Investigating inter-individual differences in short-term intra-individual variability

Abstract

Intra-individual variability over a short period of time may contain important information about how individuals differ from each other. In this paper we begin by discussing diverse indicators for quantifying intra-individual variability and indicate their advantages and disadvantages. Then we propose an alternative method that models inter-individual differences in intra-individual variability by separately considering both the amplitude of fluctuations and temporal dependency in the data. In the proposed model, temporal dependency and amplitude of fluctuations are both included as random effects. Parameter estimation is done with a multiple-step approach using maximum likelihood, or with a recommended one-step approach using a Bayesian method. The similarity and differences between the proposed method and some existing methods are discussed and investigated using diary study data from older adults. The results from empirical data analysis revealed that temporal dependency and amplitude of fluctuations have different predictability of health outcomes and thus should be modeled and considered separately.

Introduction

Traditionally, psychological research focuses on inter-individual differences in individual means in which the individual mean is interpreted as the person’s trait score and intra-individual variability around this mean over time is usually interpreted as ‘noise’ (e.g., Lord & Novick, 1968). It has been recognized for quite some time, however, that intra-individual variability (also called within-person variability, instability, or inconsistency) over a short period of time may contain important information about how individuals differ from each other (e.g. Bem & Allen, 1974; Fiske & Rice, 1955). Since then, the meaningfulness of short-term intra-individual variability has been established in diverse domains in psychological research. In the personality domain, Fleeson (2001) showed that daily measurements of constructs related to the Big Five dimensions of personality contain a considerable degree of intra-individual variability, and the amount of variability was revealed as stable (in the short run or over the course of the specific study) and meaningful individual differences, such that it could be considered a trait-like phenomenon. Moreover, Fleeson (2001) has shown that intra-individual variability in extraversion was positively related to reactivity to extraversion-relevant cues. Similarly, in the emotionality domain, Eid & Diener (1999) showed that intra-individual variability in daily affect was “sufficiently stable to be considered a psychological trait” and was sufficiently distinct from mean level scores and neuroticism to be considered a unique trait. In the perceived control domain, Eizenman et al. (1997) found that week-to-week within-person variation in perceived control in an older sample is predictive of mortality status five years later. In the cognitive domain, MacDonald, Hultch and colleagues have investigated intra-individual variability in reaction time (RT). For instance, Hultsch et al. (2002) found that individual differences in intra-individual variability of RT correlated negatively with level of performance on measures of perceptual speed, working memory, episodic memory, and crystallized abilities. Furthermore, results from MacDonald et al. (2003) showed that greater inconsistency in RT was observed for older participants even after controlling for differences in response speed levels, and variability in RT is related to changes in cognition over a six year period.

More recently, a special issue on intra-individual variability in Psychology and Aging (e.g., Ram et al., 2009) includes demonstrations of studying intra-individual variability from a variety of domains such as cognition (MacDonald et al., 2009; Schmiedek et al., 2009), movement (Newell et al., 2009), and stress and affect (Almeida et al., 2009; Sliwinski et al., 2009) with time scales varying from seconds, days, weeks, to years. In addition, an overview by Ram & Gerstorf (2009) summarized the importance, benefits, and feasibility of studying intra-individual variability from conceptual and methodological viewpoints. These studies in different domains of psychology at different time scales all indicate that inter-individual differences in intra-individual variability can be useful individual characteristics that are meaningfully predicted by, and/or predictive of, other inter-individual differences (e.g., performance or health outcomes). This legitimizes a further investigation of intra-individual variability and inter-individual differences in intra-individual variability.

When considering intra-individual variability, it is useful to distinguish between two different forms of variability: intra-individual change, which is defined as systematic change over time, such as developmental processes as growth or decline; and intra-individual variability, which is defined as relatively short-term fluctuations that are more or less reversible (Nesselroade, 1991; Nesselroade & Ram, 2004). In order to study both intra-individual variability and intra-individual change within one study, Nesselroade (1991) proposed the measurement-burst design, which consists of intensive daily or momentary assessments (e.g., daily dairy) within a burst and repeatedly measured bursts over a relative longer interval (e.g., years or decades). The idea behind this design is that the variability within a burst is useful for studying intra-individual variability, whereas the variability over bursts is useful for investigating intra-individual change. If should be noted, however, that a trend representing intra-individual change may also be present when only a single measurement burst is included. Hence, it is important to consider the possibility of intra-individual change in designs with a single measurement burst as well.

In this paper, we begin by discussing some existing statistical indicators for quantifying intra-individual variability, how to model inter-individual difference in them, and advantages and disadvantages associated with each. Next we discuss an alternative method, which is based on a multilevel extension of autoregressive models, by which the underlying process is captured. This approach allows for inter-individual differences in both the amplitude of fluctuations and the temporal dependency in the data. Inter-individual differences with respect to these two processes may be predicted by other person characteristics and predictive of performance or health outcomes. We investigate this with empirical data consisting of daily affective measurements of older adults. The similarity and differences between the proposed multilevel model and some existing methods to quantify intra-individual variability are discussed and investigated using the empirical example.

Statistical indicators of intra-individual variability

Historically, an influential paper by Fiske & Rice (1955) distinguished two types of intra-individual variability with the same stimuli over time¹ based on how the data were structured with respect to time: Type I (also called spontaneous; the order of responses is immaterial and responses at later occasions are not influenced by responses at previous occasions) and Type II (also called reactive or periodic variability). More recently, building upon Fiske & Rice (1955), Ram & Gerstorf (2009) conceptually portioned intra-individual variability into two parts: time-structured intra-individual variability (time order is important) and net intra-individual variability (time order is immaterial). To quantify intra-individual variability, a number of measures have been proposed and used under these different categories. Some of these measures focus on the amplitude of fluctuations (i.e., the amount of intra-individual variability; belongs to the Type I or net intra-individual variability category), whereas others focus on the temporal dependence (i.e., the autocorrelation; belongs to the Type II or time-structured intra-individual variability category). Yet other measures combine these two aspects of intra-individual variability. Each is described in more detail below.

Amplitude of fluctuations

An intuitively appealing–and perhaps the most widely used in psychology–measure of intra-individual variability is the intra-individual standard deviation (ISD; e.g., Nesselroade & Salthouse, 2004; Ram, Rabbitt, et al., 2005). Let y_i,t represent the observed score of individual i at occasion t. In addition, we denote the individual mean of individual i as $y_i=\frac{{\Sigma }_{t=1}^{T_i}{y}_{i,t}}{T_i}$, and we use T_i to denote the number of measurement occasions for individual i. Then the raw-score ISD of individual i from raw data is computed as

$$IS{D}_i=\sqrt{\frac{\Sigma {(y_{i,t}-y_{i.})}^2}{T_i-1}}.$$ (1)

Alternatively, one can also use the raw-score intra-individual variance of person i (i.e., $IS{D}_i^2$). Although the ISD has the advantage of reflecting the original scale of observed data, which facilitates its interpretation, the ISD² can be modeled more easily because of its convenient distribution properties (to be discussed in the next section).

Clearly, the raw-score ISD and raw-score ISD² are measures of the amplitude of intra-individual fluctuations. Although these measures are easy to compute and understand, they are also characterized by a number of disadvantages that limit their applicability. First, the ISD and ISD² are based on raw scores, and as such are sensitive to systematic intra-individual change (e.g., trends) over time. To deal with this problem, some researchers (e.g., Hultsch et al., 2008; Jahng et al., 2008) suggest detrending the data first to obtain the detrended ISD and the detrended ISD². Second, Many researchers have shown that the raw-score ISD and ISD² as well as the detrended ISD and ISD² are likely to be correlated with individual mean scores (e.g., Nesselroade & Salthouse, 2004; Shammi et al., 1998). For example, Baird et al. (2006) show that if the distribution of means is skewed and people with more extreme means have smaller intra-individual variability due to floor and ceiling effects, then a correlation between means and ISDs is artificially created. To control for the confounding effects of mean performance when using intra-individual variability as a predictor of a variable of interest, some researchers suggest dividing a person’s raw-score ISD² by his/her observed mean to produce the intra-individual coefficient of variation (i.e., the raw-score ICV; Lovie, 2005). Similarly, a detrended ICV can be obtained by dividing a person’s detrended ISD² by his/her mean score of detrended data. The ICV statistic has been criticized by Hultsch et al. (2008), however, because it ambiguously combines the main effect of ISDs, the main effect of means, and the interaction between these two. In addition, both the raw-score ICV and the detrended ICV may still be correlated with the individual means. Moreover, they could become negative (when the intra-individual mean is negative) or infinite (when the intra-individual mean is zero), which makes the modeling or interpretation of these coefficients difficult.

Analysis of Covariance (ANCOVA) has been proposed as an alternative approach to investigate inter-individual differences in ISD or ISD² while controlling for individual differences in means. In this approach, the intra-individual means are included as a covariate, the grouping variables–such as age category and gender–are included as the factors, and the ISD or ISD² is modeled as the dependent variable (e.g., Gerstorf et al., 2009). This approach is based on the assumption that the factors and the covariate are not highly correlated and thus there is no multicollinearity. In practice, this assumption may not be tenable for existing groups. Moreover, ANCOVA can be viewed as a special case of a generalized linear model with an identity link function and thus is based on the assumption that the residuals are normally distributed. This is often not true for the residuals of ISD or ISD², unless one uses an appropriate link function or an appropriate transformation. For example, Hoffman (2007) used a log function to normalize the ISD² in a multilevel model so that a linear regression model could be used as well; this eliminates the dependence of the intra-individual variance on the intra-individual mean.

An alternative approach to investigating intra-individual variability was proposed by Hultsch et al. (2008), who suggested using a repeated measures ANOVA model to decompose raw scores into four different parts: 1) systematic change over time (e.g., trends, practice or fatigue effect), 2) systematic between-group or inter-individual variation, 3) unsystematic within-group or inter-individual variation, and 4) unsystematic intra-individual variability (inconsistency). Furthermore, they suggest using the unsystematic intra-individual variability (inconsistency) portion to obtain the residual ISD or ISD², which represents intra-individual variability. One advantage of this method is that it separates intra-individual variability from intra-individual change by considering only the residual ISD or ISD² as intra-individual variability. A limitation of this method is that all the individuals in a particular group are modeled to have the same systematic change pattern over time. Moreover, the residual ISD or ISD² changes with different grouping variables included in the model, such that these residual measures should be considered as relative measures as opposed to absolute measures.

Temporal dependency

Although each of the measures described above is useful for describing the amplitude of fluctuations, they lack information about the temporal dependency in the data. The latter can be quantified using autocorrelations, which indicate the degree to which current observations are correlated with previous observations. The autocorrelations can be obtained for different lags, for which the lag refers to a specific number of occasions of measurement separating the observations that are being paired to compute the correlations. The autocorrelation at lag τ (where τ=1,2,…) is also referred to as τth-order autocorrelation, and is denoted as ρ_i(τ). The autocorrelation for person i can be estimated using

$${\widehat{\rho }}_i\left(\tau \right)=\frac{{\widehat{\gamma }}_i\left(\tau \right)}{{\widehat{\gamma }}_i\left(0\right)}$$ (2)

where ${\widehat{\gamma }}_i\left(0\right)$ is the intra-individual variance $IS{D}_i^2$ as discussed above, and ${\widehat{\gamma }}_i\left(\tau \right)$ is the auto-covariance at lag τ defined by the covariance between pairs of observations which are formed by y_it and y_i,t+τ. This lag τ auto-covariance is computed as

$${\widehat{\gamma }}_i\left(\tau \right)=\frac{1}{T_i-\tau -1}\sum _{t=1}^{T_i-\tau }(y_{i,t}-y_i.)(y_{i,t}+\tau -y_i.).$$ (3)

Larger degrees of (positive) temporal dependency (i.e., higher autocorrelations) imply that if a person deviates from his/her mean at a particular occasion, this deviation is likely to persist for a longer period of time. In contrast, a person with little temporal dependence (i.e., autocorrelations close to zero) is characterized by more or less independent scores over time.

There have been several studies in which the focus has been on inter-individual differences in temporal dependency (e.g., Kuppens et al., 2010; Suls et al., 1998; Rovine & Walls, 2006). In these studies, the data were modeled using a multilevel autoregressive model with random first-order autoregressive coefficients (multilevel AR(1) model). In the model, the first-order autoregressive coefficient, φ_i,1(1), by which the current observation is regressed upon the preceding observation is equivalent to the first-order autocorrelation, ρ_i(1), defined in Equation 2. For φ₁₍₁₎, the number in the parentheses, 1, indicates that it is an AR(1) process and the number outside the parentheses represents the specific order (e.g., 1st order in this example) of the autoregressive parameter. The random first-order autoregressive coefficients are assumed to follow a normal distribution. The first-order autoregressive parameter has been interpreted as representing an individual’s inertia (Kuppens et al., 2010; Suls et al., 1998), as the closer it is to 1, the longer it takes the person to return to his/her equilibrium after being perturbed. Furthermore, it has been shown that this parameter is related to other characteristics such as depression and neuroticism.

Combination of amplitude of fluctuations and temporal dependency

Jahng et al. (2008) argue that considering only amplitude of fluctuations (ISD or ISD²) or temporal dependency (autocorrelation) does not provide the entire picture. Instead, we should consider temporal instability, which refers to occasion-to-occasion squared differences and combines both the amplitude of fluctuations and the temporal dependency. They show that, even though two individuals may be characterized by the same amplitude of fluctuations, they can have different degrees of temporal dependency. Because a person who is characterized by a higher degree of temporal dependence will display smaller occasion-to-occasion differences than a person with a lower degree of temporal dependence, one could say that the first person varies less (from occasion to occasion) than the second person, even though their ISDs or ISD²s are the same.

To capture the occasion-to-occasion variability, Jahng et al. (2008) proposed using the mean square successive difference (MSSD; Leiderman & Shapiro, 1962; Neumann et al., 1941), which is computed as

$$MSS{D}_i=\frac{1}{T_i-1}\sum _{t=1}^{T_i-1}{(y_{i,t+1}-y_{i,t})}^2.$$ (4)

Jahng et al. (2008) have shown that, given stationary data², the MSSD can be written as a function of both the ISD² and the autocorrelation at lag 1 ($\widehat{\rho }\left(1\right)$) such that $MSS{D}_i=2IS{D}_i^2(1-{\widehat{\rho }}_i\left(1\right))$. To investigate inter-individual differences in MSSD, Jahng et al. (2008) proposed using a generalized multilevel model with a log link function to model intra-individual SSDs (SSD_i,t = (y_i,t+1 − y_i,t)²) that follow gamma distributions at the first level and then explain inter-individual differences in log of MSSD or log of the expected value of SSD by including predictors at the second level.

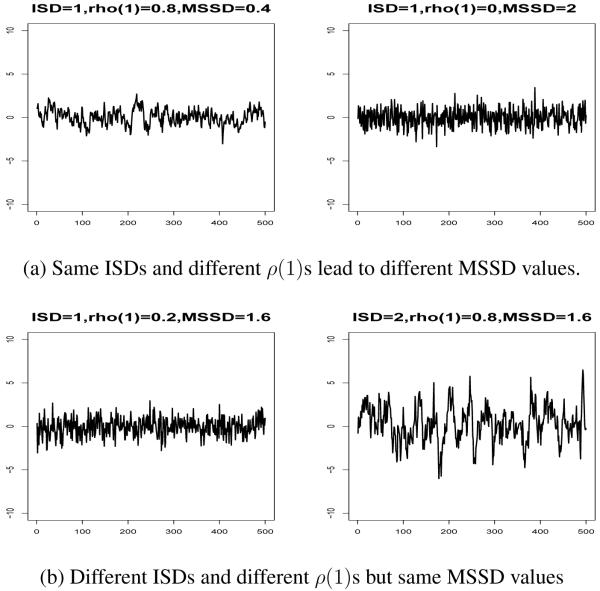
Figure 1a displays a desirable feature of the MSSD. The two processes were generated using a first-order autoregressive (AR(1)) model, which is defined as: y_t = φ₁₍₁₎y_{t − 1} + u_t, where φ₁₍₁₎ is the first-order autoregressive parameter in the AR(1) model, which is equal to ρ(1), and u_t is the unpredicted component, which is referred to as the residual or innovation in time series analysis. The first process is generated with φ₁₍₁₎ = 0.8 and u_t ~ N(0, 0.36), and the second process is generated with φ₁₍₁₎ = 0 and u_t ~ N(0, 1). This results in the same ISD² = 1, but due to the different temporal dependencies (ρ(1) = φ₁₍₁₎), the occasion-to-occasion fluctuations differ. The latter is well reflected by the squared differences in the MSSDs.

Figure 1.

Simulated time series plots.

Figure (a). Same ISDs and different ρ(1)s lead to different MSSD values.

Figure (b). Different ISDs and different ρ(1)s but same MSSD values

Another major advantage of the MSSD is that it is less sensitive to systematic intra-individual change over time (e.g., trend or practice effects over time) than the ISD and ISD² (Jahng et al., 2008). For example, consider an AR(1) process with φ₁₍₁₎ = 0.5 and u_t ~ N(0, 0.75). When there are 500 time points, the estimated MSSD is 1.00 and the estimated ISD is 1.00. If we add a linear trend to the process such that w_t = y_t + .1t = .5y_t−1 + u_t + .1t, the MSSD estimate becomes 1.008, which is still very close to the original MSSD, but the ISD estimate increases dramatically to 14.64. In this case, we do not need to detrend the data before calculating or modeling MSSD. If the linear trend is much stronger, 1t, and w_t = y_t + 1t = .5y_t−1 + u_t + 1t, the MSSD becomes 2.00 (doubled the original MSSD value) and the ISD estimate becomes 144.64. In this case, detrending the data not only affects the estimate of ISD but also results in a different MSSD. This illustrates that the MSSD is a measure that represents intra-individual variability in such a way that it is less affected by systematic intra-individual change over time.

There are, however, limitations associated with MSSD. First, similar to a problem of ICV, MSSD ambiguously combines the main effect of ISD², the main effect of ρ(1), and the interaction effect between ISD² and ρ(1). Thus, individual main effects of ISD² and ρ(1) cannot be well separated by MSSD. In Figure 1b, two AR(1) processes are shown that are obviously different, but that result in the same MSSD value. In the first process, ISD² = 1 and ρ(1) = φ₁₍₁₎ = 0.2 (meaning that u_t ~ N(0, 0.96)), whereas in the second process ISD² = 4 and ρ(1) = φ₁₍₁₎ = 0.8 (meaning that u_t ~ N(0, 1.44)). Despite the obvious difference in appearance between these two processes, the MSSD is 1.6 for each of them. Second, the intra-individual indicators such as the ISD² and ρ(1) may have very different effects on certain outcome variables (e.g., mortality), and may be differently related to other individual characteristics (e.g., personality traits). Hence, combining them in a single measure, as is done in the MSSD, may obscure important relationships and differences therein.

Note that some of the statistical indicators described above (e.g., detrended ISD, detrended ISD², and detrended ICV) are lag independent measures whereas others (e.g., autocorrelations, MSSD) are lag dependent measures. As a result, we may obtain quite different quantifications of these lag dependent indicators with different sampling schedules or different time scales. There are other ways of examining intra-individual variability. For example, Boker & Nesselroade (2002) utilized differential structural equation models (dSEM) to investigate linear relations between displacement (position or level), first-order derivative (linear rate of change), and second-order derivative (acceleration, rate of change in rate of change) to study intra-individual variability. Their perspective of studying intra-individual variability focuses on dampened oscillations by including the frequency of oscillation parameter and the dampening parameter into dSEMs, which are less lag dependent parameters and thus are less dependent of time scales. From dSEMs, we can also evaluate how quickly the dynamic system can return to equilibrium given that the model is true. Although important and interesting work, the perspective of Boker and colleagues is a different perspective looking into intra-individual variability, whereas our focus is the amplitude of fluctuations and the temporal dependency perspectives.

Modeling and estimating inter-individual differences in intra-individual variability

Instead of focusing on intra-individual amplitude of fluctuations or intra-individual temporal dependency only, or combining them as is done in the MSSD, we propose to model them using first- and higher-order AR processes. Our aim is to consider separate sources that contribute to individual differences in intra-individual variability by allowing for individual differences in ISD² and individual differences in the AR parameters, because both aspects may be meaningfully – but differently – related to other individual characteristics or outcome variables. To this end we use the following model at the intra-individual level to quantify intra-individual variability:

$$\begin{array}{cc}\hfill & y_{i,t}=Intercep{t}_i+f_i\left(tim{e}_{i,t}\right)+e_{i,t}\hfill \\ \hfill e_{i,t}& ={\varphi }_{i,1\left(K\right)}{e}_{i,t-1}+\dots +{\varphi }_{i,K\left(K\right)}{e}_{i,t-K}+u_{i,t}.\hfill \end{array}$$ (5)

The term f_i(time_i,t) reflects intra-individual linear or nonlinear change and is included for detrending the time series in order to make the time series stationary when needed. Detrending is a statistical or mathematical operation of removing trend from the series. The purpose of detrending in this study is to obtain a stationary process for the AR modeling. Determination of trend in a time series is subjective. Sometimes knowledge of the substantive system helps to identify trend. Many methods are available for detrending such as first- or higher- order differencing, parametric curve-fitting, piecewise polynomials, filtering, and loess or spline smoothing. For example, a simple linear trend in mean can be removed by subtracting a fitted straight line, which is done in the empirical study discussed in the following section. More complicated trends (e.g., seasonal trends/cycles) might require different procedures (e.g., moving averaging or parametric sinusoidal curve fitting, Ram, Chow, et al., 2005). It should be noted, however, that complex detrending models such as loess smoothing may introduce auto-covariance into the residual series and thus influence the subsequent modeling of time-dependency in the series. For detrending y_i,t in Equation 5, we recommend removing systematic change over time, but avoiding the removal of temporal dependency from the data or the introduction of artificial auto-covariance into the data, especially the autoregressive process, because we want to appropriately model temporal dependency later. The augmented Dickey-Fuller test (ADF, Dickey & Fuller, 1979; Dickey & Fuller, 1981; see also Hamilton, 1994) can be used to test stationarity before and after detrending. If the data are nonstationary, different intra-individual change functions with different change parameters (e.g., same linear change functions with different intercepts and slopes or different change functions with linear functions for some individuals and nonlinear functions for other individuals) can be included for different individuals using f_i(time_i,t). If the series is stationary, f_i(time_i,t) can be set to zero; in that case, the Intercept_i can be thought of as the person’s trait score.

After detrending the data, e_i,t represent the stationary time series for each individual i. The standard deviation and the variance of the residual e_i,t are the detrended ISD (denoted as ISD_ei) and the detrended ISD² (denoted as $IS{D}_{ei}^2$) for individual i, and they can be used to quantify the amplitude of fluctuations of person i around his/her trait score or trend.³

The detrended variable e_i,t is then modeled by an AR(K) process for individual i, which implies that it is predicted from the K preceding (detrended) values. Note that the AR parameters φ_i,k(K) as well as the error/innovation variance (the variance of u_i,t, denoted as ${\sigma }_{ui}^2$) may differ across individuals. The AR parameters φ_i,k(K), the kth order autoregressvie parameter of an AR(K) process of individual i, are used to quantify temporal dependency of intra-individual variability. These autoregressive parameters are related–but not necessarily identical–to the autocorrelation parameters ρ with the same order as defined in Equation 2 (Hamilton, 1994). The relationship between autoregressive parameters and autocorrelations is similar to the comparison of regression coefficients versus correlation coefficients. For example, in an AR(1) model, φ₁₍₁₎ is the same as ρ(1), but in an AR(2) model we have ρ(1) = φ₁₍₂₎/(1 − φ₂₍₂₎) and $\rho \left(2\right)={\varphi }_{2\left(2\right)}+{\varphi }_{1\left(2\right)}^2∕(1-{\varphi }_{2\left(2\right)})$. When the true process is a higher-order model (k > 2), the relations between τth order autoregressive parameters and τth order autocorrelations become more complex.

In order to explain inter-individual differences in the detrended $IS{D}_i^2\left(IS{D}_{ei}^2\right)$ and the autoregressive parameters φ_i,k(K), we can add predictors/covariates of interest to the model in Equation 5. Note that $IS{D}_{ei}^2$ has nonnegative values and often has a skewed distribution. Here we model it using a log link function because the distribution of the sample variance of a normally distributed variable is a chi-square distribution (Cochran’s theorem; Cochran, 1934), a special case of a gamma distribution. For an outcome with a gamma distribution, a log link function can be used (McCullagh & Nelder, 1989). A log transformation or log link function has also been used for modeling intra-individual variances (Hoffman, 2007; Hedeker et al. (2008)) and MSSD (Jahng et al., 2008). Alternatively we could consider modeling ISD_ei and use a chi distribution, but this is more difficult because the chi distribution is not in the exponential distribution family and thus it is not easily modeled in the generalized linear modeling framework (McCullagh & Nelder, 1989).

Let z_i be a column vector of predictor variables for individual i, including 1 as its first element (for an intercept). Now we can write

$$\begin{array}{cc}\hfill log\left(IS{D}_{ei}^2\right)& ={{\beta }_0}^{\prime }{z}_i+{\zeta }_{0,i}\hfill \\ \hfill {\varphi }_{i,k\left(K\right)}& ={\beta }_1^{\prime }{z}_i+{\zeta }_{1,i}\hfill \\ \hfill & \dots \hfill \\ \hfill {\varphi }_{i,K\left(K\right)}& ={\beta }_K^{\prime }{z}_i+{\zeta }_{K,i},\hfill \end{array}$$ (6)

where $IS{D}_{ei}^2$ is modeled on the predictor variables z with a log link function. The autoregressive parameters (φ_i,k(K); k = 1, .., K) are regressed on the predictor variables z with an identity function (Rovine & Walls, 2006). The residual term ζ_k,i (k = 0, .., K) is assumed to have a normal distribution with mean 0 and unknown variance, var(ζ_k,i). var(ζ_0,i) is for the inter-individual variance of $log\left(IS{D}_{ei}^2\right)$ after controlling for the predictor variables z. var(ζ_k,i) (k = 1, .., K) is for the inter-individual variance of the kth order autoregressive parameters after controlling for the predictor variables z. When z only contain a column of 1s, then the model becomes an unconditional model and var(ζ_k,i) (k = 1, .., K) can be used to study pure between-person variances in $log\left(IS{D}_{ei}^2\right)$ and φ_i,k(K).

Combining Equations 5 and 6 together, the model can be viewed as a multilevel model for modeling inter-individual differences in intra-individual variability: Equation 5 is used to quantify intra-individual variability from two sources and Equation 6 is used to explain inter-individual differences in intra-individual variability.

In addition, if we want to predict some outcome variables using intra-individual variability, we can also fit general linear models or generalized linear models with statistical indicators of intra-individual variability as predictor variables. For example,

$$E\left(Outcom{e}_i\right)=h(IS{D}_{ei}^2,{\varphi }_i)$$ (7)

where φ_i is a vector that contains the autoregressive coefficients φ_i,k(K) and h is the inverse of the link function used in the model. In this case, the link function is determined by the distribution of the outcome variable. For example, an identity function can be used when the outcome variable is normally distributed whereas a cumulative logit function can be used when the outcome variable is ordinal.

To estimate the parameters in Equations 5, 6, and 7, we can use a multiple-step approach when the number of measurements is relatively large and the number of measurements are similar across different individuals (such that the reliabilities of $IS{D}_{ei}^2$ and φ_i are relatively high). In the first step, we choose appropriate change functions to detrend individual time series and calculate the $IS{D}_{ei}^2$. Subsequently, we select appropriate autoregressive orders and estimate the autoregressive parameters for the (detrended) time series of each individual separately. In the second step, we examine inter-individual differences in the detrended variance $IS{D}_{ei}^2$ and the autoregressive parameters φ (Equation 6) and/or predict outcome variables using intra-individual variability (Equation 7). Two important advantages of the multiple-step approach are that all the steps can be easily done in existing statistical packages, and that it is flexible in that it allows idiographic trend change functions in Equation 5 as well as idiographic autoregressive orders.

This method also has disadvantages as described in Jahng et al. (2008). For example, the estimates of different statistical indicators of intra-individual variability contain measurement errors that are not considered in the multiple-step method. When the number of measurement occasions is relatively small, this problem is particularly prominent. A related question is how many observations per person is enough for the multiple-step modeling approach to be valid? The answer depends on the reliability of the statistic of interest (here $IS{D}_e^2$ and φ) in a specific study. For example, Estabrook et al. (In press) conducted a Monte Carlo simulation study of the reliability of ISD. Their results indicated that ISDs had poor reliability with insufficient assessments and was less reliable than the intra-individual sample mean, $\stackrel{‒}{X}$. Schmiedek et al. (2009) briefly studied the reliability of ISD, which also found that ISD was relatively unreliable when the number of assessments is small. Although work by Estabrook and Schmiedek and colleagues did not study the reliability of ISD² (one of the indicators of intra-individual variability of the current study), Wang & Grimm (2011) analytically derived the reliabilities of both ISD and ISD². Findings from Wang & Grimm (2011) echoed the results of the ISD from Estabrook et al. (In press) and Schmiedek et al. (2009). In addition, Wang & Grimm (2011) found that ISD² had poor reliability with insufficient assessments and was less reliable than $\stackrel{‒}{X}$. From Wang & Grimm (2011), the reliabilities of both ISD and ISD² depend on multiple factors and are functions of the sizes of the first and second moments of true intra-individual variability, the size of the measurement error variance, and the number of assessments. In comparing two studies, results showed that when the measurement scale reliability is high (e.g., .9), fewer occasions are needed to achieve the same reliability level of ISD² compared to when the measurement scale reliability is lower (e.g., .7) given the same distribution of ISD² in the two studies. Because ISD²s are often less reliable than desired, we recommend an alternative approach, a one-step approach, for modeling inter-individual differences in intra-individual variability.

A one-step approach using multilevel models can be used to estimate the parameters in Equations 5 and 6. In this approach, the data of all the individuals are analyzed simultaneously, instead of analyzing the data of each individual separately and then combining the results. The advantage of the one-step approach is that it takes uncertainty about intra-individual parameters into account. This is particularly important when the number of measurement occasions is relatively small or individuals differ a lot with respect to the numbers of measurement occasions. A disadvantage of the one-step approach is that it is based on a generalized (nonlinear) multilevel model, which makes it computationally more complicated and demanding. In addition, it is not flexible in terms of allowing idiographic trend change functions (e.g., truly different change functions). In the empirical application discussed below we therefore make a compromise by using the individually detrended data for the one-step multilevel modeling and use Bayesian estimation with noninformative priors to estimate parameters in the multilevel models because of its computational convenience for relatively more computationally complicated models (e.g., Wang & McArdle, 2008). For the purpose of illustration, we will compare the results from the one-step approach with the results from the multiple-step approach in the following section.

Our proposed model is similar to, but different from, the Mixed-effects Location Scale model proposed by Hedeker et al. (2008) for analysis of Ecological Momentary Assessment (EMA) data. In the Mixed-effects Location Scale model, both location and variability (amplitude of fluctuations) of a response variable are modeled. For modeling the variability component, a log-linear function is utilized. The location scale model has been applied in modeling variations in positive affect, negative affect, and mood (Hedeker et al., 2008, 2009). Our proposed model is similar to the Hedeker’s location scale model in that both approaches model the variability component (amplitude of fluctuations) using a log-linear function. Our proposed method is also different because it models both amplitude of fluctuations and temporal dependency whereas the Hedeker’s model focuses on only amplitude of fluctuations for intra-individual variability.

Analyzing inter-individual differences in intra-individual variability of negative affect

To illustrate the application of the methods proposed in the previous section, we use a subset of the data from the older cohort of the Notre Dame Study of Health & Well being. Participants (N = 304), ranging in age from 53 to 91, were measured daily on the PANAS scales (Watson et al., 1988) for 56 consecutive days. For data analysis convenience, we focus on the participants who completed at least 49 days of the negative affect construct (NA, N = 230; means of the NA items on the PANAS scale were used for measuring NA).

The goals of this empirical study are three-fold: 1) to compare different statistical indicators of intra-individual variability using empirical data on negative affect; 2) to investigate inter-individual differences in different intra-individual variability indicators of negative affect; and 3) to examine how inter-individual differences in different intra-individual variability indicators of negative affect predict health outcomes. To achieve the first goal, different statistical indicators of intra-individual variability discussed in previous sections will be calculated and compared numerically and graphically. For the second goal, age (M = 68.42, SD = 4.72), gender (59.4% female), and measures of the Big Five personality dimensions (sums of the items of each dimension were used; Costa & McCrae, 1991) will be used as predictors to explore inter-individual differences in intra-individual variability. With respect to the third goal we will investigate the predictive power of intra-individual variability on health outcomes. Intra-individual variability is modeled as outcomes in goal 2 whereas intra-individual variability is treated as predictors in goal 3. The time-invariant predictor variables and outcome variables were measured once before the participants received the daily diary questionnaires.

Comparing different statistical indicators of intra-individual variability

Before calculating the detrended intra-individual variances ($IS{D}_{ei}^2$) and the autoregressive parameters (φ_i), we had to decide whether detrending was needed for some individuals and to test whether the original/detrended individual time series were stationary for each individual. Individual time series plots and linear trend regression models were used to detect whether the data needed to be detrended. Based on the results, linear detrending was applied to 10 individuals. The augmented Dickey-Fuller test (ADF) was then implemented to test stationarity of each individual time series. According to the ADF test results, the original time series for the undetrended individuals and the detrended time series for the detrended individuals appeared stationary.

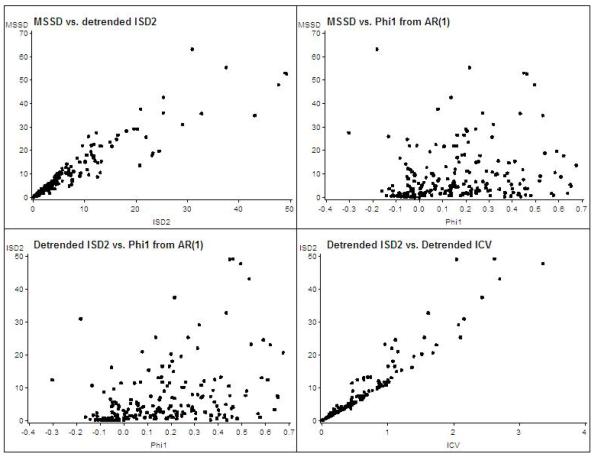
Different statistical indicators were computed to measure intra-individual variability for the empirical data. Raw-score indicators were computed based on the original data before detrending and detrended indicators were computed based on the detrended data. For the autoregressive model in Equation 5, an AR(1) and an AR(2) model were fitted to the detrended data of each individual, although an AR(1) is adequate for most individuals (i.e.,φ_2i is not significantly different from 0 for most participants). Means and standard deviations for and correlations between these indicators as well as level information (raw-score mean levels) are included in Table 1. Among these statistical indicators, ISD² and ICV can be viewed as measures of amplitude of fluctuations, whereas the φ-parameters measure temporal dependency and MSSD forms a combination of amplitude of fluctuations and temporal dependency. Figure 2 also displays scatterplots of some selected paired indicators of intra-individual variability.

Table 1.

Descriptive statistics and correlations among different statistical indicators of intra-individual variability from the empirical data.

	Raw	Raw	Detr		Raw	Detr
	M	ISD 2	ISD 2	MSSD	ICV	ICV	φ 1(1)	φ 1(2)	φ 2(2)
Mean	12.04	6.00	5.80	8.12	0.43	0.42	0.15	0.14	0.02
S.D.	2.98	8.84	8.65	10.94	0.55	0.54	0.20	0.20	0.15
Raw M	1.00
Raw ISD2	0.66	1.00
Detr ISD2	0.62	0.99	1.00
MSSD	0.56	0.94	0.94	1.00
Raw ICV	0.51	0.96	0.96	0.94	1.00
Detr ICV	0.49	0.95	0.97	0.93	0.99	1.00
φ 1(1)	0.40	0.36	0.38	0.19	0.34	0.36	1.00
φ 1(2)	0.40	0.37	0.39	0.20	0.37	0.37	0.93	1.00
φ 2(2)	0.12a	0.12a	0.13a	0.16b	0.14b	0.14b	0.18	−0.02a	1.00

Note: Raw M: raw-score mean; Raw ISD²: raw-score intra-individual variance; Detr ISD²: detrended intra-individual variance, $IS{D}_e^2$; MSSD: mean square successive difference; Raw ICV: raw-score intra-individual coefficient of variation = $\frac{ObsIS{D}^2}{ObsM}$; Detr ICV: detrended intra- individual coefficient of variation = $\frac{DetrIS{D}^2}{DetrM}$; φ₁(₁): auto-regressive parameter from the AR(1) model; φ₁(₂) and φ₂(₂): 1st order and 2nd order auto-regressive parameters from the AR(2) model. a: not significant at the .05 level. b: significant at the .05 level but not at the .01 level. All other correlations are significant at the .01 level.

Figure 2.

Scatterplots of different indicators of intra-individual variability.

Note: upper left: MSSD vs. detrended ISD²; upper right: MSSD vs. φ₁₍₁₎; lower left: detrended ISD² vs. φ₁₍₁₎; lower right: detrended ISD² vs. detrended ICV.

It should be noted that the negative affect variable did not show much systematic intra-individual change for most individuals over the short study period (56 days). Hence the raw-score ISD² was highly correlated with the detrended ISD² (r = .99) although the mean and the standard deviation of ISD² became slightly smaller after detrending than before detrending. The correlations among different measures of amplitude of fluctuations (that is, the ISD²s and ICV s), were in the range of .95 to .97, and were also highly correlated with MSSD, with correlations in the range of .93 to .94 (see also the lower right panel in Figure 2 and the upper left panel of Figure 2). In contrast, temporal dependency of the first order (i.e., φ₁₍₁₎) correlated with the measures of amplitude of fluctuations (e.g., ISD²s, ICV s) in the range of 0.34 to 0.38 (see also the lower left panel in Figure 2), and with MSSD, even less so, r = 0.19 (see also the upper right panel in Figure 2). The temporal dependency of the second order (i.e., φ₂₍₂₎) did not significantly correlate with the measures of amplitude of fluctuations, but this may be attributed to the fact that for most individuals this measure of temporal dependency did not differ from zero. Note that the low correlations between φ₁₍₁₎ and the measures of amplitude of fluctuations indicate that these are two distinct aspects of intra-individual variability that need (and deserve) to be considered and modeled separately. Furthermore, in the current data the MSSD was more closely related to measures of amplitude than to temporal dependency.

Raw-score mean levels were positively correlated with these different indicators of intra-individual variability. More specifically, correlations between raw-score mean levels and measures of amplitude of fluctuations (ISD²s, ICV s) ranged from .49 to .66 with lower, but still moderate, correlations between ICVs and raw-score mean levels. The latter shows that although the ICV was proposed as a measure to control the ISD² for mean score differences, this “corrected” measure was still correlated with the mean scores. In the current analyses, these correlations indicate that participants who had higher mean levels of negative affect tended to have higher amplitude of fluctuations. The correlation between raw-score mean levels and measures of temporal dependency (φ₁₍₁₎) was 0.4, which indicates that participants who had higher levels of negative affect also tended to have higher levels of temporal dependency, which implies that it took them longer to recover from deviations from their mean levels of negative affect.

Predicting inter-individual differences in intra-individual variability of negative affect

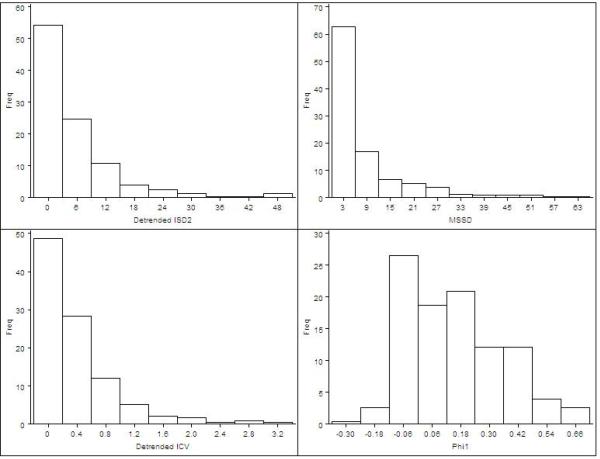
Due to extremely high correlations among some indicators of intra-individual variability in this empirical example, a subset of the discussed intra-individual variability indicators were selected to study inter-individual differences in intra-individual variability. Moreover, because the DIC values that were obtained from the AR(1) and AR(2) models (without predictors) were 42,500 and 45,020 respectively (where smaller values indicate better models; Spiegelhalter et al., 2002), we decided to focus on the AR(1) model. The indicators that we focused on were the detrended ISD², MSSD, detrended ICV, and φ₁₍₁₎.

Figure 3 displays the histograms of these indicators, from which we can see that the distributions of detrended ISD², MSSD, and detrended ICV were right skewed (or positively skewed), whereas the distribution of φ₁₍₁₎ was relatively more symmetric. The generalized linear models in Equation 6 with log link functions were applied to analyze inter-individual differences in detrended ISD² and similar generalized linear models were also applied to MSSD and detrended ICV with predictors including gender, age, and the Big Five factors. Similarly, to investigate inter-individual differences in φ₁₍₁₎, the predictors gender, age, and the Big Five factors were used in the general linear model in Equation 6. The predictors were included in the models separately. Both the multiple-step procedure and the one-step procedure are applied to analyze the detrended ISD² and φ₁₍₁₎ using the proposed models specified in Equations 5 and 6. For example, the model form with gender as the predictor is

$$\begin{array}{cc}\hfill N{A}_{i,t}& =Intercep{t}_i+f_i\left(tim{e}_{i,t}\right)+e_{i,t}\hfill \\ \hfill e_{i,t}& ={\varphi }_{i,1\left(1\right)}{e}_{i,t-1}+u_{i,t}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill log\left(IS{D}_{ei}^2\right)& =b_{00}+b_{01}Gende{r}_i+{\zeta }_{0,i}\hfill \\ \hfill {\varphi }_{i,1\left(1\right)}& =b_{10}+b_{11}Gende{r}_i+{\zeta }_{1,i}.\hfill \end{array}$$

f_i(time_i,t) is allowed to be different in both forms and parameter coefficients across different individuals.

Figure 3.

Histograms of different indicators of intra-individual variability.

Both procedures are also applied to analyze MSSD⁴. We implemented the multiple-step approach in SAS and the one-step approach in WinBUGS (See Appendix for the WinBUGS scripts for fitting the proposed model).

For the one-step approach, we first tested whether we have significant inter-individual differences in intra-individual variability indicators including detrended ISD², φ₁₍₁₎, and MSSD by fitting the unconditional multilevel models without any predictors (one model for both detrended ISD² and φ₁₍₁₎ and the other model for MSSD) to the detrended data. From the unconditional models, we can estimate inter-individual variances in the intra-individual variability indicators (var(ζ_k,i)) and their standard errors and then use the Wald test to assess significance (e.g., Fitzmaurice et al., 2004). Results revealed that we had significant inter-individual differences in these intra-individual variability indicators (detrended ISD², Z =10.67; φ₁₍₁₎ , Z =7.32; MSSD, Z =10.28), which legitimizes the further study of predicting inter-individual differences in intra-individual variability.

From Table 2, we can see that the results from the multiple-step approach with predictors were similar to the results from the one-step conditional multilevel models. The differences between these two approaches can come from three sources: 1) different estimation procedures (multiple-step vs. one-step), 2) different estimation methods (MLE vs. Bayesian), and 3) different methods of dealing with missing data. Because the proportion of missing data was relatively small and the number of measurement occasions was adequately large (the calculated reliability value of the detrended ISD² from the derived formula in Wang & Grimm (2011) was as high as .95), and because we used vague/noninformative priors in the Bayesian analyses, similar results from these two approaches were expected and observed. For a study with less reliable ISD²s and/or φs (for example, a study with shorter time series and thus more unreliable ISD²s), however, we recommend the use of the one-step approach.

Table 2.

Inter-individual differences in intra-individual variability of negative affect.

	Multiple-step approach					One-step approach
	MSSD	Detr ICV	Detr ISD2	φ 1	MSSD	Detr ISD2	φ 1
Gender	.51 (.16)	.58 (.16)	.69 (.17)	.06 (.03)	.53 (.18)	.66 (.19)	.06 (.03)
Age	−.007 (.02)	.005 (.017)	.01 (.02)	.002 (.003)	−.008 (.02)	.003 (.02)	.001 (.003)
Neuroticism	.07 (.01)	.06 (.01)	.07 (.01)	.008 (.002)	.07 (.015)	.07 (.01)	.006 (.002)
Extraversion	−.03 (.02)	−.02 (.02)	−.03 (.02)	−.003 (.003)	−.03 (.02)	−.03 (.02)	−.005 (.003)
Openness	.03 (.02)	.03 (.02)	.04 (.02)	.004 (.003)	.03 (.02)	.04 (.02)	.004 (.003)
Agreeableness	−.01 (.02)	−.02 (.02)	−.02 (.02)	−.004 (.004)	−.02 (.03)	−.02 (.02)	−.002 (.004)
Conscientiousness	−.02 (.02)	−.02 (.01)	−.02 (.02)	−.001(.003)	−.03 (.02)	−.02 (.02)	−.001 (.004)

Note: Parameter estimates are given with standard errors in parentheses. Significant effects are bolded (significance level is at 0.05). Gender: 0-male; 1-female. ICV was not analyzed by the one-step procedure because researchers usually analyze it using a two-step approach.

The analysis results showed that there were significant gender differences in both amplitude of fluctuations and temporal dependency in that (on average) females had higher amplitude of fluctuations and higher temporal dependency on negative affect than did males. In other words, females (on average) tended to have greater variation/dispersion around their average levels of negative affect than males. Furthermore, women were characterized by higher inertia than males, meaning that when they deviated from their average levels of negative affect on a particular occasion of measurement, the deviations persisted for a longer time than for males. In other words, yesterday’s negative affect level had a greater influence on today’s level of negative affect for females when compared to males. Age was not a significant predictor of inter-individual differences in amplitude of fluctuations or temporal dependency. Note that the age range was from 53 to 91, such that there could be differences between the current age group and adolescents or younger adults. With respect to the Big Five factors, the results showed that both the amplitude of fluctuations and the temporal dependency of negative affect were positively related to levels of Neuroticism in that participants who are more neurotic had higher amplitude of fluctuations (larger amounts of variations/dispersion around their average levels of negative affect) and higher temporal dependency (larger influences of yesterday’s negative affect level on today’s level) than those who are less neurotic. The latter result is consistent with earlier findings which showed that neuroticism is a positive predictor of the inertia of mood (Suls et al., 1998). None of the other Big Five factors were significant predictors of these measures of intra-individual variability.

Prediction of health outcomes using intra-individual variability

From the above analysis, we found that participants showed significant inter-individual differences in various aspects of intra-individual variability, and that these differences can be predicted from gender and Neuroticism. The next step is to study the effect of these inter-individual differences in intra-individual variability on health outcomes. The following health outcomes are considered: 1) self-rated overall health (SLFHLTH; from 6 standardized items; a high score indicates worse overall health; M = −0.14, SD = 4.38; Belloc et al., 1971); 2) chronic health problems (CHRHLTH; from 14 0-1 items; a high score reflects more chronic health problems; M = 2.44, SD = 1.45); 3) somatic health complaints (SOMHLTH; from 11 0-1 items; a high score reflects a larger number of somatic complaints; M = 2.86, SD = 1.82); 4) functional status scale (FUNCTN; a high score indicates a decreased ability to do each of these types of activities including housework, handyman type work, money management, and transportation; M = 25.81, SD = 7.61); 5) Pittsburg Sleep Quality Index (PSQI, Buysse et al., 1989; a high score on PSQI indicates worse overall sleep quality; M = 5.64, SD = 3.32); and two single items from the overall health measure scale 6) present health status compared to before (HEALTHT; How would you rate your present health status compared to five years ago? Better, About the same, Worse.) and 7) hospitalized (HOSPITAL; Have you been hospitalized this year? No; Yes, once or twice; Yes, 3 or more times.).

The first five health outcome variables are continuous and we used linear regression analysis in Equation 7 to predict them (the h function in Equation 7 is an identity function). For the two categorical single-item health variables, the generalized linear models with cumulative logit links described in Equation 7 were used. That is, for HEALTHT, we modeled $log\left(\frac{p_{better}}{p_{same}+p_{worse}}\right)$ and $log\left(\frac{p_{better}+p_{same}}{p_{worse}}\right)$, and for HOSPITAL we modeled $log\left(\frac{p_{no}}{p_{1or2}+p_{3ormore}}\right)$ and $log\left(\frac{p_{no}+p_{1or2}}{p3ormore}\right)$. These cumulative logit link functions are inverses of the h functions respectively in Equation 7 for the two models. We used the intra-individual (detrended) mean, (detrended) ISD², MSSD, (detrended) ICV, and φ₁₍₁₎ as predictors for all these health outcomes.

Because many of these predictors were (extremely) highly correlated, we began by conducting the analyses for each predictor separately. The results for the parameter estimates and standard errors are presented in Table 3 and show that not only mean levels but also intra-individual variability of negative affect predicted these health outcomes. Specifically, both the measures of amplitude of fluctuations and the measure of temporal dependency appeared more successful in predicting health outcomes compared with the mean level. For example, means of negative affect did not predict chronic health problems, somatic health complaints, and the number of hospitalizations, but temporal dependency (φ₁₍₁₎) of negative affect predicted chronic health problems and both amplitude of fluctuations (ISD²s and ICV s) and temporal dependency (φ₁₍₁₎) predicted somatic health complaints and the number of hospitalizations. To further investigate this, we also considered the detrended means, detrended ISD², and φ₁₍₁₎ simultaneously as predictors of the health outcomes, to investigate their unique contributions. The results showed that in these analyses raw means did not significantly predict any outcomes, detrended ISD² significantly predicted somatic health complaints, and φ₁₍₁₎ significantly predicted chronic health problems, somatic health complaints, sleep problems, and the number of hospitalizations (i.e., after controlling for the effect of the other two predictors).

Table 3.

Predict health outcomes using mean level and different indicators of intra-individual variability.

	SLFHLTH	CHRHLTH	SOMHLTH	FUNCTN	PSQI	HEALTHT	HOSPITAL
Predictors are entered separately
Detr M	.15 (.10)	.02 (.04)	.07 (.05)	.32 (.20)	.25 (.07)	−.11 (.05)	−.05 (.06)
MSSD	.06 (.03)	.01 (.01)	.04 (.01)	.10 (.07)	.09 (.02)	−.04 (.02)	−.04 (.02)
Detr ICV	.04 (.03)	.00 (.01)	.03 (.01)	.09 (.05)	.06 (.02)	−.023 (.012)	.0281 (.0144)
Detr ISD2	.89 (.54)	.10 (.19)	.77 (.24)	1.38 (1.03)	1.43 (.40)	−.55 (.25)	−.62 (.29)
φ 1(1)	2.76(1.45)	1.20 (.50)	2.20 (.67)	3.04 (2.67)	4.68 (1.06)	−1.40 (.67)	−2.28 (.93)
Predictors are entered simultaneously
Detr M	.01 (.14)	−.03 (.05)	−.06 (.06)	.17 (.26)	.05 (.10)	.01 (.06)	.09 (.09)
Detr ISD2	.04 (.04)	.00 (.02)	.04 (.02)	.06 (.09)	.05 (.03)	−.00 (.02)	−.039(.025)
φ 1(1)	2.08 (1.61)	1.36 (.57)	1.84 (.76)	1.45 (2.92)	3.55 (1.18)	−1.26 (.72)	−2.10 (1.03)

Note: Significant estimates (significance level α= .05) are bolded. The numbers in the parentheses are standard errors. SLFHLTH: self-rated overall health; CHRHLTH: chronic health problems; SOMHLTH: somatic health complaints; FUNCTN: functional status scale; PSQI: Pittsburg Sleep Quality Index; HEALTHT: present health status compared to before; HOSPITAL: hospitalized.

In addition, different aspects of intra-individual variability had different predictive power in predicting health outcomes. For example, for predicting the number of times hospitalized, both amplitude of fluctuations (e.g., detrended ISD²) and temporal dependency (e.g., φ₁₍₁₎) were predictive. For predicting chronic health problems, however, only temporal dependency of negative affect (measured by φ₁₍₁₎) was significant whereas amplitude of fluctuations (measured by ISD² and ICV) was not. MSSD was not significantly predictive of the above two health outcomes but the p values ranged between 0.05 and 0.06. Therefore, the results support our suggestion made earlier that amplitude and temporal dependency should be considered separately.

In sum, the estimates in Table 3 indicate that: 1) people who had higher mean levels of negative affect (Detr M) tended to have worse sleep quality and worse health status than those who had lower mean levels of negative affect; 2) people who had higher amplitude of fluctuations of negative affect (e.g., ISD² and ICV; more variations/dispersion around their average levels of negative affect) tended to have more somatic health complaints, worse sleep quality, worse health status than before, and more hospitalizations; and 3) people who had higher levels of temporal dependency (e.g., φ₁₍₁₎; larger influences of yesterday’s negative affect level on today’s level) tended to have more chronic health problems, more somatic health complaints, worse sleep quality, worse health status than before, and more hospitalizations. The latter corresponds to the idea that higher levels of inertia (i.e., autoregressive parameters) in negative affect are indicative of a maladaptive regulatory mechanism (Kuppens et al., 2010; Suls et al., 1998), which may have a detrimental effect on a number of health outcomes.

Discussion

In this study, we began by providing an overview of different ways of measuring intra-individual variability. The measures can be divided into three main categories: 1) amplitude of fluctuations (the amount of variation around the mean; time-unstructured intra-individual variability in Ram & Gerstorf (2009)), 2) temporal dependency (the magnitude of the persistence of states between measurement points; time-structured intra-individual variability in Ram & Gerstorf (2009)), and 3) a combination of both. Amplitude of fluctuations and temporal dependency represent two distinct aspects of intra-individual variability. Amplitude of fluctuations can be measured using detrended ISD²and detrended ICV; temporal dependency can be measured using autoregressive parameters in AR models such as φ₁₍₁₎ = ρ(1), φ₁₍₂₎, and φ₂₍₂₎. The MSSD combines both the amplitude of fluctuations and the temporal dependency. We discussed how to analyze inter-individual differences in intra-individual variability and two estimation procedures, including a multiple-step approach and a one-step approach. For the multiple-step approach, we obtain the estimates of intra-individual variability of each individual first and then analyze these estimates using regression models or generalized regression models to study inter-individual differences in intra-individual variability. For the one-step approach, we simultaneously predict intra-individual variability and estimate parameters describing inter-individual differences in intra-individual variability. We illustrated the use of these measures and techniques with an empirical data set consisting of 56 measurement occasions of negative affect of older adults. These different indicators and different modeling and estimation methods have different advantages and limitations, which we discuss below.

In our empirical example, because only 10 individuals showed systematic intra-individual change over time, the raw-score indicators are highly correlated with the detrended indicators. It should be noted, however, that when studying intra-individual variability, one should separate intra-individual variability from intra-individual change by detrending the data first when needed, especially for those indicators that are sensitive to intra-individual change such as ISD²s and ICV s. MSSD is much less sensitive to systematic intra-individual change and thus researchers (Jahng et al., 2008) suggest that detrending may not be needed when the amount of systematic intra-individual change is not large (e.g., 0.1t in the preceding simulation example). As shown in our simple simulation example, however, when the amount of systematic intra-individual change is large (e.g., 1t in the example), MSSD is also slightly influenced (the size was doubled without detrending) by the systematic intra-individual change, and thus detrending may also be needed in this case if one wishes to focus on intra-individual variability rather than intra-individual change.

From our empirical data analysis results, we see that intra-individual variability can help us understand inter-individual differences above and beyond intra-individual mean levels. In addition, different components of intra-individual variability can also help us better understand inter-individual differences in intra-individual variability. From Table 3, we find that amplitude of fluctuations such as ISD² and ICV showed different utility in predicting health outcomes from temporal dependency, such as φ₁₍₁₎. Inter-individual differences in amplitude of fluctuations may be different from the inter-individual differences in temporal dependency, as illustrated by the relatively low correlations between these measures in Table 1. When we combined two sources of intra-individual variability together in the MSSD, the predictive power may become smaller (see Table 3) although MSSD is highly correlated with indicators of amplitude of fluctuations, such as ISD² and ICV, based on the correlations in Table 1. This might be due to the effects of amplitude of fluctuations and of temporal dependency which could partially cancel out when the effects are in the same direction and when they are positively correlated, as implied by $MSS{D}_i=2IS{D}_i^2(1-{\widehat{\rho }}_i\left(1\right))$. Studying MSSD, however, could still bring us valuable information on inter-individual differences in intra-individual variability from the combined perspective. Therefore, we suggest studying intra-individual variability from two perspectives, namely amplitude of fluctuations and temporal dependency, at least separately using ISD²_e and φs, and jointly using MSSD if interested.

Both one-step and multiple-step approaches have advantages and disadvantages in estimating parameters in the proposed models. The one-step approach considers uncertainty in the statistical indicators of intra-individual variability. Therefore, the estimates of inter-individual differences in intra-individual variability are more accurate. The one-step approach, however, is somewhat more difficult to implement considering that the model could become a generalized multilevel model when analyzing some indicators that have skewed distributions, such as ISD² and MSSD. The two-step approach is easy to implement and the estimates of different statistical indicators of intra-individual variability can be utilized for any further modeling. When the number of occasions is smaller, however, the estimates could be less accurate. In our empirical example, the estimates from the one-step approach and the two-step approach are close mainly due to the relatively large number of occasions and thus high reliabilities of the indicators, which is also consistent with the findings from Ram, Chow, et al. (2005).

Theoretically, this real data example provides interesting information about components of aging well, especially as it relates to emotion regulation and health. That is, these analyses suggest that people who have higher levels of negative affect show greater amplitude in their emotional fluctuations and it takes them longer to recover. These individuals also have worse health outcomes (particularly somatic health, sleep disruptions, health compared to past health and number of hospitalizations). This is similar to results of research that has linked the coupled dynamics of stress and negative affect (an indicator of stress reactivity) and damping parameters (stress recovery) with resilience resources such as hardiness and social support (Montpetit et al., 2010). Thus, people who are less resistant to emotional liability and recover less easily are more susceptible to negative health and well-being outcomes in later life. The approach described in this study suggests ways of assessing emotional dis-regulation that may be useful in identifying individuals who may be at greatest risk for deleterious outcomes.

It should also be noted that different indicators of intra-individual variability may have different data requirements for calculations and modeling of inter-individual differences in them, especially in terms of the number of occasions requirement. Additionally, Hedeker et al. (2008) noted that we may have convergence or estimation issues for the mixed-effects location scale model, for example, when the number of occasions is as small as 5 and the number of individuals is as small as 20. For our proposed model, we model temporal dependency (heterogeneous AR parameters) in addition to amplitude of fluctuations (heterogeneous variances), which implies that we may need more data than the number of occasions we have from a traditional longitudinal study. With 56 occasions in the empirical study, we were able to calculate ISD², MSSD, and autoregressive parameters and model inter-individual differences in them using either the multi-step approach or the one-step approach. If we had only 3 - 7 occasions, which is the number of time points in a traditional longitudinal (panel) study, however, the estimates of autoregressive parameters would have much larger errors and it might be impossible to estimate the model parameters with convergence. For example, we tried to fit the proposed multilevel model to our data with the first 7 or 14 time points and we did not obtain convergent results. Therefore, the proposed model is more applicable for analyzing data from an intensive longitudinal study (e.g., data from a measurement burst study, experience sampling, daily diary, or EMA designs) than a traditional longitudinal (panel) study. Fortunately, in psychology, there is explosion of intensive longitudinal studies going on which makes the proposed model applicable and practical.

In addition, researchers have found that reliabilities of ISD² and ISD are lower than that of $\stackrel{‒}{X}$ and reliabilities of ISD² and ISD are generally low with few measurement occasions. Reliabilities of other indicators of intra-individual variability such as MSSD and φ, however, are still under study. Therefore, future studies should investigate the effects of different numbers of occasions on the reliabilities of more indicators of intra-individual variability such as MSSD and φ and then further study influences of the number of occasions on accuracy and precision of parameter estimates in the proposed models (both the one-step approach and the multi-step approach).

In our study, we used an identity link for an autoregressive parameter mainly because it has been used in previous research (e.g., Kuppens et al., 2010; Suls et al., 1998; Rovine and Walls, 2006). However, a more appropriate link such as a bounded inverse link function may work better for the autoregressive parameter. Future studies should investigate and compare different link functions for modeling autoregressive parameters as outcomes.

In sum, we studied inter-individual differences in intra-individual variability from both the amplitude of fluctuations and temporal dependency perspectives, separately and jointly, in this study. By studying inter-individual differences in intra-individual variability, we learn more about how these processes work and for whom. Moreover, it is possible to test how these inter-individual differences relate to important health and well-being outcomes.

WinBUGS codes for the one-step analysis on studying inter-individual differences in intra-individual variability

# Specify the model

# Data being used: detrended data

Model {

for (i in 1:N){

# response of interest at the first time point specified from an AR model

# na0 is a latent variable forinitiating the AR process

muna [i,1] < − level [i]+ phi1 [i] na0 [i]

na [i, 1] ~ dnorm (muna [i, 1], invsigu2 [i])

# responses at the second to last time points specified from the AR model

for (t in 2:T){

muna [i, t]<− level [i]+ phi1 [i] na [i, t −1]

na [i, t]~ dnorm (muna [i, t], invsigu2 [i])

}}

for (i in 1:N){

level [i]~ dnorm (0,. 000001)

# specify the prior for the latent na0 variable

na0 [i]~dnorm (0,. 000001)

# obtain a latent variable logvare2 [i]

# logvare2 [i] is the log of the intra −individual variance of individual i

# we allow heterogeneity in logvare2

invsigu2 [i] < −1/((1 − phi1 [i]*phi1 [i])* exp (logvare2 [i]))

# model inter −individual differences on logvare2 [i]

mulogvare2 [i]<− intercept 0 + beta 0*gender [i]

# I (−5,7) is added for avoiding too close to 0 values for vare2 [i]

# to avoid computing problems

logvare2 [i]~ dnorm (mulogvare2 [i], invsigzeta02) I (−5,7)

# model inter −individual difference on auto −regressive parameters

muphi1 [i]<− intercept 1 + beta 1 * gender [i]

phi1 [i]~ dnorm (muphi1 [i], invsigzeta 12) I (−1,1)

}

# priors or transformations for the model parameters

invsigzeta 02 ~dgamma (.001,. 001)

invsigzeta 12 ~dgamma (.001,. 001)

varzeta 0 <−1/ invsigzeta 02

varzeta 1 <−1/ invsigzeta 12

intercept 0 ~dnorm (0,. 000001)

intercept 1 ~dnorm (0,. 000001)

beta 0 ~dnorm (0,. 000001)

beta 1 ~dnorm (0,. 000001)

}