A Method to Model Season of Birth as a Surrogate Environmental Risk Factor for Disease

Abstract

Environmental exposures, including some that vary seasonally, may play a role in the development of many types of childhood diseases such as cancer. Those observed in children are unique in that the relevant period of exposure is inherently limited or perhaps even specific to a very short window during prenatal development or early infancy. As such, researchers have investigated whether specific childhood cancers are associated with season of birth. Typically a basic method for analysis has been used, for example categorization of births into one of four seasons, followed by simple comparisons between categories such as via logistic regression, to obtain odds ratios (ORs), confidence intervals (CIs) and p-values. In this paper we present an alternative method, based upon an iterative trigonometric logistic regression model used to analyze the cyclic nature of birth dates related to disease occurrence. Disease birth-date results are presented using a sinusoidal graph with a peak date of relative risk and a single p-value that tests whether an overall seasonal association is present. An OR and CI comparing children born in the 3-month period around the peak to the symmetrically opposite 3-month period also can be obtained. Advantages of this derivative-free method include ease of use, increased statistical power to detect associations, and the ability to avoid potentially arbitrary, subjective demarcation of seasons.

Introduction

Cancer researchers have sought to demonstrate whether a link exists between season of birth and childhood diseases such as cancer [1–13]. An early narrow window of susceptibility during prenatal development [14–15] or perhaps infancy is believed to exist for childhood cancer. These periods are characterized by rapid cell growth and division and a yet undeveloped immune system. Oncogenic viruses [16–18] and chemicals [19–20] have been shown under laboratory conditions to readily induce cancers when applied during specific periods in development versus adulthood. Therefore, evidence of an association between childhood cancer and season of birth may suggest a role for a seasonally variable environmental exposure in its etiology. Exposure to infectious agents, pesticides, indoor environmental tobacco smoke and other sources of polycyclic aromatic hydrocarbons, and use of antihistamines are a few examples of environmental factors that conceivably may follow a seasonal pattern. Other factors of interest to consider in the study of childhood cancer and seasonality include harmonic variation in population mixing, diet, temperature, humidity, sunlight/photoperiod, levels of vitamin D3 and endogenous hormones.

A number of statistical tests for the analysis of harmonic data have been presented in the literature [21–42]. This paper presents a novel and easy to use adaptation of earlier methods that is suitable for analyzing season of birth as a risk factor for diseases such as childhood cancer.

Methods

Logistic regression is used to estimate the probability for disease in relation to potential risk factors and confounding variables [43]. The technique has been widely used in epidemiologic studies, including case-control studies to examine the etiology of childhood cancer. Letting x₁,…,x_r denote a study participant’s values for the (r) predictor variables in a logistic regression model, the probability for disease (D) is computed as:

$$P(D|x_1,\dots ,x_r)=\frac{1}{1+e^{-\left(\widehat{a}+{\widehat{b}}_1{x}_1+\dots +{\widehat{b}}_r{x}_r\right)}}$$ (1)

where â,b̂₁,…,b̂_r are the intercept and coefficients estimated from the data using maximum likelihood methods. In a case-control study, the odds ratios (ORs) can be determined from the logistic regression model and are the exponentiated values of e by the corresponding estimated regression coefficients b̂₁,…,b̂_r. A p-value for a specific predictor variable may be determined by taking twice the logarithm of the ratio of the likelihood of the data under the model including the variable to the likelihood without the variable. The resulting value is compared to a χ² statistic with 1 degree of freedom.

A predictor variable in the simplest case may be expressed as a dichotomous variable, e.g., whether birth occurred in summer. However, more complex forms may be appropriate. A variable such as date of birth (DOB, coded as an integer from 1 to 365) may be expressed as a trigonometric function [44–45]. In this example, let

$$x_1=\text{cos}\left[2\text{arccos}(-1)\left(\frac{\text{DOB}-{\xi }_{\text{MAX}}}{365}\right)\right],$$ (2)

where ξ_MAX. is determined iteratively by finding the value from 1 to 365 that maximizes the coefficient b̂₁. The maximum 3-month seasonal period of risk is found by taking the 91.25 day-wide interval centered on ξ_MAX·. Analogously, the minimum risk period is found by taking the symmetrically opposite 3-month interval centered on ξ_MIN·. The seasonal association is visualized by plotting b̂₁x₁ (i.e., harmonic displacement) against DOB over the range 1 to 365. A single p-value can be obtained as described above for this predictor variable to test whether a seasonal pattern exists. An OR for disease in the maximum versus minimum 3-month seasonal period and corresponding 95% confidence interval (CI) also may be computed, using standard methods [43]. In the case of a leap year, the 29^th day of February is recoded as calendar day 59 so that the respective year consists of 365 days.

Example

Using hypothetical childhood cancer birth-date data from a case-control study (Appendix 1), we conducted analyses using the methods described above, and for comparison, the typical, more basic method to examine whether there is a seasonal pattern in children’s DOB. The identification of an underlying sinusoidal trend would be consistent with the hypothesis of a seasonally varying exposure (e.g., viruses, use of pesticides) as a possible etiologic risk factor for childhood cancer.

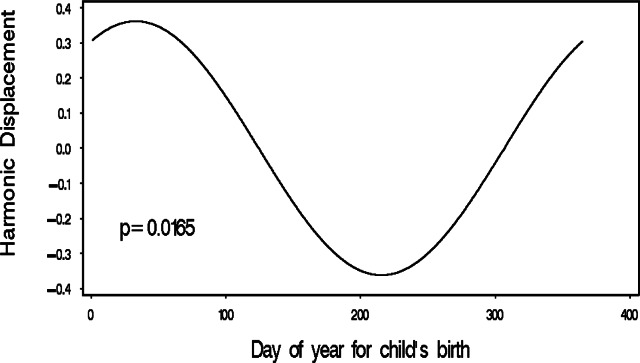
In this example, no significantly increased OR for childhood cancer (all p>0.05) was observed for pair-wise seasonal comparisons when defined in simple categorizations, here as fall (September, October, November), winter (December, January, February), spring (March, April, May), and summer (June, July, August), although the lower confidence limit for ‘winter versus summer’ was just slightly less than unity (Table 1). However, when applying equation (2) to the data in a logistic regression model, a statistically significant (p = 0.0165) seasonal pattern was observed, with peak risk occurring in early February at day 33 (Figure 1). The respective OR for childhood cancer when comparing the maximum versus minimum 3-month seasonal period was 2.2 (95% CI=1.2–4.1).

Table 1:

Odds ratios for childhood cancer by season of child’s birth using hypothetical data (Cases n = 134, Controls n = 261)

Season of birthÞ	Odds ratio	95% Confidence interval
Winter vs. Spring	1.2	(0.68–2.1)
Spring vs. Fall	1.0	(0.56–1.8)
Winter vs. Fall	1.2	(0.67–2.2)
Winter vs. Summer	1.8	(0.99–3.3)
Spring vs. Summer	1.5	(0.84–2.7)
Fall vs. Summer	1.5	(0.82–2.8)

^ÞSpring = {March, April, May}; Summer = {June, July, August}; Fall = {September, October, November}; Winter = {December, January, February}.

Figure 1:

Sinusoidal logistic regression model for hypothetical childhood cancer – birth date data.

Discussion

We have presented a simple, iterative logistic regression-based method to analyze seasonal data. The method represents a generalization of earlier trigonometric models yet is easier to apply and interpret. A novel aspect of the technique is its ability to optimally fit a sinusoidal curve to the underlying data by plotting harmonic displacement against calendar time. An additional key feature of this approach is the ability to obtain an overall p-value and an OR for disease in the “maximum versus minimum” 3-month seasonal period and a corresponding 95% CI. Whereas no single method provides a universal solution to handle harmonic data, the current method accommodates varying length of months, different populations at risk, adjustment for potentially confounding variables, and is fairly robust when used for small samples. The associated statistical test inherently will have greater family-wise power to detect a sinusoidal pattern when compared to chi-square methods or performing multiple pair-wise tests for seasonality. Analogous to a dose response relationship based upon a best-fitting monotonic model and a priori mechanism of action, multiplicity correction is not necessary for sinusoidal logistic regression because there is only one parameter and one statistical test. Furthermore, it takes into account the order of events (e.g., consecutively high/low time periods) and in contrast to pair-wise seasonal comparisons, the underlying definition of season in the current model is not arbitrary for a start and end date, but is determined via the model algorithm.

Several limitations may apply to the use of sinusoidal logistic regression. For example, parameter estimates may be biased if there is a discrepancy between observed values and values expected under the model. Accordingly, the data should be examined for goodness-of-fit using a standard procedure such as the Hosmer-Lemeshow test [46]. Erroneous results may occur in the case of multiple within-year cycles or competing out-of-phase cycles resulting in a cancelling of effects (e.g., opposing seasonal effects by histologic subgroup). A minor modification can be made to the sinusoidal function to allow for multiple cycles [25–26, 34, 40]. For example, a lunar cycle having multiple peaks per year may be modeled by substituting “365” in the denominator of equation (2) with “29.53” (i.e., the number of days in the lunar cycle). When appropriate, stratification is advised in the latter situation as a means to minimize “cancelling of effects.” Further, the lack of a seasonal effect does not necessarily rule out the etiologic importance of putative risk factors that vary in the environment seasonally. Conversely, the seasonal association of a specific risk factor with childhood cancer does not necessarily imply causality. As with any statistical test, the results of this method should be carefully interpreted in light of underlying limitations and biologic plausibility.

Appendix 1:

Hypothetical case-control data (Cases n=134, Controls n=261)

Day of birth	No. of cases	No. of controls	Day of birth	No. of cases	No. of controls	Day of birth	No. of cases	No. of controls	Day of birth	No. of cases	No. of controls	Day of birth	No. of cases	No. of controls
1	1	1	77	1	0	139	0	1	212	0	2	288	0	1
3	1	2	78	1	0	140	1	2	213	0	1	289	1	0
4	1	0	79	1	1	141	0	3	214	1	0	290	1	0
5	0	2	80	1	0	142	1	1	215	0	2	291	0	1
6	0	1	81	0	1	143	1	1	216	0	2	293	1	0
7	0	1	83	0	1	144	0	2	217	0	1	294	0	1
8	2	1	85	0	1	146	2	0	221	1	1	296	1	0
12	0	2	86	1	1	147	0	2	223	2	1	297	1	4
15	1	1	87	0	1	148	0	1	224	0	1	298	0	1
17	0	2	88	0	2	150	0	1	225	0	1	299	1	2
18	2	0	89	0	2	152	0	1	226	3	3	300	1	0
19	1	0	90	1	0	154	1	1	227	0	2	301	0	1
21	1	1	91	1	0	155	0	1	228	0	1	303	1	0
22	1	1	92	0	2	157	1	0	230	0	1	304	2	0
23	1	1	93	1	1	159	0	2	231	1	2	305	0	1
24	1	0	94	2	1	160	0	1	232	0	1	306	0	1
26	0	1	96	0	1	161	0	1	234	1	1	307	0	3
27	1	1	97	1	1	164	1	0	235	0	2	308	0	1
29	0	1	99	1	0	166	0	2	236	0	2	309	1	2
32	0	2	100	0	2	167	1	0	237	1	1	311	1	2
33	1	1	102	1	2	168	2	0	239	0	1	312	1	0
35	1	0	103	0	1	169	0	1	240	0	1	313	1	2
36	0	1	107	1	0	170	0	1	242	0	2	314	1	1
39	2	2	108	0	1	172	0	1	245	0	1	316	1	0
40	1	1	109	1	1	174	1	1	246	0	1	320	0	1
42	1	1	110	1	0	175	1	2	248	2	0	322	2	1
43	0	2	111	0	4	176	0	1	249	0	1	323	1	0
45	0	1	112	1	1	177	0	1	251	2	3	324	1	1
46	1	0	113	0	1	179	2	0	252	0	1	325	0	1
47	1	1	114	1	1	180	0	1	253	1	2	327	0	1
48	0	1	115	0	1	182	0	2	255	0	1	328	1	0
49	0	1	116	1	0	184	1	0	256	1	2	329	0	1
50	1	0	117	1	0	186	1	1	257	0	1	331	1	0
51	0	1	118	0	1	187	0	2	262	1	0	336	1	0
53	1	0	119	0	2	188	0	2	263	1	1	338	1	1
54	1	1	120	1	0	190	0	2	264	0	1	340	0	1
56	1	0	122	1	1	191	0	1	265	0	2	341	0	1
57	1	1	123	0	1	194	0	1	266	1	1	342	0	1
58	1	0	124	0	2	195	0	1	267	0	1	345	0	1
59	1	1	125	1	0	196	0	2	269	1	0	346	1	1
60	0	2	126	2	0	197	1	0	270	0	1	347	0	1
62	2	0	127	0	1	198	1	1	273	0	1	349	1	0
63	0	1	129	0	1	199	0	1	274	0	1	351	0	1
66	1	0	130	1	0	200	1	1	276	0	1	356	0	2
68	0	2	131	0	2	202	1	1	277	0	2	358	0	1
69	1	2	132	1	0	203	0	2	278	0	1	359	2	1
70	0	1	133	0	1	204	1	1	279	0	1	361	0	1
71	1	0	135	1	0	208	0	1	282	1	2	362	0	3
73	0	1	136	0	2	209	0	2	284	0	1	364	0	1
75	0	1	138	0	1	210	0	1	287	0	1	365	1	1