Abstract
In cancer biology, it is very important to understand the phenotypic changes of the patients and discover new cancer subtypes. Recently, microarray-based technologies have shed light on this problem based on gene expression profiles which may contain outliers due to either chemical or electrical reasons. These undiscovered subtypes may be heterogeneous with respect to underlying networks or pathways, and are related with only a few of interdependent biomarkers. This motivates a need for the robust gene expression-based methods capable of discovering such subtypes, elucidating the corresponding network structures and identifying cancer related biomarkers. This study proposes a penalized model-based Student’s t clustering with unconstrained covariance (PMT-UC) to discover cancer subtypes with cluster-specific networks, taking gene dependencies into account and having robustness against outliers. Meanwhile, biomarker identification and network reconstruction are achieved by imposing an adaptive 
penalty on the means and the inverse scale matrices. The model is fitted via the expectation maximization algorithm utilizing the graphical lasso. Here, a network-based gene selection criterion that identifies biomarkers not as individual genes but as subnetworks is applied. This allows us to implicate low discriminative biomarkers which play a central role in the subnetwork by interconnecting many differentially expressed genes, or have cluster-specific underlying network structures. Experiment results on simulated datasets and one available cancer dataset attest to the effectiveness, robustness of PMT-UC in cancer subtype discovering. Moveover, PMT-UC has the ability to select cancer related biomarkers which have been verified in biochemical or biomedical research and learn the biological significant correlation among genes.
Introduction
With the increasingly accumulation of genome-wide expression profiles, microarray-based method becomes a key technique for identifying cancer related genes (biomarkers) and discovering new cancer subtypes [1]. Compared with clinical and pathological risk factors, such as patient age, tumor size, and steroid receptor status, understanding the underlying genes can gain insight into cancer physiology [2]–[4], and is more effective for detection of new cancer subtypes, such as breast cancer [5], [6], ovarian cancer [7], colon cancer [8]. These subtypes may have differences in gene or protein expression, gene regulatory or protein signalling networks [9]. Predicting these subtypes from gene expression profiles can be viewed as a clustering problem, and finding the genes for prediction can be regarded as a problem of variable selection from high-dimensional unlabeled data.
One challenge of cancer subtype discovery is that the differences in network or pathway level across these subtypes may make the conventional clustering approaches based on gene expression profiles differences inadequate [9]. The discovery of these networks and pathways is very important in understanding the collective biological function of genes and their impact on the phenotypic changes of the patients [9]–[12]. In addition, biomarkers are often selected independently based on their discriminative abilities [13]. However, the genes often need to interact with others to participate in some biological processes or molecular functions [14]–[17]. Some of them may be not differentially expressed, but belong to a subnetwork which has overall discriminative activity or is a useful pathway for a specific subtype [3], [9], [18]. Therefore, the task of discovering the subtypes, elucidating their corresponding network structures, and picking out network-based biomarkers is still very important in biomedical fields.
There are various clustering methods applied on gene expression datasets for partitioning biological samples [19]. The model-based clustering which has a solid probabilistic framework is widely used in biomarker and cancer subtype discovering due to its good performance, interpretability and ease of implementation [20]. At present, the gene selection process of most approaches are designed by imposing penalty constraints on the likelihood to achieve a sparse solution.
For the penalized model-based clustering, in order to reduce the number of parameters, one common assumption is that each cluster has a diagonal covariance matrix, so the genes are assumed to be independent. Each cluster is often modeled as random variable drawn from mixture Gaussian distribution, and combined with several penalties, such as 
penalty, adaptive 
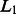penalty and group 
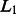penalty [21], [22]. Since the log-probability of Gaussian distribution decays quadratically with distance from the center, it is sensitive to outliers which are commonly observed in microarray experiments due to either chemical or electrical reasons [23]. A more robust penalized model-based Student’s t clustering with diagonal covariance (PMT-DC) is introduced in [24] to deal with the noise and extreme genes. They also provide a way for ranking genes according to their contributions to the clustering process with a bootstrap procedure. However, the above methods ignore dependencies among genes within cancer subtypes. A regularized Gaussian mixture model is proposed to take various dependencies into account by permitting a treatment of general covariance matrices. An expectation maximization (EM) algorithm utilizing the graphical lasso is used for parameter estimation, and achieves better subtype discovering performance and gene selection [20]. As an intermediate between a diagonal and a general covariance matrix, another idea that modeling a covariance matrix using some latent variables as done in the mixture of factor analyzers is introduced [25]. It has more constrains and is more complex than the method based on an unconstrained covariance matrix. However, it is more effective if some latent variable-induced covariance assumption holds in the gene expression dataset. Both methods have difficult to deal with the outliers due to their Gaussian assumption. These conventional penalized model-based methods only select genes based on the mean response, and ignore their implications for the underlying networks or pathways which are very important in understanding the collective biological function.
Motivated by the challenges posed by the underlying networks or pathways and outliers observed in high-dimensional gene expression dataset, and the limitations of the above methods, this study proposes a penalized model-based Student’s t clustering with unconstrained covariance (PMT-UC) for cancer subtype discovery and biomarker identification. The new proposed method is based on multivariate Student’s t distribution which makes the algorithm not be affected by extreme or unusual genes. Unlike PMT-DC with the independent assumption, in order to consider the relationship between genes and discover the cancer subtypes which differ in terms of underlying network structures, a cluster-specific unconstrained covariance is used instead of diagonal covariance. The development of the algorithms for estimating sparse graphs by applying an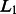 
penalty to the inverse covariance matrix [26], [27] make the idea that taking gene dependence into account feasible. We impose an adaptive 
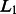penalty on the means and the inverse scale matrices to achieve network-based biomarker identification and network reconstruction. The model is fitted via an EM algorithm by utilizing the graphical lasso. A new gene selection criterion is introduced to find the following informative genes: the genes that have cluster-specific means, the genes that are not differentially expressed but interact with some discriminative genes to form a collective biological function, and the genes which have class-specific underlying network structures. By applying the new model to simulated datasets and one publicly available cancer dataset, we show that the algorithm is robust against outliers on clustering, gene selection and network reconstruction processes simultaneously, and gives competitive results with the state-of-the-art algorithms on detecting new cancer subtypes. Many identified biomarkers have been verified in biochemical or biomedical research. The Gene Ontology (GO) analysis shows that the genes in the same subnetwork selected by the new proposed method have significant biological and functional correlation.
Methods
This section introduces the penalized model-based Student’s t clustering with unconstrained covariance (PMT-UC) to select a few number of genes, that can be used to classify the 
samples into naturally occurring groups, and to discover the relationship between the genes.
The Framework of PMT-UC
Suppose that there are 
independent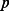 
-dimensional samples 
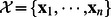, where 
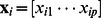represents the gene expression of 
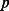genes. The genes have been standardized to have a mean 0 and variance 1 across observations.
Each sample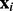 
is supposed to come from a mixture distribution with 
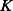components of which the probability density function is
 |
(1) |
where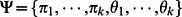 
includes all the parameters in the model, 
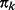is the nonnegative mixing proportion for component 
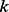with 
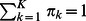, and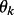 
is the unknown parameters set corresponding to 
.
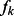Each component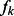 
is specified as multivariate Student’s t distribution 
with the parameters set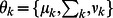 
, where 
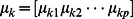is the location parameter, 
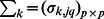is the scale matrix and 
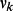is the degrees of freedom. It has the probability density
 |
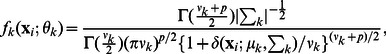(2) |
where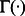 
is the gamma function, and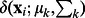 
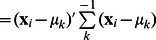denotes the Mahalanobis squared distance between 
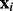and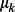 
. The mean and the covariance matrix of each Student’s t distribution is 
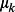and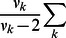 
, respectively. In general, the parameter set 
can be estimated by maximizing the log-likelihood function.
However, since the number of genes is often much more than the number of samples, the maximum likelihood estimation of 
is probably singular. The inverse scale matrix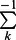 
is denoted as 
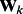with the elements 
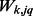. In the last few years, a number of authors introduce many approaches to yield a positive-definite covariance by increasing the sparsity of 
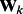[26], [27]. The structure of a network is usually constructed based on correlation or partial correlation [28]. In this paper, the partial correlation 
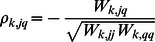can be derived from the inverse scale matrix. The partial correlation is used instead of correlation to present the relationship between two genes due to its ability of factoring out the influence of other genes. Therefore, 
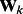can reflect the relationship between the genes for cluster 
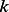and can be regarded as the networks or pathways for genes. The statement that most genes (gene products) only interact with a few genes (gene products) indicates the sparsity of 
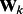in terms of biological interpretation [15]. We impose an adaptive 
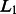penalty on the off-diagonal elements of 
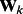to deal with the sparsity of 
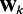[29].
In addition, the sparsity of the mean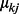 
is considered, which is often used for gene selection. The mean-based discriminative gene is defined to have cluster-specific means, no matter whether it has a common or cluster-specific variances [20]. Specifically, it has at least one nonzero 
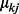since the samples have been standardized to have mean 0 for each gene. Therefore, we impose an adaptive 
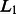penalty on each 
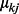to shrink it to zero [29].
Then based on the penalized log-likelihood function which consists of log-likelihood function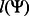 
and penalty term 
, the objective function of PMT-UC to be maximized is as follows:
 |
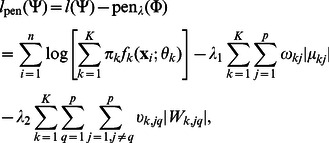(3) |
where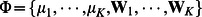 
, and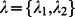 
includes the non-negative regularization parameters 
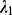and 
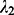for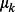 
s and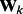 
s respectively. The regularization parameters control the sparsity of the model. The larger the values of 
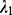and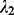 
, the more genes will be noninformative and independent. The adaptive 
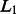penalty is a weighted version of the 
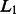penalty with a weight 
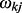or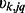 
for each component. It achieves the three desirable properties simultaneously that can produce sparse solutions, ensure consistency of model selection, and result in unbiased estimates for large coefficients [30].
Inference Algorithm
This study uses the expectation maximization (EM) algorithm [31] for optimizing the objective function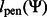 
for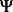 
given fixed 
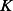and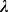 
. As in [20], [24], each sample 
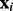is assumed to have a corresponding unobserved indicator vector 
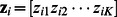, specifying the mixture component that 
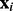belongs to. If 
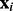comes from component 
then 
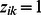, otherwise 
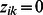. Given 
, 
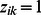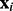follows a Student’s t distribution with the probability density function 
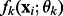. According to the fact that the Student’s t distribution can be written as a multivariate Gaussian distribution with the covariance matrix scaled by the reciprocal of a Gamma random variable, the additional missing data 
is introduced, where each element 
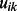of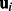 
follows the Gamma distribution [32]. Then the penalized complete-data log-likelihood of the complete data 
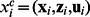is
 |
(4) |
where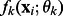 
can be expressed as the product of the probability density functions of Gaussian and Gamma distributions (see Text S1 for details).
The EM algorithm iteratively applies an expectation (E) step to calculate the expected value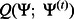 
of 
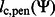with respect to the current estimation 
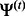of the parameters at the 
th iteration, and a maximization (M) step to find the updated parameters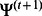 
by maximizing 
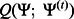, until achieving a stopping criterion 
.
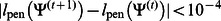E step. The value of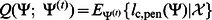 
depends on the following three expectations (see Text S2 for details).
Since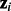 
follows the Multinomial distribution and 
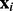comes from the mixture distribution with probability density function 
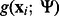, the value of 
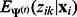is given by
 |
(5) |
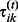can be regarded as the posterior probability of 
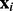belonging to the 
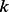th cluster. Seeing that the Gamma distribution is conjugate to itself (self-conjugate) with respect to a Gaussian likelihood function, we have
 |
(6) |
and
 |
 |
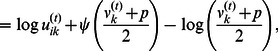(7) |
where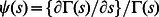 
is the Digamma function [32].
M step. Firstly, the update of 
is given by the equation
 |
with the constraint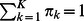 
as
 |
(8) |
Secondly, the value of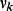 
at the 
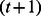th iteration is a solution of the equation
 |
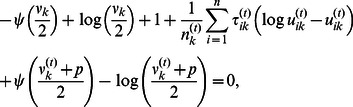(9) |
where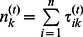 
. In this paper, since the solution of (9) is in non-closed form, the R function “nlminb” is used to find the numerical solution for 
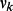[24].
Thirdly, the aim is to maximize
 |
 |
(10) |
to obtain the update for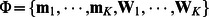 
. In the 
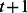step, the adaptive weights are defined to be
 |
(11) |
The parameter 
is introduced in order to provide stability and to ensure that a zero-valued component can escape from zero in the next iteration [33]. When 
is too small, the zero-valued component still has so large weight that it will remain zero in the next iteration. When 
is too large, it makes the difference between the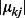 
s or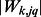 
s not significant and allows many nonzero-valued components, resulting in a complex and inaccurate model. It has been assigned several values during the experiment procedure. It is shown that 
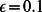is appropriate. The initial estimates 
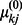and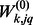 
are chosen as the results estimated by the 
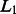penalty.
By considering the differentiability of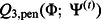 
with respect to 
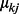for two cases that 
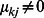and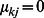 
, the updating estimate 
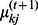is as follows (see Text S3 for details) [20]: if
 |
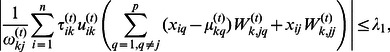(12) |
then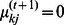 
; otherwise
 |
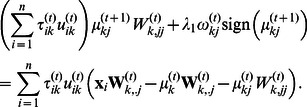(13) |
After dropping the terms unrelated to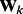 
in 
, we have
 |
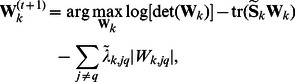(14) |
where
 |
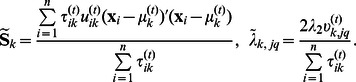This optimization problem can be solved using the graphical lasso of which the corresponding R package “glasso” is available on CRAN [27]. The graphical lasso is designed to consider the problem of estimating sparse graphs by a lasso penalty applied to the inverse covariance matrix [27]. It is first proposed for the maximization of the Gaussian log-likelihood of the data with respect to the covariance matrix. The new proposed method takes 
into account instead of the sample covariance matrix, where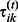 
contains a posteriori information of the sample, and 
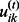can reduce the effect of the outliers on this optimization problem.
Model Selection
There are three parameters that need to be estimated before the PMT-UC algorithm, including the number of clusters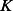 
, the penalization parameters 
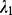and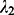 
. In this paper, the following approximate weight of evidence (AWE) criterion based on an approximation to the classification log-likelihood is used for model selection:
 |
(15) |
where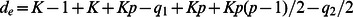 
is the effective number of parameters in the model with 
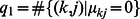and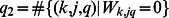 
[34], [35]. It imposes a higher penalty on more complex model than BIC and is able to identify the correct number of clusters even when the component densities are misspecified [36], [37]. A grid search is applied to find the optimal 
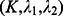which has the minimum AWE.
Subtype Discovering via Clustering
After the estimation of the parameters in PMT-UC, clusters can then be defined as samples following the similar distribution which is determined by the value of the posterior probability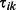 
. Given a sample, PMT-UC predicts the cancer subtype 
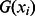of the gene expression profile 
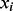by that which gives the largest posterior probability 
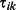, that is 
.
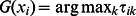Elucidating the Underlying Network Structures
We can then elucidate the cluster-specific underlying network structures based on the inverse scale matrix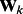 
. A cluster-specific network can be represented as undirected graph, with the genes as the vertices and edges as their relationships based on 
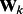. Edges connect those genes whose partial correlations derived from 
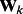are larger than 
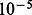. Then a subnetwork is defined as a set containing genes and edges that induces a single connected component in this network. These cluster-specific subnetworks indicate the different relationships among genes with various cancer subtypes and are regarded as the underlying network structures.
Network-based Biomarker Identification
Due to that the genes in a cell seldom act alone, but form a network of interactions [14], the biomarkers are identified as subnetworks of interacting genes instead of individual genes in this paper. Specifically, we firstly pick out the subnetworks defined above. Secondly, in consideration of the fact that the noisy gene and the informative gene are uncorrelated with each other [20], [38], the subnetworks that have at least one mean-based discriminative gene are chosen as subnetwork biomarkers. This gene selection criterion can identify genes that are not differentially expressed but interact with some discriminative genes to form a collective biological function. Finally, the remaining subnetworks of which the internal structure (the relationship between the genes) are different among 
are also regarded as biomarkers to elucidate the cluster-specific underlying network structures.
The Final Algorithm for PMT-UC
Figure 1 summarizes the detailed algorithm for discovering cancer subtypes, underlying network structures, and network-based biomarkers via PMT-UC. For any given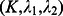 
, the result of K-means is used as the initialization for the EM algorithm. In order to avoid the local optimum of K-means, we run the entire algorithm five times with random K-means initialization, and choose the result that gives the highest value of objective function (3).
Figure 1. Summary of PMT-UC for discovering cancer subtypes, underlying network structures, and biomarkers.
Results and Discussion
Simulations
A dataset with redundant genes is simulated to evaluate the clustering, gene selection and network reconstruction performance of the method. The dataset has 
samples and 
informative genes with input dimension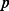 
. 
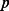is taken to be higher than sample size of each cluster so that the sample covariance of each cluster is not reversible. The first 
informative genes come from a 
-dimensional multivariate Student’s t distribution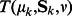 
for the 
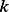th cluster. The remaining 
noisy genes which are independent of the informative genes are independently and identically distributed from univariate Student’s t distribution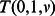 
for all clusters. The degrees of freedom 
will affect the noise level of the dataset. The lower the degrees of freedom the fatter tails the dataset will have.
Firstly, the dataset with two clusters is simulated, having 
samples for each cluster. Three cases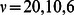 
are considered in the next experiments to explore the effects of the outliers on the performance of the method [24]. When 
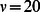, the distribution of the simulated dataset is approximate to Gaussian distribution. For each of the three cases, the following four set-ups are considered:
set-up 1 has cluster-specific means with
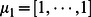and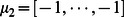 
, and common diagonal scale matrix with 
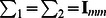, where 
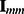is a 
-dimensional identity matrix.set-up 2 has cluster-specific means with
and 
, and common non-diagonal scale matrix with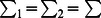 
. 
is a sparse symmetry matrix that has the diagonal elements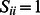 
and the non-diagonal elements 
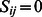with the exception of 
, 
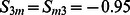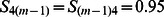.set-up 3 has cluster-specific means with
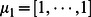and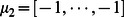 
, and uses two general sparse scale matrices generated by the similar procedure described in [9], [26]. A diagonal matrix with same positive diagonal entries is generated firstly, then a given number of nonzeros are randomly inserted in the non-diagonal locations of specified section 
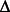of the matrix symmetrically. The number of nonzero non-diagonal entries is set to 
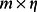. A multiple of the identity is adding to the matrix to ensure the positive definiteness. Finally, each element is divided by the corresponding diagonal element to generate the inverse scale matrix. In this set-up, 
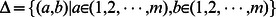and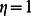 
.set-up 4 has cluster-specific means with
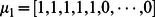and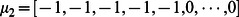 
, and similar non-diagonal scale matrices as set-up 3 with 
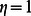and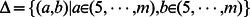 
.
Under the simulated pattern stated above, we set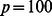 
, 
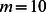and 
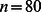similar to that introduced in [20]. For each set-up, the simulation is repeated 50 times and fitted with 
, 
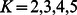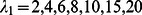, and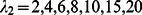 
.
PMT-UC is compared with penalized model-based Gaussian clustering with unconstrained covariance (PMG-UC) and penalized model-based Student’s t clustering with diagonal covariance (PMT-DC) in terms of the following evaluation criterions. The Rand Index (RI), the adjusted Rand Index (aRI) and the frequencies of the selected numbers (N) of clusters (K) are used to assess the ability of the method for clustering [20]. In order to quantify the ability of the method for network reconstruction, the structural hamming distance (SHD) between true and inferred networks is computed, which is the number of edge differences to transform one network to another network [9]. The smaller SHD indicates the closer approximation to the true network. The following two indexes are used for evaluation of the gene selection performance, the number of informative variables incorrectly selected to be noninformative (false negatives, FN) and the number of noninformative variables correctly selected (true negatives, TN) [20].
Effect of the parameter 
The effect of the parameter 
which is designed for the stability of the algorithm on the performance of PMT-UC is discussed in terms of the five measures introduced above (RI, aRI, SHD, FN and TN). Particularly, we run PMT-UC on a fixed dataset under the set-up 4 with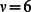 
of which the dataset has higher noise level, a fewer genes with cluster-specific means and some genes with cluster-specific network structures, with different values of 
(
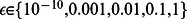). Table 1 shows the averages and standard deviations of five measures in 50 simulations with respect to various values of 
on this set-up. When 
is not too large, the algorithm performance tends to be fairly robust to the choice of 
. Since the results with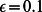 
show some improvement over the other situations, 
is set to 0.1 in the following experiments.
Table 1. The effect of the parameter 
on the performance of PMT-UC.
|
RI | aRI | SHD1 | SHD2 | FN | TN |
| 10–10 | 0.918 (0.045)§ | 0.836 (0.090) | 5.000 (0.798) | 4.565 (1.727) | 2.870 (1.792) | 89.609 (0.583) |
| 0.001 | 0.923 (0.048) | 0.846 (0.095) | 4.913 (0.949) | 4.826 (1.072) | 2.174 (1.557) | 89.565 (0.590) |
| 0.01 | 0.914 (0.049) | 0.828 (0.098) | 5.435 (1.472) | 5.043 (1.107) | 2.609 (2.210) | 89.174 (1.029) |
| 0.1 | 0.937 (0.034) | 0.873 (0.068) | 2.652 (1.229) | 2.522 (1.344) | 0.870 (0.968) | 90.000 (0.000) |
| 1 | 0.689 (0.192) | 0.380 (0.383) | 5.000 (0.000) | 5.261 (0.864) | 6.913 (2.575) | 88.478 (1.702) |
The effect of the parameter 
on the performance of PMT-UC is discussed in terms of the five measures RI, aRI, SHD, FN and TN, where SHD1 and SHD2 are the results for the first and second clusters respectively, FN is the number of informative variables incorrectly selected to be noninformative and TN is the number of noninformative variables correctly selected. In the true case,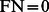 
, 
.
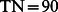c(d): c and d are the average and standard deviation of corresponding results in 50 simulations, respectively.
Effect of the initialization
The convergence of PMT-UC is studied by considering the corresponding results with respect to different initializations using K-means. This study also depends on the set-up 4 with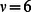 
. A simulated dataset is fixed and the entire procedure is applied ten times of which each time uses five K-means initializations. The standard deviations of the selected parameters and experiment results of these ten experiments can be regarded as the evaluation indexes for the convergence of PMT-UC. To reduce the variability, five datasets are generated, and the averages and standard deviations of results for each dataset are list in Table 2. It is shown that the clustering and gene selection results do not have significant change with different initializations. However, the complete PMT-UC algorithm has a certain variance in terms of the parameter 
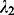and the results SHD that correspond to network reconstruction.
Table 2. The convergence of PMT-UC with respect to different initializations.
| dataset | 1 | 2 | RI | aRI | SHD1 | SHD2 | FN | TN |
| 1 | 4.0 (0.0)§ | 3.6 (0.5) | 0.91 (0.04) | 0.83 (0.07) | 3.00 (1.58) | 2.00 (1.73) | 0.40 (0.89) | 90.00 (0.00) |
| 2 | 4.0 (0.0) | 4.0 (0.0) | 0.97 (0.01) | 0.94 (0.02) | 3.20 (1.48) | 3.00 (1.58) | 0.80 (0.45) | 90.00 (0.00) |
| 3 | 4.0 (0.0) | 3.8 (0.4) | 0.95 (0.01) | 0.89 (0.02) | 1.80 (0.45) | 3.60 (0.55) | 1.20 (0.45) | 90.00 (0.00) |
| 4 | 4.0 (0.0) | 4.0 (0.0) | 0.95 (0.02) | 0.89 (0.04) | 6.40 (1.34) | 4.00 (0.71) | 1.60 (0.89) | 89.80 (0.45) |
| 5 | 4.0 (0.0) | 4.0 (0.0) | 0.95 (0.00) | 0.90 (0.00) | 1.40 (0.55) | 3.60 (0.55) | 1.00 (0.00) | 90.00 (0.00) |
The convergence of PMT-UC is explored by considering the selected parameters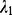 
and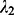 
, and the experiment results RI, aRI, SHD, FN and TN, with respect to different initializations using K-means. SHD1 and SHD2 are the results for the first and second clusters respectively, FN is the number of informative variables incorrectly selected to be noninformative and TN is the number of noninformative variables correctly selected. In the true case, 
, 
.
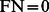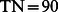c(d): c and d are the average and standard deviation of corresponding results in 10 experiments with a fixed dataset, respectively.
Clustering results
The experiment clustering results of the four set-ups with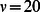 
are shown in Table 3. Since the datasets come from an approximate distribution of Gaussian distribution, both PMT-UC and PMG-UC always correctly identify the two clusters. For set-ups 1, 2, 3, PMT-UC works slightly better than PMG-UC in identifying clustering structures, as summarized by the RI or aRI in Table 3. For set-up 4, with the presence of more noise variables based on the mean, RI and aRI of PMG-UC decrease dramatically to 0.734 and 0.47. For set-up 1 with the true model with a diagonal covariance matrix, both PMT-UC and PMT-DC have similar clustering performances. The stronger the correlations among variables, the more likely for the PMT-DC to get more clusters by mistake and have poor clustering performance. Especially, for PMT-DC with the independence assumption, the dataset in set-up 4 only has five informative genes, which results in high clustering error rate.
Table 3. Comparison of performance of PMT-UC, PMG-UC and PMT-DC applied on binary-clusters simulated datasets.
| ν | Set-up | Κ | PMT-UC | PMG-UC | PMT-DC | ||||||||||||
| N | RI | aRI | FN | TN | N | RI | aRI | FN | TN | N | RI | aRI | FN | TN | |||
| 20 | 1 | 2 | 50 | 0.994 | 0.988 | 0.00 | 90.00 | 50 | 0.983 | 0.975 | 0.00 | 84.36 | 45 | 0.990 | 0.979 | 0.00 | 89.09 |
| 3 | 0 | – | – | – | – | 0 | – | – | – | – | 5 | 0.978 | 0.956 | 0.00 | 86.20 | ||
| 4/5‡ | 0 | – | – | – | – | 0 | – | – | – | – | 0 | – | – | – | – | ||
| A† | 50 | 0.994 | 0.988 | 0.00 | 90.00 | 50 | 0.983 | 0.975 | 0.00 | 84.36 | 50 | 0.988 | 0.977 | 0.00 | 88.80 | ||
| 2 | 2 | 50 | 0.998 | 0.995 | 0.00 | 89.80 | 50 | 0.971 | 0.941 | 1.86 | 84.42 | 40 | 0.981 | 0.962 | 2.00 | 89.47 | |
| 3 | 0 | – | – | – | – | 0 | – | – | – | – | 10 | 0.960 | 0.919 | 2.00 | 84.80 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 0 | – | – | – | – | ||
| A | 50 | 0.998 | 0.995 | 0.00 | 89.80 | 50 | 0.971 | 0.941 | 1.86 | 84.42 | 50 | 0.977 | 0.953 | 2.00 | 88.54 | ||
| 3 | 2 | 50 | 0.995 | 0.990 | 0.00 | 89.80 | 50 | 0.987 | 0.975 | 0.00 | 84.72 | 23 | 0.995 | 0.989 | 0.00 | 89.35 | |
| 3 | 0 | – | – | – | – | 0 | – | – | – | – | 22 | 0.929 | 0.857 | 0.00 | 85.59 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 5 | 0.861 | 0.721 | 0.00 | 76.60 | ||
| A | 50 | 0.995 | 0.990 | 0.00 | 89.80 | 50 | 0.987 | 0.975 | 0.00 | 84.72 | 50 | 0.952 | 0.904 | 0.00 | 86.42 | ||
| 4 | 2 | 50 | 0.944 | 0.889 | 0.00 | 90.00 | 50 | 0.734 | 0.470 | 7.22 | 88.84 | 39 | 0.883 | 0.767 | 5.51 | 89.64 | |
| 3 | 0 | – | – | – | – | 0 | – | – | – | – | 11 | 0.841 | 0.681 | 5.00 | 87.64 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 0 | – | – | – | – | ||
| A | 50 | 0.944 | 0.889 | 0.00 | 90.00 | 50 | 0.734 | 0.470 | 7.22 | 88.84 | 50 | 0.874 | 0.748 | 5.40 | 89.20 | ||
| 10 | 1 | 2 | 50 | 0.983 | 0.966 | 0.00 | 89.92 | 41 | 0.942 | 0.884 | 0.78 | 83.24 | 28 | 0.976 | 0.952 | 0.36 | 88.89 |
| 3 | 0 | – | – | – | – | 9 | 0.881 | 0.761 | 0.00 | 76.33 | 19 | 0.943 | 0.885 | 0.00 | 79.21 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 3 | 0.891 | 0.782 | 0.00 | 87.33 | ||
| A | 50 | 0.983 | 0.966 | 0.00 | 89.92 | 50 | 0.931 | 0.862 | 0.64 | 82.00 | 50 | 0.958 | 0.917 | 0.20 | 85.12 | ||
| 2 | 2 | 50 | 0.988 | 0.976 | 0.00 | 89.92 | 46 | 0.867 | 0.734 | 2.70 | 82.13 | 36 | 0.943 | 0.887 | 2.28 | 89.11 | |
| 3 | 0 | – | – | – | – | 4 | 0.797 | 0.593 | 1.50 | 72.50 | 13 | 0.943 | 0.887 | 1.92 | 80.31 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 1 | 0.882 | 0.764 | 4.00 | 85.00 | ||
| A | 50 | 0.988 | 0.976 | 0.00 | 89.92 | 50 | 0.861 | 0.723 | 2.60 | 81.36 | 50 | 0.942 | 0.885 | 2.22 | 86.74 | ||
| 3 | 2 | 50 | 0.992 | 0.984 | 0.00 | 88.88 | 33 | 0.922 | 0.845 | 0.00 | 82.52 | 16 | 0.873 | 0.747 | 1.63 | 88.19 | |
| 3 | 0 | – | – | – | – | 17 | 0.853 | 0.706 | 0.00 | 55.53 | 28 | 0.942 | 0.884 | 0.00 | 82.96 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 6 | 0.758 | 0.516 | 1.67 | 80.50 | ||
| A | 50 | 0.992 | 0.984 | 0.00 | 88.88 | 50 | 0.899 | 0.798 | 0.00 | 73.34 | 50 | 0.898 | 0.796 | 0.72 | 84.34 | ||
| 4 | 2 | 50 | 0.949 | 0.899 | 0.00 | 89.50 | 50 | 0.499 | 0.000 | 8.80 | 76.70 | 42 | 0.681 | 0.368 | 7.02 | 86.64 | |
| 3 | 0 | – | – | – | – | 0 | – | – | – | – | 5 | 0.796 | 0.593 | 4.80 | 85.40 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 3 | 0.644 | 0.284 | 8.33 | 84.33 | ||
| A | 50 | 0.949 | 0.899 | 0.00 | 89.50 | 50 | 0.499 | 0.000 | 8.80 | 76.70 | 50 | 0.691 | 0.385 | 6.88 | 86.38 | ||
| 6 | 1 | 2 | 50 | 0.961 | 0.922 | 0.00 | 89.70 | 40 | 0.619 | 0.240 | 6.88 | 74.75 | 32 | 0.957 | 0.914 | 0.63 | 89.75 |
| 3 | 0 | – | – | – | – | 10 | 0.868 | 0.735 | 0.00 | 81.50 | 13 | 0.872 | 0.743 | 0.92 | 84.77 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 5 | 0.503 | 0.008 | 4.00 | 90.00 | ||
| A | 50 | 0.961 | 0.922 | 0.00 | 89.70 | 50 | 0.669 | 0.339 | 5.50 | 76.10 | 50 | 0.889 | 0.779 | 1.04 | 88.48 | ||
| 2 | 2 | 50 | 0.980 | 0.961 | 0.00 | 90.00 | 45 | 0.550 | 0.101 | 8.82 | 78.20 | 46 | 0.672 | 0.351 | 4.59 | 83.00 | |
| 3 | 0 | – | – | – | – | 5 | 0.863 | 0.726 | 2.00 | 75.00 | 0 | – | – | – | – | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 4 | 0.501 | 0.001 | 10.00 | 88.50 | ||
| A | 50 | 0.980 | 0.961 | 0.00 | 90.00 | 50 | 0.581 | 0.163 | 8.14 | 77.88 | 50 | 0.659 | 0.323 | 5.02 | 83.44 | ||
| 3 | 2 | 50 | 0.952 | 0.904 | 0.10 | 89.80 | 45 | 0.502 | 0.006 | 9.89 | 88.33 | 27 | 0.542 | 0.094 | 7.85 | 80.93 | |
| 3 | 0 | – | – | – | – | 5 | 0.500 | 0.004 | 9.00 | 82.00 | 15 | 0.749 | 0.500 | 2.00 | 73.07 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 8 | 0.617 | 0.232 | 7.50 | 78.75 | ||
| A | 50 | 0.952 | 0.904 | 0.10 | 89.80 | 50 | 0.502 | 0.006 | 9.80 | 87.70 | 50 | 0.616 | 0.238 | 6.04 | 78.22 | ||
| 4 | 2 | 50 | 0.935 | 0.870 | 0.40 | 90.00 | 50 | 0.498 | 0.002 | 9.90 | 87.10 | 39 | 0.495 | 0.000 | 8.10 | 76.44 | |
| 3 | 0 | – | – | – | – | 0 | – | – | – | – | 7 | 0.507 | 0.019 | 5.86 | 67.71 | ||
| 4/5 | 0 | – | – | – | – | 0 | – | – | – | – | 4 | 0.619 | 0.234 | 1.00 | 67.00 | ||
| A | 50 | 0.935 | 0.870 | 0.40 | 90.00 | 50 | 0.498 | 0.002 | 9.90 | 87.10 | 50 | 0.506 | 0.021 | 7.22 | 74.46 | ||
The clustering and gene selection results for the four set-ups with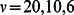 
, in terms of the average frequencies (N) of the selected numbers of clusters (K), and the average of RI, aRI, FN, and TN in 50 simulations, where FN is the number of informative variables incorrectly selected to be noninformative and TN is the number of noninformative variables correctly selected. In the true case, 
, 
, 
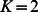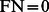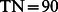. The table indicates in bold all results that perform best or that are not significantly different from each other.
: 
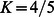denotes that 
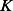can be 4 or 5.
: 
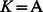denotes that 
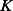can be any element of the set 
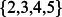which contains the predefined numbers of clusters.
To investigate the effect of the outliers, we use the smaller degrees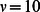 
and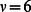 
. Table 3 also gives the results for the four set-ups with these two cases. As expected, PMG-UC performs poorly with smaller degrees, and it is more sensitive to extreme observations. For set-up 1, the clustering results of PMT-DC do not change significantly with the decreasing of degrees for its robustness and independence assumption. However, it often can not find the true clustering structures in the other three set-ups. In summary, the results for set-ups 1–4 when 
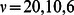demonstrate that PMT-UC has better clustering performance than PMG-UC and PMT-DC for the datasets with independent or correlated informative genes, and is robust to the outliers.
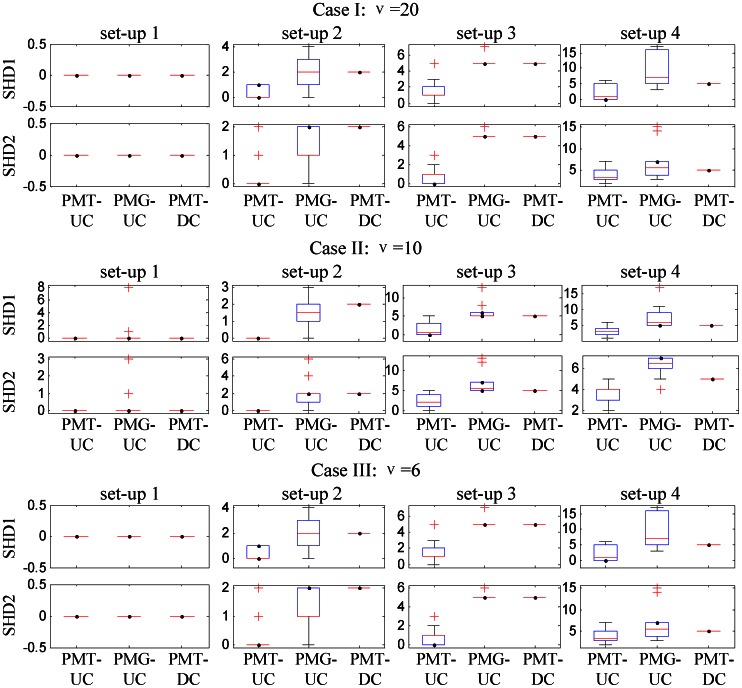
Network reconstruction
Figure 2 shows the boxplots of cluster-specific SHD between estimated and true networks over 50 simulations for the above four set-ups of the three cases when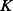 
is set to 2. In addition, we plot the average sparsity pattern which is the relative frequency matrix for PMG-UC and PMT-UC. Since PMT-DC assumes a diagonal covariance, it is not plotted here. The relative frequency matrix is comprised of the relative frequency of nonzero estimated of each element of the inverse scale matrix 
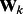over the 50 repetitions. Figure 3 shows the cluster-specific results of the first 
informative genes (see Text S4 for the results of the total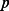 
genes). We make the following observations based on the results given in Figures 2 and 3. At all the cases, PMT-UC provides smallest SHD relative to the other two approaches. When 
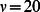with which the Student’s t distribution is similar to Gaussian distribution, both PMT-UC and PMG-UC are able to recover the sparse inverse covariance structure for set-up 1. It is shown that although both PMT-UC and PMG-UC have non-diagonal assumption, they can get the diagonal covariance as the truth by a sufficiently large penalty on the off-diagonal elements of the inverse covariance matrices. For set-up 2, PMT-UC can accurately identify the location of the nonzeros almost every simulation. Meanwhile, with the high value of the off-diagonal nonzeros of covariance, PMG-UC can also recover the inverse covariance pattern sometimes. However, when the partial correlations of the genes are not high in the set-up 3, with the 
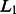penalty, PMG-UC does not have good network reconstruction performance different from that of PMT-UC. For the set-up 4, with the increasing of the noise in terms of the mean, the result of PMG-UC is obscure. When 
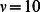or with which the dataset has higher noise level, PMG-UC is unable to recover network structure. However, PMT-UC can still discover the relationship between genes under the network.
Figure 2. Boxplots of structural hamming distance (SHD) between correct and inferred networks.
On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted individually. Results shown for PMT-UC, PMG-UC and PMT-DC in the four set-ups of three cases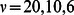 
. SHD1 and SHD2 are the results for the first and second clusters, respectively.
Figure 3. Network reconstruction for simulated datasets with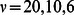 
.
TRUE:1 and TRUE:2 are the parts of the original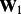 
and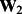 
corresponding to the first 
informative genes for the first and second clusters, respectively. PMT-UC:1 and PMT-UC:2 are the estimation of those parts of the inverse scale matrices using PMT-UC. PMG-UC:1 and PMG-UC:2 are the estimation of those parts of the inverse covariance matrices using PMG-UC.
Gene selection
The two gene selection evaluation indexes FN and TN are also summarized in Table 3. For the four set-ups, PMG-UC tends to picks out more genes which are uninformative than PMT-UC and PMT-DC. In set-ups 1 and 3, the informative genes have cluster-specific means and can be selected by all the three methods when the dataset has low noise level. For set-ups 2 and 3, there are two genes which are not differentially expressed but interact with some discriminative genes, and five genes which are also not differentially expressed but have different underlying network structures, respectively. Table 3 shows that among the three methods only PMT-UC can discover these genes.
The dataset with multiple thin-tailed clusters
For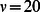 
, an additional dataset with more thin-tailed clusters is taken account into, where the number of clusters is assumed to be 5. The first two clusters are generated using the simulated pattern of set-up 4, where the values of relevant settings are not changed. The other three clusters contain more mean-based discriminative genes with 15 samples for each cluster, having 
, 
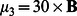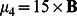, and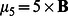 
, where 
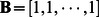, and common diagonal scale matrix. The model is fitted with 
, 
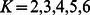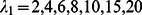, and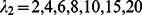 
. Table 4 presents the average results of the three algorithms in 50 simulations, including the RI and aRI with respect to the first two clusters and the other three ones. When the dataset has many thin-tailed clusters, PMT-UC tries to explain the first two clusters whose means are not too different by fat tails. Therefore, unlike the good clustering performance when the dataset has only two clusters, PMT-UC can not identify the true clustering structures of these two clusters although the informative genes are selected correctly. Since the model selection criterion of PMT-UC tends to select the sampler model with less nonzero parameters, it can not pick out the model with four or five clusters as PMT-DC does. Due to the bad initializations using K-means, PMG-UC also regards these two clusters as one although it is not so flexible as PMT-UC. The superiority of PMT-UC can not be reflected in the simulation having many thin-tailed clusters of which some clusters do not have enough mean-based discriminative genes. The good performance of algorithm may need more genes having cluster-specific means with the increasing of the number of clusters.
Table 4. Comparison of performance of PMT-UC, PMG-UC and PMT-DC applied on simulated datasets with multiple thin-tailed clusters.
| Method | Κ | N | FN | TN | RI | aRI | RI1 | aRI1 | RI2 | aRI2 |
| PMT-UC | 2 | – | – | – | – | – | – | – | – | – |
| 3 | 50 | 0.00 | 90.00 | 0.639 | 0.347 | 1.000 | 1.000 | 0.494 | 0.000 | |
| 4 | – | – | – | – | – | – | – | – | – | |
| 5 | – | – | – | – | – | – | – | – | – | |
| 6 | – | – | – | – | – | – | – | – | – | |
| A† | 50 | 0.00 | 90.00 | 0.639 | 0.347 | 1.000 | 1.000 | 0.494 | 0.000 | |
| PMG-UC | 2 | – | – | – | – | – | – | – | – | – |
| 3 | – | – | – | – | – | – | – | – | – | |
| 4 | 8 | 0.00 | 89.00 | 0.794 | 0.445 | 1.000 | 1.000 | 0.495 | 0.000 | |
| 5 | 42 | 0.00 | 89.62 | 0.793 | 0.489 | 0.993 | 0.984 | 0.497 | 0.000 | |
| 6 | – | – | – | – | – | – | – | – | – | |
| A | 50 | 0.00 | 89.52 | 0.793 | 0.482 | 0.995 | 0.987 | 0.497 | 0.000 | |
| PMT-DC | 2 | – | – | – | – | – | – | – | – | – |
| 3 | – | – | – | – | – | – | – | – | – | |
| 4 | 39 | 0.00 | 88.77 | 0.794 | 0.564 | 1.000 | 1.000 | 0.496 | 0.000 | |
| 5 | 11 | 0.00 | 88.00 | 0.797 | 0.506 | 1.000 | 1.000 | 0.502 | 0.000 | |
| 6 | – | – | – | – | – | – | – | – | – | |
| A | 50 | 0.00 | 88.60 | 0.794 | 0.551 | 1.000 | 1.000 | 0.495 | 0.000 |
The comparison of performance of PMT-UC, PMG-UC and PMT-DC applied on simulated datasets with multiple thin-tailed clusters, in terms of the average frequencies (N) of the selected numbers of clusters (K), and the average of RI, aRI, FN, and TN in 50 simulations. RI1 and RI2 are the RI with respect to the first two clusters and the last three clusters, respectively. aRI1 and aRI2 are the aRI with respect to the first two clusters and the last three clusters, respectively. In the true case,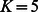 
, 
, 
.
: 
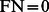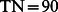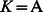denotes that 
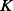can be any element of the set 
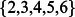which contains the predefined numbers of clusters.
Application to Real Dataset
In order to evaluate clustering capability, gene selection and network reconstruction performance of PMT-UC, experiments are carried out on one publicly available cancer dataset. This dataset is the expression profiles of 7129 genes on 72 acute leukemia samples described by Golub et al.
[39]. It includes 47 samples of acute lymphoblastic leukemia (ALL) and 25 samples of acute myeloid leukemia (AML). ALL samples consist of two subtypes: 38 B-cell ALL and 9 T-cell ALL. The following two preprocessing steps are applied to dataset as in [40] 1) thresholding, the gene expression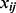 
is set to 100 if 
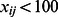and set to 16000 if 
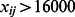; 2) filtering, the gene with 
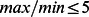or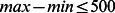 
is excluded, where 
and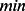 
are the maximum and minimum expression levels for a particular gene across all the samples transformation.
For the leukemia dataset, a preliminary gene screening is used that the top 300 genes with the largest sample variances across all the samples are selected [40]. The model is fitted with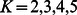 
, 
, and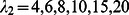 
.
Cancer subtype discovery
The clustering results of PMT-UC are compared with PMG-UC and PMT-DC. By a grid search, the optimal clustering results of three methods are shown in Table 5. PMT-DC can identify the 25 AML samples from all the 72 samples correctly. However, it cannot recognize the differences between two subtypes of ALL with the possible reason that PMT-DC assumes a diagonal covariance. Both PMT-UC and PMG-UC have better clustering performance than PMT-DC. The results in Table 5 clearly indicate that the robustness of PMT-UC make it perform better in identifying true clustering structures and gives a fewer errors in cancer subtype discovery.
Table 5. Optimal clustering results for the leukemia dataset.
| PMT-UC | PMG-UC | PMT-DC | |||||||
| Clusters (#Samples) | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| ALL-B(38) | 37 | 1 | 0 | 37 | 2 | 0 | 24 | 14 | 0 |
| ALL-T(9) | 0 | 8 | 1 | 0 | 8 | 1 | 8 | 0 | 1 |
| AML(25) | 1 | 0 | 24 | 2 | 0 | 24 | 0 | 0 | 25 |
Network structure analysis
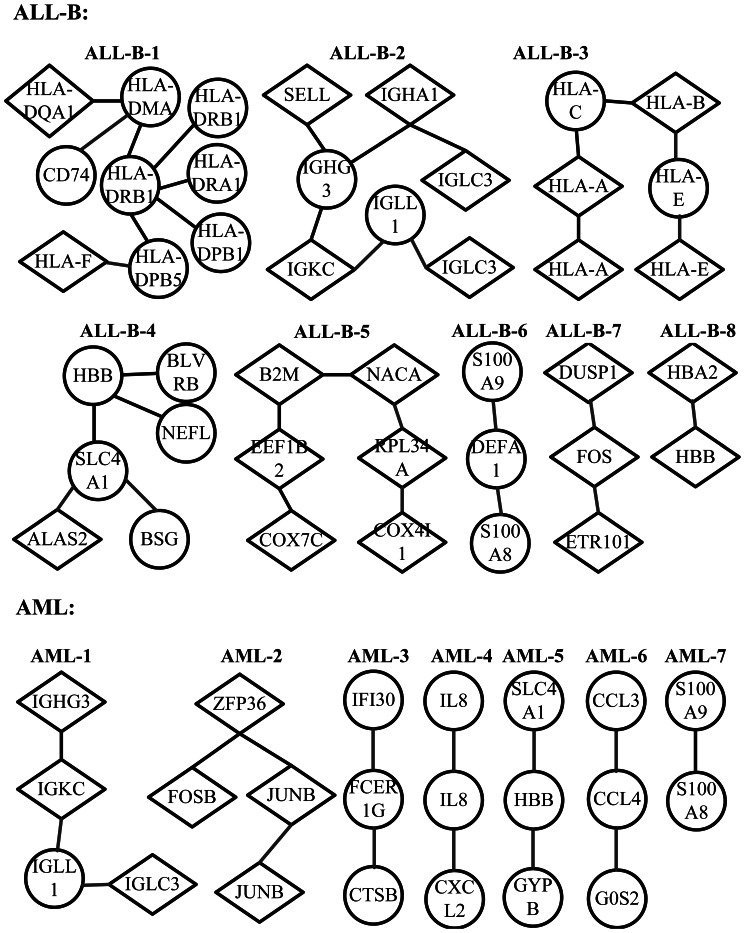
Figure 4 shows some example subnetworks based on the inverse scale matrices estimated by PMT-UC for ALL-B and AML. Each gene is labeled by its Gene Symbol. If the shape of the gene is circle, then it will have cluster-specific means, otherwise it will not have. For the ALL-T subtype, the related biomarkers identified by PMT-UC are all independent. It is shown that there are overlaps between some subnetworks corresponding to ALL-B and AML. However, these same genes interact with other different biomarkers under various cancer subtypes. Further more, the functional and biological relationships of the selected genes of each subnetwork are analyzed based on the GO annotation [41]. The P-value of a specific GO annotation is calculated using the hypergeometric distribution by the software GO::TermFinder [42]–[44]. Tables 6 and 7 list the GO analysis results for the subnetworks shown in Figure 4 of ALL-B and AML, respectively. The small P-value shows that the genes in each subnetwork have significant biological and functional correlation, and the common GO functions they share are often related to the subtypes of leukemia.
Figure 4. The subnetworks for ALL-B and AML of leukemia dataset estimated by PMT-UC.
Nodes represent human genes, and they are connected by a link if their partial correlation derived from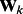 
is larger than 
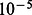. Each gene is labeled by its Gene Symbol (see Text S5 for the detailed information of the genes in each subnetwork). The shape of each node indicates whether the gene has cluster-specific means (circle) or not (diamond).
Table 6. The Gene Ontology results of the subnetwork for ALL-B of leukemia dataset.
| Subnetwork | Elements | GO Number | Ontology Description | P-value |
| ALL-B-1 | HLA-F HLA-DRB1 HLA-DRB5 | GO:0071556 | integral to lumenal side of endoplasmic | 1.1×10–20 |
| CD74 HLA-DPB1 HLA-DPA1 | reticulum membrane | |||
| HLA-DQA1 HLA-DRB1 | GO:0012507 | ER to Golgi transport vesicle membrane | 1.1×10–19 | |
| ALL-B-1 | CD74 HLA-DMA HLA-DRB1 | GO:0019886 | antigen processing and presentation of | 2.8×10–19 |
| HLA-DRB5 HLA-DPB1 HLA-DPA1 | exogenous peptide antigen via MHC class II | |||
| HLA-DQA1 HLA-DRB1 | GO:0005765 | lysosomal membrane | 6.4×10–18 | |
| ALL-B-2 | IGKC IGLC3 IGHG3 IGHA1 | GO:0003823 | antigen binding | 6.2×10–10 |
| ALL-B-2 | IGKC IGLC3 IGHG3 | GO:0006958 | complement activation, classical pathway | 1.6×10–6 |
| ALL-B-3 | The entire subnetwork | GO:0002474 | antigen processing and presentation | 1.3×10–10 |
| of peptide antigen via MHC class I | ||||
| ALL-B-4 | HBB SLC4A1 | GO:0015701 | bicarbonate transport | 6.8×10–6 |
| ALL-B-4 | ALAS2 BLVRB | GO:0042168 | heme metabolic process | 1.5×10–5 |
| ALL-B-4 | SLC4A1 NEFL | GO:0008022 | protein C-terminus binding | 8.0×10–5 |
| ALL-B-5 | EEF1B2 RPL35A | GO:0044444 | cytoplasmic part | 1.3×10–4 |
| ALL-B-5 | COX7C COX4I1 | GO:0004129 | cytochrome-c oxidase activity | 1.9×10–5 |
| ALL-B-6 | The entire subnetwork | GO:0050832 | defense response to fungus | 1.5×10–8 |
| GO:0042742 | defense response to bacterium | 1.1×10–5 | ||
| ALL-B-6 | S100A9 S100A8 | GO:0070488 | neutrophil leukocyte aggregation | 1.7×10–7 |
| GO:0002523 | leukocyte migration involved in inflammatory response | 3.7×10–6 | ||
| ALL-B-7 | DUSP1 FOS | GO:0051592 | response to calcium ion | 1.6×10–3 |
| GO:0051591 | response to cAMP | 1.6×10–3 | ||
| ALL-B-8 | The entire subnetwork | GO:0015671 | oxygen transport | 2.3×10–6 |
| GO:0031720 | haptoglobin binding | 2.1×10–8 | ||
| GO:0004601 | peroxidase activity | 4.3×10–5 |
The first column (Subnetwork) reports the name of the subnetwork introduced in Figure 4. The second column (Elements) presents the elements of subnetwork of which the functional and biological relationship are analyzed based on the GO annotation.
Table 7. The Gene Ontology results of the subnetwork for AML of leukemia dataset.
| Subnetwork | Elements | GO Number | Ontology Description | P-value |
| AML-1 | IGKC IGLC3 IGHG3 | GO:0006958 | complement activation, classical pathway | 1.6×10–6 |
| AML-2 | FOSB JUNB | GO:0071277 | cellular response to calcium ion | 4.3×10–5 |
| AML-3 | IFI30 FCER1G | GO:0019886 | antigen processing and presentation of | 2.0×10–4 |
| exogenous peptide antigen via MHC class II | ||||
| GO:0042590 | antigen processing and presentation of | 3.8×10–4 | ||
| exogenous peptide antigen via MHC class I | ||||
| AML-3 | FCER1G CTSB | GO:0009897 | external side of plasma membrane | 4.0×10–4 |
| AML-3 | IFI30 CTSB | GO:0043202 | lysosomal lumen | 6.2×10–5 |
| AML-4 | The entire subnetwork | GO:0008009 | chemokine activity | 1.4×10–5 |
| AML-5 | SLC4A1 HBB | GO:0015701 | bicarbonate transport | 6.1×10–6 |
| AML-6 | CCL3 CCL4 | GO:0031730 | CCR5 chemokine receptor binding | 1.6×10–7 |
| GO:0031726 | CCR1 chemokine receptor binding | 1.6×10–7 | ||
| AML-7 | The entire network | GO:0070488 | neutrophil leukocyte aggregation | 1.7×10–7 |
| GO:0002523 | leukocyte migration involved in inflammatory response | 3.7×10–6 |
The first column (Subnetwork) reports the name of the subnetwork introduced in Figure 4. The second column (Elements) presents the elements of subnetwork of which the functional and biological relationship are analyzed based on the GO annotation.
Specifically, for ALL-B, the smallest P-value is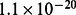 
corresponding to GO:0071556 which is related to integral to lumenal side of endoplasmic reticulum membrane. All the genes in the subnetwork ALL-B-1 except HLA-DMA share this common GO function, including HLA-DQA1 and HLA-F which do not have cluster-specific means. HLA-DMA has high correlation with the genes in the same subnetwork in term of GO:0019886 and GO:0042613. The first term is also reported to be a significant GO function for leukemia in [45], which shows the general importance of antigen presentation and antigen processing for ALL. The second term is shown to be related with B-cells [46]. The subnetwork ALL-B-2 contains all the elements of the subnetwork AML-1. The genes IGKC, IGLC3, IGHG3, IGHA1 share the common GO function GO:0003823 which is related with B cell receptor activity. In addition, the IGLL1 gene encodes Lambda5, a component of the pre-B cell receptor (pre-BCR) which plays an important role in acute lymphoblastic leukemia [47], [48]. The genes IGKC, IGLC3, IGHG3 shared by two subnetworks have the common GO function GO:0006958 which is inferred to be part of GO:0002443 (leukocyte mediated immunity). In ALL-B-2, SELL is also associated with leukocyte that mediates leukocyte rolling and leukocyte adhesion to endothelium at sites of inflammation [49]. The term GO:0002474 shared by the subnetwork ALL-B-3 is related to antigen presentation and has been reported to be highly statistically significant in subtypes of ALL [50].
Next, the subnetworks of which all the elements are not mean-based discriminative genes are taken account into. In subnetwork ALL-T-5, COX7C and COX4I1 which have common GO function cytochrome-c oxidase activity are indirectly connected by other elements. The genes are essential for maintaining the integrity of the subnetwork. HBB and HBA2 in ALL-T-8 have the function of binding with oxygen molecules and transporting them to the blood stream. They are shown to be correlated with various kinds of cancers [51]. The genes ZFP36, FOSB, JUNB belonging to AML-2 are transcription factors whose dysregulation is essential for leukemic stem cell function and that are targets for therapeutic interventions [52].
Biomarker identification
The gene selection results and biological meanings of the biomarkers selected by PMT-UC are presented in this section (see Text S6 for the detailed information of all the selected biomarkers). There are 210 genes selected as informative, including 161 mean-based discriminative genes. Most of identified biomarkers are considered to have diagnostic values for leukemia. For example, CST3 is identified as a validated target for investigating the basic biology of ALL and AML [53]. CD74 has been shown to be associated with B cell lymphocytic leukemia cell survival [54]. MPO is a lysosomal enzyme highly expressed in bone marrow cells and has been reported to be associated with risk of acute lymphoblastic leukemia [55]. TCL1A expression has been shown to delineate biological and clinical variability in B-cell lymphoma and can be regarded as a potential therapeutic target [56]. It has been shown that increased levels of LYZ in urine and serum are diagnostic indicators for some kinds of leukemia [57].
Unlike conventional penalized model-based clustering, our network-based gene selection criterion can implicate disease-related genes with low discriminative potential, such as MIF, ANP32B, METAP2, SOX4. MIF is shown to recognize the CD74 extracellular domain as a cell surface receptor, and also be associated with B cell lymphocytic leukemia cell survival as CD74 [54]. ANP32B is acted as a negative regulator for leukemic cell apoptosis and may serve as a potential therapeutic target for leukemia treatment [58], [59]. METAP2 has been detected to have high levels in B-cell acute lymphoblastic leukemia derived from germinal center B cells [60]. SOX4 has been proven to enable oncogenic survival signals in acute lymphoblastic leukemia recently [61].
Conclusions
A new robust penalized model-based network clustering for cancer subtype discovery, underlying network reconstruction and network-based biomarker identification is proposed. The multivariate Student’s t distribution used for the components of the mixture model results in robust clustering assignment. It permits a treatment of unconstrained covariance matrices to take gene dependencies into account. The network-based gene selection criterion we proposed can find the genes which have low discriminative potential, but interact with discriminative genes or have cluster-specific underlying network structures. This property is important for the discovery of disease-causing genes, because the phenotypic changes for some cancers do not regulate the level of expression.
The results for binary-clusters simulation studies have demonstrated the utility of the proposed method and its superior clustering and gene selection performance over penalized model-based Gaussian clustering with unconstrained covariance (PMG-UC) and penalized model-based Student’s t clustering with diagonal covariance (PMT-DC). Compared with PMG-UC, the network reconstruction results show that our algorithm can still discover the relationship between genes under the network even if the datasets have high noise.
The algorithm has been also applied for the analysis of a large data set consisting of leukemia cancer subtypes. The comparison of the clustering results for the three methods demonstrates that our method can handle the outliers and identify the cancer subtypes with different underlying networks or pathways. The most selected biomarkers have biological meanings and are proven to be related with leukemia. The functional and biological correlation of the genes in the same subnetwork is analyzed based on the GO annotation. The significant interaction between the genes can provide basis for the establishment of large relational network database.
Since the EM algorithm for PMT-UC is based on graphical lasso which is not feasible with high dimension, we need to apply preprocessing steps to filter some genes, which may result in the missing of the informative biomarkers. Therefore, in the future work, more efficient algorithms that can handle high-dimensional dataset are needed for the accuracy of gene selection. Moreover, the multiple-clusters simulation experiment indicates that PMT-UC should be used with caution when the dataset has more thin-tailed clusters of which some ones may do not have enough mean-based discriminative genes. The flexibility of PMT-UC may make it explain the extra clusters by fat tails. With the availability of genetic pathways or networks for genes under various conditions, we can incorporate these sources as prior information into building gene expression-based clustering and variable selection methods. They will facilitate the discovery of the true underlying clusters and biomarkers.
Supporting Information
The penalized log-likelihood of the complete data in the EM algorithm for PMT-UC.
(PDF)
Computation of the expectation of the penalized log-likelihood of the complete data for PMT-UC.
(PDF)
The updating estimate of the local parameter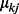 
.
(PDF)
The results for network reconstruction of the total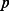 
genes of the simulated datasets.
(PDF)
The detailed information of genes in the subnetworks corresponding to B-cell ALL and AML for leukemia dataset.
(PDF)
The detailed information of all the leukemia-related biomarkers selected by PMT-UC.
(PDF)
Acknowledgments
We would like to thank the associate editor and the reviewers for careful review and insightful comments.
Funding Statement
Funding provided by National Science Foundation of China (90920007, 11171354), and the Ministry of Education of China (20120171110016). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Lee E, Chuang HY, Kim JW, Ideker T, Lee D (2008) Inferring pathway activity toward precise disease classification. PLoS Comput Biol 4: e1000217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Zhang J, Lu K, Xiang Y, Islam M, Kotian S, et al. (2012) Weighted frequent gene co-expression network mining to identify genes involved in genome stability. PLoS Comput Biol 8: e1002656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chuang HY, Lee E, Liu YT, Lee D, Ideker T (2007) Network-based classification of breast cancer metastasis. Mol Syst Biol 3. [DOI] [PMC free article] [PubMed]
- 4. Shen K, Rice SD, Gingrich DA, Wang D, Mi Z, et al. (2012) Distinct genes related to drug response identified in ER positive and ER negative breast cancer cell lines. PLoS One 7: e40900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Ng EKO, Li R, Shin VY, Jin HC, Leung CPH, et al. (2013) Circulating microRNAs as specific biomarkers for breast cancer detection. PLoS One 8: e53141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Li J, Lenferink AEG, Deng Y, Collins C, Cui Q, et al. (2012) Corrigendum: identification of high-quality cancer prognostic markers and metastasis network modules. Nat Commun 3: 655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Bentink S, Haibe-Kains B, Risch T, Fan JB, Hirsch MS, et al. (2012) Angiogenic mRNA and microRNA gene expression signature predicts a novel subtype of serous ovarian cancer. PLoS One 7: e30269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Chen LS, Hutter CM, Potter JD, Liu Y, Prentice RL, et al. (2010) Insights into colon cancer etiology via a regularized approach to gene set analysis of gwas data. Am J Hum Genet 86: 860–871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Mukherjee S, Hill SM (2011) Network clustering: probing biological heterogeneity by sparse graphical models. Bioinformatics 27: 994–1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Roy J, Winter C, Isik Z, Schroeder M (2012) Network information improves cancer outcome prediction. Brief Bioinform: In press. [DOI] [PubMed]
- 11. Taylor IW, Linding R, Warde-Farley D, Liu Y, Pesquita C, et al. (2009) Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat Biotechnol 27: 199–204. [DOI] [PubMed] [Google Scholar]
- 12. Glazko GV, Emmert-Streib F (2009) Unite and conquer: univariate and multivariate approaches for finding differentially expressed gene sets. Bioinformatics 25: 2348–2354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Wu MY, Dai DD, Shi Y, Yan H, Zhang XF (2012) Biomarker identification and cancer classification based on microarray data using laplace naive bayes model with mean shrinkage. IEEE/ACM Trans Comput Biol Bioinform 9: 1649–1662. [DOI] [PubMed] [Google Scholar]
- 14. Winter C, Kristiansen G, Kersting S, Roy J, Aust D, et al. (2012) Google goes cancer: improving outcome prediction for cancer patients by network-based ranking of marker genes. PLoS Comput Biol 8: e1002511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Barabási A, Gulbahce N, Loscalzo J (2011) Network medicine: a network-based approach to human disease. Nat Rev Genet 12: 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Kim J, Gao L, Tan K (2012) Multi-analyte network markers for tumor prognosis. PLoS One 7: e52973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Zhang XF, Dai DQ, Ou-Yang L, Wu MY (2012) Exploring overlapping functional units with various structure in protein interaction networks. PLoS One 7: e43092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Di Camillo B, Sanavia T, Martini M, Jurman G, Sambo F, et al. (2012) Effect of size and heterogeneity of samples on biomarker discovery: synthetic and real data assessment. PLoS One 7: e32200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Song WM, Di Matteo T, Aste T (2012) Hierarchical information clustering by means of topologically embedded graphs. PLoS One 7: e31929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Zhou H, Pan W, Shen X (2009) Penalized model-based clustering with unconstrained covariance matrices. Electron J Stat 3: 1473–1496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Pan W, Shen XT (2007) Penalized model-based clustering with application to variable selection. J Mach Learn Res 8: 1145–1164. [Google Scholar]
- 22. Xie B, Pan W, Shen X (2008) Penalized model-based clustering with cluster-specific diagonal covariance matrices and grouped variables. Electron J Stat 2: 168–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Murphy KP (2012) Machine learning: a probabilistic perspective. London: MIT Press.
- 24.Cozzini A, Jasra A, Montana G (2013) Model-based clustering with gene ranking using penalized mixtures of heavy-tailed distributions. J Bioinform Comput Biol : In press. [DOI] [PubMed]
- 25. Xie B, Pan W, Shen X (2010) Penalized mixtures of factor analyzers with application to clustering high-dimensional microarray data. Bioinformatics 26: 501–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Banerjee O, El Ghaoui L, d’Aspremont A (2008) Model selection through sparse maximum likelihood estimation for multivariate gaussian or binary data. J Mach Learn Res 9: 485–516. [Google Scholar]
- 27. Friedman J, Hastie T, Tibshirani R (2008) Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9: 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Lee H, Lee DS, Kang H, Kim BN, Chung MK (2011) Sparse brain network recovery under compressed sensing. IEEE Trans Med Imaging 30: 1154–1165. [DOI] [PubMed] [Google Scholar]
- 29. Zou H (2006) The adaptive lasso and its oracle properties. J Am Stat Assoc 101: 1418–1429. [Google Scholar]
- 30. Fan J, Feng Y, Wu Y (2009) Network exploration via the adaptive LASSO and SCAD penalties. Ann Appl Stat 3: 521–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Series B 39: 1–38. [Google Scholar]
- 32. Peel D, McLachlan GJ (2000) Robust mixture modelling using the t distribution. Stat Comput 10: 339–348. [Google Scholar]
- 33. Candés EJ, Wakin MB, Boyd SP (2008) Enhancing sparsity by reweighted l 1 minimization. J Fourier Anal Appl 14: 877–905. [Google Scholar]
- 34. Banfield JD, Raftery AE (1993) Model-based Gaussian and non-Gaussian clustering. Biometrics 49: 803–821. [Google Scholar]
- 35.McLachlan GJ, Peel D (2000) Finite mixture models. New York: Wiley-Interscience.
- 36. Baek J, McLachlan GJ (2011) Mixtures of common t-factor analyzers for clustering highdimensional microarray data. Bioinformatics 27: 1269–1276. [DOI] [PubMed] [Google Scholar]
- 37. Frühwirth-Schnatter S, Pyne S (2010) Bayesian inference for finite mixtures of univariate and multivariate skew-normal and skew-t distributions. Biostatistics 11: 317–336. [DOI] [PubMed] [Google Scholar]
- 38. Tadesse MG, Sha N, Vannucci M (2005) Bayesian variable selection in clustering high-dimensional data. J Am Stat Assoc 100: 602–617. [Google Scholar]
- 39. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, et al. (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286: 531–537. [DOI] [PubMed] [Google Scholar]
- 40. Dudoit S, Fridlyand J, Speed TP (2002) Comparison of discrimination methods for the classification of tumors using gene expression data. J Am Stat Assoc 97: 77–87. [Google Scholar]
- 41. Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, et al. (2000) Gene ontology: tool for the unification of biology. Nat Genet 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Yang WH, Dai DQ, Yan H (2011) Finding correlated biclusters from gene expression data. IEEE Trans Knowl Data Eng 23: 568–584. [Google Scholar]
- 43. Boyle EI, Weng S, Gollub J, Jin H, Botstein D, et al. (2004) TermFinder-open source software for accessing gene ontology information and finding significantly enriched gene ontology terms associated with a list of genes. Bioinformatics 20: 3710–3715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Zhang XF, Dai DD, Li XX (2012) Protein complexes discovery based on protein-protein interaction data via a regularized sparse generative network model. IEEE/ACM Trans Comput Biol Bioinform 9: 857–870. [DOI] [PubMed] [Google Scholar]
- 45. Alexa A, Rahnenführer J, Lengauer T (2006) Improved scoring of functional groups from gene expression data by decorrelating GO graph structure. Bioinformatics 22: 1600–1607. [DOI] [PubMed] [Google Scholar]
- 46. de Matos Simoes R, Tripathi S, Emmert-Streib F (2012) Organizational structure and the periphery of the gene regulatory network in B-cell lymphoma. BMC Syst Biol 6: 38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Nahar R, Müschen M (2009) Pre-B cell receptor signaling in acute lymphoblastic leukemia. Cell Cycle 8: 3874–3877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Payne KJ, Dovat S (2011) Ikaros and tumor suppression in acute lymphoblastic leukemia. Crit Rev Oncog 16: 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Kansas GS, Ley K, Munro JM, Tedder TF (1993) Regulation of leukocyte rolling and adhesion to high endothelial venules through the cytoplasmic domain of L-selectin. J Exp Med 177: 833–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Shand JC, Jansson J, Hsu YC, Campbell A, Mullen CA (2010) Differential gene expression in acute lymphoblastic leukemia cells surviving allogeneic transplant. Cancer Immunol Immunother 59: 1633–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Pau Ni IB, Zakaria Z, Muhammad R, Abdullah N, Ibrahim N, et al. (2010) Gene expression patterns distinguish breast carcinomas from normal breast tissues: the Malaysian context. Pathol Res Pract 206: 223–228. [DOI] [PubMed] [Google Scholar]
- 52. Steidl U, Rosenbauer F, Verhaak RGW, Gu X, Ebralidze A, et al. (2006) Essential role of Jun family transcription factors in PU. 1 knockdown–induced leukemic stem cells. Nat Genet 38: 1269–1277. [DOI] [PubMed] [Google Scholar]
- 53. Sakhinia E, Faranghpour M, Liu Yin JA, Brady G, Hoyland JA, et al. (2005) Routine expression profiling of microarray gene signatures in acute leukaemia by real-time PCR of human bone marrow. Br J Haematol 130: 233–248. [DOI] [PubMed] [Google Scholar]
- 54. Shachar I, Haran M (2011) The secret second life of an innocent chaperone: the story of CD74 and B cell/chronic lymphocytic leukemia cell survival. Leuk Lymphoma 52: 1446–1454. [DOI] [PubMed] [Google Scholar]
- 55.Krajinovic M, Sinnett H, Richer C, Labuda D, Sinnett D (2001) Role of NQO1, MPO and CYP2E1 genetic polymorphisms in the susceptibility to childhood acute lymphoblastic leukemia. Int J Cancer Suppl 97: 230–236. [DOI] [PubMed]
- 56. Aggarwal M, Villuendas R, Gomez G, Rodriguez-Pinilla SM, Sanchez-Beato M, et al. (2008) TCL1A expression delineates biological and clinical variability in B-cell lymphoma. Mod Pathol 22: 206–215. [DOI] [PubMed] [Google Scholar]
- 57. Osserman EF, Lawlor DP (1966) Serum and urinary lysozyme (muramidase) in monocytic and monomyelocytic leukemia. J Exp Med 124: 921–952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Yu Y, Shen SM, Zhang FF, Wu ZX, Han B, et al. (2012) Acidic leucine-rich nuclear phosphoprotein 32 family member B (ANP32B) contributes to retinoic acid-induced differentiation of leukemic cells. Biochem Biophys Res Commun 423: 721–725. [DOI] [PubMed] [Google Scholar]
- 59. Shen SM, Yu Y, Wu YL, Cheng JK, Wang LS, et al. (2010) Downregulation of ANP32B, a novel substrate of caspase-3, enhances caspase-3 activation and apoptosis induction in myeloid leukemic cells. Carcinogenesis 31: 419–426. [DOI] [PubMed] [Google Scholar]
- 60. Klener P, Szynal M, Cleuter Y, Merimi M, Duvillier H, et al. (2006) Insights into gene expression changes impacting B-cell transformation: cross-species microarray analysis of bovine leukemia virus tax-responsive genes in ovine B cells. J Virol 80: 1922–1938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Ramezani-Rad P, Geng H, Hurtz C, Chan LN, Chen ZS, et al. (2013) SOX4 enables oncogenic survival signals in acute lymphoblastic leukemia. Blood 121: 148–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The penalized log-likelihood of the complete data in the EM algorithm for PMT-UC.
(PDF)
Computation of the expectation of the penalized log-likelihood of the complete data for PMT-UC.
(PDF)
The updating estimate of the local parameter .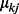
(PDF)
The results for network reconstruction of the total 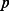genes of the simulated datasets.
(PDF)
The detailed information of genes in the subnetworks corresponding to B-cell ALL and AML for leukemia dataset.
(PDF)
The detailed information of all the leukemia-related biomarkers selected by PMT-UC.
(PDF)