Evolution of Topological Surface States in Antimony Ultra-Thin Films

Abstract

Based on an inverted bulk band order, antimony thin films presumably could become topological insulators if quantum confinement effect opens up a gap in the bulk bands. Coupling between topological surface states (TSS) from opposite surfaces, however, tends to degrade or even destroy their novel characters. Here the evolution and coupling of TSS on Sb(111) thin films from 30 bilayers down to 4 bilayers was investigated using in-situ Fourier-transform scanning tunneling spectroscopy and density functional theory computations. On a 30-bilayer sample, quasi-particle interference patterns are generated by the scattering of TSS from the top surface only. As the thickness decreases, inter-surface coupling degrades spin polarisation of TSS and opens up new wavevector-dependent scattering channels, resulting in spin degenerate states in most part of the surface Brillouin zone, whereas the TSS near the zone centre exhibit little inter-surface coupling, so they remain spin-polarised without opening a gap at the Dirac point.

Recent experimental¹,²,³,⁴,⁵ and theoretical⁶,⁷,⁸ works have demonstrated that topological surface states (TSS) support massless spin-polarised Dirac fermions due to a strong spin-orbit coupling effect. They are robust and immune to backscattering by non-magnetic defects because of protection by time-reversal symmetry⁹. Unlike the Dirac fermions in graphene with pseudospin texture, the real helical spin polarization TSS exhibit has been widely studied by surface-sensitive experiments such as angle-resolved photoemission spectroscopy (ARPES), scanning tunneling microscopy (STM) and scanning tunneling spectroscopy (STS) as summarized in recent review articles¹⁰,¹¹. TSS are attractive not only in fundamental condensed matter physics for realising novel entities such as dyons¹², imaging magnetic monopoles¹³ and Majorana fermions¹²,¹⁴, but also in practical applications in spintronics and error-tolerant quantum computing. Motivated by such perspective, special attention has been focused on thin films hosting TSS suitable for device applications. Therefore, three-dimensional (3D) topological insulator (TI) thin films approaching 2D limit have been explored. Theoretical calculations predict that an energy gap can be opened at the Dirac point by inter-surface coupling¹⁵. Some of these films may exhibit quantum spin Hall effect as that observed in HgTe quantum wells¹⁶,¹⁷. Experimental studies on Bi₂Se₃¹⁸,¹⁹ and Bi₂Te₃²⁰ confirm the existence of a thickness-dependent bandgap. However, the detail of inter-surface coupling effect, especially the intermediate state between weak and strong coupling of surface states (SS) from two surfaces, still needs to be interrogated. From topological nontrivial to trivial phases, interesting transformation must take place progressively as the overlap of electron wave functions on two surfaces increases with reducing film thickness.

Here we investigate the inter-surface coupling issue in antimony (Sb), which has a rhombohedral crystal structure and can be considered as a stacking of (111) bilayers (BL, 1 BL = 3.75 Å). There are several reasons to study Sb(111) films. Firstly, as the “parent” of the first-generation 3D TI Bi_1−xSb_x²¹, although bulk Sb is semimetal due to its negative indirect bandgap, its band order is inverted at the L point of the Brillouin zone. Sb(111) has been confirmed to possess TSS, leading to the absence of 180° backscattering and exotic transmission through atomic steps²². Next, the strongly distorted TSS Dirac cone on Sb(111) yields various scattering channels in QPI patterns, from which TSS dispersion and spin information can be extracted. Measuring the patterns at different film thickness helps us understand how the spin texture evolves as inter-surface coupling varies. Thirdly, a thin film with a large surface-to-volume ratio can make surface effect more observable. Lastly, compared with well-studied compound TIs such as Bi₂Se₃, Sb thin films provide a single-element simple system for demonstrating topological properties without much influence of residual bulk carriers from self-doping states²,⁴,²³ or spatial fluctuations of charge and potential²⁴. Therefore, by using Fourier-transform scanning tunneling spectroscopy (FT-STS), we measure the quasi-particle interference (QPI) patterns of TSS on thick and thin Sb(111) films. Combining with density functional theory (DFT) calculations, we aim to identify the scattering features in the patterns generated by the intra- and inter-surface couplings of TSS, and to examine the dependence of the couplings on film thickness and wavevector k.

Results

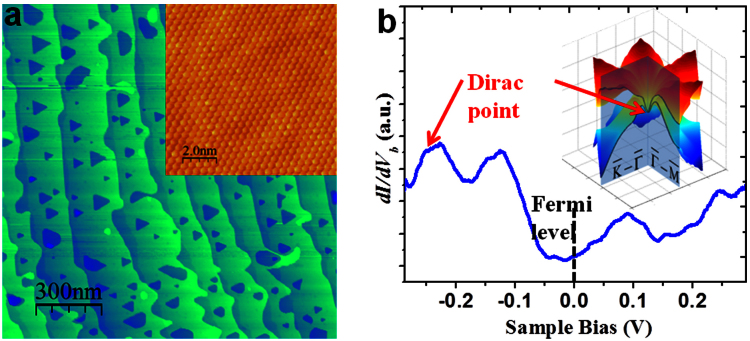
We grew Sb films on Si(111)-√3 × √3:Bi-β surface in an ultrahigh vacuum (UHV) chamber²⁵,²⁶,²⁷,²⁸. Shown in Figure 1a is a STM image of an Sb(111) film of thickness ~30 BL. Steps here are all 3.75 Å corresponding to 1 BL of Sb(111). The atomic resolution image in the inset exhibits the hexagonal lattice on the (111) surface. In Fig. 1b, a typical differential tunneling conductance dI/dV_b spectrum, where V_b is sample bias voltage and I the tunneling current, is displayed to reveal the local density of states (LDOS) of electrons in certain energy range. Unlike Bi₂Se₃ and Bi₂Te₃, Sb(111) has a strongly distorted TSS Dirac cone, with its lower part bowing up rapidly near 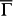point of the first surface Brillouin zone (SBZ) before bending down to merge with bulk valence bands, as shown schematically in Fig. 1b inset. Several extraordinary features of Sb(111) show up starting from the Dirac point E_D at E ≈ −240 meV (with the Fermi energy E_F at E = 0), which have also been confirmed by previous ARPES measurements¹,²⁹. The specific dispersion of TSS on Sb(111) allows us to determine E_D being at the appearance E of QPI patterns²²,³⁰.

Figure 1. Atomic and electronic structures on Sb(111).

(a) STM image of 30 BL Sb(111) film grown on Si(111)-√3 × √3:Bi-β. Imaging conditions: V_b = −3 V, I = 50 pA. The inset shows the atomic-resolution image of Sb(111) surface (V_b = 1 V, I = 250 pA). The period is about 4.31 Å. (b) dI/dV_b spectrum taken on 30-BL Sb(111) surface. The inset shows the schematic SS bands forming a Dirac point at 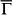on Sb(111). By cutting the bands with vertical planes passing 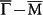and 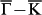axes, the dispersions lines of SS along these high symmetry directions can be obtained.

For TSS, it is generally accepted that, without magnetic field or magnetic impurities, scattering between states must obey spin conservation. That is, the scattering intensity P from a state of wavevector k and spin S to another state of 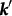and 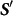depends on 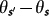, the angle between S and 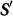, as⁵,³⁰

STS can detect the amplitude modulation of LDOS due to the scattering of momentum transfer vector 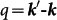⁵,³¹. After Fourier transform, the real-space modulations can be visualised as a distribution of q in the k-space, offering us information of the SS involved in scatterings and even their spin alignment at a given E. Hence, the dI/dV_b maps on 30-BL Sb(111), which can be regarded as the bulk surface, were taken under different V_b. Above E ≈ −240 meV, 6-fold symmetric patterns with dominating intensity along the 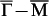direction can be identified in the FT-STS power spectra. Fig. 2a shows the coexistence of atomic structure and QPI patterns, while Fig. 2b gives its Fourier transform, which also contains both the contributions from atomic lattice (the outer 6 reciprocal lattice points) and QPI pattern near 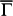at the centre. The hexagon marks the first SBZ.

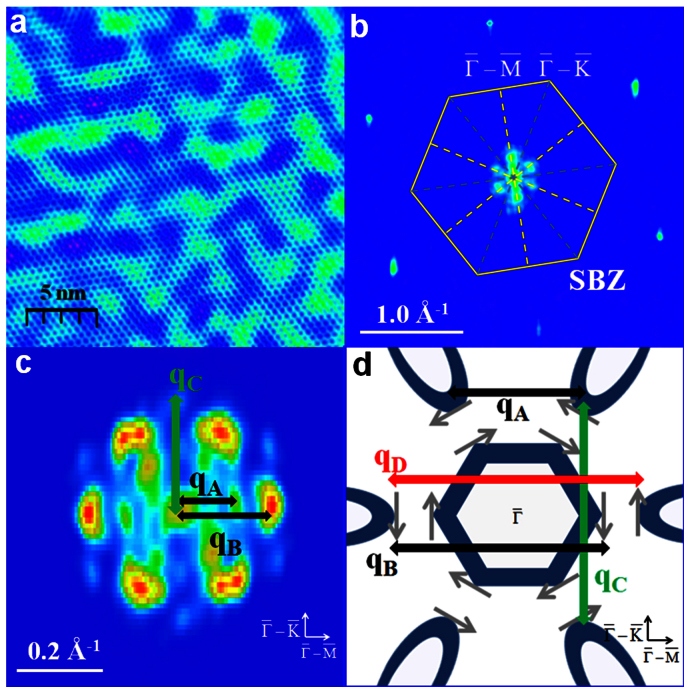
Figure 2. QPI patterns of TSS on 30-BL Sb(111).

(a) Real-space dI/dV_b map in an area of 20 nm × 20 nm taken at V_b = 40 mV, I = 120 pA. (b) Fourier transform of (a), consisting of six strong peaks along 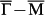. The first SBZ (yellow hexagon) and high symmetry directions are marked. (c) FT-STS pattern around 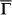with three observable scattering vectors q_A, q_Band q_C. It was taken on a 40 nm × 40 nm area at V_b = 20 mV. (d) Schematic of CEC as well as the spin texture around 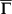, which has a central electron pocket and six hole pockets. The small grey arrows represent the spin directions. q_Aand q_B are allowed scattering vectors, while q_C is low in probability and q_D totally forbidden.

The QPI patterns are our main concern. Starting at E ≈ −40 meV, a set of spots mainly along 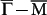and 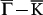appear. We use the pattern at E = 20 meV in Fig. 2c as an example to investigate the origins of these spots marked with scattering vectors q_A, q_B and q_C. From the schematic constant energy contour (CEC) in Fig. 2d with the spin texture²³, one can find that q_A along 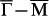represents the scattering between neighbouring hole pockets, and q_Bis that between the hole edge and the electron pocket edge across 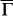. The q_Ascattering has a spin misalignment of 60°, giving a spin probability factor of ¾, while the spins are nearly parallel for the q_B, giving a probability of 1. These two scattering channels are both observed along 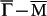in Fig. 2c with the q_Aintensity weaker than that of q_B. The q_C scattering along between the next-nearest-neighbor hole pockets with = 120°, has a probability of ¼, yielding an even weaker intensity. The q_D scattering between two hole pockets across 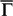, however, is totally forbidden due to antiparallel spins of two relevant states.

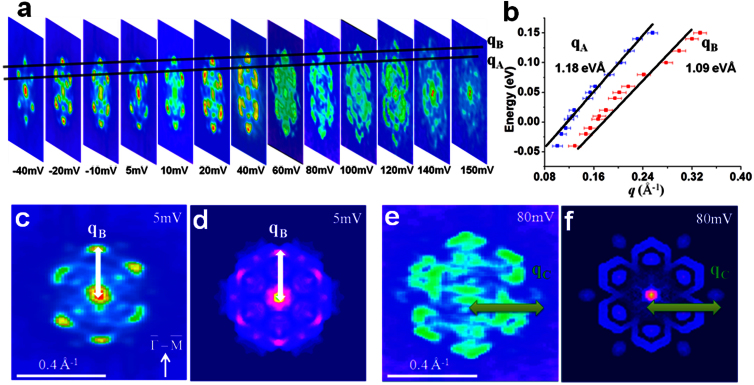
In Fig. 3a, a series of FT-STS patterns for E from −40 meV to 150 meV are displayed. Based on the magnitude of q plotted as a function of E in Fig. 3b, the dispersions of q_A and q_B are approximately linear with slopes of 1.18 eVÅ and 1.09 eVÅ, respectively. These values are close to those reported in previous STS²² and ARPES studies¹. Similar dispersions have also been obtained from our QPI patterns taken near step edges, confirming that scattering only takes place between TSS with similar spin directions. Moreover, the observed QPI patterns can be compared with DFT computational data. A QPI pattern at certain E can be simulated based on the CEC and spin texture from DFT computations as well as the spin factor given by equation (1). We re-plot the experimental QPI patterns together with the simulation patterns for E = 5 meV and 80 meV in Fig. 3c–f. Comparing the corresponding patterns, one can find a few common features. Firstly, the dominating scattering vectors q_B along 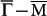appear as bright spots in all cases. Secondly, the spots centred at q_B spread more in the direction transverse to 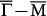at 80 meV than at 5 meV. Thirdly, the relative weak q_C spots along 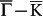become more visible at 80 meV than at 5 meV. The agreement between experimental and computational results on these key features confirms that the QPI patterns acquired on such a “thick” Sb(111) film are generated by spin-polarized TSS only on the top surface.

Figure 3. Scattering vectors in QPI patterns on 30-BL Sb(111).

(a) FT-STS maps of the same area taken at V_b from −40 mV to 150 mV are selected to extract the dispersion relationship. Each map shows two sets of scattering vectors corresponding to q_A and q_B, respectively. (b) The dispersions of q_A and q_B extracted from (a). Here the error bar corresponds to 0.05π Å⁻¹, which is determined by (2π/40) nm⁻¹. (c),(d) FT-STS mapping taken at 5 mV and the corresponding simulation pattern based on DFT computational data. (e),(f) Measured and simulated FT-STS patterns at 80 mV. q_Band q_Care marked for comparison with Fig. 2c–d.

When Sb(111) film is thin enough, however, the TSS on the top and bottom surfaces will couple eventually. It is normally believed that a gap will open up at the Dirac point and the Dirac cone will turn into Dirac hyperbola when the coupling is significant¹⁵,¹⁸. In order to gain insight into how the thickness affects the band structure, and furthermore, the coupling of SS from two surfaces, we examined a 9-BL Sb(111) film. Interestingly, according to DFT calculations, at this thickness, the coupling of states at 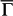is not strong enough to open a gap yet, but the inter-surface coupling of states elsewhere in k-space is already significant as revealed by FT-STS mapping. Shown in Fig. 4a is the QPI pattern on 9-BL Sb(111) at E = 20 meV. Compared with the 30-BL sample, a few changes are obvious in the pattern. Firstly, besides intensity mostly along 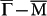in the 30 BL case, here comparable intensity along 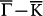can also be seen. Secondly, instead of discrete q for 30-BL Sb, 12 lobes of continuous intensity with clear cutoff vectors labeled as q_Eand q_F along 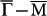and 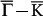, respectively, are observable on 9-BL Sb, indicating new scattering channels are effective.

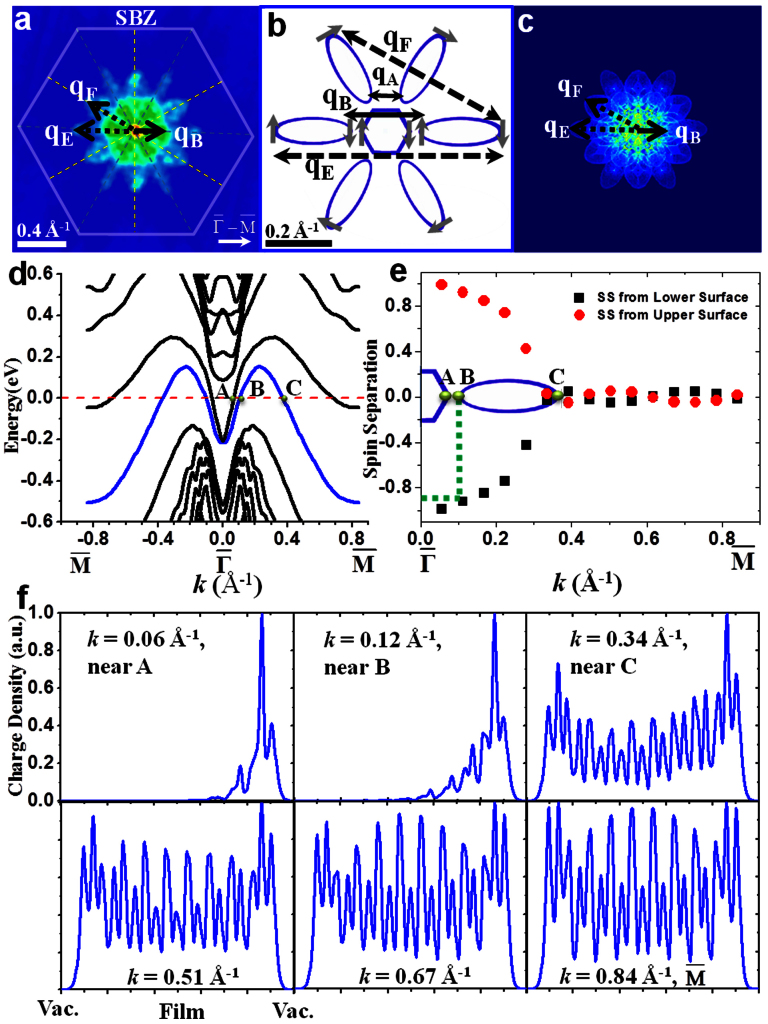
Figure 4. QPI patterns reveal strongly inter-surface coupling of TSS in 9-BL Sb(111).

(a) A representative FT-STS mapping at 20 mV. Two cutoff vectors marked as q_Eand q_F are both shown as black dashed arrows. (b) q_Eand q_F in the calculated CEC at E_F. The grey arrows illustrate the spin directions of TSS on the top surface of a thick film. Intra-surface scatterings q_Aand q_B still exist and they correspond to the central green zone with high intensities in (a). (c) The corresponding simulated QPI pattern based on DFT calculations. (d) DFT-computation band structure of 9-BL Sb(111) along 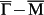. The blue lines represent the SS band chosen for computing the spin separation. (e) Spin separation as a function of k, indicating strong k-dependent inter-surface coupling of SS. A, B and C are the intersection points of CEC at E_F with k axis along 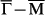. (f) The real-space distributions of SS from near 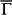to 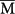obtained from DFT computations, showing that a well-defined localization of SS around 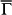but large penetration depth for states from 0.34 Å⁻¹ to .

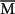Discussion

Now we discuss the origins of these new scattering channels on 9-BL Sb. Notice the scale difference between Fig. 2c and Fig. 4a. The new intensity lobes in Fig. 4a have q lengths longer than those in Fig. 2c. Specifically, the lengths of the cutoff vectors q_Eand q_F (both shown as dash-line arrows) are 0.63 Å⁻¹ and 0.54 Å⁻¹, respectively, whereas q_C = 0.25 Å⁻¹ in Fig. 2c. The q_E/q_Flength ratio takes a unique value 1.17 in the measured energy range. For comparison, the calculated CEC at E_F is shown in Fig. 4b, with superficial spin directions labeled as grey arrows assuming the upper surface separated far from the lower one. The new scattering channels are also marked in Fig. 4b, with q_E between the outer edges of opposite hole pockets along 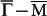, and q_F between the outer edges of next-nearest-neighbor hole pockets. Such assignments yield a 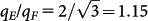, in agreement with the measured ratio. These scatterings, especially q_E, however, seem to violate spin conservation based on the superficial spin texture.

Different from thick film case, the two surfaces of 9-BL film are separated not far from each other, so a SS is no long confined to one surface. Now, it is possible for an electron in state k on one surface to scatter into a state 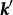with the same spin on the opposite surface. In another viewpoint, for a thick Sb(111) film, there is one TSS Dirac cone on each surface. With time-reversal and inversion symmetries, a pair of SS of a particular k are degenerate in energy but with opposite spin. They do not couple noticeably with each other since their wave functions overlap little. In a thin Sb(111) film, the coupling becomes strong if wave function overlap is significant, yielding mixing states with their spin only partially polarized or even totally degenerate. This opens up new scattering channels without violating spin conservation. Therefore, quite different from the 30-BL film where the patterns mainly originate from the so-called “intra-surface scattering”, here the QPI patterns include “inter-surface scattering”. On the other hand, the intensities in inner hexagonal zone in Fig. 4a corresponding to q_Aand q_B scatterings marked in Fig. 4b are stronger than those of q_E and q_F. This part overlaps closely with the QPI patterns on the 30-BL sample, demonstrating significant contribution from intra-surface scattering. This two-part pattern clearly shows the coexistence of intra- and inter-surface scattering events.

Based on DFT computation results of CEC and spin texture near E_F, we simulated the QPI pattern as shown in Fig. 4c, which is in good agreement with our experimental pattern in Fig. 4a. First of all, the characteristic outer lobes of comparable intensities along 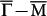and are reproduced in the simulation pattern. Secondly, the core part of the simulated pattern has stronger intensity along 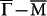, which is consistent with out observation that “intra-surface scattering” is still nontrivial. It is also worth noting that the experimental patterns were taken at 4.2 K with a 5 mV peak-to-peak modulation added to V_b, which results in an energy resolution ΔE ≈ 4.5 meV³². If this energy window is considered, the dots and arcs in the simulation pattern should be smeared out to continuous features similar to those in Fig. 4a.

Besides new features in QPI patterns, following the procedure described by Bian et al.³³,³⁴, the spin separation of SS can be defined and evaluated for our 9 BL Sb(111) film. In Fig. 4d, the electronic states in the 9 BL film obtained with DFT computation are plotted along 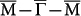. The SS bands remain cross each other at 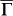, i.e., the Dirac point is intact. Due to quantum confinement effect, an indirect bandgap of ~0.3 eV can be observed for the bulk bands in Fig. 4d. Simple estimation based on bulk band parameters³⁵ gives a bandgap ~0.53 eV, whereas Zhang et al. get a value of 0.25 eV in their computations³⁶. The calculated spin separation as a function of k along 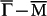for the SS bands is plotted in Fig. 4e, where the limiting values ±1 represent full spin polarization whereas 0 represents total spin degenerate. At 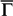, the states are fully spin-polarized, but the spin separation decreases quickly as k moves from 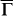towards 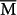, and it vanishes at k = 0.34 Å⁻¹. This k point is closer to 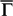than the total spin degenerate point of 20-BL Sb(111)³³, indicating that a stronger inter-surface coupling reduces spin polarization of SS.

On the other hand, the variation of spin separation shown in Fig. 4e implies a non-uniform degree of inter-surface coupling, which should depend on the SS penetration depth. The calculated real-space distributions of SS in the film normal direction are plotted in Fig. 4f for six k points of the lower SS band along 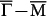. It is obvious that around 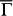the SS are well localized near the surface, so the inter-surface coupling is weak. In contrast, as k approaches 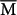, the SS become more spread over the thickness, so the coupling is stronger.

To correlate the above computational results with the observed QPI patterns, we overlay the CEC at E_F on the spin separation plot in Fig. 4e. The three points marked as A, B and C correspond to the intersections of E_F with the SS bands. The states near point B with k ≈ 0.12 Å⁻¹ are involved in the q_B scatterings in Fig. 2c and d. These states have spin separation of about ±0.9, and they are localized near surface based on Fig. 4f, so they largely maintain the character of TSS. The states at point C with k ≈ 0.34 Å⁻¹ are basically spin degenerate and spread over the whole thickness of 9 BL film. According to our DFT computations, the states at this k value in the 30 BL film exhibit SS character with a penetration depth λ ~ 5.7 BL (for comparison, λ ~ 1 BL at k = 0.12 Å⁻¹). In the 9 BL film, with such a λ value, the states originated at two surfaces can couple strongly due to significant overlap in the interior, losing TSS character. These states can scatter with any other states at the CEC of the hole pockets without violating spin conservation, resulting in the outer lobes of continuous intensity terminating at q_Eand q_F in Fig. 4a. The wave functions for the states with k ≥ 0.34 Å⁻¹ in Fig. 4f have quite large magnitude both at the surface and in the film centre. Since the magnitude does not decay when moving from film interior to the surface, these states should be considered as surface resonance states instead of quantum well states (QWSs)³⁷. QWSs derived from the bulk states, with their wave functions decaying significantly from film interior to the surface, are readily observable with ARPES³³, but they seem to contribute weakly as diffused background intensity in FT- STS QPI patterns. We explain this in terms of different surface sensitivity in these two methods. The photoelectrons detected in ARPES come from the top ~1–3 atomic layers of the sample whereas STS detects electronic states at ~3–10 Å above the top atomic layer.

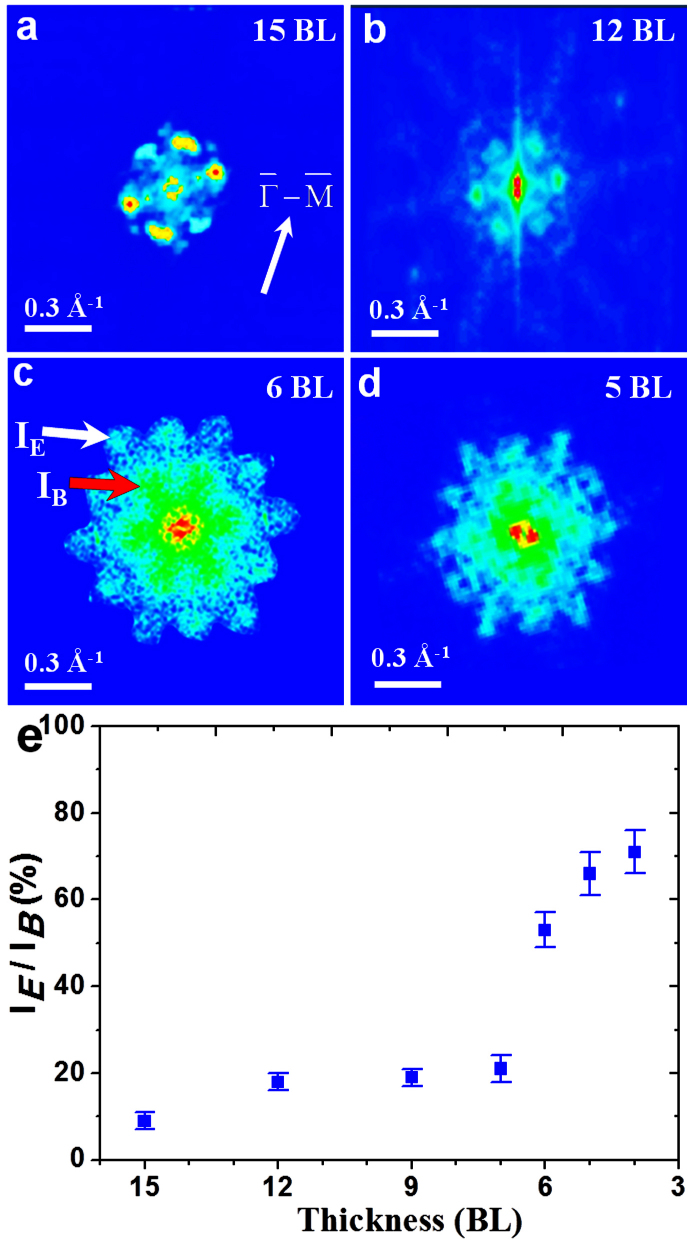
Along 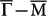, the solid- and dot-line arrows in Fig. 4a denote the end points of scattering vector q_B due to intra-surface coupling and q_E due to inter-surface coupling, respectively. The ratio of intensities at these points, I_E/I_B, in FT-STS patterns is a quantitative measure of the relative strength of intra- and inter-surface coupling. In order to analyze the thickness dependence of inter-surface coupling, we took FT-STS patterns at E = 20 meV for Sb(111) films with thickness in 4–15 BL range. In Fig. 5, the FT-STS patterns for 15, 12, 6 and 5 BL samples are displayed. The measured I_E/I_B as a function of film thickness is plotted in Fig. 5e. It shows that I_E is almost absent in 15 BL sample, and it increases as film thickness reduces from 15 to 5 BL. This monotonic trend unambiguously confirms the evolutionary process of diminishing spin polarization from thick to ultrathin films.

Figure 5. Film thickness dependence of relative strength of intra- and inter-surface couplings of TSS.

(a–d) FT-STS patterns taken on 15, 12, 6, 5 BL Sb(111), respectively. The red and green arrows mark the position of I_B due to intra-surface coupling and I_E due to inter-surface coupling. (e) Plot of I_E/I_B as a function of film thckness.

The inter-surface coupling of TSS in Bi₂Se₃ thin films has been studied both theoretically and experimentally¹⁵,¹⁸. There, the most remarkable effect is the opening of a bandgap at 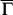for the TSS. Comparing to Sb(111), the TSS on Bi₂Se₃(111) form a fairly ideal Dirac cone with rather weak warping in the bulk bandgap⁶,⁸, so they can be considered as true surface states. Sb(111) has a highly warped Dirac cone. The SS not far from 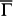penetrate quite deep into the interior, and they almost behave as surface resonance states. In 9-BL Sb(111), the inter-surface coupling of these states makes them locate more near the film centre than at the surfaces. The spin splitting of SS due to the Rashba effect, which depends on the overall potential gradient ∇V the electrons experience, is greatly reduced. To the extreme, for those states with k ≥ 0.5 Å⁻¹ in Fig. 4f with wave functions totally symmetric about the film centre, the overall ∇V = 0, so the spin polarisation is completely lost. Therefore, our results demonstrate that SS spin polarization diminishes not only with decreasing film thickness, but even more dramatically with k moving from 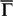to .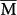

Although not an ideal TI, Sb(111) ultrathin films allow us to investigate the extraordinary scatterings between SS with nearly parallel spin directions, while in other TIs (e.g. Bi₂Se₃) possessing an ideal Dirac cone it is hard to get similar features exclusively between SS. The “distorted” Dirac cone and dramatic k-dependent penetration depth of SS in Sb thin films offer us an interesting quasi-2D system to help interpret the detailed evolution of coupling and hybridization of TSS. The dramatic change in QPI patterns with film thickness indicates that the intra- and inter-surface coupling of TSS dominates in the thick and thin film cases, respectively. The inter-surface coupling of TSS in a “thin” film shows strong k-dependence. The tuneability of relative contributions of intra- and inter-surface scatterings by changing thickness can be further explored for tailoring the surface energetic and transport properties for potential applications.

Methods

The experiments are carried out in a UHV LT-STM system. The base pressure is better than 1 × 10⁻¹⁰ Torr. Clean Si(111)-7 × 7 surface is prepared by degassing at 500°C overnight, a briefing annealing at 850°C and finally flashing at 1200°C for ~1 min. The Si(111)-√3 × √3:Bi-β surface serving as the substrate for Sb film growth in this work is prepared with 2-ML Bi deposition on Si(111)-7 × 7 at room temperature followed by annealing at ~450°C for 15 min. Bi and Sb deposition fluxes are generated from Ta boats loaded with high purity (99.999%) source materials. Prior to the deposition, the evaporators are degassed at appropriate temperature for a few hours in order to remove contaminations. Bi deposition flux is calibrated by measuring the coverage and thickness of Bi(110) films on Si(111). 1 ML of Bi(110) represents 9.3 × 10¹⁴ atom/cm². Sb is deposited on Si(111)-√3 × √3:Bi-β at 100°C to form (111)-oriented thin films with thickness from 4 BL to >30 BL. All STM images are acquired at 77 K or 4.2 K. The dI/dV_b spectra are acquired at 4.2 K using a lock-in amplifier with a modulation voltage at a frequency of 700 Hz and a peak-to-peak amplitude of 5 mV. The dI/dV_b mapping for FT-STS is normally taken in a square area of edge length ~25–40 nm, without any atomic step and other defect in the area.

First-principles DFT-based electronic structure calculations are performed using the VASP package³⁸ with a plane wave basis and a 5 × 5 k-point sampling of the Brillouin zone. In all calculations, generalized gradient approximation (GGA) in Perdew-Burke-Ernzerhof (PBE) format³⁹ and spin-orbital coupling are included. The neighbouring Sb(111) film slabs are separated with a 10-Å vacuum region along the [111] direction.

Author Contributions

G.Y., Y.P.F. and W.X. carried out the experiments; G.Y., Z.L., Y.P.F., W.X. and X.-S.W. analyzed the data; Z.L. and Y.P.F. carried out the theoretical calculations. Y.P.F. and X.-S.W. assisted in the theoretical analysis. G.Y. and X.-S.W. prepared the manuscript.