Youden index and Associated Cut-points for Three Ordinal Diagnostic Groups

Summary

Directly relating to sensitivity and specificity and providing an optimal cut-point which maximizes overall classification effectiveness for diagnosis purpose, the Youden index has been frequently utilized in biomedical diagnosis practice. Current application of the Youden index is limited to two diagnostic groups. However, there usually exists a transitional intermediate stage in many disease processes. Early recognition of this intermediate stage is vital to open an optimal window for therapeutic intervention. In this paper, we extend the Youden index to assess diagnostic accuracy when there are three ordinal diagnostic groups. Parametric and nonparametric methods are presented to estimate the optimal Youden index, the underlying optimal cut-points and the associated confidence intervals. Extensive simulation studies covering representative distributional assumptions are reported to compare performance of the proposed methods. A real example illustrates the usefulness of the Youden index in evaluating discriminating ability of diagnostic tests.

1 Introduction

The ROC (Receiver Operating Characteristic) curve has been popularly used in biomedical research to graphically illustrate the sensitivity (Se) versus 1-specificity (1-Sp) of a diagnostic test along a sequence of cut-points when there are two populations, usually healthy and diseased. Area under the ROC (AUROC) curve is the summary index from ROC curve analysis representing the global discriminative ability of a diagnostic test across all possible cut-points. The independence of cut-point property can sometimes become a disadvantage. For instance, when two markers have crossing ROC curves, it indicates that one marker performs better at some of the cut-points while the other marker appears superior at others. AUROC cannot differentiate such two markers if they happen to have an equal AUROC. For remedy, partial area under the curve has been recommended to calculate the area under curve restricted to some sensitivity or specificity region of interest (Zhang et. al., 2002 and references therein). Because of its lack of direct link to a specific pair of sensitivity and specificity, AUROC can be a rather abstract index for clinicians to understand and compute. Furthermore, an optimal cut-point which is required for diagnosis purpose is not straightforwardly available. Instead, separate computation after AUROC calculation is needed to derive an optimal cut-point, which is chosen in practice either to achieve arbitrarily preferred specificity and sensitivity, to equate sensitivity to specificity (Greiner et al, 1995) or to be closest to the perfect classification coordinate (0,1) (Grainer et al, 2000; Kitaharaa et al, 1999; Perkins and Schisterman, 2006).

In contrast, the Youden index not only summarizes the discriminatory accuracy of a diagnostic test but also provides a ready-to-use optimal cut-point for the purpose of future diagnosis. The Youden index was defined (Youden, 1950) as J(t) = Se(t) + Sp(t) −1, essentially a combinatory index of sensitivity and specificity at a cut-point t. Practically, this definition renders a maximum value of one when a diagnostic test provides a perfect separation between two populations and a minimum of zero when it classifies no better than chance. An optimal cut-point t^*, which maximizes J, i.e., t^* = argmax_t J(t) can be derived. The resulting Youden index which maximizes the overall effectiveness of a diagnostic test will be taken as the summary measure for a test’s discriminatory ability. The optimality (in the sense of overall correct classification) of t^* has been discussed in Perkins and Schisterman (2006) in comparison to the optimal cut-point from ROC curve analysis. The Youden index and cut-points for two groups has been extensively investigated in statistical literatures (Hilden and Glasziou, 1996; Fluss et al., 2005; Perkins and Schisterman, 2005, 2006; Schisterman and Perkins, 2007).

An intermediate transitional stage usually exists prior to disease onset in many disease processes. Due to the irreversible nature of most diseases, early recognition of the transitional stage will enable timely therapeutic intervention. A good diagnostic test which discriminates all three diagnostic groups will be valuable for medical practice. Current statistical research largely focuses on two-class diagnostic problems. A three-class diagnostic test is often handled as a multiple two-class problem, especially for the purpose of finding optimal cut-points (Mossman, 1999; Landgrebe and Duin, 2007). The ROC surface, a natural extension of ROC curve, has been proposed for three-group diagnostic tests while the volume under ROC surface (VUS) is taken as the global measure summarizing a test’s discriminative power (Ferri et al., 2003; Nakas et al., 2004; Xiong et al., 2006, Li and Zhou, 2009, and reference therein). As a summary measure over a whole spectrum of sensitivities and specificities, VUROC still suffers similar drawbacks as the AUROC. The Youden index for three ordinal groups, generalized from its counterpart for two populations, can overcome some of the drawbacks associated with the VUROC. In this paper, we aim to define and estimate the Youden index to rate a diagnostic test for three ordinal groups and contribute practically useful computation tools to facilitate its application in medical diagnosis. The definition of Youden index for three ordinal diagnostic groups is provided in Section 2. Parametric and non-parametric estimators to the Youden index and the optimal cut-points and their variances will be investigated under a variety of distributional assumptions in Section 3 and 4. We will compare the performance of the estimators through an extensive simulation study in Section 5. Section 6 illustrates a real example. Finally, we conclude the paper with a discussion.

2 The Youden index for three ordinal diagnostic groups

We assume that there are three ordered diagnostic groups based on the severity of a disease. Let D⁺, D⁰, and D⁻ and denote the diseased (i.e., the positive condition) group, the intermediate group (early stage/very mildly diseased), and the healthy (i.e., the negative condition) group, respectively. It is also assumed that a continuous diagnostic test (T) is measured in all the groups, under the convention that higher values of test result are associated with greater severity of the disease (when the association is opposite, negated test result can be used as a diagnostic marker). Let P_i be the probability density and F_i be the corresponding absolutely continuous and strictly increasing cumulative distribution function (CDF) of the test in group, Dⁱ, i =+, 0, −. Ideally, a pair of thresholds and t₋ and t₊, t₋ < t₊, exist for a diagnostic test to differentiate subjects among the three ordinal diagnostic groups. An intuitive decision rule is then to diagnose the subjects whose test results fall below t₋ into D⁻ and those with test results above t₊ to D⁺. The remaining subjects whose test results fall between t₋ and t₊ will be classified into the intermediate group D⁰. The probabilities of correctly classifying patients from the three groups are individually defined as: Sp(t₋)=P₋(T≤t₋)=F₋(t₋), Se(t₊) = P₊ (T≥t₊)=1−F₊(t₊), and Sm(t₋,t₊) = P₀(t₋≤T≤t₊)=F₀(t₊)−F₀(t₋). The Youden index which evaluate the diagnostic accuracy of a test marker for three ordinal groups can be thereafter defined as the sum of the three correct classification probabilities,

$$J(t_{-},t_{+})=\frac{1}{2}[Sp(t_{-})+Sm(t_{-},t_{+})+Se(t_{+})-1]=\frac{1}{2}[F_{-}(t_{-})-F_0(t_{-})+F_0(t_{+})-F_{+}(t_{+})]$$ (1)

We will suppress the dependence of the Youden index on the cut-points and abbreviate it as J later on. An optimal pair of cut-points ($t_{-}^{*},t_{+}^{*}$) can be derived by maximizing J among all possible pairs. The Youden index attained at this pair is reported as the overall diagnostic accuracy of a test,$J^{*}=J(t_{-}^{*},t_{+}^{*})$. The Youden index defined in Equation (1) falls in the practically useful range of 0~1. When a test assigns a patient to the three ordinal groups by chance, J becomes zero. When a test leads to a perfect separation among the three groups, J attains one. Further, the Youden index for three ordinal diagnostic groups is invariant under monotonic transformations on a diagnostic test (and the matching cut-points).

3 Point Estimates of the Optimal Cut-points and the Youden index

3.1 Parametric Estimates

Under the assumption of normality, P_i, i = +,0, − takes the density function of an independent normal distribution N(μ_i, σ_i) with mean μ_i, and standard deviation (SD)σ_i. Without loss of generality, we assume μ₋ <μ₀ < μ₊. Let Φ(x) denote the cumulative distribution function (CDF) of a standard normal distribution. We have,

$$Sp(t_{-})=\mathrm{\Phi }(\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}}),Se(t_{+})=1-\mathrm{\Phi }(\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}}),Sm(t_{-},t_{+})=\mathrm{\Phi }(\frac{t_{+}-{\mu }_0}{{\sigma }_0})-\mathrm{\Phi }(\frac{t_{-}-{\mu }_0}{{\sigma }_0})$$

Thus, the Youden index under the normal distribution assumption is expressed as,

$$J(t_{-},t_{+})=\frac{1}{2}\{[\mathrm{\Phi }(\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}})-\mathrm{\Phi }(\frac{t_{-}-{\mu }_0}{{\sigma }_0}])+[\mathrm{\Phi }(\frac{t_{+}-{\mu }_0}{{\sigma }_0})-\mathrm{\Phi }(\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}})]\}$$ (2)

The optimal pair of cut-points is subsequently obtained by taking partial derivatives of the above equation with respect to t₋ and t₊ separately and then setting both partial derivatives to zero:

$$\{\begin{array}{c}{t}_{-}^{*}=\frac{({\mu }_0{\sigma }_{-}^2-{\mu }_{-}{\sigma }_0^2)-{\sigma }_{-}{\sigma }_0\sqrt{{({\mu }_{-}-{\mu }_0)}^2+({\sigma }_{-}^2-{\sigma }_0^2)\text{ln}(\frac{{\sigma }_{-}^2}{{\sigma }_0^2})}}{{\sigma }_{-}^2-{\sigma }_0^2}\hfill \\ t_{+}^{*}=\frac{({\mu }_{+}{\sigma }_0^2-{\mu }_0{\sigma }_{+}^2)-{\sigma }_0{\sigma }_{+}\sqrt{{({\mu }_0-{\mu }_{+})}^2+({\sigma }_0^2-{\sigma }_{+}^2)\text{ln}(\frac{{\sigma }_0^2}{{\sigma }_{+}^2})}}{{\sigma }_0^2-{\sigma }_{+}^2}\hfill \end{array}$$ (3)

The negatively valued second derivative evaluated at the solution warrants that J achieves the maximum.

In the presence of equal group variances between D⁻ and D⁰ or/and between D⁰ and D⁺, the average of the pair of group means serves as the optimal cut-point,

$$t_{-}^{*}=\frac{{\mu }_{-}+{\mu }_0}{2}\text{or}/\text{and}{t}_{+}^{*}=\frac{{\mu }_0+{\mu }_{+}}{2}.$$

A diagnostic test may also follow gamma distributions with the group density functions $f(T;{\alpha }_i,{\beta }_i)=\frac{{\beta }_i^{{\alpha }_i}}{\mathrm{\Gamma }({\alpha }_i)}{T}^{{\alpha }_i-1}{e}^{-{\beta }_{i}T},i=+,0,-$. Let a = β₀ − β₋, b = α₋ − α₀ and c = α₋ ln(β₋) − α₀ ln(β₀) + ln(Γ(α₀)) −ln(Γ(α₋)). The closed-form solution for the lower optimal cut-point is $\text{exp}\{-lambertW(\frac{a}{b}{e}^{\frac{c}{b}})-\frac{c}{b}\}$, where the function lambertW(z) denotes the solution w satisfying we^w = z (Corless et al, 1996). The upper optimal cut-point has the same exponential expression but requires simultaneous substitution of α₀ and β₀ by α₊ and β₊, α₋ and β₋ by α₀ and β₀ in the expressions of a, b and c. If the three shape parameters (α_i) are all equivalent to α, the solutions for the optimal cut-points are simplified: $t_{-}^{*}=\alpha \frac{\text{ln}({\beta }_0)-\text{ln}({\beta }_{-})}{{\beta }_0-{\beta }_{-}}$ and $t_{+}^{*}=\alpha \frac{\text{ln}({\beta }_{+})-\text{ln}({\beta }_0)}{{\beta }_{+}-{\beta }_0}$. The resulting optimal Youden index can be calculated by using the gamma CDF functions in Equation (1). Setting α =1 supplies the solutions for exponentially distributed diagnostics tests. Estimates on the optimal cut-points and the optimal Youden index under normal and gamma distributions can be obtained by substituting the relevant parameters by their maximum likelihood estimates (MLE). Under a more general distribution assumption, application of characteristic function can be adopted (Vexler, Schisterman and Liu, 2008) but will not be investigated in the paper.

When normality is not justified, Box-Cox transformation has been frequently implemented to approximate normality (Vexler, Liu, Eliseeva and Schisterman, 2008). The Box-Cox transformation transforms a positively-valued random variable x monotonically to y through the function g: y = g(x,λ), which has the format of $y=\frac{x^{\lambda }-1}{\lambda }\text{for}\lambda \ne 0$ and the limit distribution under λ →0 leads to the log-transformation approximation, i.e., y = log(x) for λ = 0. When there are three ordinal diagnostic groups, the estimate of λ can be obtained by maximizing the overall profile log-likelihood (see Appendix) through numerical optimization algorithms.

3.2 Nonparametric Estimates

Imposing no distributional assumptions, we can estimate the optimal cut-points and the Youden index non-parametrically. The CDFs F_i, i = +,0, − can be estimated either empirically or by means of kernel smoothing (Silverman, 1986) on the basis of observed data. Fluss et al. (2005) have applied both approaches to estimating the Youden index for two populations. Denote the sample size for group Dⁱ, i = +,0,− as n_i and the test measurement of the j^th subject in the i^th diagnostic group as $x_j^{(i)}$. The empirical CDFs of the test for the three groups are estimated by,${\widehat{F}}_i(t)=\frac{1}{n_i}{\displaystyle \sum _{j=1}^{n_i}I(x_j^{(i)}\le t)},i=+,0,-$, where I(u≤t) is the indicator function returning 1 if the condition in the parenthesis holds true and 0 otherwise. With a pre-chosen kernel density function K(x) and a bandwidth h (a positive number), the group density functions can be estimated by ${\widehat{P}}_i(T=t)=\frac{1}{n_i}{\displaystyle \sum _{j=1}^{n_i}\frac{1}{h_i}K(\frac{t-x_j^{(i)}}{h_i}})$, i= +,0,−. The choice on K(x) is mostly not crucial and Gaussian kernel has been a popular choice for convenience (Wasserman, 2005). The bandwidth (h) is critical to control the degree of smoothness. Notice that we allow a different bandwidth h_i for each of the three groups. The “Normal reference rule” as in Fluss et al. (2005) can be utilized (with typos corrected): $h_i=1.06n_i^{-0.2}\text{min}\{{\widehat{\sigma }}_i,\frac{IQ{R}_i}{1.34}\}$ with IQR_i denoting the inter-quartile range of sample measurements in group Dⁱ, i=+,0,−. Besides, a popular data-based bandwidth selection method—Sheather-Jones (SJ) direct plug-in algorithm (Sheather and Jones, 1991; Sheather & Jones, 1992) can also be used. We refer readers to Loader (1999) for more details on bandwidth selection. The utilization of Gaussian kernel smoothing leads to the estimates of the group CDFs, ${\widehat{F}}_i(t)=\frac{1}{n_i}{\displaystyle \sum _{j=1}^{n_i}\mathrm{\Phi }(\frac{t-x_j^{(i)}}{h_i}}),i=+,0,-$.

Plugging in the empirical or the Gaussian kernel smoothing CDF estimates into Equation (1) gives the Youden index estimators for three ordinal groups under the two nonparametric approaches separately as following,

$$\widehat{J}(t_{-},t_{+})=\frac{1}{2}[\frac{1}{n_{-}}{\displaystyle \sum _{j=1}^{n_{-}}I(x_j^{(-)}\le t_{-})-\frac{1}{n_0}{\displaystyle \sum _{j=1}^{n_0}I(x_j^{(0)}\le t_{-})}}+\frac{1}{n_0}{\displaystyle \sum _{j=1}^{n_0}I(x_j^{(0)}\le t_{+})}-\frac{1}{n_{+}}{\displaystyle \sum _{j=1}^{n_{+}}I(x_j^{(+)}\le t_{+})}]$$

$$\widehat{J}(t_{-},t_{+})=\frac{1}{2}[\frac{1}{n_{-}}{\displaystyle \sum _{j=1}^{n_{-}}\mathrm{\Phi }(\frac{t_{-}-x_j^{(-)}}{h_{-}}})-\frac{1}{n_0}{\displaystyle \sum _{j=1}^{n_0}\mathrm{\Phi }(\frac{t_{-}-x_j^{(0)}}{h_0}})+\frac{1}{n_0}{\displaystyle \sum _{j=1}^{n_0}\mathrm{\Phi }(\frac{t_{+}-x_j^{(0)}}{h_0}})-\frac{1}{n_{+}}{\displaystyle \sum _{j=1}^{n_{+}}\mathrm{\Phi }(\frac{t_{+}-x_j^{(+)}}{h_{+}}})]$$

The optimal pair of cut-points for the above two nonparametric estimates of the Youden index can not be analytically derived. Therefore, numerical optimization algorithms have to be employed for solutions.

4 Confidence intervals for the Optimal Youden index and Cutoffs Points

4.1 Parametric Confidence Intervals

Notice that, under the normal distributions, the parametric estimates of the optimal pair of cut-points and the Youden index are functions of sample means and SDs (μ̂₋, μ̂₀, μ̂₊ and σ̂₋, σ̂₀, σ̂₊) from three independent normal distributions and it is well known that the sample mean and sample SD of a normal distribution are independent. By multivariate delta method, asymptotic variances of the optimal cut-points and the optimal Youden index can be calculated by the following equations,

$$Var({\widehat{t}}_{-}^{*})={(\frac{\partial t_{-}^{*}}{\partial {\mu }_{-}})}^{2}Var({\widehat{\mu }}_{-})+{(\frac{\partial t_{-}^{*}}{\partial {\mu }_0})}^2\text{var}({\widehat{\mu }}_0)+{(\frac{\partial t_{-}^{*}}{\partial {\sigma }_{-}})}^{2}Var({\widehat{\sigma }}_{-})+{(\frac{\partial t_{-}^{*}}{\partial {\sigma }_0})}^{2}Var({\widehat{\sigma }}_0)$$ (4)

$$Var({\widehat{t}}_{+}^{*})={(\frac{\partial t_{+}^{*}}{\partial {\mu }_0})}^2\text{var}({\widehat{\mu }}_0)+{(\frac{\partial t_{+}^{*}}{\partial {\mu }_{+}})}^{2}Var({\widehat{\mu }}_{+})+{(\frac{\partial t_{+}^{*}}{\partial \sigma 0})}^{2}Var({\widehat{\sigma }}_0)+{(\frac{\partial t_{+}^{*}}{\partial {\sigma }_{+}})}^{2}Var({\widehat{\sigma }}_{+})$$ (5)

$$Var({\widehat{J}}^{*})={(\frac{\partial J}{\partial {\mu }_{-}})}^{2}Var({\widehat{\mu }}_{-})+{(\frac{\partial J}{\partial {\mu }_{+}})}^{2}Var({\widehat{\mu }}_{+})+{(\frac{\partial J}{\partial {\mu }_0})}^{2}Var({\widehat{\mu }}_0)+{(\frac{\partial J}{\partial {\sigma }_{-}})}^{2}Var({\widehat{\sigma }}_{-})+{(\frac{\partial J}{\partial {\sigma }_{+}})}^{2}Var({\widehat{\sigma }}_{+})+{(\frac{\partial J}{\partial {\sigma }_0})}^{2}Var({\widehat{\sigma }}_0)$$ (6)

The estimates of the optimal cut-points and the Youden index are asymptotically unbiased and normally distributed. Therefore, a (1−α)×100% confidence interval (CI) for these parametric estimates can be obtained as ${\widehat{t}}_{-}^{*}\pm z_{\alpha /2}\sqrt{Var({\widehat{t}}_{-}^{*})},{\widehat{t}}_{+}^{*}\pm z_{\alpha /2}\sqrt{Var({\widehat{t}}_{+}^{*})},{\widehat{J}}^{*}\pm z_{\alpha /2}\sqrt{Var({\widehat{J}}^{*})}$ respectively, where z_α/2 represents the α/2 quantile of a standard normal. Meanwhile, $t_{-}^{*}$ and $t_{+}^{*}$ are not independent of each other due to their common dependence on μ₀ and σ₀. The covariance of the two estimates is thus derived by Taylor expansion as:

$$Cov({\widehat{t}}_{-}^{*},{\widehat{t}}_{+}^{*})=\frac{\partial t_{-}^{*}}{\partial {\mu }_0}\frac{\partial t_{+}^{*}}{\partial {\mu }_0}\text{var}({\widehat{\mu }}_0)+\frac{\partial t_{-}^{*}}{\partial {\sigma }_0}\frac{\partial t_{+}^{*}}{\partial {\sigma }_0}\text{var}({\widehat{\sigma }}_0)$$ (7)

The variances of the sample estimates of the normal parameters are well known (Patel and Read, 1996):

$$Var({\widehat{\mu }}_i)=\frac{1}{n_i}{\sigma }_i^2,Var({\widehat{\sigma }}_i)=\frac{1}{2(n_i-1)}{\sigma }_i^2,i=+,0,-$$ (8)

The partial derivatives involved in Equations (4) to (7) are presented in the Appendix. Substituting the variances of normal parameter estimates (Equation (8)) and the partial derivatives (Appendix) accordingly, we can obtain the asymptotic variance and covariance on the estimated optimal cut-points as well as the variance on the estimated optimal Youden index. The corresponding estimates can be calculated by plugging in the normal sample means and variances together with the optimal cut-point estimates.

4.2 Nonparametric Confidence Intervals

Closed-form solutions to estimate the optimal cut-points and Youden index from nonparametric approaches are not available. However, bootstrap basic quantile CIs can be computed: repeatedly draw a set of bootstrap samples, derive estimates on $t_{-}^{*},t_{+}^{*}$ and J^* from each set of bootstrap samples and finally calculate the corresponding α/2 and 1 − α/2 quantile as the lower and upper bound on the estimators respectively. A bootstrap confidence interval can be established for each proposed estimators in the paper, both parametric and non-parametric.

5 Simulation Studies

In three simulation scenarios, a diagnostic test is assumed to individually follow a normal, a log-normal or a gamma distribution. We examined in each scenario the performance of the proposed approaches: normal distribution---labeled as N, normal approximation via Box-Cox transformation---TN, empirical CDF method---EMP and kernel smoothing method with application of the normal reference rule and the Sheather-Jones algorithm for bandwidth---KS and KS-SJ separately. Table 1 displays the simulation parameters including the normal mean and SD (μ_i, σ_i, i=+,0,−) used for the Normal and Log-normal scenario and the shape and scale parameters (α_i, β_i, i=+,0,−) for the Gamma scenario. Normal/gamma parameters for the D⁻ and D⁰ group, as well as the SD (σ₊) and gamma shape parameter (α₊) for D⁺, were pre-specified while the mean and the gamma scale parameter for D⁺ (also given in Table 1) were estimated to attain a given J. We chose J to be (0.5, 0.6, 0.7, 0.8) since this is a practical range for a useful biomedical marker in three-group screening. An equal sample size of 20, 50, 100 and 200 is used for the three groups, to resemble the usual size of biomedical datasets in reality. The underlying true pair of optimal cut-points ($t_{-}^{*},t_{+}^{*}$) are also listed in Table 1. The R function “optim” with the box-constrained BFGS optimization method (Byrd et al, 1995) was used for searching the optimal cut-points in the non-parametric estimators and R package “KernSmooth” was used for implementation of SJ bandwidth calculation.

Table 1.

Parameters used for simulation scenarios. For the Log-Normal scenario, normal mean and SD parameters are shown. Detailed simulation procedures are described in Section 5.

Scenario	μ−	σ−	μ0	σ0	σ+	μ+, (or β+), t−*, t+* corresponding to J
							J=0.5	J=0.6	J=0.7	J=0.8
Normal	6	1	8	1.2	1.4	μ+	9.2031	10.0019	11.0544	13.3606
						t−*	7.0174	7.0174	7.0174	7.0174
						t+*	8.7649	9.0520	9.4941	10.5224
Log-Normal	2.5	0.45	3.5	0.6	1	μ+	4.0855	4.6033	5.2408	6.4315
						t−*	3.0046	3.0046	3.0046	3.0046
						t+*	4.1066	4.1618	4.3203	4.7019
Gamma	α-=2	β-=50	α0=2	β0=12	α+=2	β+	6.2756	4.0100	2.2150	0.6550
						t−*	0.0751	0.0751	0.0751	0.0751
						t+*	0.2265	0.2744	0.3453	0.5127

5.1 Simulation Results on J^*, $t_{-}^{*}$ and $t_{+}^{*}$ and estimations

For each scenario, 1000 datasets were independently simulated to estimate J^*, $t_{-}^{*}$ and $t_{+}^{*}$ and from each proposed method. The resulting estimations were compared in terms of bias and root mean square error (RMSE). Simulation results on J^* are shown in Table 2. At a fixed Youden index, all methods exhibit a decreasing trend in both bias and RMSE as the sample size increases under each simulation scenario. Interestingly, the two kernel smoothing estimators (both bandwidth choices) usually underestimate the Youden index while the others generally show positive biases. A similar negative bias phenomenon with the kernel smoothing estimator is also found in the Youden index for two populations (Fluss et al., 2005). The two bandwidth selection choices (normal reference rule and SJ algorithm) often result in similar performance across all scenarios though subtle superiority is observed in the latter. Unsurprisingly, when data are truly from normal, N performs the best with the smallest bias and RMSE and TN provides almost indistinguishable results. Biases resulting from kernel smoothing estimators on a normally distributed test marker are comparatively the largest among all the methods though the RMSEs at J=20 are smaller than EMP and comparable elsewhere; The Log-Normal scenario caters to the TN method. As expected, TN stands out in terms of both bias and RMSE, but with a small margin in RMSEs compared with the nonparametric estimators. KS estimators are better than EMP from both bias and RMSE though EMP produces smaller biases at large sample sizes (e.g., 200) and/or large J (J =0.7 and 0.8). In comparison, N is the worst method with the largest biases and RMSEs under the greatly skewed distribution; In the Gamma scenario, KS-SJ and TN are competitors for the best performer. KS-SJ is superior to TN at small sample sizes or/and small J while TN performs subtly better at J=0.8 and the sample size of 200. EMP can results in smaller RMSE than KS at J=0.8. Under moderate deviation from normality, N behaves the worst. Surprisingly, N noticeably outperforms the other methods at J=0.8 in the gamma scenario with the smallest RMSEs.

Table 2.

Point estimate simulation on J^*. Bias and RMSE on the optimal Youden index (J^*) estimation from five methods (N, TN, EMP, KS, KS-SJ) based on 1000 simulated datasets.

Scenario	# obs	20				50				100				200
	J	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8
Normal	Bias
	N	0.00547	0.00409	0.00265	0.00068	0.00256	0.00151	0.00047	−0.00037	0.00070	0.00033	−0.00006	−0.00046	−0.00016	−0.00025	−0.00031	−0.00024
	TN	0.00478	0.00389	0.00214	−0.00122	0.00267	0.00226	0.00112	−0.00066	0.00144	0.00137	0.00093	0.00005	0.00039	0.00041	0.00034	0.00018
	EMP	0.02178	0.02038	0.02213	0.02038	0.00928	0.00887	0.00814	0.00683	0.00481	0.00408	0.00386	0.00350	0.00244	0.00223	0.00222	0.00210
	KS	−0.02854	−0.03879	−0.04268	−0.03111	−0.02955	−0.03710	−0.03981	−0.02935	−0.02648	−0.03218	−0.03363	−0.02441	−0.02242	−0.02656	−0.02746	−0.01988
	KS-SJ	−0.02399	−0.03419	−0.03814	−0.02766	−0.02769	−0.03526	−0.03812	−0.02823	−0.02547	−0.03133	−0.03287	−0.02388	−0.02184	−0.02603	−0.02701	−0.01960
	RMSE
	N	0.06392	0.06294	0.05868	0.05048	0.04190	0.04104	0.03812	0.03253	0.02970	0.02909	0.02693	0.02292	0.02068	0.02015	0.01856	0.01580
	TN	0.06485	0.06386	0.05979	0.05209	0.04236	0.04151	0.03857	0.03322	0.03035	0.02967	0.02742	0.02329	0.02093	0.02036	0.01871	0.01592
	EMP	0.08457	0.08133	0.07500	0.06210	0.05593	0.05362	0.04961	0.04062	0.04028	0.03812	0.03485	0.02901	0.02837	0.02681	0.02420	0.02041
	KS	0.07250	0.07749	0.07664	0.06225	0.05359	0.05806	0.05803	0.04578	0.04207	0.04553	0.04501	0.03482	0.03227	0.03489	0.03451	0.02657
	KS-SJ	0.07225	0.07652	0.07522	0.06141	0.05305	0.05731	0.05729	0.04526	0.04215	0.04557	0.04498	0.03481	0.03236	0.03496	0.03455	0.02662
Log- Normal	Bias
	N	0.09082	0.06199	0.01187	−0.05147	0.09178	0.05494	−0.00088	−0.06736	0.09076	0.05128	−0.00628	−0.07370	0.08937	0.04821	−0.01039	−0.07831
	TN	0.00370	0.00422	0.00378	0.00141	0.00247	0.00221	0.00148	0.00015	0.00049	0.00054	0.00034	−0.00022	−0.00028	−0.00023	−0.00017	−0.00017
	EMP	0.01990	0.01858	0.01768	0.01865	0.00797	0.00481	0.00525	0.00599	0.00349	0.00175	0.00146	0.00344	0.00073	0.00048	0.00009	0.00111
	KS	0.00843	−0.00222	−0.02557	−0.05953	0.00454	−0.00442	−0.02710	−0.05881	0.00229	−0.00414	−0.02389	−0.05280	0.00119	−0.00292	−0.01979	−0.04616
	KS-SJ	0.00717	0.00122	−0.01440	−0.04123	0.00290	−0.00038	−0.01305	−0.03585	0.00019	−0.00104	−0.00999	−0.02866	−0.00091	−0.00092	−0.00696	−0.02194
	RMSE
	N	0.11239	0.08060	0.04833	0.07049	0.10085	0.06394	0.03171	0.07553	0.09552	0.05676	0.02553	0.07852	0.09181	0.05140	0.02147	0.08105
	TN	0.06586	0.06470	0.05984	0.05052	0.04304	0.04216	0.03890	0.03262	0.03056	0.02992	0.02757	0.02301	0.02125	0.02072	0.01894	0.01577
	EMP	0.08223	0.08307	0.07532	0.06393	0.05364	0.05278	0.04918	0.04080	0.03887	0.03821	0.03525	0.02866	0.02782	0.02692	0.02442	0.02011
	KS	0.06822	0.06060	0.05950	0.07806	0.04555	0.04020	0.04461	0.06740	0.03376	0.03006	0.03540	0.05782	0.02387	0.02145	0.02713	0.04911
	KS-SJ	0.06941	0.06373	0.05717	0.06496	0.04587	0.04248	0.03889	0.04827	0.03404	0.03161	0.02908	0.03697	0.02439	0.02272	0.02075	0.02751
Gamma	Bias
	N	0.06135	0.06186	0.04176	0.00064	0.05785	0.05770	0.03654	−0.00459	0.05577	0.05565	0.03447	−0.00630	0.05507	0.05488	0.03356	−0.00720
	TN	0.00833	0.00577	0.00357	0.00110	0.00729	0.00718	0.00623	0.00308	0.00553	0.00586	0.00540	0.00301	0.00451	0.00500	0.00471	0.00256
	EMP	0.03405	0.02305	0.02128	0.01893	0.01534	0.01033	0.01019	0.00956	0.01028	0.00822	0.00761	0.00520	0.00361	0.00204	0.00205	0.00279
	KS	0.00025	−0.00667	−0.01712	−0.03429	−0.00562	−0.01109	−0.01994	−0.03442	−0.00626	−0.01049	−0.01798	−0.03060	−0.00590	−0.00895	−0.01498	−0.02601
	KS-SJ	0.00503	−0.00102	−0.00879	−0.02390	−0.00047	−0.00467	−0.01025	−0.02204	−0.00091	−0.00383	−0.00830	−0.01782	−0.00121	−0.00309	−0.00635	−0.01382
	RMSE
	N	0.08931	0.08240	0.06197	0.04202	0.07131	0.06708	0.04675	0.02770	0.06336	0.06086	0.04039	0.02067	0.05873	0.05735	0.03647	0.01523
	TN	0.06364	0.06490	0.06149	0.05161	0.04025	0.04068	0.03849	0.03260	0.02848	0.02873	0.02719	0.02318	0.01974	0.01987	0.01869	0.01570
	EMP	0.07826	0.07619	0.07332	0.06164	0.05146	0.05022	0.04830	0.03943	0.03750	0.03596	0.03430	0.02913	0.02614	0.02523	0.02327	0.01989
	KS	0.06019	0.05855	0.05613	0.05884	0.04041	0.04031	0.04115	0.04689	0.02993	0.03036	0.03197	0.03860	0.02201	0.02191	0.02362	0.03057
	KS-SJ	0.06092	0.05880	0.05454	0.05361	0.04077	0.03975	0.03772	0.03848	0.02962	0.02910	0.02800	0.02946	0.02194	0.02089	0.01983	0.02135

The results on the upper optimal cut-point are summarized in Table 3. We omit results on the lower optimal cut-point because it is fixed across J within each scenario by our simulation design and its performance is similar to the upper optimal cut-point. Similar to the Youden index estimates, the biases and RMSEs from all methods decrease with increasing sample size. Differently, small underestimation on the upper cut-points is observed in TN instead of KS. N still performs the best in the normal scenario but generally the worst in the other two scenarios with the largest biases and RMSEs with the exception of J=0.8 in the gamma scenario. TN takes the lead in the non-normal scenarios but it results in the largest biases in the normal scenario. The two kernel smoothing estimators have similar performance but generally perform inferior to EMP. Biases from kernel smoothing estimators are larger than EMP. In terms of RMSE, KS is inferior to EMP in the Normal scenario and Log-normal scenario but is superior to EMP except at J=0.8 in the gamma scenario. KS-SJ provides slightly better performance than KS with the normal reference rule except in the normal scenario and J=0.5.

Table 3.

Point estimate simulation on t₊^*. Bias and RMSE on the upper optimal cut-point (t₊^*) estimation from five methods (N, TN, EMP, KS, KS-SJ) based on 1000 simulated datasets. True cut-points are listed for each scenario.

Scenario	# obs	20				50				100				200
	J	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8
Normal	t+*	8.7649	9.052	9.4941	10.522	8.7649	9.052	9.4941	10.522	8.7649	9.052	9.4941	10.522	8.7649	9.052	9.4941	10.522
		Bias
	N	−0.0237	−0.0135	−0.0065	0.0025	−0.0013	0.0019	0.0027	0.0028	−0.0037	−0.0024	−0.0019	−0.0015	−0.0038	−0.0030	−0.0026	−0.0022
	TN	−0.1440	−0.1294	−0.0824	0.0630	−0.0660	−0.0569	−0.0369	0.0327	−0.0228	−0.0193	−0.0140	0.0051	−0.0070	−0.0059	−0.0049	−0.0019
	EMP	−0.0746	−0.0728	−0.0632	−0.0249	−0.0128	−0.0240	−0.0144	0.0148	−0.0107	−0.0101	−0.0069	0.0002	−0.0022	−0.0016	−0.0020	0.0033
	KS	0.0318	0.0161	0.0126	0.0016	0.0338	0.0214	0.0148	0.0104	0.0289	0.0151	−0.0011	0.0023	0.0192	0.0102	−0.0004	0.0022
	KS-SJ	0.0196	0.0152	0.0108	0.0015	0.0321	0.0249	0.0126	0.0081	0.0310	0.0162	−0.0001	0.0025	0.0194	0.0127	−0.0011	0.0013
		RMSE
	N	0.3285	0.2327	0.2277	0.3255	0.2032	0.1443	0.1392	0.2000	0.1439	0.1012	0.0969	0.1394	0.0989	0.0701	0.0677	0.0974
	TN	0.4160	0.3153	0.2698	0.3549	0.2582	0.2017	0.1683	0.2224	0.1754	0.1362	0.1162	0.1473	0.1121	0.0863	0.0765	0.0998
	EMP	0.3783	0.2959	0.2875	0.3811	0.2802	0.1839	0.1562	0.2102	0.1603	0.1190	0.1068	0.1453	0.1116	0.0821	0.0779	0.1170
	KS	0.5247	0.3525	0.3053	0.3626	0.3382	0.2255	0.1874	0.2326	0.2514	0.1663	0.1395	0.1637	0.1718	0.1180	0.0964	0.1136
	KS-SJ	0.5466	0.3733	0.3211	0.3778	0.3553	0.2409	0.1977	0.2409	0.2636	0.1748	0.1425	0.1700	0.1815	0.1250	0.0997	0.1173
Log- Normal	t+*	4.1066	4.1618	4.3203	4.7019	4.1066	4.1618	4.3203	4.7019	4.1066	4.1618	4.3203	4.7019	4.1066	4.1618	4.3203	4.7019
		Bias
	N	0.2443	0.2932	0.2327	−0.0222	0.3051	0.3435	0.2767	0.0174	0.3193	0.3546	0.2854	0.0243	0.3323	0.3660	0.2956	0.0338
	TN	−0.0199	−0.0154	−0.0082	0.0034	−0.0038	−0.0021	0.0002	0.0037	−0.0040	−0.0032	−0.0019	0.0000	−0.0016	−0.0022	−0.0019	−0.0010
	EMP	0.0914	0.0934	0.0799	−0.0210	0.0762	0.0671	0.0587	0.0028	0.0387	0.0276	0.0306	0.0023	0.0134	0.0049	0.0075	0.0021
	KS	0.0831	0.1447	0.1656	0.0104	0.0560	0.1299	0.1600	0.0682	0.0325	0.0981	0.1420	0.0737	0.0171	0.0781	0.1201	0.0741
	KS-SJ	0.1020	0.1230	0.1485	−0.0086	0.0641	0.0850	0.1185	0.0396	0.0409	0.0515	0.0868	0.0469	0.0288	0.0271	0.0607	0.0491
		RMSE
	N	0.3106	0.3512	0.3104	0.2244	0.3308	0.3678	0.3095	0.1508	0.3328	0.3673	0.3026	0.1109	0.3399	0.3732	0.3053	0.0887
	TN	0.1850	0.1464	0.1388	0.1767	0.1109	0.0901	0.0854	0.1077	0.0807	0.0649	0.0599	0.0739	0.0547	0.0446	0.0418	0.0520
	EMP	0.2534	0.2399	0.2105	0.1963	0.1979	0.1797	0.1533	0.1215	0.1408	0.1181	0.1113	0.0809	0.0881	0.0669	0.0658	0.0564
	KS	0.2529	0.2456	0.2598	0.2364	0.1636	0.1875	0.2133	0.1764	0.1219	0.1393	0.1772	0.1452	0.0873	0.1075	0.1434	0.1211
	KS-SJ	0.2790	0.2433	0.2476	0.2332	0.2044	0.1719	0.1880	0.1677	0.1630	0.1273	0.1405	0.1333	0.1288	0.0931	0.1062	0.1072
Gamma	t+*	0.2265	0.2744	0.3453	0.5127	0.2265	0.2744	0.3453	0.5127	0.2265	0.2744	0.3453	0.5127	0.2265	0.2744	0.3453	0.5127
		Bias
	N	0.0620	0.0648	0.0491	−0.0357	0.0699	0.0701	0.0534	−0.0323	0.0723	0.0719	0.0551	−0.0308	0.0734	0.0727	0.0558	−0.0302
	TN	−0.0177	−0.0216	−0.0188	0.0277	−0.0072	−0.0079	−0.0060	0.0097	−0.0049	−0.0053	−0.0040	0.0054	−0.0049	−0.0050	−0.0036	0.0049
	EMP	0.0230	0.0230	0.0154	−0.0101	0.0249	0.0209	0.0164	−0.0093	0.0121	0.0062	0.0148	−0.0063	0.0109	0.0060	0.0070	−0.0037
	KS	0.0346	0.0361	0.0433	0.0026	0.0245	0.0288	0.0360	0.0188	0.0186	0.0220	0.0302	0.0182	0.0145	0.0174	0.0240	0.0161
	KS-SJ	0.0370	0.0318	0.0380	−0.0077	0.0219	0.0221	0.0276	0.0048	0.0160	0.0146	0.0213	0.0079	0.0118	0.0100	0.0153	0.0065
		RMSE
	N	0.0749	0.0790	0.0762	0.0895	0.0742	0.0759	0.0655	0.0624	0.0744	0.0748	0.0613	0.0488	0.0745	0.0742	0.0590	0.0402
	TN	0.0517	0.0479	0.0501	0.1034	0.0298	0.0283	0.0309	0.0549	0.0199	0.0184	0.0205	0.0368	0.0141	0.0129	0.0143	0.0260
	EMP	0.0786	0.0724	0.0650	0.0978	0.0580	0.0556	0.0477	0.0589	0.0479	0.0420	0.0419	0.0468	0.0391	0.0318	0.0283	0.0300
	KS	0.0748	0.0660	0.0778	0.1074	0.0474	0.0476	0.0567	0.0789	0.0359	0.0357	0.0445	0.0589	0.0269	0.0270	0.0342	0.0453
	KS-SJ	0.0830	0.0665	0.0748	0.1034	0.0529	0.0477	0.0529	0.0746	0.0411	0.0352	0.0415	0.0575	0.0309	0.0255	0.0309	0.0438

5.2 Simulation Results on Confidence Intervals

For CI, we generated 500 datasets under each scenario and for each dataset, a 95% CI was constructed by delta method for N (labeled as N-delta) and by bootstrap from 500 samplings for all methods (N, TN, EMP, KS, KS-SJ). The CIs’ coverage probabilities and widths under the three simulation scenarios are displayed in Table 4 and Table 5 for J^* and $t_{+}^{*}$ and separately (results for $t_{-}^{*}$ are omitted due to space limit). With increasing sample size, CIs produced by all the methods become narrower. Across all the scenarios, EMP leads to the widest CI on J^* while KS results in the widest CI on $t_{+}^{*}$ among all methods. N provides a high coverage probability on J^* in the Normal Scenario. The averaged coverage probability from N-delta on J is around 97% and around 95% for $t_{+}^{*}$. By comparison, the coverage probabilities of N bootstrap CIs are slightly lower but of relatively small width. TN and the nonparametric methods result in bootstrap CIs of similar coverage probabilities though the latter are often accompanied with wider CIs. CIs from N have the poorest coverage (for both J^* and $t_{+}^{*}$) under the non-normal skewed scenarios. In the Gamma scenario, the lowest coverage probability of N is nearly 0% on $t_{+}^{*}$ and 4% on J^* while the highest is only around 60% on either at Js below 0.8. Under Log-Normal scenario, the huge standard deviations lead to large variance estimation by delta-method. As a result, the width of CI on J^* has always the (practically) maximum length of 1 (the coverage probability is then 1). N-delta also has extremely poor coverage on the optimal cut-points. Noticeably, the coverage from N-delta on J^* improves when groups are more and more widely separated in the Gamma scenario. In fact, its coverage probabilities at J=0.8 rise to around 97% across sample sizes. The N bootstrap CIs are certainly better than N delta-based CIs under non-normal distributions. Across all simulation scenarios, the TN method provides optimal CIs, covering both the Youden index and the upper cut-points at a close-to-nominal probability across all situations. The KS estimators also demonstrate consistently high coverage probabilities, comparable to and sometime even higher than TN (significantly at small Js and small sample sizes), though the associated CIs are relatively wider. EMP yields CIs of high coverage probabilities for J^* across all the three scenarios, however, in comparison to TN and KS, the coverage for $t_{+}^{*}$ is much lower in the non-normal scenarios. The lowest coverage probability is around 50% in the Gamma scenario and is only around 30% in the Log-Normal scenario and the highest below 90%.

Table 4.

Confidence interval simulation on J^*. CI coverage probability and width on J^* by the five methods (N, TN, EMP, KS, KS-SJ) based on 500 simulated datasets and 500 bootstrap samples.

Scenario	# of Obs	20	20	20	20	50	50	50	50	100	100	100	100	200	200	200	200
	J	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8
Normal	Coverage Prob.
	N-delta	0.976	0.97	0.968	0.942	0.974	0.964	0.964	0.946	0.98	0.98	0.976	0.968	0.98	0.974	0.968	0.968
	N	0.922	0.914	0.91	0.902	0.956	0.934	0.936	0.934	0.942	0.944	0.954	0.952	0.944	0.956	0.952	0.96
	TN	0.932	0.906	0.91	0.9	0.946	0.932	0.934	0.936	0.93	0.94	0.952	0.946	0.938	0.948	0.95	0.956
	EMP	0.95	0.954	0.936	0.924	0.95	0.96	0.948	0.948	0.962	0.958	0.962	0.95	0.944	0.956	0.946	0.956
	KS	0.958	0.94	0.948	0.94	0.926	0.898	0.872	0.898	0.884	0.844	0.828	0.872	0.862	0.798	0.76	0.83
	KS-SJ	0.958	0.944	0.954	0.936	0.948	0.932	0.916	0.938	0.924	0.916	0.894	0.914	0.906	0.866	0.828	0.892
	Coverage Width
	N-delta	0.2966	0.2835	0.2539	0.2145	0.1903	0.1797	0.1597	0.1350	0.1350	0.1270	0.1126	0.0951	0.0953	0.0896	0.0794	0.0672
	N	0.2375	0.2331	0.2143	0.1850	0.1556	0.1520	0.1407	0.1213	0.1111	0.1084	0.1005	0.0867	0.0795	0.0776	0.0719	0.0619
	TN	0.2440	0.2391	0.2199	0.1901	0.1582	0.1544	0.1426	0.1237	0.1123	0.1093	0.1011	0.0874	0.0801	0.0782	0.0722	0.0622
	EMP	0.3172	0.3062	0.2777	0.2299	0.2103	0.2015	0.1836	0.1526	0.1502	0.1435	0.1310	0.1095	0.1074	0.1023	0.0931	0.0781
	KS	0.2547	0.2541	0.2405	0.2026	0.1684	0.1686	0.1581	0.1336	0.1224	0.1209	0.1130	0.0957	0.0892	0.0874	0.0813	0.0685
	KS-SJ	0.2609	0.2584	0.2432	0.2030	0.1739	0.1732	0.1617	0.1356	0.1268	0.1246	0.1161	0.0978	0.0921	0.0902	0.0836	0.0702
Log-Normal	Coverage Prob.
	N-delta	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
	N	0.626	0.632	0.85	0.892	0.364	0.422	0.89	0.558	0.16	0.274	0.908	0.12	0.038	0.174	0.918	0.002
	TN	0.924	0.924	0.898	0.894	0.928	0.934	0.934	0.928	0.938	0.94	0.948	0.95	0.94	0.94	0.94	0.948
	EMP	0.942	0.944	0.932	0.92	0.954	0.956	0.948	0.948	0.95	0.96	0.956	0.954	0.944	0.948	0.952	0.952
	KS	0.944	0.942	0.946	0.878	0.946	0.95	0.908	0.672	0.936	0.938	0.888	0.42	0.954	0.944	0.832	0.218
	KS-SJ	0.928	0.934	0.924	0.936	0.936	0.948	0.952	0.878	0.946	0.942	0.956	0.848	0.944	0.952	0.952	0.798
	Coverage Width
	N-delta	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
	N	0.2343	0.1936	0.1707	0.1674	0.1513	0.1201	0.1110	0.1126	0.1060	0.0849	0.0809	0.0841	0.0771	0.0626	0.0615	0.0653
	TN	0.2510	0.2461	0.2207	0.1839	0.1635	0.1596	0.1447	0.1211	0.1166	0.1131	0.1031	0.0865	0.0833	0.0810	0.0738	0.0618
	EMP	0.3049	0.2997	0.2765	0.2272	0.2018	0.1983	0.1828	0.1523	0.1441	0.1410	0.1302	0.1087	0.1042	0.1020	0.0932	0.0780
	KS	0.2587	0.2383	0.2086	0.1910	0.1724	0.1546	0.1365	0.1266	0.1251	0.1114	0.0984	0.0910	0.0906	0.0814	0.0719	0.0657
	KS-SJ	0.2622	0.2469	0.2156	0.1891	0.1744	0.1634	0.1427	0.1255	0.1264	0.1189	0.1037	0.0905	0.0921	0.0871	0.0763	0.0657
Gamma	Coverage Prob.
	N-delta	0.552	0.614	0.758	0.962	0.4	0.388	0.674	0.98	0.24	0.196	0.514	0.978	0.066	0.04	0.276	0.988
	N	0.718	0.638	0.71	0.912	0.6	0.5	0.656	0.93	0.47	0.326	0.526	0.91	0.262	0.112	0.334	0.924
	TN	0.932	0.922	0.916	0.918	0.936	0.928	0.924	0.946	0.934	0.938	0.93	0.916	0.94	0.942	0.936	0.946
	EMP	0.944	0.96	0.95	0.94	0.964	0.96	0.94	0.948	0.954	0.944	0.938	0.918	0.944	0.95	0.944	0.932
	KS	0.948	0.962	0.952	0.944	0.958	0.95	0.938	0.864	0.95	0.952	0.908	0.768	0.936	0.94	0.902	0.7
	KS-SJ	0.928	0.944	0.936	0.95	0.954	0.954	0.938	0.93	0.96	0.956	0.944	0.926	0.94	0.95	0.942	0.904
	Coverage Width
	N-delta	0.1503	0.1533	0.1553	0.2149	0.0952	0.0958	0.0978	0.1387	0.0673	0.0674	0.0689	0.0982	0.0476	0.0476	0.0486	0.0690
	N	0.2278	0.1982	0.1694	0.1527	0.1534	0.1293	0.1090	0.1000	0.1127	0.0927	0.0780	0.0717	0.0811	0.0667	0.0565	0.0521
	TN	0.2416	0.2433	0.2292	0.1914	0.1551	0.1563	0.1461	0.1233	0.1100	0.1099	0.1025	0.0864	0.0782	0.0781	0.0730	0.0615
	EMP	0.2991	0.2943	0.2729	0.2251	0.1992	0.1950	0.1803	0.1508	0.1441	0.1396	0.1290	0.1079	0.1034	0.1000	0.0920	0.0766
	KS	0.2427	0.2345	0.2119	0.1839	0.1606	0.1541	0.1397	0.1223	0.1174	0.1117	0.1012	0.0882	0.0849	0.0809	0.0731	0.0634
	KS-SJ	0.2485	0.2415	0.2187	0.1857	0.1647	0.1600	0.1443	0.1241	0.1207	0.1162	0.1048	0.0898	0.0876	0.0844	0.0762	0.0649

Table 5.

Confidence interval simulation on t₊^*. CI coverage probability and width on t₊^* by the five methods (N, TN, EMP, KS and KS-SJ) based on 500 simulated datasets and 500 bootstrap samples.

Scenario	# of Obs	20	20	20	20	50	50	50	50	100	100	100	100	200	200	200	200
	Youden	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8	0.5	0.6	0.7	0.8
Normal	Coverage Prob.
	N-delta	0.924	0.922	0.932	0.922	0.936	0.94	0.934	0.934	0.942	0.944	0.948	0.944	0.948	0.942	0.944	0.95
	N	0.93	0.926	0.908	0.894	0.922	0.948	0.928	0.922	0.938	0.944	0.942	0.934	0.936	0.93	0.942	0.942
	TN	0.916	0.93	0.93	0.918	0.942	0.948	0.928	0.934	0.936	0.942	0.952	0.938	0.932	0.938	0.942	0.944
	EMP	0.904	0.912	0.926	0.912	0.892	0.912	0.92	0.934	0.854	0.908	0.918	0.928	0.858	0.88	0.888	0.916
	KS	0.942	0.944	0.944	0.904	0.96	0.936	0.948	0.94	0.936	0.95	0.95	0.944	0.946	0.95	0.964	0.958
	KS-SJ	0.932	0.934	0.928	0.908	0.958	0.942	0.948	0.942	0.938	0.944	0.954	0.946	0.944	0.948	0.958	0.958
	Coverage Width
	N-delta	1.2991	0.8869	0.8312	1.1987	0.7953	0.5528	0.5260	0.7604	0.5547	0.3872	0.3702	0.5368	0.3907	0.2725	0.2610	0.3792
	N	1.2123	0.8723	0.8381	1.1931	0.7704	0.5473	0.5271	0.7519	0.5411	0.3810	0.3665	0.5275	0.3862	0.2697	0.2593	0.3739
	TN	1.3441	1.0216	0.9233	1.2836	0.9068	0.6977	0.6098	0.8007	0.6359	0.4886	0.4241	0.5532	0.4378	0.3308	0.2895	0.3885
	EMP	1.4494	1.1249	1.0136	1.3439	0.8559	0.6164	0.5908	0.8160	0.5253	0.3859	0.3811	0.5426	0.3507	0.2568	0.2486	0.3607
	KS	1.9313	1.3681	1.1570	1.3668	1.3315	0.9001	0.7734	0.8998	0.9771	0.6589	0.5658	0.6528	0.7208	0.4860	0.4127	0.4852
	KS-SJ	1.9497	1.4512	1.2294	1.4462	1.4019	0.9869	0.8502	0.9751	1.0418	0.7356	0.6258	0.7128	0.7800	0.5379	0.4520	0.5279
Log-Normal	Coverage Prob.
	N-delta	0.362	0.25	0.42	0.656	0.04	0.018	0.118	0.616	0.002	0	0.02	0.606	0	0	0	0.566
	N	0.77	0.662	0.798	0.774	0.26	0.142	0.414	0.874	0.03	0.006	0.102	0.902	0	0	0	0.886
	TN	0.928	0.934	0.926	0.906	0.938	0.95	0.936	0.924	0.932	0.946	0.948	0.936	0.934	0.94	0.946	0.94
	EMP	0.83	0.686	0.746	0.758	0.584	0.512	0.514	0.768	0.464	0.446	0.432	0.674	0.372	0.31	0.354	0.546
	KS	0.936	0.88	0.85	0.764	0.944	0.852	0.782	0.862	0.916	0.806	0.716	0.878	0.918	0.78	0.648	0.874
	KS-SJ	0.932	0.894	0.878	0.694	0.944	0.922	0.882	0.794	0.93	0.93	0.922	0.856	0.926	0.924	0.9	0.904
	Coverage Width
	N-delta	0.3890	0.3602	0.3767	0.4104	0.2310	0.2299	0.2411	0.2594	0.1614	0.1630	0.1707	0.1830	0.1144	0.1160	0.1213	0.1297
	N	0.6028	0.5633	0.5791	0.6222	0.4045	0.4081	0.4284	0.4597	0.3003	0.3092	0.3240	0.3477	0.2324	0.2382	0.2495	0.2674
	TN	0.7330	0.5650	0.5182	0.6606	0.4523	0.3648	0.3372	0.4085	0.3082	0.2575	0.2378	0.2833	0.2164	0.1837	0.1687	0.2000
	EMP	1.0834	0.5405	0.5097	0.5773	0.4275	0.4086	0.3571	0.3567	0.3413	0.3289	0.2846	0.2207	0.2545	0.2146	0.1900	0.1275
	KS	0.8672	0.7114	0.6539	0.6439	0.5991	0.5024	0.4913	0.4773	0.4495	0.3828	0.3788	0.3821	0.3441	0.2798	0.2872	0.3218
	KS-SJ	0.8648	0.7091	0.6394	0.6329	0.6616	0.5272	0.4856	0.4466	0.5328	0.4150	0.3827	0.3497	0.4253	0.3232	0.2901	0.2972
Gamma	Coverage Prob.
	N-delta	0.468	0.45	0.668	0.684	0.076	0.084	0.404	0.664	0.006	0	0.19	0.6	0	0	0.044	0.534
	N	0.75	0.724	0.882	0.694	0.21	0.28	0.712	0.754	0.008	0.032	0.482	0.744	0	0	0.136	0.726
	TN	0.918	0.922	0.916	0.948	0.942	0.936	0.936	0.944	0.94	0.932	0.954	0.952	0.936	0.91	0.93	0.934
	EMP	0.91	0.846	0.874	0.752	0.826	0.72	0.736	0.746	0.79	0.666	0.652	0.654	0.848	0.722	0.572	0.628
	KS	0.936	0.924	0.908	0.71	0.908	0.896	0.89	0.844	0.9	0.904	0.856	0.906	0.902	0.906	0.84	0.91
	KS-SJ	0.932	0.932	0.908	0.666	0.934	0.956	0.936	0.8	0.928	0.962	0.932	0.828	0.934	0.952	0.942	0.898
	Coverage Width
	N-delta	0.1341	0.1183	0.1422	0.1977	0.0777	0.0757	0.0917	0.1258	0.0539	0.0536	0.0650	0.0888	0.0378	0.0379	0.0460	0.0628
	N	0.1518	0.1500	0.1858	0.2550	0.0950	0.1045	0.1324	0.1823	0.0670	0.0776	0.0992	0.1369	0.0479	0.0560	0.0715	0.0993
	TN	0.1769	0.1536	0.1743	0.3846	0.1121	0.1028	0.1143	0.2119	0.0757	0.0682	0.0769	0.1409	0.0525	0.0469	0.0533	0.0984
	EMP	0.2106	0.1745	0.1812	0.2541	0.1580	0.1301	0.1199	0.1608	0.1289	0.1019	0.0922	0.1085	0.1143	0.0886	0.0753	0.0727
	KS	0.2346	0.2090	0.2259	0.2704	0.1624	0.1469	0.1644	0.2174	0.1180	0.1085	0.1217	0.1810	0.0912	0.0808	0.0916	0.1499
	KS-SJ	0.2346	0.2135	0.2224	0.2592	0.1763	0.1586	0.1665	0.1980	0.1366	0.1215	0.1270	0.1623	0.1095	0.0943	0.1001	0.1415

6 A Real Example

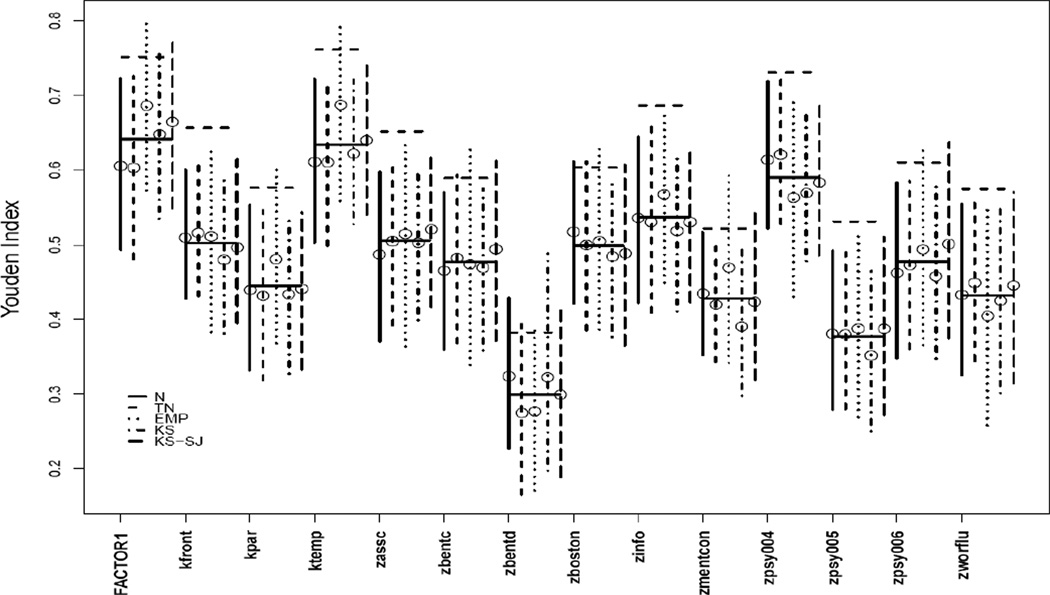
The proposed methods for the Youden index were applied to investigate the diagnostic ability of fourteen psychometric markers of Alzheimer’s disease (AD) among non-demented/mild cognitive impairment/early stage AD. The same dataset was analyzed in Xiong et al (2005) for VUS and the readers are referred to the paper for more details on the dataset. Logistic regression analyses, including the analysis of logit for dichotomous outcomes and the analysis of generalized logit for polytomous outcomes, are simple and powerful alternatives to the traditional ROC types of analyses, and are well supported by existing software packages. The connection between the binary logistic regression model and AUROC has been addressed (Qin 2003), though the connection between polytomous logistic regression and VUS has not. We implemented multinomial logit analysis and confirmed that each marker has a significant effect on predicting the AD status (all the markers have p<0.0001 based on maximum likelihood analysis of variance only that ‘zbentd’ has p=0.002). Application of a nonparametric k sample test for location based on marginal ranks (Prui and Sen, 1971; Nordhausen et al., 2010) across all the fourteen markers indicates that the markers have different distributions across the three diagnosis groups, suggesting potentially distinct diagnostic ability (p=1.55e-09). We continued to calculate the diagnostic ability summary measures—the Youden index and VUS. Figure 1 Plots for each marker the estimates on J with 95% CI, accompanied with averaged estimates of J from all methods and the averaged VUS under normal and empirical method. All markers are useful to some extent comparing the VUS measures to 1/6 and J estimates to 0 (of a useless marker) respectively. The two measures also rank the markers in similar order with subtle difference. The marker ‘zbentd’ is rated as the worst marker while ‘ktemp’ and ‘FACTOR1’ as the most discriminative, according to both the Youden index and VUS. Table 6 separately lists point estimates on J and VUS under normality for each of the 14 AD marker, accompanied with 95% CI, as well as associated optimal cut-points. The resulting optimal cut-points are not exactly equivalent but stay quite close between the two methods.

Figure 1.

Youden index and VUS for 14 psychometric markers of AD: For each marker, estimates on J (indicated by circle) under the five methods (N, TN, EMP, KS, KS-SJ) are plotted with 95% CIs (vertical lines); the solid horizontal line is the average estimates on J across all methods; the dashed horizontal line is the average of VUS estimate under normal method and by empirical estimation.

Table 6.

VUS and Youden point estimate under the normal method, followed by 95% confidence interval and associated optimal cutoff on 14 psychometric markers on Alzheimer’s disease.

marker ID	VUS				Youden index
	estimate	(95% CI)	t−*	t+*	estimate	(95% CI)	t−*	t+*
FACTOR1	0.73	(0.62,0.83)	−0.06	3.17	0.63	(0.49,0.72)	0.56	2.91
ktemp	0.75	(0.65,0.85)	−2.04	3.45	0.62	(0.5,0.72)	−1.51	3.45
kpar	0.55	(0.43,0.68)	−1.45	1.87	0.43	(0.33,0.55)	−0.54	1.60
kfront	0.66	(0.55,0.76)	−1.68	0.91	0.49	(0.43,0.6)	−1.43	1.10
zpsy004	0.72	(0.63,0.82)	−0.18	1.81	0.57	(0.52,0.72)	0.08	1.26
zpsy005	0.52	(0.41,0.63)	−1.23	1.21	0.37	(0.28,0.49)	−0.13	0.87
zpsy006	0.60	(0.48,0.71)	−0.28	2.02	0.46	(0.35,0.58)	−0.10	1.30
zinfo	0.68	(0.58,0.78)	−0.37	1.93	0.51	(0.42,0.65)	0.07	1.50
zbentc	0.59	(0.47,0.7)	−0.42	1.56	0.45	(0.36,0.57)	0.14	1.01
zbentd	0.35	(0.24,0.46)	−0.50	1.50	0.28	(0.23,0.43)	0.67	1.55
zboston	0.57	(0.46,0.69)	−0.54	1.94	0.50	(0.42,0.61)	0.17	1.92
zmentcon	0.53	(0.42,0.64)	−0.09	1.32	0.42	(0.35,0.52)	0.24	1.00
zworflu	0.57	(0.46,0.68)	−0.37	1.33	0.41	(0.33,0.55)	−0.37	0.83
zassc	0.63	(0.52,0.74)	0.03	1.37	0.50	(0.37,0.6)	−0.07	1.06

7 Discussion

Current research on diagnostic tests focuses very much on two-population diagnosis. VUROC has been used to evaluate diagnostic tests for three groups. However, VUROC has its limitations such as being computationally difficult, lacking direct link to correct classification probabilities and failing to assess two markers which have equal VUROCs but perform better at different cut-points. Most of all, it lacks an integral derivation of optimal cut-points which are required for patients diagnosis in medical practice. We extended the Youden index for three ordinal groups as an alternative measure of diagnostic accuracy. We proposed parametric and nonparametric methods for simultaneous estimation of the Youden index and the cut-points and evaluated the bias, precision and CI coverage and width of these estimators under three representative simulation scenarios. We have provided a directly applicable R package to evaluate diagnostic markers for three ordinal groups through the Youden index. We found that if groups are well separated, the parametric estimator under the normal assumption (N) performs well despite small to moderate deviation from normality but its performance is the worst otherwise. TN provides the best estimation almost in all scenarios in evaluation of both point estimates and CI properties. It may be argued that the normal and Log-normal scenario caters to TN and the gamma scenario under investigation only deviates moderately from normality, thus Box-Cox transformation can still approximate reasonably well. Kernel smoothing estimators introduce comparatively large biases but can outperform TN especially under small sample sizes and when groups are not well separated. The Sheather-Jones bandwidth selection is generally preferred to the normal reference rule for kernel smoothing estimator. In terms of point estimate for both the Youden index and optimal cut-points, EMP performs surprisingly well, especially under large sample size and for widely separated groups. However, in consideration of CI properties, EMP yields unsatisfactory coverage in non-normal scenarios.

The point estimation and variance on both the Youden index and the cut-points for three-group diagnostic tests were specifically derived for some parametric distributions. Closed form expressions are sometimes difficult to derive or may not even exist for other distributions. In contrast, flexible nonparametric estimators are distribution free and meanwhile, can provide consistently satisfactory results on point estimates and CIs. Two popular bandwidth selection methods were considered here for the kernel smoothing method for convenient and fast computation. Other bandwidth estimation algorithms may be adopted. Basic quantile bootstrap confidence intervals were calculated in the paper. However, more computationally expensive bootstrap intervals such as bias-corrected and accelerated bootstrap confidence intervals (Carpenter and Bithell, 2000; Schisterman and Perkins, 2008) may offer further improvement. In practice, it is recommended that the distribution of a marker should be examined by exploratory plots before implementation. Experiments with all of the proposed methods are encouraged for comparison. Last, we presented the Youden index as a simple combination of the three correct classification probabilities associated with the three ordinal groups by imposing equal weights. The proposed Youden index can be easily generalized by researchers in order to take disease prevalence into account or consider cost/benefit ratio in a diagnostic test.

Appendix

• The profile log-likelihood of marker measurements from three ordinal groups after implementation of Box-Cox transformation is,

  $$l(\widehat{\lambda })=-\frac{n_{-}}{2}[1+\text{log}(2\pi {\widehat{\sigma }}_{-}^2)]+(\widehat{\lambda }-1){\displaystyle \sum _{j=1}^{n_{-}}\text{log}(x_j^{(-)})}-\frac{n_0}{2}[1+\text{log}(2\pi {\widehat{\sigma }}_0^2)]+(\widehat{\lambda }-1){\displaystyle \sum _{j=1}^{n_0}\text{log}(x_j^{(0)})}-\frac{n_{+}}{2}[1+\text{log}(2\pi {\widehat{\sigma }}_{+}^2)]+(\widehat{\lambda }-1){\displaystyle \sum _{j=1}^{n_{+}}\text{log}(x_j^{(+)})}$$

Notice that we have suppressed the dependence of estimates of normal variance on λ̂.

• Partial derivatives of $t_{-}^{*}$, $t_{+}^{*}$ and J with respect to relevant parameters.

The partial derivatives of $t_{-}^{*}$ with respect to the relevant parameters can be derived as:

$$\frac{\partial t_{-}^{*}}{\partial {\mu }_{-}}=-\frac{{\sigma }_0}{b}[{\sigma }_0+\frac{{\sigma }_{-}}{\sqrt{\mathrm{\Delta }}}({\mu }_{-}-{\mu }_0)];\frac{\partial t_{-}^{*}}{\partial {\mu }_0}=\frac{{\sigma }_{-}}{b_{}}[{\sigma }_{\_}+\frac{{\sigma }_0}{\sqrt{\mathrm{\Delta }}}({\mu }_{-}-{\mu }_0)];\frac{\partial t_{-}^{*}}{\partial {\sigma }_{-}}=\frac{a_{1}b-2{\sigma }_{-}c}{b_{}^2};\frac{\partial t_{-}^{*}}{\partial {\sigma }_0}=\frac{a_{2}b+2{\sigma }_{0}c}{b_{}^2}.$$

Where b, c and Δ separately represent the denominator, numerator and the term under the square root in Equation (3.1), i.e. $b=({\sigma }_{-}^2-{\sigma }_0^2),\mathrm{\Delta }={({\mu }_{-}-{\mu }_0)}^2+({\sigma }_{-}^2-{\sigma }_0^2)\text{ln}(\frac{{\sigma }_{-}^2}{{\sigma }_0^2}),c=({\mu }_0{\sigma }_{-}^2-{\mu }_{-}{\sigma }_0^2)-{\sigma }_{-}{\sigma }_0\sqrt{\mathrm{\Delta }};a_1=2{\mu }_0{\sigma }_{-}-{\sigma }_0\sqrt{\mathrm{\Delta }}-\frac{{\sigma }_0}{\sqrt{\mathrm{\Delta }}}[{\sigma }_{-}^2\text{ln}(\frac{{\sigma }_{-}^2}{{\sigma }_0^2})+b_{}]$ and $a_2=-2{\mu }_{-}{\sigma }_0-{\sigma }_{-}\sqrt{\mathrm{\Delta }}+\frac{{\sigma }_{-}}{\sqrt{\mathrm{\Delta }}}[{\sigma }_0^2\text{ln}(\frac{{\sigma }_{-}^2}{{\sigma }_0^2})+b]$, where ln(t) is natural log.

Since $t_{+}^{*}$ has the same functional form as $t_{-}^{*}$, the partial derivatives on μ₀, μ₊, σ₀ and σ₊ can be easily written out by simultaneously substituting, in the above equations and notations, μ₋ by μ₀, μ₀, by μ₊, σ₋ by σ₀, and σ₀ by σ₊. We omit the detailed expressions here.

The partial derivatives of the Youden index with respect to the six normal parameters are represented as follows,

$$\frac{\partial J}{\partial {\mu }_{-}}=\frac{1}{2}\{\frac{\partial t_{-}^{*}}{\partial {\mu }_{-}}[\frac{1}{{\sigma }_{-}}\phi (\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}})-\frac{1}{{\sigma }_0}\phi (\frac{t_{-}-{\mu }_0}{{\sigma }_0})]-\frac{1}{{\sigma }_{-}}\phi (\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}})\};$$

$$\frac{\partial J}{\partial {\mu }_{+}}=-\frac{1}{2}\{\frac{\partial t_{+}^{*}}{\partial {\mu }_{+}}[\frac{1}{{\sigma }_{+}}\phi (\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}})-\frac{1}{{\sigma }_0}\phi (\frac{t_{+}-{\mu }_0}{{\sigma }_0})]-\frac{1}{{\sigma }_{+}}\phi (\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}})\}$$

$$\frac{\partial J}{\partial {\mu }_0}=\frac{1}{2}\{\frac{\partial t_{-}^{*}}{\partial {\mu }_0}[\frac{1}{{\sigma }_{-}}\phi (\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}})-\frac{1}{{\sigma }_0}\phi (\frac{t_{-}-{\mu }_0}{{\sigma }_0})]+\frac{\partial t_{+}^{*}}{\partial {\mu }_0}[\frac{1}{{\sigma }_0}\phi (\frac{t_{+}-{\mu }_0}{{\sigma }_0})-\frac{1}{{\sigma }_{+}}\phi (\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}})]+\frac{1}{{\sigma }_0}[\phi (\frac{t_{-}-{\mu }_0}{{\sigma }_0})-\phi (\frac{t_{+}-{\mu }_0}{{\sigma }_0})]\}$$

$$\frac{\partial J}{\partial {\sigma }_{-}}=\frac{1}{2}\{\frac{\partial t_{-}^{*}}{\partial {\sigma }_{-}}[\frac{1}{{\sigma }_{-}}\phi (\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}})-\frac{1}{{\sigma }_0}\phi (\frac{t_{-}-{\mu }_0}{{\sigma }_0})]-\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}^2}\phi (\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}})\};$$

$$\frac{\partial J}{\partial {\sigma }_{+}}=\frac{-1}{2}\{\frac{\partial t_{+}^{*}}{\partial {\sigma }_{+}}[\frac{1}{{\sigma }_{+}}\phi (\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}})-\frac{1}{{\sigma }_0}\phi (\frac{t_{+}-{\mu }_0}{{\sigma }_0})]-\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}^2}\phi (\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}})\}$$

$$\frac{\partial J}{\partial {\sigma }_0}=\frac{1}{2}\{\frac{\partial t_{-}^{*}}{\partial {\sigma }_0}[\frac{1}{{\sigma }_{-}}\phi (\frac{t_{-}-{\mu }_{-}}{{\sigma }_{-}})-\frac{1}{{\sigma }_0}\phi (\frac{t_{-}-{\mu }_0}{{\sigma }_0})]+\frac{\partial t_{+}^{*}}{\partial {\sigma }_0}[\frac{1}{{\sigma }_0}\phi (\frac{t_{+}-{\mu }_0}{{\sigma }_0})-\frac{1}{{\sigma }_{+}}\phi (\frac{t_{+}-{\mu }_{+}}{{\sigma }_{+}})]+\frac{t_{-}-{\mu }_0}{{\sigma }_0^2}\phi (\frac{t_{-}-{\mu }_0}{{\sigma }_0})-\frac{t_{+}-{\mu }_0}{{\sigma }_0^2}\phi (\frac{t_{+}-{\mu }_0}{{\sigma }_0})\}$$