A multiscale MDCT image-based breathing lung model with time-varying regional ventilation

Abstract

A novel algorithm is presented that links local structural variables (regional ventilation and deforming central airways) to global function (total lung volume) in the lung over three imaged lung volumes, to derive a breathing lung model for computational fluid dynamics simulation. The algorithm constitutes the core of an integrative, image-based computational framework for subject-specific simulation of the breathing lung. For the first time, the algorithm is applied to three multi-detector row computed tomography (MDCT) volumetric lung images of the same individual. A key technique in linking global and local variables over multiple images is an in-house mass-preserving image registration method. Throughout breathing cycles, cubic interpolation is employed to ensure C₁ continuity in constructing time-varying regional ventilation at the whole lung level, flow rate fractions exiting the terminal airways, and airway deformation. The imaged exit airway flow rate fractions are derived from regional ventilation with the aid of a three-dimensional (3D) and one-dimensional (1D) coupled airway tree that connects the airways to the alveolar tissue. An in-house parallel large-eddy simulation (LES) technique is adopted to capture turbulent-transitional-laminar flows in both normal and deep breathing conditions. The results obtained by the proposed algorithm when using three lung volume images are compared with those using only one or two volume images. The three-volume-based lung model produces physiologically-consistent time-varying pressure and ventilation distribution. The one-volume-based lung model under-predicts pressure drop and yields un-physiological lobar ventilation. The two-volume-based model can account for airway deformation and non-uniform regional ventilation to some extent, but does not capture the non-linear features of the lung.

1. Introduction

A thorough understanding of air flow in the human lung is required in order to understand the deposition of therapeutic aerosols or pollutant particles in the airways, as well as the distribution of wall shear stress for mechanotransduction to epithelial cells in maintaining water homeostasis for mucociliary clearance. This understanding is motivated on one hand by a growing interest in using aerosol drug delivery for efficient lung disease treatments [1] and on the other hand by the evidence that pollutant particle depositions in the lungs play a key role in the development of lung diseases [2]. Furthermore, cells have mechanosensing capabilities that can detect changes of the mechanical force transmitted from the organ level [3], and there is evidence of the response of human bronchial epithelial cells to mechanical force [4]. Computational fluid dynamics (CFD) has been utilized extensively to simulate respiratory flows over the past two decades [5][6]. Since particle deposition and wall shear stress are highly dependent on flow characteristics - which, in turn, are dependent on the geometrical features of the airways and regional ventilation of the lungs - it is clearly desirable to conduct subject-specific CFD modeling. However, subject-specific simulation of pulmonary air flow is challenging due to the multiscale features of airway structure and ventilation distribution. The human airway tree is composed of airway branches with increasing total cross-sectional area with each branch division, but decreasing individual diameters, varying from the order of centimeters at the trachea to the order of micrometers at the acinar level. As a result of the increase in cross-section, the flow changes from high-Reynolds number (Re) turbulent or transitional flow in the trachea to low-Re laminar flow in the distal airways.

Due to the complexity of the airway geometry, most earlier studies of air flow used either symmetric Weibel models [7] or regularly asymmetric Horsfield models [8] with the assumption of laminar flow, or use of Reynolds-Averaged Navier-Stokes (RANS) flow models [9]. Although these studies provide some insights into the characteristics of flow in systems of bifurcating tubes, the idealized airway models lack subject-specific geometrical features, and RANS models do not accurately capture the transient behaviors of turbulent or transitional flow. In order to account for subject-specific geometry and capture the complex turbulent-transitional-laminar flow characteristics, more recently several groups have been using anatomically-based airway geometries derived from in vivo computed tomography (CT) volumetric data sets. Due to the constraint of radiation dose, only one or two scans are commonly acquired with one imaged near full inspiration (total lung capacity, TLC) and/or the other at end expiration (functional residual capacity, FRC, or residual volume, RV). TLC can provide detailed information related to airway geometry, while FRC or RV provide information related to air trapping and regional tissue density under gravity loading. CFD simulations of air flow usually adopt the airway geometry extracted from TLC because more detail of the airway branch topology can be segmented from CT images acquired at a larger lung volume. A representative though not exhaustive list of such studies based on one lung volume can be found in [10]–[17]. Although only using a single volume data set, these studies have provided new insight into respiratory system function. For example, Lin et al. [13] demonstrated the dependence of flow characteristics on airway models derived from multi-detector row CT (MDCT) images acquired at TLC. Without including the upper airway in the CFD simulation (regarded as a large-scale effect), the nature of the flow was completely changed from turbulent to laminar flow.

Although the importance of anatomically-based airway geometries has been recognized, only a few generations of the central airway tree can typically be included in the CFD analysis due to the limitation of current imaging technologies. In addition to the large-scale effects that are associated with the upper airway, CFD solutions are also sensitive to the imposed boundary conditions at the exit segments of the truncated computational domains (regarded here as `small-scale' effects). Therefore, it is essential to apply physiological boundary conditions that can simultaneously: 1. capture turbulent, transitional or laminar flows at the local level in the CT-resolved airways, and 2. recover regional ventilation (air distribution) at the global organ level. This is also a common issue in simulations of other physiological flows, such as blood flows in the human arterial system [18]–[23]. Due to difficulties in measuring the in vivo pressure and flow inside the lungs, earlier CFD analyses have imposed equal pressures or flows at the exits of the airway domain, neglecting the highly non-uniform regional ventilation distribution that is typical of the lungs. An alternative subject-specific method was proposed by De Backer et al. [24][25], who specified a distribution of pressure values at the airway exits which were derived from lung or lobe expansions between two imaged lung volumes (FRC and TLC). All airway exit pressures within a specific lobe were identical. The boundary condition was used to compute steady inspiratory flow in a TLC airway geometry. Although this approach is an improvement over uniform boundary conditions, it is not sufficient to capture heterogeneity within each lung or lobe. A further alternative is the coupling to an impedance model for the respiratory system [26][27]. In this approach the impedance is estimated from a 1D model in the frequency domain, and then is transformed into the time domain to define the pressure at each specific 3D outlet. However, the 3D-impedance coupled approaches still assume uniform zero pressures at the distal ends of the alveoli units.

Recently, Lin et al. [14] proposed a method to build subject-specific 3D and 1D coupled airway geometries with seamless transition between different scales, in which the entire conducting airway tree is generated by a volume-filling method [28]. This multiscale model incorporates the desired level of geometric details at both local (3D) and global levels (with the 1D tree that links 3D airways and lung parenchyma), allowing simulations of air flow in the multiscale framework of 3D-3D (3D “large” airways coupled with 3D “small” airways) and 3D-1D (3D “large” airway coupled with 1D “small” airways) coupling. Based on this framework, Yin et al. [29] described a technique to estimate subject-specific boundary conditions by means of image registration. Two MDCT lung data sets acquired at different inflation levels were registered to derive the distribution of regional volume change, which was then passed to the 3D MDCT-resolved airways as flow boundary conditions. The image-registration-derived boundary condition was compared against the traditional uniform velocity and pressure boundary conditions. The results showed that the image-based boundary condition yielded physiologically-consistent regional distribution of flow, which was not accomplished by the other two uniform methods.

Another important aspect of air flow simulation is to consider the deformation of the airway geometry, since the lung changes in size and shape during breathing. However, in most existing CFD studies the airway geometries have been assumed to be rigid. Deformation of central airways may be small during shallow breathing in a healthy young subject; however, deformation of the central airways in deep breathing and in some diseases may not be negligible. For example, Loring et al. [30] observed significant changes in cross-sections of the trachea in patients with chronic obstructive pulmonary disease (COPD). Attempts have been made to account for airway deformation by using fluid-structure interaction (FSI) techniques [31][32]. For example, Xia et al. [32] investigated the effects of airway-parenchymal tethering and airway wall motion on flow structure and wall shear stress in a 3D MDCT-derived airway bifurcation between the 3rd and 4th generations. However the limitation of FSI is that accurate simulation relies on accurate definition of the material properties of the airway wall and parenchymal tissue in individual lungs. Such data is currently lacking in the literature. An alternative to FSI is to use an imaging-based approach to define the displacement of the airway wall. Yin et al. [33] developed a dynamic lung geometrical model by using image registration on pairs of lung images acquired at the end of full inspiration and the end of expiration, to define the displacement of each surface mesh vertex. Unlike FSI, the image-based method requires neither coupling with computational solid mechanics, nor knowing tissue mechanical properties and tethering forces a priori. Nonetheless, it requires large image data sets.

In this paper, we propose an integrative multiscale computational framework for subject-specific simulation of breathing lungs, which fuses rich image-derived deforming central airways and regional ventilation to guide CFD simulation of air flow in the human lung. We utilize three volumetric MDCT lung image data sets, a 3D-1D coupled airway model, an in-house CFD code for turbulent-laminar flow, and an in-house mass-preserving image registration method. The 3D-1D coupled airway model is multiscale because it spans over 20 generations of branching. The simulation of air flow from the mouth inlet to the lung parenchyma is multiscale because it captures turbulent-transitional-laminar flow in the regions of interest with high dimensions, and recovering regional ventilation of the whole lung. The image registration optimizes the relationship between the deformations at the scale of the whole lung and the scale of parenchymal units, linking deforming central airways with macro-scale global lung deformation as well as micro-scale local parenchymal deformation and air ventilation. The three volumetric MDCT data sets acquired at different levels of inflation allow one to interrogate the effects of non-linear time-varying lung motion and boundary conditions during breathing. In the following sections we first present an overview and detailed methods for the entire modeling process from MDCT image acquisition to CFD simulation (Section 2), then present results for the image registration and the breathing lung model (Section 3), and finally compare the three-volume-based simulation against those based on one or two volume images (Section 4).

2. Methods

2.1. Method overview

Figure 1 shows a flow chart for illustration of the proposed computational framework for a subject-specific breathing lung based on multiple volumetric lung images. First, three MDCT volumetric data sets, I₁, I₂ and I₃, are acquired at different levels of inflation in the same scanning session. A mass-preserving image registration is then performed to match any two data sets to derive transform functions, defined as a voxel-by-voxel displacement. 3D MDCT-resolved airways and lobes are segmented from the image acquired at the largest lung volume (the image I₁ in the figure); these are then used to generate a subject-specific 1D centerline airway tree, and to build the 3D-1D multiscale framework. Each terminal bronchiole of the 1D airway tree is assigned a cube-shaped region inside the lungs, representing a pulmonary acinus (also referred to as a parenchymal unit). The registration-derived transform functions are then used to deform the segmented airway geometry into the domains of other two lung volumes, establishing the correspondence of the volume-specific airway geometries. In addition, air volumes inside each parenchymal unit associated with a terminal bronchiole (at all three lung volumes) are estimated using intensity-based air fractions along with registration-derived Jacobian values. Next, non-linear interpolations are adopted to derive deforming central airway geometries and time-varying regional air volumes associated with the terminal bronchioles. The time-varying regional air volumes are used to calculate regional ventilation fractions for the 1D terminal bronchioles, which are further passed on to the 3D MDCT exit segments as boundary conditions by utilizing the connectivity information and assuming mass conservation between the 3D airway and the associated 1D airway trees. Thus, the breathing lung model with deforming central airway geometry and physiological boundary conditions is constructed and can be used for CFD simulations.

Figure 1.

A flow chart of the entire process to develop the breathing lung model.

2.2. MDCT image acquisition

A normal human subject of a non-smoking, white non-Hispanic, 20-year old male was used in this study. The subject lay supine and breathed through a mouthpiece during the scanning session. The lung volume was well-controlled with a lab-developed volume controller system, and three static volumetric images were acquired during breath-holds at 78%, 60% and 20% of vital capacity (VC), denoted by I₁, I₂ and I₃, respectively. In addition, an image of the upper airway (to the roof of the soft pallet) with opened vocal-cords was also acquired. All scans were performed with the following settings using a Siemens Sensation 64-slice MDCT scanner (Forchheim, Germany): 120 kV, 75 mAs, 0.75 mm slice thickness, 500 mm field of view. The protocol was approved by the University of Iowa's Institutional Review Board. The acquired three images were reconstructed to 772 (for I₁), 713 (for I₂), and 645 (for I₃) slices with a spacing of 0.5 mm along the z-axis. The in-plane reconstruction matrix was 512 × 512 pixels with a pixel spatial resolution of 0.65 × 0.65 mm². The three lung data sets were processed using the software package Pulmonary Workstation 2 (PW2: VIDA Diagnostics, Coralville, Iowa) to segment the lungs, lobes and central airways. The segmented airways were further skeletonized to obtain the centerlines of individual branches. The upper airway was segmented using a region growing-based approach with an optimal threshold value [34]. The central airway geometry segmented from I₁ was merged with the upper airway and further processed for smoothing rough edges and clipping off mouth and the distal airways to create faces for specification of boundary conditions. The final 3D airway model used for numerical simulations includes branches up to 9 generations.

2.3. Image registration

Image registration is performed to match any two images and derive transform functions. A mass-preserving registration algorithm is adopted to estimate local tissue (parenchyma plus blood) and air fraction within the lung and to minimize the local tissue volume difference. Given I(x) as the Hounsfield unit (HU) for a voxel at location x in the lung region Ω, the tissue and air fractions can be estimated as [35][36]

$${\gamma }_{\mathit{air}}\left(I\right(\mathbf{x}\left)\right)=\frac{H{U}_{\mathit{tissue}}-I\left(\mathbf{x}\right)}{H{U}_{\mathit{tissue}}-H{U}_{\mathit{air}}},{\gamma }_{\mathit{tissue}}\left(I\right(\mathbf{x}\left)\right)=\frac{I\left(\mathbf{x}\right)-H{U}_{\mathit{air}}}{H{U}_{\mathit{tissue}}-H{U}_{\mathit{air}}}$$ (1)

where HU_air and HU_tissue refer to the HUs of air and tissue and can be estimated from samples at the center of the trachea (air) and aorta (blood), respectively. In this work, we used −1000 for HU_air and 55 for HU_tissue.

In registering two images, one image is used as the reference image and the other is the floating image. An optimal transform function, which is defined in the domain of the reference image, is obtained after registration. Based on Eq. (1), we can then define the similarity measure as the sum of squared local tissue volume difference (SSTVD) for a pair-wise registration:

$$E_{ij}=\sum _{\mathbf{x}\in \Omega }{\left[{\upsilon }_i\left(\mathbf{x}\right){\gamma }_{\mathit{tissue}i}\left(I_i\right(\mathbf{x}\left)\right)-{\upsilon }_j\left({\mathbf{T}}_{ij}\right(\mathbf{x}\left)\right){\gamma }_{\mathit{tissue}j}\left(I_j\right({\mathbf{T}}_{ij}\left(\mathbf{x}\right)\left)\right)\right]}^2$$ (2)

where T_ij(x) is the transform function between the two images i and j to be registered. υ_i and υ_j are the volumes of corresponding local regions in the two images, respectively, and υ_j can be calculated from the Jacobian value J_T of the deformation as υ_j = υ_iJ_T. The transform function is described by a composite operation of multi-level B-splines and a sufficient condition is imposed to ensure a one-to-one mapping even for a registration pair with large volume difference. Parameters of the transform function are optimized by a limited-memory, quasi-Newton minimization approach in a multi-resolution framework. For complete details, please refer to [37]. With the pair-wise registration, the transform function T₁₂ is obtained from the registration pair I₁ – I₂ with I₁ as the reference image and I₂ as the floating image, and T₂₃ is from the registration pair I₂ – I₃ with I₂ as the reference image and I₃ as the floating image. A composite operation of T₁₂ and T₂₃ is then set as a start point for the registration pair I₁ – I₃, which has the maximum deformation, to obtain the transform function T₁₃. Once the registration is performed, the resulting transform function can be used to transform the floating image domain into the reference image domain from an Eulerian viewpoint, obtaining the warped image. The transform function can also be used to deform any meshes in the reference image into the floating image domain from a Lagrangian viewpoint. The different viewpoints are adopted to transform image and mesh because an image is defined in a discrete domain while a mesh is defined in a continuous domain. In the following sections, for simplicity we will use the words “warped” and “deformed” to distinguish the transformed image and mesh.

Although 3D MDCT-derived airway geometries can be segmented for all three images, they provide no correspondence information and cannot be used for interpolations. With image registration, we can transform the airway segmented from the image I₁ into the domains of images I₂ and I₃ to obtain the deformed airways at I₂ and I₃ using the transform functions T₁₂ and T₁₃, respectively. The segmented airway at I₁, and the deformed airways at I₂ and I₃ have the same node and connectivity information, thus providing the correspondence information for interpolation. The registration-deformed airway is then compared against the airway segmented from the corresponding image to ensure the accuracy of the mapping.

In addition, with the image registration we can track the air volume within each cube-shaped region across the three image domains. Let Ω_a denote an acinus region in image I₁. The air volumes inside Ω_a at the three lung volumes can then be estimated from intensity-based air fractions along with registration-derived local Jacobian values as follows:

$$\begin{array}{cc}\hfill {\upsilon }_{\mathit{air}1}& =\sum _{\mathbf{x}\in {\Omega }_a}{\upsilon }_1\left(\mathbf{x}\right){\gamma }_{\mathit{air}}\left(I_1\right(\mathbf{x}\left)\right)\hfill \\ \hfill {\upsilon }_{\mathit{air}2}& =\sum _{\mathbf{x}\in {\Omega }_a}{J}_{12}\left(\mathbf{x}\right){\upsilon }_1\left(\mathbf{x}\right){\gamma }_{\mathit{air}}\left(I_2\right({\mathbf{T}}_{12}\left(\mathbf{x}\right)\left)\right)\hfill \\ \hfill {\upsilon }_{\mathit{air}3}& =\sum _{\mathbf{x}\in {\Omega }_a}{J}_{13}\left(\mathbf{x}\right){\upsilon }_1\left(\mathbf{x}\right){\gamma }_{\mathit{air}}\left(I_3\right({\mathbf{T}}_{13}\left(\mathbf{x}\right)\left)\right)\hfill \end{array}$$ (3)

where υ₁ is the volume of a voxel in image I₁ and γ_air is the air fraction based on Eq. (1). Jacobian values J₁₂ and J₁₃ reflect the volume contraction/expansion relative to I₁ and can be calculated from T₁₂ and T₁₃, respectively.

2.4. 3D–1D multiscale framework

We have previously shown a two-volume-based approach to estimate subject-specific boundary conditions by means of image registration [29]. Although it provides physiologically-meaningful boundary conditions and CFD simulation shows improved results over the more simplistic boundary conditions, the distribution of air ventilation fractions at distal ends (outlets) remains unchanged during breathing. With the availability of three volumetric lung data sets, we extend this approach with improved non-linear interpolation to derive time-varying regional ventilation.

The current 1D airway model is generated using the volume filling method proposed in [28]. This takes the lobes as “boundary conditions” and the skeleton of the 3D MDCT-resolved central airway tree as “initial conditions”. The lobes are first filled with a group of uniformly distributed seed points, where each seed point corresponds to a region approximately representing a pulmonary acinus. The locations of the seed points are defined at the largest lung volume (the image I₁ in this work) with the assumption that the lung is uniformly expanded. The number of seed points is approximately equal to the expected number of terminal bronchioles (30,000), which also determines the size of each acinus. The algorithm then works recursively by associating the seed points with the nearest peripheral branch in the respective lobe, calculating the center of mass of each group of seed points, splitting each group into two using the plane defined by the “parent” branch and the group's center of mass, and then creating branches that point towards the center of mass of the two point groups. A generated branch is declared as a terminal bronchiole if it is shorter than a user-defined limit or if it supplies only a single seed point. The combination of the generated 1D tree and the MDCT-derived 3D tree then provides a coupled multiscale framework with a seamless transition between scales.

Since each terminal bronchiole of the 1D airway tree is associated with a specific cube-shaped region of lung, it is reasonable to assume that change in air volume with time in each cube is equivalent to air flow for the corresponding terminal bronchiole. By tracking regional air volumes across different registered image data sets, we can then derive air flow rates at terminal bronchioles. By tree connectivity and mass conservation, we can then derive the flow rates at the 3D terminal airways.

2.5. Global to local linkage

The image registration described in section 2.3 can produce the Lagrangian mapping between any pair of MDCT volumetric images of the same subject. By linear interpolation between two images, one can construct any lung geometry whose volume lies between the two given volumes. However, the trajectories of any material points in the lung are straight lines between matching points in the two images and the distributions of flow rate fractions remain unchanged during a breathing cycle. With three volumes of MDCT images, cubic interpolation can be utilized to more accurately derive intermediate variables, such as air volume and airway surface. In this work, constrained cubic interpolation is adopted to avoid non-physiological overshoot between corresponding points at three lung volumes [38]. The total lung air volumes V₁, V₂ and V₃ of the three images I₁, I₂ and I₃ acquired at 78%, 60% and 20% VC are 6.08, 5.40 and 3.75 l, respectively, as marked in Figure 2. Since the lung is scanned at breath-hold for optimal spatial resolution without time information, we assume a sinusoidal waveform (Eq. (4)) with a normalized time period of 1 to fit the three lung air volumes. The maximum volume V₁ is at the normalized reference time t* = 0.5 and the minimum volume V₃ is at t* = 0 and 1. If the lung is scanned dynamically, the real time associated with the image can replace the reference time and the actual waveform of the flow rate at the mouth can replace the sinusoidal waveform.

$$V\left(t^{\ast }\right)=V_3+\frac{{\left(\Delta V\right)}_{\text{max}}}{2}(1-\text{cos}(2\pi t^{\ast }\left)\right)$$ (4)

where (ΔV)_max = V₁ − V₃. This sinusoidal reference breathing waveform is introduced to facilitate construction of cubic interpolation functions (which requires four data points per segment) using a limited number of image-derived data. The inverse function of Eq. (4) reads

$$t^{\ast }=\frac{1}{2\pi }{\text{cos}}^{-1}\left(1-\frac{2(V-V_3)}{{\left(\Delta V\right)}_{\text{max}}}\right)$$ (5)

With V = V₂, we have the corresponding $t\ast =t_2^{\ast }$. With the reference times $(t_1^{\ast },t_2^{\ast },t_3^{\ast })$ for lung volumes (V₁, V₂, V₃) and for the corresponding local variables (f₁, f₂, f₃), a cubic interpolation function for a local variable as a function of t* can be constructed as:

$$f\left(t^{\ast }\right)=a+b{t}^{\ast }+c{t}^{\ast 2}+d{t}^{\ast 3}$$ (6)

where the coefficients a, b, c, and d are computed for the reference time window, denoted by the dashed (dot-dashed) line in Figure 2, between 0 and $t_2^{\ast }$ ($t_2^{\ast }$ and 0.5), using local variables at the reference times of $-t_2^{\ast }$, 0, $t_2^{\ast }$, and 0.5 (0, $t_2^{\ast }$, 0.5, and 1 − $t_2^{\ast }$). Note that for CT images acquired at lung volume i there is only one single V_i value, thus a global variable, whereas there are numerous local f_i values. For example, the coordinates of a nodal point on the airway surface can be treated as a local variable f_i. If f₁ of a nodal point at V₁ is known, f₂ and f₃ of the same point at the other two lung volumes can be determined by registration. The trajectory of that nodal (Lagrangian) point can be approximated by Eq. (6). While the reference lung volume curve in Figure 2 is bounded by V₁ and V₃ (roughly corresponding to TLC and FRC, respectively), we can choose an arbitrary breathing (flow-rate) waveform imposed at the mouthpiece inlet and an end-expiratory volume V_EE, which can be greater than V₃. By time integration of the flow-rate waveform beginning from V_EE, we can get the “global” lung air volume V(t) at any instant of the breathing cycle. Then, the mapping between V_i and f_i illustrated in Figure 2 yields “local” variables f(t) at the same instant. At the end of inspiration, the volume V_EI shall be less than V₁. Both the coordinates of airway surface nodal points and the local air volume contents at terminal bronchioles are computed in this manner. The algorithm is summarized as follows:

Figure 2.

A schematic of the interpolation of time-varying local variable during a specific breathing cycle, with respect to global lung volume and reference time. Dashed (red) and dot-dashed (blue) lines represent two sections of respective interpolation curves based on three image data. Solid circles denote three image-derived data points.

Algorithm 1.

1. Compute the global air volume V(t) at time t of a breathing waveform.

2. Find the reference time t* for V(t) using Eq. (5).

3. Identify the corresponding reference time window for t* to construct the interpolation function.

4. Compute the local variable f using Eq. (6).

In the case of utilizing linear interpolation based on two images (I₁, I₃), Eqs. (4) and (5) remain the same, whereas the interpolation function becomes a straight line, thus c and d in Eq. (6) are zero.

2.6. Time-varying local ventilation fraction

At the terminal bronchioles, the local time-varying flow rate q(t) can be obtained by taking the time derivative of the interpolation function of the local air volume computed from Eq. (3).

$$q\left(t\right)=\frac{d{\upsilon }_{\mathit{air}}\left(t\right)}{dt}=\frac{d{t}^{\ast }}{dt}\frac{d}{d{t}^{\ast }}\left(a+b{t}^{\ast }+c{t}^{\ast 2}+d{t}^{\ast 3}\right)=\left(b+2c{t}^{\ast }+3d{t}^{\ast 2}\right)\frac{d{t}^{\ast }}{dt}$$ (7)

where υ_air (t) can be derived from (υ_air1, υ_air2, υ_air3) by interpolation and dt*/dt is uniform in space at a given instant t during a breathing cycle. Thus, the flow rate fraction at the terminal bronchiole i can be calculated by

$$q_i^{\ast }\left(t\right)=\frac{q_i\left(t\right)}{\sum _{j=1}^N{q}_j\left(t\right)}$$ (8)

where N is the number of terminal bronchioles in the entire lung. By airway tree connectivity and mass conservation, the flow rate fraction at a distal end j of the 3D airway can be determined as

$$Q_j^{\ast }\left(t\right)=\sum _{i=M\left(j\right)}^{M(j+1)-1}{q}_i^{\ast }\left(t\right)=\frac{\sum _{i=M\left(j\right)}^{M(j+1)-1}{q}_i\left(t\right)}{\sum _{i=1}^N{q}_i\left(t\right)}$$ (9)

where M(j) is the pointer to the beginning index of the array that contains all terminal bronchioles generated from the 3D MDCT-derived distal end airway branch j. In addition, the total flow rate at all outlets is calculated by mass conservation

$$Q_{\mathit{mouth}}+\underset{\Gamma }{\int }{\overrightarrow{u}}_{\mathit{awy}}\cdot \overrightarrow{n}d\Gamma +Q_{\mathit{dist}}=0$$ (10)

where ${\overrightarrow{u}}_{\mathit{awy}}$ is the velocity of an airway surface element during deformation, $\overrightarrow{n}$ is the unit vector in wall normal direction, and Γ depicts the airway surface. Q_mouth is the total volumetric flow rate given at the proximal inlet (mouthpiece) and Q_dist is the total flow rate at all distal ends of 3D airway with the positive direction pointing out of 3D domain. Combining with Eq. (9), the flow rate at an individual 3D distal end, j, is then determined by

$$Q_j=Q_j^{\ast }{Q}_{\mathit{dist}}.$$ (11)

The Dirichlet velocity boundary condition is then employed based on the obtained flow rate and the cross-section area at each distal end by assuming a parabolic velocity profile. This boundary condition, however, does not take into consideration of secondary flow. Quantitative analysis near boundaries shall then be avoided.

2.7. CFD simulation

Large eddy simulation (LES) is adopted to capture laminar, transitional and turbulent flow. The governing equations consist of the filtered continuity equation and Navier-Stokes equations for incompressible flow in an arbitrary Lagrangian-Eulerian (ALE) framework for moving mesh:

$$\frac{\partial u_j}{\partial x_j}=0$$ (12)

$$\frac{\partial u_i}{\partial t}+(u_j-u_j^{ALE})\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[(\nu +{\nu }_T)\frac{\partial u_i}{\partial x_j}\right]$$ (13)

where u_i, $u_i^{ALE}$, p, ρ, ν, and ν_T are the i-th components of fluid and grid velocities, pressure, density, kinematic viscosity, and subgrid-scale eddy viscosity, respectively. The density and the kinematic viscosity of the air are 1.2 kg/m³ and 1.7 × 10⁻⁵ m²/s, respectively. The subgrid-scale eddy-viscosity model proposed by Vreman [39] is adopted to account for transitional and anisotropic flow characteristics, and becomes zero in the laminar regime. A pressure-Poisson equation is solved to enforce the continuity equation (12). A fractional four-step and implicit characteristic Galerkin based finite element scheme is employed to solve the governing equations.

In order to capture the turbulent laryngeal jet, as shown in [13], the upper airway geometry is included in the computational domain. A mesh with 608,389 nodal points and 2,842,900 tetrahedral elements is generated based on previous sensitivity studies of similar airway models [10], and is further divided into 192 or 384 partitions for message passing interface (MPI)-based parallel computation. In addition, a fine mesh with 2,668,038 nodal points and 13,410,079 tetrahedral elements is used for the mesh sensitivity test. The average grid width ratio of the refined mesh to the original mesh is about 0.6 as shown in Figure 3. A spatio-temporal convergence test is conducted using the flow condition at the peak inspiration of deep breathing, having a flow rate of about 920 ml/s and the Reynolds number (Re) of about 3,500 in the trachea. Time steps of 5.0 × 10⁻⁶ s and 2.0 × 10⁻⁶ s are chosen for the original mesh and the refined mesh, respectively, to satisfy the Courant–Friedrichs–Lewy (CFL) condition. The mean and turbulence statistics are computed based on 80 data sets with an interval of 0.006 s. Figure 3 shows the isosurface of instantaneous air speed at 5.5 m/s color-coded by pressure contours and the mean speed in a vertical plane, the normalized turbulent kinetic energy by the mean speed in the trachea for the two meshes. They are in good agreement. Pressure drops to distal airways have the average relative error of 4.4% and the difference is not statistically significant (p > 0.05). The mesh sensitivity test results indicate that the original mesh is adequate for the current study.

Figure 3.

Comparison between (a) the original and (b) the refined meshes for a case at an inspiratory flow rate of about 920 ml/s. The cross-sectional mesh in the trachea, isosurface of instantaneous air speed at 5.5 m/s color-coded by the pressure contour, mean speed in a vertical plane of the trachea, and normalized turbulent kinetic energy of the laryngeal jet in dashed box are shown from left to right. Arrows mark the high turbulent region.

3. Image registration and breathing lung model

3.1. Registration accuracy

The registration method has previously been validated using hundreds of landmarks for different pairs of volumetric MDCT data sets, and the method has been shown to be effective at registering intra-subject lung MDCT data sets [37]. Figure 4 shows the comparison of a sagittal section from (a) the image I₁, (b) the warped image of I₂, and (c) the warped image of I₃ at the same axial location. The sagittal sections are oriented such that the diaphragm is at the bottom, the dorsal surface (nearest the scanner table) is on the right and the ventral surface is on the left. In addition, sections from the original images I₂ and I₃ at the same axial location are also shown in (d) and (e), respectively, for reference. All panels (a)–(e) have the same heights and widths. The comparison shows that the warped images (b) and (c) have good anatomic correlations with (a), indicating that registrations are able to recover the deformations among the three original images.

Figure 4.

Visual assessment of registration accuracy. A sagittal slice from (a) the image I₁, (b) the warped image of I₂, (c) the warped image of I₃, (d) the image I₂, and (e) the image I₃ at the same axial locations, respectively. All panels have the same sizes.

3.2. Registration-derived airway deformations

Figure 5 shows 3D airway geometries segmented from the three lung volumetric images: (red, green, blue) for (I₁, I₂, I₃). We can see that the airway geometry deforms with changes in lung volumes. As the lung volume decreases, the lengths of the branches become shorter and the airways contract towards the apex, which results in smaller airway volume.

Figure 5.

3D MDCT-derived airway geometries segmented from the three lung volumetric images: Red for I₁, green for I₂, and blue for I₃.

To further demonstrate the capability of registration in matching the deformation of the airway geometries, we compare the airways directly segmented from I₂ and I₃ against the airways that are transformed from I₁ using the transform functions T₁₂ and T₁₃, shown in Figures 6 and 7, respectively. In Figure 6(a), the airway of I₂, shown in green, is superimposed over the deformed airway at I₂, shown in pink. Figures 6(b) and (c) present the comparisons between the two geometries at two selected cross sections, where the extracted curves from the airway of I₂ are shown in green and the ones from the deformed airway are shown as pink dots. The curves extracted from the undeformed airway geometry of I₁ at those two cross-sections are shown in red as a reference. In Figure 7 the airway of I₃ is shown in blue and the deformed airway at I₃ is shown in orange. Similarly to Figures 6(b) and (c), Figures 7(b) and (c) show the curves extracted from the airway of I₃ (blue) and the deformed airway (orange dot) at the two cross sections. The undeformed airway geometry of I₁ is also displayed in red. These comparisons clearly indicate that the deformed airways obtained from image registration match well with the airways segmented from the images. More importantly, the deformed airways are obtained by applying the transform functions onto the I₁ airway; thus, they all have the same node and connectivity information, establishing the correspondences among the three domains. The airway at I₁, the deformed airway at I₂, and the deformed airway at I₃ can then be used as the base geometries for interpolation.

Figure 6.

Comparison between the segmented airway from I₂ (60% VC) and the airway deformed from I₁ with the transform function T₁₂: (a) whole airway from I₂ (green) and the deformed airway (pink); (b) the extracted curves from the I₂ (green) and from the deformed airway (pink dot) at a cross-section in the middle of trachea; (c) the extracted curves from the I₂ (green) and from the deformed airway (pink dot) at a cross-section after the carina. The undeformed airway geometry from I₁ at those two cross-sections are shown in red in both (b) and (c). In addition, an interpolated airway at 60%VC using the linear interpolation between the two lung volumes at I₁ and I₃ is also shown in gray (surface or curves) to demonstrate the insufficiency of the linear interpolation.

Figure 7.

Comparison between the segmented airway from I₃ (20% VC) and the airway deformed from I₁ with the transform function T₁₃: (a) whole airway from I₃ (blue) and the deformed airway (orange); (b) the extracted curves from the I₃ (blue) and from the deformed airway (orange dot) at a cross-section in the middle of trachea; (c) the extracted curves from the I₃ (blue) and from the deformed airway (orange dot) at a cross-section after the carina. The undeformed airway geometry from I₁ at those two cross-sections are shown in red in both (b) and (c).

Owing to cubic spline interpolation, the trajectories of the airway geometry exactly pass the base geometries and C₁ continuity of each path is guaranteed. By contrast, a linear interpolation would lead to C₁ discontinuities at the intersection of two pairs of linear interpolations. In addition, the dynamic model derived from the three lung volumes can track the lung motion more precisely by comparing against the model based on two lung volumes. Non-linear interpolation can be utilized with the three lung volumes while only linear interpolation is available with the two lung volumes. Non-linear interpolation is more physiological than linear interpolation between two lung volumes, or piece-wise linear interpolations between three volumes, since lung elasticity is non-linear. To demonstrate the insufficiency of linear interpolation, we calculate the interpolated airway at 60% VC using the linear interpolation between the two lung volumes I₁ and I₃ and show it (in gray) in Figure 6. This clearly illustrates the differences between the interpolated airway at 60% VC and the undeformed airway of I₂.

3.3. Registration-derived regional ventilation

Figures 8(a) and (b) show the 3D-1D coupled airway tree in the respective coronal and sagittal views. The color-coded 1D airways generated from the distal ends of the 3D airway depicts the relative locations of 1D sub-trees in the five lobes. Upper lobes are placed in relatively ventral and apical regions, while lower lobes are in dorsal and basal regions. The distributions of air volume associated with each terminal bronchiole are shown from a sagittal view in Figures 9(a)–(c) for the three imaged lung volumes. The unit of air volume is mm³. In Figure 9(a) there is a gravitational gradient with less air in the dependent (dorsal) region than in the nondependent (ventral) region. In Figure 9(b), air volume increases but the gravitational gradient still exists. In Figure 9(c) the air volume increases more and becomes uniformly distributed in the whole lung. All these observations follow well the recognized physiology of ventilation in subjects positioned in the supine body posture [40]–[44]. For I₁, the lung volume is close to TLC and all alveoli inside the lungs are close to full expansion, thus leading to uniform air volume distribution in Figure 9(c). When air is exhaled from the lung, due to the motion of the diaphragm and the effect of gravity, the dorsal region recoils more than the ventral region so that less air is left in the dorsal region, forming the ventral-dorsal gradient.

Figure 8.

3D MDCT-resolved airway and generated 1D centerline airway from two views: (a) coronal and (b) sagittal. The generated airways are shown in different colors for each lobe: red for left upper lobe (LUL), green for left lower lobe (LLL), cyan for right upper lobe (RUL), blue for right middle lobe (RML) and pink for right lower lobe (RLL).

Figure 9.

The distributions of air volume associated with each terminal bronchiole for three data sets: (a) I₃, (b) I₂ and (c) I₁. The unit is mm³.

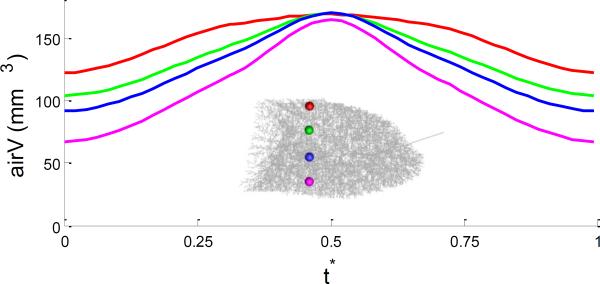
The air volume associated with each terminal bronchiole at any intermediate step can then be derived from the three states by interpolation. Again, owing to the cubic interpolation, the regional air volumes change non-linearly with time. To illustrate the temporal variation of local air volumes, Figure 10 presents the curves of air volumes at four locations selected from ventral to dorsal regions inside the lungs. The locations are marked with spheres in different colors and the curves of air volumes at the four locations are plotted in the same colors as the corresponding locations with respect to the reference time t*. This figure further illustrates the recognized lung physiology of ventilation in subjects positioned in the supine body posture. At the end of expiration, acini in the non-dependent regions are filled with more air. As the lung expands from 20% VC (V₃) to 78% VC (V₁), dependent regions expand more than non-dependent regions as air flows into the lung and eventually all regions fully expand, resulting in uniform distributions of air volume inside the lung.

Figure 10.

Time-varying air volume associated with terminal bronchioles for four selected locations in the lung. The locations are marked with spheres in different colors and the curves of air volume at the four locations are plotted in the same colors as the corresponding locations.

3.4. Breathing lung model

By combining the deforming airway geometry and time-varying local air volume, we can construct the breathing lung model. The four panels shown in Figure 11 correspond to four different time points in a breathing curve between lung volume V₃ and V₁: (a) t* = 0, (b) t* = 1/6 (≈0.17), (c) t* = 1/3 (≈0.33), (d) t* = 1/2 (0.5), with t* as the reference time, and (a) and (d) correspond to the lung volumes V₃ and V₁, respectively. The deforming airway geometry and the heterogeneous time-varying air volume distribution are clearly indicated. Similarly, we can calculate the flow rate fraction according to Eq. (8) during a breathing cycle. The four panels shown in Figure 12 correspond to four different times at: (a) t* = 0.01, (b) t* = 1/6 (≈0.17), (c) t* = 1/3 (≈0.33), (d) t* = 0.49. Figures 12(a) and (d) correspond to the lung volumes slightly greater than V₃ and slightly less than V₁, respectively, and are chosen for demonstration because the flow rates calculated by Eq. (7) at t* = 0 and t* = 0.5 are zero. The figures clearly show that the flow rate fraction varies with lung inflation during breathing. A noticeable regional dependency of the time-varying flow rate fraction distribution is also observed. At the end of expiration, all regions inside the lung are smaller than during inspiration, but the dependent regions are smaller than the non-dependent regions due to gravitation effects. At a small lung volume, air is able to flow into all regions inside the lung, resulting in a relatively uniform distribution of flow rate fractions. As the lung volume increases, the non-dependent regions first reach their maximum capacities, whereas the dependent regions are still expanding so that more air flows into the dependent regions than the non-dependent regions. Thus, the dependent regions have larger flow rate fractions than the non-dependent regions, as shown in Figures 12(c) and (d). This tendency at the lung periphery is reflected in the larger airways due to mass conservation.

Figure 11.

Moving airway geometry and the distribution of air volumes associated with terminal bronchioles extracted from the breathing lung model at four different time points in a breathing cycle between the lung volumes V₃ and V₁: (a) t* = 0; (b) t* = 0.17; (c) t* = 0.33; (d) t* = 0.5. (a) and (d) correspond to the lung volume, V₃, and lung volume, V₁, respectively.

Figure 12.

Deforming airway geometry and time-varying regional air flow fraction distribution associated with terminal bronchioles at different time points in a breathing cycle between the lung volumes V₃ and V₁: (a) t* = 0.01; (b) t* = 0.17; (c) t* = 0.33; (d) t* = 0.49.

The time-varying local ventilation at the terminal bronchioles leads to definition of the flow rate fractions at all 33 outlet boundaries of the 3D airway model. Figure 13(a) first shows the time-varying flow rate fractions at all the outlet boundaries derived from three images (I₁, I₂, I₃). The constant flow rate fractions derived from two images (I₁, I₃) are shown in Figure 13(b) for comparison. Four selected outlet boundaries 6, 13, 16, and 25 demarcated by boxed numbers are located in the ventral (and vertically middle) region, the basal region, the basal dorsal region, and the ventral region, respectively, as shown in Figure 13(c). Figure 13(d) shows the changes of flow rate fractions from V₃ to V₁. The flow rate fractions decrease at all the outlets in the left upper lobe (LUL), they all increase in the right lower lobe (RLL), and most of them increase in the left lower lobe (LLL). The highest decrease is observed in the right middle lobe (RML), in which the inflation will be the least among the five lobes due to its limited size. The changes in regional flow rate fractions from V₃ to V₁ are not trivial. Figure 13(e) illustrates the regional distribution of the increases of flow rate fractions normalized by the average flow rates shown in Figure 13(b). Relative changes vary from −80% (decrease) to +60% (increase) and they exhibit high correlations with the ventral-to-dorsal locations. The increase of relative local flow rate fraction is greater near the dorsal region and less near the ventral region. The boundary 16 in the dorsal basal region has the greatest increase, and the boundary 25 has the greatest decrease.

Figure 13.

Time varying ventilation at distal ends of 3D model. (a) The time-varying flow rate fractions with respect to the global lung volume and (b) the two-image-based constant flow rate fractions at distal ends of 3D airway model illustrated in (c). (c) A side (left) view of 3D airway model. The upper airway is not shown. Boxed numbers denote the indices of four selected boundaries. (d) The flow rate fraction increase at each outlet of 3D airway model. (e) The ventral-to-dorsal dependency of the flow rate fraction increases at normalized by the average values between V₁ and V₃.

Accordingly, the lobar ventilation fractions also vary with time, showing a similar regional dependency of time-varying ventilation. Figure 14 shows the sum of the flow rate fractions over all airways in the five lobes at four selected reference times based on three images (I₁, I₂, I₃). The constant lobar fractions obtained from two images (I₁, I₃) and those based on the assumption of uniform velocity at the outlets for one image (I₁) are also displayed for comparison. It is noted that the lobar ventilation fractions derived from the three images are time dependent. The ventilation fractions decrease in the upper and middle lobes whereas they increase in the lower lobes, being consistent with the results in Figure 13(d). More specifically, the LUL experiences the largest (25.5%) decrease in ventilation fraction from 0.235 at t* = 0.01 to 0.175 at t* = 0.49, whereas the LLL undergoes the largest (28%) increase from 0.25 at t* = 0.01 to 0.32 at t* = 0.49. In addition, with regards to the spatial distributions, the lower lobes (LLL and RLL) have greater flow fractions than the upper and middle lobes (LUL, RUL and RML), being consistent with physiological observations. In contrast to the three-volume-based time-varying results, the two-volume-based lobar ventilation fractions remain constant, but are approximately equal to the time-average three-volume-based lobar ventilation fractions. Nonetheless, the one-volume-based results deviate greatly from those using two and three volume images, especially in the lower lobes.

Figure 14.

Comparison of lobar ventilation (flow rate fractions) of three-volume-based regional ventilation model at 4 reference times of deep breathing with the two-volume-based constant regional ventilation model and the one-volume-based model with uniform velocity.

4. CFD results

In this section, we consider four different cases to examine the effect of the number of volumetric lung images and the effect of rigid versus compliant airway models. Two of these cases are conducted in a normal breathing condition, and the other two are in a deep breathing condition. Table 1 summarizes the major parameters and conditions for these four cases.

Table 1.

Comparison of CFD simulation cases

Case	I	II	III	IV
Number of images used	3	1	3	2
Airway deformation	Deforming (non-linear trajectory)	Rigid	Deforming (non-linear trajectory)	Deforming (linear trajectory)
VEE (l)	3.75	6.08	3.75	3.75
VEI (l)	4.25	6.08	6.08	6.08
VEI–VEE(l)	0.5	0	2.33	2.33
Outlet BC	Time-varying regional ventilation	Uniform velocity	Time-varying regional ventilation	Time-constant regional ventilation
Peak flow rate (ml/s)	327	327	918	918
Peak Re at the trachea	1250	1250	3511	3511
Average pressure drop1 at peak inspiration (Pa)	56	33	372	357

¹The average pressure drop is for the 3D model (not for 3D–1D)

4.1. Normal breathing simulation

The first case (Case I) utilizes the three-volume-based lung model and simulates the air flow during normal breathing. The deforming airway geometry is considered. The initial airway geometry is near the image I₃ at the beginning of the inspiration and the airway motion is constrained in the normal breathing range (corresponding lung volume range of (V₃, V₃ + 500 ml)). A sinusoidal flow-rate waveform with a time period of 4.8 s and an amplitude of 327 ml/s is imposed at the mouthpiece inlet, resulting in a tidal volume of 500 ml. The Reynolds number in the airway is defined as

$$\mathrm{Re}=\frac{UD}{\nu }=\frac{Q}{A}\frac{D}{\nu }=\frac{4Q}{\pi D^2}\frac{D}{\nu }=\frac{4Q}{\pi \nu D}$$ (14)

where U, D, Q, and A are the average velocity, average diameter, flow rate, and average cross-sectional area in an airway segment. The Reynolds number in the trachea reaches a maximum of 1,250 at the peak inspiratory flow rate of 327 ml/s. A time step of 1.0 × 10⁻⁵ s is chosen to satisfy the CFL condition. The simulation results at peak inspiration and expiration are shown in Figure 15. An isosurface of air speed at 2 m/s color-coded by pressure is shown in Figure 15(a) for inspiration and (c) for expiration. In addition, the contours of air speed in the vertical y-z cross-section are plotted in Figure 15(b) for inspiration and (d) for expiration. On inspiration, the airway constriction at the glottis induces the turbulent laryngeal jet [10][13]. On expiration, free-shear jet-like flows are formed when air flows from child (small) branches to parent (large) branches, resembling pipe flow in a sudden expansion.

Figure 15.

Demonstration results of 3D LES of normal breathing. (a) and (c) show the isosurface at air speed of 5 m/s color-coded by pressure contours. (b) and (d) show the instantaneous air speed contours in a vertical plane through the trachea (a) and (b) are snapshots at the peak inspiration, and (c) and (d) are at the peak expiration.

The average pressure drop from the mouthpiece inlet to the distal ends of the 3D airway model is about 56 Pa at peak inspiration. With the 3D-1D coupled framework, we can further estimate the pressure drop from the distal ends of 3D airway segments to the terminal bronchioles using the 1D entry flow model of Pedley et al. [45]. The average pressure drop from the mouthpiece inlet to the terminal bronchioles calculated based on 3D-1D coupled simulation is found to be 78 Pa. The average pressure drop in the lower lobes (LLL and RLL) is 110 Pa. These values are within the typical range of pressure drop in normal breathing, which is about 1 cmH20 (~98 Pa) [41]. The relatively higher pressure drop in the lower lobes than the upper lobes is also physiologically consistent with known regional variation of pressure drop in the lung.

4.2. Effect of the number of volumetric image data sets

In this section, we compare air flow simulations based on one image (I₁), two images (I₁, I₃), and three images (I₁, I₂, I₃) in order to investigate the effect of the number of image data sets on flow patterns. Case I, already presented in Section 4.1, utilizes all three images to account for the non-linear deforming airway and time-varying regional ventilation. The deforming airway geometry is near FRC with the deformation in the normal breathing range. Case II is based on a single image I₁ at 78% VC rather than image I₃ at 20% VC to mimic the scenario that, if only one image is available, the image scanned at a larger lung volume is desirable to obtain more generations of airways. With one image, the distribution of regional ventilation cannot be derived for boundary conditions. Consequently, the air speeds at the boundaries of the 3D terminal airway segments are assumed constant and are obtained by dividing the flow rate at the mouthpiece inlet by the sum of the areas of the peripheral boundaries. The same flow-rate waveform is used in both cases.

The results of Cases I and II are depicted in Figure 16 (17) at peak inspiration (expiration). The central airway tree in Case I is shorter because it corresponds to the airway geometry near FRC. At peak inspiration (expiration), the average pressure difference between the mouth and all the outlets is 55.7 Pa (42.4 Pa) in Case I, while it is 33.1 Pa (32.9 Pa) in Case II. That is, the rigid airway model under-predicts 40.5% (22.3%) of the pressure drop at peak inspiration (expiration) because the rigid airway derived from I₁ is larger than the deforming airway during normal breathing. The percent differences in pressure drops in the five lobes (LUL, LLL, RUL, RML, RLL) using Case I as the reference are (22%, −6%, 21%, 7%, 73%) at peak inspiration and (13%, −35%, 11%, −4%, 61%) at peak expiration. In addition, differences are also observed at distal airways between the two cases. The flow ventilation in Case I is specific to the subject because it is derived from MDCT images (see Section 3.3). Case II, however, does not warrant realization of subject-specific regional ventilation. The difference in flow ventilation leads to the difference in pressure drop. As enlarged in Figures 16(c) and 16(d) (17(c) and 17(d)) for inspiratory (expiratory) flow, the pressures at individual outlets deviate noticeably with the difference up to 149% (92%) for inspiration (expiration) with reference to Case I. The pressure drop is overall greater in the pathway of dorsal branches in Case 1 due to the ventral-dorsal regional ventilation tendency. However, this tendency is not observed in Case 2.

Figure 16.

Comparison of isosurface of air speed at 2 m/s color-coded by the pressure contour at the peak inspiratory flow between (a) the three-image-based realistic normal breathing case and (b) the single-image based case near 78%VC with traditional boundary condition (uniform flow). The left lung in the dashed boxes of (a) and (b) are enlarged in (c) and (d), respectively.

Figure 17.

Comparison of pressure distribution at the peak expiratory flow between (a) the three-image-based realistic normal breathing case and (b) the single-image based case near 78%VC with traditional boundary condition (uniform flow). The left lung in the dashed boxes of (a) and (b) are enlarged in (c) and (d), respectively.

Next, Cases III and IV based on three and two images are compared. Both cases simulate air flow during deep breathing with lung volume deforming from about V₃ to V₁. A sinusoidal breathing waveform with a period of T = 8 s is imposed at the mouthpiece inlet to produce a maximum volume change (inhaled air volume) of ~2.33 l, which is almost five times the normal breathing cases (Cases I and II). Pressure distributions are shown in Figures 18(a) and (b) for Cases III and IV at an inspiratory phase of t/T = 0.15. Both cases exhibit similar pressure distributions in the large airways. However, the degrees of airway geometry deformation and the pressure distributions in distal small airways are different. For example, at t/T = 0.15, the pressure drop in the LLL (dashed box, shown in the enlarged view in Figure 18(c)) is smaller in Case III than in Case IV but it is reversed in the RUL (solid box). At a later time t/T = 0.30 with a greater inflation level, the pressure drops in the lowest two distal airway segments increase in Case III while the pressure remains nearly the same in Case IV. Those two distal airways correspond to the boxed 13 and 16 outlet boundaries in Figure 13, in which the flow rate fractions increase as the lung expands. An increase in flow rate fraction during breathing contributes to an increase in pressure drop. On the other hand, the pressure drops at the boxed 6 and 25 outlet boundaries - in which the flow rate fractions decrease with time in Case III - decrease with time as compared with Case IV. The small airways associated with these boundaries are located in the ventral and vertically middle regions as shown in Figure 13. In addition, the deforming airways in Cases III and IV at the same dimensionless time (the same global lung volume) are different. Figure 18(b) shows that the three-volume-based airway (Case III) is slightly smaller than the two-volume-based one (Case IV). This is because in Case III the intermediate image I₂ poses an additional constraint in constructing, via cubic interpolation, non-linear deforming airways. Figure 19 illustrates non-linear trajectories of some selected nodes on the airway surface between images I₁ and I₃. The black lines show trajectories of selected nodes derived from the three images (I₁, I₂, I₃). These nodes move along non-linear trajectories, which pass through their corresponding nodes at images I₁, I_2, and I₃. In contrast, for the two-volume-based model the surface nodal points are constrained to move along line trajectories between their corresponding nodes at images I₁ and I₃. The differing trajectories of the airway surface nodes result in different deforming airway models. Figure 20 compares the volumes of the 3D airway models for Cases III and IV as a function of the global lung volume in the range of V₃ and V₁. The 3D airway volume in Case III is smaller than that of Case IV except near the maximum lung volume. Furthermore, the change of 3D airway volume is very small compared to the change of lung volume. From V₃ to V₁, the current 3D airway volume (of up to 7 generations) only increases by 8 ml, which is only 0.36% of the global lung volume change (V₁ − V₃ = 2.33 l). For normal breathing (Case I), the 3D airway volume increases by 1.4 ml from end expiration to end inspiration, which is 0.28% of the global lung volume change of 500 ml.

Figure 18.

Comparison of pressure drop at an inspiratory phase of t/T = 0.15 of deep breathing, using the approaches based on (a) three images and (b) two images. (c) Enlarged views of LLL (dashed box) from (a) (left) and (b) (right). (d) The same views at later time t/T = 0.30.

Figure 19.

Connected lines of black symbols show trajectories of selected local points in the airway during non-linear deformation. The airway surfaces of I₁ and I₃ are denoted by the light gray and the light green, respectively.

Figure 20.

Change of volume in 3D airway with respect to the global lung volume based on the cubic interpolation from three images (solid line) and the linear interpolation from two images (dashed line).

Another observation from Case III of the three-volume-based deep breathing simulation is that the local Re can reach the maximum before or after the global peak flow rate. Figure 21(a) shows four selected outlet boundaries of boxed 6, 25, 13, and 16 in Figure 13. The x-axis is the normalized inflation level V_n = (V − V₃)/(V₁ − V₃), which correlates with the intermediate phase during a sinusoidal breathing cycle, and V_n = 0.5 corresponds to the peak inspiration. Boundaries 6 and 25, at which the flow rate fractions decrease, reach the maximum Re earlier at V_n = 0.41 for boundary 6 and V_n = 0.38 for boundary 25. On the other hand, boundaries 13 and 16, at which the flow rate fractions increase, reach the maximum Re later at V_n = 0.56 for boundary 13 and V_n = 0.74 for boundary 16. Such an asymmetric flow feature is not present in the two-imaged-based model as shown in Figure 21(b). Figures 21(c) and (d) show the variations of flow rates and diameters at those exit boundaries of the ending airway segments. The earlier or later occurrences of maximum Re values at these segments than the global peak flow appear to be correlated with their respective time-varying flow rates and diameters, and mainly affected by the flow rates.

Figure 21.

Changes of Reynolds numbers at selected outlets of 3D airway corresponding to the (a) three- and (b) two-image-based breathing lung model, and changes of (c) flow rates and (d) diameters corresponding to the three-image-based model.

5. Discussion

In this paper, we proposed a technique to build a multiscale breathing lung model from MDCT volumetric data sets acquired at different inflation levels. Pair-wise mass-preserving image registration was performed to match any two data sets to derive transform functions. The transform functions were then used to deform the airway geometries to establish correspondence for interpolation. Comparisons between the deformed airways and the targets show good agreement. In addition, local air volumes for lung parenchyma at three inflation levels were estimated with intensity-based air fractions along with registration-derived Jacobian values. Given three images, a cubic spline interpolation was utilized to build a breathing lung model with deforming airway geometry and non-uniform changes in local air volumes. Subject-specific boundary conditions for the 3D MDCT-resolved central airways at an instant were then produced based on regional air volumes in a 3D-1D coupling multiscale framework. The proposed breathing lung model derived from three images was then used for CFD simulations and was compared against the one- and two-image-based models. When only one image is available, the distribution of regional ventilation cannot be derived for boundary conditions and the airway geometry is assumed to be rigid. Using more than one image allows one to model physiologically-consistent (or anatomically-based) local variables, most importantly including airway deformation between the volumes of given images. With two volumes, airway surface trajectory is restricted to a straight line that connects corresponding nodes at two images, and regional ventilation distribution is constant with time. When three images are utilized, the smooth surface trajectory and time-varying regional air volume distribution can be obtained by cubic interpolation, consequently providing the temporal variation of local flow rate fractions. Due to the lack of subject-specific airway motion and boundary conditions, the one-image-based model yields non-physiological flow results with arbitrary lobar ventilation distributions and under-predicted pressure drops. The two-image-based model accounts for airway deformation and non-uniform regional ventilation to some extent and shows improved results against the one-volume-based methods. However, due to the straight-line trajectories and time-invariable ventilation, it does not capture some flow details, such as pressure drop and airway deformation.

Since airway deformation and regional ventilation are derived from MDCT images of an individual, the breathing lung model is subject-specific. In addition, the proposed framework combines both the 3D and 1D airway trees, considers the regional ventilation from a local voxel to global sub-lung regions, and accounts for turbulent-transitional-laminar flows. Thus the proposed model is multiscale. In regions of interest, at a local level, we can capture accurate air flow-induced wall stresses needed for future study of mechanotransduction (in 3D) and, at the global level, we can recover whole lung ventilation and airway resistance.

Image-derived data allows subject-specific air flow simulation of the human lung. The range of breathing conditions to which the model is applicable is improved by using multiple image data. A brief comparison is presented in Table 2. The three-volume-based model is capable of predicting the dynamic behavior of regional air volume distributions and modeling the non-linear motions of the airway geometry, while the two-volume-based model implies constant flow rate fractions at distal outlets and straight-line trajectories of airway deformation during breathing cycles. As shown in the previous section, some local pressures increases faster than other regions as the local flow rate fraction increases according to the lung inflation. This implies that the local airway resistance increases compared to the global airway resistance, which may cause abnormal behaviors in the related region of the lung. The model constructed from three or more volumetric lung images or even 4D CT can definitely yield improved flow results since more information can be extracted to estimate regional ventilation and airway motion. However, with the constraint of radiation dose, one or two lung images are commonly acquired. If two lung images are available, the CFD model should definitely be constructed from both of them. Even though some flow features, such as changes of local pressure with time, cannot be captured, the two-volume-based model is able to account for physiological boundary conditions and airway motions. If only one image is available, we need to assume reasonable physiological boundary conditions at the ending segments, which may be approximately described by some simple mathematic ventilation models or using the lobar ventilation fractions presented in this paper.

Table 2.

Comparison of capability for different number of image data.

Number of image data	1	2	3	More than 3
Subject-specific geometry	Yes	Yes	Yes	Yes
Regional ventilation BC	N/A	Time-constant	Time-varying	Time-varying
Moving airway	N/A	Linear interpolation of local points (C0 continuous)	Non-linear interpolation (C1 continuous)	Non-linear interpolation (C1 continuous)
Breathing cycle specificity	No	Limited	Yes	Yes
Correspondence to global lung volume	Rigid with given single volume	Linear trajectory of individual surface nodes may cause volumetric defect.	Same capability as more image based approach regarding algorithm	Interpolation error may decrease if number of images increases.

It is noted that some limitations exist for the proposed method. First, all components for the breathing lung models are directly derived from images, which are captured in a certain body posture (for example, supine position in this work). If suitable material properties are chosen, models for soft tissue mechanics [46][47] are able to account for the displacement and motion of the lung in any posture. Combining the advantages of both registration and tissue mechanics approaches might be a good direction for future work. In addition, due to radiation dose limit, only one image was acquired for the upper airway and thus, the deformations of upper airways, including the glottis, is assumed rigid in this study. The most obvious motions of upper airways are related to the opening/closure of vocal cord. Mouth cavity should have little deformation. The glottis motion depends on breathing maneuvers and it is larger on inspiration than on expiration. Stanescu et al. [48] reported a correlation between glottis opening, lung volume and flow rate during panting and slow expirations. Using their correlation to estimate the area change associated with the change of the airflow rate in the range of 150–342 ml/s and the corresponding air volume change of about 142 ml on inspiration, the glottis area is estimated to vary by about 9%, resulting in a constriction varying between 55% and 59%. Given the convective nature of the flow and with the above range of variation in constriction, the level of turbulent fluctuation is not expected to change dramatically. For expiratory flow, the change of the glottis area is even smaller and will have little effects on the flow in the central airways. This is because the glottis is located on the downstream side of the flow in the trachea during expiration. Some possible future studies can be performed by accounting for the realistic deformation from multiple images by using image registration. The expected outcome of including the upper airways is to produce physiologically-consistent intensity of flow disturbance in the central airways during inspiration. Furthermore, although the current 1D model accounts for individual image information, such as the central airway and lung boundary, some underlying assumptions may cause uncertainties of the tree structure and are limited to normal lungs. With regards to uncertainties, the effects of the generated 1D tree structure on the 3D boundary conditions should be subtle since the 3D boundary conditions depend on the affected parenchyma regions, instead of the local 1D airway structures. For example, the acinus density could have been substantially increased and this would have changed the ventilation of each individual acinus but not the summed ventilation at the level of the 3D model. In order to evaluate the effects of the 1D airway tree structures, we have performed uncertainty analysis. Three 1D trees were generated by adjusting the seed point densities: tree A with 30,306 terminal bronchioles (used in this paper), tree B with 25,999 terminal bronchioles and tree C with 36,422 terminal bronchioles. The results showed that the differences of the air volumes associated with 3D MDCT ending branches are not statistically significant (p = 0.71 between tree A and tree B, p = 0.98 between tree A and tree C). With regards to the second aspect, the 1D tree modeling method is likely to be a reasonable first approximation for modeling the distribution of asthmatic airways within the lung (or with some modification such as [49]) when there is no evidence of lung tissue loss. For the emphysematic lung, the extent to which the algorithm would need to be modified depends on the degree of emphysema. For severe emphysema, where the distribution of the terminal bronchioles at TLC could be far from uniform, it may be necessary to distribute the `seed points' for tree growing non-uniformly (assuming that we have some a priori knowledge of the distribution of the acini).