FreeSurfer

Abstract

FreeSurfer is a suite of tools for the analysis of neuroimaging data that provides an array of algorithms to quantify the functional, connectional and structural properties of the human brain. It has evolved from a package primarily aimed at generating surface representations of the cerebral cortex into one that automatically creates models of most macroscopically visible structures in the human brain given any reasonable T1-weighted input image. It is freely available, runs on a wide variety of hardware and software platforms, and is open source.

Introduction

FreeSurfer is suite of powerful tools that provide extensive and automated analysis of key features in the human brain. This includes volumetric segmentation of most macroscopically visible brain structures (Fischl et al., 2002, 2004a), segmentation of hippocampal subfields (Van Leemput et al., 2009), inter-subject alignment based on cortical folding patterns (Fischl et al., 1999b), segmentation of white matter fascicles using diffusion MRI (Yendiki et al., 2008), parcellation of cortical folding patterns (Desikan et al., 2006; Destrieux et al., 2010; Fischl et al., 2004b), estimation of architectonic boundaries from in vivo data (Fischl et al., 2008, 2009; Hinds et al., 2008; Yeo et al., 2009), mapping of the thickness of cortical gray matter (Fischl and Dale, 2000), and the construction of surface models of the human cerebral cortex (Dale et al., 1999; Fischl et al., 1999a).

It is this last functionality—the construction of cortical surface models—that was the motivation for the development of the software that would eventually become FreeSurfer. The surface reconstruction code traces its roots to Anders Dale's Ph.D. dissertation work with Marty Sereno in the early 1990s (Dale, 1994), in which the surface models were used to solve the EEG/MEG inverse problem (Dale, 1994; Dale et al., 2000). The EEG/MEG inverse problem is that one records electromagnetic signals outside the skull with electrodes (for EEG) or magnetometers/gradiometers (for MEG), but one wishes to recover the set of currents inside the brain that gave rise to the measured signals. This is a fundamentally ill-posed problem in that an infinite distribution of source currents can give rise to the same measurements. Thus one must apply some constraints in order to obtain a solution. In this case, Anders and Marty wanted to use the fact that pyramidal neurons in the cortex are thought to be the source of the vast majority of the EEG/MEG signal. Cortical surface models would therefore give them access to the location of the pyramidal neurons. Further, because the processes of these neurons are typically oriented perpendicular to the cortical surface, the surface models would also provide orientation constraints on the underlying dipoles. Thus, the surface models allowed a strong and neurobiologically plausible set of constraints to be applied to the inverse problem, resulting in a linear inversion that minimized the L2 norm of the solution and provided some of the first spatiotemporal movies of estimated human brain activity (Dale, 1994).

Prior to Anders’ dissertation work, others had attempted to construct surface models, as it was widely recognized how useful they would be for both visualization and analysis purposes. Most previous attempts had focused on the construction of the so-called “pial” surface, which represents the “top” of the cortical gray matter, ideally above layer I and below the pial. Unfortunately, this surface is impossible to directly visualize or reconstruct from MRI as there are many locations in the brain where adjacent banks of a sulcus are closer than 1 mm or so resolution achievable with MRI. Attempts to model this boundary directly lead to either topologically “correct” models (i.e. topologically equivalent to a sphere) that did not extend into deep sulci and thus excluded large regions of the brain, or geometrically reasonable models that included huge topological “defects”— holes and handles in the surface models. The fundamental insight that Anders and Marty had that enabled surface model construction was that the gray/white boundary, or the “bottom” of the gray matter, did not suffer from these problems given that adjacent banks are separated by at least twice the width of the gray matter, or an additional 3–7 mm. This added spacing was critical as it meant the gray/white surface could be resolved directly across the vast majority of the cortex.

The tools that came from this work provided surface models with adequate geometric accuracy that worked reasonably well with a specific and known MRI sequence, but did not constrain the topology of the surface models, nor did they provide estimates of the pial surface in addition to the gray/white boundary. They were thus of limited utility for cross-subject registration, in which having a correct topology allows one to construct an invertible map, or for cortical morphometry, which requires models of both the gray/white boundary as well as the pial surface to measure cortical thickness and volume. In addition, they required many hours of user intervention to construct each surface model, most notably for manually correcting large topological defects, which was tedious, labor intensive and had a steep learning curve.

Historical context

It is worth first pointing out that the history of surface-based analysis of cortical structure and function predates computer algorithms, and owes much to the pioneering work of people like David Van Essen and Eric Schwartz. David has always been one of the great proponents of “cortical cartography” and his early work with Heather Drury (Drury, 1997; Drury et al., 1996, 1997, 1998) laid the algorithmic foundation for what would become the CARET package for surface-based analysis that is widely used today. Eric, who among other things was both my and Doug Greve's Ph.D. advisor (in fact he mistook us for each other the first day either of us met him), was the first person to recognize the importance of surface-based computer analysis and developed the first computational flattening algorithm (Schwartz, 1990; Schwartz et al., 1989) for generating planar representations of cortical properties. This algorithm is the basis for the one in use in FreeSurfer today both for flattening as well as for regularizing spherical transformation and registration.

This is the only scientific paper that I've ever written in which a reviewer requested more “juicy details” of the history of the development of a set of ideas. Okay, here goes. When I arrived at MGH in 1996 the prototypes of some of the tools that would become FreeSurfer were being used mainly in the study of retinotopic representations in early visual cortex. This resulted in a set of studies that helped lay the framework of our current understanding of the human visual system (Hadjikhani et al., 1998; Halgren et al., 1999; Mendola et al., 1999; Sasaki et al., 2001; Sereno et al., 1995; Tootell et al., 1995, 1997,1998). These studies almost never happened, as Anders and Marty seriously considered working with Brian Wandell and colleagues at Stanford as opposed to Roger Tootell's MGH group. The decision to come to MGH led to a fierce competition with the remarkably productive Stanford group, who published a collection of seminal papers on the use of fMRI for mapping visual cortex (e.g. (Boynton et al., 1996; Engel et al., 1997; Teo et al., 1997; Wandell, 1999; Wandell et al., 1999)).

In this period before FreeSurfer formally existed, there were an array of prominent imaging laboratories that were frustrated and in some cases angry at Anders for not releasing the code for surface reconstruction that he developed as part of his Ph.D. work with Marty Sereno. In my view, this was an unfair expectation, as releasing code without supporting it is never enough. The only thing that makes people more annoyed than not having access to code, is having access but not being able to get questions about it answered, and expecting a single graduate student/postdoc to devote his time to support isn't feasible. Anders, Marty, Doug and I were committed to releasing FreeSurfer, and did so with the help of Thomas Witzel at the Human Brain Mapping meeting in Dusseldorf in 1999, which included Marty writing about 10,000 lines of tcl/tk code in the week leading up to the meeting (this is how csurf was created, which I'm pretty sure only Marty still uses).

Two years later I met Steve Smith giving demos of the FSL tools, which had been released in June of 2000, and we began a collaboration that has continued to this day. Our partnership has involved a yearly course that has been a near catastrophe in almost every instance, including the 2005 course in which, during setup, we plunged large parts of a major Boston hotel into total darkness every time we powered on the course machines (they had gotten our power requirements wrong by about an order of magnitude). This course was also notable as it was that year that Jenni Pacheco became the FS(L) champion baguette jouster by battering some poor stranger into near unconsciousness with a large piece of bread (all in good fun of course). The 2003 course held in Santa Monica, CA (near the beach) was particularly memorable due to the arrival of the first apparent participant, who came into the course room and asked “Where is the free surfer course, dude?”. He ended up being quite disappointed in the subject material.

Topology correction

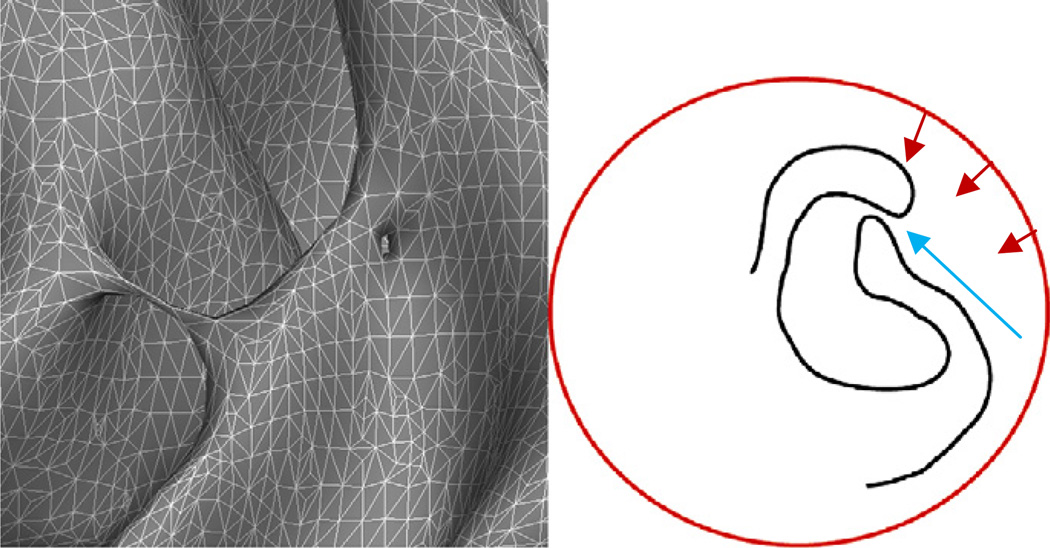
Previous work in cortical surface reconstruction had focused on topological accuracy by deforming a surface with a known topology to lie at the specified interface in the imaging data (e.g. either gray/white or pial) (MacDonald, 1998; MacDonald et al., 1994,2000). The issue with these models is the difficulty of generating surfaces that accurately follow the entire boundary of interest, as illustrated in Fig. 1. The left-hand image exhibits typical topological defects: a bridge across the banks of a sulcus and a hole in the wall of a gyrus. These are topologically equivalent, but any accurate topology correction procedure must resolve them differently—cutting the handle and filling the hole. The right-hand drawing demonstrates the difficulty of using a topologically-constrained deformable surface to accurately model the entire cortex. The deformable surface (shown in red) is typically driven by an energy functional designed to move it towards the true surface (a portion of which is shown in black). The cortex contains many deep folds with narrow openings, such as the one indicated by the blue arrow. It is exceedingly difficult to design an energy functional that will push enough surface area through this type of narrow opening then move it away from the (true) black surface that lies near the opening and across the sulcus to the un-modeled surface on the other side.

Fig. 1.

Left: examples of two geometrically different topological defects that are topologically equivalent: a handle that bridges a sulcus, and a hole in the bank of a gyrus. Right: a graphical example of the difficulty of using surface deformation techniques to model the cortical surface. Typically we want a smooth surface, but much of the cortical surface is buried deep inside folds forcing surfaces to pass through regions (indicated by the blue arrow) where the evolving surface has to bunch up to get enough surface area inside the fold to model the surface. Another problem is finding energy terms that will draw the surface into the deep fissure, and away from the narrow opening, which also means pulling it away from the true cortical surface to traverse the sulcal opening and arrive at the boundary on the other side.

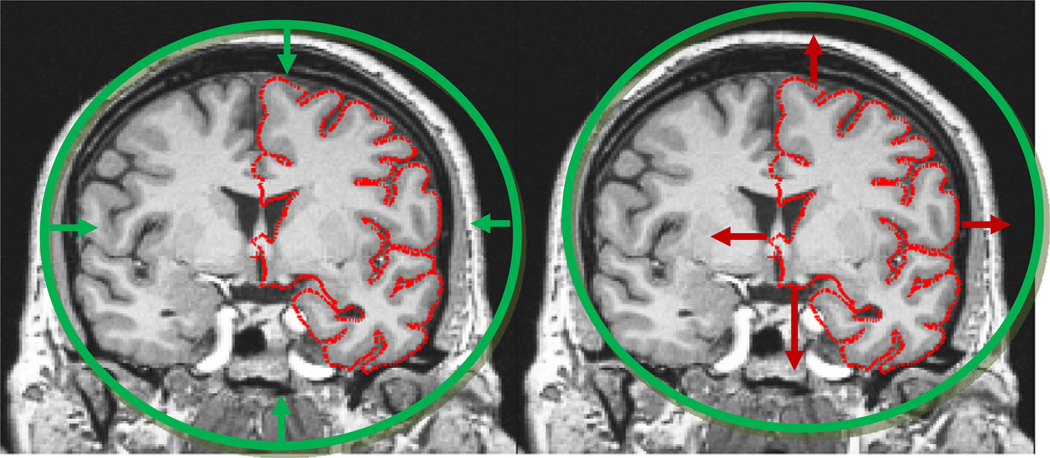
The deformable surface approach when applied to brain images is illustrated in Fig. 2, right. Here we can again see the difficulty of pushing the surface through the many narrow openings into deep sulci, while obtaining a smooth surface at the end of the procedure. In order to resolve this problem, we had the insight that while driving a spherical model to lie at each point of the cortical surface was extremely difficult, the opposite approach, that of taking a cortical surface, regardless of its topology, and driving it outwards towards the surface of a sphere, is relatively easy (Fischl et al., 2001). The fundamental notion of topological equivalence states that if the original surface is not topologically equivalent to a sphere, that is if it contains topological defects, then it is not possible to find a continuous, one-to-one and invertible (i.e. homeomorphic) mapping. More interestingly, we realized that the regions in which the mapping was many-to-one were precisely those that contained topological defects. This enabled us to localize the defects, and limit the topology correction to what is typically only a small fraction of the surface and thus allowed us to focus on geometric accuracy everywhere else.

Fig. 2.

Left: the approach taken with deformable models. A surface of known topology but incorrect geometry (a sphere) is driven by an energy functional towards the desired pial surface shown in red. The difficulty stems from finding terms that will generate a smooth surface but will allow it to pass through an intermediate representation that can push enough surface area into e.g. the sylvian fissure. Right: in contrast, deforming the topologically incorrect surface model outwards to the surface of the sphere is a relatively simple computational problem.

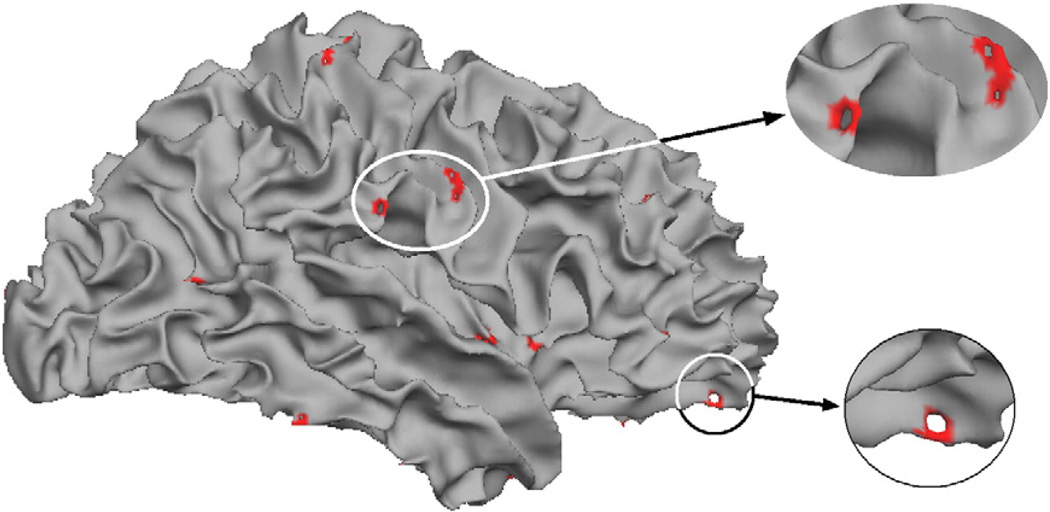
Fig. 3 shows a typical surface model before correction with the detected topological defects shown in red. As can be seen, less than 1% of the surface area is contained within the defects.

Fig. 3.

Example of the typical spatial distribution of topological defects.

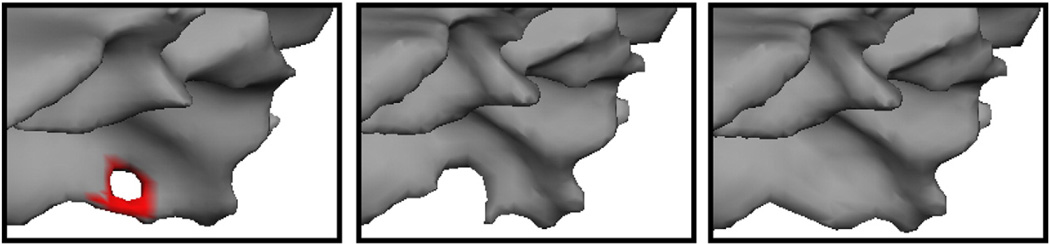
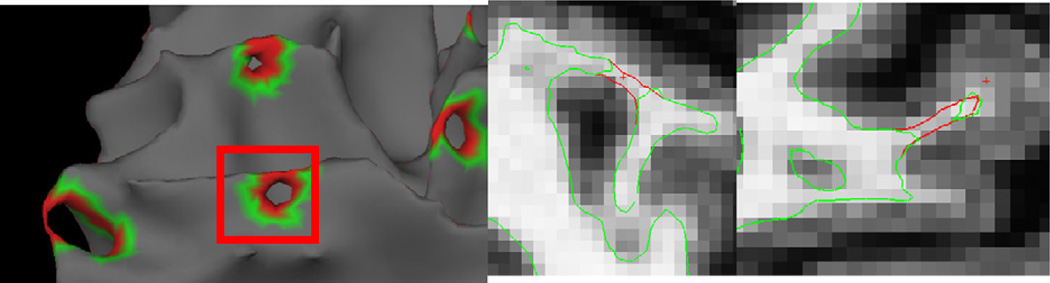
A second problem we needed to resolve was how to correct the existing defects and obtain an accurate surface model. An example of a defect localized with this procedure is given in Fig. 4, left, as well as two possible corrections show in the center (cutting the handle) and right (filling the hole). In this case it turns out that the right-hand correction leads to a geometrically accurate surface, while the center one eliminates some of the cortex from being modeled. ¹ Note that it is impossible to tell from the rendering of the surface models which is the correct solution. It is only by considering the intensity volume—that is that the surface should contain white matter in the interior and gray matter outside—that one is able to choose the correct topological manipulation to generate an accurate surface (see Fig. 5 for an example of what the MRI volume looks like after filling a hole).

Fig. 4.

Example of a topological defect (left), an inaccurate correction (center) and an accurate correction (right) (thanks to Florent Ségonne).

Fig. 5.

Example of a surface defect (left), and it's representation in two orthogonal slices (center and right). The red portion in the left-hand image represents the region found to contain the defect. The red portion of the surface in the center and right images represent the surface that has been added to fill the hole.

Surface deformation and thickness estimation

The accuracy requirements on surface placement depend on what they will be used for. For example, for EEG/MEG source estimation, a surface misplacement of one or two mm will have little effect on the computed solution. Similarly, for analyzing and visualizing functional data that is typically acquired with voxels that are greater than 3 mm on each side (although this is changing!) surface accuracy is not critical. However, if one's goal is to measure morphometric changes associated with disease state, neuropsychological variables or age for example, one is typically aiming to detect changes on the order of ½ mm. This naturally places significantly greater constraints on the geometric accuracy of the resulting surfaces.

Surface-deformation techniques had been commonly utilized to attempt to generate accurate models of various boundaries from MRI (Davatzikos and Prince, 1995; Davatzikos et al., 1996; MacDonald et al., 2000). Unfortunately, it was difficult to directly use these techniques to construct surface representations with the requisite degree of accuracy for a number of reasons. First, isointensity surfaces, which assume that the MRI intensity of the gray/white and pial surface interfaces are constant over space, do not generate accurate enough surfaces. This is due to variance in the histological makeup of cortical gray matter and the subjacent white matter as well as acquisition artifacts such as variable RF penetration, dielectric resonance and nonuniform receive coil sensitivity profiles that all conspire to cause the MR intensity of a given tissue type to vary over space. For example, cortical gray matter in motor cortex is significantly brighter than in frontal cortex, due to its higher myelin content (which can be quantified with T1 mapping in MRI (Fischl et al., 2004a)).

Second, the surfaces must be constrained to not self-intersect and to maintain their topology. Eulerian methods that elegantly handle the first problem that existed at the time did not have an easy way to impose topological constraints (a feature that was usually an asset to these techniques, but not in this problem domain),² and also suffered from an inability to accurately model two interfaces that pass through the same voxel, something that occurs frequently when adjacent banks of a sulcus are almost touching. Finally, surface deformations were typically constrained to generate smooth surfaces either by a so-called “spring” term or curvature minimization. Unfortunately the cortex contains many locations of high curvature in which these terms underestimate the extent of for example small fingers of white matter.

In order to resolve these problems, we developed a surface deformation procedure that adaptively determined the MR intensity of the boundaries in question at each point in the cortex (Fischl and Dale, 2000). Instead of using curvature minimization or spring terms that seek a flat surface, we modeled the surface with local quadratic patches that constrained the surfaces to be well-modeled using a second order polynomial as opposed to a plane. This allowed us to prevent noise-induced oscillations in the surfaces while avoiding underestimation in regions of high curvature. Finally, we borrowed techniques from the computer graphics literature to implement fast triangle–triangle intersection (Möller, 1997) that provided a hard constraint and prevented the surface from developing self-intersections. The combination of these approaches yielded a procedure that generates models of the gray/white and pial surfaces that were topologically correct, handled acquisition artifacts and tissue variability, was robust to variations in sequence parameters and generated models that were accurate enough to reliably measure the thickness of the gray matter of the human cerebral cortex and detect pathology induced variations of less than ¼ mm.

One point that must be addressed is how one can validate the accuracy of the thickness measures. This is of course a critical question as any neurobiological interpretation of results depends on the thickness measures accurately reflecting the width of the cortical gray matter. Towards that end, we have performed an extensive (and extremely dull!) series of validation studies. This includes direct comparison of the thickness measures we compute against histological thickness measures in the same tissue (Rosas et al., 2002), using published measures of average thickness such as von Economo (1929) in motor cortex, somatosensory cortex, gyral cortex, sulcal cortex and overall average cortical thickness (Fischl and Dale, 2000), comparison with manual measures from MRI in disease and control populations (Kuperberg et al., 2003), estimation of the stability of the thickness measures with respect to scanner platform, sequence type and analysis degrees of freedom (Han et al., 2006), voxel geometry and amount of acceleration (Wonderlick et al., 2009), as well as their robustness and sensitivity for detecting correlations with cognitive measures that are stable across scan session, scanner manufacturer and field strength (Dickerson et al., 2008). Taken together, this wide array of studies gives us confidence that we are in fact measuring the thickness of the cortical gray matter in a manner that is accurate and stable to an array of acquisition variables in a neurobiologically meaningful and clinically relevant manner.

Whole-brain segmentation

The surface models provided an excellent basis for the analysis of the structural and functional properties of the cerebral cortex, but not for subcortical and ventricular structures. At the time, segmentation tools were limited to a small number of tissue classes (e.g. gray matter, white matter and CSF) or subcortical structures (e.g. Louis Collins’ excellent work (Collins and Evans, 1997)). However, no tools existed that would provide a labeling of each voxel in the brain into semantically meaningful classes such as hippocampus, amygdala, thalamus, etc.…. Part of the difficulty in generating such a segmentation was the variability in the histological composition of these structures. For example, while pallidum and caudate are both gray matter nuclei, the significantly higher myelin content of the pallidum make its T1-weighted MR intensity considerably higher than that of the caudate. Even more difficult was the modeling of structures such as the thalamus that showed variability within its boundaries, with darker appearing tissue at the midline and a gradient of brighter intensities as one moves more laterally. In order to resolve these issues we took a Bayesian approach and decomposed the problem into formulating a more realistic image likelihood term as well as a more sophisticated prior model.

For the image likelihood we chose to relax the assumption that tissue classes could be well-modeled by one or a mixture of a small number of Gaussians that are spatially stationary. Instead, we used a separate model for each structure for each point in space. This allowed us to account for within-structure heterogeneity that occurs commonly in thalamus, hippocampus and elsewhere, but also by keeping the distributions of e.g. pallidum and caudate separately, instead of modeling all “gray matter” together, we were able to use significantly sharper and hence more informative distributions, making the segmentation problem less ambiguous. For the image prior term, like others we used a prior on structure identity given spatial location, however we augmented this to include models of the stereotypical spatial relationships found between anatomical structures. For example, while hippocampus and amygdala are similar in terms of image intensity, their spatial location relative to one another is quite consistent: amygdala is always in front of and above hippocampus, never below or behind it. To encode this, we used a Markov Random Field (MRF) model, which had been previously used extensively in computer vision (Geman and Geman, 1984). Typical MRF modeling at the time was stationary (e.g. the same probabilities for voxel a being label l₁ given voxel b being label l₂ regardless of spatial location), and isotropic (e.g. the spatial relationship between voxels a and b was not considered other than whether they were neighbors or not). In order to constrain the segmentations to be neuroanatomically plausible, we extended the MRF model to be spatially nonstationary, so that the probabilities were allowed to vary over space, and anisotropic, so that we could model the probability that hippocampus was below amygdala separately from the probability that it was above it. These more sophisticated models allowed us to utilize a training set of manually labeled images to bootstrap a procedure for whole-brain segmentation that was as accurate as extensively trained manual raters were capable of creating, as well as being robust to pathology (Fischl et al., 2002,2004a).

Contributors

Many people have contributed to FreeSurfer over the years, and I would like to acknowledge them. First and foremost are Anders Dale and Marty Sereno who developed some of the initial tools, and also had many of the key technological and neuroscientific insights that made FreeSurfer possible. Doug Greve, who understands the intricacies of fMRI analysis as well as anyone in the world, is the primary author of almost all the functional analysis tools distributed with FreeSurfer (FS-FAST). Other early contributors and developers include Sean Marrett, Kevin Teich, Yasunari Tosa and Thomas Witzel, and more recently Ruopeng Wang and Krish Subramanian as well as Richard Edgar who reported a number of binaries to run on the GPU with remarkable speed increases. Nick Schmansky has been the lead engineer for many years, and is responsible for taking a loosely organized set of binaries and turning it into a well-documented, extensively tested, easy to install and use (relatively!) suite of tools. Andre van der Kouwe has been the key developer of sequences that are optimal with respect to brain morphometry, and more recently M. Dylan Tisdall has worked with Andre to develop structural sequences with embedded real-time motion correction that promise to open up structural imaging to an array of clinical populations that were difficult or impossible to image previously. FreeSurfer has also been blessed with an array of talented, responsible and dedicated research assistants, including Jenni Pacheco, Allison Stevens, Khoa Nguyen, Michelle Roy, Sita Kakunoori, Louis Vinke, Priti Srinivasan, Brian T. Quinn, Maureen Glessner, Evelina Busa, and Niranjini Rajendran. More recently Allison has taken on the larger role of organizing pretty much everything to do with FreeSurfer, including courses, documentation, lab meetings and research projects. Anastasia Yendiki, in collaboration with Tim Behrens and Saad Jbabdi at Oxford, has developed and integrated automated tractography into FreeSurfer (Yendiki et al., 2011), Lilla Zöllei in collaboration with Gheorghe Postelnicu developed a combined volume and surface registration that aligns cortical folding patterns as well as subcortical and ventricular structures (Postelnicu et al., 2009a; Zöllei et al., 2010), and more recently has been working on extending our tools to build segmentations and surface models of newborns; Rudolph Pienaar has worked on web-based frontends for running FreeSurfer processes and also created tools for analyzing curvature properties of surface models with a focus on development (Pienaar et al., 2008); Eric Halgren, David Salat and Jean Augustinack have contributed critical neuroscientific and neuroanatomical expertise; Arthur Liu was Anders’ first graduate student and the unfortunate person tasked with doing surface reconstructions before the process was automated, and carried out important early work developing inverse solutions and comparing EEG and MEG (Liu et al., 2002); Florent Ségonne developed the hybrid watershed skull stripping algorithm still in use in FreeSurfer (Ségonne et al., 2004), and also many volumetric and surface-based algorithms for topology correction, and evolving fronts under topological control (Ségonne et al., 2003,2005a,2005b,2007); Jon Polimeni has pushed forward the use of the surface models for laminar modeling; Oliver Hinds developed tools for automatically predicting the location of V1 from folding patterns as part of his Ph.D. work with Eric Schwartz at BU; Martin Reuter has developed tools for rigid registration that are unbiased and extremely accurate in the presence of nonlinearities such as B0 distortions, and tongue/jaw/eye movement (Reuter et al., 2010), and has taken over primary responsibility for the ongoing development of our longitudinal analysis stream, and also worked with Peter Sand to develop and validate prototype tools for registering histological and block-face images to high-resolution ex vivo MRI; Peng Yu was an MIT Ph.D. student who implemented spherical wavelets and applied them to the study of cortical folding patterns (Yu et al., 2007); Xiao Han came from Jerry Prince's lab and wrote code for estimation of intensity distributions that made the segmentation procedures insensitive to pulse sequence (Han and Fischl, 2007), Rahul Desikan worked with Ron Killiany to develop a gyral-based cortical parcellation (Desikan et al., 2006), similar to Christophe Destrieux's earlier Ph.D. work with Eric Halgren, Koen van Leemput is one of the world's experts in segmentation of medical imaging data, and has developed techniques for segmenting hippocampal subfields in standard resolution data using information from a high-resolution training set (Van Leemput et al., 2009); B.T. Thomas Yeo did his doctoral work at MIT with Polina Golland and myself working on an array of surface-based tools for spherical filter banks including wavelets (Yeo et al., 2008), on fast diffeomorphic surface-based registration (Yeo et al., 2010a,2010b), and for computing registration functionals that are optimized for specific tasks, such as alignment of Brodmann areas (Yeo et al., 2010a,2010b); and finally, last but certainly not least is Mert Sabuncu, who was Polina's postdoc and is currently faculty at MGH whose work involves cutting edge segmentation using probabilistic label fusion (Sabuncu et al., 2010), and is more recently working on imaging genetics, multivariate pattern analysis, and longitudinal statistics.

Conclusion

The development of a set of key technologies enabled the development of FreeSurfer, an array of image analysis tools designed to be automated, robust, accurate and relatively easy to use. This included automated geometric accurate topology correction (Fischl et al., 2001), surface-based inter-subject alignment (Fischl et al., 1999a, 1999b) and whole-brain segmentation (Fischl et al., 2002, 2004a). Although in many ways these still represent the core functionality of FreeSurfer, it has also evolved tremendously since that time. For example, we have recently adopted a liberal open source license that allows great freedom in the use of our source code (http://surfer.nmr.mgh.harvard.edu/fswiki). FreeSurfer is constantly being improved and extended, with our most recent release including tools for accurate cross-modal intra-subject registration (Greve and Fischl, 2009), combined volume and surface cross-subject registration (Postelnicu et al., 2009b), probabilistic estimation of cytoarchitectonic boundaries (Fischl et al., 2008), automated tractography (Yendiki et al., 2009), and longitudinal analysis (Reuter and Fischl, 2011; Reuter et al., 2010). It has been used to improve our understanding of an array of neurological disorders (Becker et al., 2008; Desikan et al., 2010a,b; Dickerson et al., 2009; Gold et al., 2005; Kuperberg et al., 2003; Manoach et al., 2007; Milad et al., 2005; Oliveira et al., 2010; Rauch et al., 2005; Rosas et al., 2002,2005,2006,2010; Sabuncu et al., 2011; Sailer et al., 2003; Stufflebeam et al., 2011), the genetic basis of neuroanatomical variability and change (Kremen et al., 2010; Panizzon et al., 2009), as well as healthy development (Isaacs et al., 2008; Martinussen et al., 2005) and aging (Fjell et al., 2005,2006; Salat et al., 2004,2005a,2005b,2009; Walhovd et al., 2004,2005a, 2005b, 2006).