A novel CT acquisition and analysis technique for breathing motion modeling

Abstract

Purpose

To report on a novel technique for providing artifact-free quantitative 4DCT image datasets for breathing motion modeling.

Methods

Commercial clinical four-dimensional computed tomography (4DCT) methods have trouble managing irregular breathing. The resulting images contain motion-induced artifacts that can distort structures and inaccurately characterize breathing motion. We have developed a novel scanning and analysis method for motion-correlated CT that utilizes standard repeated fast helical acquisitions, a simultaneous breathing surrogate measurement, deformable image registration, and a published breathing motion model.

Results

The motion model differs from the CT-measured motion by an average of 0.72 mm, indicating the precision of the motion model. The integral of the divergence of one of the motion model parameters is predicted to be a constant 1.11 and is found in this case to be 1.09, indicating the accuracy of the motion model.

Conclusions

The proposed technique shows promise for providing motion-artifact free images at user-selected breathing phases, accurate Hounsfield units, and noise characteristics similar to non-4D CT techniques, at a patient dose similar to or less than current 4DCT techniques.

Breathing motion has been managed in radiation therapy treatment planning by acquiring a 4-dimensional computed tomography (4DCT) during CT simulation. The 4DCT image data set is acquired using one of two methods: low-pitch helical (Ford et al., 2003) or ciné acquisition sequences (Pan, 2005). A simultaneous breathing surrogate measurement is conducted to retrospectively subdivide acquired projections or images according to breathing phase. There are two widely used descriptions of the breathing cycle; amplitude-based and phase-angle based (Lu et al., 2006, Abdelnour et al., 2007, Santoro et al., 2009, Wink et al., 2006). Under conditions of regular breathing, defined as breathing with a consistent breathing depth, either of the acquisition techniques and breathing cycle definitions will provide clinically useful images. The challenge with current commercial 4DCT techniques is that many if not most patients, especially lung cancer patients, do not breathe regularly and the resulting 4DCT images are plagued with artifacts and their subsequent use in treatment planning is more qualitative than quantitative (Chen et al., 2004). Figure 1 shows an example of a clinical 4DCT scan. The image data set, used for clinical treatment planning, has image artifacts caused by the commercial system’s inability to manage irregular breathing. This letter introduces a new 4DCT acquisition and analysis protocol that decreases motion-induced artifacts, averages the acquired images to reduce image noise, and provides the user with a resulting image at user-selected breathing phases with accurate Hounsfield Units.

Figure 1.

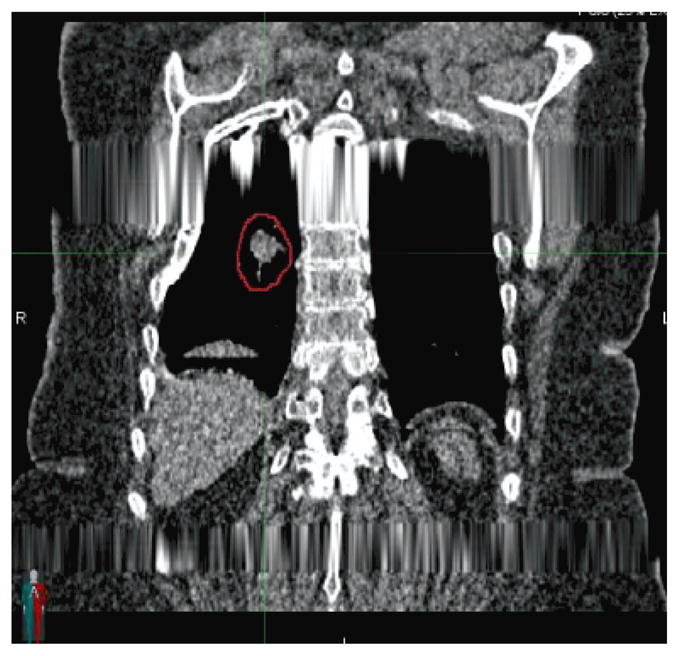
Example of a coronal slice through a commercial clinical 4DCT scan. Artifacts caused by improperly managed irregular breathing are evident in the scan.

The new imaging protocol was demonstrated under an IRB-approved protocol by scanning an abdominal cancer patient using a 64 slice CT scanner (Siemens Definition Flash) with a pitch of 1.2, scanner rotation period of 0.285s, nominal beam collimation (longitudinal field of view) of 3.84 cm (64×0.6mm), 512 × 512 voxel reconstruction with a 50 cm field of view, 169 mA (40 effective mAs), and 120 kV. This protocol required 2.5 seconds to scan the entire lungs. The patient was scanned 25 times using alternating scanning directions, and the entire scanning sequence took 140 s.

The breathing cycle was monitored with a bellows-based system that was strapped around the patient’s abdomen and stretched and contracted during breathing. A pressure transducer monitored the internal bellows air pressure and an amplification circuit followed by an analog-to-digital converter was monitored by an independent computer. That computer also monitored the CT scanner beam-on signal to synchronize the breathing with the CT data. Once the scans were acquired, they were synchronized to the breathing data and each slice was assigned a breathing amplitude and breathing rate (the time derivative of the amplitude). The voltage signal was smoothed using a fifth order moving polynomial and the signal change rate was smoothed using a third order polynomial.

The proposed process was intended to provide anatomically accurate images of the lungs at user selected breathing phases. This was extended to the Hounsfield Unit values to provide the most accurate CT scans. In order to determine the Hounsfield Unit values at a user selected tidal volume, the Hounsfield Units were converted to relative air content of each voxel by linearly interpolating the HU values between air as measured in the trachea and soft tissue as measured in the liver. At each voxel, the relative air contents of the 25 scan acquisitions were correlated against the bellows voltage signal and the relationships fit to a linear polynomial. The bellows voltage itself was proportional to air content and tidal volume, but there was value in modeling the breathing motion as a function of air content or tidal volume rather than voltage (for example, the relationship in Equation 2). To convert voltage to air content the linear relationship between the two was used to determine that the sum of the first-order terms (the ratio of air content to bellows voltage) of all the voxels provided the ratio of total air content to bellows voltage. Based on our earlier work, which specified the motion model parameters as a function of tidal volume rather than air content, the air content was converted to tidal volume by dividing it by 1.11 to account for the effect of body temperature and humidity on lung air density relative to room air density.

The resulting scans (example in figure 2A for a scan acquired during exhalation) showed no signs of the streaking artifacts or subdividing of the liver into multiple sections evidenced in figure 1. Although difficult to visualize in figure 2A, because the image was acquired during respiration, there was distortion of the tissues caused by the relative motion of the tissues and the scanner. It was the relative tissue positions, including their distortion in each scan, that were used to measure breathing motion. The 25 images were segmented to isolate the lungs, trachea and main-stem bronchi. A B-spline registration algorithm (Klein et al., 2010, Staring et al., 2007) was used to register the first segmented image to the subsequent 24 segmented images. The similarity metric was the Mattes mutual information (Mattes et al., 2001) with no penalty term applied. The optimizer was an iterative stochastic gradient descent (Thevenaz and Unser, 2000) and a 5-level multi-resolution approach was taken to avoid local minima using a Gaussian pyramid with a subsampling factor of 2 in each dimension, providing B-spline grid spacings of 160 mm, 80 mm, 40 mm, 20 mm, and 10 mm. These registrations were conducted separately for the lungs and other tissues to allow modeling of the shear motion between the lungs and chest wall. To determine the motion model parameters for each voxel, the 5D breathing motion model proposed by Low et al. (Low et al., 2005) was applied to the deformably registered voxel locations:

$$\overrightarrow{X}=\overrightarrow{X_0}+\overrightarrow{\alpha }\left(\overrightarrow{X_0}\right)v+\overrightarrow{\beta }\left(\overrightarrow{X_0}\right)f$$ (1)

where v and f referred to the tidal volume and airflow, respectively, $\overrightarrow{X_0}$ referred to the tissue position at zero tidal volume (defined here as the 5^th percentile tidal volume) and zero airflow, α⃗ related the breathing motion to the depth of breathing, and β⃗ related the breathing motion to the rate of breathing (modeling motion hysteresis). The 25 positions of each voxel of the first image as determined using the deformable image registration, along with the tidal volume and airflow corresponding to the original slice locations of the registered voxels, were used to determine the motion model parameters $\overrightarrow{X_0},\overrightarrow{\alpha }(\overrightarrow{X_0})$, and $\overrightarrow{\beta }(\overrightarrow{X_0})$, using linear regression. Linear interpolation was used when the registered position lay between slices. The breathing motion model tissue position predictions in the 25 images were compared against the deformably registered tissue positions to evaluate the CT acquisition, motion model, and registration accuracy. Discrepancies between the model and registered tissue positions could not be assigned to specific error sources such as limitations in the model, but served to identify an upper bound to the model imprecision.

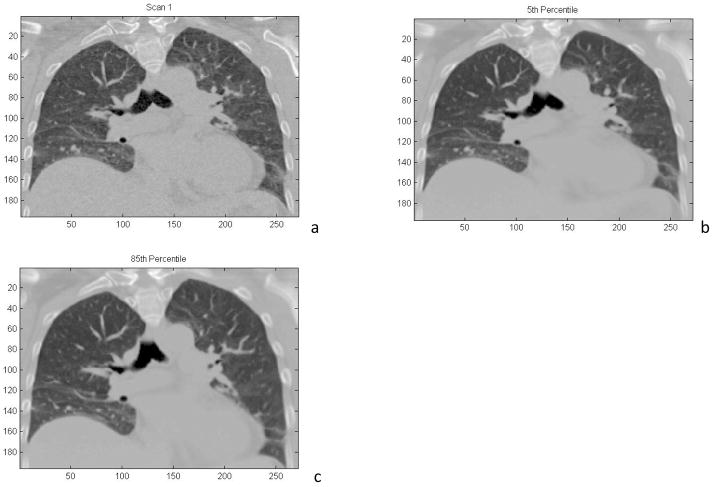
Figure 2.

a) Coronal reconstruction of a 4DCT image acquired during free breathing. b) Coronal reconstruction of a 4DCT image using all 25 acquired scans, reconstructed at the 5th percentile tidal volume. c) Coronal reconstruction of a 4DCT image using all 25 acquired scans, reconstructed at the 85th percentile tidal volume.

The motion model as described in Equation 1 was used to deform the 25 images to specified breathing phases. The Hounsfield Units assigned to the voxels were interpolated from the Hounsfield Unit linear fit described above. Figure 2a shows an example of the first acquired image deformed to the 5^th percentile tidal volume (tidal exhalation, v = f = 0). Contrast the image quality in Figure 2 with that of Figure 1.

The discrepancy between the breathing motion model and the 25 positions corresponding to the 25 scans was determined. Figure 3 shows the mean discrepancy between the model and the image-registration-measured positions for all 25 scans at a mid-sagittal slice. The image geometry shown in the figure corresponded to the first acquired CT scan. As can be seen in this figure, most of the lung exhibited a discrepancy of less than 1 mm, however regions in the left lung and near the heart exhibited mean discrepancies of greater than 1 mm. This may have been due to uncompensated and unmodeled cardiac motion. The total mean discrepancy between the breathing motion model and the tissue motion was 0.72 mm±0.18 mm (1 standard deviation), indicating that the breathing motion model and registration process had a high level of accuracy.

Figure 3.

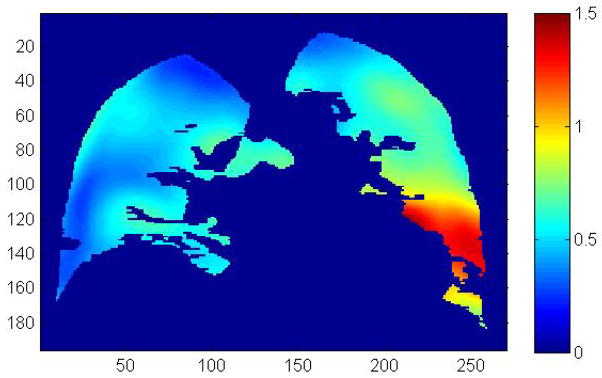
Mean discrepancy (in millimeters) between the breathing motion model and the measured tissue positions averaged over all 25 scans. The color scale is in millimeters, the distance scales are in voxels (0.98 mm).

Because the images had been coregistered, they were deformed to a common geometry and averaged, reducing the statistical image noise. Figure 2b and 2c show the exhalation (5^th percentile tidal volume) and inhalation (85^th percentile tidal volume = 378 ml) breathing states, respectively, with an image composed of the average of the 25 acquired data sets. The noise characteristics were reduced as evidenced by the reduced mottle in the liver, but residual image registration errors also reduced the sharpness of the subsequent image. The pixel-to-pixel noise in the liver was 46 HU and 8 HU for the single image (Figure 2a) and 25-image average (Figure 2b), respectively. The noise reduction was close to the expected ratio of 5.

Low et al. (Low et al., 2010) applied mass conservation to the 5D breathing motion model and determined that for all cases

$$\int \overrightarrow{\nabla }·\overrightarrow{\alpha }dv=1.11$$ (2)

where ∇⃗ was the divergence operator, and the integral was taken over the entire lungs. This equation served to provide a level of quality assurance on the registration, model fitting, and voltage to tidal volume conversion. For the patient presented in Figure 2, the integral was 1.09, indicating a high level of accuracy.

In addition to providing improved breathing motion model data, the proposed protocol showed promise in improving the process of clinical 4DCT. The acquisition process required no additional hardware; the surrogate we used was identical to the system used in the clinical 4DCT process provided by Philips. While the bellows voltage was converted to tidal volume, this would not be required for clinical 4DCT. Inhalation and exhalation could be defined by percentiles rather than tidal volume, however converting voltage to tidal volume allowed use of Equation 2 for quality assurance. The research scan acquisition sequence was a set of repeated routine fast helical CT scans. For the 5D model development, we used 25 sequential and unsynchronized CT scans, but a prospective gating algorithm could be developed to optimize and minimize the number of scan acquisitions required to accurately model lung motion. The clinical implementation could produce a series of artifact-free CT scans at user-selected breathing phases, defined as a set of amplitudes or phases. The clinical protocol used to acquire the image in Figure 1 delivered 600 mAs. The effective mAs used in the 25 scans acquired as part of this research study was 1000 mAs. The CTDIvol was 4.22 cGy and the DLP was 122 cGy cm for all 25 scans. Through the use of prospective gating, we anticipate that only 5 scans would be required to generate the motion model and consequently provide images at arbitrary breathing phases, resulting in an exposure of only 200 mAs.

We are continuing to develop this acquisition and analysis technique. In addition to monitoring breathing, we also monitored the electrocardiogram. This will allow us to determine if residual errors near the heart were due to cardiac motion, in which case we will add a cardiac motion term to our breathing motion model. We will also conduct phantom-based measurements to validate the assertions that the deformation seen in the free breathing images are quantitatively related to the breathing motion.