THE DISCOUNTED REPRODUCTIVE NUMBER FOR EPIDEMIOLOGY

Abstract

The basic reproductive number, , and the effective reproductive number, , are commonly used in mathematical epidemiology as summary statistics for the size and controllability of epidemics. However, these commonly used reproductive numbers can be misleading when applied to predict pathogen evolution because they do not incorporate the impact of the timing of events in the life-history cycle of the pathogen. To study evolution problems where the host population size is changing, measures like the ultimate proliferation rate must be used. A third measure of reproductive success, which combines properties of both the basic reproductive number and the ultimate proliferation rate, is the discounted reproductive number . The discounted reproductive number is a measure of reproductive success that is an individual’s expected lifetime offspring production discounted by the background population growth rate. Here, we draw attention to the discounted reproductive number by providing an explicit definition and a systematic application framework. We describe how the discounted reproductive number overcomes the limitations of both the standard reproductive numbers and proliferation rates, and show that is closely connected to Fisher’s reproductive values for different life-history stages

1. Introduction

The theory of biological evolution provides a dynamic method for predicting past and future population change. If we know a population’s current composition and we can identify the fittest individuals, we can predict that population’s future composition. However, when converting theory to prediction we stumble at one particular point: how does nature determine fitness? Fitness is a flexible concept that can be defined in different ways depending on the evolutionary problem being addressed (Mayr, 1997). The evolutionary ecology concept of fitness is conventionally defined as the “reproductive success” of a phenotype or adaptation. This convention bypasses the complexities of population genetics (that inherited genotypes differ from expressed phenotypes according to Mendel’s laws) but is a reasonable approximation under weak selection (Lande, 1982; Charlesworth, 1990).

In infectious disease research, the most commonly invoked measure of reproductive success is the basic reproductive number 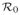(Dublin and Lotka, 1925). In a demographic sense, 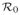is the total number of offspring a typical individual expects to have over the course of a lifetime in a naive population. For infectious diseases, this means the number of new infections caused by a typical case in a completely susceptible population. In several archetypal epidemiology models, strains of disease with higher 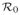values out-compete strains with lower 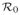values, leading to a rule-of-thumb that evolution maximizes 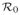. This phenomenon has been exploited to derive a number of useful results concerning pathogen evolution in the context of vaccination (Gandon et al., 2001, 2003). In populations that are not completely susceptible, 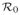is replaced by an effective reproductive number representing the number of new cases created, conditional on the population’s state. But Bremermann and Thieme (1989) have shown that even in some cases where populations are not completely susceptible, 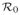can be used to predict the asymptotic outcomes of some nonlinear competition models.

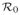maximization does not always correctly predict evolutionary changes in strain frequencies, however. If, for example, at the beginning of an epidemic, there are two strains of a virus: one strain that kills its host in 2 days while causing 2 new cases at the end of those 2 days, and a second strain that kills its host in 6 days while causing 3 new cases at the end of those 6 days, the second strain has a larger 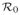(3 versus 2). However, the relative frequency of the second strain will decrease over time. In 6 days, the first strain will have been transmitted though 3 generations, for a total of 8 descendant infections compared to the 3 descendant infections of the second strain. If both strains start with a single case, then after a month, there will clearly be more cases of strain one than strain two although strain two has the larger 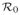value.

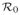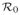The above argument applies for both naive populations with and non-naive population states where we use the effective reproductive number . Both and ignore the timing of reproduction events, treating all reproduction events as having the same value. If the population size is not changing, all reproductive events do indeed have the same value, and reproductive success can be predicted by 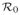or . But if the population size is changing, early reproductive events have more value than late reproduction events.

In situations where the population size is growing, reproductive success is often measured in terms of the ultimate proliferation rate r of the strains. Biologically, r is the asymptotic instantaneous rate of change in abundance of a population of identical individuals after the population structure has settled down to a stable stage distribution (Keyfitz, 1968). Although no population can grow indefinitely, and the allowance for indefinite growth superficially violates one of the fundamental premises of Darwin and Wallace’s theory of evolution, r is a measure of reproductive success that receives regular use in both theory and practice (Bulmer, 1994; McGraw and Caswell, 1996; Caswell, 2001). Comparative analysis of the ultimate proliferation rates r of different strains can correctly predict evolutionary changes in strain frequency not just when population sizes are changing, but also when the total population size is stationary (r = 0).

However, the dichotomy between the ultimate proliferation rate and the basic reproductive value is unsettling. A better mathematical theory of fitness would not require this ad-hoc distinction between populations that are changing size and populations that are not changing size. The ultimate proliferation rate is often more difficult to calculate than a reproductive number when comparing novel mutant strains with a wild-type population, especially when considering a subpopulation having a different life history than the population as a whole. Another issue is that the ultimate proliferation rate has the connotation of a population-scale concept, describing how the size of a specific subpopulation changes in time as the population structure converges to a stationary distribution. By contrast, reproductive numbers have a connotation associated with individuals. As each individual case of an infection has a basic reproductive number, so each mutation in an evolving population has the potential to create a new strain with its own reproductive number.

Instead of having to deal with both the ultimate proliferation rate and the basic reproductive number, there is an equivalent alternative approach. Here we describe a third measure of reproductive success equally valid in contexts of both growing and static background populations: the discounted reproductive number . The discounted reproductive number is a measure of reproductive success that is an individual’s expected lifetime offspring production discounted by the background population growth rate. We provide an explicit definition and systematic application framework for the discounted reproductive number. Although other authors have used the discounted reproductive number for life-history optimization (Goodman, 1982; McNamara, 1991; McNamara et al., 2001), its merits remain under-recognized. Furthermore, the fundamentally comparative and game-theoretic nature of the discounted reproductive number has not been made explicit. In this work, we illustrate the versatility of the discounted reproductive number as a fitness measure that subsumes the two most common measures, the basic reproductive number and the ultimate proliferation rate. We also show that is closely connected to Fisher’s reproductive values for different life-history stages. Our results show how the standard concept of reproductive numbers extends naturally to solve a wide array of evolution problems.

2. Mathematical methods and results

To define measures of reproductive success within a quantitative framework, we consider the family of continuous-time, stage-structured population models described by a (possibly nonlinear) matrix equation of the form

$$\frac{\text{d}\mathbf{n}}{\text{d}t}=(\mathbf{F}+\mathbf{T})\mathbf{n},$$ (1)

where n is a vector of population abundances at each life stage, F is a non-negative matrix of reproduction rates, and T is the negative of an M-matrix¹ describing the transition rates of a Markov process, and F + T is irreducible and primitive. Formally, there are many different splittings of the system into fecundity and transition components such that F + T = F̃ + T̃ with F ≠ F̃ and T ≠ T̃. Biologists may argue that life-cycle structure dictates a canonical splitting. Our results will hold for all splittings provided the non-degeneracy condition λ₀(F + T) > λ₀(T) holds, where the notation λ₀(·) represents the matrix’s largest real eigenvalue.

The ultimate proliferation rate is the largest real eigenvalue of the growth operator:

$$r={\lambda }_0(\mathbf{F}+\mathbf{T}),$$ (2)

which is the eigenvalue with largest real part. The general methods for calculation of 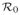and are closely related to the theory of Markov decision processes developed by Howard (1960) and to branching process theory (Ulam, 1990). The basic reproductive number can be thought of as the expected number of offspring produced in each life-history stage, weighted by the probability of surviving and entering that stage, and summed over all stages. The basic reproduction number of an epidemic is the expected number of new cases in a naive population. 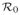is calculated (Cushing and Yicang, 1994; Caswell, 2001; Diekmann et al., 1990; van den Driessche and Watmough, 2002) as

$${\mathcal{R}}_0={\lambda }_0(-{\mathbf{FT}}^{-1}).$$ (3)

In situations where the expected number of new cases is conditional on a population state other than the naive state, the calculation is the same and the result is called an effective reproductive number . Note that the difference between 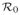and is simply whether the matrices F and T, as functions of the population state, are evaluated at a naive or non-naive state. In what follows, we will refer only to , although the statements also hold for .

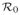A third measure of reproductive success that combines both the basic reproductive number and the ultimate proliferation rate is the discounted reproductive number . The discounted reproductive number represents the number of off-spring an individual expects to have over the course of a lifetime, discounted for expected changes in population size. The conceptual origins of the discounted reproductive number begin with the r–K theory of selection introduced by Margalef (1959) and MacArthur and Wilson (1967). The r–K selection theory was originally envisioned as a continuum between r selected species in resource-rich environments that evolve to maximize productivity and K selected species in resource-scarce environments that evolve to maximize efficiency. The nomenclature derives from the simple logistic-growth model

$$\frac{\text{d}n}{\text{d}t}=rn\left(1-\frac{n}{K}\right)$$ (4)

where r represents the per-capita growth rate and K denotes the carrying capacity. In application, however, r–K selection has most often been treated as a polar dichotomy because there is no natural continuum between the carrying capacity K, measured in the same units as the population’s size, and the growth rate r, measured in units of inverse time. Although it is a convenient caricature, r–K selection theory has been largely abandoned.

The discounted reproductive number supplies the missing spectrum to r–K selection theory, with K selection corresponding to static populations without discounting, and r selection corresponding to any scenario with positive population growth. The concept of discounting has a long history in economics tracing back to Fibonacci’s 13th-century work (Goetzmann, 2005). In the later part of the 20th century, some researchers have observed that the discount rate also plays an important role in evolutionary population biology because it provides a means to account for costs associated with delays in reproduction (Goodman, 1982). has appeared repeatedly throughout the historical development of evolutionary theory, although not explicitly by this name. Taylor et al. (1974) showed that the proliferation rate and are equivalent fitness measures in the special case of a discrete-time, age-structured model. Schaffer (1974) also implicitly employed the discounted reproductive number in his study of life-history evolution. Li and Schneider (2002) later extended this by studying models with general stage structure in discrete time. Goodman (1982) seems to be the first author to treat the discount rate as a free parameter, although he takes pains to downplay any originality in his paper. Goodman further suggests a method for optimizing in an age-structured model. The method implicitly requires that an equilibrium strategy have a form of convergent stability (Eshel, 1983) to guarantee that it will be found. McNamara refers specifically to as the “discounted maximum future expected reward” (McNamara, 1991) or the “discounted lifetime reproduction success” (McNamara et al., 2001). plays an important role in studies of evolution based on dynamic programming approaches to fitness (McNamara, 1991) and alternative versions of adaptive topographies (McNamara, 1993; Lande, 1982).

The discounted reproductive number is defined in a manner similar to the basic reproductive number, except that the number of offspring from each stage is also weighted to reduce the value of offspring produced later in time, relative to offspring produced earlier. Thus, the discounted reproductive number is defined as

$${\mathcal{R}}_{\text{d}}={\lambda }_0\left(\mathbf{F}{(\delta \mathbf{I}-\mathbf{T})}^{-1}\right),$$ (5)

where δ is the discount rate. In general, we take δ > λ₀(T) so that an inverse exists. Since all known species are mortal, λ₀(T) < 0.

Just like , can be defined for other common life-history models in addition to the continuous-time matrix models presented here. For a McKendrick–von Foerster model,

$$\frac{\partial n}{\partial t}+\frac{\partial n}{\partial a}=-\mu (a)n\text{and}n(0,t)={\int }_0^{\infty }m(a,t)n(a,t)\text{d}a,$$ (6)

where a is the age of a cohort, the discounted reproductive number is given by

$${\mathcal{R}}_{\text{d}}={\int }_0^{\infty }{\text{e}}^{-\delta a}\ell (a)m(a)\text{d}a,$$ (7a)

with

$$\ell (a)=exp\left({\int }_0^a-\mu (\widehat{a})\text{d}\widehat{a}\right).$$ (7b)

For the discrete-time matrix model

$${\mathbf{n}}_{t+1}=(\mathbf{F}+\mathbf{T}){\mathbf{n}}_t,$$ (8)

the discounted reproductive number is given by

$${\mathcal{R}}_{\text{d}}={\lambda }_0\left(\theta \mathbf{F}{(\mathbf{I}-\theta \mathbf{T})}^{-1}\right),$$ (9)

where θ is the discrete-time discounting ratio (Li and Schneider, 2002). The equation = 1 is a special case which leads to the well-known Euler–Lotka eigen-value problem (Kot, 2001) and Fisher’s reproductive value (Fisher, 1930) for age-structured populations.

3. Properties of

Inspecting equations (3) and (5), we see that when there is no discounting (δ = 0), = . Further, positive discount rates always result in discounted reproductive numbers smaller than the basic reproductive number.

Proposition 1

The discounted reproductive number is a decreasing function of the discount rate δ and is bounded below by 0.

Proof

Define the discounted generation matrix

$$\mathbf{G}=\mathbf{F}{(\delta \mathbf{I}-\mathbf{T})}^{-1},$$ (10)

so that = λ₀(G). By the properties of M-matrices, G exists for all δ > λ₀(T). The discounted generation matrix can be rewritten as

$$\mathbf{G}={\int }_0^{\infty }\mathbf{F}{\text{e}}^{-(\delta \mathbf{I}-\mathbf{T})t}\text{d}t.$$ (11)

Since multiplication by a scalar commutes over all matrices, we can decompose the matrix exponential to the form

$$\mathbf{G}=\mathbf{F}{\int }_0^{\infty }{\text{e}}^{-\delta t}{\text{e}}^{\mathbf{T}t}\text{d}t.$$ (12)

Because −T is an M-matrix, the matrix exponential and hence the whole integrand must be non-negative (Berman and Plemmons, 1979, p. 146). Perron–Frobenius theory tells us that the dominant eigenvalue of a non-negative matrix is non-negative (Horn and Johnson, 1985), so = λ₀(G) ≥ 0.

By inspection, the integrand is decreasing in δ. Because F is also non-negative, we see that G is a component-wise strictly decreasing function of δ in the sense that either ∂G_ij/∂δ < 0 or G_ij = 0. Take h such that for sufficiently small ε,

$$\mathbf{G}(\delta )\ge (1-h\epsilon )\mathbf{G}(\delta )\ge \mathbf{G}(\delta +\epsilon )\ge \mathbf{0}.$$ (13)

If for two matrices A and B where B ≥ A ≥ 0 component-wise, then λ₀(B) ≥ λ₀(A) ≥ 0 (Horn and Johnson, 1985, p. 491), so

$${\lambda }_0(\mathbf{G}(\delta ))\ge {\lambda }_0((1-h\epsilon )\mathbf{G}(\delta ))=(1-h\epsilon ){\lambda }_0(\mathbf{G}(\delta ))\ge {\lambda }_0(\mathbf{G}(\delta +\epsilon ))\ge 0.$$ (14)

It follows that either λ₀(G(δ)) = 0, or λ₀(G(δ)) > λ₀(G(δ + ε)) ≥ 0 in the limit as ε approaches 0 from above.

As = λ₀(G), we conclude that is decreasing in the discount rate δ, and strictly decreasing so long as is positive.

Note that this proof holds for any T and F satisfying our assumptions, so there is a continuous cone of discounted reproductive numbers for any alternative splitting F̃ + T̃ = F + T, but all of these ’s have the same relationship to the ultimate proliferation rate r: the discounted reproductive number is 1 if reproduction is discounted at the ultimate proliferation rate.

Proposition 2

= 1 if and only if δ = r.

Proof

We need to show that the dominant eigenvalue of F(rI − T)⁻¹ is 1. Since r is the dominant eigenvalue of the primitive matrix F + T, the left eigenvector v corresponding to r is unique (up to scaling) and can be taken to be positive (Horn and Johnson, 1985). Moreover, v is the only positive left eigenvector for any eigenvalue (Chow, 1983, p. 914). Then

$${\mathbf{v}}^{\text{T}}(\mathbf{F}+\mathbf{T}-r\mathbf{I})={\mathbf{v}}^{\text{T}}[\mathbf{F}-(r\mathbf{I}-\mathbf{T})]=0,$$ (15)

where v^T denotes the transpose of v. Since −T is an M-matrix and r = λ₀(F+T) > λ₀(T), the matrix rI − T also satisfies the definition of an M-matrix. Because the inverse of an M-matrix is non-negative (Horn and Johnson, 1991, p. 117), (rI − T)⁻¹ exists and is non-negative. If we multiply by this inverse,

$${\mathbf{v}}^{\text{T}}[\mathbf{F}{(r\mathbf{I}-\mathbf{T})}^{-1}-\mathbf{I}]=0.$$ (16)

We now see that v is a positive left eigenvector of F(rI − T)⁻¹ corresponding to the eigenvalue of 1.

Perron–Frobenius theory tells us that for a non-negative matrix A, if an eigenvalue e has a modulus smaller than the dominant modulus, then the eigenvector for e is not strictly positive. Contrapositively, if A is non-negative and v is a positive eigenvector, then the corresponding eigenvalue has modulus equal to the dominant eigenvalue (Chow, 1983, p. 914). Since v is a positive left eigenvector of the nonnegative matrix F(rI − T)⁻¹, we must have λ₀(F(rI − T)⁻¹) = 1. Thus, if δ = r, = 1.

Conversely, let δ ≠ r. By Proposition 1, is strictly decreasing in δ when > 0, so ≠ 1.

4. Comparison of fitness measures

To demonstrate that the discounted reproductive number is equivalent to the basic reproductive number and the ultimate proliferation rate as a fitness measure, consider a very large population where a small number of individuals possess a mutant phenotype π that differs from the population’s resident phenotype π̄. The life-history and fecundity matrices of individuals depend both on the mutant phenotype and on the resident phenotype, which we will denote using subscripts. The mutant phenotype has basic reproductive number

$$\mathcal{R}(\overline{\pi },\overline{\pi })={\lambda }_0(-{\mathbf{F}}_{\pi ,\overline{\pi }}{\mathbf{T}}_{\pi ,\overline{\pi }}^{-1}),$$ (17)

ultimate proliferation rate

$$r(\pi ,\overline{\pi })={\lambda }_0({\mathbf{F}}_{\pi ,\overline{\pi }}+{\mathbf{T}}_{\pi ,\overline{\pi }}),$$ (18)

and discounted reproductive number

$${\mathcal{R}}_{\text{d}}(\pi ,\overline{\pi })={\lambda }_0\left({\mathbf{F}}_{\pi ,\overline{\pi }}{[\delta (\overline{\pi })\mathbf{I}-{\mathbf{T}}_{\pi ,\overline{\pi }}]}^{-1}\right),$$ (19)

where

$$\delta (\overline{\pi })=r(\overline{\pi },\overline{\pi })={\lambda }_0({\mathbf{F}}_{\overline{\pi },\overline{\pi }}+{\mathbf{T}}_{\overline{\pi },\overline{\pi }}).$$ (20)

We have chosen the discount rate δ(π̄) to be the ultimate proliferation rate of individuals with the resident phenotype because this is the population’s baseline growth rate against which the mutant phenotype is competing. Although all phenotypes with (π, π̄) > 1 will increase in number, only phenotypes with an ultimate proliferation rate larger than that of the resident population will increase in frequency.

A mutant phenotype can only invade a population if it has a greater fitness in the current environment than the resident phenotype. If we define the relative fitness of a phenotype as W(π, π̄), with the convention that W(π̄, π̄) = 1, then a mutation can invade when W(π, π̄) > 1. A resident phenotype is a strict Nash equilibrium of the population game if all possible mutations have a lower fitness than the resident phenotype (W(π, π̄) < 1 for all π ≠ π̄). This and other evolutionary properties of a fitness measure can be assessed using the pairwise invasion test map

$$S(W)=\{\begin{array}{lll}-1\hfill & i\text{f}\hfill & W<1,\hfill \\ 0\hfill & \text{if}\hfill & W=1,\hfill \\ +1\hfill & \text{if}\hfill & W>1.\hfill \end{array}$$ (21)

As examples, we re-derive and generalize results from Mylius and Diekmann (1995) and Bulmer (1994, p. 77) describing the circumstances when each fitness measure is equivalent.

Comparison 1

When a population is at a stable size (i.e., no growth, r = 0), the pairwise invasion test of relative fitness measured in terms of the basic reproductive number is the same as the pairwise invasion test of relative fitness measured in terms of the discounted reproductive number.

Proof

We need to prove

$$S\left(\frac{\mathcal{R}(\pi ,\overline{\pi })}{\mathcal{R}(\overline{\pi },\overline{\pi })}\right)=S\left(\frac{{\mathcal{R}}_{\text{d}}(\pi ,\overline{\pi })}{{\mathcal{R}}_{\text{d}}(\overline{\pi },\overline{\pi })}\right).$$ (22)

Because there is no asymptotic growth of the population (r(π̄, π̄) = 0), there is no discounting (δ(π̄) = 0) and the discounted reproductive numbers are equal to the basic reproductive numbers. The ratio of the mutant discounted reproductive number to the resident discounted reproductive number is then the same as the ratio of the basic reproductive numbers:

$$\frac{\mathcal{R}(\pi ,\overline{\pi })}{\mathcal{R}(\overline{\pi },\overline{\pi })}=\frac{{\mathcal{R}}_{\text{d}}(\pi ,\overline{\pi })}{{\mathcal{R}}_{\text{d}}(\overline{\pi },\overline{\pi })}.$$ (23)

Thus, the population games are identical, and the pairwise invasion tests must also be identical.

does not correctly measure fitness, however, when a population’s size is growing or decaying because it gives all reproduction events equal weight. In a growing population, reproduction events next year are worth less than reproduction events this year. Both the ultimate proliferation rate and the discounted reproductive number are suitable alternatives in these cases.

Comparison 2

The pairwise invasion test of relative fitness measured in terms of the ultimate proliferation rate is the same as the pairwise invasion test of relative fitness measured in terms of the discounted reproductive number.

Proof

In order for 1 to remain the critical value for invasion, as in the definition (21) of S(W), we will use the exponential of the ultimate proliferation rate, e^r(π,π̄), instead of the ultimate proliferation rate. Consequently, the relative fitness of π with respect to π̄ is

$$\frac{{\text{e}}^{r(\pi ,\overline{\pi })}}{{\text{e}}^{r(\pi ,\overline{\pi })}}={\text{e}}^{r(\pi ,\overline{\pi })-r(\overline{\pi },\overline{\pi })}.$$ (24)

Thus, we need to show that

$$S\left({\text{e}}^{r(\pi ,\overline{\pi })-r(\overline{\pi },\overline{\pi })}\right)=S({\mathcal{R}}_{\text{d}}(\pi ,\overline{\pi })).$$ (25)

The tests are equal if they are equal at each point (π, π̄). If r(π, π̄) −r(π̄, π̄) = 0, then the discounted reproductive number has a discount rate equal to the proliferation rate and by Proposition 2, (π, π̄) = 1. Now by Proposition 1, if r(π, π̄)−r(π̄, π̄) < 0, then the discount rate is faster than the proliferation rate and (π, π̄) < 1. If r(π, π̄) − r(π̄, π̄) > 0, then the discount rate is slower than the proliferation rate and (π, π̄) > 1. The tests are therefore equal.

Comparisons 1 and 2 show that the discounted reproductive number subsumes the two most common measures of fitness, r and . To show how can be combined with population-level and individual-level models to study evolutionary strategies, let n(t) be the macroscopic state of the resident population, e(t) be the state of the environment, and p(t) be the probability density of the life-history state space over time for an individual with the mutant phenotype π. We refer to p(t) as the microscopic state, because it is the life-history state of a single individual. We refer to n(t) as the population’s macroscopic state because it is a combination of all other individuals’ states. Mathematically, the macroscopic and microscopic dynamics are driven by separate but related processes. From the microscopic perspective of the individual, life is stochastic, but from the macroscopic perspective of a large population, the dynamics are treated as deterministic. If we use a Markov process to describe the life of an individual, and a system of ordinary differential equations to describe changes in a population, the relative fitness of an individual with phenotype π is given by the discounted reproductive number

$$W(\pi ,\overline{\pi })={\int }_0^{\infty }{\text{e}}^{-\delta t}{\mathbf{v}}^{\text{T}}\mathbf{F}\mathbf{p}(t)\text{d}t,$$ (26a)

where

$$\frac{\text{d}\mathbf{P}}{\text{d}t}=\mathbf{T}(\mathbf{n},\mathbf{e},\pi )\mathbf{p}$$ (26b)

governs the dynamics of the microscopic state, and

$$\frac{\text{d}\mathbf{n}}{\text{d}t}={\mathbf{g}}_{\mathbf{n}}(\mathbf{n},\mathbf{e},\overline{\pi }),$$ (26c)

$$\frac{\text{d}\mathbf{e}}{\text{d}t}={\mathbf{g}}_{\mathbf{e}}(\mathbf{n},\mathbf{e},\overline{\pi })$$ (26d)

govern the dynamics of the macroscopic state and the environment. Here, T is the transition-rate matrix of the life-history Markov process, δ = r(π̄, π̄) is the population’s proliferation rate, F is the fecundity matrix, and the vector v is the reproductive value for each state. The use of v was introduced by Fisher (1930), who suggested it be interpreted as the relative expected future lifetime contribution to reproductive output for individuals in each state when π = π̄. The population’s proliferation rate δ discounts future reproduction relative to current reproduction.

Consider a system that is stationary in the sense that the resident population is growing at rate δ(π̄) with fixed proportions of life-history states so that n(t) = e^δ(π̄)tn^* and the resource is at steady state, i.e. e(t) = e^*. The dynamic equations can be reduced by substituting n(t) = e^δ(π̄)tn^* and e(t) = e^* into system (26) and requiring that the equation for the microscopic state, p, be at steady state, resulting in the system of equations:

$$\delta (\overline{\pi }){\mathbf{n}}^{\ast }={\text{e}}^{-\delta (\overline{\pi })t}{\mathbf{g}}_{\mathbf{n}}\left({\text{e}}^{\delta (\overline{\pi })t}{\mathbf{n}}^{\ast },{\mathbf{e}}^{\ast },\overline{\pi }\right)={\mathbf{g}}_{\mathbf{n}}({\mathbf{n}}^{\ast },{\mathbf{e}}^{\ast },\overline{\pi }),$$ (27a)

$$\mathbf{0}={\mathbf{g}}_{\mathbf{e}}\left({\text{e}}^{\delta (\overline{\pi })t}{\mathbf{n}}^{\ast },{\mathbf{e}}^{\ast },\overline{\pi }\right)={\mathbf{g}}_{\mathbf{e}}({\mathbf{n}}^{\ast },{\mathbf{e}}^{\ast },\overline{\pi }),$$ (27b)

$$\mathbf{T}({\text{e}}^{\delta (\overline{\pi })}{\mathbf{n}}^{\ast },{\mathbf{e}}^{\ast },\pi )=\mathbf{T}({\mathbf{n}}^{\ast },{\mathbf{e}}^{\ast },\pi ).$$ (27c)

Under these equilibrium conditions, the probability of being in each state at a given time is

$$\mathbf{p}(t)=e^{\mathbf{T}t}\mathbf{p}(0).$$ (28)

It follows that²

$$W(\pi ,\overline{\pi })={\mathbf{v}}^{\text{T}}\mathbf{F}{(\delta \mathbf{I}-\mathbf{T})}^{-1}\mathbf{p}(0).$$ (30)

We want to choose the reproductive values v such that the relative fitness W(π, π̄) correctly predicts changes in strategy frequency of long times; mathematically,

$$S(W(\pi ,\overline{\pi }))=S({\text{e}}^{r(\pi ,\overline{\pi })-\delta (\overline{\pi })}).$$ (31)

If we choose v to be the left eigenvector associated with the dominant eigenvalue of F (δI − T)⁻¹, normalized such that v^Tp(0) = 1, then

$$W(\pi ,\overline{\pi })={\mathcal{R}}_{\text{d}}(\pi ,\overline{\pi }){\mathbf{v}}^{\text{T}}\mathbf{p}(0)={\mathcal{R}}_{\text{d}}(\pi ,\overline{\pi }).$$ (32)

Applying Comparison 2, we find that for this choice of v,

$$S(W(\pi ,\overline{\pi }))=S({\mathcal{R}}_{\text{d}}(\pi ,\overline{\pi }))=S({\text{e}}^{r(\pi ,\overline{\pi })-r(\overline{\pi },\overline{\pi })})=S({\text{e}}^{r(\pi ,\overline{\pi })-\delta (\overline{\pi })}).$$ (33)

Thus, the relative fitness W(π, π̄) correctly predicts which strategies π can replace the resident strategy π̄ provided that the reproductive value v is defined in terms of a left eigenvector. The reproductive value v is a generalization of Fisher’s reproductive value because it depends on both the invading phenotype π and the resident phenotype π̄, whereas for Fisher’s reproductive value it is traditionally assumed that π = π̄. The definition of the reproductive values in terms of an eigenvector of F (δI − T)⁻¹ may seem to preclude the practical use of equation (26a). However, often F has only 1 nonzero row, corresponding to birth into only one life-history stage, and v^TF is a scalar multiple of that row. In this case, the condition v^Tp(0) = 1 completely characterizes v^T.

Given a fitness function, we can then compare strategies and determine which strategies are Nash equilibria. A phenotype π̄ is a Nash equilibrium strategy if (π*, π*) > (π*, π*) for all π ≠ π. When is a smooth function, the Nash condition is equivalent to $\frac{\partial {\mathcal{R}}_{\text{d}}}{\partial \pi }(\overline{\pi },\overline{\pi })=0$ and $\frac{{\partial }^2{\mathcal{R}}_{\text{d}}}{\partial {\pi }^2}(\overline{\pi },\overline{\pi })<0$.

5. Applications of

The discounted reproductive number is easy to apply, although closed-form solutions are uncommon. As a first example, let us calculate for a simplification of the classic problem of maturation-time evolution. Consider a population with two life-history states, juvenile and adult, that grows linearly according to

$$\frac{\text{d}{y}_1}{\text{d}t}=-f(\overline{\pi })y_1-{\mu }_1{y}_1+u(\overline{\pi })y_2,$$ (34)

$$\frac{\text{d}{y}_2}{\text{d}t}=f(\overline{\pi })y_1-{\mu }_2{y}_2,$$ (35)

where π̄ is the resident phenotype strategy. An individual with phenotype π has life-history transition-rate matrix

$$\mathbf{T}=\left[\begin{array}{cc}-f(\pi )-{\mu }_1& 0\\ f(\pi )& -{\mu }_2\end{array}\right]$$ (36)

and fecundity matrix

$$\mathbf{F}=\left[\begin{array}{cc}0& u(\pi )\\ 0& 0\end{array}\right].$$ (37)

Applying equation (27), we find the discounted reproductive number

$$W(\pi ,\overline{\pi })={\mathcal{R}}_{\text{d}}(\pi ,\overline{\pi })=\frac{u(\pi )f(\pi )}{[f(\pi )+{\mu }_1+\delta (\overline{\pi })][{\mu }_2+\delta (\overline{\pi })]},$$ (38)

where the discount rate

$$\delta (\overline{\pi })=\frac{\sqrt{{[f(\overline{\pi })+{\mu }_1-{\mu }_2]}^2+4u(\overline{\pi })f(\overline{\pi })}-f(\overline{\pi })-{\mu }_1-{\mu }_2}{2}.$$ (39)

Let us extend this model to pathogen evolution in epidemiology. Consider incubation-period evolution in the susceptible-exposed-infectious-recovered (SEIR) model

$$\stackrel{.}{S}=\eta -mS-\beta (\overline{\pi })SI,$$ (40a)

$$\stackrel{.}{E}=\beta (\overline{\pi })SI-f(\overline{\pi })E-mE-{\mu }_{E}E,$$ (40b)

$$\stackrel{.}{I}=f(\overline{\pi })E-\gamma I-mI-{\mu }_{I}I,$$ (40c)

$$\stackrel{.}{R}=\gamma I-mR.$$ (40d)

Here S is the number of people who are susceptible, E is the number exposed, I is the number infectious, and R is the number recovered. The birth rate is given by η, m is the background death rate, μ_E is the infection-induced death rate during the exposed stage, μ_I is the infection-induced death rate during the infectious stage, and γ is the recovery rate. The infection rate, β, and the incubation rate, f, are both functions of pathogen phenotype.

The dynamics of System (40) are well understood. If

$$\left(\frac{\beta }{f+m+{\mu }_E}\right)\left(\frac{f}{\gamma +m+{\mu }_I}\right)\frac{\eta }{m}\le 1,$$ (41)

then the disease-free stationary solution is globally attracting. Otherwise, there is a unique, globally attracting stationary solution with known Lyapunov function (Korobeinikov and Maini, 2005).

In infectious-disease modeling, the pathogens are the organisms of interest, and they only exist in infected human hosts. Therefore, we only need the exposed (E) and infectious (I) compartments of the host population to model the pathogen population. The life-history transition-rate matrix for an infection with type π is

$$\mathbf{T}=\left[\begin{array}{cc}-f(\pi )-{\mu }_E-m& 0\\ f(\pi )& -\gamma -{\mu }_I-m\end{array}\right]$$ (42)

and the fecundity matrix for the creation of new infections is

$$\mathbf{F}=\left[\begin{array}{cc}0& \beta (\pi )S\\ 0& 0\end{array}\right].$$ (43)

We apply equation (5) and find

$${\mathcal{R}}_{\text{d}}=\frac{\beta (\pi )Sf(\pi )}{[f(\pi )+{\mu }_E+m+\delta (\overline{\pi })][\gamma +{\mu }_I+m+\delta (\overline{\pi })]}$$ (44)

with

$$\delta =\frac{-2m-f(\overline{\pi })-{\mu }_E-\gamma -{\mu }_I+\sqrt{{[f(\overline{\pi })+{\mu }_E-\gamma -{\mu }_I]}^2+4\beta (\overline{\pi })Sf(\overline{\pi })}}{2}.$$ (45)

In this calculation, S is treated as a constant. There are two natural cases of equation (40) where this is reasonable. First, early in an epidemic, the number of infections is small while S is large and relatively constant. In this case, S is fixed and independent of the resident phenotype π̄. Second, late in an epidemic, the dynamics approach the endemic steady-state solution, where S is again constant. In this case, the steady-state depends on the resident phenotype π̄;

$$S(\overline{\pi })=min\left\{\frac{\eta }{m},\frac{(\gamma +m+{\mu }_I)(f(\overline{\pi })+m+{\mu }_E)}{\beta (\overline{\pi })f(\overline{\pi })}\right\}.$$ (46)

As an example, let f(π) = π and $\beta (\pi )=\frac{b_0\pi }{1+b_1{\pi }^2}$ (Fig. 1). Example contour plots of (π, π̄) early and late in an epidemic are shown in Figure 2. The condition above are used to show that the points where the 1-contours cross in Figure 2 are Nash equilibria.

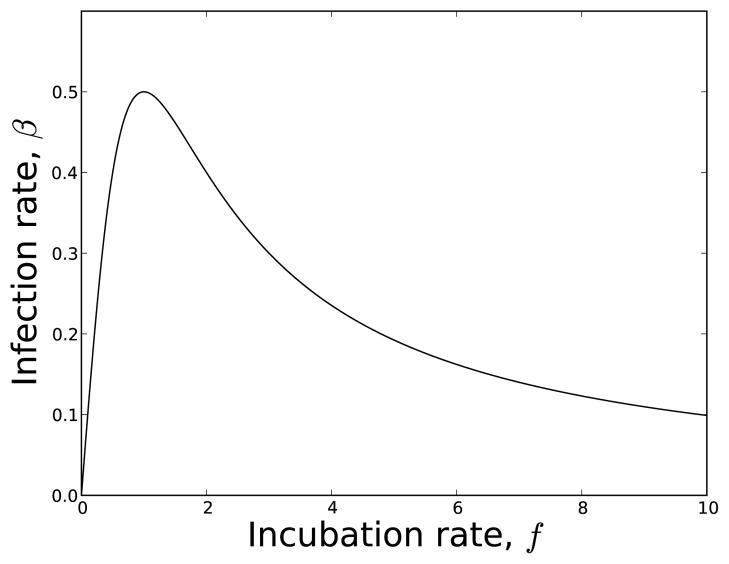
Figure 1.

Transmission rate, β vs. incubation rate, f used in our example for equation (40) and Figure 2. The functional forms are f(π) = π and $\beta (\pi )=\frac{b_0\pi }{1+b_1{\pi }^2}$ with b₀ = b₁ = 1.

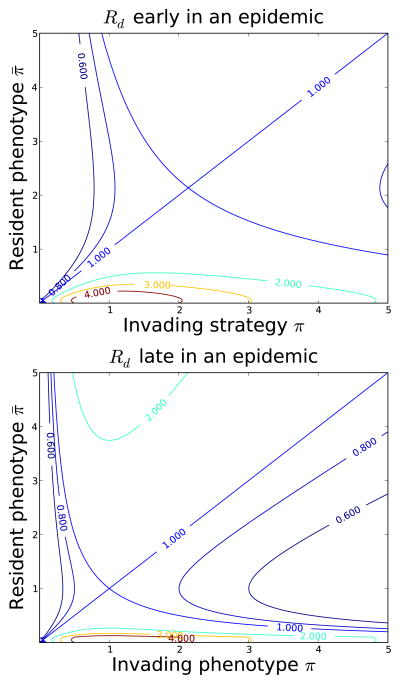
Figure 2.

Contour plots of (π, π̄) early (top) and late (bottom) in the course of an epidemic described by equation (40). Nash equilibria correspond to the phenotypes where the 1-contours intersect. At the start of an epidemic, the number of susceptibles is independent of the strategies and the number of infections is growing exponentially. However, near the end of an epidemic, the number of susceptible individuals at dynamic equilibrium depends on the population’s resident phenotype π̄, although there is no net change in the number of susceptible individuals per unit time. Because of these differences, the Nash equilibrium π* for the rate of leaving the exposed class is more than twice as large early compared to late in the epidemic. Parameter values μ_E = μ_I = 0, γ = 10, m = 1/60, η/m = 100. The early plot is for the naive population, S = 100. For the late plot, S is given by equation (46).

The value of the discount rate differs at different points in an epidemic, as does the number of susceptibles S. Early in an epidemic almost all individuals are susceptible and the number of infections grows exponentially. Thus, the discount rate is large. Over time, however, the excess of susceptibles is exhausted and the population-dynamics approach an endemic stationary solution with the discount rate also approaching 0. The evolutionary pressures on the pathogen change as the discount rate varies between these extremes. The discount rate is faster early in the epidemic when the number of susceptibles is largest and the number of infections is growing quickly, favoring short incubation periods (large π). Late in the epidemic, discounting is slow, and longer incubation periods can pay off with greater transmission. Figure 2 shows how these differences play out in moving the Nash equilibrium from short incubation early in the epidemic to longer incubation periods late in the epidemic.

6. Discussion

We have shown that the discounted reproductive number unifies several disparate measures of fitness within a single framework while providing a mechanistic basis for the derivation of new results. The discounted reproductive number allows us to systematically account for the timing of transmission events to study changes in frequency in a way not possible with the reproductive number . Although we illustrated the use of with ordinary differential equation models, we also showed how is formulated for difference equation and partial differential equation models. We have applied to model changes in host behavior when virulence changes with the age of the host (Reluga et al., 2007) and here to describe changes in pathogen selection over the course of an epidemic. In addition, can be used in studies of the evolution of clutch size, senescence, growth, and other evolutionary trade-offs, including co-evolution, like that between host and pathogen. We also have shown that (π, π̄) is closely connected to Fisher’s reproductive values for different life-history strategies. Therefore, the discounted reproductive number is broadly applicable to other studies where it is reasonable to assume populations are near dynamic equilibrium or growing exponentially.

For many models, the reproductive number is easier to derive and takes a simpler form than the ultimate proliferation rate r. When discount rate δ is treated as a free parameter, which may suffice for some kinds of analysis, is as easy to derive and as simple in form as . However, when δ is taken to be the ultimate proliferation rate of the resident population r(π̄, π̄), the determination of (π, π̄) involves the complexity of calculating both r and .

The proofs of Proposition 1 and Proposition 2 rely on our assumption that the demography matrix F + T is irreducible and primitive. It is not immediately clear what form the results would take if either of these conditions were relaxed. Of particular interest is the fact that the splitting of F + T needed to define , as well as , is not unique. A similar issue is present and more onerous when matrix models are generalized to branching-process models of demography. This suggests two points. First, the mathematics is not capturing some parts of the biology, since fecundity can not be defined arbitrarily in practice. Second, while each splitting defines a different , there seem to be no significant mathematical differences between these splittings in practice. These points suggest a need for a practical convention to aid in comparative analyses. Some readers may note a close connection between the concept of the discounted reproductive number as a function of the discount rate δ and the concept of a Laplace transform. This connection may provide a convenient avenue for mathematical applications of in new research.

Evolutionary population game theory based on the discounted reproductive number has a number of limitations. While convenient, population game theory based on is an asymptotic theory with well-known shortcomings (Abrams et al., 1993). The theory has primarily been applied in settings where population dynamics are stationary or growing exponentially. Equation (5) assumes the matrices F and T are stationary. If transition rates or fecundities are not stationary, the integrals in equation (11) and equation (26a) do not have general closed-form solutions. Similar issues arise in attempts to apply and r in situations where dynamics oscillate. Further generalizations are needed to accommodate dynamic programming formulations and Lyapunov-exponent descriptions of fitness in settings with periodic and chaotic population dynamics (McNamara et al., 2001 ; Metz et al., 1992 ). We have also sidestepped the challenges associated with frequency-dependent selection by restricting our attention to population games. In general, alternative mathematical approaches should be used if the evolutionary dynamics of a biological system are not easily summarized in terms of asymptotic properties.

In summary, we have provided an explicit definition and systematic application framework for extending the reproductive number to the discounted reproductive number. We demonstrated that the discounted reproductive number is a versatile fitness measure that subsumes the two most common measures of fitness, the basic reproductive number and the ultimate proliferation rate.

Figure 3.

Nash equilibrium strategy (π*) at the start of an epidemic, depending on the initial population size (N = η/m). Parameter values are m = 1/60, μ_E = μ_I = 0, γ = 1/3, and b₀ and b₁ as in Figure 1.

Terminology

Here we briefly outline the terminology we use to describe a variety of matrices that arise in population modeling.

A matrix A = [a_ij] is non-negative if all its entries are non-negative, a_ij ≥ 0. Likewise, A is positive if its entries are all positive, a_ij > 0.

A Z-matrix is a square matrix whose off-diagonal entries are all non-positive, a_ij ≤ 0 for i ≠j. A Z-matrix can be written as Z = αI − P, where P is a non-negative matrix. An important property of Z-matrices is that the matrix exponential e^−Zt is non-negative for all t ≥ 0 (Berman and Plemmons, 1979, p. 146).

An M-matrix is a Z-matrix that can be decomposed as M = αI − P for some non-negative matrix P and some α > λ₀(P), where λ₀ denotes the largest real eigenvalue of the matrix. The real part of all the eigenvalues of an M-matrix are positive. Moreover, the inverse of an M-matrix is non-negative (Horn and Johnson, 1991, p. 117). See Horn and Johnson ( 1991) and Berman and Plemmons ( 1979) for expositions on M-matrix theory.

A matrix A being irreducible means, in population terms, that each life stage can ultimately produce every other life stage, either by transition between life stages or by production of offspring. (See, for example, Caswell ( 2001, p. 81).) Note that this definition implies that the matrix must be square. An example of a reducible matrix would be the projection matrix from a model that includes post-reproductive adults: the post-reproductive life stage cannot produce newborns or any other life stage.

A non-negative matrix P is primitive if there exists an integer z such that P^z is positive (Horn and Johnson, 1985). Note that primitive implies irreducible. Otherwise, we define the matrix A to be primitive if there exists α > 0 such that A = P − αI, with P non-negative and primitive. Note that A primitive implies that it is irreducible, as with non-negative matrices, and that it is the negative of a Z-matrix, A = −Z. For a primitive matrix A = P − αI, by Perron–Frobenius theory, the eigenvalue of maximum modulus of P is real and positive (Horn and Johnson, 1985). Therefore, the largest real eigenvalue, λ₀(P), is the eigenvalue of maximum modulus. This implies that λ₀(A) = λ₀(P) − α is real and is the eigenvalue of A with the largest real part.