Abstract
Regulating physical size is an essential problem that biological organisms must solve from the subcellular to the organismal scales, but it is not well understood what physical principles and mechanisms organisms use to sense and regulate their size. Any biophysical size-regulation scheme operates in a noisy environment and must be robust to other cellular dynamics and fluctuations. This work develops theory of filament length regulation inspired by recent experiments on kinesin-8 motor proteins, which move with directional bias on microtubule filaments and alter microtubule dynamics. Purified kinesin-8 motors can depolymerize chemically-stabilized microtubules. In the length-dependent depolymerization model, the rate of depolymerization tends to increase with filament length, because long filaments accumulate more motors at their tips and therefore shorten more quickly. When balanced with a constant filament growth rate, this mechanism can lead to a fixed polymer length. However, the mechanism by which kinesin-8 motors affect the length of dynamic microtubules in cells is less clear. We study the more biologically realistic problem of microtubule dynamic instability modulated by a motor-dependent increase in the filament catastrophe frequency. This leads to a significant decrease in the mean filament length and a narrowing of the filament length distribution. The results improve our understanding of the biophysics of length regulation in cells.
Keywords: biophysics, cytoskeleton, microtubules, motor proteins, kinesin-8, length regulation, dynamic instability
1. Introduction
A fundamental question in biology is how organisms control the size of subcellular structures, cells, organs, and whole organisms. The physical principles underlying the sensing and control of size in biology are not well understood; indeed, whether there are general principles or mechanisms in size control is unclear [1–3]. In particular, the regulation of polymer length is important for the organization of the cellular cytoskeleton. Regulation of cytoskeletal filaments affects both the size of subcellular organelles such as the mitotic spindle [4, 5] and the structure of cells themselves [6, 7]. Microtubules are an important cytoskeletal filament that contribute to cell structure, affect the distribution of other cytoskeletal filaments, move chromosomes during cell division, and serve as tracks for transport within the cell. This paper focuses on the regulation of microtubule length.
Microtubules undergo complex, nonequilibrium polymerization dynamics, known as dynamic instability, characterized by stochastic switching between distinct growing and shrinking states. When dynamic microtubules polymerize in vitro from purified tubulin protein, dynamic instability leads to a broad distribution of polymer lengths [8]. However, in cells other proteins are also present which modify microtubule dynamics, particularly at the plus ends of microtubules [9]. This allows cells to control tubulin polymerization dynamics to give microtubules of regulated length. A relatively well-studied example of length regulation of microtubule-based structures is the control of flagellar length in Chlamydomonas reinhardtii, where the assembly and disassembly of the flagellum is controlled to give a fixed flagellar length [10]. However, in general it is not well understood how cells control the length of their microtubules.
Recently an example of physically-based microtubule length detection and control was proposed, based on motor proteins that walk with directional bias on a microtubule and shorten a stabilized (non-polymerizing) microtubule from its plus end [11–13]. If the motors are processive (unbinding slowly from the microtubule), then a long filament can accumulate large numbers of motors at its end, and the shortening rate is high; for a short filament fewer motors reach the end, and shortening slows. This length-dependent depolymerization has been demonstrated for the kinesin-8 protein Kip3p moving on stabilized microtubules. The physical interactions of motors moving on the filament allow a physical process (the rate of depolymerization) to vary with the filament length, thereby allowing sensing of the length [12–14]. By coupling this length-sensitive depolymerization with other processes (for example, a constant filament growth rate) a specific filament length or narrow filament-length distribution could in principle be achieved [12].
To understand the biological relevance of length-dependent depolymerization, it is important to make a connection between the biophysically measured effects of purified proteins on stabilized microtubules and the more complex situation in cells. Stabilized microtubules have little or no intrinsic length dynamics, while in cells microtubules undergo dynamic instability. Other proteins can also modify microtubule dynamics. Therefore, the kinesin-8 length-dependent depolymerization process will be affected by microtubule length fluctuations and the presence of other proteins at microtubule tips. In general, any biophysical mechanism of length regulation must be robust to noise in the cellular environment.
Recent work suggests that direct length-dependent depolymerization may not be occurring in cells; instead, kinesin-8 proteins may act to promote catastrophe (the transition from growing to shrinking). Extensive experiments have demonstrated that deletions or knockdowns of kinesin-8 proteins in cells result in longer microtubules and mitotic spindles as well as an increase in chromosome loss in mitosis [11,15–21]. Other work has shown that kinesin-8 activity is associated with destabilization of microtubules and other alterations in microtubule dynamics [11–13,15,20,22–35]. While the molecular mechanisms of kinesin-8 protein function are not clear, it appears that not all kinesin-8 proteins are able to depolymerize stabilized microtubules [26,35,36]. Both experimental evidence [11, 25, 29, 35] and modeling work [37] suggest that in cells kinesin-8 proteins may act to promote catastrophe of dynamic microtubules. Therefore, it is necessary to understand the consequences of length-dependent changes in microtubule dynamic instability to predict the effects of these motors in cells. This will improve our general question of how length-sensing mechanisms are altered by fluctuations and dynamics in biological systems.
Previous theory and modeling work has addressed aspects of kinesin 8 behavior and length regulation. Several papers have focused on modeling the physical effects important to describe the length-dependent depolymerization of otherwise static filaments [13,14,38] or filaments with simplified polymerization kinetics [39–41]. To our knowledge, previous work has not examined the effect of catastrophe-promoting motors on the length distribution of microtubules undergoing dynamic instability. Tischer et al. used a similar formalism to that in this paper in a model for how length-dependent microtubule catastrophe and rescue rates affect the density of cargo-carrying motors along microtubules, an effect that could be used to target cargo delivery to specific cellular locations [42].
In this paper, we develop a simplified physical theory to compare two scenarios for length regulation: for length regulation by depolymerization we calculate the steady-state length that is reached by a constantly growing filament balanced by depolymerizing motors, while for length regulation by altering catastrophe we consider filaments undergoing dynamic instability with alterations in the dynamics due to motors. We consider two possible mechanisms of motor action at the microtubule tip, both the minimal model in which motor effects (depolymerization or catastrophe) increase in proportion to the motor density [14, 38, 41] and the cooperative model in which motor effects (depolymerization or catastrophe) increase in proportion to the flux of motors to the filament end [13]. These two models show important differences in their effects on length regulation, suggesting that cellular length regulation could be sensitive to the precise mechanism. We find consistent qualitative agreement between mean-field theory and stochastic simulation; in some parameter regimes the two approaches agree quantitatively.
2. Motor dynamics along filament
The mean-field density of the motors along the filament, ρ(x, t), in units of motors per unit length is described by [43]
| (1) |
On the right hand side, the first term describes biased motion of the motors with speed v, where crowding effects reduce the motor flux [43] and ρmax is the maximum possible motor density. The second term describes binding of motors to unoccupied sites at rate per unit length konc. The third term describes unbinding of motors from occupied sites at rate koff. This formulation assumes a continuum limit in which the lattice spacing a → 0 so that the motor density can be treated as continuous in x. The bulk motor concentration c is assumed constant, i.e., the binding of motors to the filament is assumed not to deplete the pool of motors in the bulk. Note that we do not consider protofilament interactions within a microtubule, so we are effectively considering a single-protofilament microtubule (figure 1).
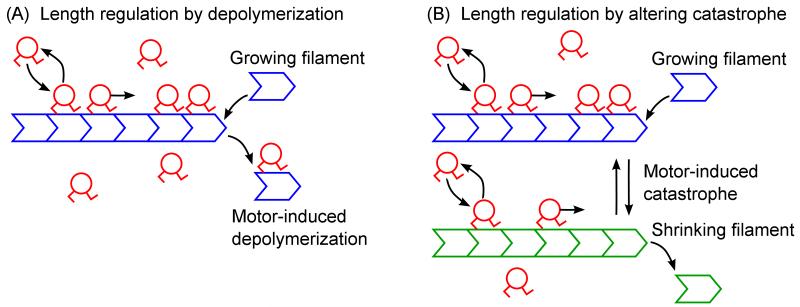
Figure 1.
Schematic of the model. (A) Model of length regulation by depolymerization. Filament growth at the plus end is balanced by motor-induced depolymerization. Motors bind to and unbind from the filament, move toward the filament plus end, and catalyze removal of filament subunits from the plus end. This leads to a length-dependent depolymerization rate, so a single filament length is favored, depending on the model parameters. (B) Model of length regulation by altering catastrophe. The filament undergoes dynamic instability at its plus end, characterized by stochastic transitions between growing (blue) and shrinking (green) states. Motors bind to and unbind from the filament, move toward the filament plus end, and catalyze catastrophe (transition from the growing to the shrinking state) at the filament plus end. Motor effects make the catastrophe frequency length dependent, which leads to a broad distribution of filament lengths determined by the properties of the motors.
For relatively low motor density, we neglect crowding effects in the drift term, which makes the density equation linear. In addition, we work with the motor fractional occupancy p(x, t) = ρ(x, t)/ρmax, so the density equation can be written
| (2) |
With the initial condition p(x, t) = 0 at time t = 0 and the boundary condition p(x = 0, t) = 0, the solution to this equation is
| (3) |
The steady-state occupancy away from the filament ends is p0 = konc/(koffρmax + konc), the time scale τ = 1/(koff + konc/ρmax), and the length scale λ = v/(koff + konc/ρmax) = vτ. At long time, the density approaches the steady state profile which is constant away from the filament end but has a boundary layer for small x where transport effects and boundary conditions change the motor density away from p0 [39,43,44].
3. Length regulation by depolymerization
Here we study the regulation of filament length assuming the motors directly depolymerize the filament from its plus end, an effect which is balanced by a constant rate of filament growth (figure 1A). This approach neglects fluctuations due to microtubule dynamic instability, and so the resulting length is deterministically reached. We suppose that a filament grows with constant speed u.
We consider two simple models for the dynamics of the plus end end. (We assume that the filament minus end is not dynamic.) For density-controlled depolymerization, the motor-induced depolymerization rate is proportional to the motor occupancy at the end [14,38,41]. For flux-controlled depolymerization, the motor-induced depolymerization rate is proportional to the motor flux to the end [13,38]. We assume that the motors move faster than the growth (v > u), so the motors track the end as observed experimentally. We therefore assume that the motor occupancy away from the filament end reaches the steady-state value p(x) = p0(1 – e−x/λ).
Dimensional analysis suggests that the filament length reached should be related the boundary layer length scale λ = v/(koff + konc/ρmax) = vτ, the obvious length scale that can be constructed from the rates in the problem. However, the steady-state filament length is quite different from λ and is controlled by the dynamics at the end of the filament.
This model is related to recent work that also considered the balance between depolymerizing motors and filament kinetics described by constant growth [39, 41] or treadmilling [40]. The model here is simplified compared to the previous work, to allow the derivation of analytic expressions for the length achieved and to allow comparison to the results for filaments undergoing dynamic instability.
3.1. Density-controlled depolymerization
In the density-controlled model, we assume that the depolymerization rate is proportional to the motor density at the terminal site of the microtubule [14]. We assume that only the motor occupancy at the last site of the filament is important for depolymerization, i.e., we neglect possible cooperative effects. Define pe(t) to be the average motor occupancy at the last site on the filament, and the filament length is L(t). The mean-field density-dependent depolymerization model is:
| (4) |
| (5) |
The first term on the right side of equation (4) represents the stepping of motors from the site adjacent to the end to the terminal site on the filament, at rate . The density at the penultimate site on the filament is p(L – a, t), where a is the lattice spacing, assumed small. If the motor dynamics at the end are faster than the typical time scale of density changes in the bulk of the filament, we can treat the motor density away from the end quasi-statically assuming it is unaffected by the end dynamics. Thus, we write p(L – a, t) ≈ p(L, t), where p(x, t) is the motor occupancy for a region far from the filament end. Because the kinetics of motor removal may be different at the end of the filament, we include crowding effects at the last site even though they are neglected elsewhere along the microtubule. The second term on the right side of equation (4) describes unbinding of the motor at the end. In equation (5), the filament lengthens at constant speed u and shortens at a rate proportional to the motor density at the end, with a maximum speed w.
Note that in this model the unbinding of the motor from end of the filament (controlled by the term with rate in equation (4)) is decoupled from the depolymerization rate (controlled by the term with rate wpe in equation (5)). This means that we allow processive depolymerization, with a single motor able to remove an average of monomers from the filament.
The steady-state length in the density-controlled model Lden is reached when and , which implies pe = u/w and
| (6) |
| (7) |
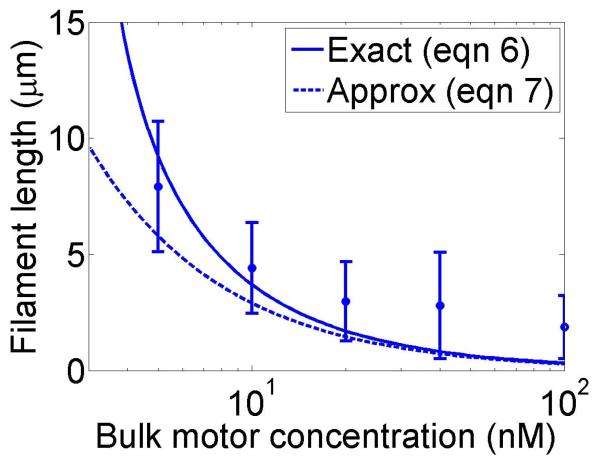
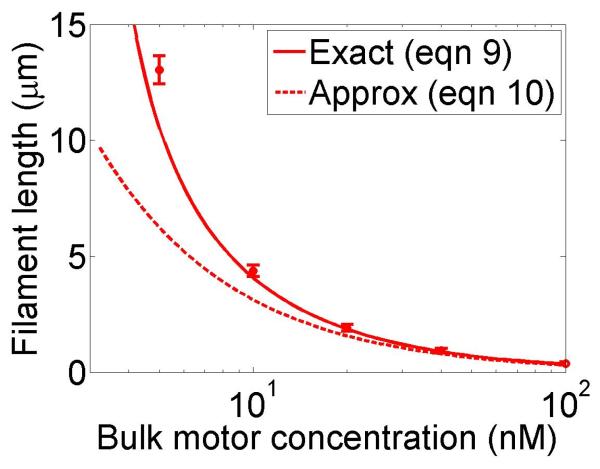
The approximate solution in equation (7) applies when the second term inside the logarithm of equation (6) is small. Note that there is no steady-state solution if either w < u (in this case the motors can never remove dimers quickly enough to keep up with the growth) or . Therefore the motor occupancy must be larger than the critical value for a steady-state length to occur, implying a minimum bulk motor concentration of . In practice given measured motor parameters, reasonable values of the steady-state length require w quite similar to u; the requirement for such fine-tuning of the depolymerization rate suggests that this length-regulation mechanism is not highly robust (figure 2).
Figure 2.
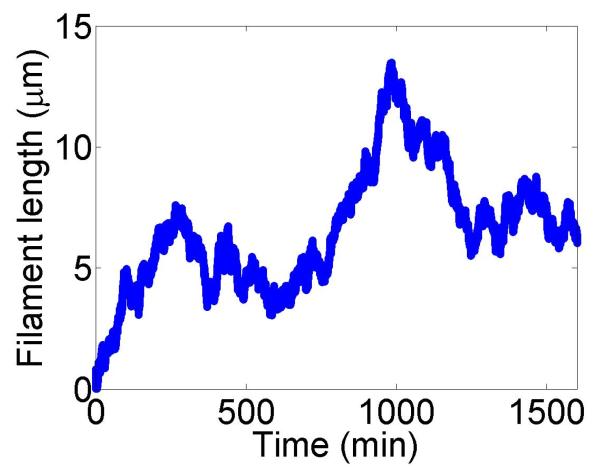
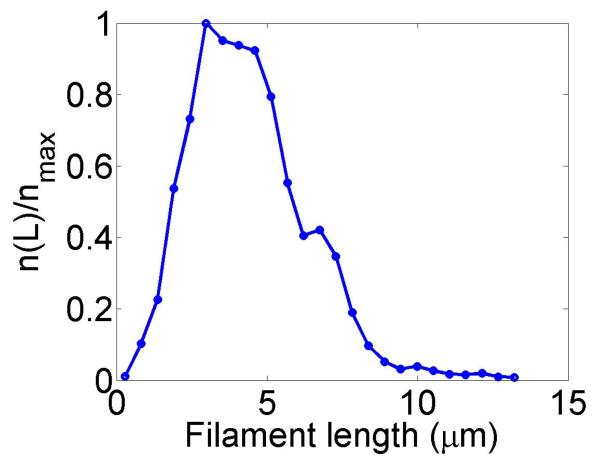
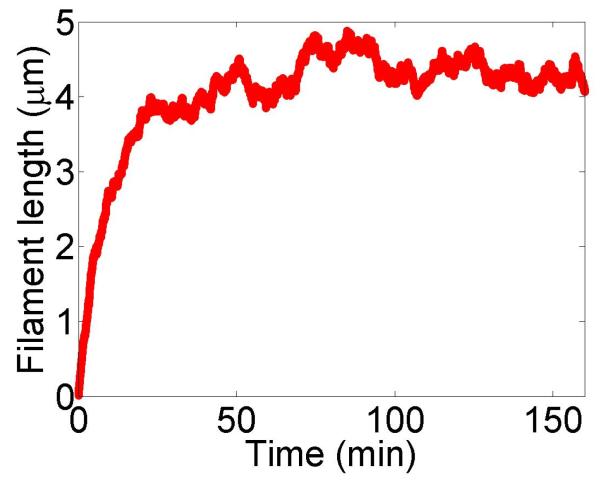
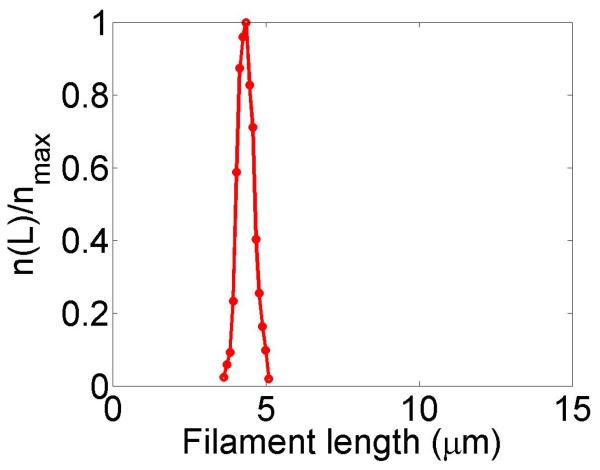
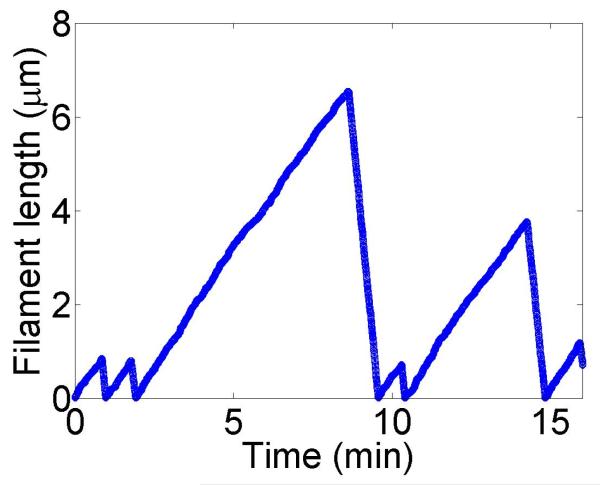
Filament dynamics and steady-state filament length for length regulation by depolymerization. Blue (top), density-controlled depolymerization; red (bottom), flux-controlled depolymerization. Left, example trace of filament length versus time in the stochastic simulation for c = 10 nM. Middle, normalized filament length distribution in the stochastic simulation for c = 10 nM, averaged from 10 stochastic simulations after removal of the initial transient. Right, steady-state filament length predictions of mean-field theory and the stochastic simulation (error bars are standard deviations of steady-state length distributions). The steady-state length varies rapidly with the bulk motor concentration. The two models give similar predictions, and the approximate expressions (eqns 7 and 10) for the steady-state length are within a factor of two of the exact expressions (eqns 6 and 9) except for very low bulk motor concentrations. The mean-field theory uses the parameters v = 3 μm min−1, kon = 2 nM−1μm−1 min−1, koff = 0.25 min−1, min−1, w = 1.025 μm min−1, a = 8 nm, δ = 8 nm, and ρmax = 125 μm−1; for the density-controlled model u = 1.0 μm min−1 while for the flux-controlled model u = 0.5 μm min−1. The stochastic simulation uses the same parameters except w = 1.5 μm min−1 and min−1 off for the density-controlled model.
We show the dependence of the steady-state length on the bulk motor concentration in figure 2. We use parameters similar to those found in experiments [11,13]. The results of stochastic simulation of density-controlled depolymerization agree qualitatively with the predictions of the mean-field theory (figure 2, details of the simulations are described in section 5). The best agreement occurs when the stochastic simulation uses a slightly larger motor-induced depolymerization speed w and a slightly lower motor unbinding rate from the filament end than the mean-field theory. In this case the mean filament lengths reached in the two models are similar, but the stochastic simulation shows large fluctuations about the mean length. This is intuitively reasonable since in this model depolymerization is controlled by the motor occupancy at the terminal site of the filament, which undergoes significant fluctuations.
3.2. Flux-controlled depolymerization
Varga et al. found that their experimental data for depolymerization of stabilized microtubules by Kip3p are consistent with filament depolymerization being determined by the flux of motors to the end [13]. In this model, a motor would in principle remain bound to the filament end forever, unless displaced from the tip by the arrival of another motor. When unbinding, each motor is assumed to shorten the microtubule by a length δ (where δ could equal the lattice spacing a if each motor removes exactly one tubulin dimers, but could differ from a depending on the motor depolymerization processivity). Therefore the depolymerization speed is w = δJ(L), where is the flux of motors to the end of the filament. Note that steric interactions between motors that decrease the flux are neglected here. The length of the microtubule changes in time according to
| (8) |
At steady state, and the motor occupancy is the steady-state value. Therefore u = δρmaxvp(Lss), and the steady-state length in the flux-controlled model is
| (9) |
| (10) |
As above, the approximate solution applies when the second term inside the logarithm is small. Note that there is no steady-state solution if u/(vδp0ρm) ≥ 1. This implies that the motor density must be larger than the critical value p0c = u/(vδρmax) for a steady-state length to occur; this corresponds to a critical bulk motor density cc = koffρmaxu/(kon(vδρmax – u)). This requires vδρmax > u; in practice, for parameters for the budding-yeast motor Kip3 vδρmax must be a few times u to get steady-state lengths of a few microns.
We show the dependence of the steady-state length on the bulk motor concentration in figure 2. The results of stochastic simulation of flux-controlled depolymerization agree quantitatively with the predictions of the mean-field theory for identical parameters (figure 2, details of the simulations are described in section 5). Compared to the density-controlled depolymerization model, the flux-controlled depolymerization model shows decreased fluctuations and a relatively narrow length distribution. This may occur because in this model depolymerization is controlled by the motor flux to end of the filament, which is a collective property of multiple motors.
The structures of the steady-state solutions are similar in the two models, having the approximate form (equations (7) and (10)) L ~ u/konc times a factor with units of inverse length related to how motors are removed from the end. These approximations to L make clear the strong dependence of the steady-state length on the bulk motor concentration, implying that length regulation by this mechanism requires tight regulation of the motor concentration c. In the density-controlled model the motor unbinding rate from the end of the filament and the difference w – u between the maximum speed of depolymerization and the filament growth rate are important in controlling the length reached. In the flux-controlled model the steady-state length takes a simple form, depending primarily on u, konc, and δ.
In both cases, there is a minimum motor occupancy required to reach a steady-state length, as expected, because a minimum number of motors is required for depolymerization to balance polymerization. The steady-state filament length is quite different from the dimensional length scale λ which characterizes the motor density profile.
4. Length regulation by altering catastrophe
In cells, microtubule filaments typically don’t grow constantly as in the simple model above, but instead undergo dynamic instability, characterized by long-lived growing and shrinking regimes with transitions between these two states. Studies of Kip3p in cells [11] and in vitro [29] and of other kinesin-8 motors [25, 35], as well as modeling work [37] suggest that in cells these proteins may act to promote catastrophe (the transition from growing to shrinking) of dynamic microtubules. Therefore, it is necessary to understand the consequences of length-dependent changes in filament dynamics (rather than merely shortening) to predict the effects of these motors in cells.
Here we develop a theory of motors that promote filament catastrophe in a length-dependent manner. The number probability density n(L) = nG(L)+nS(L) for filaments of length L is made up of two populations, growing (G) and shrinking (S) filaments. The total number of filaments is N = ∫n(L) dL. In this model, we neglect pauses (neither growth nor shrinkage) exhibited by dynamic microtubules in cells. The distributions evolve according to
| (11) |
The terms in the first equation represent filament growth with speed u, catastrophe with frequency fc, and rescue with frequency fr. The terms in the second equation represent filament shortening with speed w, catastrophe, and rescue. At steady state, . The solution to this equation (consistent with the boundary condition that the number of filaments drops to zero as L → ∞) is nS = (u/w)nG. Then the steady-state equation for the total number of filaments n = nG + nS simplifies to
| (13) |
If the catastrophe and rescue rates are spatially constant, the microtubule length distribution is exponential, n(L) = n0 exp(–(fc/u – fr/w)L), so the distribution is a bounded exponential if fc/u > fr/w and has characteristic length uw/(fcw – fru).
In the case of length-dependent rates, we have the formal solution
| (14) |
Here, we assume that only the catastrophe rate fc(L) varies with length (as observed for the kinesin-8 motors Klp5/6 in fission yeast cells [25]), and other rates are all constant. Then
| (15) |
4.1. Density-controlled catastrophe
As above, we assume that the motors move faster than the filament growth, so the motors track the end and the motor density is at steady state. In the density-controlled catastrophe model, we assume that the catastrophe frequency increases linearly with the motor occupancy at the end of the filament:
| (16) |
The motor occupancy at the end is determined by equation (4). At steady state, the occupancy at the end of the growing filament is
| (17) |
with b = (v – u)p0/a. Using the integral
| (18) |
the length distribution is
| (19) |
where is the maximum possible increase in the catastrophe frequency in the density-controlled model. We see two effects due to motors: first, there is an effective increase in the catastrophe rate of Δfden. Second, there is an additional multiplicative factor in the length distribution. This factor approaches one in the limit of short filaments (L ⪡ λ) and for typical experimental parameters varies slowly with L.
Note that in this model the unbinding of the motor from end of the filament is controlled by the rate constant . This means that a motor can processively track the end of a depolymerizing filament, and this processivity tends to increase motor concentration at the end of the filament and therefore enhance the filament-shortening effects of motors.
4.2. Flux-controlled catastrophe
In the flux-controlled catastrophe model, we assume that the catastrophe frequency increases linearly with the flux of motors to the end:
| (20) |
The flux to the end of the microtubule is J = p(L)ρmax(v – u). Note that in this model α is dimensionless and that steric interactions between motors that decrease the flux are neglected. The length distribution is then
| (21) |
where Δfflux = α(v – u)ρmaxp0 is the maximum possible increase in the catastrophe frequency in the flux-controlled model. Again, we see two effects from the length-dependent catastrophe: there is an effective increase in the catastrophe rate of Δfflux, and there is an additional multiplicative factor in the length distribution which is an exponential of an exponential of the length. This factor approaches 1 in the limit of short microtubules (L ⪡ λ) and approaches the constant factor as L → ∞; for typical experimental parameters this factor is of order 1.
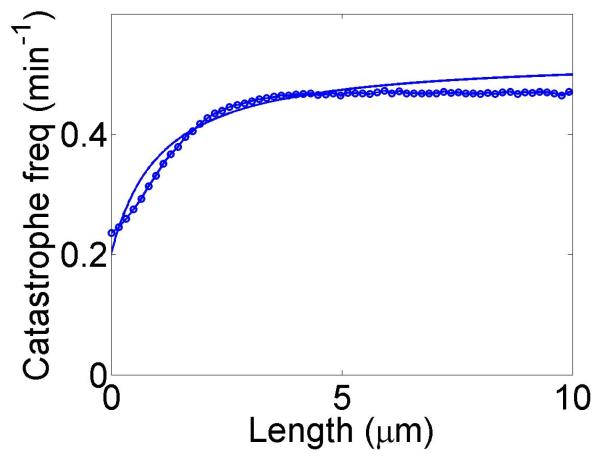
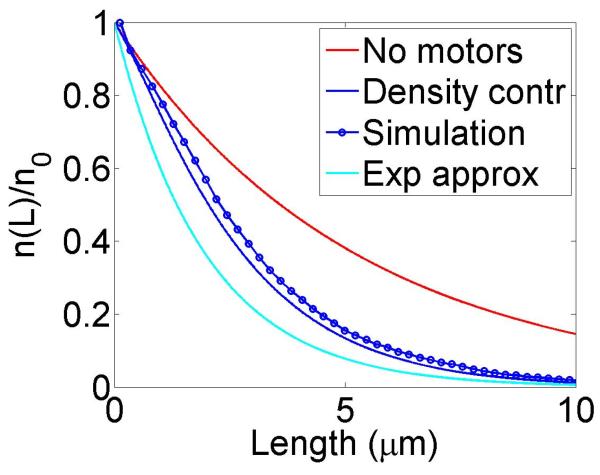
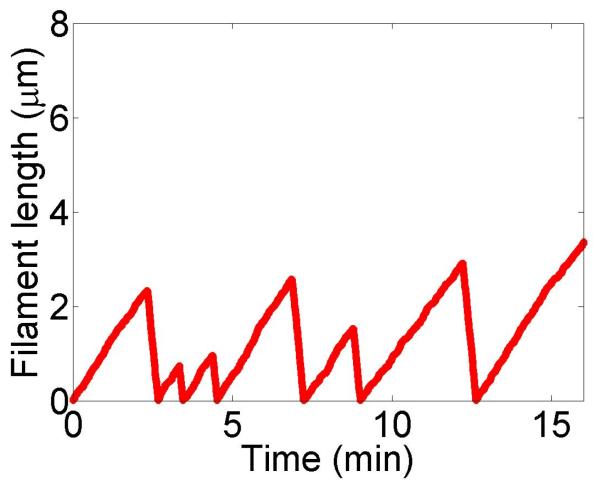
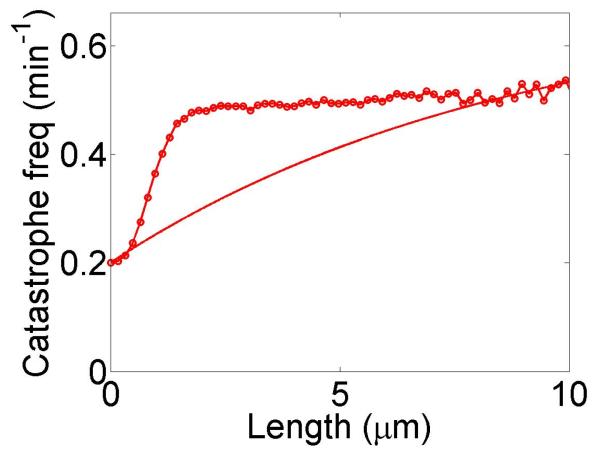
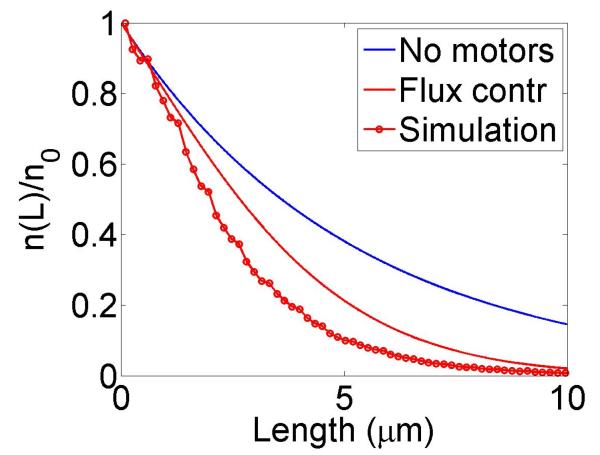
We show simulations of filament length as a function of time, calculations of the variation of catastrophe frequency with filament length and filament length distributions in figure 3. We chose parameters from experiments on the increase in catastrophe frequency associated with the kinesin-8 motor Klp5/6 in fission yeast [25], which found a catastrophe frequency fc = 0.2 min−1 in cells lacking kinesin-8 motors and a length-dependent increase in the catastrophe frequency up to a maximum of 0.5 min−1 for filaments 8 μm long in cells containing motors. With the correct choice of parameters, the length-dependent increase in catastrophe frequency due to motors is qualitatively similar to that measured by Tischer et al. [25].
Figure 3.
Dynamics of length regulation by altering catastrophe. Top, density-controlled model. Bottom, flux-controlled model. Left, example trace of filament length versus time in the stochastic simulation. Middle, catastrophe frequency as a function of filament length, comparing mean-field theory (line) and stochastic simulation (points). Right, length distribution of dynamic filaments for the model with and without motors, comparing mean-field theory and stochastic simulation. The presence of the motors leads to a significant decrease in the mean filament length. This figure uses the parameters v = 3 μm min−1, u = 1 μm min−1, w = 7 μm min−1, minimum catastrophe frequency fc = 0.2 min−1, rescue frequency fr = 0.05 min−1, a = 8 nm, and ρmax = 125 μm−1. For the density-controlled model the parameters are kon = 1 nM−1μm−1 min−1, koff = 0.25 min−1, min−1, bulk motor concentration c = 2 nM, and α = 0.35 min−1. The simulation of the density-controlled model has the same parameters except min−1 and α = 0.38 min−1. For the flux-controlled model the parameters are kon = 3 nM−1μm−1 min−1, koff = 0.25 min−1, bulk motor concentration c = 4 nM, and α = 7 × 10−3. The simulation of the flux-controlled model has the same parameters as the corresponding mean-field theory except kon = 1.5 nM−1μm−1 min−1 and α = 2 × 10−3.
The results of stochastic simulation are shown for comparison with mean-field theory. For density-controlled catastrophe, there is excellent agreement between stochastic simulation results and mean-field theory if the parameters and α are slightly modified. The flux-controlled catastrophe model predictions of the dependence of catastrophe frequency on filament length show only rough qualitative agreement with mean-field theory; the shapes of the curves are quite different. Even this level of agreement requires modification of the parameters kon and α.
4.3. Mean filament length
The length-dependent catastrophe induced by motors changes the microtubule length distribution in two ways: the effective catastrophe frequency increases, and the length distribution is multiplied by an additional function. When the additional change in the functional form due to this multiplication can be neglected, including only the effective increase in the catastrophe frequency gives a simple result for the change in mean filament length. The approximate length distribution is
| (22) |
We define , the mean filament length in the absence of motors, and the mean length including motor effects is . The mean length is
| (23) |
The fractional change in the mean length is
| (24) |
This expression is an approximation that typically overestimates the change in filament length due to motors, but has the advantage that it has a simple analytical form that can be used to understand which parameters control the mean length. The mean filament length is related to the maximum increase in catastrophe frequency that can be achieved by the motors. In the density-controlled model , and in the flux-controlled model Δfflux = α(v – u)ρmaxp0.
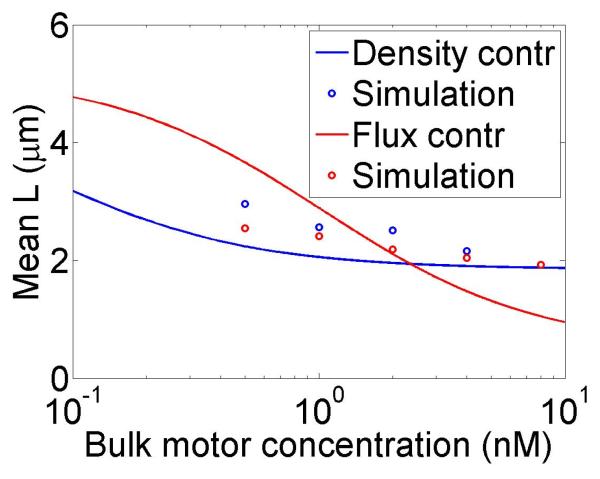
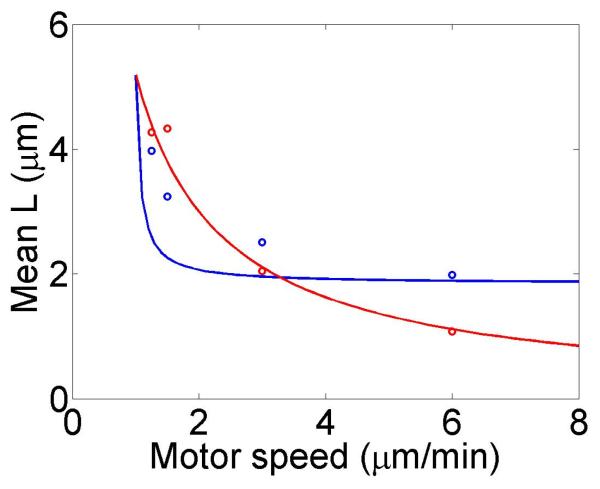
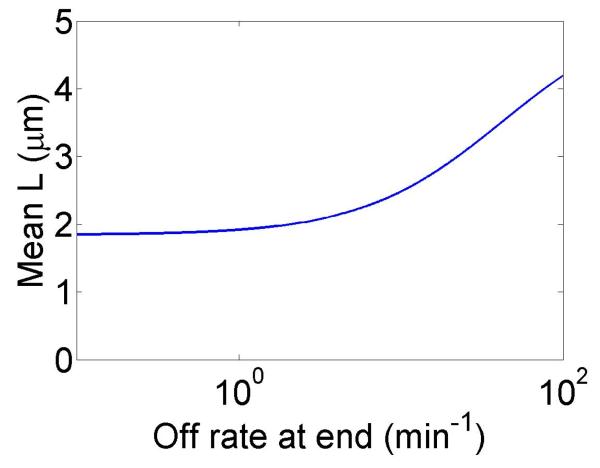
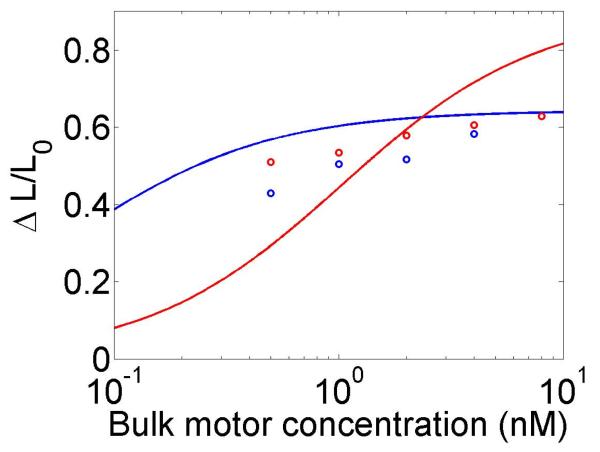
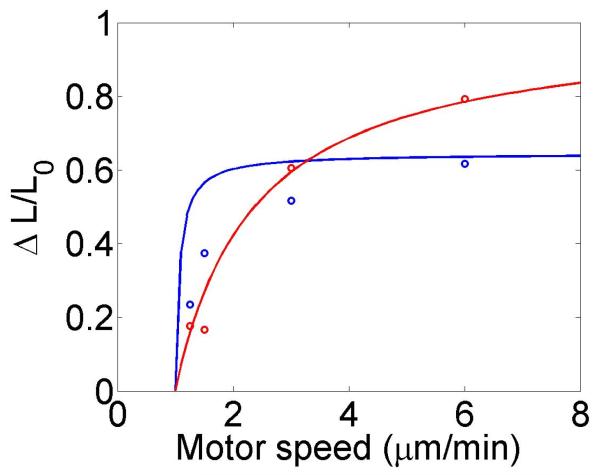
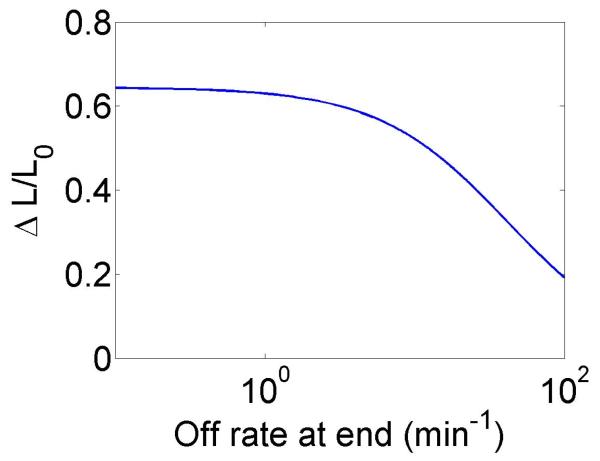
The change in the mean filament length varies with the bulk motor concentration (through the occupancy p0), the difference between the filament growth speed and the motor walking speed, and the motor unbinding rate from the filament end in the density-controlled model (figure 4). This suggests that in cells length regulation could be tuned by altering motor concentration, motor/filament velocity, or motor off rate at the end of the filament in the density-controlled model. For typical experimental parameters, the fractional change in mean filament length varies from 0.1 to 0.9 with changes in these parameters. While changes in bulk motor concentration can alter the mean filament length, relatively large changes in the concentration (over two orders of magnitude) lead to only modest changes in mean filament length. We find that in comparison to stochastic simulation the approximate expressions calculated above tend to overstate the changes in mean filament length achievable through bulk motor density changes. Particularly for the flux-controlled model, mean filament length is more sensitive to alterations in motor speed. Varying motor speed over a factor of 4 allows approximately factor of 10 change in the mean filament length. Comparison to stochastic simulations shows that mean filament length changes due to variation in motor speed are accurately captured by the approximate model.
Figure 4.
Mean filament length and changes in filament length as a function of motor parameters. Left, variation as a function of bulk motor concentration. Center, variation as a function of motor speed. Right, variation as a function of in the density-controlled model. This figure uses the same parameters as figure 3 except where noted in varying the bulk motor concentration and motor speed: v = 3 μm min−1, u = 1 μm min−1, w = 7 μm min−1, minimum catastrophe frequency fc = 0.2 min−1, rescue frequency fr = 0.05 min−1, a = 8 nm, and ρmax = 125 μm−1. For the density-controlled model the parameters are kon = 1 nM−1 μm−1 min−1, koff = 0.25 min−1, min−1, bulk motor concentration c = 2 nM, and α = 0.35 min−1. The simulation of the density-controlled model has the same parameters except min−1 and α = 0.38 min−1. For the flux-controlled mean-field model the parameters are the same as for the density-controlled mean-field model except kon = 3 nM−1μm−1 min−1 and α = 7 × 10−3. The simulation of the flux-controlled model has the same parameters as the corresponding mean-field theory except kon = 1.5 nM−1μm−1 min−1 and α = 2 × 10−3.
In the density-controlled model, the rate constant controls the residence time of a motor at the end of a filament. In the limit that this rate becomes large compared to other rates in the problem, the motors rapidly unbind upon reaching the filament end and the changes in filament length due to motors become smaller.
The increase in catastrophe due to motors can shift the filament length distribution from the unbounded growth regime to the bounded growth regime. If fr/w > fc/u, the filament dynamics are in the unbounded growth regime, with no defined mean filament length. If the increase in catastrophe due to motors Δf is large enough, the presence of motors can shift the distribution back to the bounded growth regime characterized by an exponential length distribution and a well-defined mean filament length. This requires that Δf > fru/w – fc. This relationship implies a minimum motor concentration to shift from unbounded to bounded growth.
5. Stochastic simulation
We developed a kinetic Monte Carlo simulation of the model as shown in figure 1. The model considers a single filament (equivalent to representing a microtubule by a single protofilament) made up of a varying number of monomers. Each motor occupies a single filament monomer. Typical time scales of motor and filament processes are of order seconds to minutes, so we chose a simulation time step of 0.01 s. At each time step a number of monomers equal to the total number of monomers currently in the the filament is randomly sampled and one step of the polymerization dynamics at the end of the filament is performed. Each site on the filament except the last site has the same rules: a motor can bind to an empty site, if the next site forward is empty a motor can step forward, and a motor can unbind to create an empty site.
The behavior of the last site (the end of the filament) varies depending on the model considered. In the model of length regulation by depolymerization (figure 1A), the filament can grow by addition of a monomer. Growth is independent of motor occupancy at the last site. The filament can shrink by one monomer depending on the motor occupancy at the end of the filament. In the density-controlled depolymerization model, removal of the terminal monomer can occur if the terminal site is occupied by a motor. In this model the motor can processively track the depolymerizing filament: if the penultimate site is empty, the motor at the last site steps backward when the terminal monomer is removed. If the second-to-last site is occupied, the motor on the terminal site is removed when the terminal monomer is removed. The motor at the terminal site can also directly unbind from the filament without removal of a monomer. In the flux-controlled depolymerization model, removal of the terminal monomer occurs when the last and penultimate sites are both occupied by motors and the motor at the penultimate site attempts a forward step. In this case the terminal motor and monomer are both removed.
In the model of length regulation by catastrophe (figure 1B), the filament stochastically switches between growing and shrinking states. Speeds of growth and shrinkage as well as the rescue frequency are independent of motor occupancy at the last site. The catastrophe frequency is increased depending on the motor occupancy at the end of the filament. In the density-controlled catastrophe model, the catastrophe frequency is increased by α if the terminal site is occupied by a motor. In this model the motor can processively track the depolymerizing filament: if the filament is shortening and the penultimate site is empty, the motor at the last site steps backward when the terminal monomer is removed. If the second-to-last site is occupied, the motor on the terminal site is removed when the terminal monomer is removed. The motor at the terminal site can also directly unbind from the filament without removal of a monomer. In the flux-controlled catastrophe model, the increase in the catastrophe frequency by α occurs when the last and penultimate sites are both occupied by motors and the motor at the penultimate site attempts a forward step. In this case the terminal motor is removed independent of whether or not a catastrophe occurs.
In all versions of the model, if the filament fully depolymerizes (0 sites remain) a new filament is nucleated containing 1 site. For each parameter set we performed 5-10 simulations of 106 – 108 time steps.
6. Conclusion
We have considered an example of biophysical length regulation by motors that walk along a filament and promote filament shortening, inspired by experiments on the effects of kinesin-8 motor proteins on microtubule dynamics. The motors bind to microtubules and move toward their plus ends, and the presence of motors at the filament end alters microtubule polymerization dynamics.
The first mechanism we considered is a simplified model of length regulation, in which the motors directly catalyze depolymerization of the filament from its plus end. When the action of the motors is balanced by a constant filament polymerization rate, a steady-state filament length can be reached. This mechanism neglects any fluctuating filament dynamics: only a single steady-state length is reached. In the stochastic simulation, fluctuations due to stochastic motor/filament dynamics lead to a spread about the mean length but the distribution of filament lengths remains strongly peaked. There is a minimum bulk motor concentration on the filament to reach a steady-state length, because if there are too few motors, motor-induced depolymerization can never be fast enough to balance the intrinsic polymerization. In addition, inequalities involving the motor motion constrain the parameter regime where steady-state solutions are possible. The steady-state filament length differs from the length scale λ which characterizes the motor density profile. The steady-state filament length depends sensitively on the bulk motor concentration, implying that this mechanism of length regulation requires tight control of total motor number to operate successfully.
Other recent theory work has addressed length regulation due to depolymerizing motors and filament kinetics described by constant growth [39, 41] or treadmilling [40]. Govindan et al. considered a similar model for motor motion, but used an absorbing boundary condition for motors at the filament plus end, an approximation that doesn’t apply to filaments with biologically realistic growth and shrinkage rates. Their work found an exponential filament length distribution for typical parameter values corresponding to Kip3 [39]. Melbinger et al. improved the model of Govindan et al. by studying in detail how effects of motor crowding near the microtubule end control the depolymerization dynamics. They discovered a parameter regime in which filament length is well regulated, and how the length depends on motor kinetics [41]. Johann et al. considered the related problem of how length regulation can be achieved by depolymerizing motors on filaments that undergo treadmilling dynamics (addition of subunits at one end and removal at the other) [40].
In the model of length regulation by depolymerization we have discussed, constant growth is balanced by length-dependent depolymerization. In the balance-point model of flagellar length regulation in Chlamydomonas, a constant rate of flagellar disassembly is balanced by a length-dependent rate of flagellar assembly, leading to a fixed flagellar length [10, 45]. While the underlying microscopic mechanisms of flagellar length regulation differ from those discussed here, the conceptual similarity is striking. Perhaps this basic idea of regulating length by making assembly or disassembly length-dependent while the other process (disassembly or assembly) is length independent could be a general paradigm for length regulation, at least of microtubule-based structures.
A more biologically relevant model for the length regulation of dynamic microtubules is length regulation by altering catastrophe, in which the filament undergoes dynamic instability characterized by long-lived growing and shrinking states with transitions between growth and shrinkage. The effect of the motors at the end is then not to directly depolymerize the filament but to increase the catastrophe frequency. We calculate how the filament length distribution is altered by the motor-dependent increase in catastrophe frequency, and derive a simple approximate expression that relates the mean filament length to the maximum increase in catastrophe frequency that can be achieved by the motors. The mean filament length varies modestly with bulk motor concentration but is sensitive to the difference between the filament growth speed and the motor walking speed.
The increase in catastrophe frequency associated with the kinesin-8 motor Klp5/6 in fission yeast cells was measured by Tischer et al. [25], who found a catastrophe frequency fc = 0.2 min−1 in cells lacking Klp5/6 and a length-dependent increase in the catastrophe frequency up to a maximum of 0.5 min−1 for filaments 8 μm long in cells containing motors. With the correct choice of parameters, our model displays a length-dependent increase in catastrophe frequency due to motors which is qualitatively similar to that measured by Tischer et al. Using these parameters in our model, changes in the mean length of a factor of 2 can be achieved by this mechanism.
Acknowledgments
The authors thank Robert Blackwell, Matt Glaser, Loren Hough and Dick McIntosh for useful discussions. This work was supported by NSF CAREER Award DMR-0847685, NSF MRSEC Grant DMR-0820579, and NIH training grant T32 GM-065103.
Footnotes
PACS numbers: 87.16.dp,87.10.Ed,87.15.rp,87.16.ad,87.16.Ka,87.16.Nn,87.18.Tt
Contributor Information
Hui-Shun Kuan, Program in Chemical Physics and Biofrontiers Institute, University of Colorado at Boulder.
M. D. Betterton, Department of Physics and Biofrontiers Institute, University of Colorado at Boulder mdb@colorado.edu
References
- [1].Day SJ, Lawrence PA. Measuring dimensions: the regulation of size and shape. Development. 2000;127(14):2977–2987. doi: 10.1242/dev.127.14.2977. [DOI] [PubMed] [Google Scholar]
- [2].Hafen E, Stocker H. How are the sizes of cells, organs, and bodies controlled? PLoS Biology. 2003;1(3):e86. doi: 10.1371/journal.pbio.0000086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Mike Cook and Mike Tyers. Size control goes global. Current Opinion in Biotechnology. 2007 Aug;18(4):341–350. doi: 10.1016/j.copbio.2007.07.006. [DOI] [PubMed] [Google Scholar]
- [4].Goshima G, Wollman R, Stuurman N, Scholey JM, Vale RD. Length control of the metaphase spindle. Current Biology. 2005;15(22):1979–1988. doi: 10.1016/j.cub.2005.09.054. [DOI] [PubMed] [Google Scholar]
- [5].Walczak Claire E., Mitchison Timothy J., Desai Arshad. XKCM1: a xenopus kinesin-related protein that regulates microtubule dynamics during mitotic spindle assembly. Cell. 1996 Jan;84(1):37–47. doi: 10.1016/s0092-8674(00)80991-5. [DOI] [PubMed] [Google Scholar]
- [6].Rivero F, Koppel B, Peracino B, Bozzaro S, Siegert F, Weijer CJ, Schleicher M, Albrecht R, Noegel AA. The role of the cortical cytoskeleton: F-actin crosslinking proteins protect against osmotic stress, ensure cell size, cell shape and motility, and contribute to phagocytosis and development. Journal of Cell Science. 1996 Nov;109(11):2679–2691. doi: 10.1242/jcs.109.11.2679. [DOI] [PubMed] [Google Scholar]
- [7].Revenu C, Athman R, Robine S, Louvard D. The co-workers of actin filaments: from cell structures to signals. Nature Reviews Molecular Cell Biology. 2004;5(8):635–646. doi: 10.1038/nrm1437. [DOI] [PubMed] [Google Scholar]
- [8].Marileen Dogterom and Stanislas Leibler. Physical aspects of the growth and regulation of microtubule structures. Physical Review Letters. 1993 Mar;70(9):1347–1350. doi: 10.1103/PhysRevLett.70.1347. [DOI] [PubMed] [Google Scholar]
- [9].Anna Akhmanova and Casper C Hoogenraad. Microtubule plus-end-tracking proteins: mechanisms and functions. Current Opinion in Cell Biology. 2005 Feb;17(1):47–54. doi: 10.1016/j.ceb.2004.11.001. [DOI] [PubMed] [Google Scholar]
- [10].Marshall Wallace F., Qin Hongmin, Brenni Mónica Rodrigo, Rosenbaum Joel L. Flagellar length control system: Testing a simple model based on intraflagellar transport and turnover. Molecular Biology of the Cell. 2005 Jan;16(1):270–278. doi: 10.1091/mbc.E04-07-0586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Gupta ML, Carvalho P, Roof DM, Pellman D. Plus end-specific depolymerase activity of Kip3, a kinesin-8 protein, explains its role in positioning the yeast mitotic spindle. Nature Cell Biology. 2006;8(9):913–923. doi: 10.1038/ncb1457. [DOI] [PubMed] [Google Scholar]
- [12].Varga V, Helenius J, Tanaka K, Hyman AA, Tanaka TU, Howard J. Yeast kinesin-8 depolymerizes microtubules in a length-dependent manner. Nature Cell Biology. 2006;8(9):957–962. doi: 10.1038/ncb1462. [DOI] [PubMed] [Google Scholar]
- [13].Varga Vladimir, Leduc Cecile, Bormuth Volker, Diez Stefan, Howard Jonathon. Kinesin-8 Motors Act Cooperatively to Mediate Length-Dependent Microtubule Depolymerization. Cell. 2009;138(6):1174. doi: 10.1016/j.cell.2009.07.032. [DOI] [PubMed] [Google Scholar]
- [14].Hough LE, Schwabe A, Glaser MA, McIntosh JR, Betterton MD. Microtubule depolymerization by the kinesin-8 motor kip3p: a mathematical model. Biophysical Journal. 2009;96(8):3050–3064. doi: 10.1016/j.bpj.2009.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].West Robert R, Malmstrom Terra, Troxell Cynthia L, McIntosh JR. Two related kinesins, klp5+ and klp6+, foster microtubule disassembly and are required for meiosis in fission yeast. Molecular Biology of the Cell. 2001;12(12):3919–32. doi: 10.1091/mbc.12.12.3919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].West Robert R, Malmstrom Terra, McIntosh J Richard. Kinesins klp5(+) and klp6(+) are required for normal chromosome movement in mitosis. Journal of Cell Science. 2002;115:931–40. doi: 10.1242/jcs.115.5.931. [DOI] [PubMed] [Google Scholar]
- [17].Garcia Miguel Angel, Koonrugsa Nirada, Toda Takashi. Two kinesin-like Kin I family proteins in fission yeast regulate the establishment of metaphase and the onset of anaphase A. Current biology. 2002;12(8):610–21. doi: 10.1016/s0960-9822(02)00761-3. [DOI] [PubMed] [Google Scholar]
- [18].Garcia MA, Koonrugsa N, Toda T. Spindle-kinetochore attachment requires the combined action of Kin I-like Klp5/6 and Alp14/Dis1-MAPs in fission yeast. EMBO Journal. 2002;21(22):6015–6024. doi: 10.1093/emboj/cdf611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Savoian MS, Gatt MK, Riparbelli MG, Callaini G, Glover DM. Drosophila Klp67A is required for proper chromosome congression and segregation during meiosis i. Journal of Cell Science. 2004;117(16):3669–3677. doi: 10.1242/jcs.01213. [DOI] [PubMed] [Google Scholar]
- [20].Mayr MI, Hummer S, Bormann J, Gruner T, Adio S, Woehlke G, Mayer TU. The human kinesin Kif18A is a motile microtubule depolymerase essential for chromosome congression. Current Biology. 2007;17(6):488–498. doi: 10.1016/j.cub.2007.02.036. [DOI] [PubMed] [Google Scholar]
- [21].Jaqaman K, King EM, Amaro AC, Winter JR, Dorn JF, Elliott HL, Mchedlishvili N, McClelland SE, Porter IM, Posch M, et al. Kinetochore alignment within the metaphase plate is regulated by centromere stiffness and microtubule depolymerases. The Journal of Cell Biology. 2010;188(5):665–679. doi: 10.1083/jcb.200909005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Gandhi R, Bonaccorsi S, Wentworth D, Doxsey S, Gatti M, Pereira A. The drosophila kinesin-like protein KLP67A is essential for mitotic and male meiotic spindle assembly. Molecular Biology of the Cell. 2004;15(1):121–131. doi: 10.1091/mbc.E03-05-0342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Gatt MK, Savoian MS, Riparbelli MG, Massarelli C, Callaini G, Glover DM. Klp67A destabilises pre-anaphase microtubules but subsequently is required to stabilise the central spindle. Journal of Cell Science. 2005;118(12):2671–2682. doi: 10.1242/jcs.02410. [DOI] [PubMed] [Google Scholar]
- [24].Unsworth Amy, Masuda Hirohisa, Dhut Susheela, Toda Takashi. Fission yeast kinesin-8 Klp5 and Klp6 are interdependent for mitotic nuclear retention and required for proper microtubule dynamics. Molecular Biology of the Cell. 2008;19(12):5104. doi: 10.1091/mbc.E08-02-0224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Tischer Christian, Brunner Damian, Dogterom Marileen. Force- and kinesin-8-dependent effects in the spatial regulation of fission yeast microtubule dynamics. Molecular Systems Biology. 2009 Mar;5 doi: 10.1038/msb.2009.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Du Y, English CA, Ohi R. The kinesin-8 Kif18A dampens microtubule plus-end dynamics. Current Biology. 2010;20(4):374–380. doi: 10.1016/j.cub.2009.12.049. [DOI] [PubMed] [Google Scholar]
- [27].Peters Carsten, Brejc Katju∣[scaron]∣a, Belmont Lisa, Bodey Andrew J., Lee Yan, Yu Ming, Guo Jun, Sakowicz Roman, Hartman James, Moores Carolyn A. Insight into the molecular mechanism of the multitasking kinesin-8 motor. The EMBO Journal. 2010 Sep;29(20):3437–3447. doi: 10.1038/emboj.2010.220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Wang H, Brust-Mascher I, Cheerambathur D, Scholey JM. Coupling between microtubule sliding, plus-end growth and spindle length revealed by kinesin-8 depletion. Cytoskeleton. 2010;67(11):715–728. doi: 10.1002/cm.20482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Gardner Melissa K., Zanic Marija, Gell Christopher, Bormuth Volker, Howard Jonathon. Depolymerizing kinesins Kip3 and MCAK shape cellular microtubule architecture by differential control of catastrophe. Cell. 2011 Nov;147(5):1092–1103. doi: 10.1016/j.cell.2011.10.037. [DOI] [PubMed] [Google Scholar]
- [30].Masuda Natsuko, Shimodaira Tetsuhiro, Shiu Shu-Jen, Tokai-Nishizumi Noriko, Yamamoto Tadashi, Ohsugi Miho. Microtubule stabilization triggers the plus-end accumulation of Kif18A/kinesin-8. Cell Structure and Function. 2011 Jan;36(2):261–7. doi: 10.1247/csf.11032. [DOI] [PubMed] [Google Scholar]
- [31].Mayr Monika I., Storch Marko, Howard Jonathon, Mayer Thomas U. A non-motor microtubule binding site is essential for the high processivity and mitotic function of kinesin-8 Kif18A. PLoS One. 2011 Nov;6(11):e27471. doi: 10.1371/journal.pone.0027471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Stumpff Jason, Du Yaqing, English Chauca A., Maliga Zoltan, Wagenbach Michael, Asbury Charles L, Wordeman Linda, Ohi Ryoma. A tethering mechanism controls the processivity and kinetochore-microtubule plus-end enrichment of the kinesin-8 Kif18A. Molecular cell. 2011 Sep;43(5):764–75. doi: 10.1016/j.molcel.2011.07.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Su X, Qiu W, Gupta ML, Jr, Pereira-Leal JB, Reck-Peterson SL, Pellman D. Mechanisms underlying the dual-mode regulation of microtubule dynamics by Kip3/kinesin-8. Molecular cell. 2011;43(5):751. doi: 10.1016/j.molcel.2011.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Weaver LN, Ems-McClung SC, Stout JR, LeBlanc C, Shaw SL, Gardner MK, Walczak CE. Kif18A uses a microtubule binding site in the tail for plus-end localization and spindle length regulation. Current Biology. 2011 doi: 10.1016/j.cub.2011.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Erent M, Drummond DR, Cross RA. S. pombe kinesins-8 promote both nucleation and catastrophe of microtubules. PloS One. 2012;7(2):e30738. doi: 10.1371/journal.pone.0030738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Grissom PM, Fiedler T, Grishchuk EL, Nicastro D, West RR, McIntosh JR. Kinesin-8 from fission yeast: A heterodimeric, plus-end–directed motor that can couple microtubule depolymerization to cargo movement. Molecular Biology of the Cell. 2009;20(3):963–972. doi: 10.1091/mbc.E08-09-0979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Brun Ludovic, Rupp Beat, Ward Jonathan J., Nédélec François. A theory of microtubule catastrophes and their regulation. Proceedings of the National Academy of Sciences. 2009 Dec;106(50):21173–21178. doi: 10.1073/pnas.0910774106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Reese Louis, Melbinger Anna, Frey Erwin. Crowding of molecular motors determines microtubule depolymerization. Biophysical Journal. 2011 Nov;101(9):2190–2200. doi: 10.1016/j.bpj.2011.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Govindan BS, Gopalakrishnan M, Chowdhury D. Length control of microtubules by depolymerizing motor proteins. Europhysics Letters. 2008 Aug;83(4):40006. [Google Scholar]
- [40].Johann Denis, Erlenkämper Christoph, Kruse Karsten. Length regulation of active biopolymers by molecular motors. Physical Review Letters. 2012 Jun;108(25):258103. doi: 10.1103/PhysRevLett.108.258103. [DOI] [PubMed] [Google Scholar]
- [41].Melbinger Anna, Reese Louis, Frey Erwin. Microtubule length regulation by molecular motors. Physical Review Letters. 2012 Jun;108(25):258104. doi: 10.1103/PhysRevLett.108.258104. [DOI] [PubMed] [Google Scholar]
- [42].Tischer Christian, ten Wolde Pieter Rein, Dogterom Marileen. Providing positional information with active transport on dynamic microtubules. Biophysical Journal. 2010 Aug;99(3):726–735. doi: 10.1016/j.bpj.2010.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Parmeggiani A, Franosch T, Frey E. Totally asymmetric simple exclusion process with Langmuir kinetics. Physical Review E. 2004 Oct;70(4) doi: 10.1103/PhysRevE.70.046101. [DOI] [PubMed] [Google Scholar]
- [44].Nowak Sarah A., Fok Pak-Wing, Chou Tom. Dynamic boundaries in asymmetric exclusion processes. Physical Review E. 2007;76(3):031135–11. doi: 10.1103/PhysRevE.76.031135. [DOI] [PubMed] [Google Scholar]
- [45].Engel Benjamin D., Ludington William B., Marshall Wallace F. Intraflagellar transport particle size scales inversely with flagellar length: revisiting the balance-point length control model. The Journal of Cell Biology. 2009 Oct;187(1):81–89. doi: 10.1083/jcb.200812084. [DOI] [PMC free article] [PubMed] [Google Scholar]