Reaching for Words and Non-Words: Interactive effects of word frequency and stimulus quality on the characteristics of reaching movements

Abstract

Word frequency and stimulus degradation produce large and additive effects in the onset latencies of lexical decision responses. The influence of these two variables was examined in a lexical decision task where continuous arm reaching responses were required and movement trajectories were tracked. The results yielded the typical additive pattern of word frequency and stimulus degradation on reaction time and movement duration. Importantly, however, an examination of movement trajectories revealed interactive effects of word frequency and stimulus degradation that emerged for the early part of the movement. These findings suggest that factors thought to influence early stages of stimulus identification continue to influence the dynamics of the response after response initiation, motivating a need to reevaluate current models of lexical decision performance. Moreover, this work highlights how the dynamics of naturalistic multi-dimensional responses provide a richer source of information about decision-making processes than discrete uni-dimensional measures.

Additive effects of stimulus quality (SQ) and word frequency (WF) on reaction time (RT) have been found in a number of visual word recognition studies using the lexical decision task (LDT: Becker & Killion, 1977; Plourde & Besner, 1997; Yap & Balota, 2007). Hence, recognition of a low frequency (LF) word like “gorge” is just as affected by stimulus degradation as a high frequency (HF) word like "large". Strong additive effects of these variables are inconsistent with the general thrust of interactive activation models of word recognition (e.g., Coltheart et al., 2001; McClelland & Rumelhart, 1981) in which SQ and WF should multiplicatively influence word recognition performance. Within such models, degradation has more time to influence the activation function for LF than for HF words, since the representations for LF words are further from threshold.

Additive factors logic (Sternberg, 1969) explains these results by arguing that manipulations of SQ and WF influence separate stages of processing during the LDT (Borowsky & Besner, 1993). In particular, an early stage may involve perceptual normalization where stimuli are "cleaned up". At a later stage, individuals recover familiarity-based information (i.e. how orthographically and phonologically similar the stimulus is to a word) to assist their word or non-word decision (Balota & Chumbley, 1984). Stimulus quality is thought to influence the former stage while WF influences the latter. Additive influences have been found for mean reaction time (RT) and the detailed parameters of reaction time distributions when legal non-words (e.g., FLIRP) are used (Yap, Balota, Tse & Besner, 2008).

In most models of the LDT, SQ and WF exert their influence prior to response execution. Effectors, like the hands and fingers simply translate the more central, final decision into action. However, some work reveals that these factors show a persisting influence on features of the response after initiation (Abrams & Balota, 1991; Balota & Abrams, 1995). When participants categorized word and non-word targets by moving a response handle to one side or the other, WF and SQ produced additive effects not only on response latency but also movement duration, and parameters related to movement force (Balota & Abrams, 1995). High frequency and non-degraded words produced faster, more forceful movements than LF and degraded words. Moreover, work by Coles, Gratton, Bashore, Eriksen, and Donchin (1985) has shown that response competition in the flanker task influences both the characteristics of event related potentials and features of the motor response. In this and other conflict scenarios (see Coles, Gratton & Donchin, 1988 for a review), recordings of the lateralized readiness potential (LRP) indicate that information incompatible with the correct response may prime the inappropriate response before stimulus evaluation is completed. These studies support the idea that stimulus information continuously accumulates over time to influence features of a response other than latency.

Recently, there is increasing interest in the use of continuous response measures to illuminate the dynamics of information processing over time. For example, in the psycholinguistics literature eye-tracking has revealed that, even in the earliest moments of spoken language comprehension, visual context information can influence the processing of syntactic ambiguities (Tanenhaus, Spivey-Knowlton, Eberhard & Sedivy, 1995). Studies which track the coordinates of continuous responses, such as movements of a computer mouse towards a visual target, have shown evidence of response competition in the curvature of movement trajectories (see Song & Nakayama, 2009, for a relevant review) in a variety of tasks. These include selecting a picture that matches a cue word in the presence of distracting phonological competitors (Spivey, Grosjean, Knöblich & McClelland, 2005), classifying typical and atypical category exemplars (Dale, Kehoe & Spivey, 2007), and categorizing nouns according to their color in the presence of masked color primes (Finkbeiner, Song, Nakayama & Caramazza, 2008). With high competition between response options, trajectories towards the correct target have greater curvature, exhibiting an attraction towards the competing response. For instance, the reaching response to a picture of a candle will curve more towards the opposite target if the name of that target shares the same first syllable (i.e., candy), than if it does not (i.e., dog) (Spivey et al., 2005). Continuous motor responses may, therefore, reveal the dynamics of such processing over time as individuals resolve competing stimulus influences even after response initiation; they may also better reflect natural movement in the environment than the simple discrete movements typically measured in RT tasks.

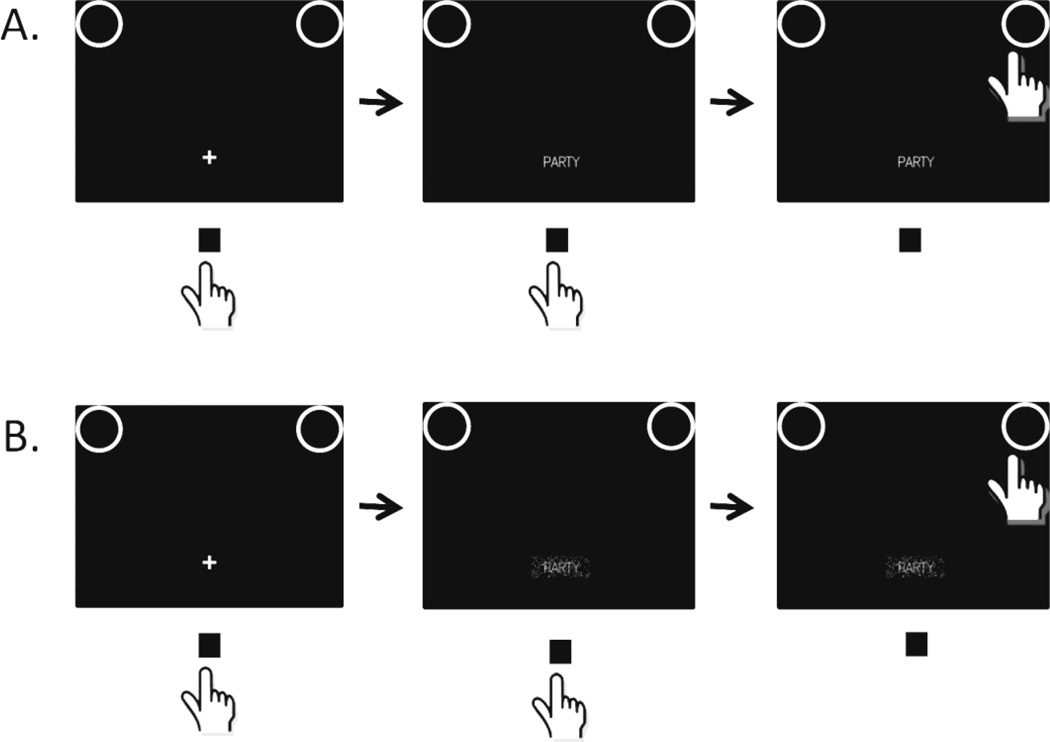
The current study extends the Balota and Abrams (1995) investigation of WF and SQ to a more natural three-dimensional movement. The procedure is displayed in Figure 1, wherein participants were required to move their hand from a starting point to a target location as quickly and as accurately as possible. Although Balota and Abrams found additive influences of these variables, the dependent variables used were uni-dimensional, i.e., the movement was constrained by a handle that could only move left to right horizontally. More natural movements involve all three dimensions. It is possible that in the Balota and Abrams study, constraining the response to one dimension may have simplified the motor programs and minimized the opportunity to detect more complex patterns of behavior as have been observed in the recent work looking at two-dimensional mouse coordinates by Dale et al. (2007) and Spivey et al. (2005). Indeed, using the three dimensional procedure it may be possible to discover that competition from the non-word response option, reflecting people’s uncertainty about the identity of word stimuli, continues to influence trajectories throughout the course of movement responses for LF degraded words. In contrast, if the additivity of SQ and WF on lexical decision processing implicates separate processing stages, reflecting more general characteristics of lexical processing, then one should find the same additive effects observed by Balota and Abrams (1995) even in naturalistic unconstrained three-dimensional movements.

Figure 1.

Events during a single trial in the lexical decision task with an example A) clear and B) degraded stimulus. The position of the participant’s index finger was tracked during the trial. In these examples the word response was assigned to the right target circle while the non-word response was assigned to the left target circle.

Method

Participants

Thirty-two students (mean age = 18.88, SD = .87; 11 males) from the Psychology department undergraduate pool consented to participate in this study for course credit. They were right-handed, native English speakers with normal or corrected-to-normal visual acuity. An additional participant completed the study but was eliminated due to a high error rate.

Apparatus

Stimuli were displayed on a 15-inch Viewsonic VG150 LCD monitor positioned approximately 46 cm in front of the participant at a 44 degree angle from the horizontal table surface. The monitor was situated in a box under a glass cover which provided a surface upon which to make reaching responses. Letters were presented in an uppercase sans serif font. Each letter was 12.7 mm in height, subtending a visual angle of approximately 1.58°. Participants wore a glove on their right hand with an Ascension Technology (Burlington, VT) Flock of Birds 25.4 × 25.4 × 20.3 mm sensor attached to the top of the index finger. This system sampled the sensor’s position in three dimensions at a rate of 100 Hz. Responses were made to target circles (48 mm diameter) in the upper corners of the monitor; one circle was assigned to the word while the other was assigned to the non-word response. Testing occurred in a dimly lit room.

Stimuli

The stimuli consisted of 200 words and 200 length-matched pronounceable non-words. HF words had mean counts of 1,227 counts per million, whereas LF words had counts of 44 per million based on the HAL corpus (Lund & Burgess, 1996). For HF words, the mean length was 4.73 letters (SD = .96), and the mean orthographic neighborhood size (N) (Coltheart, Davelaar, Jonasson, & Besner, 1977) was 4.77 (SD = 4.47). LF words had a mean length of 4.78 letters (SD = .85), and a mean N of 4.82 (SD = 4.37). HF and LF words did not differ in length or orthographic neighborhood size (all t < 1). The non-word mean N was 3.16 (SD = 3.67). All stimuli and their relevant characteristics can be found in a supplemental appendix.

Half of the HF, LF words and non-words were visually-degraded by the presence of additional illuminated pixels. A pixilated mask was created by randomly illuminating 3% of the pixels in the area in which the letter strings were presented. This degradation method has been used in prior work demonstrating additive effects of SQ and WF on RT and other response features (Balota & Abrams, 1995). Examples of a non-degraded and degraded trial are shown in Figure 1. Word and non-word assignment to the degraded condition was counterbalanced across two lists; all stimulus items were presented in each list, but items degraded in the first list were non-degraded in the second list. Within-list stimulus order was randomized for each participant.

Procedure

Each participant was assigned to one of four LDT conditions resulting from the factorial combination of the two counterbalanced stimulus lists and the two possible circle assignments (left or right) to the "word" response. When a letter string appeared at the bottom of the screen participants were told to indicate quickly and accurately whether it spelled a word or non-word by reaching their right hand to the appropriate response circle.

As shown in Figure 1, participants placed their right index finger on a black square at the base of the display aligned with their body midline. This served as the home position. A fixation cross at the bottom of the screen brightened and, after 800 ms, was replaced by a letter string. Participants were instructed to move their index finger to the correct circle and to remain there until the letter string disappeared (2,500 ms after its appearance) and a tone was presented indicating that participants should return to the home position for the next trial. If participants made an error, feedback appeared on the computer screen for 1500 ms. Feedback was given for incorrect responses, failures to move, and movements that were either premature or did not end close enough to a response circle.

Participants first completed 20 practice trials. Test stimuli were presented in 13 blocks with rest periods between. The first 12 blocks had 31 trials each while the last block contained the final 28 trials. Performance was monitored on a display in a separate room. After every few blocks the experimenter checked with participants to encourage them to rest their eyes and reaching arm and reminded them to make rapid responses while still valuing accuracy.

Data Analysis

Each movement trajectory was differentiated and filtered to achieve smooth velocity profiles. To determine the start and end of the movements we computed a composite velocity in the forward and horizontal dimensions. Movement start was defined as the first moment in time when the velocity exceeded 100 inches per second such that, subsequently, velocity exceeded 500 inches per second for at least 30 ms. Movement end was defined as the first time after movement initiation at which the velocity dropped below 100 for at least 30 ms. RT was defined as the interval between the appearance of the letter string and the start of the movement. Movement duration (MD) was the interval between movement start and movement end.

To assess movement trajectories, we evaluated positional changes in the lateral (left-right) dimension, which distinguished the two response options. We used both a distance-based and a time-based assessment. For the distance-based measure, the lateral position was examined at five equally-spaced locations, each representing 20% of the total distance forward along a path from the home location to a point midway between the two targets (i.e., perpendicular to the lateral dimension). We could then evaluate how far people deviated laterally at the same relative distance travelled forward in each trajectory, regardless of the time taken to reach that location. Percent forward distance (PFD) was treated as a within-subjects independent variable in analyses of forward distance-normalized trajectories. The time-based assessment evaluated lateral position at every 10 ms time point (TP) after movement initiation up to 200 ms (approximately 1/3 of the total MD). This was intended to evaluate how trajectories were impacted during the earliest portion of the movement. Note that while we examined positional changes in the lateral dimension as our dependent variable, these movements were not independent of movements in the forward dimension.

For each participant we eliminated trials where the RT was less than 100 ms, participants failed to move (the response finger never moved outside of a 2 × 2 × 2 inch tolerance range around the home position), they moved too early (100 ms after the letter string appeared on the screen the position of the finger was outside of the 2 inch³ tolerance range), the final position was not near a target (at the farthest point reached forward the finger was positioned less than an inch laterally toward either target circle), or the wrong target was reached (at the farthest point reached forward, the finger was positioned more than 1-inch laterally towards the wrong target).

Trials were also excluded if the RT was more than 2.5 standard deviations from each participant’s mean. Trimming, based both on RT and on the factors listed above, removed 5.8% of the trials (3.2% due to incorrect responses and 2.6% due to other factors). The mean RT, MD, and movement data from the remaining trials were used for analysis. Accuracy data were converted into rationalized arcsine units (RAUs) for analysis. We conducted a series of repeated-measures ANOVAs at the subject and item level for analysis, and in cases where sphericity was violated the Huynh-Feldt correction was applied.

Results

Reaction time, movement duration, and accuracy

Table 1 shows the means and standard deviations of RT, MD and accuracy (both in RAU and proportion correct for ease of interpretation) across subjects for the different stimulus conditions. As expected, for RT we found large main effects of WF, F₁(1, 31) = 79.36, p < .001, η_p² = .72, MSE = 706.80, F₂ (1, 198) = 86.07, p < .001, η_p² = .30, MSE = 2326.52, and SQ, F_s (1, 31) = 146.81, p < .001, η_p² = .83, MSE = 1012.30, F₂ (1, 198) = 450.01, p < .001, η_p² = .69, MSE = 1102.89. More importantly, there was no hint of an interaction, p₁ = .507, p₂ = .886. Similarly, for MD, main effects of WF, F₁ (1, 31) = 35.29, p < .001, η_p² = .53, MSE = 284.95, F₂ (1, 198) = 25.03, p < .001, η_p² = .11, MSE = 1528.21, and SQ, F₁ (1, 31) = 22.74, p < .001, η_p² = .42, MSE = 246.92, F₂ (1, 198) = 15.47, p < .001, η_p² = .07, MSE = 1425.36, emerged with no interaction between these factors, p₁ = .307, p₂ = .613. Individuals were slower to initiate and complete movements for LF and degraded words. Turning to accuracy we found main effects of WF, F₁ (1, 31) = 53.12, p < .001, η_p² = .63, MSE = 63.17, F₂ (1, 198) = 25.51, p < .001, η_p² = .11, MSE = 190.38, and SQ, F₁ (1, 31) = 5.89, p = .021, η_p² = .16, MSE = 49.08, F₂ (1, 198) = 3.89, p = .050, η_p² = .02, MSE = 57.15, due to higher accuracy for HF and non-degraded words. The interaction was not significant, p₁ = .272, p₂ = .434. When word and non-word stimuli were compared analyses of RT and MD revealed main effects of lexicality and SQ (all p₁ < .01, all p₂ < .001) coupled with an absence of an interaction between these factors. There were no reliable effects on accuracy.

Table 1.

Mean response latency (RT), movement duration (MD) and accuracy (ACC) as a function of word frequency, lexicality, and stimulus quality

	Clear
	HF		LF		NW
	M	SD	M	SD	M	SD
RTa,b,c,d (ms)	491.96	75.59	536.14	86.12	578.86	94.25
MD a,b,c,d (ms)	564.31	100.73	584.77	104.64	600.51	105.72
ACC a,b	.99	.02	.96	.04	.97	.03
RAU a,b	113.01	5.63	105.94	8.57	105.90	7.15

		Degraded
	HF		LF		NW
	M	SD	M	SD	M	SD
RT a,b,c,d (ms)	562.42	92.45	601.97	103.77	644.84	114.48
MD a,b,c,d (ms)	580.29	111.02	595.28	113.14	609.56	116.53
ACC a,b	.99	.02	.94	.05	.97	.03
RAU a,b	111.17	6.14	99.77	9.36	105.71	6.98

Note. HF = high frequency; LF = low frequency; NW = Non-word.

^aA reliable frequency effect (at least p < .05 or better).

^bA reliable degradation effect when HF and LF words were evaluated (at least p < .05).

^cA reliable lexicality effect (at least p < .05 or better).

^dA reliable degradation effect when words and non-words were evaluated (at least p < .05).

Movement trajectory

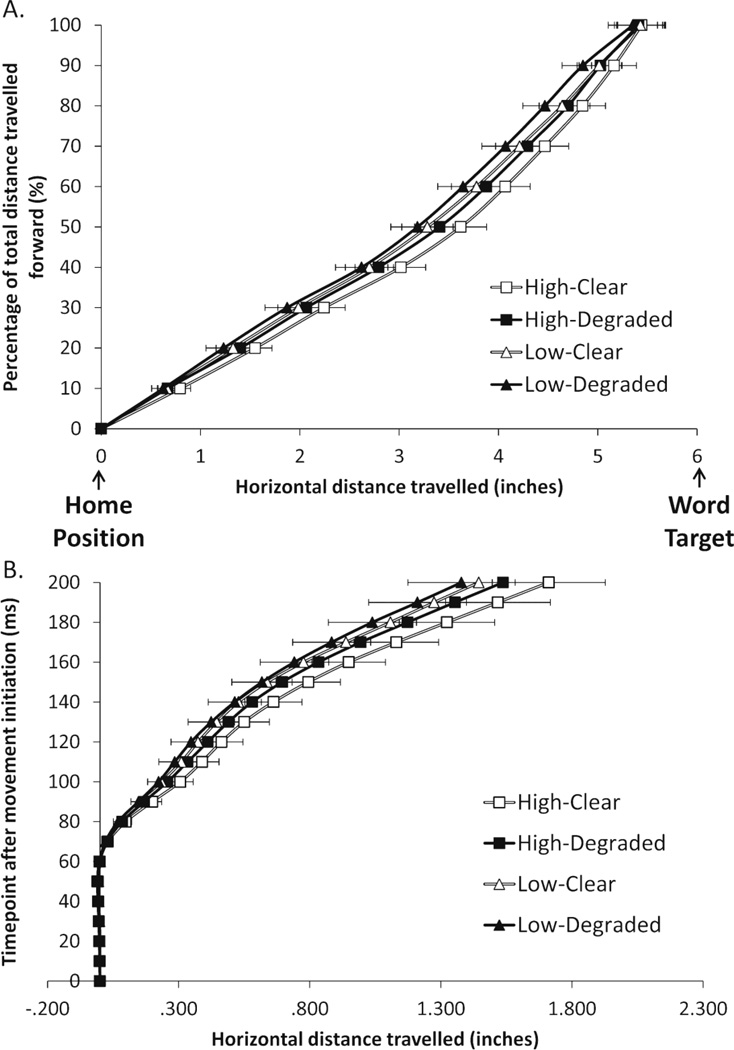
Figure 2 panel A displays the distance-normalized mean trajectories for each of the WF conditions plotted with lateral deviation on the x-axis and percent forward distance (PFD) on the y-axis. The ANOVA yielded a reliable three-way interaction among WF, SQ and PFD (20%, 40%, 60%, 80%, and 100%), F₁ (3, 84) = 3.57, p = .021, η_p² = .10, MSE = .019, F₂ (2, 473) = 3.56, p = .022, η_p² = .02, MSE = .09, suggesting that the degree to which SQ influenced performance in the two frequency conditions differed across the course of movement.¹ The analysis of the time-locked horizontal deviations also revealed a three-way interaction of WF, SQ and TP, F₁ (2, 59) = 3.28, p = .047, η_p² = .10, MSE = .037, F₂ (2, 333) = 3.28, p = .047, η_p² = .02, MSE = .179. These data are shown in Figure 2 panel B. Interestingly, this analysis also revealed a trend towards a significant two-way interaction of SQ × WF for the subjects-level analysis, F₁ (1, 31) = 3.96, p = .056, η_p² = .11, MSE = .059, with a significant effect emerging at the items-level, F₂ (1, 198) = 4.55, p = .034, η_p² = .02, MSE = .228. Clear HF words appear to pull away from the other conditions relatively early in the movement. Note, however, as illustrated by the plots of the distance-normalized degradation effects for HF and LF words in Figure 3, that the effect of stimulus degradation for HF words decreases slightly later in the movement. LF words, on the other hand, show minimal early impact of degradation, with an increased effect appearing in the later portion of the movement before resolving at movement’s end. Thus, it appears that WF and SQ have interactive influences on movement trajectories, especially during the early part of the movements.

Figure 2.

Panel A shows the horizontal deviations toward the word target for each 20% portion of the total distance travelled forward (represented on the y-axis). Panel B shows the horizontal deviations toward the word target for each 10 ms time point after movement initiation. In both panels data are plotted for HF and LF word responses under clear and degraded conditions. Note that all data have been plotted as if the word response target was on the right side of the screen, even though this was counterbalanced across participants. Error bars are ± 1 standard error around the mean.

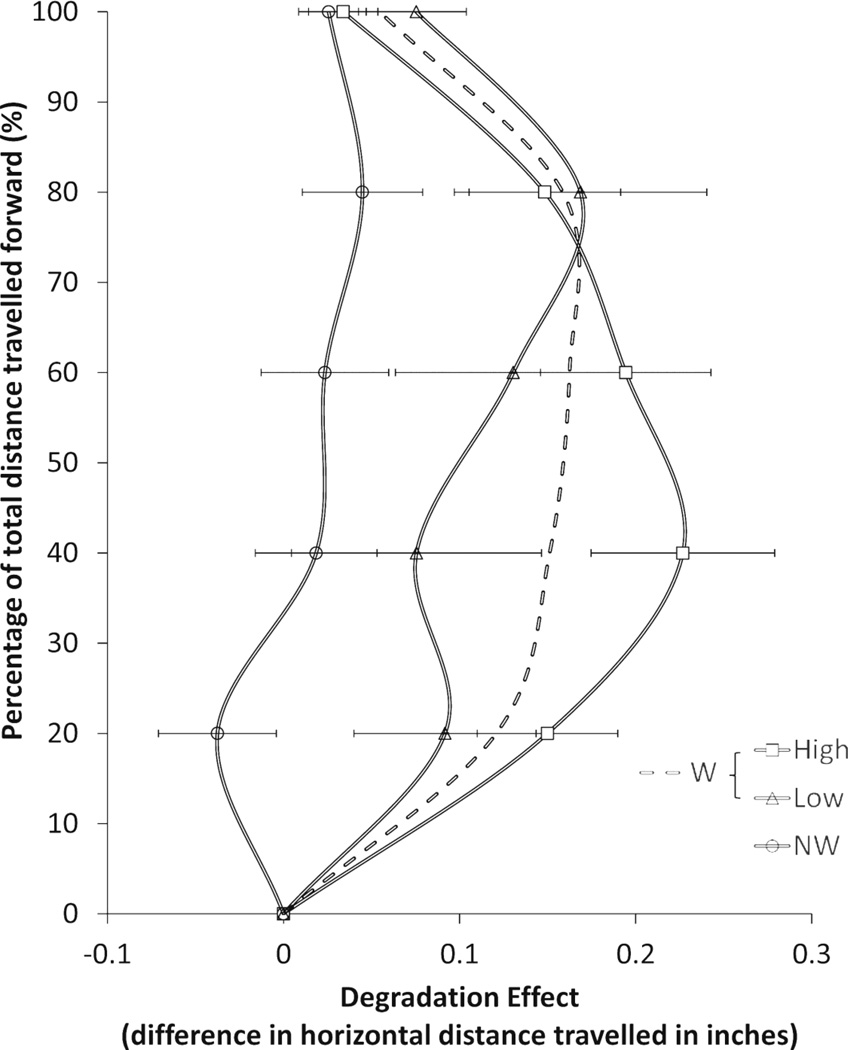
Figure 3.

The degradation effect (the difference in the horizontal distance travelled for clear versus degraded stimuli) across response movements for HF and LF words and for non-words (NW). The dashed line shows the degradation effect for word (W) stimuli combined. Larger x-axis values represent larger differences between clear and degraded conditions for the indicated stimulus type. The degradation effect was much larger for HF as compared to LF words for the beginning portion of people's movements, with the degradation effect increasing towards the end of movements for LF words. Additionally, stimulus degradation had a larger impact on word as compared to non-word trajectories throughout the course of response movements. Specifically, responses for degraded words moved less directly towards the word target than responses for clear words. However, degradation of non-words had little impact on how directly responses moved towards the non-word target. Error bars are ± 1 standard error around the mean.

Turning to a comparison of the horizontal deviations at each PFD for words versus non-words, a reliable lexicality by SQ interaction was obtained, F₁ (1, 31) = 6.99, p = .013, η_p² = .18, MSE = .075, F₂ (1, 398) = 8.68, p = .003, η_p² = .02, MSE = .375. As Figure 3 shows, it is clear that SQ had an impact on words, but little impact on non-word stimuli. However, the three-way interaction among lexicality, SQ and PFD was not reliable (p₁ = .091, p₂ = .126) indicating that the influence of stimulus degradation in the word and non-word conditions did not significantly change across the course of PFD. Analysis of the deviations across TP also revealed a significant SQ × WF interaction, F₁ (1, 31) = 5.86, p = .022, η_p² = .16, MSE = .008, F₂ (1, 398) = 5.80, p = .017, η_p² = .01, MSE = .214, with a significant three-way interaction emerging for the item-level analysis, F₂ (2, 675) = 3.22, p = .049, η_p² = .01, MSE = .167. Thus, at the item level the strength of the lexicality x SQ interaction may shift across the earliest portion of the movement.

Discussion

The present study used a reaching task to investigate the influence of WF and SQ on the dynamics of reaching to visual targets in the LDT. Balota and Abrams (1995) found with uni-dimensional measures the typical additive effects of SQ and WF in both onsets and movement dynamics. We replicated these additive effects in RT, MD and accuracy. However, multidimensional movement trajectories revealed interactive effects that differed across the course of movement. As shown in Figure 2, trajectories for LF and degraded words were farther from the word response option than those for clear HF words. This pattern is indicative of increased response uncertainty for LF and degraded stimuli, leading to response trajectories exhibiting an attraction to the non-word response target. Figure 3 illustrates the differential interactive effects of WF and SQ across distance-normalized trajectories--degrading LF words only slightly increased the existing level of response uncertainty during the early portion of movements with larger increases seen towards the end of movements. Degrading HF words, on the other hand, increased early response uncertainty followed by later reductions. Movement trajectories also revealed interactive effects of lexicality and SQ that were not found for uni-dimensional response measures (RT, MD and accuracy) when words and non-words were examined, but the strength of this interaction did not significantly change across the course of movement.

The interactive effect of WF and SQ on multi-dimensional response characteristics indicates that some lexical decision processes may persist during motor programming, and possibly throughout the course of continuous responses. Work has shown that masked orthographic primes presented just before a stimulus influence movement trajectories (Finkbeiner et al., 2008). When the prime and stimulus were incongruent, movement initially curved towards the target matching the prime and then corrected to the appropriate target, despite prime identity being unavailable to conscious awareness. Therefore, early perceptual processes may measurably influence the unfolding of the response, especially when the response is extended in time and space. Given this, it may be that some aspects of perceptual normalization and access to familiarity-based information occur in parallel and influence programming of the early portion of response trajectories. While it is possible that these influences primarily impact the initial motor program, some feedforward models of reaching suggest that feedback processes influence the integration of sensory and motor information during ongoing movements (Desmurget & Grafton, 2000).

Because the present paradigm tracks responses across time and distance, one may consider an analogue with Ratcliff, Gomez and McKoon's (2004) diffusion model of binary choices in the LDT where noisy information about the stimulus accumulates over time toward one of two response decision criteria. This model accounts for WF effects on RT and accuracy by postulating different drift rates for words of different frequencies. However, like other models, it has difficulty accounting for additive effects of SQ and WF, and, in fact, should predict interactive effects if both factors influence drift rates. This model and interactive-activation models (McLelland & Rumelhart, 1981) of word recognition predict that degradation should have a larger impact on LF as compared to HF words. Although the present results revealed interactive effects on movement dynamics, our finding of a larger effect for HF versus LF words early in movement is inconsistent with this prediction. Of course, these models were designed to explain patterns in RT and accuracy, not the dynamics of response execution. Yet, our finding of additive effects on RT and MD would appear to place constraints on the most straightforward predictions from both interactive activation and diffusion type models.

The additive effects of SQ and WF on mean RTs and MDs would naturally fall from a normalization process that is influenced by SQ and a lexical retrieval process influenced by WF (see Borowsky & Besner, 1993). However, interactive effects on movement trajectories are inconsistent with this interpretation. Perhaps in the current LDT, individuals set a liberal response initiation criterion, starting movements before familiarity information has been fully processed. Indeed, latencies to begin movements in our study were shorter (sometimes by more than 100 ms) than the RTs typically found for the LDT (Balota & Abrams, 1995; Yap & Balota, 2007). Uncertainty due to either degradation or LF may engage an additional analytic process that influences early aspects of movements, i.e., pulling movements to the non-word response dimension. In contrast, clear HF words have sufficient familiarity to negate this additional checking and hence drive the movements more directly to the “word” response. This can account for the larger effect of degradation on HF as compared to LF words since only degraded HF words but both clear and degraded LF words would be impacted by the added processing time required by this secondary analytic process.

In this light, these results could be viewed as consistent with a recent model proposed by Resulaj, Kiani, Wolpert and Shadlen (2009) with multiple decision criteria to account for changes of direction during reaching. These include a "response initiation" criterion coupled with a "change of mind" criterion. They demonstrate that even when the stimulus disappears after response initiation--preventing acquisition of additional information about the stimulus--there is evidence for changes of mind in movement trajectories. Namely, information in the processing stream that was not used for planning response initiation may be accessed later to determine whether movement direction should be adjusted. "Changes of mind" are most prevalent under time pressure, presumably due to a more liberal setting for the initial response criterion. It is unclear whether information accumulated about a stimulus that remains accessible after response initiation can further influence these changes of mind. However, a two-criterion model may prove useful for interpreting the results from the current study and may, perhaps, be successfully incorporated into existing models of lexical decision, such as multiple-stage models (Borowsky & Besner, 1993), that do account for additive effects of WF and SQ on uni-dimensional responses. We look forward to future work exploring this possibility.

Though the present data cannot distinguish whether feedforward, feedback, or some combination of these processes lead to the interactive patterns seen in multidimensional response trajectories, it is clear that factors which impact early processing of the stimulus also influence the kinematics of reaching responses in the LDT. While additive effects remain for uni-dimensional response features, a multidimensional investigation of the movement trajectory implicates interactive influences of WF and SQ that change over the evolution of the movement. These findings have important implications for models of lexical decision performance and provide further evidence of the richness of movement dynamics after response initiation. Indeed, future work may benefit from exploring how decision processes evolve when the stimulus is presented after movement initiation. Although most mental chronometric studies emphasize the point in time at which a microswitch is triggered, we would argue that most natural movements are constantly taking into consideration multiple dimensions of a stimulus as they unfold across time. Tracking movement trajectories in standard cognitive tasks is a useful way to further understand these influences.