Efficiency Loss Caused by Linearity Condition in Dimension Reduction

Summary

Linearity, sometimes jointly with constant variance, is routinely assumed in the context of sufficient dimension reduction. It is well understood that, when these conditions do not hold, blindly using them may lead to inconsistency in estimating the central subspace and the central mean subspace. Surprisingly, we discover that even if these conditions do hold, using them will bring efficiency loss. This paradoxical phenomenon is illustrated through sliced inverse regression and principal Hessian directions. The efficiency loss also applies to other dimension reduction procedures. We explain this empirical discovery by theoretical investigation.

1. Introduction

In the sufficient dimension reduction literature, two essential conditions are linearity and constant variance. Denote X the p-dimensional random covariate vector, and let the dimension reduction subspace be the column space of a full rank p × d matrix β. The linearity condition assumes E(X | β^TX) = PX, where P = ∑β(β^T∑β)⁻¹ β^T is a p × p matrix and ∑ = cov(X). The constant variance condition assumes cov (X | β^TX) = Q, where Q = ∑ – P∑P^T. These two conditions have played a central role throughout the development of the sufficient dimension reduction literature. For example, the linearity condition, sometimes jointly with the constant variance condition, permitted the establishment of sliced inverse regression (Li, 1991), sliced average variance estimation (Cook and Weisberg, 1991), directional regression (Li and Wang, 2007), discretization-expectation estimation (Zhu, et al, 2010b), cumulative slicing estimation (Zhu, et al, 2010a), ordinary least squares (Li and Duan, 1989), and principal Hessian directions (Li, 1992; Cook and Li, 2002), etc. It is no exaggeration to call linearity and constant variance the fundamental conditions of dimension reduction.

It is a different story regarding the validity of the linearity and constant variance conditions and how to verify them in practice. Hall and Li (1993) showed that the linearity condition would hold in an asymptotic sense when p goes to infinity. Yet whether the asymptotically true result suffices for a finite dimensional problem remains unclear. This has prompted researchers to relax these conditions. For example, Li and Dong (2009) and Dong and Li (2010) replaced the linearity condition by a polynomial condition. Ma and Zhu (2012) completely eliminated both conditions.

Following the relaxation of the linearity and constant variance conditions, a natural question arises: What do we lose by ignoring these conditions when they hold? It is natural to conjecture that this will cause estimation variance inflation. However, our discovery is exactly the opposite.

We illustrate this paradoxical phenomenon empirically. Consider

$$\begin{array}{cc}\hfill \text{Model}\mathrm{I}:Y& ={\beta }_1^{T}X∕\{0.5+{({\beta }_2^{\mathrm{T}}X+1.5)}^2\}+\epsilon ,\hfill \\ \hfill \text{Model}\mathrm{II}:Y& ={\left({\beta }_1^{\mathrm{T}}X\right)}^2+{\left({\beta }_2^{T}X\right)}^2+\epsilon ,\hfill \end{array}$$

where β₁ = 10^−1/2(1, 1, 1, 1, 1, 1, 1, 1, 1, 1)^T, β₂ = 10^−1/2(1,−1, 1,−1, 1,−1, 1,−1, 1,−1)^T and ε is a standard normal random variable. Thus, p = 10, d = 2 and β = (β₁, β₂) in these models. We generate X from a multivariate standard normal distribution. Thus both the linearity and the constant variance conditions hold. For Model I, we implement classical sliced inverse regression and its semi-parametric counterpart where the linearity condition is not used. For Model II, we compare classical principal Hessian directions and its semi-parametric counterpart where neither condition is used. Here, the sliced inverse regression and principal Hessian directions are identical to their semi-parametric counterparts, except that the sliced inverse regression and principal Hessian directions utilize the linearity and the constant variance conditions to obtain E(X | β^TX) and cov(X | β^TX), while their semi-parametric counterparts estimate E(X | β^TX) and cov(X | β^TX) nonparametrically. See Ma and Zhu (2012) for details on these semi-parametric estimators. We generate 1000 data sets each of size n = 200, and summarize the results in Figure 1. To make a fair comparison, we estimate the kernel matrix of the classical sliced inverse regression by using kernel smoothing rather than the usual slicing estimation. This allows us to avoid selecting the number of slices, which usually adversely affects the performance. Thus, sliced inverse regression is implemented in its improved form.

Fig. 1.

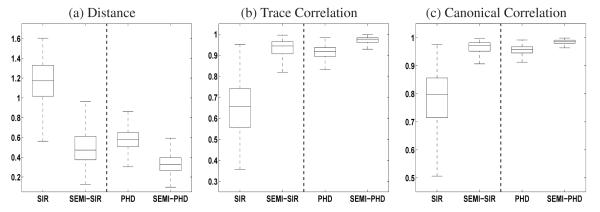
Comparison of sliced inverse regression (SIR) and principal Hessian directions (PHD) with their semiparametric counter parts (SEMI-SIR, SEMI-PHD) in model (I) (left half in each panel) and model (II) (right half in each panel). Results are based on 1000 simulated data sets with sample size n = 200.

Figure 1(a) contains the box plots of the four estimation procedure results, measured by a distance between the estimated and the true dimension reduction subspaces. This distance is defined as the Frobenius norm of $\widehat{P}-P$, where P is as defined before, $\widehat{P}=\Sigma \widehat{\beta }{\left({\widehat{\beta }}^{\mathrm{T}}\Sigma \widehat{\beta }\right)}^{-1}{\widehat{\beta }}^{\mathrm{T}}$ and $\widehat{\beta }=({\widehat{\beta }}_1,{\widehat{\beta }}_2)$ is obtained from the aforementioned estimation procedures. This distance criterion is widely used to evaluate the performance of different estimation procedures, with a smaller distance indicating better estimation of the dimension reduction subspace. Figure 1(a) shows clearly that the semi-parametric counterparts outperform their classical versions. Thus, not taking advantage of the linearity condition or the constant variance condition, although both are satisfied, seems to bring a gain in estimating the dimension reduction subspaces.

Figure 1(b) contains the box plots of the same results measured by the trace correlation, defined as trace $\left(P\widehat{P}\right)∕d$. A larger value of this criterion indicates better performance. Figure 1(b) demonstrates again that the semi-parametric counterparts outperform their classical versions respectively, once again indicating that not taking advantage of the linearity or the constant variance condition, even though both hold, brings a gain.

Finally, Figure 1(c) shows the results by yet another popular criterion, the canonical correlation, defined as the average of d canonical correlation coefficients between ${\widehat{\beta }}^{\mathrm{T}}X$ and β^TX. Under this measure, larger values indicate better estimation results, and the conclusion from Figure 1(c) is consistent with those from Figure 1(a) and Figure 1(b).

Having observed these unexpected results, our goal here is to demonstrate that the improvement is not merely a sporadic phenomenon. This improvement is theoretically verifiable. Because it is already well understood that using the linearity and the constant variance conditions when they do not hold causes bias, here we consider exclusively the case when the covariate vector satisfies the linearity condition and, if required, the constant variance condition. This means that the aforementioned original methods, such as sliced inverse regression and principal Hessian directions, are valid and will provide consistent estimation. Although this is the classical setting of the dimension reduction literature and seems well understood, we will formally establish that if we ignore the linearity and the constant variance conditions, and instead, estimate the conditional expectation E(X | β^TX) or more generally E{a(X) | β^TX} nonparametrically, then the performance of sufficient dimension reduction methods will improve. The improvement is in the asymptotic variance of the estimated dimension reduction subspace, in that not using the linearity or the constant variance condition will yield a more efficient estimator than using them, even when these conditions are indeed true.

2. Some Preliminaries

We first lay out the central subspace and the central mean subspace models and some notation we use throughout. Let Y be a univariate response variable and X and β be defined as in Section 1. Throughout this paper we assume that X satisfies both the linearity and the constant variance conditions. Using an invariance property (Cook, 1998, page 106), we assume without loss of generality that E(X) = 0 and cov(X) = I_p. The essence of the sufficient dimension reduction literature is to assume that Y depends on X only through a few linear combinations β^TX, then to identify the space spanned by the columns of β. There are mainly two types of links between Y and X that are commonly studied, one is the conditional distribution, and the other is the conditional mean function. Specifically, in the first model type (Li, 1991; Cook, 1998), one assumes that

$$F(y\mid X)=F(y\mid {\beta }^{\mathrm{T}}X),y\in \mathbb{R},$$ (1)

where F (y | X) = pr(Y ≤ y | X) denotes the conditional distribution function of Y given X. The smallest column space of β satisfying (1) is called the central subspace, S_Y |X. In the second model type (Cook and Li, 2002), one assumes that the conditional mean function satisfies

$$E(Y\mid X)=E(Y\mid {\beta }^{\mathrm{T}}X).$$ (2)

The corresponding smallest column space of β is called the central mean subspace S_E(Y|X). Estimating S_Y|X and S_E(Y|X) is the main purpose of sufficient dimension reduction. In the following development, we focus on the classical sliced inverse regression and principal Hessian directions methods as representative estimators for S_Y|X and S_E(Y|X) respectively, although the conclusion applies to other sufficient dimension reduction method as well.

To further ensure that the identifiability of S_Y|X or S_E(Y|X) implies the identifiability of β, we require the upper d × d sub-matrix of β to be the identity matrix. Through this parameterization, estimating S_Y|X or S_E(Y|X) is equivalent to estimating the lower (p – d) × d sub-matrix in β. This sub-matrix contains all the unknown parameters involved in the estimation of S_Y|X or S_E(Y|X) and uniquely defines the corresponding space S_Y|X or S_E(Y|X). The particular parameterization is simple and enables us to study the properties of the space estimation through studying the properties in estimating the parameters in β. Other parameterizations can also be used.

We further introduce two matrix operators. We use vecl(β) to denote the length (p – d)d vector formed by the concatenation of the columns in the lower (p – d) × d sub-matrix of β, and use vec(M) to denote the concatenation of the columns of an arbitrary matrix M.

3. Theoretical Explanation of the Paradoxical Phenomenon

Following Ma and Zhu (2012), to identify S_Y|X in model (1), the sliced inverse regression solves for the parameters contained in β from an estimating equation based on the relation

$$E\left[E\right(X\mid Y\left)\right\{X^T-E(X^{\mathrm{T}}\mid {\beta }^{\mathrm{T}}X)\left\}\right]=0.$$ (3)

When the linearity condition holds, (3) simplifies to

$$\mathit{QE}\left\{E\right(X\mid Y\left)X^T\right\}=Q\mathrm{cov}\left\{E\right(X\mid Y\left)\right\}=0,$$

where Q = I_p – P = I_p – β (β^Tβ) β^T. Consequently, solving (3) is equivalent to calculating the eigen-space of the matrix cov{E(X | Y)} associated with its d nonzero eigenvalues.

Similarly, to identify in S_E(Y|X) in model (2), the principle Hessian directions method solves for the parameters contained in β from an estimating equation based on the relation

$$E\left[\right\{Y-E\left(Y\right)\left\}\right\{{\mathit{XX}}^{\mathrm{T}}-E({\mathit{XX}}^{\mathrm{T}}\mid {\beta }^{\mathrm{T}}X)\left\}\right]=0.$$ (4)

When both the linearity and the constant variance conditions hold, (4) simplifies to

$$E\left[\right\{Y-E\left(Y\right)\left\}{\mathit{XX}}^{\mathrm{T}}\right]=\mathit{PE}\left[\right\{Y-E\left(Y\right)\left\}{\mathit{XX}}^{\mathrm{T}}\right]P.$$

Thus, solving (4) is equivalent to computing the eigen-space of the matrix E [{Y – E(Y)} XX^T] associated with its d nonzero eigenvalues.

To simultaneously consider both the sliced inverse regression in (3) and the principal Hessian directions in (4), we consider a unified form

$$E\left[g^{\ast }\right(Y\left)\right\{a^{\ast }\left(X\right)-E(a^{\ast }\mid {\beta }^{\mathrm{T}}X)\left\}\right]=0,$$ (5)

where g* is a fixed function of Y that satisfies E(g* | X) = E(g* | β^TX), and a* is a fixed function of X. Clearly (5) contains both sliced inverse regression and principal Hessian directions as special cases, by choosing g* = E(X | Y) and a* = X^T to yield (3) or g* = Y – E(Y) and a* = XX^T to yield (4). Denote the observations by (X_i,Y_i)(i = 1,…,n). To facilitate our subsequent inference procedure, we further perform the following operations. We first vectorize the sample version of (5), then we perform a generalized method of moment treatment to reduce the number of estimating equations to (p – d)d, then finally we simplify these estimation equations to obtain

$$\sum _{i=1}^n\sum _{j=1}^q\left[g_j\right(Y_i\left)\right\{a_j\left(X_i\right)-E(a_j\mid {\beta }^{\mathrm{T}}{X}_i)\left\}\right]=0,$$ (6)

where g_j(Y) is a scalar or column vector that satisfies E(g_j | X) = E(g_j | β^TX), and a_j is a row vector, for j = 1,…,q. A more detailed description of how to obtain (6) from (5) is given in the Appendix. We also assume (6) has a unique solution when n → ∞. We remark here that (6) is equivalent to (5) when n → ∞, hence we can view (6) as a compact expression of the sample version of (5).

We now study the asymptotic properties of the estimating equation (6), both when the E(a_j | β^TX)s are known and when they are estimated nonparametrically. The analysis of (6) for q > 1 can be readily obtained after we study (6) for q = 1, so in the sequel, whenever appropriate, we shall focus on the case q = 1 in (6) and ignore the subscript j.

When we decide to give up using any properties of the covariate X such as linearity or constant variance, we need to estimate E(a | β^TX) nonparametrically. For example, we can estimate E(a | β^TX) through

$$\widehat{E}(a\mid {\beta }^{\mathrm{T}}X)=\sum _{i=1}^n{K}_h({\beta }^{\mathrm{T}}{X}_i-{\beta }^{\mathrm{T}}X)a\left(X_i\right)/\sum _{i=1}^n{K}_h({\beta }^{\mathrm{T}}{X}_i-{\beta }^{\mathrm{T}}X).$$

Here K_h(·) = K(·/h)/h is a kernel function and h is a bandwidth which can be estimated by leave-one-out cross-validation. Replacing E(a | β^TX) in (6) with $\widehat{E}(a\mid {\beta }^{\mathrm{T}}X)$, we obtain an estimator $\widehat{\beta }$ by solving the equation

$$\sum _{i=1}^{n}g\left(Y_i\right)\left\{a\right(X_i)-\widehat{E}(a\mid {\beta }^{\mathrm{T}}{X}_i\left)\right\}=0.$$ (7)

Cross-validation is one possible way of selecting h, and its validity in the nonparametric context can be found in Härdle, et al (1988). In the semiparametric context, the final estimate is insensitive to the bandwidth choice. This is reflected in the condition (C4), where a range of bandwidths is allowed, all of which will yield the same first order asymptotic property of the estimation on β. In terms of finite sample performance, bandwidth has also been observed to have low impact, see for example Maity et al (2007). Theorem 1 states the asymptotic properties of $\widehat{\beta }$.

Theorem 1

Under the regularity conditions given in the Appendix, $\widehat{\beta }$ satisfies

$$\begin{array}{cc}\hfill & -n^{1∕2}A\mathrm{vecl}(\widehat{\beta }-\beta )\hfill \\ \hfill =& n^{-1∕2}\sum _{i=1}^n\mathrm{vec}\left[\right\{g\left(Y_i\right)-E(g\mid {\beta }^{\mathrm{T}}{X}_i)\left\}\right\{a\left(X_i\right)-E(a\mid {\beta }^{\mathrm{T}}{X}_i)\left\}\right]+o_p\left(1\right),\hfill \end{array}$$ (8)

where

$$A=E\left(\frac{\partial \mathrm{vec}\left[\right\{g\left(Y\right)-E(g\mid {\beta }^{\mathrm{T}}X)\left\}\right\{a\left(X\right)-E(a\mid {\beta }^{\mathrm{T}}X)\left\}\right]}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\right).$$

Hence, when $n\to \infty ,n^{1∕2}\mathrm{vecl}(\widehat{\beta }-\beta )\to \mathcal{N}\{0,A^{-1}{B}_1{\left(A^{-1}\right)}^{\mathrm{T}}\}$ in distribution, where

$$B_1=\mathrm{cov}\left(\mathrm{vec}\right[\left\{g\right(Y)-E(g\mid {\beta }^{\mathrm{T}}X\left)\right\}\left\{a\right(X)-E(a\mid {\beta }^{\mathrm{T}}X\left)\right\}\left]\right).$$

Remark 1

We consider only the situation where g* and hence g are fixed functions. In practice, sometimes g* and hence g are estimated, thus more careful notation is ${\widehat{g}}^{\ast }$ and $\widehat{g}$. However, as long as the estimated function $\widehat{g}$ converges to g at a proper rate (Mack and Silverman, 1982), the first order result in Theorem 1 stays unchanged if we replace g with $\widehat{g}$.

Alternatively, E(a* | β^TX) may have a known form, say E(a* | β^TX) = h*(β^TX, β), where h*(·) is a known function. This will further yield a known form for E(a_j | β^TX) in (6), which we denote h_j(β^TX, β) (j = 1,…, q). For example, under the linearity condition, for a*(X) = X^T, h*(β^TX, β) = PX = β^T(β^Tβ)⁻¹(β^TX); under both the linearity and the constant variance conditions, for a*(X) = XX^T, h*(β^TX, β) = Q + PXX^TP = I_p – β(β^Tβ)⁻¹β^T + β(β^Tβ)⁻¹(β^TX)(β^TX)^T(β^Tβ)⁻¹β. This allows us to solve a simplified version of (6). For q = 1 and ignoring the subscript j, we only need to solve

$$\sum _{i=1}^{n}g\left(Y_i\right)\left\{a\right(X_i)-h({\beta }^{\mathrm{T}}{X}_i,\beta \left)\right\}=0$$ (9)

to obtain an estimator $\tilde{\beta }$. The asymptotic properties of $\tilde{\beta }$ are given in Theorem 2.

Theorem 2

Assume h is differentiable with respect to β, then $\tilde{\beta }$ satisfies

$$-n^{1∕2}A\mathrm{vecl}(\tilde{\beta }-\beta )=n^{-1∕2}\sum _{i=1}^n\mathrm{vec}\left[g\right(Y_i\left)\right\{a\left(X_i\right)-E(a\mid {\beta }^{\mathrm{T}}{X}_i)\left\}\right]+o_p\left(1\right),$$ (10)

where A is given in Theorem 1. Hence, when n → ∞, $n^{1∕2}\mathrm{vecl}(\tilde{\beta }-\beta )\to \mathcal{N}\{0,A^{-1}{B}_2{\left(A^{-1}\right)}^{\mathrm{T}}\}$ in distribution, where

$$B_2=\mathrm{cov}\left(\mathrm{vec}\right[g\left(Y\right)\left\{a\right(X)-E(a\mid {\beta }^{\mathrm{T}}X\left)\right\}\left]\right).$$

A direct comparison between B₁ and B₂ reveals the difference between $\widehat{\beta }$ from solving (7) and $\tilde{\beta }$ from solving (9), as stated in Proposition 1.

Proposition 1

Under the conditions in Theorems 1 and 2, $n\left[\mathrm{cov}\left\{\mathrm{vecl}\right(\tilde{\beta }\left)\right\}-\mathrm{cov}\left\{\mathrm{vecl}\right(\widehat{\beta }\left)\right\}\right]$ is positive definite when n → ∞.

Combining the results in Theorems 1, 2 and Proposition 1, we are now ready to state the main results in Theorem 3. Its proof combines that of Theorems 1, 2 and Proposition 1, and is omitted to avoid redundancy.

Theorem 3

Let $\tilde{\beta }$ and $\widehat{\beta }$ solve (6) with E(a_j | β^TX) replaced by h_j(β^TX, β) and by its nonparametric kernel estimator $\widehat{E}(a_j\mid {\beta }^{\mathrm{T}}X)$ respectively. Under the regularity conditions given in the Appendix, $n\left[\mathrm{cov}\left\{\mathrm{vecl}\right(\tilde{\beta }\left)\right\}-\mathrm{cov}\left\{\mathrm{vecl}\right(\widehat{\beta }\left)\right\}\right]$ is positive definite when n → ∞.

We emphasize that $\tilde{\beta }$ and $\widehat{\beta }$ solve the same estimating equation (6), except that $\tilde{\beta }$ takes advantage of the known forms of E(a_j | β^TX) while $\widehat{\beta }$ does not. They are estimators of the same parameter β. Therefore, Theorem 3 states the interesting result that by giving up using the linearity and constant variance conditions, we enjoy a decreased estimation variance.

In estimating the central subspace S_Y|X, any function of Y is a qualified g* function, because E(g* | X) = E(g* | β^TX) by the model assumption (1). Specifically, choose g*(Y ) = E(X | Y), a*(X) = X^T, and h*(β^TX,β) = β^T(β^Tβ)⁻¹(β^TX). After vectorizing and using a generalized method of moments to reduce the number of estimating equations, the over-identified estimating equation ${\sum }_{i=1}^n{g}^{\ast }\left(Y_i\right)\left\{a^{\ast }\right(X_i)-E(a^{\ast }\mid {\beta }^{\mathrm{T}}{X}_i\left)\right\}=0$ reduces to (6). Theorem 3 then directly shows that giving up using the h_j functions, hence giving up the linearity condition, will reduce the variance of sliced inverse regression. In estimating the central mean subspace S_E(Y|X) defined in (2), Y – c is the only qualified g* function, where c is an arbitrary constant. Specifically, choose g*(Y) = Y – E(Y), a*(X) = XX^T, h*(β^TX,β) = I_p – β(β^Tβ)⁻¹β^T + β(β^Tβ)⁻¹(β^TX)(β^TX)^T(β^Tβ)⁻¹β. Vectorizing the estimating equations and using the generalized method of moments to reduce the number of estimating equations will again yield an estimating equation of the form (6). Theorem 3 shows that giving up the linearity and constant variance conditions will reduce the variance of principal Hessian directions.

Ma and Zhu (2012) studied many other forms of the sufficient dimension reduction estimators that use the linearity and constant variance conditions. Those estimators can all be written in the form (6). Following Theorem 3, these estimators suffer the same efficiency loss as sliced inverse regression and principal Hessian directions, in that their estimation variance can be decreased by nonparametric estimation of E(a_j | β^TX). Since we work in the semiparametric framework, our analysis does not apply when Y is categorical and X is multivariate normal given Y. Under these two conditions, the model is parametric and the sliced inverse regression is the maximum likelihood estimator and cannot be further improved.

To keep the vital information simple and clear, we have presented the inverse regression methods in their idealistic forms, where the knowledge E(X) = 0 and cov(X) = I is directly incorporated into estimation. In practice, one might need to replace E(X) with $\overline{X}$ and cov(X) with $\widehat{\mathrm{cov}}\left(X\right)$, and proceed with the estimation. Denote the resulting estimator $\check{\beta }$. However, the estimation of E(X) and cov(X) does not recover the efficiency loss caused by using the linearity and constant variance conditions. In other words, $n\left[\mathrm{cov}\left\{\mathrm{vecl}\right(\check{\beta }\left)\right\}-\mathrm{cov}\left\{\mathrm{vecl}\right(\widehat{\beta }\left)\right\}\right]$ is still a positive definite matrix. We omit the proof because it is very similar to the proofs of Theorems 1, 2, Proposition 1 and Theorem 3.

4. Discussion

The surprising discovery that the linearity and constant variance conditions cause efficiency loss reminds us of the situation widely experienced in using inverse probability weighting idea to handle missing covariates. There it is well known that using the true weights yields a less efficient estimator than using the estimated weights. Such a phenomenon has been well studied in Henmi and Eguchi (2004), and a nice geometrical explanation was provided there. However, our problem shows several important differences. First, the efficiency improvement in the inverse probability weighting scheme can be obtained through any valid parametric estimation of the weights, while the efficiency improvement is not guaranteed when we view the linearity condition as a truth, and replace it with an arbitrary valid parametric estimation. This makes the geometric explanation in Henmi and Eguchi (2004) invalid in our context. Second, our efficiency gain is achieved through replacing the linearity condition with a nonparametric estimation, while only parametric estimation is considered in Henmi and Eguchi (2004).

Finally, having focused on the drawback of using the linearity and the constant variance conditions when they do hold, we acknowledge that using these conditions does ease the computation. When these conditions hold, a nonparametric estimation procedure can be avoided, which results in less programming effort and fast computation. However, nonparametric estimation is more or less routine in modern statistics, while the linearity and constant variance conditions remain uncheckable. As estimation is the eventual goal and this is better achieved without using the linearity or constant variance conditions, whether or not they hold, one would expect that giving up computational convenience for better statistical results can be sensible.

Appendix 1.

A.1. Obtaining (6) from (5)

We first vectorize the estimating function in (6) to obtain

$$f(Y,X,{\beta }^{\mathrm{T}}X)=\left(\begin{array}{c}\hfill g^{\ast }\left(Y\right)\left[a_1^{\ast }\right(X)-E\{a_1^{\ast }\left(X\right)\mid {\beta }^{\mathrm{T}}X\left\}\right]\hfill \\ \hfill ⋮\hfill \\ \hfill g^{\ast }\left(Y\right)\left[a_1^{\ast }\right(X)-E\{a_1^{\ast }\left(X\right)\mid {\beta }^{\mathrm{T}}X\left\}\right]\hfill \end{array}\right).$$ (A.1)

Here we assume a* contains l columns, denoted $a_1^{\ast },\dots ,a_l^{\ast }$. Assume $g^{\ast }\left(Y\right)a_1^{\ast }\left(X\right)$ contains l’ rows. We then perform the generalized method of moments step to obtain

$$D_f(Y,X,{\beta }^{\mathrm{T}}X)=\sum _{j=1}^l{D}_j{g}^{\ast }\left(Y\right)\left[a_j^{\ast }\right(X)-E\{a_j^{\ast }\left(X\right)\mid {\beta }^{\mathrm{T}}X\left\}\right]=\sum _{j=1}^l{g}_j\left(Y\right)\left[a_j^{\ast }\right(X)-E\{a_j^{\ast }\left(X\right)\mid {\beta }^{\mathrm{T}}X\left\}\right],$$

where

$$D=(D_1,\dots ,D_l)=E\left\{\frac{\partial f^{\mathrm{T}}(Y,X,{\beta }^{\mathrm{T}}X)}{\partial \mathrm{vecl}\left(\beta \right)}{D}^{\ast }\right\}$$

has (p – d)d rows and D_j is a (p – d)d × l’ matrix, j = 1,…,l. Here D* is an arbitrary positive-definite ll’ × ll’ matrix, with the optimal choice being D* = E(ff^T)⁻¹, and g_j(Y) = D_jg*(Y). In (A.1) $a_j^{\ast }\left(X\right)$ is either a scalar, such as in sliced inverse regression, or a column vector, such as in principal Hessian directions. When the $a_j^{\ast }\left(X\right)\mathrm{s}$ are column vectors, we further expand the matrix multiplication $g_i\left(Y\right)\left[a_j^{\ast }\right(X)-E\{a_j^{\ast }\left(X\right)\mid {\beta }^{\mathrm{T}}X\left\}\right](j=1,\dots ,l)$ so that eventually, after simplification through combining terms that are redundant, each summand contains a scalar function $a_j^{\ast }$ and a scalar or column vector g_j(Y). We use q to denote the total number of summands. By now the form of Df(Y,Xβ^TX) is almost the desired form in (6), except that if several different $a_j^{\ast }\left(X\right)-E\left\{a_j^{\ast }\right(X)\mid {\beta }^{\mathrm{T}}X\}$ are multiplied by the same g_j(Y) functions, we can write them more concisely by forming a row vector of the corresponding $a_j^{\ast }$’s and this is what we name a_j in (6). For example, writing X = (X₁,…,X_p)^T, for sliced inverse regression, we have

$$\mathit{Df}(Y,X,{\beta }^{\mathrm{T}}X)=\sum _{j=1}^p{D}_{j}E(X\mid Y)\{X_j-E(X_j\mid {\beta }^{\mathrm{T}}X\left)\right\},$$

hence q = p, g_j(Y) = D_jE(X | Y), which is a column vector, and a_j(X) = X_j, which is a scalar, in (6). For principal Hessian directions, we have

$$\begin{array}{cc}\hfill \mathit{Df}(Y,X,{\beta }^{\mathrm{T}}X)& =\sum _{j=1}^p\{Y-E(Y\left)\right\}{D}_j\left\{\right({\mathit{XX}}_j-E({\mathit{XX}}_j\mid {\beta }^{\mathrm{T}}X)\}\hfill \\ \hfill & =\sum _{k=1}^p\sum _{j=1}^p\{Y-E(Y\left)\right\}{D}_{\mathit{jk}}\{X_k{X}_j-E(X_k{X}_j\mid {\beta }^{\mathrm{T}}X\left)\right\},\hfill \end{array}$$ (A.2)

where D_j has dimension (p – d)d × p, and D_jk stands for the kth column of D_j. We rewrite (A.2) into a matrix form as

$$\sum _{k=1}^p\{Y-E(Y\left)\right\}\{X^{\mathrm{T}}D{.}_{,k}{X}_k-E(X^{\mathrm{T}}D{.}_{,k}{X}_k\mid {\beta }^{\mathrm{T}}X\left)\right\},$$ (A.3)

where D_·,k is a p × (p – d)d matrix with jth row $D_{\mathit{jk}}^{\mathrm{T}}(k=1,\dots ,p)$. Using (A.3) to form (6), we hence have q = p, g_j(Y) = Y – E(Y), a scalar, and a_j(X) = X^TD_·,jX_j, a row vector, in (6).

A.2. List of regularity conditions

(C1) The univariate kernel function K(·) is symmetric, has compact support and is Lipschitz continuous on its support. It satisfies

$$\int K\left(u\right)\mathit{du}=1,\int u^{i}K\left(u\right)\mathit{du}=0(i=1,\dots ,m-1),0\ne \int {\mid u\mid }^{m}K\left(u\right)\mathit{du}<\infty .$$

Thus K is a m-th order kernel. The d-dimensional kernel function is a product of d univariate kernel functions, that is, $K_h\left(u\right)=K(u∕h)∕h^d={\prod }_{j=1}^d{K}_h\left(u_j\right)={\prod }_{j=1}^{d}K(u_j∕h)∕h^d$ for u = (u₁,…, u_d)^T. Here we abuse notation and use the same K regardless of the dimension of its argument.

(C2) The probability density function of β^TX, denoted by f(β^TX), is bounded away from zero and infinity.

(C3) Let r(β^TX) = E{a(X) | β^TX}f(β^TX). The (m – 1)-th derivatives of r(β^TX) and f(β^TX) are locally Lipschitz-continuous as functions of β^TX.

(C4) The bandwidth h = O(n^−κ) for (2m)⁻¹ < κ < (2d)⁻¹. This implies m > d.

A.3. Technical details

Let $\widehat{f}\left({\beta }^{\mathrm{T}}{X}_i\right)={(n-1)}^{-1}{\sum }_{j\ne i}{K}_h(X_j^{\mathrm{T}}\beta -X_i^{\mathrm{T}}\beta )$ and $\widehat{r}\left({\beta }^{\mathrm{T}}{X}_i\right)={(n-1)}^{-1}{\sum }_{j\ne i}{K}_h(X_j^{\mathrm{T}}\beta -X_i^{\mathrm{T}}\beta )a\left(X_j\right)$. Write ${\eta }_i={\beta }^{\mathrm{T}}{X}_i,\eta ={\beta }^{\mathrm{T}}X,{\widehat{\eta }}_i={\widehat{\beta }}^{\mathrm{T}}{X}_i$,

Lemma A1

Assume E (ε | η) = 0. Under Conditions (C1)-(C3), we have

$$\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\left\{\widehat{E}(a\mid {\eta }_i)-E(a\mid {\eta }_i)\right\}=O_p\left\{h^m∕n^{1∕2}+h^{2m}+{\log }^{2}n∕\left({\mathit{nh}}^d\right)\right\}.$$

Proof of Lemma A1

Recall that $r\left(\eta \right)=E(a\mid \eta )f\left(n\right)$ from condition (C3), and $\widehat{r}\left(\eta \right)=\widehat{E}(a\mid \eta )\widehat{f}\left(\eta \right)$. We write

$$\begin{array}{cc}\hfill \frac{1}{n}\sum _{i=1}^n{\epsilon }_i\left\{\widehat{E}(a\mid {\eta }_i)-E(a\mid {\eta }_i\right\}& =\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\left\{\frac{\widehat{r}\left({\eta }_i\right)}{\widehat{f}\left({\eta }_i\right)}-\frac{r\left({\eta }_i\right)}{f\left({\eta }_i\right)}\right\}\hfill \\ \hfill & =\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\left\{\frac{\widehat{r}\left({\eta }_i\right)-r\left({\eta }_i\right)}{f\left({\eta }_i\right)}\right\}-\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\left[\frac{r\left({\eta }_i\right)\left\{\widehat{f}\right({\eta }_i)-f({\eta }_i\left)\right\}}{f^2\left({\eta }_i\right)}\right]\hfill \\ \hfill & -\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\left[\frac{\left\{\widehat{r}\right({\eta }_i)-r({\eta }_i\left)\right\}\left\{\widehat{f}\right({\eta }_i)-f({\eta }_i\left)\right\}}{f\left({\eta }_i\right)\widehat{f}\left({\eta }_i\right)}\right]\hfill \\ \hfill & +\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\left[\frac{r\left({\eta }_i\right){\left\{\widehat{f}\right({\eta }_i)-f({\eta }_i\left)\right\}}^2}{f^2\left({\eta }_i\right)\widehat{f}\left({\eta }_i\right)}\right].\hfill \end{array}$$ (A.4)

By the uniform convergence of nonparametric regression (Mack and Silverman, 1982), the third and the fourth summations are order $O_p\{h^{2m}+{\log }^{2}n∕({\mathit{nh}}^d\left)\right\}$. The first two summations in the right hand side of (A.4) have similar structures, thus we explain in detail only the first one. We write $n^{-1}{\sum }_{i=1}^n\widehat{r}\left({\eta }_i\right){\epsilon }_i∕f\left({\eta }_i\right)$ as a second-order U-statistic:

$$\frac{1}{n}\sum _{i=1}^n\frac{\widehat{r}\left({\eta }_i\right)}{f\left({\eta }_i\right)}{\epsilon }_i=\frac{1}{2n(n-1)}\sum _{i\ne j}{K}_h({\eta }_i-{\eta }_j)\left\{{\epsilon }_{i}a\right(X_j)∕f({\eta }_i)+{\epsilon }_{j}a(X_i)∕f({\eta }_j\left)\right\}.$$

By using Lemma 5.2.1.A of Serfling (1980, page 183), it follows that

$$\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\frac{\widehat{r}\left({\eta }_i\right)}{f\left({\eta }_i\right)}-\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\frac{E\left\{K_h\right({\eta }_i-{\eta }_j\left)E\right(a\mid {\eta }_j)\mid {\eta }_i\}}{f\left({\eta }_i\right)}=O_p\left\{1∕\left({\mathit{nh}}^{d∕2}\right)\right\},$$ (A.5)

because the difference on the left hand side is a degenerate U-statistic. Next we show that

$$\frac{1}{2}\sum _{i=1}^n{\epsilon }_i\left[\frac{E\left\{K_h\right({\eta }_i-{\eta }_j\left)E\right(a\mid {\eta }_j)\mid {\eta }_i\}-r\left({\eta }_i\right)}{f\left({\eta }_i\right)}\right]=O_p\left(n^{-1∕2}{h}^m\right).$$ (A.6)

Following similar arguments in Lemma 3.3 of Zhu and Fang (1996) for calculating the bias term, we easily have $\underset{X_i}{\sup }\mid E\left\{K_h\right({\eta }_i-{\eta }_j\left)E\right(a\mid {\eta }_j)\mid {\eta }_i\}-r\left({\eta }_i\right)\mid =O\left(h^m\right)$ by assuming that the (m – 1)-th derivative of r(η) is locally Lipschitz-continuous. This proves (A.6). Combining (A.5) and (A.6), we obtain

$$\frac{1}{2}\sum _{i=1}^n{\epsilon }_i\left\{\frac{\widehat{r}\left({\eta }_i\right)-r\left({\eta }_i\right)}{f\left({\eta }_i\right)}\right\}=O_p\left\{1∕\left({\mathit{nh}}^{d∕2}\right)+h^m∕n^{1∕2}\right\}.$$

This result together with (A.4) entails the desired result, which completes the proof.

Lemma A2

Under Conditions (C1)-(C4), we have

$$\sum _{i=1}^{n}E(g\mid {\eta }_i)\left\{E(a\mid {\eta }_i)-\widehat{E}(a\mid {\eta }_i)\right\}=\sum _{i=1}^{n}E(g\mid {\eta }_i)\left\{E\right)(a\mid {\eta }_i)-a\left(X_i\right)\}+o_p\left(n^{1∕2}\right).$$

Proof of Lemma A2

Using the definition of the function r(·) in condition (C3), and the bandwidth conditions nh^2d → ∞ and nh^4m → 0 in (C4), we obtain

$$\begin{array}{cc}\hfill & \sum _{i=1}^{n}E(g\mid {\eta }_i)\left\{E(a\mid {\eta }_i)-\widehat{E}(a\mid {\eta }_i)\right\}\hfill \\ \hfill =& \sum _{i=1}^{n}E(g\mid {\eta }_i)\left[\frac{r\left({\eta }_i\right)\left\{\widehat{f}\right({\eta }_i)-f({\eta }_i\left)\right\}}{f^2\left({\eta }_i\right)}-\frac{\left\{\widehat{r}\right({\eta }_i)-t({\eta }_i)}{f\left({\eta }_i\right)\}}\right]+o_p\left(n^{1∕2}\right).\hfill \end{array}$$

Furthermore, since the bandwidth h satisfies nh^2m → 0 under condition (C4), Lemma A.2 of Zhu and Zhu (2007) yields

$$\begin{array}{cc}\hfill & \sum _{i=1}^{n}E(g\mid {\eta }_i)\frac{r\left({\eta }_i\right)\left\{\widehat{f}\right({\eta }_i)-f({\eta }_i\left)\right\}}{f^2\left({\eta }_i\right)}\hfill \\ \hfill =& \sum _{i=1}^n\left[E\right(g\mid {\eta }_i\left)E\right(a\mid {\eta }_i)-E\{E(g\mid {\eta }_i)E(a\mid \eta )\left\}\right]+o_p\left(n^{1∕2}\right).\hfill \end{array}$$ (A.7)

Similarly, invoking Lemma A.3 of Zhu and Zhu (2007), we obtain

$$\sum _{i=1}^{n}E(g\mid {\eta }_i)\frac{\left\{\widehat{r}\right({\eta }_i)-r({\eta }_i\left)\right\}}{f\left({\eta }_i\right)}=\sum _{i=1}^n\left[E\right(g\mid {\eta }_i\left)a\right(X_i)-E\{E(g\mid \eta )E(a\mid \eta )\left\}\right]+o_p\left(n^{1∕2}\right).$$ (A.8)

Combining (A.7) and (A.8), we obtain the results of Lamma A2.

Proof of Theorem 1

We rewrite the estimating equation ${\sum }_{i=1}^{n}g\left(Y_i\right)\left\{a\right(X_i)-\widehat{E}(a\mid {\widehat{\eta }}_i\left)\right\}=0$ to obtain

$$-\sum _{i=1}^{n}E(g\mid {\eta }_i)\left\{a\right(X_i)-\widehat{E}(a\mid {\widehat{\eta }}_i\left)\right\}=\sum _{i=1}^n\left\{g\right(Y_i)-E(g\mid {\eta }_i\left)\right\}\left\{a\right(X_i)-\widehat{E}(a\mid {\widehat{\eta }}_i\left)\right\}.$$ (A.9)

We first study the left hand side of (A.9):

$$\begin{array}{cc}\hfill \sum _{i=1}^{n}E(g\mid {\eta }_i)\left\{a\right(X_i)-\widehat{E}(a\mid {\widehat{\eta }}_i\left)\right\}& =\sum _{i=1}^{n}E(g\mid {\eta }_i)\left\{a\right(X_i)-E(a\mid {\eta }_i\left)\right\}+\sum _{i=1}^{n}E(g\mid {\eta }_i)\left\{E\right(a\mid {\eta }_i)\hfill \\ \hfill & -\widehat{E}(a\mid {\eta }_i)\}+\sum _{i=1}^{n}E(g\mid {\eta }_i\left)\right\{\widehat{E}(a\mid {\eta }_i)-\widehat{E}(a\mid {\widehat{\eta }}_i)\}.\hfill \end{array}$$ (A.10)

From Lemma A2, the summation of the first two terms on the right hand side of (A.10) is o_p(n^1/2). Using Taylor’s expansion and the weak law of large numbers, denoting Kronecker product as ⊗, i.e. M ⊗ B = (m_ijB) for any matrices M and B, we rewrite the vectorized form of the third summation on the right hand side of (A.10) as

$$\begin{array}{cc}\hfill \mathrm{vec}\left[\sum _{i=1}^{n}E(g\mid {\eta }_i)\left\{\widehat{E}\right(a\mid {\eta }_i)-\widehat{E}(a\mid {\widehat{\eta }}_i\left)\right\}\right]& =-\sum _{i=1}^n\left\{\frac{\partial \widehat{E}(a^{\mathrm{T}}\mid {\eta }_i)}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes E(g\mid {\eta }_i)\right\}\mathrm{vecl}(\widehat{\beta }-\beta )+o_p\left(n^{1∕2}\right)\hfill \\ \hfill & =-\mathit{nE}\left\{\frac{\partial \widehat{E}(a^{\mathrm{T}}\mid \eta )}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes E(g\mid \eta )\right\}\mathrm{vecl}(\widehat{\beta }-\beta )+o_p\left(n^{1∕2}\right).\hfill \end{array}$$

Using $\partial \mathrm{vec}\left({\mathit{fg}}^{\mathrm{T}}\right)∕\partial X^{\mathrm{T}}=g\otimes \partial f∕\partial X^{\mathrm{T}}+\partial g∕\partial X^{\mathrm{T}}\otimes f$, we obtain that

$$\begin{array}{cc}\hfill A& =E\left(\frac{\partial \mathrm{vec}\left[\right\{g\left(Y\right)-E(g\mid \eta )\left\}\right\{a\left(X\right)-E(a\mid \eta )\left\}\right]}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\right)\hfill \\ \hfill & E\left[{\left\{a\right(X)-E(a\mid \eta \left)\right\}}^{\mathrm{T}}\otimes \frac{\partial \left\{g\right(Y)-E(g\mid \eta \left)\right\}}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\right]+E\left[\frac{\partial {\left\{a\right(X)-E(a\mid \eta \left)\right\}}^{\mathrm{T}}}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes \left\{g\right(Y)-E(g\mid \eta \left)\right\}\right]\hfill \\ \hfill & =-E\left[{\left\{a\right(X)-E(a\mid \eta \left)\right\}}^{\mathrm{T}}\otimes \frac{\partial E(g\mid \eta )}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\right]-E\left[\frac{\partial E{(a\mid \eta )}^{\mathrm{T}}}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes \left\{g\right(Y)-E(g\mid \eta \left)\right\}\right]\hfill \\ \hfill & =-E\left[\left\{a\right(X)-E{(a\mid \eta )\}}^{\mathrm{T}}\otimes \frac{\partial E(g\mid \eta )}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\right],\hfill \end{array}$$

where the last equality is because E(g | X) = E(g | η). Hence

$$E\left\{\frac{\partial E(a^{\mathrm{T}}\mid \eta )}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes E(g\mid \eta )\right\}+A=-E\left(\frac{\partial \mathrm{vec}\left[E\right(g\mid \eta \left)\right\{a\left(X\right)-E(a\mid \eta )\left\}\right]}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\right)=0,$$

since E [E (g | η) {a(X) – E(a | η)}] = 0 for all β. Thus, the vectorized form of the left hand side of (A.9) is $-nA\mathrm{vecl}(\widehat{\beta }-\beta )+o_p\left(n^{1∕2}\right)$. Next we study the right hand side of (A.9). We write

$$\begin{array}{cc}\hfill & \sum _{i=1}^n\left\{g\right(Y_i)-E(g\mid {\eta }_i\left)\right\}\left\{a\right(X_i)-\widehat{E}(a\mid {\widehat{\eta }}_i\left)\right\}\hfill \\ \hfill =& \sum _{i=1}^n\left\{g\right(Y_i)-E(g\mid {\eta }_i\left)\right\}\left\{a\right(X_i)-E(a\mid {\eta }_i\left)\right\}+\sum _{i=1}^n\left\{g\right(Y_i)-E(g\mid {\eta }_i\left)\right\}\left\{E\right(a\mid {\eta }_i)-\widehat{E}(a\mid {\eta }_i\left)\right\}\hfill \\ \hfill & +\sum _{i=1}^n\left\{g\right(Y_i)-E(g\mid {\eta }_i\left)\right\}\left\{\widehat{E}\right(a\mid {\eta }_i)-\widehat{E}(a\mid {\widehat{\eta }}_i\left)\right\}.\hfill \end{array}$$

Because E {g(Y_i) – E(g | η_i) | η_i} = 0, a direct application of Lemma A1 entails that the second term is of order O_P {n^1/2h^m + nh^2m + (log² n)h^−d}, which is o_p(n^1/2) when nh^2d → ∞ and nh^4m → 0. By Taylor expansion, the vectorized form of the third term is

$$\begin{array}{cc}\hfill & \mathrm{vec}\left[\sum _{i=1}^n\left\{g\right(Y_i)-E(g\mid {\eta }_i\left)\right\}\left\{\widehat{E}(a\mid {\eta }_i)-\widehat{E}(a\mid {\widehat{\eta }}_i)\right\}\right]\hfill \\ \hfill =& -\sum _{i=1}^n\left[\frac{\partial \widehat{E}(a^{\mathrm{T}}\mid {\eta }_i)}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes \left\{g\right(Y_i)-E(g\mid {\eta }_i\left)\right\}\right]\mathrm{vecl}(\widehat{\beta }-\beta )+o_p\left(n^{1∕2}\right)\hfill \\ \hfill =& -\mathit{nE}\left[\frac{\partial E(a^{\mathrm{T}}\mid \eta )}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes \left\{g\right(Y)-E(g\mid \eta \left)\right\}\right]\mathrm{vecl}(\widehat{\beta }-\beta )+o_p\left(n^{1∕2}\right)\hfill \\ \hfill =& o_p\left(n^{1∕2}\right),\hfill \end{array}$$

where the last equality is again because E(g | X) = E(g | η). The proof of Theorem 1 is completed by combining the results concerning the left and right hand sides of (A.9).

Proof of Theorem 2

A standard Taylor expansion around β yields

$$\begin{array}{cc}\hfill 0=& n^{-1∕2}\sum _{i=1}^n\mathrm{vec}\left[g\left(Y_i\right)\left\{a\left(X_i\right)-h({\tilde{\eta }}_i,\tilde{\beta })\right\}\right]\hfill \\ \hfill =& n^{-1∕2}\sum _{i=1}^n\mathrm{vec}\left[g\right(Y_i\left)\right\{a\left(X_i\right)-h({\eta }_i,\beta )\left\}\right]\hfill \\ \hfill & +n^{-1}\sum _{i=1}^n{\phantom{\mid }\frac{-\partial \left[\mathrm{vec}\right\{g\left(Y_i\right)h({\eta }_i,\beta )\left\}\right]}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\mid }_{\beta ={\beta }^{\ast }}{n}^{1∕2}\left\{\mathrm{vecl}\right(\tilde{\beta }-\beta \left)\right\}+o_p\left(1\right)\hfill \\ \hfill =& n^{-1∕2}\sum _{i=1}^n\mathrm{vec}\left[g\right(Y_i\left)\right\{a\left(X_i\right)-E(a\mid {\eta }_i)\left\}\right]-E\left\{\frac{E(a^{\mathrm{T}}\mid \eta )}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes g\left(Y\right)\right\}{n}^{1∕2}\left\{\mathrm{vecl}\right(\tilde{\beta }-\beta \left)\right\}+o_p\left(1\right),\hfill \end{array}$$

where β* is on the line connecting $\tilde{\beta }$ and β. From the proof of Theorem 1, we have

$$E\left\{\frac{\partial E(a^{\mathrm{T}}\mid \eta )}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes g\left(Y\right)\right\}=E\left\{\frac{\partial E(a^{\mathrm{T}}\mid \eta )}{\partial \mathrm{vecl}{\left(\beta \right)}^{\mathrm{T}}}\otimes E(g\mid \eta )\right\}=-A.$$

Thus, we have

$$0=n^{-1∕2}\sum _{i=1}^n\mathrm{vec}\left[g\right(Y_i\left)\right\{a\left(X_i\right)-E(a\mid {\eta }_i)\left\}\right]+{\mathit{An}}^{1∕2}\left\{\mathrm{vecl}\right(\tilde{\beta }-\beta \left)\right\}+o_p\left(1\right),$$

hence the theorem is proven.

Proof of Proposition 1

From Theorem 1 and 2, we can easily obtain that

$$\begin{array}{cc}\hfill B_2-B_1=& \mathrm{cov}\left(\mathrm{vec}\right[E(g\mid \eta )\left\{a\right(X)-E(a\mid \eta \left)\right\}\left]\right)\hfill \\ \hfill & +\mathrm{cov}\left(\mathrm{vec}\right[\left\{g\right(Y)-E(g\mid \eta \left)\right\}\left\{a\right(X)-E(a\mid \eta \left)\right\}],\hfill \\ \hfill & \mathrm{vec}\left[E\right(g\mid \eta \left)\right\{a\left(X\right)-E(a\mid \eta )\left\}\right])\hfill \\ \hfill & +\mathrm{cov}\left(\mathrm{vec}\right[E(g\mid \eta )\left\{a\right(X)-E(a\mid \eta \left)\right\}],\hfill \\ \hfill & \mathrm{vec}\left[\right\{g\left(Y\right)-E(g\mid \eta )\left\}\right\{a\left(X\right)-E(a\mid \eta )\left\}\right])\hfill \\ \hfill =& \mathrm{cov}\left(\mathrm{vec}\right[E(g\mid \eta )\left\{a\right(X)-E(a\mid \eta \left)\right\}\left]\right),\hfill \end{array}$$

which is clearly positive definite. The last equality holds because E(g | X) = E(g | η). Hence $\mathrm{cov}\left\{\mathrm{vecl}\right(\tilde{\beta }\left)\right\}-\mathrm{cov}\left\{\mathrm{vecl}\right(\widehat{\beta }\left)\right\}=n^{-1}{A}^{-1}(B_2-B_1){\left(A^{-1}\right)}^{\mathrm{T}}$ is positive definite.