PRACTICAL ISSUES IN BUILDING RISK-PREDICTING MODELS FOR COMPLEX DISEASES

Abstract

Recent genome-wide association studies have identified many genetic variants affecting complex human diseases. It is of great interest to build disease risk prediction models based on these data. In this article, we first discuss statistical challenges in using genome-wide association data for risk predictions, and then review the findings from the literature on this topic. We also demonstrate the performance of different methods through both simulation studies and application to real-world data.

1. INTRODUCTION

An important topic in genetic studies of human diseases is the prediction of individual risk of succumbing to a particular disease. This knowledge can assist physicians in disease prevention, diagnosis, prognosis, and treatment (Collins and McKusick, 2001). Traditional approaches to assessing patients’ disease risk with a significant genetic component are primarily achieved through nongenetic risk factors and family history information, but the limitation of this approach in risk prediction is apparent as it is expected that a better prediction rule can be achieved if we can incorporate known genetic variations affecting disease risk in such modeling. For Mendelian diseases, such as cystic fibrosis (Rowe et al., 2005) and Huntington’s disease Walker (2007), where one major gene is responsible for most of the disease cases in a population, disease risk prediction is relatively straightforward. But for common diseases where many genes, nongenetic risk factors, and their interactions jointly affect disease risk, risk prediction is far more challenging. For example, mutations at BRCA1 and BRCA2 are routinely screened to predict breast cancer and ovarian cancer risk. However, these mutations only account for a small proportion of cancer cases (Armstrong et al., 2000; Levine and Hughes, 1998).

Recent advances in genome-wide association studies (GWAS) have led to the discoveries of hundreds of chromosomal regions associated with risk for dozens of diseases (Guyon and Elisseff, 2003; Marchiori et al., 2005). One natural question following these successes is how to most effectively translate these exciting discoveries into better disease risk prediction models. One intuitive approach is to use identified associated single-nucleotide polymorphisms (SNPs) to construct the risk prediction model for the corresponding diseases. In fact, several companies (e.g., PreventionGenetics [http://www.preventiongenetics.com] and deCode [http://www.decode.com]) already offer so-called personalized genomics services that provide individualized disease-risk estimates based on genome-wide SNP genotyping for relatively modest fees. However, these commercial tests are neither sensitive nor specific. The major challenge in using GWAS data for risk prediction is the very large number of genetic markers that can be potentially used in deriving a disease risk model, but this challenge has not been well addressed in the literature.

This paper is organized as follows. Section 2 reviews some common procedures adopted in establishing risk prediction models in the high-dimensional data setting, which GWAS belong to. Section 3 discusses major practical issues that are frequently encountered in risk model building. Section 4 provides an overview of work that has been published on risk prediction using a GWAS approach for complex diseases. And finally, Section 5 provides an illustration of the aforementioned statistical issues using results from simulation studies, and a real data set is analyzed in Section 6. We conclude this paper in Section 7.

2. CLASSIFICATION METHODS BASED ON HIGH-DIMENSIONAL DATA

In a typical GWAS setting, the number of covariates (SNPs and Copy Number Variations (CNVs)) is in the range of hundreds of thousands, whereas the sample size (the number of study participants) is generally on the order of a few thousands, or only a few hundreds. Therefore, constructing a risk prediction model using GWAS data is an instance of classification under high dimensionality.

Various statistical and machine learning methods have been used to analyze high-dimensional data arising from genomics and proteomics studies, but most classification algorithms perform suboptimally when thousands of features are used for prediction simultaneously. Therefore, it is a common practice to use feature selection techniques to identify features that are most predictive of a phenotype first. The selected features are then used to develop a classifier or a prediction model. In this section, we review a few commonly used methods in feature selection, classification, and model evaluation, in the high-dimensional data setting.

2.1. Feature Selection

Feature selection is often perceived as a major bottleneck of supervised learning (Guyon and Elisseff, 2003; Marchiori et al., 2005). When the number of features far exceeds the number of samples, it becomes highly desirable to remove less relevant features before proceeding to derive a classification model. Empirical evidence suggests that by selecting a subset of features, the prediction performance often improves and, in addition, more biological insight into the nature of the prediction problem may be gained. Therefore, feature selection is a critical step in the analysis of high-dimensional data.

The feature selection problem in classification can be considered as a combinatorial optimization problem to find the feature set that maximizes the prediction accuracy based on these features. Ideally, to seek an optimal subset of features, all combinations of features will need to be tried, and the combination that yields the best classification performance should be selected (Ressom et al., 2008).

However, this approach is computationally infeasible because the number of such subsets is an exponential function of the number of features. In practice, three feature selection strategies are commonly used: filter, wrapper, and embedded (Marchiori et al., 2005). The filter strategy selects features primarily based on the general characteristics of the data set without involving any learning algorithm. In the wrapper method, feature selection relies on the “usefulness” criterion; e.g., features are selected based on their contribution to the performance of a given type of classifier. In the embedded approach, feature selection is part of the training procedure of a classifier. Like the wrapper method, the implementation of this approach also depends on the type of the classifier. Filter-based methods, such as t-statistic (Golub et al., 1999; Ressom et al., 2008; Slonim et al., 2000), signal-to-noise ratio, and correlation; wrapper-based methods, such as forward addition and backward elimination; and embedded methods, such as shrunken centroid, recursive feature elimination (Guyon et al., 2002), and CART, are widely adopted in practice.

In the GWAS setting, relevant features are often selected via filtering. This can be achieved by evaluating each feature individually for its marginal association with the disease phenotype, for instance, through a chi-square association test. Then all the features can be ranked by the significance of their disease association, often measured by p values or z scores. Assuming that those SNPs most significantly associated with disease are also good classifiers, a significance cutoff threshold can be applied, and features below the cutoff level are included in the classification model.

This cutoff threshold can be either chosen in an ad hoc fashion or determined from formal statistical procedures. Recently, Donoho and Jin (2008) proposed a strategy of feature selection by thresholding of feature z scores based on the notion of higher criticism. In addition, they also showed that higher criticism thresholding yields asymptotically optimal error rate classifiers in the rare/weak feature model, where the fraction of useful features is small and the useful features are each too weak to be of much use on their own.

Although the filter model is very attractive due to its computational efficiency, it suffers from the following limitations: (1) It selects features based on the “relevance” instead of the “usefulness” criterion; (2) redundant features might be retained after the filtering step as a result of the high degree of dependency among the markers; and (3) features having strong discriminating power jointly, but weak individually, could be ignored (Ressom et al., 2008).

2.2. Classification Methods

Many classification algorithms have been utilized for classification in the high-dimensional setting. In this section, we review four commonly used classification methods for high-dimensional data: linear discriminant analysis (LDA), logistic regression, random forests, and support vector machine (SVM).

Linear discriminant analysis (LDA) aims to find the linear combination of features that best separates two or more classes of samples (McLachlan, 2004). When the response variable is a binary outcome, as in the setting of case-control studies, consider a set of observations x for each sample with class label y = 0 or 1. LDA approaches the problem by assuming that the conditional density functions p(x⃗ | y = 1) and p(x⃗ | y = 0) are both normally distributed. Under this assumption, the Bayes optimal solution is to predict an individual as being from the second class if the likelihood ratio is below a threshold. Under the assumptions of homoscedasticity and full-rank covariance matrix, the decision rule is only a linear combination of the features.

Logistic regression assumes that the outcome variable follows a binomial distribution and that the log odds (or logit) is a linear combination of the predictor variables.

Random forests (Breiman, 2001; Ressom et al., 2008) is a classification method based on “growing” an ensemble of decision tree classifiers. To classify a new individual, the features from this individual are used for classification using each classification tree in the forest. Each tree gives a classification, or “voting,” for a class label. The decision is based on the majority votes over all the trees in the forest. Random forests has better performance over the single tree classifier such as classification and regression tree (CART) (Lewis, 2000).

Support vector machine (SVM; Guyon et al., 2002; Ressom et al., 2008) is a kernel-based system. For a given set of training samples and kernel, SVM finds a linear separating hyperplane with the maximal margin in a higher dimensional space. During the operation phase, the optimal hyperplane and the corresponding decision function are used to determine the class labels for new samples.

2.3. Model Evaluation

It is important to quantify a classifier’s ability to serve as a general model, whose input–output relationships (derived from the training data set) apply equally well to new sets of data (previously unseen test data). However, a nontrivial drawback of many machine learning-based classification algorithms is that they are not based on a probabilistic model, and consequently, there is no confidence interval or probability level associated with models trained using them to classify a new set of test data.

The most appropriate approach to assessing prediction accuracy of a classifier is through the application of this classifier to a set of independent samples in a way that reflects all sources of variability to be experienced in broad application of the classifier. However, before investing valuable time and resources necessary into such an “external validation,” predictive accuracy can be estimated from the same data set used to develop the classifier through resampling methods (Simon, 2007). These methods, such as k-fold cross-validation and bootstrap, provide “internal estimates” of prediction accuracy of classification models.

In k-fold cross-validation, data are divided into k subsets of approximately equal size. We train the model k times, each time leaving out one of the subsets from training, and using this subset to evaluate the classifier performance. If k equals the sample size, this method is called “leave-one-out” cross-validation. In cross-validation, the number of samples in the training sample is less than the full sample size, and therefore cross-validation methods are likely to bias the classification error upward. As a result, a bootstrap estimate of the classification error maybe more accurate. This is achieved by drawing random samples (with replacement) of the same sample size as that of the original to form the training data. This process is repeated B times. A classifier can be built from each bootstrap data set, and the performance of this classifier can be assessed using those out of bag samples not included in the training data. The overall behavior of the prediction accuracies can be obtained by summarizing results from these B bootstrap runs.

A potential problem associated with the bootstrap approach is that when using the same data set for building and validating a classifier, biases are likely to arise. To correct for this bias, Efron and Tibshirani (1993) developed the 0.632 rule. This method was based on a weighted average of the estimate of the leave-one-out bootstrap and the resubstitution estimate. For the 0.632 bootstrap, the weight of the leave-one-out bootstrap estimate is 0.632 and the weight for the learning set is 0.368. The 0.632 bootstrap estimate can be very downward biased, however, for high-dimensional data (Efron and Tibshirani, 1993; Molinaro et al., 2005; Simon, 2007). For instance, in the situation where the genotype data are uninformative for predicting the phenotype, the true prediction error is 0.5 for a balanced case control cohort, and the leave-one-out bootstrap is unbiased because there is no penalty associated with developing classifiers based on a reduced number of distinct cases in the learning set, because no classifier that performs better than the flip of a coin is possible. Even in this situation, the resubstitution error can be close to zero (Simon et al., 2003). Since the 0.632 bootstrap estimate is a weighted average of the leave-one-out bootstrap estimate and the resubstitution estimate, the result is also downward biased.

To improve on the bias of the 0.632 bootstrap, Efron and Tibshirani (1993) developed the 0.632+ bootstrap. With the 0.632+ bootstrap, the weight for the leave-one-out bootstrap is not a fixed value but is adjusted based on an estimate of the degree to which the data is overfit. Molinaro et al. (2005) found that the 0.632+ bootstrap performed well except for high-dimensional data in cases where the classes were well separated. In those cases, the 0.632+ estimate could be much greater than the true value.

To assess the overall performance of a classifier, commonly used evaluation criteria are confusion matrices and receiver operating characteristic (ROC) curves. A confusion matrix presents information about actual and predicted classifications made by a classifier. In a confusion matrix, let true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) denote the four different possible outcomes of prediction for a two-class case with classes “1” (“yes”) and “0” (“no”). A false positive is when the outcome is incorrectly classified as “yes” (or “positive”), when it is in fact “no” (or “negative”). A false negative is when the outcome is incorrectly classified as negative when it is in fact positive. True positives and true negatives are correct classifications. Various performance measures commonly used include the following:

$$\begin{array}{l}\text{Sensitivity}=\frac{TP}{TP+FN}\\ \text{Specificity}=\frac{TN}{TN+FP}\\ \text{Positive}\text{predictive}\text{value}=\frac{TP}{TP+FP}\\ \text{Negative}\text{predictive}\text{value}=\frac{TN}{TN+FN}\\ \text{Overall}\text{classification}\text{accuracy}=\frac{TP+TN}{TP+TN+FP+FN}\end{array}$$

The ROC curve represents the combination of sensitivity and specificity for each possible cutoff value of the continuous test result that can be considered to define positive and negative test outcomes. It is the probability that given a random pair of individuals, between whom one will develop the disease and the other will not, the classifier will assign the former a positive test result and the latter a negative result. Theoretically, the AUC can take values between 0 and 1, where a perfect classifier will take the value of 1. However, the practical lower bound for random classification is 0.5, and classifiers with an AUC significantly greater than 0.5 have at least some ability to discriminate between cases and controls.

In a recent paper by Lu and Elston (2008), the authors propose to use the optimal ROC curve to design a predictive genetic test, which provides a quick evaluation of newly found potential risk conferring genetic variants for potential clinical practice. By calculating out the likelihood ratios of the multi-locus genotypes at the genetic loci of interest between cases and controls, an empirical optimal ROC curve can be obtained, and the corresponding AUC can then be derived using the trapezoid rule. The authors claim the proposed test is asymptotically more powerful than tests built on any other existing method. When applying it on a type II diabetes data set, they discovered that the AUC of the new test (AUC = 0.671) is higher than for the existing test (AUC = 0.580).

3. STATISTICAL ISSUES IN RISK PREDICTION USING GWAS DATA

As described earlier, various methods have been proposed and applied for classification analysis using high dimensional genomics and proteomics data. In contrast to other genomics (e.g., microarray gene expression data) and proteomics data (e.g., mass spectrometry data), there are a number of unique challenges for GWAS data. In this section, we discuss three issues particularly pertinent to risk assessment in the GWAS setting: small effect size, unknown genetic model, and prevalence adjustment.

3.1. Small Effect Size

For diseases caused by single genes with large effect sizes, establishing a risk prediction model based on genotype information is clearly a useful approach for modeling disease risk. However, for diseases with complex inheritance, there is ongoing debate about whether genetic profiling will be useful in clinical care and public health. Some foresee that this will be a critical step toward personalized medicine, in which the development of complex diseases can be predicted by simple DNA tests, but others argue that the era of using genetic profiling to predict disease risk is not quite here yet, because common complex diseases such as psychiatric disorders, cancer, diabetes, heart disease, and asthma are likely to be affected by many genes and mutations, most of which only confer a small effect on disease risk (Holtzman and Marteau, 2000; Vineis et al., 2001).

From recent GWAS studies on complex traits, although a few variants of large effects (allelic odds ratio OR > 2) have been discovered, the vast majority of the effect sizes of risk alleles are small, typically with OR < 1.5, and many around 1.1 and 1.2 (Bertram et al., 2007; Ioannidis et al., 2006), which are the limits of detection given the experimental sample sizes employed to date. Moreover, the observed effect sizes may still represent the upper tail of true effect sizes. Given the effect sizes of the variants detected so far, study samples on the order of 10,000 cases and controls would be needed to detect variants that can explain the majority of genetic variance. However, the sample size in a typical GWAS study is usually in the range of thousands or even hundreds, although more samples may be gathered through research consortia. Thus, the combination of weak effect and relatively small sample size presents a major challenge in identifying the true association signals, compromising the ability to extract most relevant risk-predicting features to include in the prediction model.

3.2. Unknown Genetic Model

SNP genotypes are often represented in a GWAS data set as a three-level categorical variable, i.e., homozygotes with respect to one of two alleles (typically the minor allele), or heterozygotes. One common approach for parameterizing an SNP effect is to choose a particular mechanism by which the genetic variant affects the disease phenotype, and to introduce the corresponding predictor variable into the regression models (Holford et al., 2005). For instance, if there is an additive effect for each copy of a particular allele, i.e., the difference between 0 and 1 copy is the same as that between 1 and 2 copies, then the three genotypes can be coded as 0, 1, and 2. Similarly, if the effect is dominant, then either 1 or 2 copies would have the same effect, but these would be different from 0 copy.

Thus, the key in choosing the regressor variable to represent an SNP is to appropriately specify its mode of action, and if this selection is correct then one has the assurance that the estimated effect is both unbiased and optimal. However, this would be unrealistic because researchers are typically analyzing an SNP to determine whether it has an effect, usually without knowing its mode of action on the response (Holford et al., 2005). Sometimes prior information coming from the observed resemblance between relatives is available to inform about the mode of gene action, and if most observed genetic variations are additive, then it makes sense to model SNP effects as additive. Generally, although fitting a one-degree-of-freedom additive model is quite robust to departures from additivity, the exact genetic architectures for many SNPs remain unknown (Lettre et al., 2007).

One apparent solution to address this problem is to test several genetic models, but this increases the multiple testing burdens, which may decrease power. It is therefore useful to determine which genetic model, or combination of models, maximizes power to detect disease susceptibility loci in genetic association studies, when the true genetic model is unknown.

Lettre et al. (2007) compared various analytical strategies that use different genetic models to analyze genotype–phenotype information from association studies of quantitative traits in unrelated individuals. They generated simulated data sets where the minor alleles are causal with an additive, dominant, or recessive mode of inheritance over a range of allele frequencies. They then calculated power to detect these causal alleles using one or a combination of statistical models in a standard regression framework, including corrections for the multiple testing introduced from analyzing multiple models. According to their results, maximal power is achieved, unsurprisingly, when testing a single genetic model that agrees with the actual underlying mode of action of the causal allele. When the inheritance pattern of the causal allele is unknown, the co-dominant model, a single two degrees of freedom test, has a satisfactory overall performance in any of the three simple modes of inheritance simulated. Alternatively, it is slightly more powerful to analyze all three genetic models together, but only if the significance thresholds used to correct for analyzing multiple models are appropriately determined (such as by permutation). Finally, they discovered that a commonly employed approach, testing the additive model alone, performs poorly for recessive causal alleles when the minor allele frequency is not close to 50%.

In addition to the marginal effects exerted by single SNPs on the onset of complex disease traits, accumulating evidence (Sing et al., 2003; Williams et al., 2004) indicates that gene-gene interactions may also contribute to complex diseases (Hoh and Ott, 2003; Hirschhorn and Daly, 2005; Wang et al., 2005). Examples include Alzheimer’s disease (Martin et al., 2006), breast cancer (Ritchie et al., 2001; Smith et al., 2003), coronary heart disease (Nelson et al., 2001), dyslipidemia (Putt et al., 2004), schizophrenia (Becker et al., 2005; Qin et al., 2005), and type II diabetes (Cho et al., 2004). These interaction effects are rarely taken account of in a risk model, often due to issues such as data sparsity, computational burden, overfitting, and multiple testing (Musani et al., 2007). It is possible that nonreplication of some association studies (Hirschhorn et al., 2002; Ioannidis et al., 2001) is partly due to interactions among disease-associated loci (Cardon and Bell, 2001; Hirschhorn et al., 2002; Williams et al., 2004). It is worth noting that under a continuous threshold model (e.g., probit or logit), gene effects can be additive on the unobserved liability scale but will be nonadditive on the observed binary risk scale. Based on the current GWAS data, there seems to be very little evidence of nonadditivity on the liability scale.

3.3. Prevalence Adjustment

What is common among many complex diseases is a low incidence probability, and for this reason, case-control studies are frequently used in genetic association studies. Many traditional risk modeling approaches for prediction (e.g., logistic regression) are not effective through the case-control studies because the study design produces a biased sample due to the fact that the proportion of cases in the sample is not the same as the population of interest.

To address this issue, in 1972, Anderson presented the intercept-adjusted maximum likelihood estimation (Anderson, 1972) to obtain the predicted probability of disease Y given covariates W with case-control study data. Let q₀ denote the prevalence of the disease, and the addition of log[q₀/(1 − q₀)] to a logistic regression model intercept yields the true logistic regression function P^*(Y = 1 | W).

More recently, Rose and van der Laan (2008) introduced the use of case-control weighted models for prediction with case-control study data. Through simulations, they demonstrated that the case-control weighted model performed similarly to intercept adjustment when the number of covariates and interaction terms was small. When the simulation included a larger number of covariates and was limited to main effect terms, case-control weighting outperformed intercept adjustment.

When evaluating the performance of a binary diagnostic test, although sensitivity and specificity measure the intrinsic accuracy of a diagnostic test that is independent of the prevalence rate, they do not provide information on the diagnostic accuracy for a particular patient. To obtain this information, we need to use positive predictive value (PPV) and negative predictive values (NPV), defined earlier. Since PPV and NPV are functions of both the intrinsic accuracy and the prevalence of the disease, constructing confidence intervals for PPV and NPV for a particular patient in a population with a given prevalence of disease using data from a case-control study is not a trivial task. Mercaldo et al. (2005) proposed a method for the estimation of PPV and NPV using estimates of sensitivity and specificity in a case-control study. For PPV and NPV, standard, adjusted, and their logit-transformed based confidence intervals were compared using coverage probabilities and interval lengths. Based on the results from their simulation study, the adjustment using the logit transformation outperformed the addition of the continuity correction in terms of coverage probabilities, and both logit methods are preferred over the untransformed methods.

4. SIMULATION AND EMPIRICAL STUDIES IN THE LITERATURE

Simulation studies have been performed in the past to provide theoretical ground for the validity of using the GWAS approach in risk prediction. In 2006, Janssens et al. investigated predictive testing for complex diseases using multiple genes by simulation. They examined diseases controlled by up to 400 risk loci, and demonstrated that a good (AUC = 0.80) to excellent (AUC = 0.95) discriminative accuracy can be obtained by simultaneously testing multiple susceptibility genes. Higher discriminative accuracies are obtained when genetic factors play a larger role in the disease, as indicated by the proportion of explained variance. For each value of the proportion of explained variance, rare diseases (lower value of the prevalence parameter) reached higher AUCs than common diseases. Based on their results, Janssens et al. (2006) speculated that the upper bound of discriminative accuracy of future genetic profiling can be estimated from the heritability and prevalence of disease.

One limitation of the Janssens et al. model lies in its unrealistic assumption of individuals’ true genetic risk being known without error, so that the correlation between genetic risk and disease status is simply the square root of the broad-sense heritability on the observed scale. To address this shortcoming, Wray et al. (2007) revisited the Janssens et al. simulation study, and considered four disease scenarios based on realistic combinations of disease prevalence, K = 0.05 or 0.10, and heritabilities of the disease on the observed scale, h² = 0.1 or 0.2. They also considered two distributions of risk allele frequencies underlying the disease corresponding to the common-disease common-variant hypothesis and to the neutral allele hypothesis. Their findings suggest that when the number of loci contributing to the disease is >50, a large case-control study is needed to identify a set of risk loci in predicting the disease risk of an independent sample of healthy individuals. For instance, for diseases controlled by 1,000 loci with mean relative risk of 1.04, a case-control study with 10,000 cases and controls are required to select loci that can explain >50% of the genetic variance; also, the top 5% of people with the highest predicted risk are three to seven times more likely to suffer the disease than the population average, depending on heritability and disease prevalence.

Simulation studies are often time consuming and computationally intensive. In a recent paper, Daetwyler et al. (2008) derived a simple deterministic formula to estimate the prediction accuracy of predicted genetic risk from case control studies using a genome-wide approach, assuming a dichotomous disease phenotype with an underlying continuous liability. The derived expression for accuracy is composed of the product of the ratio of number of phenotypic records per number of risk loci and the observed heritability, and this formula will help researchers gain some insight of the sample size appropriate to attain their target prediction accuracy.

One should interpret the results from these simulation studies with cautions, because none of the simulation/methodology papers presented thus far takes issues such as methodological problems in genotyping, subtle population stratification effects, or important gene–environment interaction effects into account. In real-world applications, however, these are not negligible problems, which may significantly influence the performance of a classifier. Therefore, the prediction performance for genetic risk given in these papers may only represent the upper bound of accuracy achievable. In fact, a number of large-scale risk prediction analyses on several common human diseases using the GWAS approach have been published in medical journals, but the results from these real-world studies unfortunately are not very encouraging.

One of the disease traits for which the GWAS approach has been most successful is type 2 diabetes. Together with candidate gene approaches, 18 common variants have now been convincingly shown to be associated with the disease (Saxena et al., 2007; Scott and Mohlke, 2007; Sladek, 2007; Steinthorsdottir, 2007; Zeggini et al., 2008). In 2008, Lango et al. assessed the risk predicting capability of these 18 independent loci in 2,598 control subjects and 2,309 case subjects from the Genetics of Diabetes Audit and Research Tayside Study (Hana et al., 2008). They discovered that individuals carrying more risk alleles had a higher risk of type 2 diabetes, but the AUC for these variants was merely 0.60. The AUC for prediction based on traditional clinical variables such as age, BMI, and gender was much higher, at 0.78. Adding the genetic risk variants to these clinical variables only marginally increased the AUC to 0.80.

Meigs et al. conducted a similar diabetes study in 2,377 participants of the Framingham Offspring Study (James et al., 2008). They created a genotype score from the number of risk alleles and used logistic regression to generate AUC to indicate the extent to which the genotype score can discriminate the risk of diabetes when used alone and when in addition to clinical risk factors. The AUC was 0.534 without the genotype score and 0.581 with the score. In a model adjusted for gender and self-reported family history of diabetes, the AUC was 0.595 without the genotype score and 0.615 with the score.

Another recent risk study on diabetes was published by Lyssenko et al. (2005). By using a Cox proportional hazard model, common variants in several genes were studied for their ability to predict type 2 diabetes in 2,293 individuals participating in the Botnia study in Finland. After a median follow-up of 6 years, 132 (6%) people developed type 2 diabetes. The hazard ratio for risk of developing type 2 diabetes was statistically significant for the risk genotypes of those examined variants. Based on this large prospective study, the authors concluded genetic testing might become a future approach to identify individuals at risk of developing type 2 diabetes.

In a risk prediction analysis on asthma, Bureau et al. (2005) illustrated the application of random forests with a data set of asthma cases and unaffected controls genotyped at 42 SNPs in ADAM33, a previously identified asthma susceptibility gene. Applying random forests to the 131 cases and 217 controls yielded a misclassification rate of 44%.

Traditionally, the predictors included in a genetic risk model are those variants most significantly associated with disease phenotype (e.g., variants with the largest odds ratios) in GWAS. However, Jakobsdottir et al. (2009) raised skepticism on such approach. Their paper argues that strong association does not guarantee effective discrimination between cases and controls, and excellent classification (high AUC) does not guarantee good prediction of actual risk. In supporting their claim, an age-related macular degeneration dataset was examined. By using an additive model of three variants, the AUC is 0.79, but assuming prevalences of 15%, 5.5%, and 1.5%, only 30%, 12%, and 3% of the group were classified as high-risk cases (although a recent paper suggests better risk prediction for AMD can be obtained when including not only genetic, but also demographic, and environmental variables in the set of predictors; Seddon et al., 2009). Additionally, they presented examples for four other diseases for which strongly associated variants have been discovered. In type 2 diabetes, their classification model of 12 SNPs has an AUC of only 0.64, and two SNPs achieve an AUC of only 0.56 for prostate cancer. Finally, in Crohn’s disease, a model of five SNPs has an AUC of 0.66. Based on these results, the authors suggested that strong association, although very valuable for establishing etiological hypotheses, does not guarantee effective discrimination between cases and controls. It is worth noting that in the Jakobsdottir et al. paper, the AUCs were derived from prediction models only including a very small number of predictors. However, prediction performance can be improved with a large number of weak predictors, each of which is merely nominally significant, especially for diseases such as bipolar disorder and coronary heart disease (Evans et al., 2009).

In summary, although published simulation studies seem to suggest that risk prediction using GWAS approach holds great promises, with real data sets the prediction performance remains quite modest for common complex diseases.

5. SIMULATION STUDIES

Previously published simulation studies revolve around only one or several steps in the process of risk model establishment, but a comprehensive analysis involving all stages of prediction model building is still lacking. In this section, we conduct simulations to systematically investigate the impact of sample size, effect size, feature selection, classification methods, and model evaluation (internal vs. external validation) on the performance of risk prediction models.

To model the disease risks associated with genetic profiles, we adopt a modified version of the Janssens et al. (2006) simulation scheme. The posterior odds of disease are calculated by multiplying the prior odds (e.g., $\frac{\text{prevalence}}{1-\text{prevalence}}$) by the likelihood ratio (LR) of the genetic profile.

By fixing the prevalence of the disease, the minor allele frequency, the number of subjects in the study, and the ORs of the homozygous and heterozygous risk genotypes, the LR of single causal SNP genotypes can be derived. Assuming a multiplicative risk model on the odds scale and no statistical interaction between the genes, the LR of a genetic profile can be obtained by multiplying the LRs of single causal SNP genotypes. Finally, posterior odds are converted into disease risk. (e.g., $=\frac{\text{odds}}{1+\text{odds}}$). The proportion of explained variance by genetic factors can be calculated as

$$1-\frac{\sum \text{risk}\ast (1-\text{risk})}{\text{prevalence}\ast (1-\text{prevalence})\ast \text{sample}\text{size}}$$

In our simulation study, we investigate the role of effect size in prediction performance by considering three disease scenarios, and the median odds ratios of the causal SNPs in the three disease scenarios are 1.13, 1.31, and 1.48, corresponding to weak, medium, and strong effect size, respectively. As described in the previous section, published simulation studies suggest the upper bound of AUCs likely being a function of disease prevalence and heritability. To make a fair comparison among the three disease scenarios, we set population parameters (e.g., prevalence and heritability) roughly equal for each scenario. This is achieved by first fixing prevalence at 0.1 for all of the disease scenarios; then, through simulations, we determine the number of causal loci needed in each disease to achieve similar heritability given prespecified ORs and minor allele frequencies.

Following the simulation scheme described earlier, we simulated a population of size 150,000 and 100,000 noncausal markers. For the set of causal loci in each disease, Minor Allele Frequencies (MAFs) are simulated from a uniform distribution, and we assume that each single SNP has two alleles and that all genotypes are in Hardy–Weinberg equilibrium. Causal SNPs are further assumed to be independent, i.e., no linkage disequilibrium. For the three disease scenarios in the direction of increasing effect size, the number of causal loci included in the genetic profile is 30, 60, and 300, and the heritability on the observed scale is 0.294, 0.281, and 0.292, respectively.

The distributions of ORs for the causal SNPs in these three diseases are summarized in Fig. 1.

Figure 1.

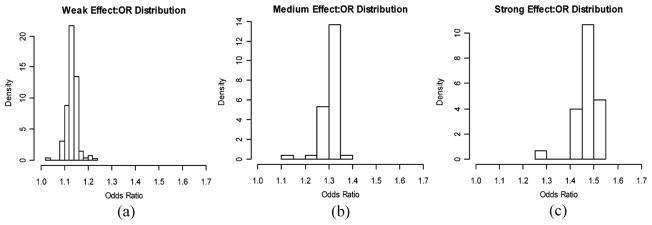
Odds ratio distributions for the causal SNPs in the three disease scenarios with different effect sizes.

In each of three disease scenarios, we vary the following simulation parameters used in risk model construction:

1. Number of features: Feature sets containing 20, 50, 100, 200, 300, and 400 most significantly associated SNPs are used to construct the prediction models, respectively. Some of these features may be true signals whereas many others are not associated with disease.

2. Sample size: We consider samples consisting of 500 (including both cases and controls), 1000, 2000, 5000, and 10,000 individuals. Seventy percent of the subjects are used as the discovery cohort, whereas the remaining 30% are used as the validation cohort, following a sevenfold cross-validation resampling scheme.

3. Classification algorithms: We consider three commonly used classification methods: logistic regression, risk-score logistic regression, and SVM. In the risk-score logistic regression, the sum of risk alleles in the genetic profile is calculated as a risk score, which serves as a proxy for the risk of a subject developing disease. The risk score is then treated as the single predictor in the logistic regression framework for model training and validation. In the SVM approach, SNP genotypes in the feature set are used as predictors, and radial kernel function is used for classification. For each set of simulation parameters, the prediction performance was evaluated based on the median AUC of the model on the validation cohorts among 50 cross-validation runs. Both “internal” validation (generated with seven fold cross-validation) and “external” validation cohort (an independent validation cohort) are used for model evaluation.

We first summarize the results for derivation and validation cohorts generated from internal validation (e.g., cross-validation) scheme. We summarize the relationship between prediction performance and the simulation parameters one at a time by plotting the median AUC (among 50 cross-validation runs) versus the parameter of interest.

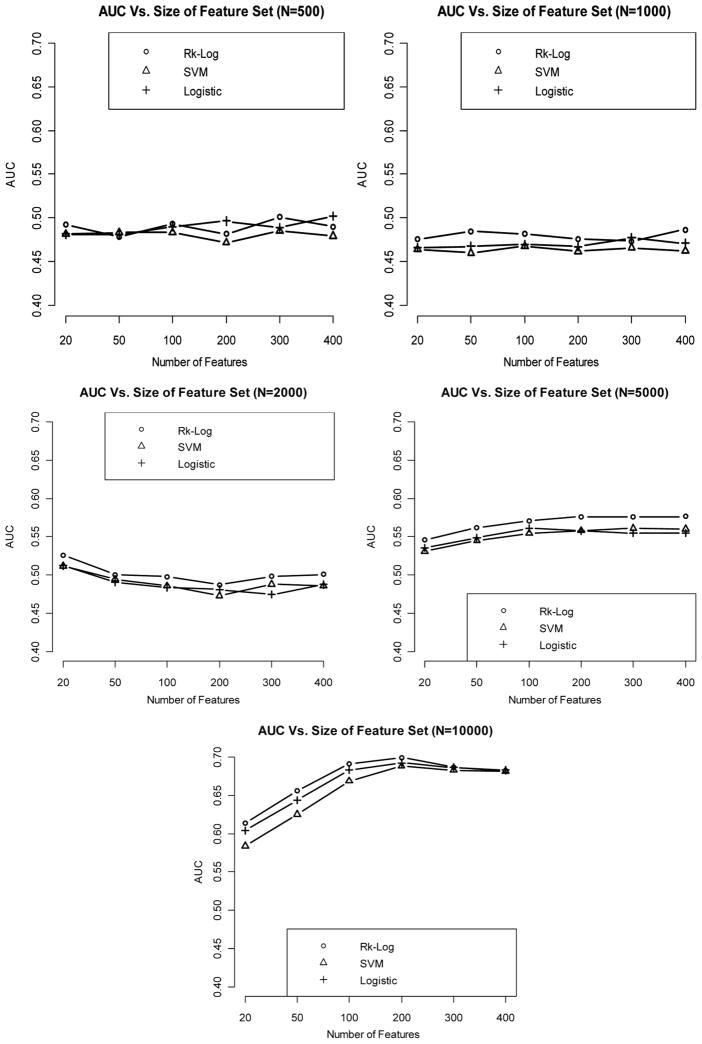
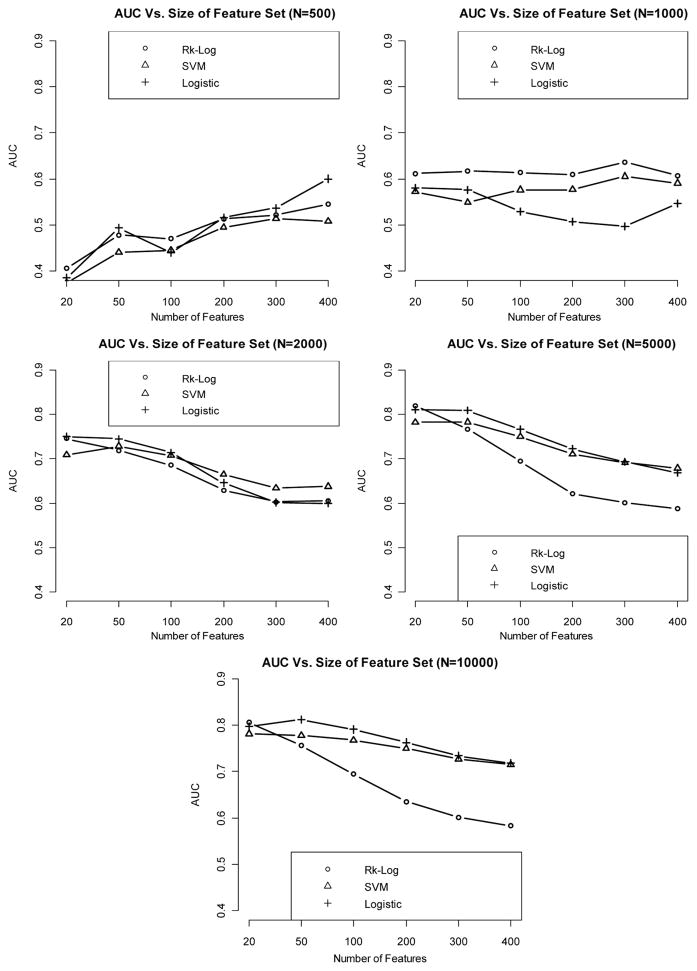
When the effect size is weak, it appears that even with sample size as large as 10,000, we cannot get satisfactory classification performance (e.g., AUC < 0.7). Logistic regression and logistic risk score method consistently outperform SVM at all levels of sample size and feature set size (Fig. 2).

Figure 2.

Relationship between AUC (median AUC among 50 CV runs) and number of features included in the model, with sample size varying from 500 to 10,000, when the effect size is weak.

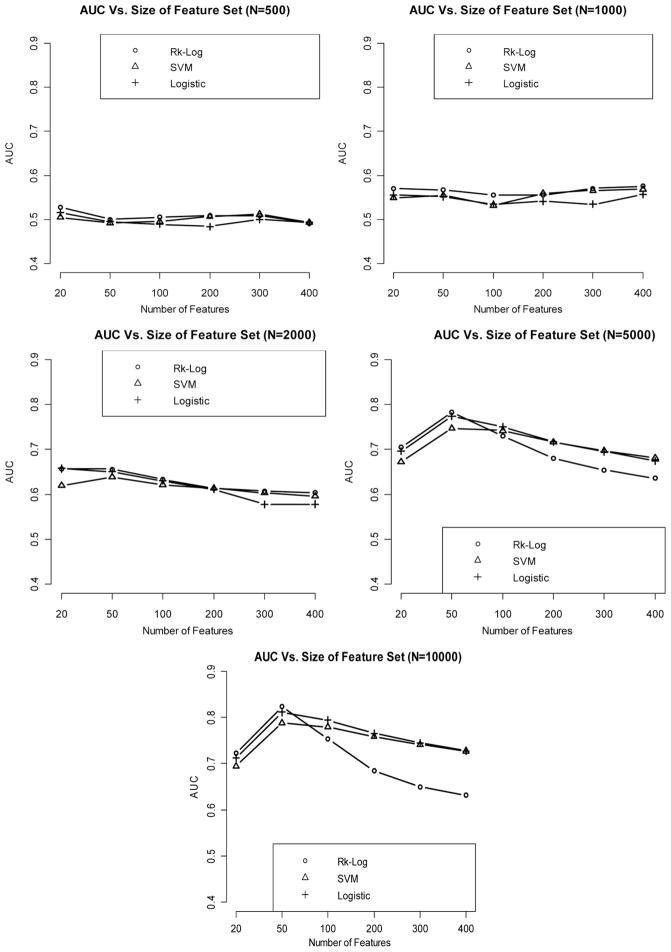
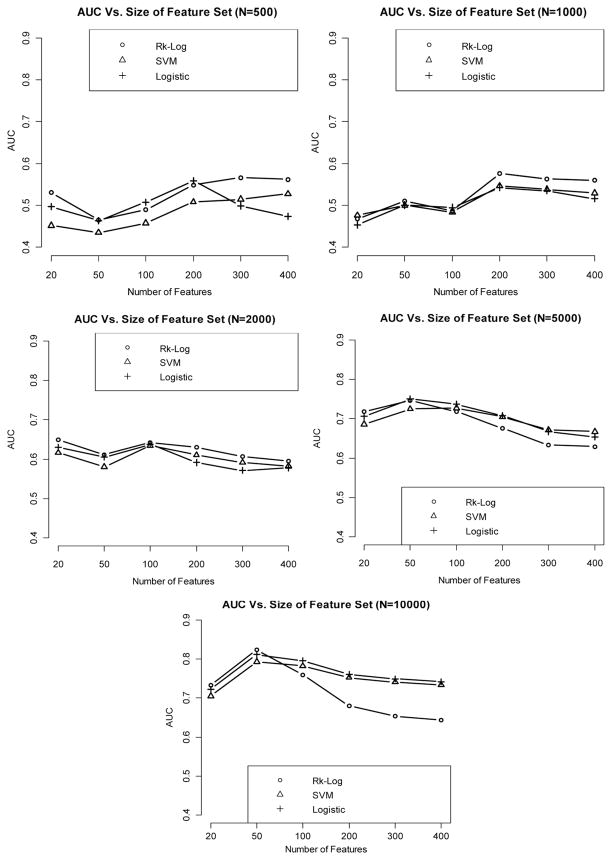
When the effect size is medium, the AUC increases in general as the sample size increases. Classification performance is generally improved when comparing the AUCs of medium-effect-size classifiers against their counterparts in the weak-effect-size setting.

Risk score method and logistic regression continue to yield better classification accuracies than SVM (Fig. 3).

Figure 3.

Relationship between AUC (median AUC among 50 CV runs) and number of features included in the model, with sample size varying from 500 to 10,000, when the effect size is medium.

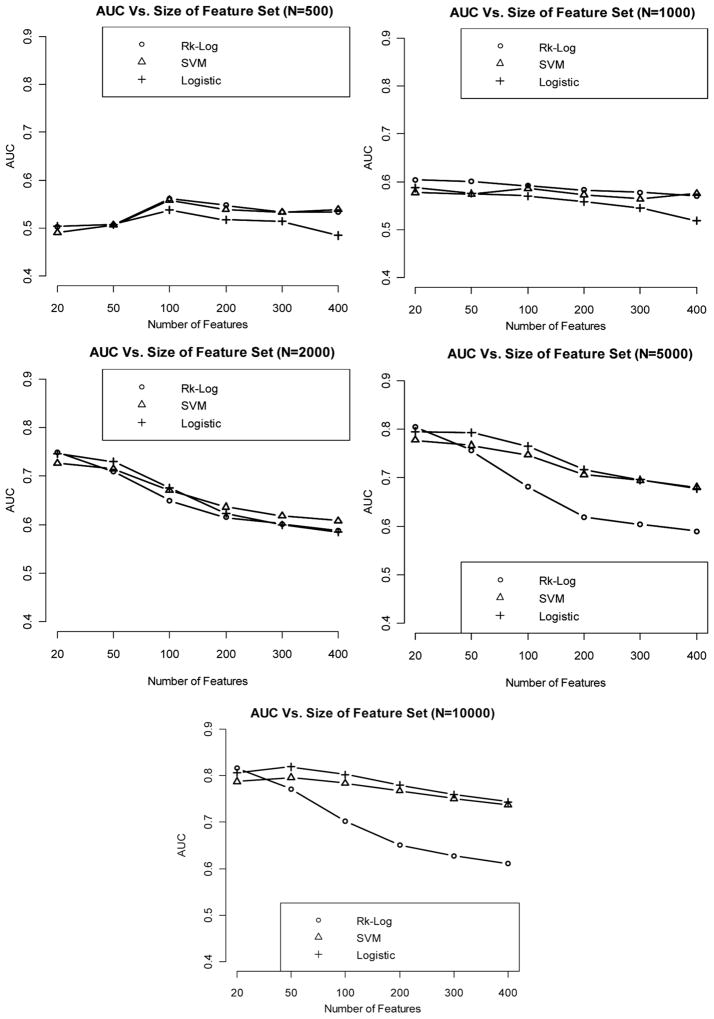
Prediction performance continues to improve as the effect size increases. In addition, in the setting of strong effect size, the performance of SVM starts to become more comparable to that of risk score and logistic regression methods (Fig. 4).

Figure 4.

Relationship between AUC (median AUC among 50 CV runs) and number of features included in the model, with sample size varying from 500 to 10,000, when the effect size is strong.

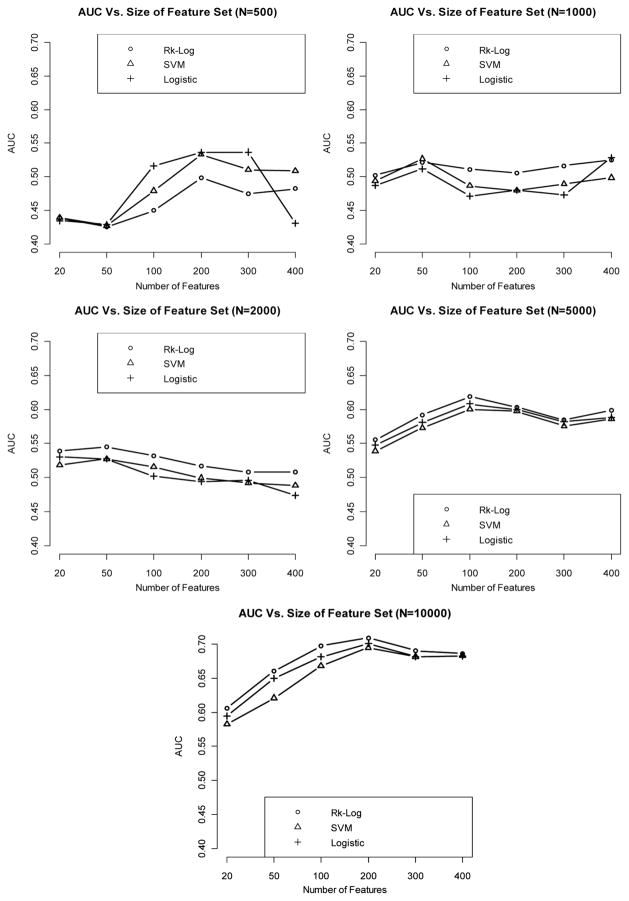
When using an independent cohort as an external validation, we observe that internal validation in general yields lower AUCs than given by the external validation, especially when sample size is very small (N = 500). However, the difference in AUC between the two validation strategies diminishes when sample size becomes very large (N = 10.000). AUC is generally increased with a larger effect size and a bigger sample size. In addition, risk score method and logistic regression generate more superior classification performance than the SVM method. The results are summarized in Figs. 5–7.

Figure 5.

Relationship between AUC and number of features included in the model, with sample size varying from 500 to 10,000, when the effect size is weak, using an independent validation set.

Figure 7.

Relationship between AUC and number of features included in the model, with sample size varying from 500 to 10,000, when the effect size is strong, using an independent validation set.

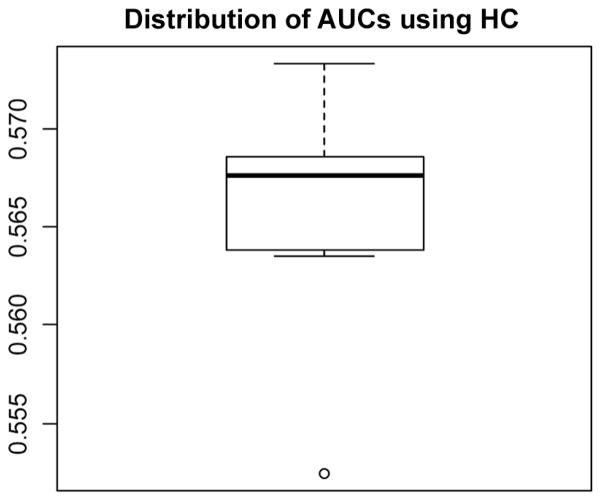
Finally, we examine the performance of HC thresholding (Donoho and Jin, 2008) in selecting features from a simulated data set with weak effect size and sample size of 5000, resembling a realistic GWAS setting. The boxplot for the distribution of AUCs across 50 cross-validation runs is provided in Fig. 8.

Figure 8.

Distribution of AUCs across the 50 cross-validation runs, on a data set with weak effect size and sample size of 5000.

Using higher criticism thresholding, the median AUC is 0.568 across 50 cross-validation runs. Based on the HC criterion, a range between 545 and 7361 features (a median of 1379 features) across different cross-validation runs are selected; however, compared to our previous results, we see that when sample size is 5000 and effect size is weak, AUC peaks at feature set size of around 200.

6. CASE STUDY

In this section, we develop risk prediction models based on a Crohn’s disease (CD) data set. Crohn’s disease is a subtype of inflammatory bowel disease, and many variants are believed to be associated with CD; however, each only exerts a small to medium effect.

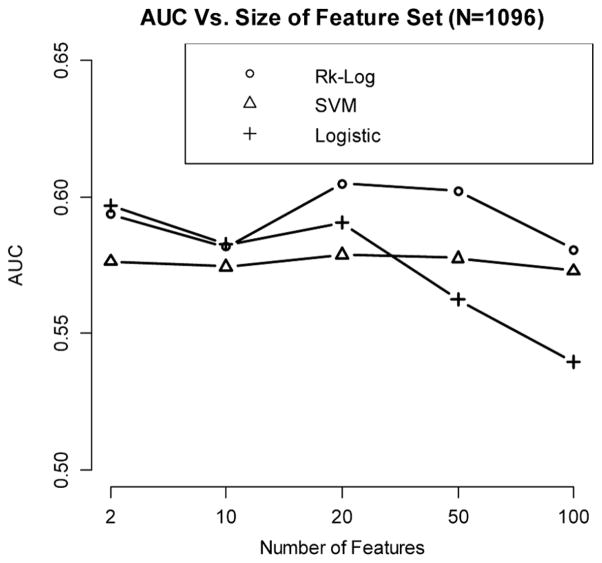
In this data set, we have 1096 participants (549 controls, and 547 cases) with non-Jewish European ancestry, and 308,330 markers are analyzed (Fig. 9). The most significantly associated SNPs are selected as features. We investigate the relationship between AUC (median AUC among 50 cross-validation runs) and the number of features included, using the risk score method, SVM, and logistic regression. Derivation and validation cohorts are generated using a sevenfold cross validation scheme. From the analysis results, we observe that risk score method generates better prediction accuracy than SVM and logistic regression, and the best performance is obtained when including 20 SNPs in the model.

Figure 9.

Relationship between AUC and the number of features for a CD data set.

7. CONCLUSIONS

During the past few years, scores of GWA studies have been conducted for many common complex diseases, and the findings from such studies raise hope that genetic profiling could help identifying those high risk individual, who may benefit from preventive interventions. However, when using GWAS data to build risk prediction models, the number of predictors substantially outnumbers the number of study participants; in this high-dimensional setting, most classification algorithms often fail to deliver the most optimal performance, and error estimates derived from common resampling schemes used for “internal validation” can be biased. In addition, there are a number of unique challenges under GWAS setting, such as small effect size, unknown genetic model, and prevalence adjustment, which further increase the difficulty of building a satisfactory classifier using GWAS data.

Our simulation studies suggest that prediction performance of risk models is very sensitive to the effect size of genetic variants on the disease, the number of samples included in the study, and the number of features included in the final model. And when the effect size is very weak (median odds ratio for causal SNPs is less than 1.2), which applies to many common complex diseases, prediction accuracy remains very modest even when sample size is increased to 10,000.

As described previously, a major bottleneck in the process of risk model establishment is feature selection. Currently, the main approach within genetic diagnostics is to test individuals only at well-established loci known to affect risk of complex disease. However, for many diseases, the established loci could only collectively explain a small portion of the genetic contribution, which suggests that a lot more disease-associated genetic variants (especially for those less common variants) are yet to be discovered. Therefore, estimates of risk based upon the known locus associations are likely to change dramatically in the next few years, raising questions on the stability of the current risk estimates (Kraft and Hunter, 2009). In fact, several papers (Kraft and Hunter, 2009; Mihaescu et al., 2009) demonstrate that updating risk factor profile may generate contradictory information about an individual’s risk status over time. In the light of that, including both only nominally significant variants and established risk loci seems to be an attractive alternative to using only the known loci alone. However, in a recent paper, Evans et al. (2009) showed that the addition of nominally significant variants (summarized in the form of genome-wide score) to known variant information produced only a limited increase in discriminative accuracy but was most effective for bipolar disorder, coronary heart disease and type II diabetes, and concluded that this small improvement in discriminative accuracy is unlikely to be of diagnostic or predictive utility.

Finally, from a practical standpoint, in order for genetic diagnostics to be widely adopted in clinics and hospitals, the “clinical utility” (Kraft and Hunter, 2009) of genetic tests is critical. A few papers argue that the statistics used during the discovery stage of the research (such as odds ratios or p values for association) are not the most appropriate measures for evaluating the predictive value of genetic profile, and that other measures such as sensitivity, specificity, and positive and negative predictive values are more useful when proposing a genetic profile for risk prediction (Kraft and Hunter, 2009; Kraft et al., 2009; Mihaescu et al., 2009).

In conclusion, although it is clear that genetic profiling can generate useful information in assessing individuals’ risk for certain complex disease, there are also many practical statistical issues that limit its full utility at the present time. There is a great need to develop more appropriate and efficient statistical tools to address this highly critical issue presented from genome-wide association studies.

Figure 6.

Relationship between AUC and number of features included in the model, with sample size varying from 500 to 10,000, when the effect size is medium, using an independent validation set.