Intrinsic Regression Models for Medial Representation of Subcortical Structures

Abstract

The aim of this paper is to develop a semiparametric model for describing the variability of the medial representation of subcortical structures, which belongs to a Riemannian manifold, and establishing its association with covariates of interest, such as diagnostic status, age and gender. We develop a two-stage estimation procedure to calculate the parameter estimates. The first stage is to calculate an intrinsic least squares estimator of the parameter vector using the annealing evolutionary stochastic approximation Monte Carlo algorithm and then the second stage is to construct a set of estimating equations to obtain a more efficient estimate with the intrinsic least squares estimate as the starting point. We use Wald statistics to test linear hypotheses of unknown parameters and establish their limiting distributions. Simulation studies are used to evaluate the accuracy of our parameter estimates and the finite sample performance of the Wald statistics. We apply our methods to the detection of the difference in the morphological changes of the left and right hippocampi between schizophrenia patients and healthy controls using medial shape description.

1 Introduction

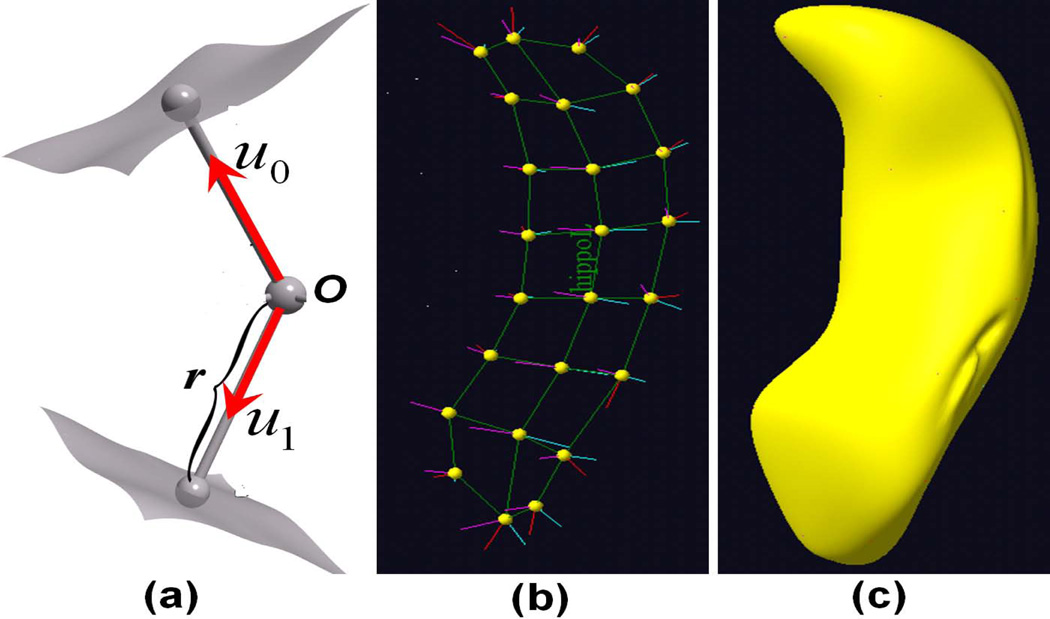
The medial representation of subcortical structures provides a useful framework for describing shape variability in local thickness, bending, and widening for subcortical structures (Fletcher et al., 2004). In the medial representation framework, a geometric object is represented as a set of connected continuous medial primitives, called medial atoms. See Figure 1 for a hippocampus example. For 3-dimensional objects, these medial atoms are formed by the centers of the inscribed spheres and by the associated spokes from the sphere centers to the two respective tangent points on the object boundary. Specifically, a medial atom $\mathbf{m}={({\mathbf{O}}^T,r,{\mathbf{s}}_0^T,{\mathbf{s}}_1^T)}^T$ is formed by a position O, the center of the inscribed sphere; a radius r, the common spoke length; and (s₀, s₁), the two unit spoke directions (Pizer et al., 2003; Styner et al., 2004). A medial atom can be regarded as a point on a Riemannian manifold, M(1) = R³ × R⁺ × S² × S², where S² is the sphere in R³ with radius one. A medial representation model consisting of K medial atoms can be described as the direct product of K copies of M(1), i.e., $M{(1)}^K={\displaystyle {\prod }_{i=1}^K}M(1)$. The existing statistical analytical methods for the medial representation include principal geodesic analysis, the estimation of extrinsic and intrinsic means, and a permutation test for comparing medial representation data from two groups (Fletcher et al., 2004). The scientific interests of some neuroimaging studies, however, typically focus on establishing the association between subcortical structure and a set of covariates, particularly diagnostic status, age, and gender, thus requiring a regression modeling framework for medial representation.

Figure 1.

(a) A medial representation model $\mathbf{m}={({\mathbf{O}}^T,r,{\mathbf{s}}_0^T,{\mathbf{s}}_1^T)}^T$ at an atom, where O is the center of the inscribed sphere, r is the common spoke length, and (s₀, s₁) are the two unit spoke directions; (b) a skeleton of a hippocampus with 24 medial atoms; (c) the smoothed surface of the hippocampus.

There are several challenging issues including multiple directions on S² and the complex correlation structure among different components of M(1) in developing medial representation regression models with a set of covariates. Although there is a sparse literature on regression modeling of a single directional response and a set of covariates of interest (Mardia and Jupp, 1983; Jupp and Mardia 1989), these regression models of directional data are based on particular parametric distributions, such as the von Mises-Fisher distribution (Mardia, 1975; Mardia and Jupp, 1983; Presnell et al., 1998). For instance, existing circular regression models assume that the angular response follows the von Mises-Fisher distribution with either the angular mean η_i or the concentration parameter κ_i being associated with the covariates x_i (Gould, 1969; Johnson and Wehrly, 1978; Fisher and Lee, 1992). However, it remains unknown whether it is appropriate to directly apply these parametric models for a single directional measure to simultaneously characterize the two spoke directions at each atom, which are correlated. Moreover, the two spoke directions may be correlated with other components of each atom and this provides further challenges in developing a parametric model to simultaneously model all components of each atom of the medial representation.

The rest of this paper is organized as follows. In Section 2, we formulate the semiparametric regression model and introduce the two-stage estimation procedure for estimating the regression coefficients. Then, we establish asymptotic properties of our estimates and then develop Wald statistics to carry out hypothesis testing. Simulation studies in Section 3 are used to assess the finite sample performance of the parameter estimates and Wald test statistics. In Section 4, we illustrate the application of our statistical methods to the detection of the difference in morphological changes of the hippocampi between schizophrenia patients and healthy controls in a neuroimaging study of schizophrenia.

2 Theory

2.1 Inverse Link functions

Suppose we have an exogenous q × 1 covariate vector x_i and a medial representation for a particular sub-cortical structure, denoted by M_i = {m_i(d) : d ∈ 𝒟}, for the i–th subject, where d represents an atom of the medial representation. For notational simplicity, we temporarily drop atom d from our notation. We formally introduce a semiparametric regression model for medial representation responses and covariates of interest from n subjects. The regression model involves modeling a conditional mean of a medial representation response m_i at an atom given x_i, denoted by μ_i(β) = μ(x_i, β), where β is a p × 1 vector of regression coefficients in ℬ ⊂ R^p. Thus, μ(·, ·) is a map from R^q × R^p to M(1) and μ_i(β) = (μ_oi(β)^T, μ_ri(β), μ_0i(β)^T, μ_1i(β)^T)^T, which is a 10 × 1 vector and μ_oi(β), μ_ri(β), μ_0i(β), and μ_1i(β) are the ‘conditional means’ of the location O_i, the radius r_i, and the two spoke directions s_0i and s_1i respectively, given x_i, for the i-th subject. Note that for spoke directions, we borrow the term conditional mean for random variables in Euclidean space.

We need to formalize the notion of conditional mean explicitly. For the location component of a medial representation, we may set μ_oi(β) = (g₁(x_i, β₁), g₂(x_i, β₂), g₃(x_i, β₃))^T, where g_k(·, ·) is a known inverse link function and β_k is a p_k × 1 coefficient vector for k = 1, 2, 3. There are many different ways of specifying g_k(x_i, β_k). The simplest one is the linear inverse link function $g_k({\mathbf{x}}_i,{\mathit{\beta }}_k)={\mathbf{x}}_i^T{\mathit{\beta }}_k$. We may also represent g_k(x_i, β_k) as a linear combination of basis functions {ψ_j(x_i) : j = 1, …, J}, such as B-splines, that is $g_k({\mathbf{x}}_i,{\mathit{\beta }}_k)={\displaystyle {\sum }_{j=1}^J}{\psi }_j({\mathbf{x}}_i){\beta }_{\mathit{\text{kj}}}$, in which β_kj is the j-th component of β_k. In this way, we can approximate a nonlinear function of x_i using the linear combination of basis functions. For the radius component, we may use μ_ri(β) = g₄(x_i, β₄), where β₄ is a p₄ × 1 coefficient vector for a medial representation radius. Since a radius is always positive, a natural inverse link function is $g_4({\mathbf{x}}_i,{\mathit{\beta }}_4)=\text{exp}({\mathbf{x}}_i^T{\mathit{\beta }}_4)$, among other possible choices.

As the two spoke directions at each atom of a medial representation are spherical responses, we develop a link function μ_0i(β) ∈ S² for the first spoke direction at a specific atom for notational simplicity. Let x_i,d be a q_d × 1 vector of all the discrete covariates, x_i,c are a q_c × 1 vector of all the continuous covariates and their potential interactions with x_i,d, β_5d and β_5c are the regression parameters corresponding to x_i,d and x_i,c, respectively, and β₅ contains all unknown parameters in β_5d and β_5c. From now on, all covariates have been centered to have mean zero. We assume that all first spoke directions associated with the same discrete covariate vector x_i,d are concentrated around a center on the sphere given by

$${\mathbf{g}}_5({\mathbf{x}}_{i,d},{\mathit{\beta }}_{5d})={(\text{sin}(\theta ({\mathbf{x}}_{i,d}))\text{cos}(\varphi ({\mathbf{x}}_{i,d})),\text{sin}(\theta ({\mathbf{x}}_{i,d}))\text{sin}(\varphi ({\mathbf{x}}_{i,d})),\text{cos}(\theta ({\mathbf{x}}_{i,d})))}^T,$$ (1)

where θ(x_i,d) and ϕ(x_i,d) are, respectively, the colatitude and the longitude, and β_5d includes all unknown parameters θ(x_i,d) and ϕ(x_i,d) for different x_i,d.

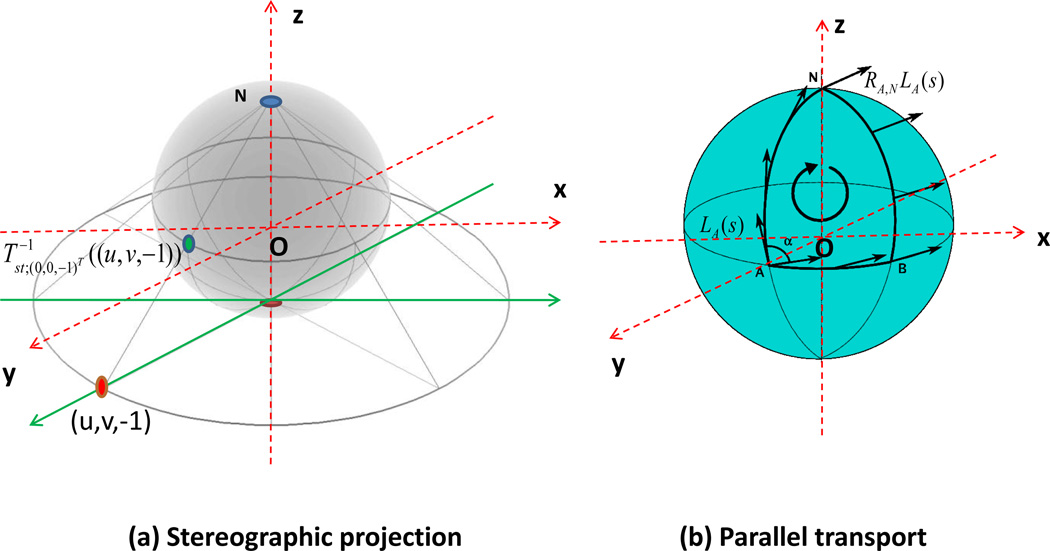
We then describe the stereographic projection of projecting μ_0i(β) on the plane with base point g₅(x_i,d, β_5d), denoted by T_{st;g5(xi,d,β5d)}(μ_0i(β)) (Downs, 2003). A graphic illustration of the stereographic projection $T_{\mathit{\text{st}};(0,0,1)}^{-1}(u,v,-1)$ is given in Figure 2 (a). The stereographic projection T_{st;g5(xi,d,β5d)}(μ_0i(β)) is defined as the point of intersection for the plane passing through g₅(x_i,d, β_5d) with the normal vector g₅(x_i,d, β_5d), which is given by g₅(x_i,d, β_5d)^T {(u, v, w)^T − g₅(x_i,d, β_5d)} = 0 for (u, v, w) ∈ R³, and the line passing through −g₅(x_i,d, β_5d) and μ_0i(β): μ_0i(β) − t{g₅(x_i,d, β_5d) + μ_0i(β)} for t ∈ (−∞, ∞). With some calculation, it can be shown that T_{st;g5(xi,d,β5d)}(μ_0i(β)) is given by

$$T_{\mathit{\text{st}};{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\beta }_{5d})}({\mathit{\mu }}_{0i}(\mathit{\beta }))=\frac{2{\mathit{\mu }}_{0i}(\mathit{\beta })}{1+{\mathit{\mu }}_{0i}{(\mathit{\beta })}^T{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\mathit{\beta }}_{5d})}-\frac{{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\mathit{\beta }}_{5d})\{{\mathit{\mu }}_{0i}{(\mathit{\beta })}^T{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\mathit{\beta }}_{5d})-1\}}{1+{\mathit{\mu }}_{0i}{(\mathit{\beta })}^T{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\mathit{\beta }}_{5d})}.$$

Figure 2.

Graphic illustration of (a) stereographic projection and (b) parallel transport. In panels (a) and (b), N and O denote the north pole (0, 0, 1) and the origin (0, 0, 0), respectively, and the red dash lines are the x, y, and z-axes. In panel (a), the red point (u, v, −1) is a selected point on the plane z = −1 and the green point $T_{\mathit{\text{st}};{(0,0,1)}^T}^{-1}((u,v,-1))$ is the inverse map of the stereographic projection mapping from (u, v, −1) back to S². In panel (b), the point A is on S², L_A(s) is in T_AS², and R_A,NL_A(s) ∈ T_NS² is the parallel transport of L_A(s) from A to the north pole N.

Let R be a rotation matrix in SO(3) such that R^T = R⁻¹ and det(R) = 1, where det(R) denotes the determinant of R and SO(3) is the set of 3 × 3 rotation matrices. By applying the rotation matrix R to both g₅(x_i,d, β_5d) and μ_0i(β), we have

$$T_{\mathit{\text{st}};R{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\beta }_{5d})}(\mathbf{R}{\mathit{\mu }}_{0i}(\mathit{\beta }))=\mathbf{R}{T}_{\mathit{\text{st}};{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\beta }_{5d})}({\mathit{\mu }}_{0i}(\mathit{\beta })).$$ (2)

We consider a specific rotation matrix for rotating s₁ = (s_1,u, s_1,v, s_1,w)^T ∈ S² to s₂ = (s_2,u, s_2,v, s_2,w)^T ∈ S², denoted by R_s1,s2, such that R_s1,s2s₁ = s₂. We need to calculate $\eta =\text{arccos}({\mathbf{s}}_1^T{\mathbf{s}}_2)=\text{arccos}(s_{1,u}{s}_{2,u}+s_{1,v}{s}_{2,v}+s_{1,w}{s}_{2,w})$ and s₃ = s₁ × s₂/‖s₁ × s₂‖ = (s_3,u, s_3,v, s_3,w)^T, where s₁ × s₂ = (s_1,vs_2,w − s_1,ws_2,v, s_1,ws_2,u − s_1,us_2,w, s_1,us_2,v − s_1,vs_2,u)^T and ‖·‖ is the Euclidean norm of a vector. Then, R_s1,s2 is given by

$$\left(\begin{array}{ccc}\hfill s_{3,u}^2{c}_{\eta }+\text{cos}(\eta ),\hfill & \hfill s_{3,u}{s}_{3,\upsilon }{c}_{\eta }-s_{3,w}\text{sin}(\eta ),\hfill & \hfill s_{3,u}{s}_{3,w}{c}_{\eta }+s_{3,\upsilon }\text{sin}(\eta )\hfill \\ \hfill s_{3,u}{s}_{3,\upsilon }{c}_{\eta }+s_{3,w}\text{sin}(\eta ),\hfill & \hfill s_{3,\upsilon }^2{c}_{\eta }+\text{cos}(\eta ),\hfill & \hfill s_{3,\upsilon }{s}_{3,w}{c}_{\eta }-s_{3,u}\text{sin}(\eta )\hfill \\ \hfill s_{3,u}{s}_{3,w}{c}_{\eta }-s_{3,\upsilon }\text{sin}(\eta ),\hfill & \hfill s_{3,\upsilon }{s}_{3,w}{c}_{\eta }+s_{3,u}\text{sin}(\eta ),\hfill & \hfill s_{3,w}^2{c}_{\eta }+\text{cos}(\eta )\hfill \end{array}\right),$$ (3)

where c_η = 1 − cos(η).

The inverse link function μ_0i(β) is explicitly given as follows. By letting R = R_{g5(xi,d,β5d),(0,0,−1)^T} in (2), in which (0, 0,−1)^T is the south pole of S², we have

$$T_{\mathit{\text{st}};{(0,0,-1)}^T}({\mathbf{R}}_{{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\beta }_{5d}),{(0,0,-1)}^T}{\mathit{\mu }}_{0i}(\mathit{\beta }))={\mathbf{R}}_{{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\beta }_{5d}),{(0,0,-1)}^T}{T}_{\mathit{\text{st}};{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\beta }_{5d})}({\mathit{\mu }}_{0i}(\mathit{\beta })).$$ (4)

We assume that

$$T_{\mathit{\text{st}};{(0,0,-1)}^T}({\mathbf{R}}_{{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\beta }_{5d}),{(0,0,-1)}^T}{\mathit{\mu }}_{0i}(\mathit{\beta }))={({\mathbf{x}}_{\mathit{\text{ic}}}^T{\mathit{\beta }}_{5c},-1)}^T,$$ (5)

where β_5c is a q_c × 2 matrix. Let $T_{\mathit{\text{st}};{(0,0,-1)}^T}^{-1}$ be the inverse map of the stereographic projection mapping from the plane with base point (0, 0, −1) back to S² such that

$$T_{\mathit{\text{st}};{(0,0,-1)}^T}^{-1}((u,v,-1))=(\frac{4u}{u^2+v^2+4},\frac{4v}{u^2+v^2+4},\frac{u^2+v^2-4}{u^2+v^2+4}).$$

Please see Fig. 2 (a) for details. Note that R_{g5(xi,d,β5d),(0,0,−1)^T} ∈ SO(3), the inverse link function μ_0i(β) is given by

$${\mathit{\mu }}_{0i}(\mathit{\beta })={\mathbf{R}}_{{(0,0,-1)}^T,{\mathbf{g}}_5({\mathbf{x}}_{i,d},{\beta }_{5d})}{T}_{\mathit{\text{st}};{(0,0,-1)}^T}^{-1}({({\mathbf{x}}_{i,c}^T{\mathit{\beta }}_{5c},-1)}^T).$$ (6)

When β_5c = 0 indicating no continuous covariate effect, μ_0i(β) reduces to g₅(x_i,d, β_5d). Similarly, for the second spoke direction, we introduce β_6d and β_6c as the regression parameters corresponding to x_i,d and x_i,c, respectively, and then we define g₆(x_i,d, β_6d) and μ_1i(β), respectively, as the center associated with the same discrete covariate vector x_i,d and the inverse link function by following (1) and (6). We have discussed various inverse link functions for μ (x_i, β), but these link functions can be misspecified for a given data set. To avoid such misspecification, we may estimate these inverse link functions nonparametrically. It is a topic for future research.

2.2 Intrinsic regression model

Now, we introduce a definition of a residual to ensure that μ_i(β) is the proper conditional mean of m_i given x_i. For instance, in a classical linear model, the response is the sum of the regression function and the residual, and the conditional mean of the response equals the regression function. Given two points m_i and μ_i(β) on the manifold, we need to define the residual or difference between them. At μ_i(β), we have the tangent space of M(1), denoted by T_μi(β)M(1), which is a Euclidean space representing a first order approximation of the manifold M(1) near μ_i(β). We calculate the projection of m_i onto T_μi(β)M(1), denoted by L_μi(β)(m_i), as follows:

$${\mathrm{L}}_{{\mathit{\mu }}_i(\mathit{\beta })}({\mathbf{m}}_i)={({\mathbf{O}}_i-{\mathit{\mu }}_{\mathit{\text{oi}}}(\mathit{\beta }),\text{log}(r_i/{\mu }_{\mathit{\text{ri}}}(\mathit{\beta })),{\mathrm{L}}_{{\mathit{\mu }}_{0i}(\mathit{\beta })}{({\mathbf{s}}_{0i})}^T,{\mathrm{L}}_{{\mathit{\mu }}_{1i}(\mathit{\beta })}{({\mathbf{s}}_{1i})}^T)}^T,$$ (7)

where L_μki(β)(s_ki) = arccos(μ_ki(β)^T s_ki)s̃_ki/‖s̃_ki‖, in which s̃_ki = s_ki − {μ_ki(β)^T s_ki}μ_ki(β) for k = 0, 1. Thus, L_μi(β) (m_i) can be regarded as the residual or difference between m_i and μ_i(β) in T_μi(β)M(1). Geometrically, L_μi(β)(m_i) is associated with the Riemannian Exponential and Logarithm maps on M(1).

We introduce the Riemannian Exponential and Logarithm maps on M(1). Let the tangent vector θ = (θ_o, θ_r, θ_s0, θ_s1)^T ∈ T_mM(1), where θ_o ∈ R³ is the location tangent component, θ_r ∈ R is the radius tangent component, and θ_s0 and θ_s1 ∈ R³ are the two directional tangent components. Let γ_m(t; θ) be the geodesic on M(1) passing through γ_m(0; θ) = m ∈ M(1) in the direction of the tangent vector θ ∈ T_mM(1). The Riemannian Exponential map, denoted by Exp_m(·), maps the tangent vector θ at m to a point m₁ ∈ M(1) and Exp_m(θ) = γ_m(1; θ). The Riemannian Logarithm map, denoted by L_m(m₁), maps m₁ ∈ M(1) onto the tangent vector θ = L_m(m₁) ∈ T_mM(1). The Riemannian Exponential map and Logarithm map are inverses of each other, that is Exp_m(L_m(m₁)) = m₁.

Because a medial representation is the product space of several spaces, the Riemannian Exponential/Logarithm map for M(1) is the product of the Riemannian Exponential/Logarithm maps for each space. Let $\mathbf{m}={({\mathbf{O}}^T,r,{\mathbf{s}}_0^T,{\mathbf{s}}_1^T)}^T\text{ and }{\mathbf{m}}_1={({\mathbf{O}}_1^T,r_1,{\mathbf{s}}_{0,1}^T,{\mathbf{s}}_{1,1}^T)}^T$ be two points in M(1) and θ ∈ T_mM(1). We give the explicit form of the Exponential and Logarithm maps for each space of interest. For the space of locations, Exp_o(θ_o) = O + θ_o, and L_o(O₁) = O₁ − O. For the space of radiuses, Exp_r(θ_r) = r exp(θ_r) and L_r(r₁) = log(r₁/r). For the space S², Exp_s0(θ_s0) = cos(‖θ_s0‖₂)s₀ + sin(‖θ_s0‖₂) θ_s0/‖θ_s0‖₂. Let ${\tilde{\mathbf{s}}}_{0,1}={\mathbf{s}}_{0,1}-({\mathbf{s}}_0^T{\mathbf{s}}_{0,1}){\mathbf{s}}_0\ne 0$. If s₀ and s_0,1 are not antipodal (s₀ ≠ −s_0,1), we can get ${\mathrm{L}}_{{\mathbf{s}}_0}({\mathbf{s}}_{0,1})=\text{arccos}({\mathbf{s}}_0^T{\mathbf{s}}_{0,1}){\tilde{\mathbf{s}}}_{0,1}/{\Vert {\tilde{\mathbf{s}}}_{0,1}\Vert }_2$. Thus, for the space M(1), the Riemannian Exponential and Logarithm maps are, respectively, given by

$${\text{Exp}}_{\mathbf{m}}(\mathit{\theta })={({\mathbf{O}}^T+{\mathit{\theta }}_o^T,r\text{exp}({\theta }_r),{\text{Exp}}_{s_0}{({\mathit{\theta }}_{s_0})}^T,{\text{Exp}}_{s_1}{({\mathit{\theta }}_{s_1})}^T)}^T,$$ (8)

$${\mathrm{L}}_{\mathbf{m}}({\mathbf{m}}_1)={({\mathbf{O}}_1^T-{\mathbf{O}}^T,\text{log}(r_1/r),{\mathrm{L}}_{{\mathbf{s}}_0}{({\mathbf{s}}_{0,1})}^T,{\mathrm{L}}_{{\mathbf{s}}_1}{({\mathbf{s}}_{1,1})}^T)}^T.$$ (9)

Although the L_μi(β)(m_i) ∈ T_μi(β)M(1) are in different tangent spaces, we can use parallel transport to translate them to the same tangent space at an overall base point, denoted by B(β). We choose B(β) = (0, 0, 0, 1, g̅₅(β_5d)^T, g̅₆(β_6d)^T)^T, where g̅₅(β_5d) and g̅₆(β_6d) are the mean directions of g₅(x_i,d, β_5d) and g₆(x_i,d, β_6d) for all possible x_i,d, respectively. We use parallel transport formulated by a rotation matrix,

$$\mathbf{R}({\mathit{\mu }}_i(\mathit{\beta })\Rightarrow \mathbf{B}(\mathit{\beta }))=\text{diag}\{{\mathbf{I}}_3,1,{\mathbf{R}}_{{\mathit{\mu }}_{0i}(\mathit{\beta }),{\overline{\mathbf{g}}}_5({\mathit{\beta }}_{5d})},{\mathbf{R}}_{{\mathit{\mu }}_{1i}(\mathit{\beta }),{\overline{\mathbf{g}}}_6({\mathit{\beta }}_{6d})}\},$$ (10)

to translate L_μi(β)(m_i) ∈ T_μi(β)M(1) into {R(μ_i(β) ⇒ B(β))}L_μi(β)(m_i) ∈ T_B(β)M(1). An illustration of the parallel transport is given in Figure 2 (b). Finally, we define the rotated residual of m_i with respect to μ_i(β) as

$${\mathbf{ℰ}}_i(\mathit{\beta })=\{\mathbf{R}({\mathit{\mu }}_i(\mathit{\beta })\Rightarrow \mathbf{B}(\mathit{\beta }))\}{\mathrm{L}}_{{\mathit{\mu }}_i(\mathit{\beta })}({\mathbf{m}}_i)\text{ for }i=1,\dots ,n.$$ (11)

The ℰ_i(β) are uniquely defined in the same tangent space T_B(β)M(1), which is a Euclidean space.

The intrinsic regression model for medial representations M(1) at an atom is then defined by

$$\begin{array}{cc}E\{{\mathbf{ℰ}}_i(\mathit{\beta })|{\mathbf{x}}_i\}=\mathbf{0},\hfill & E[\{\mathbf{R}({\mathit{\mu }}_i(\mathit{\beta })\Rightarrow \mathbf{B}(\mathit{\beta }))\}{\mathrm{L}}_{{\mathit{\mu }}_i(\mathit{\beta })}({\mathbf{m}}_i)|{\mathbf{x}}_i]=\mathbf{0}\hfill \end{array}$$ (12)

for i = 1, …, n, where the expectation is taken with respect to the conditional distribution of ℰ_i(β) given x_i (Le, 2001). In model (12), the nonparametric component is the distribution of m_i given x_i, which is left unspecified, while the parametric component is the mean function μ_i(β), which is assumed to be known. Moreover, our model (12) does not assume a homogeneous variance across all atoms and subjects. This is also desirable for real applications, because between-subject and between-atom variabilities can be substantial.

At atom d, let ℰ_i(β, d) be {R(μ_i(β, d) ⇒ B(β, d))}L_μi(β,d)(m_i(d)), where μ_i(β, d) is the conditional mean of m_i(d) given x_i. Model (12) leads to an intrinsic regression model for M(1)^K given by

$$E\{{\mathbf{ℰ}}_i(\mathit{\beta },d)|{\mathbf{x}}_i\}=\mathbf{0}$$ (13)

for all d ∈ 𝒟 and i = 1, …, n. As a comparison, consider a multivariate regression model Y_i = X_iβ + ε_i and E(ε_i | x_i) = E(Y_i − X_iβ | x_i) = 0, where Y_i is a p_y × 1 vector and X_i is a p_y × p design matrix depending on x_i. It is clear that ℰ_i(β, d) is closely related to ε_i = Y_i − X_iβ in the multivariate regression model and thus the intrinsic regression model (13) for M(1)^K can be regarded as a generalization of a standard multivariate regression.

The key advantage of translating tangent vectors on different tangent spaces to the same tangent space is that we can directly apply most multivariate analysis techniques in Euclidean space to the analysis of ℰ_i(β) (Anderson, 2003). By using parallel transport to obtain ℰ_i(β), we can explicitly account for correlation structure among ℰ_i(β) and then construct a set of estimation equations to calculate a more efficient parameter estimate. Please refer to the next section for details.

2.3 Two-stage estimation procedure

We propose a two-stage estimation procedure for computing parameter estimates for the semi-parametric medial representation regression model (12) as follows.

Stage 1 is to calculate an intrinsic least squares estimate of the parameter β, denoted by β̂_I, by minimizing the square of the geodesic distance,

$${\widehat{\mathit{\beta }}}_I={\text{argmin}}_{\mathit{\beta }}{D}_n(\mathit{\beta })={\text{argmin}}_{\mathit{\beta }}{\displaystyle \sum _{i=1}^n}{D}_{n,i}(\mathit{\beta })={\text{argmin}}_{\mathit{\beta }}{\displaystyle \sum _{i=1}^n}\text{dist}{\{{\mathbf{m}}_i,{\mathit{\mu }}_i(\mathit{\beta })\}}^2,$$ (14)

where D_n,i(β) = dist{m_i, μ_i(β)}² and dist{m_i, μ_i(β)} is the shortest distance between m_i and μ_i(β) on M(1). Since D_n(β) can be written as the sum of four terms: $D_n^{(1)}(\mathit{\beta })={\displaystyle {\sum }_{i=1}^n}{\{{\mathbf{O}}_i-{\mathit{\mu }}_{\mathit{\text{oi}}}(\mathit{\beta })\}}^T\{{\mathbf{O}}_i-{\mathit{\mu }}_{\mathit{\text{oi}}}(\mathit{\beta })\},D_n^{(2)}(\mathit{\beta })={\displaystyle {\sum }_{i=1}^n}{[\text{log}(r_i)-\text{log}\{{\mu }_{\mathit{\text{ri}}}(\mathit{\beta })\}]}^2,D_n^{(3)}(\mathit{\beta })={\displaystyle {\sum }_{i=1}^n}{[\text{arccos}\{{\mathbf{s}}_{0i}^T{\mathit{\mu }}_{0i}(\mathit{\beta })\}]}^2\text{ and }{D}_n^{(4)}(\mathit{\beta })={\displaystyle {\sum }_{i=1}^n}{[\text{arccos}\{{\mathbf{s}}_{1i}^T{\mathit{\mu }}_{1i}(\mathit{\beta })\}]}^2$, we can minimize $D_n^{(k)}(\mathit{\beta })$ for k = 1, 2, 3, 4 independently when they do not share any common parameters.

Computationally, we develop an annealing evolutionary stochastic approximation Monte Carlo algorithm (Liang, 2011) for obtaining β̂_I, whose details can be found in the supplementary report. Moreover, according to our experience, the traditional optimization methods including the quasi-Newton method do not perform well for optimizing D_n(β) and strongly depend on the starting value of β. When μ_i(β) takes a relatively complicated form, D_n(β) is generally not concave and can have multiple local modes. For instance, since μ_1i(β) is a nonlinear function of β and $D_n^{(4)}(\mathit{\beta })$ may not be a concave function of β over ℬ, our prior experiences have shown that the quasi-Newton method for optimizing $D_n^{(4)}(\mathit{\beta })$ can easily converge to local minima.

The estimate β̂_I is closely associated with the intrinsic mean (Bhattacharya and Patrangenaru, 2005) and does not involve the concept of parallel transport. If we replace |arccos(s)|² by 1 − s in $D_n^{(3)}(\mathit{\beta })\text{ and }{D}_n^{(4)}(\mathit{\beta })$, then our fitting procedure in Stage 1 is effectively a maximum likelihood estimation for a model with the Fisher-distributed errors on the sphere and thus β̂_I is an extrinsic estimate. It will be shown in Theorem 1 below that β̂_I is a consistent estimate, but β̂_I is not efficient, since it does not account for the correlation among the different components of medial representations.

Stage 2 is to calculate a more efficient estimator of β, denoted by β̂_E, which is a solution of

$${\displaystyle \sum _{i=1}^n}{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}{\mathbf{ℰ}}_i(\mathit{\beta })=\mathbf{0},$$ (15)

where ĥ_E(x_i) = ∂_βμ_i(β̂_I){R(μ_i(β̂_I) ⇒ B(β̂_I))}⁻¹ = ∂_βμ_i(β̂_I){R(B(β̂_I) ⇒ μ_i(β̂_I))}, $\mathbf{V}(\mathit{\beta })={\displaystyle {\sum }_{i=1}^n}{\mathbf{ℰ}}_i(\mathit{\beta }){\mathbf{ℰ}}_i{(\mathit{\beta })}^T/n$, and V̂ = V(β̂_I).

The equation (15) in Stage 2 is invariant to the rotation matrix R(B(β) ⇒ P₀), where P₀ = (0, 0, 0, 1, 0, 0, 1, 0, 0, 1)^T representing the center at the origin (0, 0, 0)^T, the unit radius r = 1, and the two spoke directions pointing towards the north pole (0, 0, 1)^T. Specifically, we can use the rotation matrix R(B(β) ⇒ P₀) to rotate ℰ_i(β) to {R(B(β) ⇒ P₀)}ℰ_i(β) for all i. Correspondingly, ĥ_E(x_i) and V⁻¹ are, respectively, changed to ĥ_E(x_i){R(B(β) ⇒ P₀)}^T and {R(B(β) ⇒ P₀)}V⁻¹{R(B(β) ⇒ P₀)}^T. Thus, after applying the rotation R(B(β) ⇒ P₀), we can show that ĥ_E(x_i)V⁻¹ℰ_i(β) equals

$${\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\{\mathbf{R}(\mathbf{B}(\mathit{\beta })\Rightarrow {\mathbf{P}}_0)\}}^T\{\mathbf{R}(\mathbf{B}(\mathit{\beta })\Rightarrow {\mathbf{P}}_0)\}{\mathbf{V}}^{-1}{\{\mathbf{R}(\mathbf{B}(\mathit{\beta })\Rightarrow {\mathbf{P}}_0)\}}^T\{\mathbf{R}(\mathbf{B}(\mathit{\beta })\Rightarrow {\mathbf{P}}_0)\}{\mathbf{ℰ}}_i(\mathit{\beta }),$$

which is independent of R(B(β) ⇒ P₀).

Model (12) is a conditional mean model (Chamberlain, 1987; Newey, 1993). The conditional mean model implies that E{h(x_i)ℰ_i(β)} = E[h(x_i)E{ℰ_i(β) | x_i}] = 0 for any vector function h(·), which may depend on β. After some algebraic calculations, it can be shown that calculating β̂_I is equivalent to solving ${\partial }_{\mathit{\beta }}{D}_n(\mathit{\beta })=-2{\displaystyle {\sum }_{i=1}^n}{\partial }_{\mathit{\beta }}{\mathit{\mu }}_i(\mathit{\beta })\mathbf{R}(\mathbf{B}(\mathit{\beta })\Rightarrow {\mathit{\mu }}_i(\mathit{\beta })){\mathbf{ℰ}}_i(\mathit{\beta })=\mathbf{0},$ that is, h_I(x_i) = ∂_βμ_i(β)R(B(β) ⇒ μ_i(β)). However, it has been shown (Chamberlain, 1987; Newey, 1993) that the optimal function has the form h_opt(x_i, β) = E{∂_βℰ_i(β) | x_i}var{ℰ_i(β) | x_i}⁻¹, which achieves the semiparametric efficiency bound for β. Therefore, h_I(x_i) is not an optimal function and thus the intrinsic least squares estimate in Stage 1 is not an efficient estimator.

Since E{∂_βℰ_i(β) | x_i} and var{ℰ_i(β) | x_i} for each β do not have a simple form, we must estimate them nonparametrically, which leads to a nonparametric estimate of h_opt(x, β), denoted by ĥ_opt(x, β). Although we may solve the estimating equations ${\mathbf{F}}_n(\mathit{\beta })={\displaystyle {\sum }_{i=1}^n}{\widehat{\mathbf{h}}}_{\mathit{\text{opt}}}(x_i,\mathit{\beta }){\mathbf{ℰ}}_i(\mathit{\beta })=\mathbf{0}$ to calculate the efficient estimator of β, it can be computationally challenging to solve F_n(β) since nonparametrically, estimating the 8 × p matrix E{∂_βℰ_i(β) | x_i} and the 8 × 8 inverse matrix of var{ℰ_i(β) | x_i} can be very unstable for a relatively small sample size. Thus, we replace var{ℰ_i(β) | x_i} by var{ℰ_i(β)} and approximate E{∂_βℰ_i(β) | x_i} by ∂_βμ_i(β)R(B(β) ⇒ μ_i(β)). Moreover, in order to avoid calculating ∂_βμ_i(β)R(B(β) ⇒ μ_i(β)) and var{ℰ_i(β)} during each numerical iteration, we calculate them at β̂_I and then construct the objective function ${\displaystyle {\sum }_{i=1}^n}{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}{\mathbf{ℰ}}_i(\mathit{\beta })=\mathbf{0}$ for calculating β̂_E. The two-stage estimation procedure leads to substantial computational efficiency, since solving the complex estimating equations (15) is relatively easy starting from β̂_I. An alternative way is to directly minimize ${\{{\displaystyle {\sum }_{i=1}^n}{\partial }_{\mathit{\beta }}{\mathit{\mu }}_i(\mathit{\beta })\mathbf{R}(\mathbf{B}(\mathit{\beta })\Rightarrow {\mathit{\mu }}_i(\mathit{\beta }))\mathbf{V}{(\mathit{\beta })}^{-1}{\mathbf{ℰ}}_i(\mathit{\beta })\}}^2$, which is much more complex than D_n(β) and thus is computationally difficult.

As a comparison between β̂_E and β̂_I, we consider a multivariate nonlinear regression model Y_i = F(x_i, β) + ε_i with E(ε_i | x_i) = E{Y_i − F(x_i, β) | x_i} = 0 and var(ε_i | x_i) = Σ, where F(x_i, β) is a vector of nonlinear functions of x_i and β. In this case, ℰ_i(β) = ε_i = Y_i − F(x_i, β), ${\widehat{\mathit{\beta }}}_I={\text{argmin}}_{\mathit{\beta }}{\displaystyle {\sum }_{i=1}^n}{\{{\mathbf{Y}}_i-\mathbf{F}({\mathbf{x}}_i,\mathit{\beta })\}}^T\{{\mathbf{Y}}_i-\mathbf{F}({\mathbf{x}}_i,\mathit{\beta })\}$, and ĥ_E(x_i) = ∂_βF(x_i, β̂_I). Then, Σ can be estimated by using $\widehat{\mathbf{V}}={\displaystyle {\sum }_{i=1}^n}\{{\mathbf{Y}}_i-\mathbf{F}({\mathbf{x}}_i,{\widehat{\mathit{\beta }}}_I)\}{\{{\mathbf{Y}}_i-\mathbf{F}({\mathbf{x}}_i,{\widehat{\mathit{\beta }}}_I)\}}^T/n$. Equation (15) reduces to ${\displaystyle {\sum }_{i=1}^n}{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}\{{\mathbf{Y}}_i-\mathbf{F}({\mathbf{x}}_i,\mathit{\beta })\}=\mathbf{0}$, whose solution is just β̂_E. Under mild conditions, it can be shown that compared with β̂_I, β̂_E is a more efficient estimator of β and its asymptotic covariance is given by ${\{{\displaystyle {\sum }_{i=1}^n}{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}{\widehat{\mathbf{h}}}_E{({\mathbf{x}}_i)}^T\}}^{-1}$. In the context of highly concentrated spoke data, our intrinsic regression model reduces to the multivariate nonlinear regression model and similar to the multivariate nonlinear regression model, the two-stage approach can increase statistical efficiency in estimating β.

2.4 Asymptotic properties

We establish consistency and asymptotic normality of β̂_I and β̂_E. The following assumptions are needed to facilitate the technical details, although they are not the weakest possible conditions.

Assumption A1. The data {z_i = (x_i, m_i) : i = 1, …, n} form an independent and identical sequence.

Assumption A2. β_* is an interior point of the compact set ℬ ⊂ R^p and is the unique solution for the model, E {h_E(x)ℰ(β)} = 0, where h_E(x) = ∂_βμ_i(β_*){R(B(β_*) ⇒ μ_i(β_*))}V(β_*)⁻¹. Moreover, β_* is an isolated point of the set of all minimizers of the map D(β) = E[dist{m, μ(x, β)}²] on ℬ, denoted by I_ℬ.

Assumption A3. In an open neighborhood of β_*, μ(x, β) has a second-order continuous derivative with respect to β and ‖L_μ(β)(m)‖, ‖∂_μL_μ(β)(m)‖, ‖∂_βμ(x, β)‖ and $\Vert {\partial }_{\mathit{\beta }}^2\mu (\mathbf{x},\mathit{\beta })\Vert$ are bounded by some integrable function G(z) with E{G(z)²} < ∞.

Assumption A4. In an open neighborhood of β_*, the rank of $E\{{\partial }_{\mathit{\beta }}^2{D}_{n,i}(\mathit{\beta })\}$ is p and E[{∂_βD_n,i(β)}^⊗2] is positive definite, where a^⊗2 = aa^T for a given vector a.

Assumption A1 is needed just for notational simplicity and can be easily modified to accommodate independent and non-identically distributed scenarios. Assumption A2 is an identifiability condition. Assumptions A3 and A4 are standard conditions for ensuring the first order asymptotic properties including consistency and asymptotic normality of M-estimators when the sample size is large (van der Vaart and Wellner, 1996). We obtain the following theorems, whose detailed proofs can be found in the Appendix.

Theorem 1. (a) If assumptions A1, A2, and A3 are true, then β̂_I and β̂_E converge to β_* in probability as n → ∞, where β_* is the solution of (12).

(b) Under assumptions A1–A4, we have

$${[E{\displaystyle \sum _{i=1}^n}\{{\partial }_{\mathit{\beta }}{D}_{n,i}{({\widehat{\mathit{\beta }}}_I)}^{\otimes 2}\}]}^{-1/2}E\{-{\partial }_{\mathit{\beta }}^2{D}_n({\widehat{\mathit{\beta }}}_I)\}({\widehat{\mathit{\beta }}}_I-{\mathit{\beta }}_{*})\to N(\mathbf{0},{\mathbf{I}}_p)$$ (16)

as n → ∞, where I_p is a p × p identity matrix and → denotes convergence in distribution.

(c) Under assumptions A1–A4, we have

$${[{\displaystyle \sum _{i=1}^n}{\{{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}{\mathbf{ℰ}}_i({\widehat{\mathit{\beta }}}_E)\}}^{\otimes 2}]}^{-1/2}\{{\displaystyle \sum _{i=1}^n}{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}{\partial }_{\mathit{\beta }}{\mathbf{ℰ}}_i{({\widehat{\mathit{\beta }}}_E)}^T\}({\widehat{\mathit{\beta }}}_E-{\mathit{\beta }}_{*})\to N(\mathbf{0},{\mathbf{I}}_p)$$ (17)

as n → ∞.

Theorem 1 has several important applications. Theorem 1 (a) establishes the consistency of β̂_E and β̂_I. According to Theorems 1 (b) and (c), we can consistently estimate the covariance matrices of β̂_E and β̂_I. For instance, the covariance matrix of β̂_E, denoted by Σ̂_E, can be approximated by

$${\{{\displaystyle \sum _{i=1}^n}{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}{\partial }_{\mathit{\beta }}{\mathbf{ℰ}}_i{({\widehat{\mathit{\beta }}}_E)}^T\}}^{-1}[{\displaystyle \sum _{i=1}^n}\{{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}{\mathbf{ℰ}}_i{({\widehat{\mathit{\beta }}}_E)\}}^{\otimes 2}]{\{{\displaystyle \sum _{i=1}^n}{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\widehat{\mathbf{V}}}^{-1}{\partial }_{\mathit{\beta }}{\mathbf{ℰ}}_i{({\widehat{\mathit{\beta }}}_E)}^T\}}^{-T}.$$ (18)

Moreover, we can use Theorem 1 (c) to construct confidence cones of β̂_E and its functions. Since Theorem 1 only establishes the asymptotic properties of β̂_E when the sample size is large, these properties may be inadequate to characterize the finite sample behavior of β̂_E for relatively small samples. In the case of small samples, we may have to resort to higher order approximations, such as saddlepoint approximations and bootstrap methods (Butler, 2007; Davison and Hinkley, 1997).

Our choices of which hypotheses to test are motivated by scientific questions, which involve a comparison of medial representation components across diagnostic groups. These questions usually can be formulated as testing linear hypotheses of β as follows:

$$\begin{array}{ccc}{H}_0:\mathbf{A}\mathit{\beta }={\mathbf{b}}_0\hfill & \text{vs}.\hfill & H_1:\mathbf{A}\mathit{\beta }\ne {\mathbf{b}}_0,\hfill \end{array}$$ (19)

where A is an r × p matrix of full row rank and b₀ is an r × 1 specified vector. We test the null hypothesis H₀ : Aβ = b₀ using a Wald test statistic W_n defined by

$$W_n={(\mathbf{A}{\widehat{\mathit{\beta }}}_E-{\mathbf{b}}_0)}^T{(\mathbf{A}{\widehat{\mathbf{\Sigma }}}_E{\mathbf{A}}^T)}^{-1}(\mathbf{A}{\widehat{\mathit{\beta }}}_E-{\mathbf{b}}_0).$$ (20)

We are led to the following theorem.

Theorem 2. If the assumptions A1–A4 are true, then the statistic W_n is asymptotically distributed as χ²(r), a chi-square distribution with r degrees of freedom, under the null hypothesis H₀.

An asymptotically valid test can be obtained by comparing sample values of the test statistic with the critical value of a χ²(r) distribution at a pre-specified significance level α. However, for a small sample size n, we observed relatively low precision of the chi-square approximation. Instead, we calibrate W_n with a critical value of $F_{r,n-r}^{1-\alpha }r(n-1)/(n-r)$, which leads to a slightly higher precision of the F approximation, where $F_{r,n-r}^{1-\alpha }$ is the upper α-percentile of the F_r,n−r distribution. That is, we reject H₀ if $W_n\ge F_{r,n-r}^{1-\alpha }r(n-1)/(n-r)$, and do not reject H₀ otherwise. The reason that the F approximation outperforms the chi-square approximation is due to the fact that the F approximation explicitly accounts for sample uncertainty in estimating the covariance matrix of Aβ̂_E.

3 Simulation studies and real data

3.1 Double directional data with covariates

We generated double directional responses as follows:

$$\begin{array}{cc}{\mathbf{R}}_{{\mathit{\mu }}_{0i}(\mathit{\beta }),{(0,0,-1)}^T}{\mathrm{L}}_{{\mathit{\mu }}_{0i}(\mathit{\beta })}({\mathbf{s}}_{0i})={\mathbf{ℰ}}_{0i},\hfill & {\mathbf{R}}_{{\mathit{\mu }}_{1i}(\mathit{\beta }),{(0,0,-1)}^T}{\mathrm{L}}_{{\mathit{\mu }}_{1i}(\mathit{\beta })}({\mathbf{s}}_{1i})={\mathbf{ℰ}}_{1i},\hfill \end{array}$$

where μ_0i(β) and μ_1i(β) were set according to (6), in which x_i,d’s were fixed at 1 and x_i,c’s were independently simulated from a N(0, 1) distribution. It is assumed that both μ_0i(β) and μ_1i(β) were, respectively, centered around g₅(x_i,d, β_5d) = (u₀, v₀, w₀)^T and g₆(x_i,d, β_6d) = (u₁, v₁, w₁)^T according to (1) such that

$$\frac{u_0}{1-w_0}={\beta }_{5d,1}=1.2,\frac{v_0}{1-w_0}={\beta }_{5d,2}=1.2,\frac{u_1}{1-w_1}={\beta }_{6d,1}=0.8,\text{and }\frac{v_1}{1-w_1}={\beta }_{6d,2}=0.8.$$

In addition, we imposed two constraints as follows:

$${\mathit{\beta }}_{5c}={({\beta }_{5c,1},{\beta }_{5c,2})}^T={\mathit{\beta }}_{6c}={({\beta }_{6c,1},{\beta }_{6c,2})}^T={(1,1)}^T.$$

We generated the errors ℰ_0i and ℰ_1i in T_(0,0,−1)(S²) from a 4-dimensional normal distribution, N(0, 0.5Σ) with Σ being specified as

$$\mathbf{\Sigma }=\left(\begin{array}{cc}\hfill {\mathbf{\Sigma }}_0\hfill & \hfill {\mathbf{\Sigma }}_{01}\hfill \\ \hfill {\mathbf{\Sigma }}_{01}\hfill & \hfill {\mathbf{\Sigma }}_1\hfill \end{array}\right),{\mathbf{\Sigma }}_0={\mathbf{\Sigma }}_1=\left(\begin{array}{cc}\hfill 1\hfill & \hfill {\rho }_1\hfill \\ \hfill {\rho }_1\hfill & \hfill 1\hfill \end{array}\right),{\mathbf{\Sigma }}_{01}={\rho }_2\left(\begin{array}{cc}\hfill 1\hfill & \hfill {\rho }_1\hfill \\ \hfill {\rho }_1\hfill & \hfill 1\hfill \end{array}\right).$$

Subsequently, we rotated ℰ_0i onto the tangent space T_μ0i(β) (S²) and ℰ_1i onto the tangent space T_μ1i(μ)(S²), and then we used the Exp map defined in the supplementary report to obtain the responses s_0i and s_1i. We set n = 40, 80, and 120, ρ₁ = ρ₂ = 0.5, and then we simulated 2000 datasets for each case to compare the biases and the root-mean-square error of the two estimates: β̂_I and β̂_E. As seen in Table 1, β̂_E has smaller root-mean-square error than β̂_I for every component of β, but some components of β̂_E can be more biased.

Table 1.

Bias (×10⁻³) and MS (×10⁻²) of β̂_I and β̂_E for double directional case. Bias denotes the bias of the mean of the estimates; MS denotes the root-mean-square error. For each parameter, the first row is for β̂_I and the second is for β̂_E. Moreover, the constraints β_5c,1 = β_6c,1 and β_5c,2 = β_6c,2 are imposed.

	n = 40		n = 80		n = 120
	Bias	MS	Bias	MS	Bias	MS
β5d,1 = 1.2	3.15	13.26	4.35	10.04	4.22	7.75
	3.40	13.10	4.36	9.82	3.98	7.60
β5c,1 = β6c,1 = 1	9.29	19.19	1.74	12.76	7.43	10.31
	8.93	18.02	0.89	12.09	7.27	9.81
β5d,2 = 1.2	9.44	13.69	2.05	10.19	0.86	7.80
	9.81	13.29	0.88	9.59	0.43	7.69
β5c,2 = β6c,2 = 1	6.90	18.55	5.00	13.08	0.64	10.53
	6.74	17.50	5.67	12.44	0.62	9.99
β6d,1 = 0.8	5.18	16.85	3.23	9.74	2.49	7.93
	5.69	12.91	3.10	9.65	2.69	7.76
β6d,2 = 0.8	2.34	14.84	1.31	9.78	0.86	8.47
	1.32	13.06	0.98	9.71	0.91	8.07

We also calculated the mean of the estimated standard error estimates and the relative efficiencies for all the components in β̂_E and evaluated the finite sample performance of the Wald statistic W_n for hypothesis testing. The results are quite similar to those from the single directional case in the supplementary file, so we did not present them here to preserve space.

3.2 Schizophrenia study of the hippocampus

We consider a neuroimaging dataset about the medial representation shape of the hippocampus structure in the left and right brain hemisphere in schizophrenia patients and healthy controls, collected at 14 academic medical centers in North America and western Europe. The hippocampus, a gray matter structure in the limbic system, is involved in processes of motivation and emotions, and plays a central role in the formation of memory.

In this study, 238 first-episode schizophrenia patients (53 female, 185 male; mean/standard deviation age, female 25.1/5.69 years; male 23.6/4.55 years) were enrolled who met the following criteria: age 16 to 40 years; onset of psychiatric symptoms before age 35; diagnosis of schizophrenia, schizophreniform, or schizoaffective disorder according to DSM-IV criteria; and various treatment and substance dependence conditions. 56 healthy control subjects (18 female, 38 male; mean/standard deviation age, female 24.8/3.30 years; male 25.3/4.21 years) were also enrolled. Neurocognitive and magnetic resonance imaging (MRI) assessments were performed at the first visit time.

The brain MRI data were first aligned to the Montreal Neurological Institute (MNI) space. Hippocampi were segmented in the MNI space and then their medial representations were reconstructed from those binary segmentations (Styner et al., 2004). Subsequently, these hippocampus medial representations were realigned by using a rigid body variation of the standard Procrustes method. The resulting alignment leads to a shape representation that is invariant to translation and rotation, but not to scale. Scaling information is retained for studying changes in overall size or volume.

The aim of our study was to investigate the difference of medial representation shape between schizophrenia patients and healthy controls while controlling for other factors, such as gender and age. The response of interest was the hippocampus medial representation shape at the 24 medial atoms of the left and right brain hemisphere (Figure 1). Covariates of interest were Whole Brain Volume (WBV), race including Caucasian, African American and others, age in years, gender, and diagnostic status including patient and control.

The covariate vector is x_i = (1, gender_i, age_i, diag_i, race1_i, race2_i, WBV_i)^T, where diag is the dummy variable for patients versus healthy controls, and race1 and race2 are, respectively, dummy variables for Caucasians and African Americans versus other races. For the location component on the medial representation, we set μ_O(x, β) = (x^T β₁, x^T β₂, x^T β₃)^T, where β_k (k = 1, 2, 3) are 7 × 1 coefficient vectors. For the radius component on the medial representation, we set μ_r(x, β) = exp(x^T β₄), where β₄ is a 7 × 1 coefficient vector. For the directional components on the medial representation, we used μ₀(x_i, β) as defined in (6), in which x_i,d = (gender_i, diag_i, race1_i, race2_i)^T, x_i,c = (age_i, WBV_i)^T, ${\mathit{\beta }}_5={({\mathit{\beta }}_{5d}^T,{\mathit{\beta }}_{5c}^T)}^T$ for s₀ and ${\mathit{\beta }}_6={({\mathit{\beta }}_{6d}^T,{\mathit{\beta }}_{6c}^T)}^T$ for s₁. Therefore, we have the coefficient vector $\mathit{\beta }={({\mathit{\beta }}_1^T,{\mathit{\beta }}_2^T,{\mathit{\beta }}_3^T,{\mathit{\beta }}_4^T,{\mathit{\beta }}_5^T,{\mathit{\beta }}_6^T)}^T$. Then we used the two-stage estimation procedure to obtain estimates of β and conducted hypothesis testing using Wald statistics. Since the primary goal of the study is to investigate the difference of medial representation shape between schizophrenia patients and healthy controls, we paid special attention to the terms in β associated with diagnostic status.

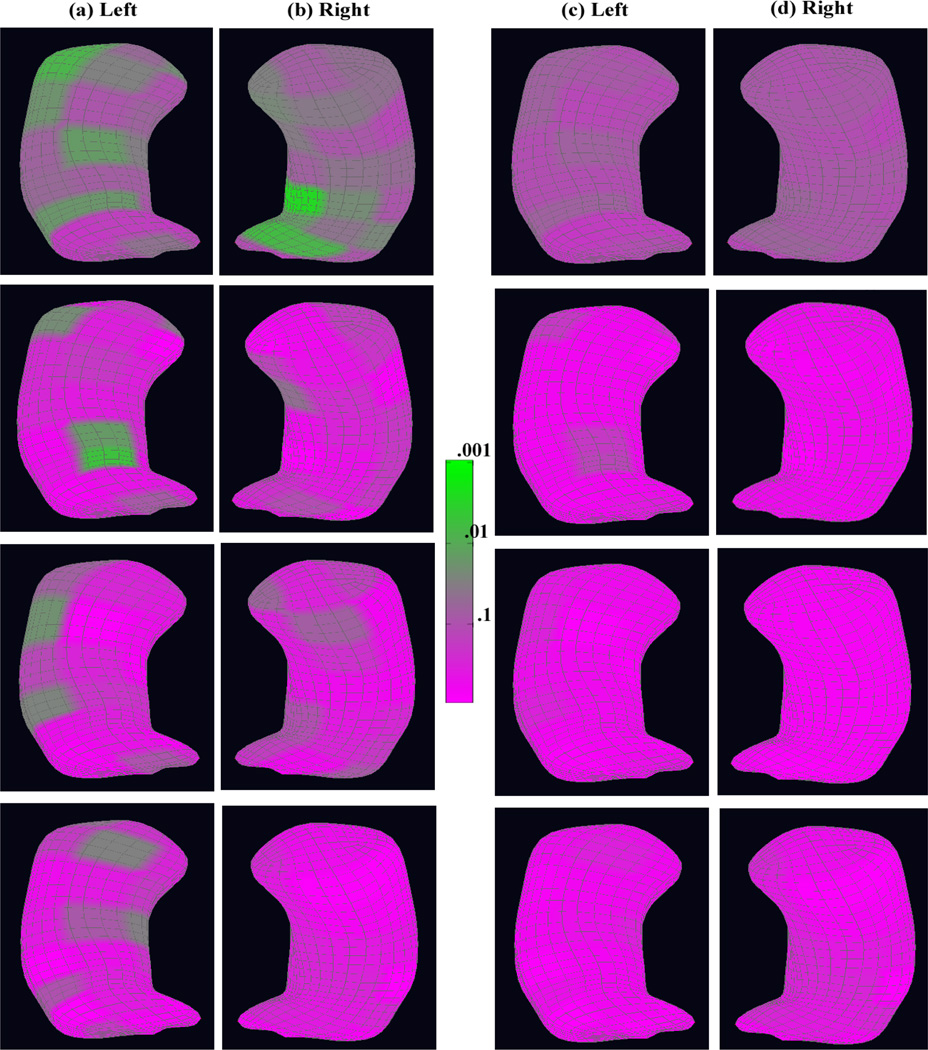
First, we examined the overall diagnostic status effect on the whole medial representation structure. The p-values of the diagnostic status effects across the atoms of both the left and right reference hippocampi are shown in the first row (a) and (b) of Figure 3. The false discovery rate approach (Benjamini and Hochberg, 1995) was used to correct for multiple comparisons, and the corresponding adjusted p-values are shown in the first row (c) and (d) of Figure 3. There was a large significant area in the left hippocampus and also some in the right hippocampus. The significance area remains almost the same after correcting for multiple comparisons, but with an attenuated significance level.

Figure 3.

The coded p–value maps of the diagnostic status effects from the schizophrenia study of the hippocampus: rows 1, 2, 3, and 4 are for the whole medial representation structure, radius, location, and two directions, respectively: at each row, the uncorrected p–value maps for (a) the left hippocampus and (b) the right hippocampus; the corrected p–value maps for (c) the left hippocampus and (d) the right hippocampus after correcting for multiple comparisons.

We also examined each component on the medial representation separately. For the radius component of the medial representation, we presented the p-values of the diagnostic status effects across the atoms in the second row (a) and (b) of Figure 3 and the adjusted p-values in the second row (c) and (d). Before correcting for multiple comparisons, we observed a significant diagnostic status difference in the medial representation thickness at the central atoms near the posterior side in the left hippocampus and in some areas in the right hippocampus, whereas we did not observe much of a significant diagnostic status effect after correcting for multiple comparisons.

For the location component of the medial representation, we showed the p-values of the diagnostic status effects in the third row (a) and (b) of Figure 3 and the corresponding adjusted p-values in the third row (c) and (d). We observed significant diagnostic status differences mainly located around the anterior and lateral side of the left hippocampus though with clearly reduced significance after correcting for multiple comparisons. Similar lateral results have also been observed by Narr et al. (2004).

Similarly, for the two spoke directions on the medial representation, the p-values of the diagnostic status effects are shown in the last row (a) and (b) of Figure 3 and the corresponding adjusted p-values are shown in the last row (c) and (d). Before correcting for multiple comparisons, there was some significant area around the anterior, posterior, and the medial side of the left hippocampus, but not much in the right hippocampus. There was still some significance for the diagnostic status effect around the same areas in the left hippocampus after correcting for multiple comparisons, but nothing in the right hippocampus. The posterior orientation effect of hippocampal differences in schizophrenia has also been shown by Styner et al. (2004) and basically constitutes a local bending change in that region. The anterior effect is novel and located at the intersection of the hippocampal Cornu Ammonis 1 and Cornu Ammonis 2 regions.

We also examined the overall age effect on the whole medial representation structure. The color-coded p-values of the age effect across the atoms of both the left and right reference hippocampi are shown in the first row (a) and (b) of Figure 4. The false discovery rate approach was used to correct for multiple comparisons, and the corresponding adjusted p-values are shown in the first row (c) and (d) of Figure 4. There was a large significant area in the right hippocampus and also some in the left hippocampus. The significance area remains almost the same after correcting for multiple comparisons, but with an attenuated significance level.

Figure 4.

The color-coded p–value maps of the age effect from the schizophrenia study of the hippocampus: row 1, 2, 3, and 4 are for the whole medial representation structure, radius, location, and two directions, respectively: at each row, the uncorrected p–value maps for (a) the left hippocampus and (b) the right hippocampus; the corrected p–value maps for (c) the left hippocampus and (d) the right hippocampus after correcting for multiple comparisons.

Additionally, we looked at each component on the medial representation separately. For the radius component of the medial representation, the color-coded p-values of the age effect across the atoms are shown in the second row (a) and (b) of Figure 4 and the adjusted p-values are shown in the second row (c) and (d). Before correcting for multiple comparisons, there was a small age effect in the medial representation thickness at the central atoms near the posterior side in the left hippocampus and in some areas in the right hippocampus. However, there was not much of a significant diagnostic status effect after correcting for multiple comparisons.

For the location component of the medial representation, the color-coded p-values of the age effect are shown in the third row (a) and (b) of Figure 4 and the corresponding adjusted p-values are shown in the third row (c) and (d). Significant age effects were mainly located around the anterior and lateral side of the left hippocampus though with clearly reduced significance after correcting for multiple comparisons.

For the two spoke directions on the medial representation, we showed the color-coded p-values of the age effect in the last row (a) and (b) of Figure 4 and the corresponding adjusted p-values are in the last row (c) and (d). Even after correcting for multiple comparisons, we observed significant areas around the anterior, posterior, and the medial side of the right hippocampus and some areas in the left hippocampus.

Finally, following suggestions from a reviewer, we examined the overall diagnostic status effect without accounting for other factors. The p-values of the diagnostic status effects are shown in Figure 5. Inspecting Figure 5 reveals a small significant area in the left and right hippocampi before and after correcting for multiple comparisons. Comparing with Figure 3, we feel that such attenuation in Figure 5 may be caused by omitting other factors such as age that are believed to be associated with the variability of the medial representation of subcortical structures.

Figure 5.

The coded p–value maps of the diagnostic status effects without accounting for other factors from the schizophrenia study of the hippocampus: rows 1, 2, 3, and 4 are for the whole medial representation structure, radius, location, and two directions, respectively: at each row, the uncorrected p–value maps for (a) the left hippocampus and (b) the right hippocampus; the corrected p–value maps for (c) the left hippocampus and (d) the right hippocampus after correcting for multiple comparisons.

4 Discussion

We have proposed a semiparametric model for describing the association between the medial representation of subcortical structures and covariates of interest, such as diagnostic status, age and gender. We have developed a two-stage estimation procedure to calculate the parameter estimates and used Wald statistics to test linear hypotheses of unknown parameters. We have used extensive simulation studies and a real dataset to evaluate the accuracy of our parameter estimates and the finite sample performance of the Wald statistics.

Many issues still merit further research. The two-stage estimation procedure can be easily modified to simultaneously estimate all parameters across all atoms and imposing some structures (e.g., spatial smoothness) on the matrix of regression parameters across all atoms while accounting for the correlations between different components of different atoms. This generalization requires a good estimate of the covariance matrix of ℰ_i(β) across all atoms. We may consider a shrinkage estimator of the covariance matrix of all ℰ_i(β) as a linear combination of the identity matrix and the sample covariance matrix V(β) (Ledoit and Wolf, 2004). Moreover, for the matrix of regression parameters across all atoms, we may consider its sparse low-rank matrix factorization to identify the underlying latent structure among all atoms (Witten, Tibshirani, and Hastie, 2009; Dryden and Mardia, 1998; Fletcher et al., 2004), which will be a topic of our future research. It is interesting to develop Bayesian models for the joint analysis of medial representation data of subcortical structures (Angers and Kim, 2005; Healy and Kim, 1996).

Appendix: Proofs of Theorems 1 and 2

We need the following lemma throughout the proof of Theorems 1 and 2.

Lemma 1. (i) Under Assumption A1, if f(z, β) is a vector of continuous functions in β for any β in a compact set ℬ and z, then

$$\underset{\delta \to 0}{\text{lim}}P(\underset{\mathit{\beta },{\mathit{\beta }\prime }_{\in \mathit{ℬ},}{\Vert \mathit{\beta }\prime -\mathit{\beta }\Vert }_2<\delta }{\text{sup}}{\Vert f(\mathbf{z},\mathit{\beta })-f(\mathbf{z},\mathit{\beta }\prime )\Vert }_2>\epsilon )=0{\forall }_{\epsilon }>0.$$ (21)

(ii) In addition to the assumptions in (i), if f(z, β) also satisfies sup_β∈ℬ ‖f(z, β)‖₂ ≤ G₁(z) and E {G₁(z)} < ∞, then

$$\underset{{\mathit{\beta }}_{\in \mathit{ℬ},}{\Vert \mathit{\beta }\prime -\mathit{\beta }\Vert }_2<\delta }{\text{sup}}{\Vert E\{f(\mathbf{z},\mathit{\beta })-f(\mathbf{z},\mathit{\beta }\prime )\}\Vert }_2\to 0\mathit{\text{ as }}\delta \to 0$$ (22)

$$\begin{array}{ccc}\mathit{\text{and\hspace{1em}}}\hfill & \frac{1}{n}{\displaystyle \sum _{i=1}^n}[f({\mathbf{z}}_i,\mathit{\beta })-E\{f({\mathbf{z}}_i,\mathit{\beta })\}]\hfill & \mathit{\text{\hspace{1em}\hspace{1em}is stochastically equicontinuous on }}\mathit{ℬ}.\hfill \end{array}$$ (23)

(iii) In addition to the assumptions in (ii), if E {G₁(z)^r} < ∞ for any r > 1, then

$$\underset{{\mathit{\beta }}_{\in \mathit{ℬ}}}{\text{sup}}\Vert \frac{1}{n}{\displaystyle \sum _{i=1}^n}[f({\mathbf{z}}_i,\mathit{\beta })-E\{f({\mathbf{z}}_i,\mathit{\beta })\}]{\Vert }_2\to 0$$ (24)

in probability, as n → ∞.

(iv) In addition to the assumptions in (ii), if $E\left\{{\text{sup}}_{{\mathit{\beta }}_{\in \mathit{ℬ},}{\Vert \mathit{\beta }\prime -\mathit{\beta }\Vert }_2<\delta }{\Vert f(\mathbf{z},\mathit{\beta })-f(\mathbf{z},\mathit{\beta }\prime )\Vert }_2^2\right\}\le C{\delta }^{\psi }$ for any δ > 0 in a neighborhood of 0 and some constants C and ψ, then

$$\begin{array}{cc}\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}[f({\mathbf{z}}_i,\mathit{\beta })-E\{f({\mathbf{z}}_i,\mathit{\beta })\}]\hfill & \mathit{\text{\hspace{1em}\hspace{1em}is stochastically equicontinous on\hspace{1em}}}\mathit{ℬ}.\hfill \end{array}$$ (25)

The assumptions and result (21) of Lemma 1 (i) correspond to Jennrich’s (1969) Theorem 2. The results in Lemma 1 (ii) correspond to Andrews’ (1992) Lemma 3. The results in Lemma 1 (iii) correspond to Andrews’ (1992) Theorem 1. The result in Lemma 1 (iv) is a special case of Andrews’ (1994) Theorems 4 and 5.

Lemma 2. Let E(β, β′) be E {dist(μ(x, β), μ(x, β′))²}. We assume that (i) ℬ is a compact set; (ii) there is a point β ∈ ℬ such that D(β) < ∞ and sup_β′∈ℬ E(β, β′) < ∞; (iii) E(β, β′) is a continuous function in β and β′. Then, I_ℬ is an non-empty compact set.

Proof of Lemma 2. It follows from the triangle inequality that

$$\text{dist}{(\mathbf{m},\mathit{\mu }(\mathbf{x},\mathit{\beta }\prime ))}^2\le \text{dist}{(\mathbf{m},\mathit{\mu }(\mathbf{x},\mathit{\beta }))}^2+\text{dist}{(\mathit{\mu }(\mathbf{x},\mathit{\beta }),\mathit{\mu }(\mathbf{x},\mathit{\beta }\prime ))}^2+2\text{dist}(\mathit{\mu }(\mathbf{x},\mathit{\beta }),\mathit{\mu }(\mathbf{x},\mathit{\beta }\prime ))\text{dist}(\mathbf{m},\mathit{\mu }(\mathbf{x},\mathit{\beta })).$$

Using the Schwarz inequality and the assumptions of Lemma 2, we have

$$D(\mathit{\beta }\prime )\le D(\mathit{\beta })+E(\mathit{\beta },\mathit{\beta }\prime )+2\sqrt{D(\mathit{\beta })E(\mathit{\beta },\mathit{\beta }\prime )}<\mathrm{\infty }$$

for any β′ ∈ ℬ. Thus, D(β) is a real continuous function of β in a compact set, which yields that I_ℬ is an non-empty set. Since ℬ is a compact set, it is trivial that I_ℬ is a compact set.

Proof of Theorem 1. We prove Theorem 1 (a) in two parts. The first part proves weak consistency of β̂_E. We set f(z, β) = dist(m, μ(β))² = ℰ(β)^T ℰ(β). It follows from Assumption A3 that sup_β∈ℬ dist(m, μ(β))² ≤ G(z)². Thus, Lemma 1 (ii) and (iii) yield that sup_β∈ℬ |n⁻¹D_n(β) − D(β)| → 0 in probability and D(β) is continuous in β uniformly over β ∈ Θ. Since I_ℬ is a compact set and β_* is an isolated point, β̂_I is a consistent estimator of β_*. Furthermore, we can show that ${\text{sup}}_{{\mathit{\beta }}_{\in \mathit{ℬ}}}|n^{-1}{\displaystyle {\sum }_{i=1}^n}[{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\mathbf{ℰ}}_i(\mathit{\beta })-E\{{\widehat{\mathbf{h}}}_E({\mathbf{x}}_i){\mathbf{ℰ}}_i(\mathit{\beta })\}]|\to 0$ in probability. Using similar arguments, we can show that β̂_E is also a consistent estimator of β_*. Using the results of Lemma 1, we can show the asymptotic normality of β̂_E and β̂_I under conditions A1–A4 (Andrews, 1999).

Proof of Theorem 2. Using standard arguments, we can easily prove Theorem 2. Specifically, as n → ∞, since it follows from Theorem 1 (ii) that ${\widehat{\mathbf{\Sigma }}}_E^{-1/2}({\widehat{\mathit{\beta }}}_E-{\mathit{\beta }}_{*})\to N(\mathbf{0},{\mathbf{I}}_p),{(A{\widehat{\mathbf{\Sigma }}}_E{A}^T)}^{-1/2}A({\widehat{\mathit{\beta }}}_E-{\mathit{\beta }}_{*})\to N(\mathbf{0},{\mathbf{I}}_r)$, which finishes the proof of Theorem 2.