A Comparison of Logistic Regression, Logic Regression, Classification Tree, and Random Forests to Identify Effective Gene-Gene and Gene-Environmental Interactions

Abstract

Genome wide association studies (GWAS) have identified numerous single nucleotide polymorphisms (SNPs) that are associated with a variety of common human diseases. Due to the weak marginal effect of most disease-associated SNPs, attention has recently turned to evaluating the combined effect of multiple disease-associated SNPs on the risk of disease. Several recent multigenic studies show potential evidence of applying multigenic approaches in association studies of various diseases including lung cancer. But the question remains as to the best methodology to analyze single nucleotide polymorphisms in multiple genes. In this work, we consider four methods—logistic regression, logic regression, classification tree, and random forests—to compare results for identifying important genes or gene-gene and gene-environmental interactions. To evaluate the performance of four methods, the cross-validation misclassification error and areas under the curves are provided. We performed a simulation study and applied them to the data from a large-scale, population-based, case-control study.

Introduction

Genome-wide association studies (GWA) have identified numerous single nucleotide polymorphisms (SNP) that are associated with a variety of common human diseases. For many diseases, multiple disease-associated SNPs have been discovered [Davis et al. 2010; Kathiresan et al. 2009; Meigs et al. 2008; Morrison et al. 2007]. The marginal effect of these disease-associated SNPs, however, is generally quite modest, and so individual disease-associated SNPs are not very useful for predicting the risk of disease. Because of the weak marginal effect of most disease-associated SNPs, attention has recently turned to evaluating the combined effect of multiple disease-associated SNPs on the risk of disease. As knowledge regarding genetic susceptibility to common diseases has increased, interactions among genetic variants, as well as gene-environmental interactions and epigenetic processes, are likely to play a significant role in determining susceptibility to the diseases. In the past, the majority of studies have been single-gene studies, which directly test the effects of only a single nucleotide polymorphism (SNP) in a candidate gene on disease development [Hook et al. 2011; Sobrin et al. 2011; Dong et al., 2008; Jo et al., 2008; Houlston et al., 2004].

More recently, researchers have acknowledged that lung cancer is a multigenic disease that is more likely associated with the combined effects of multiple genes, not a single gene effect. Several recent studies have shown the potential of applying multigenic approaches in association studies of various diseases [Scherer et al. 2011; Heit et al. 2011; Cote et al., 2009; Kathiresan et a. 2008; Schwartz et al. 2007; Gerger et al. 2007; Imyanitov et al. 2004]. The question remains as to the best methodology to analyze SNPs in multiple genes. In this work, we consider four methods - logistic regression [Cote et al., 2009], classification tree [Brieman et al. 1984], random forests [Breiman 2001], and logic regression [Ruczinski et al., 2003] - to compare the results for identifying important genes or gene-gene and gene-environmental interactions. Logistic regression models have been most popularly used in measuring the association between the susceptibility of a disease and genetic and/or environmental risk factors. However, traditional parametric statistical analyses become more difficult and often inefficient for investigating interactions because the number of polymorphisms leads to a dramatic increase in the number of interaction terms requiring a large study population and the need to address multiple comparisons.

To deal with increasing amounts of information from SNPs, nonparametric methods offer a possible alternative. Classification and regression tree methods (CART) are the most commonly used nonparametric methods that require no distributional assumptions. CART uses tree building methods, a form of binary recursive partitioning, and classifies subjects or predicts the outcome by selecting the most important genetic and environmental risk factors available from the study population. This method is becoming more widely used in cancer research [Goel et1 al., 2009; Wang et al., 2007; Toschke et al., 2005; Lemon et al., 2003; Zhang et al. 2000]. Nonetheless, the tree models are highly unstable to small changes in the data, the major drawback of CART analysis. Due to the instability, each tree shows highly varied predictions, and interpretation can be severely affected by the random variability of the data. An alternative to solving the problem of instability is ensemble methods such as bagging, boosting, and random forests. The methods depend on many sets of trees rather than a single tree. In the random forest method, introduced by Breiman, each tree is built based on recursive partitioning, and the prediction is made on the average of an ensemble of trees rather than of a single tree. A growing number of applications of random forests indicate a wide range of application areas in cancer research [Wu et al., 2011; Rizk et al., 2010; Buness et al., 2009; Abrahantes et al., 2008]. A fourth method, logic regression, is an adaptive (generalized) regression methodology to find predictors that are Boolean (logical) combinations of the original predictors. Since Ruczinski [2003] proposed this approach, several studies have applied logic regression methods to identify important SNP interactions [Kooperberg et al., 2006, 2005, 2001; Ruczinski et al., 2004].

The goal of these analyses is to provide a comprehensive comparison among four methods: logistic regression, classification tree method, random forests, and logic regression, and apply these methods to a moderate sized case-control study of lung cancer in women. The statistical analysis of interactions using these four methods is explained in the next section, and then model validation methods are discussed. To investigate advantages and disadvantages of those four methods, we conducted a simulation study involving the interaction effects among binary outcomes representing SNPs and environmental factors. Then we applied the methods to a case-control study to identify important, higher-order, multiplicative interactions for identifying lung cancer risk. The data used in this work came from a population-based study in metropolitan Detroit and were analyzed using four methods. To evaluate the performance of the four methods, we used cross-validation methods and areas under the curves. Finally, we discuss methodological and practical issues encountered when using these methods in a case-control study setting.

Materials and Methods

Statistical Methods for Analysis of Interactions

Assuming that we want to identify important main or interaction effects among genetic and environmental risk factors, when the response variable (Y) is the disease phenotype to be predicted by multiple effects, (X₁, …, X_k), a traditional logistic regression model can be considered. The logistic model including both single factors and two-way interactions terms of genetic and environmental factors is,

$$p=\frac{1}{1+\text{exp}(-({\beta }_0+\sum _{i=1}^p{\beta }_i{X}_i+\sum _{j=1}^{p-1}\sum _{k=2}^p{\beta }_{jk}{X}_j{X}_k))}$$

where p is the probability that disease status = 1 for given values of the predictors. To find the most parsimonious model that explains the data, we performed a model building procedure by using forward selection that included both 7 environmental risk factors (age, BMI, pack-years of cigarette smoking, education, history of obstructive lung disease, family history of lung cancer, and hormone replacement therapy) and 11 candidate genotypes. To assess which single factor and interaction risk factors were important and whether the addition of genotype information into this model would improve the fit, we used the likelihood ratio test to calculate the statistical significance of nested models as new terms were added. Even though a logistic regression model is the most popular model to analyze the association between discrete responses and multiple predictor variables, the traditional logistic models have a few fundamental limitations in multigenic studies. First, when the number of main effects increases, the number of interaction terms shows a dramatic increase, which results in loss of power because of large degrees of freedom. Furthermore, the magnitude of the interaction effect in nonlinear models does not equal the marginal effect of the interaction term, and its statistical significance is not calculated by standard software. Analysis based on subsets of the predictors can be used to improve power because there are fewer degrees of freedom. A tree-based method and logic regression are alternatives to the traditional logistic regression analysis. Tree-based methods [Breiman et al. 1984] employ a multistage decision process that attempts to identify a strong relationship between input values (predictive variables) and target values (response variable).

Unlike the logistic regression, tree-based methods do not assume a prespecified relationship between the response and predictors. A tree-based method generates primarily the classification tree on the predictor variables, which are constructed by recursively partitioning the data into successively more homogeneous subsets with respect to the variables of interest. The most discriminative variable is selected to partition the dataset into subsets, and partitioning is repeated until the nodes are homogeneous enough to be terminal. The output is a tree diagram with the branches determined by the splitting rules and a series of terminal nodes that contain the response frequency. The tree-building process leads to the terminal nodes (or leaves) when the nodes cannot be divided anymore and need to be pruned to avoid overfitting and to increase efficiency. The Gini criterion was used to express the decrease in the node impurity function. The Gini index is one of the most commonly used tree-building criteria with entropy (or information gain) to measure node impurity for categorical target values, especially for the categorical target values. The Gini index measures purity of categorical data, which equals 0 for a pure node. The Gini index can be obtained by $\text{Gini index}=1-\sum _{j=1}^r{P}_j^2$ where P_j is a relative frequency of class j in a node.

The splitting process is repeated on each of the two resulting regions of the previous step and continues until the stopping rule stops the process. This large tree is pruned using cost-complexity pruning. The biggest drawback of a tree method is that they are instable for the small changes in observations. More accurate predictions can be obtained by combining many suitably chosen trees, or tree-based ensembles. Breiman [2001] proposed a random forest that is an ensemble method that fits many classifications of trees resampled by the bootstrap method and then combines the predictions from all the trees. Classification tree approaches use all predictors and all individuals to make a single tree, but random forests make a forest of many trees (ntree), which are based on a random selection of predictors (mtry) and individuals by using the bootstrap resampling method. Thus, random forests are an average of multiple classification trees. Error rates are computed for each observation by using the out-of-bag predictions and then averaged over all observations. Because the out-of-bag observations are not used in fitting the trees, the out-of-bag estimates are essentially cross-validated accuracy estimates. We want the smallest set of SNP-SNP and SNP-environment interactions to achieve good diagnostic ability.

Variable importance finds the most relevant predictors. At each split of each tree, a variable contributed to the importance of the impurity measure. We accumulate the reduction of the impurity measure to find a measure of relative importance of the variables. We permute the predictor values of the OOB sample at every tree; the accumulation of resulting decrease in prediction accuracy over all trees is also a measure of importance. The variable importance of X_j in a tree t is the difference of the number of correct predictions with between-predictor variables including the original variable X_j and predictor variables including the permuted variable X_j^* for the out-of-bag observations. Let i be the subject index, j be the variable index, and B^(t) be the out-of-bag observations for a tree t, with t ∈ {1,…,ntee}.

Then the variable importance of variable X_j in tree t (VI^(t) (X_j)) is

$$V{I}^{(t)}(X_j)=\frac{1}{\left|B^{(t)}\right|}(\sum _{i\in B^{(t)}}I(y_i=y_i^{(t)})-\sum _{i\in B^{(t)}}I(y_i=y_{i,j^{*}}^{(t)}))$$

where ${\stackrel{⌢}{y}}_i^{(t)}$ is the prediction based on the variables including the original variable X_j for observation i, and ${\stackrel{⌢}{y}}_{i,j^{*}}^{(t)}$ is the prediction based on the variables including the permuted variable X_j^* for observation i. Then the variable importance of each variable is computed by averaging over all trees. Thus, the variable importance indicates how much the original association with the response is broken after randomly permuting the predictor X_j. The variable with higher variable importance indicates the more importance among variables used in random forests. Variable importance is used to find the smallest set of predictor variables to achieve good prediction ability [Strobl et al., 2009; Alvarez et al., 2005; Hastie et al. 2001]. Ruczinski [2003] proposed a logic regression that is an adaptive regression methodology that aims to find combinations of binary variables that are highly associated with an outcome. Let X, …, X_k be binary variables, and Y be a response variable.

The logic regression model is of the form,

$$g\{\mathrm{E}(\mathrm{Y}|\mathrm{X})\}={\beta }_0+\sum _{i=1}^p{\beta }_i{L}_i+\sum _{i=1}^q{\beta }_{i+p}{Z}_{i+p}$$

where g(·) is a link function relating the response variable and the related covariates, β_i, i = 0,…, p and β_i+p, i = 1,…, q are regression parameters, Z_i are additional confounders, and L_i is a Boolean expression of the binary predictors X_js. The link function can be a linear regression for continuous outcomes and logit function for binary outcomes. An example of a Boolean expression is X₃ ∧ X₄, which indicates an interaction between two variables of X3 and X4, and [(X₁ ∩ X₂) ∪ (X₃ ∩ X₁₉)], which expresses a combined information of two interactions: X1 and X2, and X3 and X19. Therefore, the logic regression is simply a combination of Boolean expressions. Logic regression uses a “simulated annealing algorithm” to try to find Boolean statements in the regression model that minimize the scoring function associated with the model type, estimating the regression coefficients simultaneously with the Boolean expressions. A score function that reflects the quality of the model is given for each regression model such as the residual sum of squares for linear regression and the binomial deviance for logistic regression. To find the best logic regression model, we need to perform model selection procedure using cross-validation or permutation tests.

Model Validation

Model assessment needs to be performed to validate the effectiveness of the four models that identified important single and combined variable effects, and compare their predictive power. We applied the hold-out method for the cross-validation. For k-fold cross-validation, the data are split into k approximately equal groups (typically 3 to 10). Each of the k subsets of the data is left out in turn, the model is fit for the remaining data, and the results used to predict the outcome for the subset that has been left out. The cross-validation estimate of prediction error, CV(θ), is then calculated:

$$CV(\theta )=\frac{1}{n}\sum _{k=1}^K\sum _{i\in C_k}L(y_i,{\stackrel{⌢}{f}}^{-k}(x_i,\theta ))$$

The notation of x_i = (x_i1, ⋯, x_ip) is a vector of predictors, y_i is a response, C_k is the indices of observations in the k th fold, and L(y_i, f̑^−k (x_i, θ)) is a loss function that measures the error between the observed values, y_i, and the predicted values, f̑^−k (x_i, θ). The predicted values come from the data that removed the k th fold. Prediction error is usually taken as the squared difference between observed and predicted in a regression model, L(y, f̑(x) = (y − f̑(x))², and as 0–1 loss for classification models, L(y, f̑(x)) = 1{y ≠ f̑(x)}.

Once prediction errors are obtained for all k subset groups, the total error is averaged as dividing by the number of groups [Tibshirani et al., 2009; Bouckaert et al., 2008; Efron et al., 1983]. For comparison purpose, areas under the curves (AUC) were computed for all four classifier methods. We used Statistical Analysis Software (SAS; V 9.2, Cary, North Carolina) and the R software (Version 2.12.1, www.r-project.org).

Results

Simulation Study

A simulation study was performed to examine which mining method(s) shows better prediction among the four methods (logistic regression, logic regression, classification tree and random forests). We generated 10 binary predictors and a case-control disease status of 1000 unrelated subjects. Let X₁, X₂, …, X₁₀ be predictors (SNPs or environmental factors) and Y be an outcome. Predictor variables were generated from a Bernoulli distribution with a probability of 0.5 and were randomly associated with the outcome. Therefore, individual predictors were not statistically significant with the outcome. We further considered two interaction terms, X₁ ∩ X₂ and X₃ ∩ X₄, that were highly associated with the outcome for finding better classification performance of the classifiers that are able to correctly identify important interactions. When the interactions are true, the disease status has the probability of 0.8 from a Bernoulli distribution. We considered all single predictors and two-way interactions to find the best logistic model. The multiple logistic approach and stepwise selection procedure identified six single predictors (X₁, X₂, X₃, X₄, X₈, X₁₀) and four interactions (X₁ ∩ X₂, X₁ ∩ X₄, X₂ ∩ X₃, and X₃ ∩ X₄). The best logistic model is

$$\text{log}\left(\frac{P(Y=1)}{P(Y=0)}\right)=-0.88+0.23X_1+0.17X_2+0.20X_3+0.03X_4+1.58X_1{X}_2+1.58X_3{X}_4-0.74X_1{X}_4-0.64X_2{X}_3$$

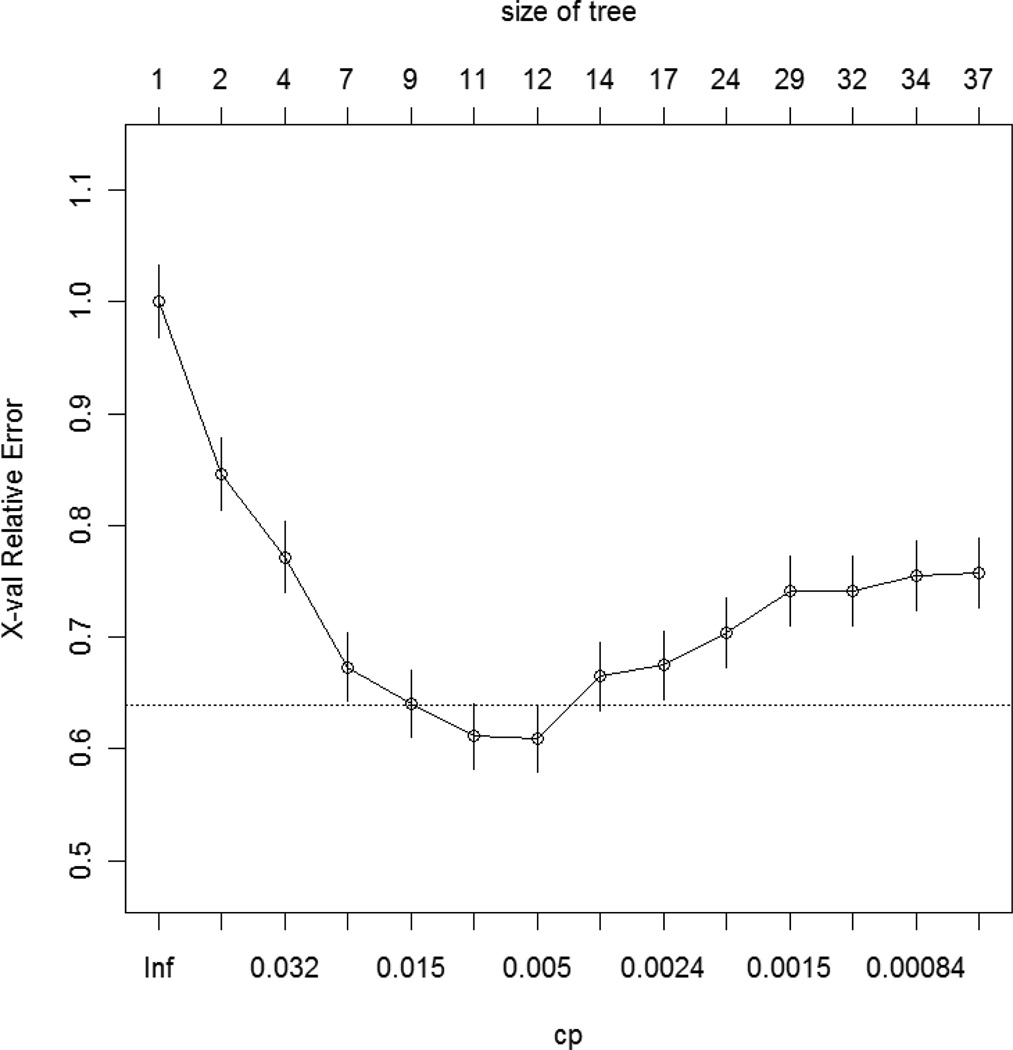
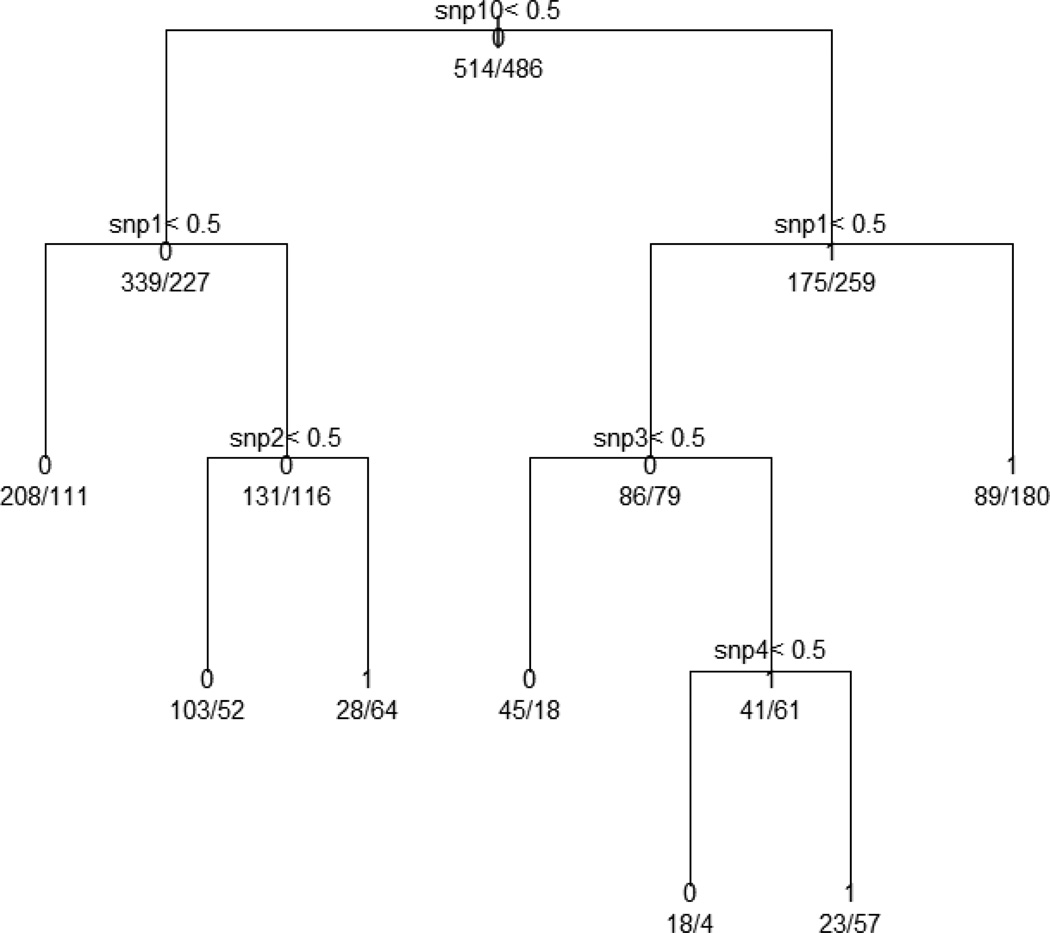
With the above best fit model, we calculated the probabilities that a subject has a disease for given values of the predictors. The optimal decisions are based on the posterior class probabilities P(y|x). For binary classification problems, we can write these decisions as 1 if the logit of the probability that disease status = 1 is greater than 0, and 0 for otherwise. The cross-validation prediction error was 0.3481, and the AUC was 0.6836. The recursive partitioning algorithm was applied to grow the trees while the grown trees were pruned using a cross-validation technique. Once we built the unpruned trees by using the Gini index as a splitting criterion, then we found the complexity parameter to lead to an optimal tree size. The (10-fold) cross-validation error rates were used to prune the tree by using the standard “1 – SE” rule. Based on the rule, we set the threshold complexity parameter to 0.018. Figure 1 is a plot of the relationship between the cost-complexity parameter (cp), cross-validation error (x-val Relative Error), and tree size. Figure 2 is classification tree analysis of the simulated data set including genetic risk factors and environmental factors showing cut-off values for snp10, snp1, snp2, snp3, and snp4.

Figure 1.

A plot of the relationship between the cost-complexity parameter (cp) and cross-validation error (x-val Relative Error), and tree size (size of tree). The dashed horizontal line represents one standard deviation of the minimum cross-validation error.

Figure 2.

Classification tree analysis of simulated data set including genetic risk factors and environmental factorsshowing cut-off values for snp10, snp1, snp2, snp3, and snp4. The target variable is the prevalence and the analysis produces seven terminals. The prevalence in the entire population was 48.6% (486/1000), and the first split is performed on snp10. This produces two subgroups with respective prevalence of 40.1% (227/566) and 59.7% (259/434).We investigated the subgroups with higher prevalence than the entire population. Among seven terminal nodes, only three were higher in prevalence than the entire population: the combination of snp10=1, snp1=0, snp3=1 and snp4=1 shows the highest prevalence (71.3%), the combination of snp10=0, snp1=1 and snp2=1 has the second highest prevalence (69.6%), the combination of snp10=1 and snp1=1 shows 66.9% in prevalence.

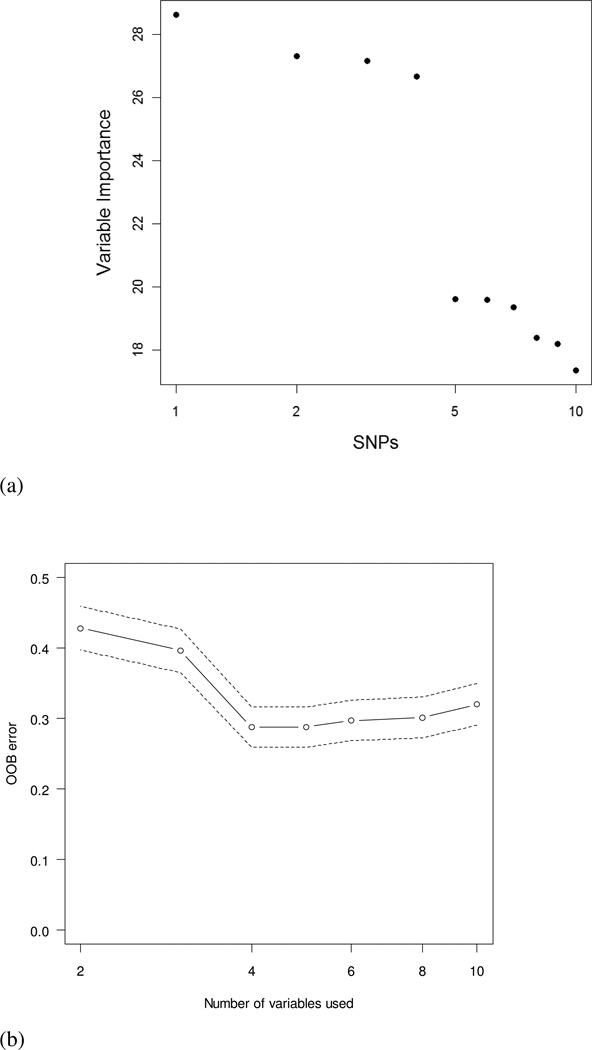
The target variable is the disease rate, and the analysis produces seven terminals. The disease rate in the entire population was 48.6% (486/1000), and the first split is performed on snp10. This produces two subgroups with respective disease rate of 40.1% (227/566) and 59.7% (259/434). We investigated the subgroups with higher disease rate than the entire population. Among seven terminal nodes, only three were higher in disease rate than the entire population: the combination of snp10=1, snp1=0, snp3=1, and snp4=1 shows the highest disease rate (71.3%), the combination of snp10=0, snp1=1, and snp2=1 has the second highest disease rate (69.6%), and the combination of snp10=1 and snp1=1 shows 66.9% in disease rate. The tree method identified two important interactions of snp1 and snp2, and snp3 and snp4 with high disease rate. For this tree model, the cross-validation error is 0.3310, and AUC is 0.6853. The random forests method was performed to find the important variables based on (1) the size of variable importance and (2) out-of-bag error rates. The random forests perfectly identified four important variables of SNP1, SNP2, SNP3, and SNP4. As seen in Figure 3 (a), the importance values for all SNPs were calculated to assess the relevance of each variable over all trees of the ensemble. The plot showed the first four variables were more valuable than the other SNPs because the first four had the higher importance values (SNP1=28.6, SNP2=27.2, SNP3 = 27.3, and SNP4=26.7). The other six SNPs have importance values less than 20. Therefore, the random forests method exactly divides all SNPs into two groups.

Figure 3.

(a) Variable importance plot on all SNPs. The importance values for all SNPs were calculated to assess the relevance of each variable over all trees of the ensemble. The plot showed the first four variables were more valuable than the other SNPs because the first four had the higher importance values; (b) A plot of out-of-bag error rates against the number of variables used. The plot showed that the four variable models had the smallest error rate.

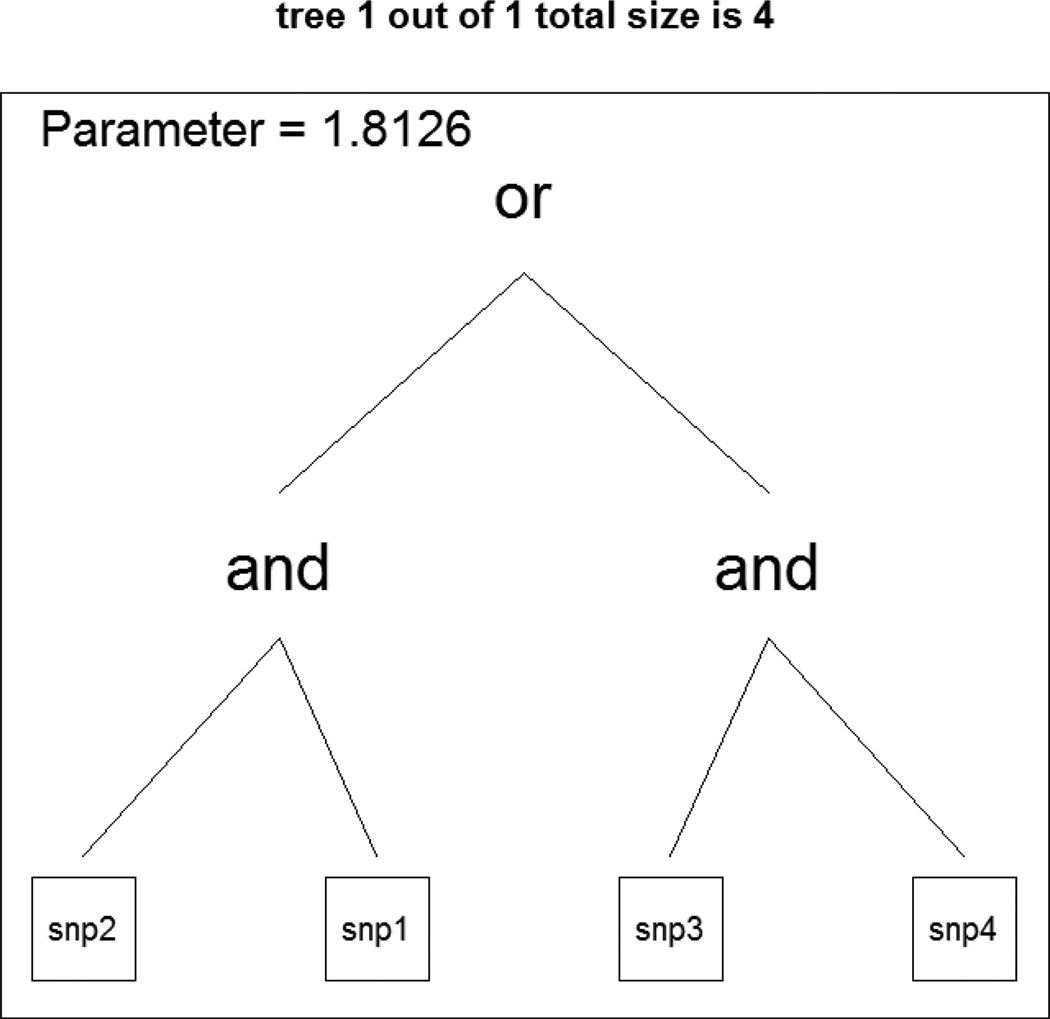
Figure 3 (b) showed that the model including four variables of X₁, X₂, X₃, and X₄ showed minimum out-of-bag error rates of 0.288. The cross-validation error for the random forests method was 0.2224, the smallest among all four methods. The random forests method had the largest area under the curve of 0.8795. The logic regression model was executed to examine the identification ability of important interactions among generated 10 variables. We picked the parameters of simulated annealing with START=2 and END=−1 that found the best annealing parameters in R:{LogReg} package. With those parameters, the acceptance rate was over 90% and no acceptances were after log-temperature of −0.5. The logic regression identified a best model including a Boolean expression of (snp₁ ∩ snp₂) or (snp₃ ∩ snp₄) that minimized the scoring function. Simultaneously, the logic regression estimated the regression coefficients of the logic regression as follows: Y = −0.892 + 1.81L where Y is a disease status and L is a logic expression of (snp₁ ∩ snp₂) or (snp₃ ∩ snp₄). Figure 4 shows the tree of the Boolean expression. The cross-validation error was 0.3220, which was slightly better than the logistic regression and classification tree methods. The area under the curve was 0.7110, which was larger than that for logistic regression and classification tree. Table I summarizes the cross-validation errors and the areas under the curves for all four models. As expected, the random forests method showed best performance with the smallest cross-validation error and the largest AUC, the logic regression showed the second best method, classification tree was third, and the logistic regression showed the worst classification ability.

Figure 4.

This is a logic tree of (snp₁ ∩ snp₂) or (snp₃ ∩ snp₄), and the coefficient of the logic tree is 1.8126.

Table 1.

Resubmission errors, cross-validation errors and area under the curves from simulated data including 10 SNPs and 1000 subjects using four different classifiers of logistic regression, classification trees, random forests, and logic regression.

	Variables identified	Resubmission Error	Cross- validation error	AUC
Logistic Regression	snp1&snp2	0.3350	0.3481	0.6836
	snp1&snp4
	snp2&snp3
	snp2&snp4
	snp3&snp4
Classification Trees	snp1&snp4&snp10	0.3250	0.3257	0.6853
	snp1&snp2
	snp1&snp10
Logic Regression	snp1&snp2	0.2880	0.3220	0.7110
	snp3&snp4
Random Forests	snp1&snp2	0.2200	0.2224	0.8795
	snp3&snp4

Women’s Epidemiology of Lung Cancer Study

Data

The case-control study design and description were described in detail elsewhere [Cote et al. 2009]. In summary, female lung cancer patients aged 18–74 who were diagnosed with nonsmall-cell carcinoma in Wayne, Macomb, and Oakland counties between November 1, 2001, and October 31, 2005, were enrolled through the population-based Metropolitan Detroit Cancer Surveillance System (MDCSS), a participant in the National Cancer Institute’s Surveillance, Epidemiology, and End Results (SEER) program. Control subjects were selected through random telephone dialing and were frequency matched to cases on race and 5-year age group. In total, 1031 women (504 cases and 527 controls) were willing to complete a detailed, in-person interview and to provide DNA samples. Among the 1031 women, the largest subpopulation was white smokers: 177 controls and 339 cases (n=516). Eleven polymorphisms were considered, and all nonbinary polymorphisms were represented by a binary variable coding a dominant effect of these polymorphisms. Supplementary Table I details the distribution of genetic polymorphisms evaluated and the estimated ORs and adjusted ORs for white women who had ever smoked (n=516). Demographic and environmental data were also measured at baseline. The variables included in these analysis were age, pack-years of smoking, use of hormone replacement therapy (ever/never), family history of lung cancer in a first degree relative (yes/no), personal history of chronic obstructive lung disease (yes/no), education completed in years, and body mass index (BMI). For better comparison of logic regression with classification tree, random forests and logistic regression methods, binary variables were created for three continuous variables: body mass index, pack-years of cigarette smoking, and education in years. The results from CART analysis were used as respective cut-off values. Pack-years of cigarette smoking were divided in two with a cut-off of 18.5 packs per year, while body mass index and years of education were dichotomized at 25 and 14.5, respectively. Supplementary Table II shows demographic and environmental characteristics for white women who had ever smoked (N=516).

Results

Two logistic regression, a logic regression and classification tree, and random forests methods were applied to identify a panel of genetic and environmental risk factors that are associated with lung cancer risk. Five models from four methods were developed: (1) a logistic regression model including single factors (no interaction effects, Model 1), (2) a logistic regression model including interaction terms (Model 2), (3) a classification tree model (Model 3), (4) a logic regression model (Model 4), and (5) random forest model (Model 5). The endpoint for all four methods was lung cancer status of study subjects, which had a value 1 for cases and 0 for controls. Predictor variables considered were 11 polymorphisms and 7 environmental risk factors.

Logistic regression

Two logistic regression models were considered to select the best combination of risk factors using a stepwise variable selection procedure to identify important genetic and environmental risk factors associated with lung cancer. Single factors selected by stepwise logistic regression are listed in Table II (denoted by Model 1).

Table 2.

Estimates of main effects for environmental and genetic risk factors from the most parsimonious model, white ever smoking women (Model 1).

	OR (95% CI)	p-value
Age at diagnosis/interview	0.99 (0.98–1.02)	0.8972
Family history of lung cancer	2.49 (1.37–4.51)	0.0026
History of chronic obstructive lung disease	1.93 (1.19–3.12)	0.0068
Pack years of cigarette smoking	1.04 (1.03–1.05)	<0.0001
Body mass index	0.93 (0.90–0.97)	0.0006
XRCC1 A/A genotype	1.91 (1.01–3.60)	0.0474
GSTM1 null	1.38 (0.90–2.12)	0.1402
COMT A/G or G/G genotype	1.13 (0.70–1.82)	0.6197

The factors were family history of lung cancer, history of chronic obstructive lung disease, pack-years of cigarette smoking, and body mass index as environmental risk factors associated with lung cancer and XRCC1 A/A genotype as the genetic risk factor associated with lung cancer. Model 1 revealed significant positive associations between lung cancer and (1) family history of lung cancer (OR=2.49 [1.37–4.51]), (2) history of chronic obstructive lung cancer (OR=2.01 [1.21–3.34]), (3) pack-years of cigarette smoking (OR=1.04 [1.03–1.05]), and (4) XRCC1 A/A genotype (OR=1.91 [1.01–3.60]). There was a negative association between body mass index and lung cancer (OR=0.93 [0.90–0.97]). Two SNPs in addition to XRCC1 A/A were selected in the final model, namely GSTM1 (P=0.14), and COMT A/G or G/G genotype (P=0.62) because the likelihood ratio test showed a better fit when these two variables were added into the final model. Interestingly, education years, history of chronic obstructive lung diseases, and hormone therapy use were not associated with lung cancer status. Model 2 extended Model 1 by incorporating gene-gene, gene-environmental, or environmental-environmental interactions. Table III lists identified single and interaction genetic and environmental factors selected by a logistic stepwise selection method. The selected factors included (1) family history of lung cancer; history of chronic obstructive lung disease; education in years; pack-years of cigarette smoking; body mass index; GSTM1, GSTP1 A/A, or A/G genotype; and XRCC1 A/A genotype as single factors and (2) body mass index and education in years, pack-years of cigarette smoking and education in years, and body mass index and GSTM1 as two-way interaction factors. The −2 log-likelihood criteria for model fitting for both Model 1 and Model 2 were 517.8 and 488.5, respectively. The cross-validation errors are 0.255 for Model 1 and 0.2236 for Model 2 while AUC’s are 0.7948 and 0.8147 respectively.

Table 3.

Estimates of main and interaction effects for environmental and genetic risk factors from the most parsimonious model, white ever smoking women (Model 2)

	OR (95% CI)	p-value
Family history of lung cancer	2.30 (1.24–4.27)	0.0083
History of chronic obstructive lung disease	1.91 (1.12–3.26)	0.0169
Pack years of cigarette smoking	1.02 (1.01–1.04)	<.0001
Body mass index (BMI)	0.71 (0.57–0.89)	0.0032
Education	0.39 (0.23–0.65)	0.0003
GSTM1 null	19.1 (1.91–191)	0.0121
XRCC1 A/A genotype	1.94 (1.01–3.75)	0.0483
GSTP1 A/A or A/G genotype	2.31 (1.15–4.64)	0.0181
BMI and Education	1.02 (1.01–1.04)	0.0051
BMI and GSTM1	0.91 (0.84–0.99)	0.0213
Smoking and Education	1.004 (1.00–1.01)	0.0323

Classification tree method

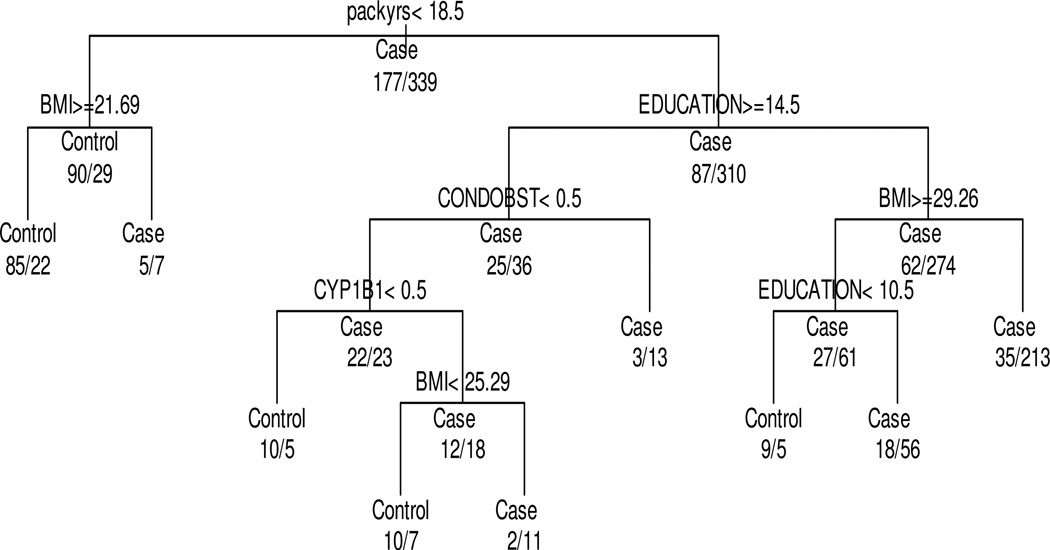
Classification tree method produced nine multiplicative interactions and identified four important multiplicative interactions (Figure 5). The target value was disease rate of lung cancer (number of cases/total number), and the overall disease rate was 65.7% (339/516). We believe that this disease rate was improved with appropriate further partitions, and a primary interest was to find the route that led to best disease rate. The classification tree analysis detected five environmental and genetic risk factors as important predictors associated with lung cancer: pack-years of cigarette, education years, body mass index, history of chronic obstructive lung disease, and CYP1B1 C/C genotype. Cigarette pack-years were the best predictor, and education was the second best predictor for lung cancer. For pack-years, the classification tree analysis yielded a split point (threshold) of 18.5 packs/year. This produced two subgroups with respective lung cancer disease rate of 24% (<18.5 pack-years) and 78% (≥18.5 pack-years). This latter subgroup was further partitioned on the basis of education, and the classification tree analysis yielded a split point (threshold) of 14.5 years of education. The resultant groups had lung cancer rates of 59% (education ≥14.5 years) and 81.5% (education <14.5 years). We verified the results produced by the classification tree method by using logistic regression models. Table IV shows results of multivariable logistic regression analyses for four effective pathways of genetic and environmental factors for lung cancer identification after adjusting for age, BMI, and family history of lung cancer. The P-values of all subgroup combinations except the third combination were statistically significant, indicating that the classification tree method for identifying important multiplicative interactions worked well. The lowest lung cancer disease rate (21%; n=102) was observed among of lighter smoking women (<18.5 pack-years) and BMI >21.3, indicating that, for this subgroup, only 21% of White women who have ever smoked have lung cancer. This result corresponds to a (negative) likelihood ratio of 21%/66% = 0.32, indicating that the lung cancer risk in the entire study population was reduced to one-third among this subgroup. The cross-validation error is 0.2235 and AUC is 0.8159, which are slightly better than Model 2.

Figure 5.

Classification tree analysis of environmental and genetic risk factors for lung cancer showing cut-off values for cigarette packs a year, education years, body mass index, chronic obstructive disease history, and CYP1B1 C/G or G/G genotype. The target variable is the prevalence and the analysis produces nine terminals. The prevalence in the entire population was 65.7% (339/516), and the first split is performed on cigarette packs a year with a split point of 18.5 packs/year. This produces two subgroups with respective prevalence of 24% (29/119) and 78.1% (310/397).

Table 4.

Results of multivariable logistic regression analyses for four important combinations of genetic and environmental risk factors identified by classification tree methodsafter adjusting for age, BMI, family history of lung cancer, pack years of smoking, and obstructive lung disease history

Node	Subgroup	Prevalence in percentage (case/total)	Likelihood ratio over overall average prevalence	p-value using logistic regression models *
1	Packs in years greater than 18.5, education years less than 14.5, body mass index less than 29.26	86%(213/248)	86%/66%=1.30	0.0004
2	Packs in years greater than 18.5, education years greater than 14.5, CONDOBST=0, CYP1B1=1 or 2, body mass index greater than 25.28	85% (11/13)	85%/66%=1.29	0.0079
3	Packs in years greater than 18.5, education years greater than 14.5, CONDOBST=1	81% (13/16)	81%/66%=1.23	0.3238
4	Packs in years greater than 18.5, education years greater than 10.5 and less than 14.5, body mass index greater than 29.26	76% (56/74)	76%/66%=1.15	0.0252

^*adjusted by age, BMI, family history of lung cancer

Logic regression method

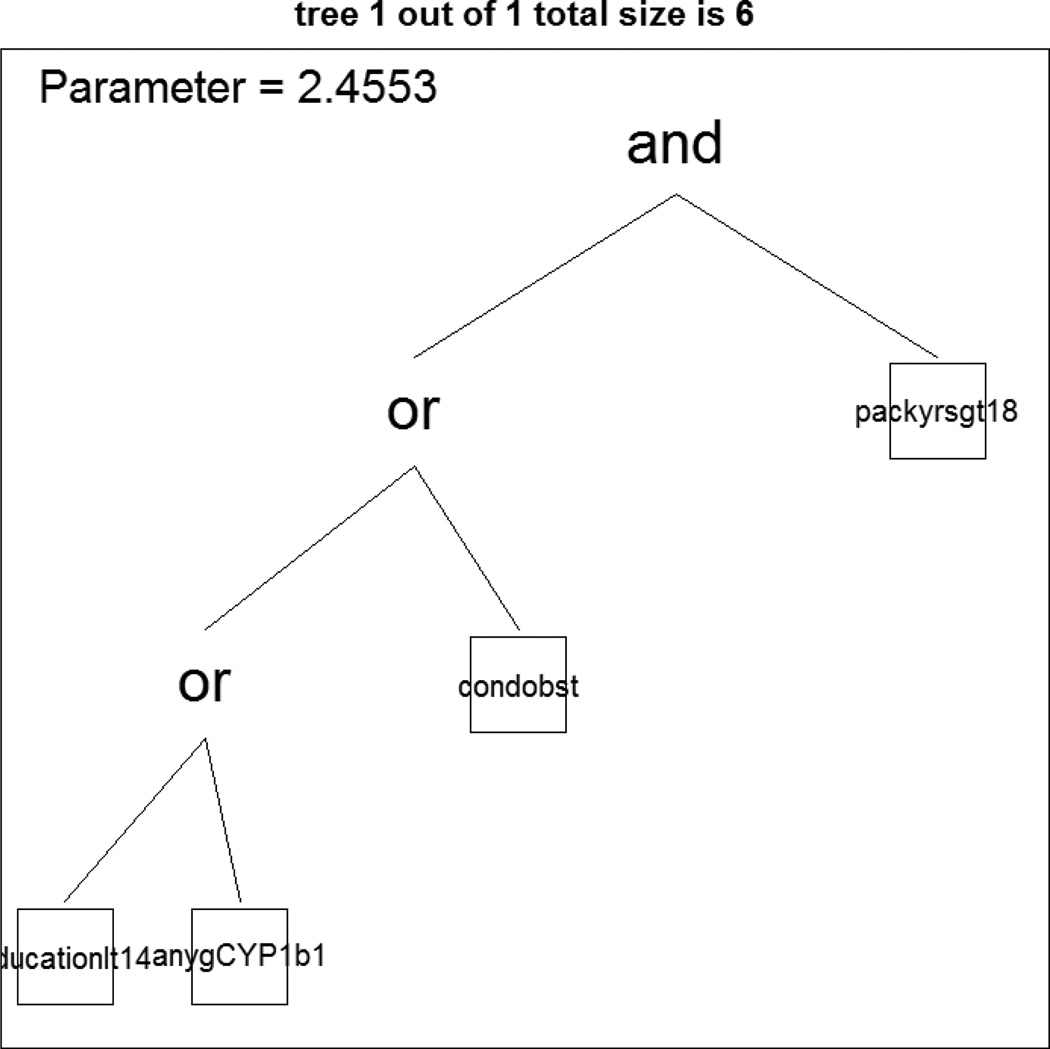
In order to determine best parameters of the simulated annealing algorithm, we examined the acceptance rates with different starting log-temperatures and looked at what level of ending temperature. We determined 3 as starting log-temperature and -1 as ending log-temperature. To find the best model, we used the cross-validation approach with 3 for the number of trees and 8 for the number of tree leaves. The cross-validation plot showed that the scores of ntree=1 and nleaves=6 resulted in the minimum score (data not shown). The logic regression identified a best model including a Boolean expression (Figure 6) of pack-years of cigarette smoking (packyrs) and (education level or CYP1b1 or history of chronic obstructive lung disease), and estimated the regression coefficient of logic regression as follows:

1. Y = −1.133 + 2.45L

where Y is a disease status and L is the logic expression noted above. The cross-validation error was 0.2137, which was slightly better than two logistic regressions and classification tree method. The AUC was 0.8207, which was larger than that for logistic regression and classification tree methods.

Figure 6.

The plot shows the tree of the Boolean expression, which includes a tree of cigarette smoking (packyrs) and (education level or CYP1b1 or history of chronic obstructive lung disease).

Random Forest

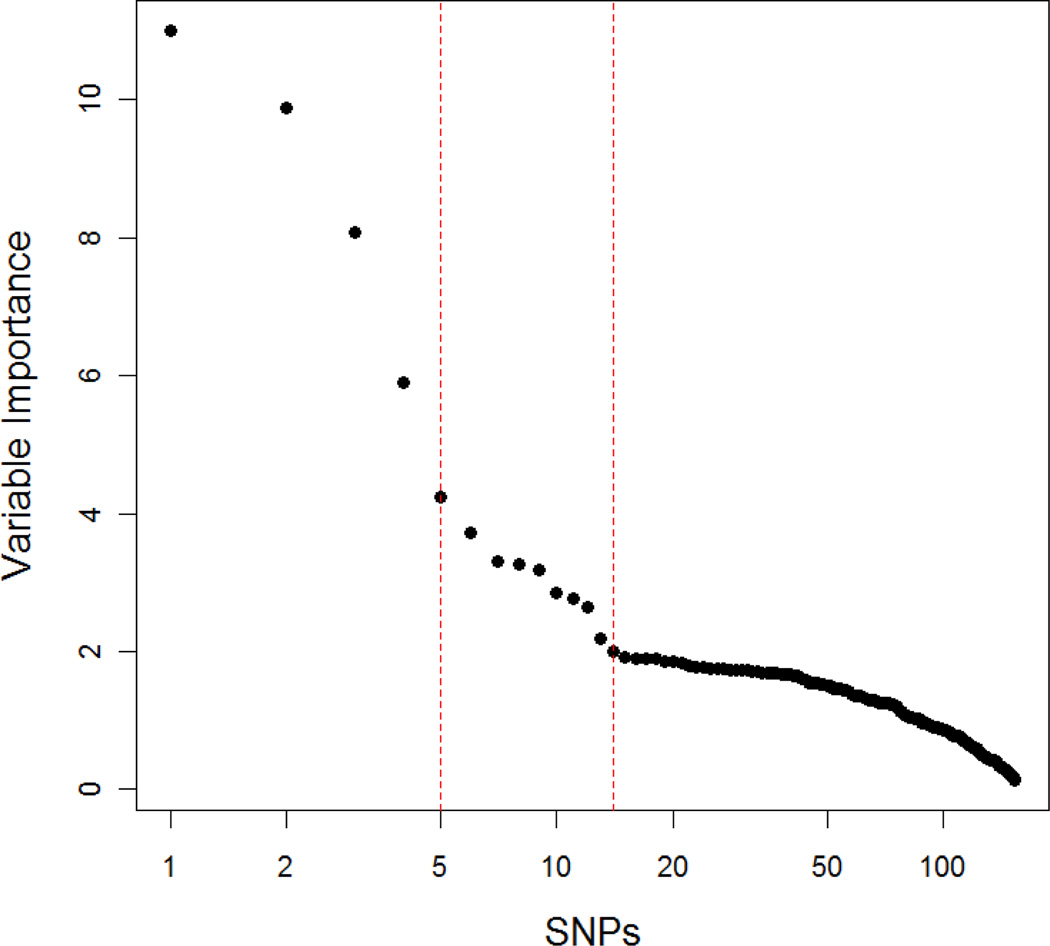
The random forests identified pack-years of cigarette smoking as the most important variable and education level as the second most important variable. Because our study did not have many variables, we applied 1000 for the number of trees and 5 for randomly preselected predictor variables for each split. The pack years variable was more than twice as high as education level. Education, history of chronic obstructive lung disease, BMI, GSTP1, and CYP1b1 were identified as relatively important variables. The interaction between pack-years of cigarette smoking and education was the second highest multifactor variable in significance; pack-years was highest. Figure 7 shows the variable importance among single and multifactor variables. The top four single and multi-factors were the single factor of pack-years and three two-way interactions of pack-years and education, pack years and GSTP1, and pack-years and CYP1b1. The cross-validation error for random forests method was 0.1627, the smallest among all five models. The random forests method had the largest AUC (0.8267) as seen in Table V.

Figure 7.

The variable important among single and multi-factors variables. The left dashed line is a cut-off for top 4 variable(s) in the variable important values, while the dashed right line indicates variables on top 14 in the variable importance. The single and multi-factors of top 4 variable important were a single factor of pack years of cigarette smoking, and three two-way interactions of pack years of cigarette smoking and education, pack years of cigarette smoking and GSTP1, and pack years of cigarette smoking and CYP1b1.

Table 5.

Cross-validation errors and area under the curves from five different models of two logistic regressions, classification trees, random forests, and logic regression.

	Models	Pathways	Cross- validation error	AUC
Model 1	Logistic Regression	Single variables	0.2255	0.7948
Model 2	Logistic Regression	Two-way interactions	0.2236	0.8147
Model 3	Classification trees	Multi-way interactions	0.2235	0.8159
Model 4	Logic Regression	Multi-way interactions	0.2137	0.8207
Model 5	Random Forests	Multi-way interactions	0.0627	0.8267

Discussion

This work aims to compare the effectiveness for identifying important genes or gene-gene and gene-environmental interactions among four classification methods of logistic regression, classification tree, random forests, and logic regression models. We started with the assumption that a multigenic study increases the chance of detection of disease because it considers gene-gene interactions and gene-environmental interactions, and environmental-environmental interactions. Logistic regression models and a tree-based study are selected to perform this purpose since these are two of the most commonly used model building procedures. A logic regression model is also considered because it is a generalized regression model to produce the importance of interactions among disjointed pairs of risk factors. In addition to a classification tree which has been a popular nonparametric classifier in medical research during last a decade, random forests method is included because it is a generalized version of classification tree method by allowing multiple classification tree and averaging those results. An interesting in this study is to incorporate environmental factors into our three analysis models since it is reasonable to assume that inclusion of these factors would further improve the diagnostic ability.

Table VI lists variables identified by each model. Throughout the five models, pack-years were the most dominant variable among both genetic and environmental risk factors. Education, chronic obstructive lung disease, and BMI were the second most dominant variables. GSTM1, CYP1b1, GSTP1, and XRCC1 were important polymorphisms as genetic risk factors. It is interesting that two logistic analyses identified GSTM1 and XRCC1 as important risk factors, but CART and random forests analyses identified only one polymorphism (CYP1b1) as an important risk factor. No genetic factors (GSTM1, XRCC1, or COMT) were identified by stepwise selection or by nonparametric methods. Based on our results, random forests showed the best performance while logic regression was second best. Classification tree method was slightly better than the two logistic analyses. For a model including single and two-way interactions, 64 degrees of freedoms were needed. Because each variable has around 10 samples, a model including two-way interactions is acceptable. However, 164 degrees of freedoms were necessary to consider three-way interaction terms, and we needed 329 degrees of freedoms for additional four-way interactions. It is not possible for a logistic model to include interactions equal to or less than four-way interactions because the number of variables exceeds the number of samples.

Table 6.

Variable list identified by each model.

	Environmental risk factors					Genetic risk factors
Mode l	bm i	packyr s	Famhis t	condobs t	educatio n	CYP1b 1	GSTM 1	GSTP 1	CYP1A 1	XRCC 1	COM T
1	✓	✓	✓	✓			✓			✓	✓
2	✓	✓	✓	✓	✓		✓	✓		✓
3	✓	✓		✓	✓	✓
4		✓		✓	✓	✓			✓
5		✓			✓	✓		✓

Model 1 (logistic regression with single factors), Model 2 (logistic regression with two-way interactions), Model 3 (classification trees model), Model 4 (logic regression), and Model 5 (random forests method).

In summary, logistic regression should not be used when the number of predictor variables is greater than the number of subjects, and a reduction of power results because the degrees of freedom increase dramatically including higher-order interactions in the model. The classification tree algorithm rapidly selects significant features resulting in a classification tree with binary split criteria, and enables automatic classification of lung cancer patients and control subjects on the basis of their individual genetic profile. Logic regression is a generalized regression methodology for predicting the outcome in classification and regression problems based on Boolean combinations of logic variables. Even though a logic regression is able to include continuous covariates, the predictors must be binary in order to be considered as a Boolean combination. This can be somewhat limiting when compared to other tree-based classifiers.

If a continuous variable is transformed into a dichotomous variable to apply logic regression, information about the variable be reduced, which might lead to loss of power in detecting important predictors. Nonetheless, several studies have shown that logic regression can be a good tool in identifying important SNP-SNP interactions [Kooperberg et al. 2005; Ruczinski et al, 2004]. As mentioned earlier, small changes in data lead to large changes in classification tree results, which produce instable results. Random forests method is an ensemble method, which reduces variability of trees by averaging multiple trees from bootstrapped data sets. Random forests have been widely applied in genetics and related disciplines within the past few years, because the approach applies to random subsets, which can be applicable with many more variables than observations (small subjects large predictor). This fact has added much to the popularity of random forests. Logistic regression analyses demonstrate the importance of each predictor to be able to explain the outcome variable. The odds ratios are a core statistic in logistic regression. Unfortunately, they do not provide information about relative priorities or importance among the predictive variables. Logic regression, classification tree, and random forests methods can answer this problem. In general, it is known that logistic regression and classification tree deliver very similar results with respect to the variables identified [Muller et al., 2008; Schwarzer et al., 2003]. Our work also supports this. All four methods have advantages and disadvantages in classification ability and practical applicability. Based on this study, random forests method shows best performance, but the complimentary application of four techniques seems to be an efficient procedure for better performance of analyzing and interpreting the results of multigenic studies.