A Model-Based fMRI Analysis with Hierarchical Bayesian Parameter Estimation

Abstract

A recent trend in decision neuroscience is the use of model-based fMRI using mathematical models of cognitive processes. However, most previous model-based fMRI studies have ignored individual differences due to the challenge of obtaining reliable parameter estimates for individual participants. Meanwhile, previous cognitive science studies have demonstrated that hierarchical Bayesian analysis is useful for obtaining reliable parameter estimates in cognitive models while allowing for individual differences. Here we demonstrate the application of hierarchical Bayesian parameter estimation to model-based fMRI using the example of decision making in the Iowa Gambling Task. First we use a simulation study to demonstrate that hierarchical Bayesian analysis outperforms conventional (individual- or group-level) maximum likelihood estimation in recovering true parameters. Then we perform model-based fMRI analyses on experimental data to examine how the fMRI results depend upon the estimation method.

How we make decisions to obtain rewards and avoid punishments is a fundamental topic across research areas including psychology, economics, neuroscience, and computer science. In the last decade, decision neuroscience researchers have begun to approach decision making from an interdisciplinary perspective – integrating quantitative models with neural signals. For example, early pioneering studies demonstrated that the phasic responses of midbrain dopamine neurons can be well described by the temporal-difference reinforcement learning algorithm (Montague, Dayan, & Sejnowski, 1996; Schultz, Dayan, & Montague, 1997). More recently, human functional magnetic resonance imaging (fMRI) studies have shown that blood-oxygen-level-dependent (BOLD) activations in brain regions including the striatum and orbitofrontal cortex correlate with prediction error signals from the temporal-difference learning model (McClure, Berns, & Montague, 2003; O’Doherty, Dayan, Friston, Critchley, & Dolan, 2003). These fMRI studies used the method of “model-based fMRI,” in which a mathematical model of behavior provides a framework to study neural mechanisms of reward learning. In model-based fMRI, predictions derived from a mathematical model of choice behavior are correlated with fMRI data to determine brain areas related to postulated decision-making processes. This method is increasingly popular in decision neuroscience because it provides insight into the neural correlates of predicted cognitive processes and can be useful to discriminate competing theories of brain function (see O’Doherty, Hampton, & Kim, 2007 for a review and methodological recipe).

The first step in model-based fMRI is to estimate the free parameters in the mathematical model of behavior. Getting accurate parameter estimates is important not only because parameter estimates reflect psychological traits (such as the learning rate or the balance of exploitation and exploration), but also because they affect the results of the subsequent model-based fMRI analysis (e.g., Tanaka et al., 2004). Most previous studies with model-based fMRI have used group-level analysis with maximum likelihood estimation (MLE). In group-level analysis, free parameters are assumed to be homogenous across participants and no individual differences are taken into account. It might be tolerable to ignore individual differences in simple conditioning tasks where most participants behave similarly, but it is inappropriate in complex tasks where substantial individual differences exist. In order to take into account individual differences, an alternative approach is individual-level analysis. However, using MLE for individual-level analysis can lead to noisy and unreliable estimates if the amount of information from each individual is limited, as is often the case in neuroimaging studies. We propose the use of hierarchical Bayesian analysis (HBA) to reconcile the tension between individual differences and reliable parameter estimation.

Hierarchical Bayesian analysis (HBA) is an advanced branch of Bayesian statistics (Berger, 1985) that employs the basic principles of Bayesian statistical inference (Gelman, Carlin, Stern, & Rubin, 2004). One of the advantages of HBA is that, whereas MLE finds a point estimate for each parameter that maximizes the likelihood of the data, HBA finds a full posterior distribution of belief across the range of values a parameter can take on. A second advantage of HBA is that it allows for individual differences while pooling information across individuals in a coherent way. Both individual and group parameter estimates are found simultaneously in a mutually constraining fashion. By capturing the commonalities among individuals, each individual’s parameter estimates tend to be more stable and reliable because they are informed by the group tendencies.

In this paper, we apply HBA to model-based fMRI analysis of the Iowa Gambling Task (IGT) (Bechara, Damasio, Damasio, & Anderson, 1994) and compare it with other estimation methods. The remainder of this article is organized as follows. First, we briefly explain the IGT and a mathematical model for the task. Second, we briefly explain the procedures of MLE and HBA and then use simulated data with known true parameter values to examine which method recovers the values more accurately. To tease apart the relative contributions of Bayesian estimation and the use of a hierarchical approach, we estimate parameters using each of the following methods: MLE at the group level (MLE-Group), MLE at the individual level (MLE-Ind), non-hierarchical Bayesian analysis (Bayes-Ind), and HBA. Third, we present model-based fMRI analyses using parameter estimates from MLE-Group, MLE-Ind, and HBA and show how the choice of method influences the fMRI results.

Iowa Gambling Task

The IGT is a well-established task used to study decision-making processes in normal participants and decision-making deficits in clinical populations including substance abusers and patients with brain lesions (Bechara, Damasio, Tranel, & Damasio, 1997; Bechara et al., 2001). The goal of the task is to maximize monetary gains while repeatedly choosing cards from one of four decks. Each selection results in a monetary gain, draw, or loss. There are two “good” decks with long-term gains and two “bad” decks with long-term losses. However, the typical win is larger for the bad decks than the good decks, putting the magnitude of the potential immediate gain into opposition with the long-term cumulative outcome from the decks. Furthermore, one bad and one good deck have infrequent larger losses, while the other bad and good deck have more frequent smaller losses. Participants need to learn from experience which decks are advantageous for good performance. It is a challenging task and even healthy control participants show substantial individual differences in behavioral performance.

Prospect Valence Learning (PVL) Model

We used the Prospect Valence Learning (PVL) model (Ahn, Busemeyer, Wagenmakers, & Stout, 2008) to mathematically model participants’ decision-making processes. The model assumes that the evaluation of outcomes follows the Prospect utility function which has diminishing sensitivity to increases in magnitude and loss aversion, i.e. different sensitivity to losses versus gains. Specifically, the utility, u(t)on trial t of each net outcome x(t) is expressed as:

$$u(t)=\{\begin{array}{cc}x{(t)}^{\alpha }& \text{if}x(t)\ge 0\\ -\lambda {\mid x(t)\mid }^{\alpha }& \text{if}x(t)<0\end{array}.$$ (1)

Here α is a shape parameter (0< α <1) that governs the shape of the utility function and λ is a loss aversion parameter (0 < λ <5) that determines the sensitivity of losses compared to gains. Net outcomes were scaled for cognitive modeling so that the highest net gain becomes 1 and the largest net loss becomes −11.5 (Busemeyer & Stout, 2002). As α gets close to 1, the utility gets close to the objective outcome amount, and as α gets close to 0, it becomes more like a step function. If an individual has a value of loss aversion (λ) greater than 1, it indicates that the individual is more sensitive to losses than gains. A value of λ less than 1 indicates that the individual is more sensitive to gains than losses.

Based on the outcome of the chosen option, the expectancies of decks were updated on each trial using the decay-reinforcement learning rule (Erev & Roth, 1998). When tested with the Bayesian information criterion (BIC; Schwarz, 1978), previous studies consistently showed that this rule had the best post-hoc model fit (Ahn, et al., 2008; Yechiam & Busemeyer, 2005, 2008) compared to others including the delta rule (Rescorla & Wagner, 1972). The decay-reinforcement learning rule assumes that the expectancies of all decks decay (are discounted) with time and then the expectancy of the chosen deck is added to the current outcome utility:

$$E_j(t)=A·E_j(t-1)+{\delta }_j(t)·u(t).$$ (2)

The parameter A is a recency parameter (0 < A <1), which determines how much the past expectancy is discounted. δ_j(t) is a dummy variable which is 1 if deck j is chosen and 0 otherwise.

Using the updated expectancies, the softmax choice rule (Luce, 1959) was then used to compute the probability of choosing each deck j. It has a sensitivity (or exploitiveness) parameter, θ(t), which governs the degree of exploitation versus exploration.

$$Pr[D(t+1)=j]=\frac{e^{\theta (t)·E_j(t)}}{{\displaystyle \sum _{k=1}^4}{e}^{\theta (t)·E_k(t)}}$$ (3)

Sensitivity, θ(t), is assumed to be trial-independent and was set to 3^c−1 (Ahn, et al., 2008; Yechiam & Ert, 2007). Here c is called consistency and was limited from 0 to 5 so that the sensitivity ranges from 0 (random) to 242 (almost deterministic). In sum, the PVL model used in this study has four free parameters reflecting distinct psychological constructs: A, recency; α, utility shape; c, choice sensitivity; and λ, loss aversion.

Simulation Study

To compare the performance of HBA to the other methods in accurately recovering parameter values, we simulated 30 participants performing the IGT (100 trials per participant) assuming that they behaved according to the PVL model. To be as realistic as possible, we based the simulated data on the actual fMRI study reported in a later section. The number of subjects and trials were matched to those of the actual study, and when generating stimulated data we used parameters estimated from the actual dataset. Specifically, the parameters of the simulation agents were the posterior means of the parameters found using HBA for the real participants.¹

The four free model parameters of each simulated participant were then estimated in four different ways and compared to determine which method recovered the true parameter values most accurately. The four methods are: MLE at the group level (MLE-Group), MLE at the individual level (MLE-Ind), non-hierarchical Bayesian analysis at the individual level (Bayes-Ind), and HBA. HBA yields posterior distributions of the group parameters (HBA-Group) and each individual’s parameters (HBA-Ind), so we report them separately. MLE-Group and MLE-Ind are the most widely used approaches in the decision neuroscience field, so we were most interested in comparing estimates from these approaches with those from HBA. The inclusion of Bayes-Ind allowed us to learn something about the degree to which the advantages of HBA were due to the use of Bayesian estimation versus being due to the use of a hierarchical model.

Parameter Estimation Methods

Maximum likelihood estimation

For MLE-Group, point estimates were made for each parameter that maximized the sum of log likelihood across all participants (e.g., Daw, O’Doherty, Dayan, Seymour, & Dolan, 2006). We used a combination of grid-search (100 different initial grid positions) and simplex search methods (Nelder & Mead, 1965) implemented in the R programming language (R Development Core Team, 2009).² For MLE-Ind, a set of parameters were estimated that maximized the log likelihood of each individual’s one-step-ahead model predictions, again using the combination of grid-search and simplex search methods in R.

Bayesian estimation

For HBA, it is assumed that the parameters of individual participants are generated from parent distributions, which are modeled with independent beta distributions for each parameter:

$$\begin{array}{l}{\alpha }_i~\mathit{Beta}({\mu }_{\alpha },{\sigma }_{\alpha }),\\ {\lambda }_i^{\prime }~\mathit{Beta}({\mu }_{\lambda };{\sigma }_{\lambda }),{\lambda }_i=5·{\lambda }_i^{\prime },\\ A_i~\mathit{Beta}({\mu }_A,{\sigma }_A),\\ c_i^{\prime }~\mathit{Beta}({\mu }_c,{\sigma }_c),c_i=5·c_i^{\prime }.\end{array}$$ (4)

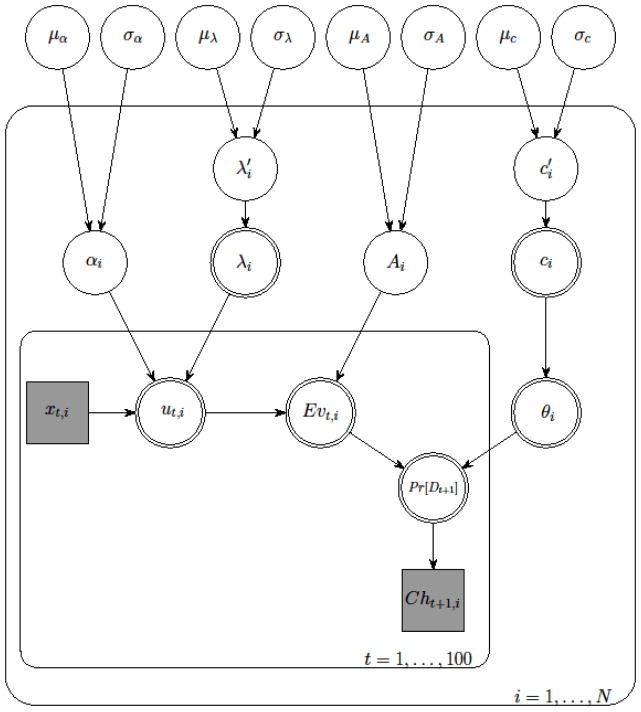
As implied in the equations above, α_i and A_i were limited to values between 0 and 1 and λ_i and c_i were limited to values between 0 and 5. Here μ_z and σ_z are the mean and the standard deviation of the beta distribution of each group-level parameter z (i.e. α, λ, A, and c).³ The Bayesian method needs the specification of the prior distributions for the parameters and we used uniform distributions for μ_z and σ_z, which provide flat priors and thus assume no a priori knowledge about these parameters. The range of each μ_z was set between 0 and 1 and each σ_z was set between 0 and $\sqrt{{\mu }_z(1-{\mu }_z)/3}$ so that each distribution was prevented from being bimodal. Different diffuse priors were also tested (e.g., uniform distributions for the beta means and diffuse gamma distributions for their precisions) and they resulted in almost identical posterior distributions. The hierarchical Bayesian model is represented graphically in Figure 1.

Figure 1.

Graphical depiction of the hierarchical Bayesian analysis for the Prospect Valence Learning model. Clear shapes indicate latent variables, shaded shapes indicate observed variables; single outlines indicate probabilistic functions of input, double outlines indicate deterministic functions of input; circles indicate continuous variables, squares indicate discrete variables; rounded rectangular plates indicate replication over the indexing variable. See the main text for a description of the individual parameters.

Finally, the observed data matrix from all participants was used to compute the posterior distributions for all parameters according to Bayes rule. Posterior inference was performed using the Markov chain Monte Carlo (MCMC) sampling scheme in OpenBUGS (Thomas, O’Hara, Ligges, & Sturtz, 2006), an open source version of WinBUGS (Spiegelhalter, Thomas, Best, & Lunn, 2003), and BRugs, its interface to R (R Development Core Team, 2009). WinBUGS (and OpenBUGS) implements various MCMC computational methods and it is relatively user-friendly and easy to program, thus has greatly facilitated Bayesian modeling and its applications (Cowles, 2004). A total of 50,000 samples were drawn after 70,000 burn-in samples with three chains.

For non-hierarchical Bayesian analysis, we again used beta distributions for each participant’s parameters. However, no hyper (group) parameters were assumed and priors of each participant’s parameters were uniform beta distributions (e.g.,α_i ~ Beta(1,1)). We used the same number of burn-in samples and real samples as the HBA analyses. For each parameter, the Gelman-Rubin test (Gelman, et al., 2004) was run to confirm the convergence of the chains. All parameters had Rhat values of 1.00 (in most parameters) or at most 1.04, which suggested MCMC chains converged to the target posterior distributions. OpenBUGS codes used for all Bayesian analyses are available at http://www.ahnlab.org/home/research/.

Results and Discussion

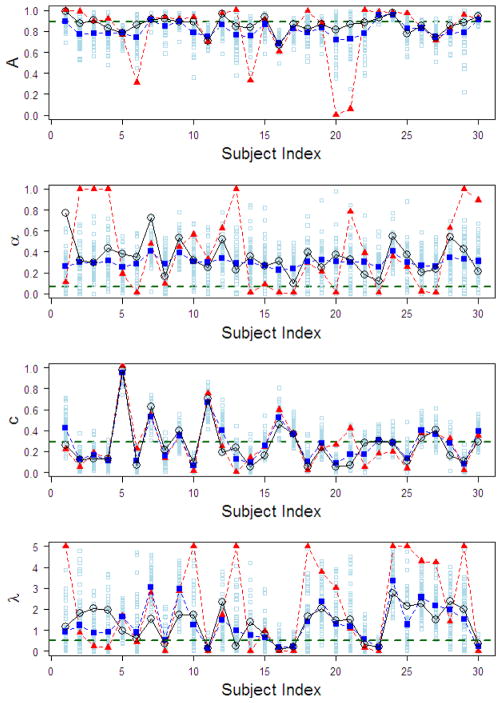
Figure 2 shows the results of the simulation study focusing on comparisons between HBA-Ind and MLE (MLE-Ind and MLE-Group) methods. Wetzels et al. (2010) showed that parameter estimates of an individual’s data are not reliable in the Expectancy Valence Learning (EVL) model (Busemeyer & Stout, 2002), which closely resembles the PVL model. However, their claim was based on parameter values estimated with each individual’s data only, not all individuals’ data in a group. In our dataset, parameter estimates of the PVL also show some discrepancy from actual values when using each individual’s data only (MLE-Ind in Figure 2). In particular, note that some MLE-Ind estimates are on the parameters’ boundary limits, indicating insufficient information in each individual participant’s data. However, when estimated with HBA, parameter estimates (HBA-Ind in Figure 2) show much less discrepancy with actual values compared to MLE-Ind estimates.

Figure 2.

For the simulation study, parameter estimates of the four free parameters in the PVL model for each simulated participant from both HBA and MLE. Shown in the graphs are: true parameter values (black circles), MLE-Ind estimates (red triangles), mean HBA-Ind estimates (big blue squares), MLE-Group estimates (red horizontal dashed lines), and 50 random samples from the posterior distribution of the HBA estimate for each participant (small sky-blue squares). A = recency; α = utility shape; c = choice sensitivity; λ = loss aversion. HBA = hierarchical Bayesian analysis; MLE = maximum likelihood estimation; Ind = individual-level estimates; Group = group-level estimates.

The HBA results lead to two interesting observations. First, by capturing the dependency between all participants, the HBA estimates regress towards the group mean when there is not much information in individual participants’ data (“shrinkage”, Gelman, et al., 2004). Second, HBA can also be sensitive to individual differences when there is enough information, which is demonstrated in the estimates for the learning parameter (A). Although the performance of the HBA was not perfect, estimated values from HBA were overall more accurate than those from MLE. Note that we reached the same conclusion when running additional simulations with different true parameter values and different numbers of subjects and trials. Regarding MLE-Group estimates, A and c parameter estimates are around the mean values of individual values but α and λ estimates are quite different from them.

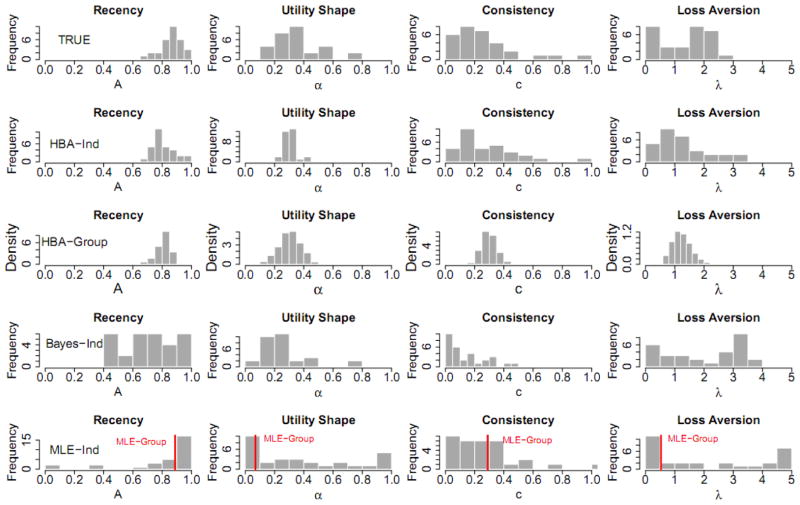
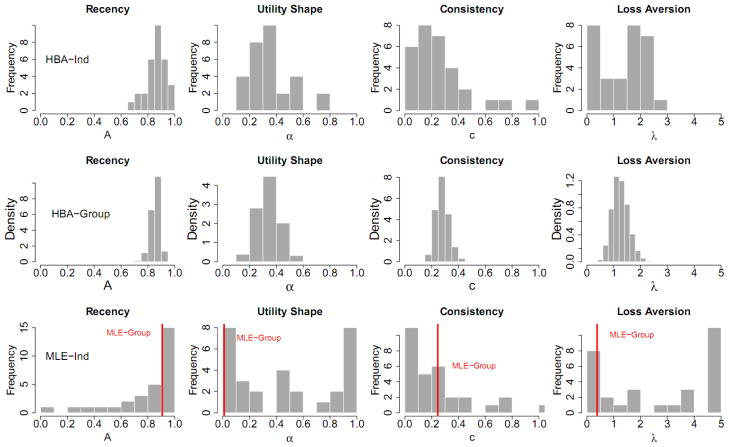
Figure 3 plots the distribution of posterior means for individual participants’ parameter estimates computed from each method (except for HBA-Group, for which distribution densities of group parameters are plotted). When compared to the true values, the results suggest HBA performs better than Bayes-Ind and MLE-Ind in recovering true values. The fact that the HBA-Ind estimates are closer to the true values than Bayes-Ind estimates provides empirical support that using a hierarchical approach indeed helps get more accurate estimates.

Figure 3.

For the simulation study, histograms of the true parameter values and the parameter estimates from each estimation method for all of the simulated participants (except for the third row, which shows the posterior distributions of the group parameters for HBA-Group). HBA = hierarchical Bayesian analysis; MLE = maximum likelihood estimation; Bayes = non-hierarchical Bayesian analysis; Ind = individual-level estimates; Group = group-level estimates.

The posterior distributions of parameters for HBA-Group closely resemble the true parameter distributions. However, these distributions are narrower because they represent the variance in the group estimates, not the variance among individuals.

The results in Figure 3 also give some insight into why the MLE-Group estimates of α and λ are so far from the actual values. The MLE-Group estimates are around the mode of the MLE-Ind distributions. For parameter A, most participants’ true values are around the mode, so the MLE-Group estimate looks acceptable. However, for parameters α and λ, the modes of MLE-Ind parameters are near the lower bounds, thus MLE-Group estimates are dissimilar from the overall patterns of actual values. Note that these results are not because of the estimation method (MLE) but because of the assumption made in the estimation, namely that all participants use the same parameter values. Indeed, if the same assumption is used with Bayesian estimation, the posterior means of the parameters are very close to the MLE-Group estimates (results not shown here for brevity). In sum, the results of the simulation study suggest that HBA is the best among these methods for estimating free parameters of the PVL model accurately.

Model-Based fMRI Study

Having confirmed the utility of HBA in estimating behavioral parameters, we then wanted to examine how fMRI results would depend upon the choice of estimation method. We ran model-based fMRI analyses of actual data using parameter estimates from three of the estimation methods (HBA, MLE-Ind, and MLE-Group). We included both the individual and group estimates from HBA (HBA-Ind and HBA-Group). By using group and individual estimates with both MLE and HBA, we could consider the effects of method and analysis level separately. We hypothesized that HBA would yield more power than MLE because its parameter estimates would be more accurate (as revealed by the simulation study) and thus its model predictions would better reflect participants’ actual cognitive processes. When MLE-Group and HBA-Group are compared to each other, we also predicted that MLE-Group would yield more power at the second level (group) than the first level (individual), whereas HBA-Group would conversely yield more power at the first level (individual) than the second level (group). This follows from the fact that MLE-Group simply finds a group average parameter, but HBA-Group provides more individualized fits constrained toward the group mean. Regarding comparisons between individual estimates and group estimates, we predicted that MLE-Group would yield more power than MLE-Ind because, according to the simulation study, MLE-Ind estimates would be noisy and unreliable.

Methods

Participants

We recruited participants from the student body of Indiana University, Bloomington. They were required to be at least 18 years of age, right-handed, and to meet standard health and safety requirements for entry into the magnetic resonance imaging scanner. They were paid $25/hour for participation, plus performance bonuses based on points earned during the task. A total of 30 participants (mean age 21.7 years, age range 18–29, 16 females) were used in all reported analyses.

Design and procedure

Participants performed the IGT for a block of 100 trials.⁴ During the task, there were 4 decks of cards labeled A, B, C, and D from left to right. Two of the decks are considered bad decks: a net-loss/frequent-loss deck, with 50% loss trials, a mean loss of 25 points per trial, and a gain of 100 on non-loss trials; and a net-loss/rare-loss deck, with 10% loss trials, a mean loss of 25 points per trial, and a gain of 100 on non-loss trials. The other two decks are considered good decks: a net-gain/frequent-loss deck, with 50% loss trials, a mean gain of 25 points per trial, and a gain of 50 on non-loss trials; and a net-gain/rare-loss deck, with 10% loss trials, a mean gain of 25 points per trial, and a gain of 50 on non-loss trials. The two bad decks were always adjacent with the frequent-loss deck to the left of the rare-loss deck. The two good decks were also kept adjacent with the frequent-loss deck to the left of the rare-loss deck. The order of the bad and good decks was counterbalanced across participants.

The specific sequences of gains and losses for each deck were the same as in the original task design (Bechara, et al., 1994). However, unlike in the original design, each trial outcome was presented as a net gain, draw, or loss, the participant started with an initial sum of 1000 points, and the entire task was performed on a computer using E-Prime 1.2 (Psychology Software Tools Inc., 2006).

Participants were instructed to select cards from the decks. They were informed that the goal was to maximize earnings, and that they would receive a monetary bonus based on the number of points they accumulated. They were informed of the 3 second period in which to make each selection and the running point total at the bottom of the screen. They were told nothing about the order of the decks or how the order might change from block to block.

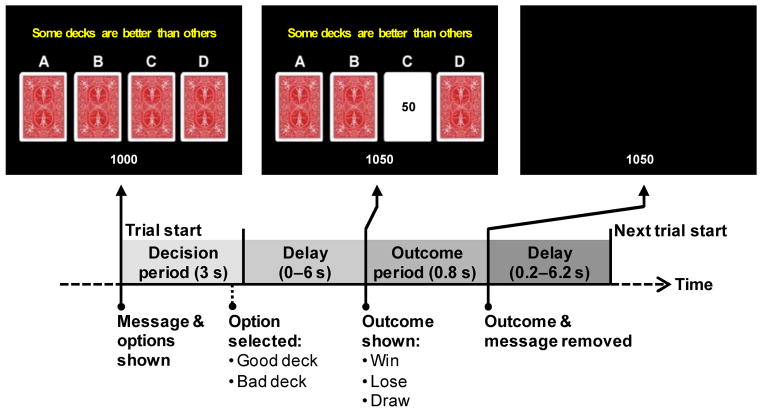
The timing and presentation of a trial is presented schematically in Figure 4. The participant’s running point total was displayed throughout the block at the bottom of the screen. At the start of a trial, a message (“Some decks are better than others”) and the 4 decks of cards (labeled A, B, C, and D from left to right) were presented. The participant had 3 seconds to select a deck by pressing one of their middle or index fingers on buttons corresponding in a spatially compatible way to the decks. If the participant failed to respond within 3 seconds, then the trial was considered a no-response trial. After the response deadline, there was an exponentially distributed delay of 0, 2, 4, or 6 seconds. Following the variable delay, a card from the chosen deck was flipped over to reveal the outcome as a negative, zero, or positive point value, and the running total was updated. On no-response trials, the outcome was always a loss of 100 points, in order to encourage participants to make a choice on every trial. The feedback remained visible for 0.8 seconds, after which the message, cards, and outcome were removed for an exponentially-distributed ITI of 0.2, 2.2, 4.2 or 6.2 seconds before the next trial began. The variable-length delays between choice and outcome and between trials were designed to allow the brain activity associated with the decision period to be estimated separately from that associated with response to the outcome (Ollinger, Corbetta, & Shulman, 2001; Ollinger, Shulman, & Corbetta, 2001).

Figure 4.

Time-course of the Iowa Gambling Task in a rapid event-related fMRI design.

fMRI collection and preprocessing

Imaging data were collected on a 3.0 Tesla Siemens Magnetom Trio. For each participant, functional blood oxygenation-level dependent (BOLD) data were collected using echo planar imaging with free induction decay for a block of 360 whole brain volumes with an echo time (TE) of 25 ms, a repetition time (TR) of 2000 ms and a flip angle of 70°. Images were collected in 33 axial slices in interleaved order with 3 mm thickness and 1 mm spacing between slices. Each slice consisted of a 64 by 64 grid of 3.4375 by 3.4375 by 3 mm voxels. For each participant, a structural scan was collected using three dimensional TurboFLASH imaging.

Each participant’s functional volumes were checked for transient spike artifacts in individual slices using a custom algorithm implemented in MATLAB R2007a 7.4.0. Preprocessing of the data was done using SPM5 (Wellcome Trust Centre for Neuroimaging, 2005). The raw DICOM images were first converted to NIfTI format. Slice timing correction was then performed on the functional images using SPM5’s Fourier phase shift interpolation with the first slice as reference. Motion correction was then performed using SPM5’s least squares six parameter rigid body transformation. The structural scan was then skull-stripped using BET2 (Péchaud, Jenkinson, & Smith, 2006) with default parameters. The structural scan was then coregistered with the motion-corrected functional scans using SPM5’s affine transformation with the mean functional image as reference. The images for each participant were then registered to MNI space using SPM5’s normalization procedure by first performing a 12-parameter affine transformation within a Bayesian framework using regularization to the ICBM space template followed by a non-linear deformation using discrete cosine transform basis functions.. The source image was the structural scan with an 8mm Gaussian smoothing kernel and the template was SPM5’s MNI Avg152, T1 at 2 mm³ along with its associated weighting mask. The resulting normalized images were written with 2 mm³ voxels. Finally, the normalized images were smoothed using an 8 mm³ FWHM Gaussian kernel.

Model-based fMRI analysis

For model-based fMRI analysis (Daw, et al., 2006; McClure, et al., 2003; O’Doherty et al., 2004; O’Doherty, et al., 2007; Tanaka, et al., 2004), model-generated regressors were convolved with a canonical hemodynamic response function (HRF) and then correlated against BOLD fMRI signals to determine brain areas related to the specific decision-making processes (using parametric modulation in SPM5). We used choice probability of the chosen option at the time of decision (onset of deck presentation) as the regressor of interest. The choice probability is a relative measure of the expected value signal (Daw, et al., 2006). Ventromedial prefrontal cortex (vmPFC) is known to encode reward (Daw, et al., 2006; Knutson, Taylor, Kaufman, Peterson, & Glover, 2005), and IGT performance is impaired in vmPFC lesion patients (Bechara, et al., 1994), so we hypothesized that the choice probability computed by the model for the chosen option on each trial would be correlated with activation of vmPFC at the time of decision making.

In order to increase statistical power, we used summed probabilities for choosing either good or bad decks. In other words, if a good deck was chosen on a given trial, we used the summed probability of choosing either good deck, and if a bad deck was chosen on a trial, we used the summed probability of choosing either bad deck. Analyzing the IGT results in terms of good and bad decks is a common practice (e.g., Bechara, et al., 1994; Bechara, et al., 1997).

For model-based fMRI with HBA, the regressors were generated directly from the posterior distributions of each participant’s parameters (HBA-Ind) or group parameters (HBA-Group) and the means of the posterior predictive distributions were used as input to SPM5.⁵ For regressors from MLE, regressors were generated from each participant’s point estimates (MLE-Ind) or group point estimates (MLE-Group). In every case, all regressors were standardized into z-scores within each participant (mean=0, standard deviation=1) before being entered into SPM5.

First-level analysis of the preprocessed fMRI data was performed using SPM5. A general linear model (GLM) was run for each participant using SPM5’s canonical hemodynamic response function with no derivatives, a micro-time resolution of 16 time-bins per scan, a high-pass filter cutoff at 128 seconds using a residual forming matrix, autoregressive AR(1) to account for serial correlations, and restricted maximum likelihood (ReML) for model estimation. The model included a constant term, six motion regressors using the parameters of the motion correction performed during preprocessing, the model-generated regressor and nuisance regressors. Nuisance regressors included objective outcomes and the absolute value of loss outcomes at the feedback period, reaction times, and onsets of no-response trials (mean number of no-response trials = 1.8).

Group-level analyses were conducted using two approaches. The first approach was a whole-brain analysis which assumes that activations for a given contrast will be in the same location for all participants. This approach used voxel-by-voxel one-sample t-tests to test if the beta coefficients across participants were significantly different from zero. For activation maps in vmPFC, we used a threshold of p < 0.001, uncorrected, with a cluster threshold of 8 contiguous voxels. This approach was selected because it is the most commonly used group-level analysis for model-based fMRI analysis. The second approach was a form of region-of-interest (ROI) analysis where the voxel with peak activation within an a priori ROI is selected for each participant. Our ROI was vmPFC, defined as Brodmann area 25 dilated by 1 mm using the WFU Pick Atlas (Lancaster et al., 2000; Maldjian, Laurienti, Kraft, & Burdette, 2003). The peak values for each participant from this ROI were tested at the second-level using an uncorrected one-sample t-test. This approach was selected because past work has suggested that the peak voxel best reflects the underlying neural activity (Arthurs & Boniface, 2003), and because this approach allows for individual differences in the particular location of activity.

Results and Discussion

Parameter estimation

Model parameters were estimated from the actual behavioral data with three different methods (HBA, MLE-Ind, and MLE-Group). Table 1 shows the parameter estimates from each method and Figure 5 illustrates the histograms of parameter estimates from each method. Again, MLE-Ind estimates are often on the boundaries of parameter ranges and MLE-Group estimates of α and λ are near the lower bound of zero. Unlike the simulation study, we do not know true values of these parameters, so we cannot tell which method is the best for estimating them. However, the previous simulation study and other studies (Fridberg et al., 2010; Shiffrin, Lee, Kim, & Wagenmakers, 2008; Wetzels, et al., 2010) that examined this issue suggest that the HBA estimates probably better reflect individuals’ true internal characteristics.

Table 1.

Comparison of PVL Model Parameters by Method of Parameter Estimation

Method	A	α	c	λ
μ (HBA-Group)	0.86	0.34	0.29	1.25
Mean of MLE-Ind estimates	0.80	0.48	0.26	2.71
MLE-Group	0.91	0.01	0.25	0.38

Note. Parameter estimates from the 30 participants in the fMRI study. A = recency; α = utility shape; c = choice sensitivity; λ = loss aversion. HBA = hierarchical Bayesian analysis; MLE = maximum likelihood estimation; Ind = individual-level estimates; Group = group-level estimates.

Figure 5.

For the model-based fMRI study, histograms of each participant’s parameter estimates with each estimation method. Note that the HBA-Ind parameters in the first row were used as the true parameters in the simulation study. HBA = hierarchical Bayesian analysis; MLE = maximum likelihood estimation; Ind = individual-level estimates; Group = group-level estimates.

Model-based fMRI

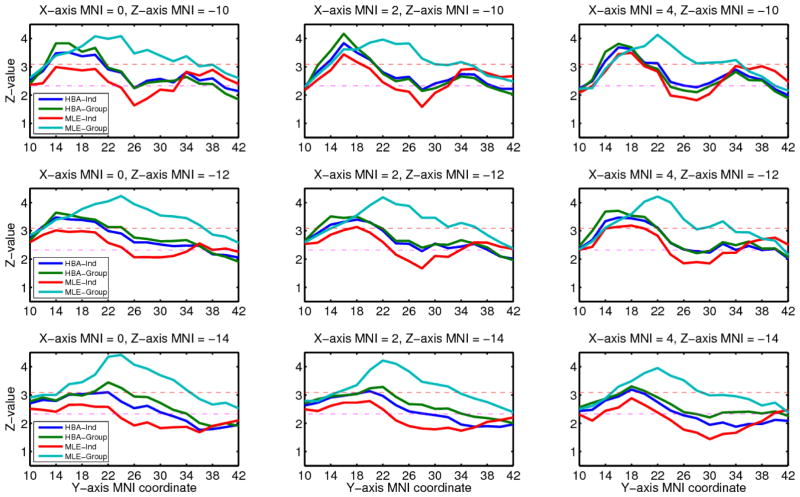
In order to focus on the comparison of estimation methods, we limited our fMRI analysis to correlations between choice probability for the chosen option and decision-time activation in the vmPFC. We found such correlations with all four estimation methods using both approaches to the group-level fMRI analysis. The results from each estimation method and each analysis approach are summarized in Table 2, and the activation maps from the whole-brain analysis are shown in Figure 6. To compare the models in more detail, we plotted z-values for all four methods from the whole-brain analysis within a rectangle of MNI space ranging from 0 to 4 in x-coordinates, 10 to 42 in y-coordinates, and −14 to −10 in z-coordinates (Figure 7). This region includes the vmPFC peak activations found with each of the four methods.

Table 2.

Comparison of PVL Model-Based fMRI Findings by Method of Parameter Estimation and Analysis Approach

Estimation method	Whole-brain analysis			ROI analysis
	Max z-value	Cluster size (kE)	Peak MNI coordinates	Mean peak z-value	Mean MNI coordinates
HBA-Ind	3.84	54	[2, 16, −10]	5.20	[0, 12, −14]
HBA-Group	4.17	74	[2, 16, −10]	5.31	[0, 12, −12]
MLE-Ind	3.49	14	[4, 18, −10]	4.99	[0, 12, −14]
MLE-Group	4.41	444	[0, 24, −14]	5.06	[0, 12, −12]

Note. Regions in vmPFC correlating significantly with the choice probability for the chosen option assigned by the PVL model. Cluster size in voxels. vmPFC = ventromedial prefrontal cortex; PVL = prospect valence learning; ROI = region of interest; HBA = hierarchical Bayesian analysis; MLE = maximum likelihood estimation; Ind = individual-level estimates; Group = group-level estimates.

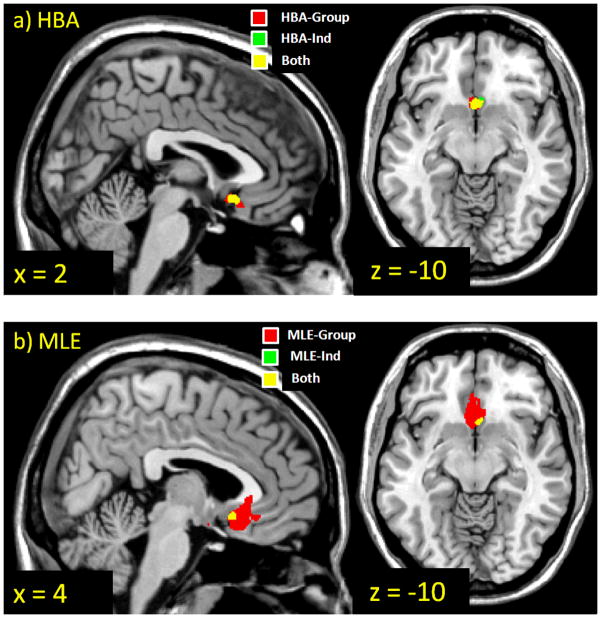
Figure 6.

Brain regions whose decision-time activation correlates significantly with the choice probability assigned by the PVL model using parameter estimates from each estimation method. Thresholded at p < .001, uncorrected, cluster size >= 8 voxels. HBA = hierarchical Bayesian analysis; MLE = maximum likelihood estimation; Ind = individual-level estimates; Group = group-level estimates.

Figure 7.

The z-values as a function of MNI coordinates for decision-time activation correlated with the choice probability assigned by the PVL model using parameter estimates from each estimation method. Red dashed lines indicate thresholds for p < .001 (z = 3.06), and pink dashed lines indicate thresholds for p < .01 (z = 2.33). HBA = hierarchical Bayesian analysis; MLE = maximum likelihood estimation; Ind = individual-level estimates; Group = group-level estimates.

With the whole brain analysis, for HBA and especially MLE, group methods showed higher peak z-values and larger regions of activation than individual methods. The MLE-Group method produced the largest vmPFC region correlating with the choice probabilities. The activation maps for HBA-Ind, HBA-Group, and MLE-Ind are quite similar in shape and their peak coordinates match, but the map for MLE-Group is qualitatively different. The peak of activation is shifted forward along the y-axis for MLE-Group compared to the other methods.

With the ROI analysis, which searches the ROI to find the voxel with the best model fit separately for each individual, the group methods again showed higher peak z-values than the individual methods. However, unlike the whole-brain approach, both of the HBA methods yielded higher z-values than either of the MLE methods. Furthermore, the mean locations of the peaks were almost the same for all four methods.

The differences found here between estimation methods in terms of their ability to account for the fMRI data are relatively small. However, it is still interesting to note that to the extent that there are differences, HBA was more successful when the method of analysis allowed for individual differences in the locations of activation. This suggests that in order for HBA’s advantage in accounting for individual differences in behavior to carry over to the fMRI analysis, that analysis must also allow for individual differences. In addition, HBA-Ind yielded more power than MLE-Ind in both whole brain and ROI analyses, which suggests that allowing some extra parameters in the hierarchical model is helpful in terms of fMRI power when estimating each subject’s parameters separately.

What is less clear is why the HBA-Group method outperformed HBA-Ind in the ROI analysis, given that the simulation study suggested that HBA-Ind does the best job of accounting for individual differences in parameter estimates. Further investigation should be done to characterize these patterns across a wider range of brain regions, tasks, and model predictions.

General Discussion

The simulation study compared two Bayesian methods (HBA and Bayes-Ind) and two MLE methods (MLE-Ind and MLE-Group) in their performance recovering true parameters and the results suggest that HBA is the best method for obtaining accurate individual and group parameter estimates. While the HBA estimates were close to the true parameter values, the MLE-Ind estimates were often stuck on bounds and some MLE-Group estimates diverged markedly from the true parameter means. Individual estimates from the non-hierarchical Bayesian method (Bayes-Ind) were uninformed by other participants’ data and were often too vague and less accurate than HBA estimates.

Subsequent model-based fMRI results were generally consistent with the behavioral results. We predicted that a method that performed well in the stimulation study would yield more significant activations when employed for model-based fMRI. We evaluated this prediction in the vmPFC for the correlation of decision-time activity and choice probabilities for the chosen options. As predicted, the HBA-Ind method yielded more vmPFC activation than MLE-Ind, MLE-Group yielded more activation than MLE-Ind, and HBA-Group out-performed MLE-Group in the ROI analysis. However, in the whole-brain analysis MLE-Group yielded the largest vmPFC activation, which was not expected. The best overall performance with respect to power was found with HBA-Group, with the more flexible prior assumption that there may be individual differences in peak voxel location. Nonetheless, when the simplifying assumption was made that there are no individual differences in peak voxel location, then MLE-Group yielded more power than HBA-Group. To our knowledge, this is the first model-based fMRI study with HBA estimation, so further research is needed to confirm and extend the results of this study.

We demonstrated the use of hierarchical Bayesian parameter estimation with model-based fMRI, and compared this method to other non-hierarchical and non-Bayesian methods. As our results suggest, there may be a number of advantages to using HBA in studies correlating modeling predictions with both behavior and neural signals. In particular, obtaining more reliable parameter estimates from behavior may in turn better capture individual differences in neural activations underlying the behavior. If participants’ data contain enough information, then using non-hierarchical individual-level analysis (MLE-Ind or Bayes-Ind) for model-based fMRI might be sufficient. However, for many real-world scenarios, where only a limited number of trials are collected for each participant, our findings support the use of a hierarchical analysis (e.g., HBA). Although we applied the HBA to model-based fMRI, it can also be used for model-based EEG analysis (Mars et al., 2008) and model-based single-cell monkey electrophysiology analysis. HBA has been recently utilized in many areas including biostatistics, economics and cognitive modeling and has proven to be a useful method. We believe it will also be a valuable tool in model-based fMRI and hope this study will help researchers in decision neuroscience better understand and adopt HBA for their work.