The Impact of Model Uncertainty on Benchmark Dose Estimation

Abstract

We study the popular benchmark dose (BMD) approach for estimation of low exposure levels in toxicological risk assessment, focusing on dose-response experiments with quantal data. In such settings, representations of the risk are traditionally based on a specified, parametric, dose-response model. It is a well-known concern, however, that uncertainty can exist in specification and selection of the model. If the chosen parametric form is in fact misspecified, this can lead to inaccurate, and possibly unsafe, lowdose inferences. We study the effects of model selection and possible misspecification on the BMD, on its corresponding lower confidence limit (BMDL), and on the associated extra risks achieved at these values, via large-scale Monte Carlo simulation. It is seen that an uncomfortably high percentage of instances can occur where the true extra risk at the BMDL under a misspecified or incorrectly selected model can surpass the target BMR, exposing potential dangers of traditional strategies for model selection when calculating BMDs and BMDLs.

1. INTRODUCTION

An important issue in modern quantitative risk assessment is estimation of the occurrence of adverse outcomes in a target population ⁽¹⁾. This is typically accomplished by estimating the risk function, R(x), associated with the adverse effect over a broad range of exposure values, x. Often, R(x) is defined as the probability of an adverse response at exposure level x. Below, we focus on settings where the argument x in the risk function represents the dose of a toxic agent. Unknown parameters that characterize R(x) are then estimated using the observed proportions of adverse responses at a small number of exposure levels covering the range of interest. This is commonly referred to as the quantal response setting in toxicological risk analysis.

Once R(x) has been estimated, a subsequent goal is quantification of the exposure level that produces a low rate of adverse responses in the target population. This involves inversion of the estimated risk function to determine the benchmark dose (BMD) that corresponds to a given, low-level benchmark response (BMR) ^{(2, 3)}. Rather than focusing on R(x), it is common in the quantal response setting to define the BMR in terms of a benchmark level of extra risk, R_E(x) = {R(x) − R(0)}/{1 − R(0)}, which adjusts the risk for background or spontaneous effects not associated with exposure to the toxic agent ^{(4, §4.2)}. The BMD is then determined by setting R_E(x) equal to the BMR∈(0,1) and solving for x. To emphasize dependence on BMR, it is common to add a clarifying subscript via the notation BMD_100BMR. For example, we denote the benchmark exposure level with an extra risk of 0.01 (or 1%) as BMD₀₁.

Risk assessors increasingly employ the benchmark dose approach as the basis for setting exposure limits or other ‘points of departure’ (PODs) when assessing hazardous environmental stimuli ⁽⁵⁾. The United States Environmental Protection Agency (EPA) and the Organisation for Economic Co-operation and Development (OECD) provide guidance on BMD calculation for carcinogen risk analysis ^{(6, 7)}, and use of the BMD is growing for risk assessments over a number of toxicological endpoints ^(8-10).

Despite the dramatic rise in the BMD’s adoption over the past few decades, a number of issues related to the approach remain open and unsolved. Perhaps the most important of these is how selection of the parametric model for R(x) impacts the statistical characteristics of BMD estimators. Few graphical diagnostics exist that allow a risk assessor to unambiguously select a particular R(x) function for a given quantal data set. In many cases, a number of candidate models will provide a good visual fit to the observed proportions, especially at higher exposures; however, these models produce very different BMDs in the lower exposure range ^{(11, 12)}. The intertwined issues of model uncertainty, model selection, and model adequacy are therefore of great importance in benchmark analysis.

Herein, we consider selection of R(x) when BMD calculation is the goal of the risk analyst. As part of our evaluation, we study the consequences of using statistical model selection techniques to determine the ‘best’ model among a suite of candidates for a given data set. The potential impact of the approach will be studied by calculating the true extra risk at the estimated BMD_100BMR and exploring its characteristics both when the selected model is correct and when it is not. Section 2 describes the formal aspects of the model-fitting process and the statistical model selection technique. Section 3 details a Monte Carlo simulation study to examine the small-sample operating characteristics of these various selection strategies. Section 4 discusses the potential implications of our simulation results on the basic practice of risk assessment and on future research in this area.

2. BENCHMARK ANALYSIS

2.1. Statistical model for quantal-response data

For quantal data in the form of proportions, Y_i/N_i, the numerators are assumed to be independent binomial variates Y_i ~ Bin(N_i, R(x_i)) at each exposure or dose index i, where the proportion denominator N_i is the number of subjects tested, i = 1, …, I. As introduced above, R(xi) models the unknown probability that an individual subject will respond at dose x_i ≥ 0, via some assigned parametric specification. For instance, the ubiquitous logistic dose-response model is R(x) = 1/(1 + exp{−β₀ − β₁x}), while the similarly popular probit model is R(x) = Φ(β₀ + β₁x), where Φ(·) is the standard normal cumulative distribution function (c.d.f.). The unknown β-parameters are estimated from the data; maximum likelihood is a favored approach ^{(4, §A.4.3)}. The maximum likelihood estimator (MLE) of the BMD, $\mathrm{B}\widehat{\mathrm{M}}{\mathrm{D}}_{100\mathrm{BMR}}$, is found by setting the estimated extra risk function, ${\widehat{\mathrm{R}}}_{\mathrm{E}}\left(x\right)$, equal to the chosen BMR and solving for x.

To account for uncertainty in the estimation process, a 95% lower confidence limit on the true BMD, denoted by BMDL_100BMR, is also calculated ⁽¹³⁾. If the model for R(x) is correct, the associated BMDL should be at or below the true benchmark dose 95% of the time in repeated sampling. A 100(1 − α)% BMDL is built from the statistical features of the $\mathrm{B}\widehat{\mathrm{M}}\mathrm{D}$; e.g., the one-sided ‘Wald’ lower limit employs the asymptotic properties of the MLE to yield

$${\mathrm{BMDL}}_{100\mathrm{BMR}}=\mathrm{B}\widehat{\mathrm{M}}{\mathrm{D}}_{100\mathrm{BMR}}-{\mathrm{z}}_{\alpha }\mathit{se}\left[\mathrm{B}\widehat{\mathrm{M}}{\mathrm{D}}_{100\mathrm{BMR}}\right],$$ (2.1)

where zα = Φ⁻¹(1 − α) and $\mathit{se}\left[\mathrm{B}\widehat{\mathrm{M}}{\mathrm{D}}_{100\mathrm{BMR}}\right]$ is the large-sample standard error of the MLE ^{(4, §A.5.1)}.

2.2. Dose-response modeling and estimation

In addition to the logistic and probit forms, a wide variety of possible dose-response functions exists for modeling R(x). In toxicology and carcinogenicity testing, the models generally correspond to functions available from the US EPA’s BMDS software program for performing BMD calculations ⁽¹⁴⁾. Table I provides a selection of eight such dose-response models that we most often see in practice, along with their BMDs for a given BMR. The models are taken from a collection employed by Wheeler and Bailer ^{(15, 16)}. (Wheeler and Bailer also presented a possible data generating model based on the gamma distribution c.d.f., but did not use it in their calculations. In a similar vein, we do not consider the gamma model here.) Notice that certain models impose restrictions on selected parameters; these are listed in Table I to correspond with the most common constraints seen in the risk assessment literature.

Table I.

Selected quantal dose-response models common in toxicological and carcinogenic risk assessment

Model	Code	R(x)	BMD	Restrictions/Notes
Logistic	1	$\frac{1}{1+\exp \{-{\beta }_0-{\beta }_{1}x\}}$	$\frac{1}{{\beta }_1}\log \left\{\frac{1+e^{-{\beta }_0}\mathrm{BMR}}{1-\mathrm{BMR}}\right\}$	−
Probit	2	Φ(β0 + β1x)	$\frac{{\mathrm{Q}}_{\mathrm{BMR}}-{\beta }_0}{{\beta }_1}$	QBMR = Φ−1{BMR[1 −Φ(β0)] + Φ(β0)}
Quantal-linear	3	1 − exp{−β0 − β1x}	$\frac{-\ln (1-\mathrm{BMR})}{{\beta }_1}$	β0 ≥ 0, β1 ≥ 0
Quantal-quadratic	4	γ0 + (1−γ0)(1−exp{−β1x2})	$\sqrt{\frac{-\ln (1-\mathrm{BMR})}{{\beta }_1}}$	0 ≤ γ0 ≤ 1, β1 ≥ 0
Two-stage	5	1 − exp{−β0 − β1x − β2x2}	$\frac{-{\beta }_1+\sqrt{{\beta }_{1^2}+4{\beta }_2{\mathrm{T}}_{\mathrm{BMR}}}}{2{\beta }_2}$	βj ≥ 0, j = 0,1,2 TBMR = −log(1 − BMR)
Log-logistic	6	${\gamma }_0+\frac{1-{\gamma }_0}{1+\mathit{exp}\{-{\beta }_0-{\beta }_1\log [x\left]\right\}}$	$\exp \left\{\frac{{\mathrm{L}}_{\mathrm{BMR}}-{\beta }_0}{{\beta }_1}\right\}$	0 ≤ γ0 ≤ 1, β1 ≥ 0 LBMR = log{BMR/(1−BMR)}
Log-probit	7	γ0 + (1−γ0)Φ(β0 + β1log[x])	$\exp \left\{\frac{{\Phi }^{-1}\left(\mathrm{BMR}\right)-{\beta }_0}{{\beta }_1}\right\}$	0 ≤ γ0 ≤ 1, β1 ≥ 0
Weibull	8	γ0 + (1−γ0)[1–exp{−eβ0xβ1}]	$\exp \left\{\frac{{\mathrm{W}}_{\mathrm{BMR}}-{\beta }_0}{{\beta }_1}\right\}$	0 ≤ γ0 ≤ 1, β1 ≥ 1 WBMR = log{−log(1−BMR)}

Notes: The quantal linear (Model 3) model is also referred to as the ‘one-stage’ model or as the ‘complementary-log’ model, and may equivalently appear as γ₀ + (1 − γ₀)(1 − exp{−β₁x}), where γ₀ = 1 − exp{−β₀}.

The two-stage model (Model 5) and the quantal-linear/one-stage model (Model 3) are special cases of the more general ‘Multi-stage’ model in carcinogenesis testing ^{(4, §4.2.1)}.

We denote the unknown parameters of each model in Table I via the generic parameter vector b; e.g., with the log-probit model 7, β = [γ₀ β₀ β₁]^T. To find the corresponding MLEs we maximize the log-likelihood $\mathit{l}\left(\beta \right)={\sum }_{i=1}^{\mathrm{n}}\left\{{\mathrm{Y}}_i\log \right[\mathrm{R}\left(x_i\right)]+({\mathrm{N}}_i-{\mathrm{Y}}_i\left)\log \right[1-R\left(x_i\right)\left]\right\}$, up to a constant not dependent upon β. In all cases the usual regularity conditions hold for the large-sample distribution of the MLEs to approach Gaussian ^{(17, §10.6)}, although where constraints exist on the elements of β we require that the true values of those constrained parameters lie in the interior of the parameter space. Consequent large-sample standard errors are built from the inverse of the Fisher information matrix, using standard likelihood theory. With these, we find $\mathit{se}\left[\mathrm{B}\widehat{\mathrm{M}}{\mathrm{D}}_{100\mathrm{BMR}}\right]$ for use in (2.1) via a multivariate Delta-method approximation ^{(4, §A.6.2)}.

2.3. Model selection under uncertainty

The models in Table I are some of the most popular forms chosen by risk analysts for describing toxicological dose-response patterns; the number of instances where they are employed is larger than can be reasonably reviewed here. Whether the chosen form is actually correct for any given data set is of course uncertain, and as we note above, there is a concern that this level of model uncertainty can be extensive in practice, at least as regards BMD estimation.

To explore this issue more closely, we consider two basic, often-seen approaches for the model selection strategy. The first simply assumes one and only one model in Table I is valid for a given data set, and operates with that model for all benchmarking and other inferences. (We have heard this called the “pet model” strategy—perhaps derisively—since the analyst unilaterally favors a single model and essentially ignores any model uncertainty.) The second is to allow for uncertainty in the modeling process and select the model from a larger suite of Q >1 models, such as the list in Table I. Selection is based on some statistical information quantity such as Akaike’s ⁽¹⁸⁾ Information Criterion:

$${\mathrm{AIC}}_q=-2{\widehat{\mathit{l}}}_q+2{\nu }_q,$$

where ${\widehat{\mathit{l}}}_q$ is the maximized log-likelihood and ν_q is the number of free parameters to be estimated under model M_q (q = 1, …, Q). Notice that this is the “lower-is-better” form of the AIC. As a comparative selection statistic, the AIC has become popular in benchmark analysis ^(19-23), hence our focus on it here. Once selected, the model with the best (lowest) AIC is employed to perform the fit and calculate the $\mathrm{B}\widehat{\mathrm{M}}\mathrm{D}$ and BMDL. Note that in practice no additional statistical adjustment is made for this data-based selection when calculating the confidence limit, despite the fact that without such an adjustment the true confidence level of the BMDL often differs from the nominal 95% level ^{(24, §7.4)}.

3. SIMULATION STUDY

3.1. Simulation design

To compare the two basic strategies for model determination described in §2.3, we conducted a large-scale, Monte Carlo, simulation study. Due to their wide acceptance and popularity for benchmark analysis with quantal data, we centered our attention on the Q = 8 models in Table I. For the study design we chose I = 4 exposure levels: x₁ = 0.0, x₂ = 0.25, x₃ = 0.5, x₄ = 1.0, corresponding to a standard design in carcinogenicity assessment ⁽²⁵⁾. Equal numbers of subjects, N_i = N, were taken per dose group. We considered three different possibilities for the per-dose sample sizes: N = 25, 50, or 1000; the latter approximates a ‘large-sample’ setting and provides a glimpse at how the methods perform asymptotically, while the former two fall in the range of values that are more commonly used in practice.

For the true dose-response patterns we set background risks at x = 0 between 1% and 30%. The other risk levels were increased to produce a variety of (strictly) increasing forms, ending with high-dose risks at x = 1 between 10% and 90%. To set the parameters for each model, we fixed R(x) at x = 0 and x = 1 and solved for two unknown parameters. For the 3-parameter models ^(5–8), we additionally fixed R(x) at x = ½, and then solved for the third unknown parameter. The resulting parameter configurations for the various models are given in Table II. Each model/configuration pairing was simulated 2,000 times using the standard four-dose design.

Table II.

Models and configurations for the Monte Carlo evaluations

			Configuration
		A	B	C	D	E	F
	Constraint:	R(0) = 0.01	0.01	0.10	0.05	0.30	0.10
		R(1) = 0.10	0.20	0.30	0.50	0.75	0.90
Model code	Parameters
1	β 0	−4.5951	−4.5951	−2.1972	−2.9444	−0.8473	−2.1972
	β 1	2.3979	3.2088	1.3499	2.9444	1.9459	4.3944
2	β 0	−2.3263	−2.3263	−1.2816	−1.6449	−0.5244	−1.2816
	β 1	1.0448	1.4847	0.7572	1.6449	1.1989	2.5631
3	β 0	0.0101	0.0101	0.1054	0.0513	0.3567	0.1054
	β 1	0.0953	0.2131	0.2513	0.6419	1.0296	2.1972
4	γ 0	0.0100	0.0100	0.1000	0.0500	0.3000	0.1000
	β 1	0.0953	0.2131	0.2513	0.6419	1.0296	2.1972

			Configuration
		A	B	C	D	E	F
	Constraint:	R(0) = 0.01	0.01	0.10	0.05	0.30	0.10
		R(½) = 0.04	0.07	0.17	0.30	0.52	0.50
		R(1) = 0.10	0.20	0.30	0.50	0.75	0.90
Model code	Parameters
5	β 0	0.0101	0.0101	0.1054	0.0513	0.3567	0.1054
	β 1	0.0278	0.0370	0.0726	0.5797	0.4796	0.1539
	β 2	0.0675	0.1761	0.1788	0.0622	0.5501	2.0433
6	γ 0	0.0100	0.0100	0.1000	0.0500	0.3000	0.1000
	β 0	−2.3026	−1.4376	−1.2528	−0.1054	0.5878	2.0794
	β 1	1.6781	1.8802	1.7603	1.3333	1.9735	3.3219
7	γ 0	0.0100	0.0100	0.1000	0.0500	0.3000	0.1000
	β 0	−1.3352	−0.8708	−0.7647	−0.0660	0.3661	1.2206
	β 1	0.7808	0.9794	0.9456	0.8189	1.2261	1.9626
8	γ 0	0.0100	0.0100	0.1000	0.0500	0.3000	0.1000
	β 0	−2.3506	−1.5460	−1.3811	−0.4434	0.0292	0.7872
	β 1	1.6310	1.7691	1.6341	1.0716	1.4483	1.9023

Every simulated data set was fit using all Q = 8 models shown in Table I. MLEs of the BMD₀₁ and the BMD₁₀ along with their corresponding 95% Wald lower confidence limits, BMDL₀₁ and BMDL₁₀, were computed. The AIC from each qth model’s fit to every data set was also computed. While we could have considered other model selection strategies based on other criterion such as the BIC (Bayesian Information Criterion), we chose to focus on the AIC herein since it is the approach used most often by most risk assessors in practice.

All our calculations were performed in the R programming environment ⁽²⁶⁾ 64-bit version 2.13.1 on a Windows® workstation. The simulated data were generated using standard R routines for quantal data. The models were fit to the data to produce MLEs using either the standard R function glm for Models 1 and 2, box-constrained optimization via the R function optim for Models 3–5 ⁽²⁷⁾, or the R package drc ⁽²⁸⁾ for Models 6–8. A large subset of the resulting model fits were compared with the corresponding results from the EPA’s publicly available BMDS 2 software ⁽¹⁴⁾. No significant differences were found between the two packages for any of the quantities we evaluated. We employed the R package because of its more advanced capabilities for generating and managing the large data structures needed.

3.2. Monte Carlo results: single-model coverage evaluations

The first aspect studied in our simulations was the capacity of the BMDL to provide a valid lower confidence bound on the BMD if the model fit to the data is in fact correct. (No data-based selection is considered: we assume the analyst has a single model in mind and operates with it exclusively. This is the “pet model” scenario.) When the true model is correctly specified and used to build the BMDL via (2.1), statistical likelihood theory tells us that the coverage rates should approximate and approach the nominal 95% level as N increases ^{(17, §10.4)}. Happily, our simulated BMDLs exhibited stable, if slightly conservative coverage. Median coverage across all models and parameter configurations at N = 25 subjects/dose was 0.978 (interquartile range (IQR) = 0.013) at BMR = 0.01 and 0.977 (IQR= 0.016) at BMR = 0.10, while at N = 50 subjects/dose they were 0.986 (IQR = 0.011) at BMR = 0.01 and 0.980 (IQR = 0.020) at BMR = 0.10. At the larger sample size of N = 1000, the asymptotic effects began to take hold, as the average coverage rates dropped to 0.966 (IQR = 0.009) at BMR = 0.01 and 0.963 (IQR = 0.004) at BMR = 0.10.

These results require correct model specification, however. To study the effects of model misspecification, we extended our single-model coverage evaluations by fitting every possible incorrect model and calculating the resulting BMDLs. That is, we took simulated data from each of the eight models in Table I and in turn fit the other seven, incorrect models to each data set. (Again, no model selection was applied: each model was fit singularly, if purposefully incorrect.) Our results for this misspecification scenario were alarming: we found that coverage rates could literally take on any value between 0% and 100% across the constellation of models and parameter configurations we studied. Every model exhibited at least one instance of 0% coverage under some form of misspecification, and for some models BMDL coverage in the 0–25% range was about as common as coverage in the 95–100% range. Indeed, the variation in coverage rates actually increased as N grew large, with many model/configuration combinations showing lower coverage rates at N = 1000 than at N = 25. (This was not wholly unexpected: the large-sample consistency of MLEs is violated under model misspecification, and as a result the true coverage is not guaranteed to be at, or even near, the 95% level.) Worse still, we found no discernible pattern in the unstable coverage across models or configurations. Any model from Table I could produce a misspecification coverage rate of 0%, 25%, 50%, 95%, or 100%, as could any parameter configuration in Table II. (To save space, detailed results are not shown here but are available from the authors.)

In the presence of model misspecification, we conclude that the associated BMDL can perform in a completely unpredictable and possibly unstable manner, and that the analyst has no guidance on when this might occur. Construction and use of singly specified, “pet” model BMDLs must be performed with essentially unambiguous assurance that the chosen model is correct. If not, the BMDL will cover the true benchmark dose at an unpredictable level of confidence. A consequence of this effect will resurface in §3.4, below, when we discuss the capacity of the true extra risk function to attain the desired BMR when evaluated at a misspecified BMDL.

3.3. Monte Carlo results: model selection evaluations

Given the unpredictable nature of the single-model BMDLs seen in §3.2, we next evaluated the effects of employing a formal model-selection strategy when model uncertainty is a concern. In particular, can we identify the correct dose-response model for a given data set by selecting the fitted model with the smallest AIC? To assess this, we calculated the percentage of times the correct model was chosen among all simulated data sets across all configurations for a given model in Table I. The somewhat surprising results are reported in Tables III, IV, and V, representing per-dose sample sizes of N = 25, 50, and 1000, respectively. The true, correct model ^(1–8) is listed across the rows of each table and the AIC-selected model (also 1–8) is shown across the columns. The cells within a row indicate the percentage of times each of the eight candidate models was selected when the data were generated using the model indicated for that row. (Some rounding can occur.) Thus the table diagonals give the percentage of times the correct model was chosen. Disturbingly, for the smaller per-dose sample sizes of N = 25 and N = 50 the diagonal rates are noticeably low for every model configuration; only Model 3 was properly selected as the correct model over 50% of the time. (This is an intriguing observation: Model 3 is the only strictly concave dose-response function in Table I.) In general, Models 1–4, which are two-parameter models, exhibited much higher correct-selection percentages than the three-parameter forms given by Models 5–8. Indeed, at the smaller sample sizes, the three-parameter models all had less than a 6% chance of being properly selected as the correct model.

Table III.

AIC-based model selection percentages over all configurations (A–F) in Table II for per-dose sample size of N = 25

	Selected
	Model	1	2	3	4	5	6	7	8
Correct	1	16.9	14.5	26.4	35.9	0.1	3.9	1.5	0.9
	2	15.3	14.7	29.1	35	0.1	3.5	1.3	0.8
	3	8.4	9.1	56.5	19.6	0	4.5	1.9	0.1
	4	15.4	13.6	20.8	42.7	0	4.3	2	1.1
	5	12.2	13.5	34.6	33.5	0.1	3.5	1.6	0.9
	6	12.6	11.5	32.1	35.7	0	3.9	3.4	0.8
	7	12.9	11.5	31.8	36.2	0	3.5	3.3	0.7
	8	12.3	13.3	33.8	34.5	0	3.5	1.7	0.9

Table IV.

AIC-based model selection percentages over all configurations (A–F) in Table II for per-dose sample size of N = 50

	Selected
	Model	1	2	3	4	5	6	7	8
Correct	1	17.6	18.1	21.9	35	0.4	3.4	2.4	1.2
	2	15.8	18.7	25.3	34	0.4	2.8	1.9	1
	3	7.4	8.7	61.9	13.6	0.2	5.1	3	0.1
	4	15.3	14.8	15.4	45.3	0.2	3.7	3.7	1.6
	5	12.5	15.7	33.2	32.3	0.2	3	2.2	0.9
	6	12.4	12	30.6	34.7	0.1	3.5	6	0.9
	7	12.3	12	29.8	35.8	0	3.4	5.9	0.8
	8	12.6	15.2	32.2	33.5	0.2	3	2.4	0.9

Table V.

AIC-based model selection percentages over all configurations (A–F) in Table II for per-dose sample size of N = 1000

	Selected
	Model	1	2	3	4	5	6	7	8
Correct	1	41.5	29.9	2.6	15	1.6	1.1	5	3.3
	2	27.5	44.1	4.1	13	3.7	1.4	4.3	1.9
	3	1.1	3.8	77.4	0	2.4	4.3	9.9	1
	4	14.3	10	0.1	58.1	1.3	2.3	9.8	4.2
	5	20.2	24.4	12.8	18.3	7.9	3	9.1	4.4
	6	11.2	13.4	6.9	17.8	5.3	14.2	27.5	3.7
	7	7.7	8.8	3.3	21.4	2.8	11.8	41.1	3.1
	8	18.4	18.8	11	22.9	7.1	4.1	12.5	5.2

In the off-diagonal cells of each table—indicating an incorrect selection—there is an obvious preference for selecting lower-order models. The chances of selecting the correct model improve only at the larger sample size of N = 1000, but even at this very large sample size the highest percentage of proper selection is only 77.4% (at Model 3). The preference for lower-order models remains, with the three-parameter models correctly selected well less than 50% of the time. [These results appear somewhat paradoxical, since the AIC criterion is generally thought to prefer higher-order models. The effect is less substantial than often expected, however; see Claeskens and Hjort ^{(24, §8.3)}.] Even when accounting for potential model uncertainty by applying an established selection technique, we find that the process of dose-response modeling can be fraught with pitfalls, at least when employing the traditional four-dose design.

In addition to considering the rate at which the individual models were either correctly or incorrectly selected, we also considered the coverage characteristics of the associated BMDLs for the selected model based on AIC. We computed the percentage of times that the BMDL from the AIC selected model was below the corresponding benchmark dose from the true underlying model. Overall, the observed percentages were quite disconcerting and often times quite far from the target value of 95%. The coverage percentages associated with a BMR of 0.1 were generally only marginally higher than those percentages associated with a BMR of 0.01. These percentages ranged from roughly 50% to 100% across all combinations of model, configuration and dose group size. Based on the model misspecification rates discussed above, one might guess that the models with more parameters would lead to lower coverage percentages. However, we found these percentages to be much more consistent across model than configuration. For the smaller dose group sizes (N=25 and N=50), the coverage percentages tended to be on the conservative side (above 95%) in most cases, but for the more steep configurations (D-F) the percentages were often times much lower in 60% to 80% range. While these results did not vary a great deal across the models, the lowest coverage percentages were actually observed for Models 1-4. The impact of sample size on these values was interesting in that there was no observed convergence to the nominal 95% level at the larger dose group size of N=1000. Indeed many of the model/configuration pairings that were conservative for the smaller dose group sizes drifted into the 80% range at the larger dose group size while those pairings that were originally on the low side only increased marginally at the higher dose group value.

3.4. Monte Carlo results: extra risk evaluations

Given the large number of times that an incorrect dose-response model was selected in §3.3, we next attempted to quantify the impact of model misspecification. We already saw in §3.2 that the BMDL’s coverage characteristics under an incorrectly specified model can vary wildly and unpredictably. We next assessed how this translated to the core quantity of interest: the achieved extra risk at the estimated benchmark points. For each simulated data set the true extra risk was computed at the $\mathrm{B}\widehat{\mathrm{M}}\mathrm{D}$ and the BMDL using the correct model’s extra risk; i.e., we calculated $R_{\mathrm{E}}\left[\mathrm{B}\widehat{\mathrm{M}}{\mathrm{D}}_{100\mathrm{BMR}}\right]$ and R_E(BMDL_100BMR). We reasoned that if a model selection method is performing well, even in the face of model misspecification, the true R_E(x) values at the resulting $\left[\mathrm{B}\widehat{\mathrm{M}}{\mathrm{D}}_{100\mathrm{BMR}}\right]$ would hopefully cluster about the reference BMR—either 0.1 or 0.01, as the case may be in our study. Similarly, since all our models are monotone increasing functions we expect roughly 95% of the true R_E(BMDL_100BMR) values should rest below the corresponding reference BMR (preferably not too far below). By contrast, if the model selection/model specification process has gone awry, these various extra risks will differ greatly from the target BMR. Since we focus on the BMDL, we report results below for only the R_E(BMDL_100BMR) calculations.

The magnitude of the true R_E values also allows us to detect and quantify the actual extra risk in settings where estimates deviate significantly from the target BMR. Such detection is most important in situations where the true R_E exceeds the BMR, indicating potentially greater extra risk than desired by the risk manager.

The true, achieved R_E values calculated from our simulations were separated into three sets for comparison. The first comparison set contains the true extra risks when the correct model (‘CM’) was fit to the simulated data. This represents an ideal standard where we expect about 95% of the consequent R_E(BMDL_100BMR) values to be (slightly) below the BMR. The second comparison set contains the true R_E values that result from incorrectly fitting all of the other models (‘OM’) to the simulated data; e.g., if the data were generated under the logistic, Model 1, we calculated BMDL_100BMRs when all the other models ^(2–8) were fit to the data, and then determined the (true) logistic R_E at each of these seven BMDLs. This OM set provides an overall look at the range of true extra risks that can occur if an incorrect model is specified for a given data set. The third set contains the true R_E values if active, AIC-based selection was conducted prior to computation of the BMDL. The acronym ‘SM’ will denote this in what follows. Note that this last set is not mutually exclusive from the previous two, as the selected model is obviously either the correct model or one of the other, incorrect models. The SM set describes the impact of AIC-based model selection on the resulting extra risks.

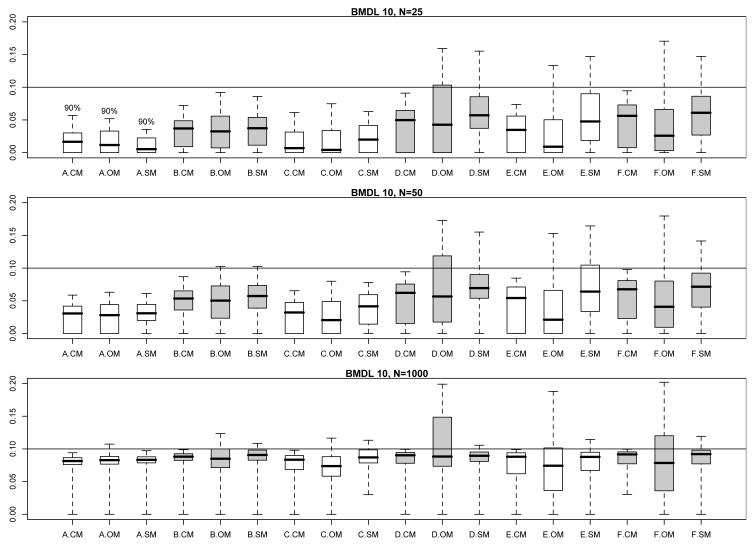
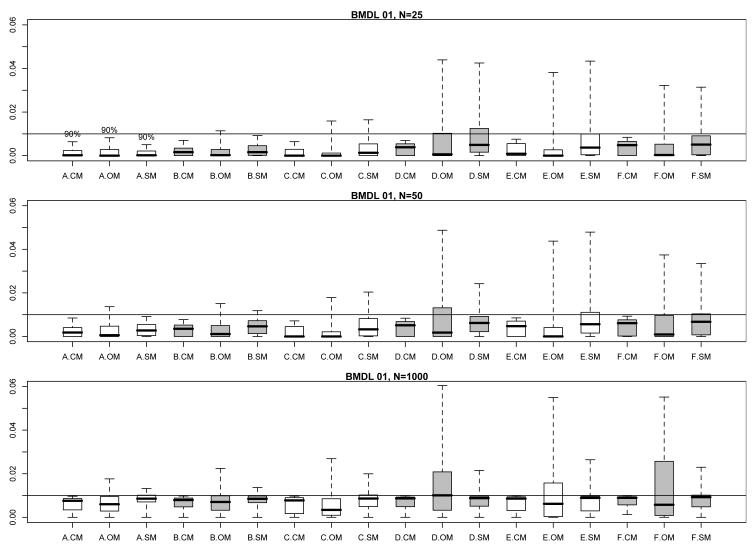
Figs. 1 and 2 encapsulate the extensive information available in these extra risk evaluations. They display modified boxplots of the true values for R_E(BMDL₁₀) (Fig. 1) and R_E(BMDL₀₁) (Fig. 2) stratified by parameter configuration and by comparison set (CM, OM, or SM) at each per-dose sample size. Thus each modified boxplot pools true extra risks across all models in the pertinent comparison set. The boxplots have been modified from the traditional format so that their upper hinges represent the 95th percentile of the true extra risk values for that configuration/comparison group combination (but, also see below). This avoids display of extremely large extra risks that extend the vertical range and limit the amount of visible information across the comparison boxplots. This was especially a problem for smaller sample sizes with configurations A and B, which have a very shallow risk function. Shallow risk functions can produce very flat response patterns; the consequent BMDLs are then driven far from zero and the associated, true values of R_E(BMDL_100BMR) reach close to one.

Fig. 1.

Modified boxplots of the true extra risk at calculated 95% BMDLs from the simulation results in §3; BMR = 0.10. (See text for details of the modifications.) Results are pooled across all eight models from Table I. Three boxplots are displayed for each parameter configuration, A–F, from Table II. A ‘.CM’ suffix corresponds to BMDLs calculated under the correct dose-response model in Table I. A ‘.OM’ suffix corresponds to BMDLs incorrectly calculated under the other models in Table I. A ‘.SM’ suffix corresponds to BMDLs calculated under the model actively selected from minimizing the AIC. The upper comparison graphic presents results for a per-dose sample size of N = 25, the middle graphic for a per-dose sample size of N = 50, and the lower graphic for a per-dose sample size of N = 1000. Shadings separate different configurations.

Fig. 2.

Modified boxplots of the true extra risk at calculated 95% BMDLs from the simulation results in §3; BMR = 0.01. (See text for details of the modifications.) Results are pooled across all eight models from Table I. Three boxplots are displayed for each parameter configuration, A–F, from Table II. A ‘.CM’ suffix corresponds to BMDLs calculated under the correct dose-response model in Table I. A ‘.OM’ suffix corresponds to BMDLs incorrectly calculated under the other models in Table I. A ‘.SM’ suffix corresponds to BMDLs calculated under the model actively selected from minimizing the AIC. The upper comparison graphic presents results for a per-dose sample size of N = 25, the middle graphic for a per-dose sample size of N = 50, and the lower graphic for a per-dose sample size of N = 1000. Shadings separate different configurations.

In addition to providing a more comparative graphic, the modified boxplots also allow one to visually estimate the coverage probability of the associated BMDLs: when the modified upper hinge is above the reference BMR (the horizontal line in each figure) this suggests that fewer than 95% of the simulated BMDLs lie below the true BMD, hence coverage for that BMDL falls short of the nominal 95% level. On the other hand, if the upper hinge is below the BMR, then the BMDL values are conservative in nature.

We made one additional modification to the boxplots in Figs. 1 and 2: as noted above, the shallow dose response for configuration A led to very large BMDLs and consequent extra risks near 1.0. Even when limited to the 95th percentile, the upper hinges for configuration A were so high that visually clarity was obscured in the graphic. To compensate, we set the upper hinge for configuration A boxplots to only the 90^th percentile. This is indicated by the “90%” symbol above the hinges in each figure.

The comparisons in Figs. 1 and 2 indicate that the CM BMDLs are generally conservative at smaller sample sizes, as their displayed upper hinges are often below the BMR. This corresponds with our coverage evaluations in §3.2, above. As the sample size increases to N = 1000, the CM upper hinges converge appropriately to the BMR reference value, which again validates the large-sample coverage characteristics of the underlying Wald confidence limit.

The patterns of variation in Figs. 1 and 2 for the true extra risks under the incorrect model fits (OM) and the AIC-selected model fits (SM) are far more problematic. Perhaps not surprisingly, the interquartile ranges (IQRs) of the CM boxplots are typically much smaller than those of the OM boxplots, while those for the SM boxplots fall somewhere in between. For the combination of shallow dose-response curves (configurations A–C) and small sample size (N = 25 or 50), the OM and SM extra risks occasionally appear conservative. As the sample size increases to N = 1000, however, both the OM and SM upper hinges move above the BMR, although this may only be for a small amount. The corresponding third quartiles tend to match closely with the target BMR, suggesting corresponding substandard coverage percentages in the 75% range for the underlying BMDLs.

For the configurations (D–F) with richer and steeper curvilinearity, the OM and SM extra risks in Figs. 1 and 2 exhibit much greater variability: wider IQRs and upper hinges extending alarmingly beyond the target BMR are more the rule. This is true across all sample sizes. Perhaps the worst-case example occurs with OM configuration D at a per-dose sample size of N = 1000. In this case, roughly 50% of the true R_E values exceed the target BMR (in both Fig. 1 and Fig. 2). In Fig. 1, the corresponding upper hinge extends up to 0.20 indicating true extra risks double that of the target value. In Fig. 2, the corresponding upper hinge reaches an extra risk of 0.06; not as disturbing in absolute value, but now six-fold larger than the BMR in a relative sense. The picture is not quite as bleak for SM values across the steeper configurations (D–F), but we still find upper hinges well above the target BMRs at all sample sizes.

4. DISCUSSION

The results of our simulation study in §3 should be reason for pause among practicing risk analysts. As a regulatory tool, the goal of the BMDL approach is to help set low exposure levels that limit the (extra) risk of an adverse effect to predetermined levels, quantified via the BMR. While much prior study on the BMDL has emphasized statistical characteristics such as coverage probability—and for completeness we include similar evaluations here—our results focus on the true extra risk achieved at the estimated BMDL. Our simulations expose an uncomfortably high percentage of cases where the true extra risk at a misspecified or incorrectly selected BMDL can surpass the target BMR; exceedances can surpass six times the desired level in the most extreme cases. In many risk assessment scenarios, we expect that such an exceedance in extra risk would be deemed unacceptable. It has been known for some time ^{(11, 12)} that a variety of models can fit a dose-response pattern fairly well in the observed data range, and yet provide disparate $\mathrm{B}\widehat{\mathrm{M}}\mathrm{Ds}$ and BMDLs at low doses. Our evaluations further drive home this point, now in terms of a potential, undesirable increase in extra risk when an incorrect model is used to calculate a $\mathrm{B}\widehat{\mathrm{M}}\mathrm{D}$ or BMDL.

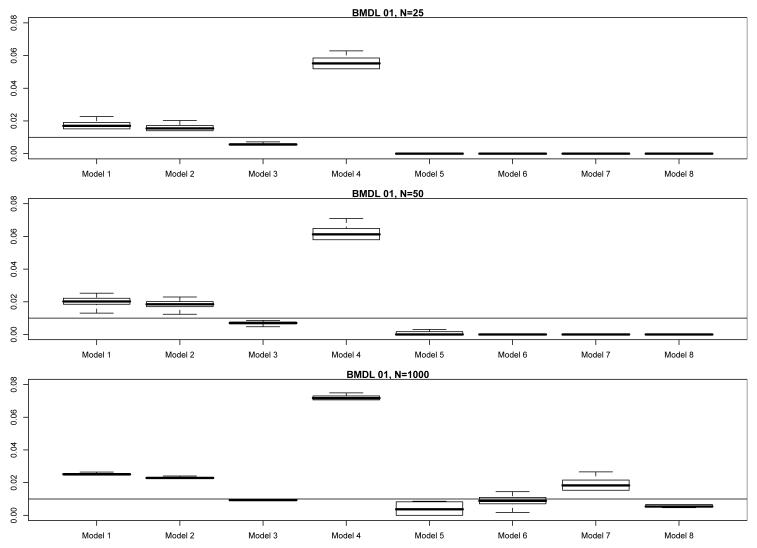
While the results in §3 provide a broad description of the consequences when fitting an incorrect model to dose-response data, quantifying the impact of any particular misspecification is quite difficult to do. As we have seen, the impacts of model misspecification fluctuate, and depend on the particular nature of the incorrectly fitted model, the underlying/correct model, the sample size, etc. For example, return to the simulation results in §3 and consider Model 3 from Table I, the popular quantal-linear model R(x) = 1 − exp{−β₀ − β₁x}. Fix the underlying parameterization from Table II as configuration D. In Fig. 3 we display modified boxplots, as per §3.4, of the true values of R_E(BMDL₀₁), stratified horizontally by actual model fit, and vertically by per-dose sample size, N. As expected, when Model 3 is correctly fit to the data, the boxplots are fairly tight and rest slightly below the target BMR. When an incorrect model is fit to the data, however, the results vary: at N = 25 and N = 50, fitting Models 1, 2, and 4 produces anticonservative extra risks ranging from two to almost eight times that of the target BMR = 0.01, but the three-parameter model fits exhibit conservative extra risks that lie well below the BMR. At N = 1000, however, the true extra risks for Models 1, 2, and 4 tighten up, and they are now joined by those from Model 7 in moving up and away from the BMR. The Model 7 extra risks now exhibit larger IQRs, however, as do those from Models 5 and 6. The extra risks from Model 4 are perhaps most disturbing: they consistently rest six-times as high, and often higher, as the target BMR. (Model 4 is the quantal-quadratic function, which though more flexible than the strictly concave quantal-linear Model 3, is very similar in mathematical form. Apparently, this similarity is irrelevant: the increased flexibility is driving the BMDLs too far above the true BMD and the corresponding extra risks too far above the BMR.)

Fig. 3.

Modified boxplots of the true extra risk at calculated 95% BMDLs from the simulation results in §3 for Model 3 under configuration D; BMR = 0.01. (See text for details of the modifications.) The upper comparison graphic presents results for a per-dose sample size of N = 25, the middle graphic for a per-dose sample size of N = 50, and the lower graphic for a per-dose sample size of N = 1000.

The results in Fig. 3 illustrate that the impacts of model misspecification depend largely on which model is fit to the data. In some cases, an incorrect model leads to conservative BMDLs and extra risks, while in others an incorrect model has the more drastic impact of inflating the BMDLs and pushing true extra risks to several times the desired BMR.

Our simulation results also suggest that a simple, AIC-based selection strategy does not solve the problems of model misspecification. We found that the selection process more often than not identifies an incorrect model. AIC-based selection does help reduce the magnitude of exceedances above BMR seen in the values of R_E(BMDL_100BMR), compared to no selection and incorrect specification. These reductions do not always drop excessive extra risks down to the target BMR, however. In addition, the nominal 95% confidence level for the BMDL can erode after model selection is implemented: we observed coverage rates down to 75% for some SM model/configuration combinations.

In practice, the situation may be even more complex than presented here. Given our warnings, risk analysts might be tempted to expand the suite of models being fit, in order to increase their odds of selecting a correct form. There is just as much possibility, however, that this will increase the chance of selecting an incorrect model and damage the risk estimation process even further. In such settings, the analyst may literally be “searching in the dark” for the appropriate $\mathrm{B}\widehat{\mathrm{M}}\mathrm{D}$ and BMDL, and in the best case can only hope to find values that produce extra risk values that are vaguely in the vicinity of the desired BMR for the agent under study. Furthermore, the results of model selection appear to be even more negatively impacted in situations where the risk function changes steeply over the observed dose range.

Readers should be careful in how they generalize the results described above to all dose-response studies. For example, based on Tables III–V one should not trust that lower-order models would typically be best for quantal data sets simply because they appear to be selected more often. Likewise, one should not consider model selection to be unimportant for studies with small/shallow increases in the observed dose response. For any realized set of quantal data, the true coverage probability or the true extra risk at the BMDL may be distinctly better or worse than what we present here.

Perhaps our most important conclusion is that the quality of a parametrically calculated BMDL appears unpredictable in the presence of model uncertainty. We do not feel this is a testament against the BMD approach; in fact, we are strong supporters of its continued and expanded use in quantitative risk assessment. Our message and call is for much more careful use of the method in practice, and for further research to develop advanced statistical techniques that better incorporate the effects of model uncertainty. We are exploring a number of possibilities towards these ends, including model averaging approaches and approaches based on focus-based inference. We hope to report on them in future manuscripts.

Lastly, although we did not focus on it here, we recognize that dose selection and design also impact the qualities of the BMDL ^(29-31). We concentrated on a four-dose design due to its popular use in toxicology ⁽³²⁾. Clearly, however, the limited amount of information available in only four distinct doses makes powerful model selection and efficient parameter estimation extremely difficult. Further research is also necessary to determine how designs with more, well-placed doses can overcome the issue of model uncertainty and improve risk estimation in benchmark analysis.