Coaching Competency and (Exploratory) Structural Equation Modeling: A Substantive-Methodological Synergy

Abstract

Objectives

The purpose of this manuscript was to provide a substantive-methodological synergy of potential importance to future research in the psychology of sport and exercise.

Design

The substantive focus was the emerging role for, and particularly the measurement of, athletes’ evaluations of their coach's competency within conceptual models of effective coaching. The methodological focus was exploratory structural equation modeling (ESEM), a methodology that integrates the advantages of exploratory factor analysis and confirmatory factor analysis (CFA) within the general structural equation model.

Method

The synergy was a demonstration of when a new and flexible methodological framework, ESEM, may be preferred as compared to a more familiar and restrictive methodological framework, CFA, by reanalyzing existing data.

Results

ESEM analysis on extant datasets suggested that for responses to the Athletes’ Perceptions of Coaching Competency Scale II – High School Teams (APCCS II-HST), a CFA model based on the relevant literature plus one post hoc modification, offered a viable alternative to a more complex ESEM model. For responses to the Coaching Competency Scale (CCS), a CFA model based on the relevant literature did not offer a viable alternative to a more complex ESEM model.

Conclusions

The ESEM framework should be strongly considered in subsequent studies validity studies - for new and/or existing instruments in the psychology of sport and exercise. A key consideration for deciding between ESEM and the accompanying rotation criterion and CFA in future validity studies should be level of a priori measurement theory.

Factor analysis has been closely linked with investigations of construct validity in psychology for several decades (Nunnally, 1978). Investigations of construct validity (e.g., scale development) in exercise and sport have frequently occurred in studies where only factor analytic measurement model(s), exploratory and/or confirmatory, were specified – typically guided by important, yet incomplete, a priori substantive measurement theory (Myers, Ahn, & Jin, 2011a). Incomplete substantive measurement theory often manifests as model error and offers a possible explanation as to why the majority of construct validity studies in psychology fail the test of exact fit under a strictly confirmatory approach (Jackson, Gillaspy, & Purc-Stephenson, 2009).¹ Construct validity studies that incorporate an exploratory methodological approach typically reduce model error, as compared to a confirmatory approach, but may fail to adequately incorporate a priori substantive measurement theory (Asparouhov & Muthén, 2009).

What constitutes a sufficient degree of a priori substantive measurement theory, and therefore should lead to a preference for a more restrictive confirmatory approach versus a more flexible exploratory approach, is an emerging area of methodological research of potential importance to substantive research in the psychology of sport and exercise. Simulation research suggests that a key consideration for deciding between exploratory structural equation modeling (ESEM; Asparouhov & Muthén, 2009) and confirmatory factor analysis (CFA; Jöreskog, 1969) in future validity studies should be level of a priori substantive measurement theory (Myers, Ahn, & Jin, 2011b). In the Myers et al. simulation study model-data fit was manipulated (as a proxy for level of a priori substantive measurement theory) with small but non-zero values in both the pattern coefficient matrix and in off-diagonals of the residual covariance matrix. Under exact (with ESEM having errors of inclusion) and close (with both ESEM and CFA having errors of exclusion) model-data fit, CFA generally performed at least as well as ESEM in terms of parameter bias, and was cautiously recommended when a priori substantive measurement theory can be viewed as at least close. Under only approximate model-data fit, on balance, ESEM performed at least as well as CFA and was cautiously recommended when a priori substantive measurement theory can be viewed as only approximate.

This invited manuscript demonstrates by way of an extant conceptual model (i.e., coaching competency) when a new and flexible methodological framework, ESEM, may be preferred as compared to a more familiar and restrictive methodological framework, CFA, within a substantive-methodological synergy format (Marsh & Hau, 2007). For spatial reasons this manuscript focuses primarily on the synergy by way of relevant empirical examples. Fuller reviews of both the relevant substance (Myers & Jin, 2013) and technical aspects of the broader methodology (e.g., Asparouhov & Muthén, 2009) are available elsewhere. From this point forward the acronym, (E)SEM, is used when referring to both ESEM and CFA simultaneously.

Coaching Competency: The Substance

The Coaching Competency Scale (CCS; Myers, Feltz, Maier, Wolfe, & Reckase, 2006) was derived via minor changes to the Coaching Efficacy Scale (CES; Feltz, Chase, Moritz, & Sullivan, 1999). The CES was developed to measure a coach's belief in his or her ability to influence the learning and performance of his or her athletes. The specific factors measured—instructional technique, motivation, character building, and game strategy—purposely overlap with key expected competency domains articulated in the National Standards for Athletic Coaches (National Association for Sport and Physical Education, 2006) and are congruent with self-efficacy theory (Bandura, 1997). According to Horn's (2002) model of coaching effectiveness, however, why a coach's beliefs (e.g., coaching efficacy) are related to athletes’ self-perceptions and performance is due to the influence that these beliefs exert on a coach's behavior. But, the influence that a coach's behavior exerts on athletes’ self-perceptions, motivation, and performances is mediated, at least in part, by athletes’ evaluations of their coach's behavior. The purpose of the CCS, therefore, was to measure athletes’ evaluations of their head coach's ability to affect the learning and performance of athletes. There is evidence that measures derived from both the CCS relate to theoretically relevant variables (e.g., Bosselut, Heuzé, Eys, Fontayne, & Sarrazin, 2012).

The measurement model for the CCS posited that four latent variables covary and influence responses to 24 items. From this point forward the terms competency and efficacy were generally not included alongside any particular dimension of coaching competency. Motivation was defined as athletes’ evaluations of their head coach's ability to affect the psychological mood and skills of athletes. Game strategy was defined as athletes’ evaluations of their head coach's ability to lead during competition. Technique was defined as athletes’ evaluations of their head coach's instructional and diagnostic abilities. Character building was defined as athletes’ evaluations of their head coach's ability to influence the personal development and positive attitude toward sport in their athletes. Myers, Feltz et al. (2006) referred to this multidimensional construct as coaching competency. High school and lower division collegiate athletes of team sports comprise populations for which the CCS was intended.

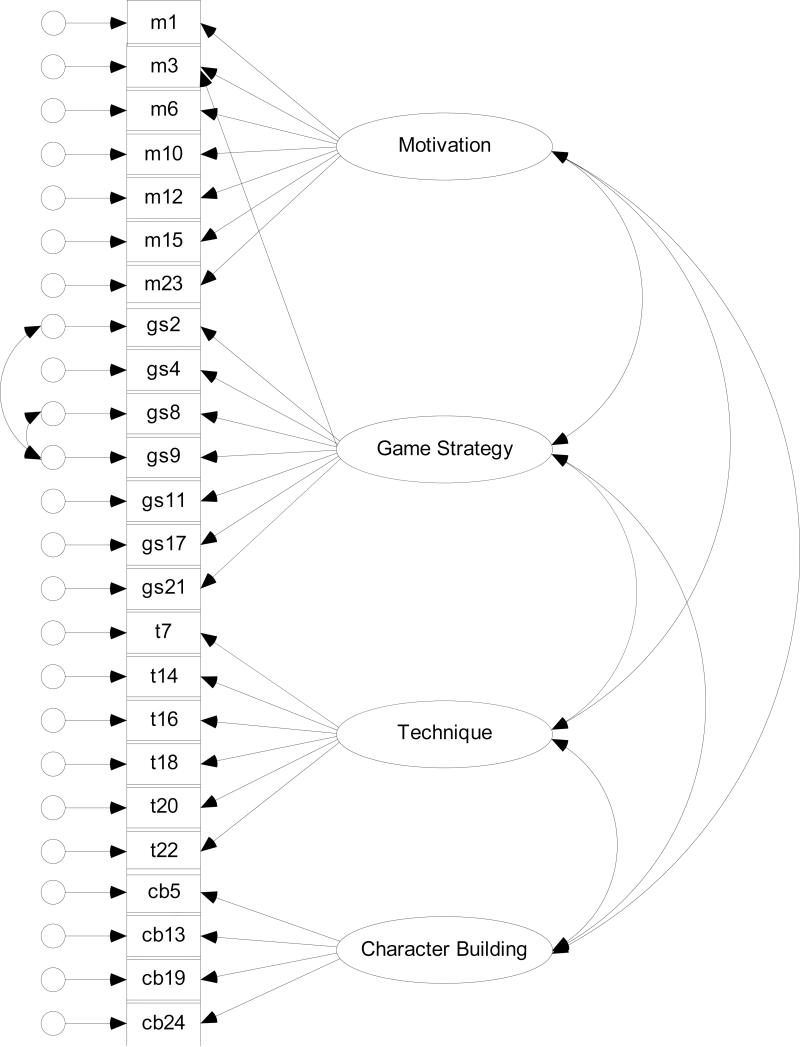
Model-data fit within the CFA framework for the CCS (as well as the CES - see Myers & Jin, 2013) has generally not met heuristic values for close fit (e.g., Hu & Bentler, 1999). Myers, Feltz, et al. (2006) reported the following model-data fit for non-division I collegiate athletes (N = 585) clustered within men's (g = 8) and women's (g = 24) teams: χ²(246) = 1266, CFI = .91, Tucker-Lewis index (TLI) = .90, and RMSEA = .09. Post hoc modifications by Myers, Feltz, et al. included allowing a motivation item to also indicate game strategy and freeing the covariance between two pairs of residual variances (see Figure 1). Interfactor correlations in the Myers, Feltz et al. study ranged from r_{technique, character building} = .80 to r_{game strategy, technique} = .92. Given the high interfactor correlations, Myers, Feltz, et al. explored models with fewer latent variables, all of which yielded statistically significant worse fit.

Figure 1.

Athlete-level a priori measurement model for the CCS

Responses to the CCS have a history of dependence based on athletes nested within teams. Myers, Feltz, et al. (2006) reported item-level intraclass correlation coefficients (ICC) ranging from .22 to .44, M = .32, SD = .05. Multilevel CFA is an appropriate methodology when data violate the assumption of independence (Muthén, 1994). Simulation research has indicated, however, that a relatively large number of groups (~100) may be necessary for optimal estimation, particularly at the between-groups level (Hox & Maas, 2001). When group-level sample size is not large, imposing a single-level model on the within-groups covariance matrix, S_W, as opposed to the total covariance matrix, S_T, controls for probable biases in fitting single-level models to multilevel data (Julian, 2001). Myers, Feltz, et al. modeled the S_W.

The Coaching Efficacy Scale II-HST (CES II-HST) was derived via major changes to the CES as detailed in Myers, Feltz, Chase, Reckase, and Hancock (2008) and Myers, Feltz, and Wolfe (2008). The Athletes’ Perceptions of Coaching Competency Scale II – High School Teams (APCCS II-HST) was derived via minor changes to the CES II-HST as detailed in Myers, Chase, Beauchamp, and Jackson (2010). Thus, moving from either CES to the CES II-HST, or the CCS to the APCCS II-HST, resulted in non-equivalent measurement models. There is evidence that measures derived from the APCCS II-HST relate to theoretically relevant variables (Myers, Beauchamp, & Chase, 2011) in a doubly latent multilevel model (Marsh et al., 2012).

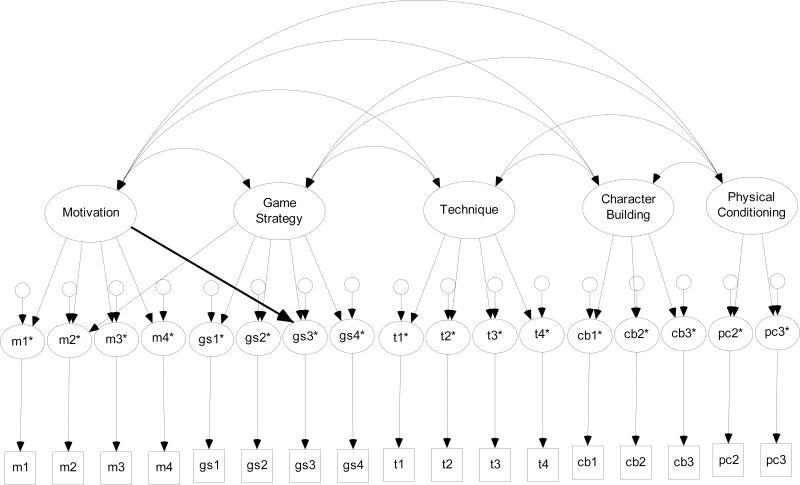
The measurement model for the APCCS II-HST occurred at two-levels in Myers et al. (2010) because there was strong evidence for dependence due to the clustering of athletes (N = 748) within teams (G = 74). Specifically, ICCs ranged from .18 to .35, M = .29, SD = .05. There was evidence for close fit for the multilevel measurement model: ${\chi }_R^2\left(201\right)$ ranged from 375, p < .001, to 405, p < .001, RMSEA = .04, CFI = .99, TLI = .99, SRMR_within = .03, and SRMR_between = .04.² Evidence also was provided for both the stability of all latent variables and for the reliability of composite scores. There is evidence, at least in regard to a crude comparison of model-data fit, that the measurement model underlying responses to the APCCS II-HST may be better understood (by researchers) than the measurement model underlying responses to the CCS. While Myers et al. took a multilevel approach, the focus of this manuscript was on the athlete-level (Level 1) model only.

The measurement model for the APCCS II-HST specified that five dimensions of coaching competency covary and influence responses to 17 indicators. Motivation (M) was measured by four items and was defined as athletes’ perceptions of their head coach's ability to affect the psychological mood and psychological skills of her/his athletes. Game strategy (GS) was measured by five items and was defined as athletes’ perceptions of their head coach's ability to lead his/her athletes during competition. Technique (T) was measured by four items and was defined as athletes’ perceptions of their head coach's ability to utilize her/his instructional and diagnostic skills during practices. Character building (CB) was measured by three items and was defined as athletes’ perceptions of their head coach's ability to positively influence the character development of his/her athletes through sport. Physical conditioning (PC) was measured with two items and was defined as athletes’ perceptions of their head coach's ability to prepare her/his athletes physically for participation in her/his sport. Figure 2 depicts the athlete-level measurement model put forth by Myers et al. (2010) - less the bolded arrow.³

Figure 2.

Athlete-level a priori measurement model for the APCCS II-HST. Thick (bolded) arrow denotes a post hoc modification proposed in this manuscript.

There is growing evidence for the importance of coaching competency in coaching effectiveness models. An important foundational question for this emerging line of research going forward is: how best to derive measures from responses to the CCS and APCCS II-HST? In cases where the population of interest is high school team sports the APCCS II-HST, and its proposed measurement model, seems appropriate. In cases where the population of interest is not high school team sports the CCS, and its less well understood measurement model, may be appropriate. While the measurement model for CCS appears to be understood at a level below typical close-fitting CFA standards, it also seems to be understood better than imposition of a mechanical EFA model would imply. Perhaps a framework situated between traditional EFA and traditional CFA would be appropriate for deriving measures from responses to the CCS.

(Exploratory) Structural Equation Modeling: The Methodologies

Asparouhov and Muthén (2009) introduced ESEM as a methodology that integrates the relative advantages of both EFA and CFA within the general structural equation model (SEM). A technical paper (Asparouhov & Muthén) and a substantive-methodological synergy (Marsh et al., 2009) introduced ESEM to the methodological community. The general ESEM allows for parameterizations beyond EFA, but given the measurement focus of this manuscript, only reduced versions of ESEM (i.e., EFA and Multiple-Group EFA in ESEM) are reviewed.⁴ Prior to introducing the reduced equation below, however, a brief history is provided because this history may inform how researchers have decided between EFA and CFA over the last few decades.

Over a century ago Spearman (1904) articulated what has become to be known as EFA. Several decades after this articulation, EFA became a widely used multivariate analytic framework in many disciplines. Over the past few decades, however, some limitations in the way EFA is typically implemented in software, in addition to rotational indeterminacy more generally, has likely impeded the use of the technique in favor of CFA - even when the level of a priori measurement theory was insufficient to warrant a confirmatory approach.⁵ Examples of limitations in the way that EFA has typically been implemented in software include the absence of standard errors for parameter estimates, restrictions on the ability to incorporate a priori content knowledge into the measurement model, an inability to fully test factorial invariance, and an inability to simultaneously estimate the measurement model within a fuller structural model.

The most commonly used measurement model within SEM likely is Jöreskog's (1969) CFA (Asparouhov & Muthén, 2009). CFA provides standard errors for parameter estimates, allows a priori content knowledge to guide model specification, provides a rigorous framework to test factorial invariance, and allows the measurement model to be a part of a fuller structural equation model. An often overlooked but necessary condition for appropriate use of CFA, however, is a sufficient level of a priori measurement theory. Absence of such theory often results in an extensive post hoc exploratory approach guided by modification indexes. Such an approach is susceptible to producing an accepted model that is inconsistent with the true model – despite possible consistency with a particular dataset (MacCallum, Roznowski, & Necowitz, 1992). EFA, not CFA, may often be the better framework for post hoc explorations in search of a well-fitting measurement model (Browne, 2001).

A common misspecification in CFA is when nonzero paths from latent variables to measurement indicators are fixed to zero. This type of misspecification often results in upwardly biased covariances between the latent variables and biased estimates in the non-measurement part of the structural equation (Asparouhov & Muthén, 2009). Both of these problems can, and probably have, impeded research in sport and exercise psychology. An example of upwardly biased covariances between latent variables may have occurred in Myers, Feltz, et al. (2006). It is impossible, however, to know for certain that biased (upwardly or downwardly) parameter estimates are observed in any case where the population parameter values are unknown.

In Mplus (Muthén & Muthén, 1998-2010), the ESEM approach integrates the relative advantages of EFA and CFA within SEM. Like EFA, ESEM imposes fewer restrictions on the measurement model than common implementations of CFA and integrates advances in possible direct rotations of the pattern matrix. Like CFA, ESEM can be part of a general SEM which affords much greater modeling flexibility than observed in the traditional EFA framework. In fact, within a single SEM specification, both CFA and ESEM can be imposed simultaneously. This latter point is of special interest because when sufficient a priori measurement theory exists, the more parsimonious CFA is preferred (Asparouhov & Muthén, 2009). An important methodological question within the psychology of sport and exercise research going forward is: What constitutes a sufficient degree of a priori substantive measurement theory, and therefore should lead to a preference for a more restrictive (i.e., parametrically parsimonious) CFA approach versus a more flexible (i.e., parametrically non-parsimonious) EFA approach?

EFA in ESEM

EFA in ESEM can be written with two general equations: one for the measurement model and one for the latent variable model (Bollen, 1989). Given the focus of this manuscript neither equation will be provided here but a review of each equation is available in Appendix A of the supplemental electronic-only materials. It is important to note, however, that as compared to ESEM, the form of the measurement equation is identical for CFA but more restrictions typically are placed on it by the researcher (e.g., many elements within the pattern matrix, Λ, are fixed to 0). Thus, a primary difference between EFA in ESEM and CFA is the restrictions placed on Λ.

Rotation

Direct analytic rotation of the pattern matrix is based on several decades of research within the EFA framework as detailed in Browne (2001) and summarized in Appendix B_1 of the supplemental electronic-only materials. Geomin rotation (Yates, 1987) is the default rotation criterion in Mplus and, therefore, may be used frequently in practice. Geomin, however, “...fails for more complicated loading matrix structures involving three or more factors and variables with complexity 3 and more;...For more complicated examples the Target rotation criterion will lead to better results” (Asparouhov & Muthén, p. 407). Target rotation has been developed over several decades and can be thought of as “a non-mechanical exploratory process, guided by human judgment” (Browne, p.125). It is important to note that a solution will be mathematically equivalent under either target or geomin rotation. Simulation research suggests, however, that in some cases the factors may be defined more consistent with a well-developed a priori theory under target rotation as compared to geomin rotation (Myers, Jin, & Ahn, 2012).

Multiple-Group EFA in ESEM

Measurement invariance is necessary to establish that measures are comparable across groups for which inferences are sought (Millsap, 2011). Providing evidence for measurement invariance across groups for which an instrument is intended is an important facet of validity evidence (AERA, APA, NCME, 1999). Until very recently, however, fully testing for measurement invariance across groups forced researchers to use the CFA framework (Asparouhov & Muthén, 2009). Multiple-group EFA in ESEM allows researchers to fully test for measurement invariance across groups within an exploratory framework.

Measurement of Coaching Competency within (E)SEM: The Synergy

EFA in ESEM

An important question for the emerging line of research involving coaching competency within coaching effectiveness models going forward is: how best to derive measures from responses to the CCS and APCCS II-HST? An important methodological question within effective coaching research going forward is: how can researchers apply (E)SEM to evaluate models of effective coaching? The purpose of this section was to attempt to address both questions by demonstrating how (E)SEM may be used guided by content knowledge to develop better, or confirm existing, measurement models for coaching competency.

Two primary research questions drove subsequent analyses on extant datasets. Extant datasets were used for both demonstration purposes and to see if the new ESEM approach offered benefits not available when each dataset was originally analyzed. The first question was: how many factors were warranted to explain responses to the APCC II-HST/CCS? The first question was answered in two steps. Step 1, number of factors (m), considered the fit of a particular ESEM model. Step 2, m, considered the relative fit of a ESEM model as compared to a more complex alternative.⁶ Thus, m denoted number of factors and not necessarily the number of factors consistent with substantive a priori measurement theory. Nested models were compared with the change in the likelihood ratio χ² (robust) test, $\Delta {\chi }_R^2$, with the DIFFTEST command (Asparouhov & Muthén, 2010).⁷ The approach taken in Step 2 was susceptible to over-factoring and inflated Type I error (Hayashi, Bentler, & Yuan, 2007). Therefore α was set to .01 for these comparisons (.05 otherwise) and the interpretability of the estimated rotated pattern matrix ${\widehat{\Lambda }}^{\ast }$ also was considered (i.e., incorporating content knowledge) when deciding which model to accept. The second question was: could a more parsimonious CFA model, based on the relevant literature, offer a viable alternative to a more complex ESEM model? If the answer to Question 2 was no, a follow-up question was: which rotation method was preferred? Consistent with weaknesses of the $\Delta {\chi }_R^2$ with real data and imperfect theories (Yuan & Bentler, 2004) and the utility of strict adherence to the null hypothesis testing framework with regard to the assessment of model-data fit (Marsh et al., 2004), a collection of fit indices were considered.

Methods

APCCS II-HST data from Myers et al. (2010) were re-analyzed. Athlete-level sample size was 748 and team-level sample size was 74. Seven relevant sports were represented. Girls’ (n = 321, g = 35) and boys’ (n = 427, g = 39) teams were included. Age data ranged from 12 to 18 years (M =15.46, SD = 1.51).

CCS data from Myers, Feltz, et al. (2006) were reanalyzed. Athlete-level sample size was 585 and team-level sample size was 32. Data were collected from lower division intercollegiate men's (g = 8) and women's (g = 13) soccer and women's ice hockey teams (g = 11). Age data ranged from 19 to 23 years (M =19.53, SD = 1.34).

At the time of the writing of this manuscript ESEM could not be fitted within a multilevel framework in Mplus (L. Muthén, personal communication, January 11, 2013). The multilevel nature of the data was handled via the TYPE = COMPLEX command. This resulted in modeling S_T with non-independence accounted for in the computation of standard errors and in relevant model-data fit indices and parallels an approach taken in Asparouhov and Muthén (2009, p. 412). Models were not fit to S_W because summary data are not allowed in Mplus for ESEM (T. Nguyen, personal communication, February 22, 2013).

APCCS II-HST data were treated as ordinal due to the four-category rating scale structure (Finney & Distefano, 2006). Weighted least squares mean- and variance-adjusted (WLSMV; Muthén, 1984) estimation was used.⁸ CCS data were treated as continuous and normal, with a correction for non-normality, due to the original ten-category rating scale structure. Geomin rotation (ε value varied based on m: .0001 when m = 2, .001 when m = 3, .01 when m ≥ 4) was used for Question 1. Target rotation was used for Question 2. Key input files for subsequent examples are available in Appendix E of the supplemental electronic-only materials.

Deriving Measures from the APCCS II-HST: Question 1

The null hypothesis for exact fit was rejected until six factors were extracted. For fuller results see Table 1s in Appendix C of the supplemental electronic-only materials. From this point forward a Table/Figure number denoted with an “s” suggests that the Table/Figure is located in the supplemental electronic-only materials. The sixth factor of ${\widehat{\Lambda }}^{\ast }$, however, was judged as not interpretable and likely the result of over-factoring as only three elements (m1, t4, c3) in this column were statistically significant and the interfactor correlations for this factor ranged from .07 to .17 – each of which was statistically non-significant. The five factor solution (i.e., Model 5) was accepted despite exhibiting statistically significant worse fit than the sixth factor solution, $\Delta {\chi }_R^2\left(12\right)=31,p=.002$. There was evidence for close fit of Model 5: ${\chi }_R^2\left(61\right)=88$, p = .013. RMSEA = .02, CFI = 1.00, and TLI = .99. Elements within ${\widehat{\Lambda }}^{\ast }$ were generally consistent with expectations (compare Table 1 to Figure 2). Interfactor correlations ranged from r_PC,CB = .54 to r_GS,T = .76. Only 4 of the 66 cross-loadings that were estimated in the ESEM approach, and inconsistent with Figure 2 (e.g., m1 on GS), were statistically significant (standardized loadings ranged from .24 to .27). A reasonable answer to Question 1 was: five factors explained responses to the APCC II-HST.

Table 1.

Geomin-Rotated Pattern Coefficients (Λ*), Standard Errors (SE), Geomin-Rotated Standardized Pattern Coefficients (Λ*⁰), and Percentage of Variance Accounted For (R²)

	Factor 1 = GS			Factor 2 = PC			Factor 3 = T			Factor 4 = M			Factor 5 = CB
Item	λ*p1	SE	λ*p10	λ*p2	SE	λ*p20	λ*p3	SE	λ*p30	λ*p4	SE	λ*p40	λ*p5	SE	λ*p50	R2
gs1	1.07	.24	0.63	0.09	.09	0.05	0.22	.14	0.13	0.15	.13	0.09	-0.07	.09	-0.04	.65
gs2	1.32	.19	0.74	0.04	.08	0.02	0.04	.09	0.02	-0.08	.09	-0.05	0.24	.13	0.14	.68
gs3	0.67	.18	0.45	-0.07	.08	-0.05	0.23	.14	0.15	0.35	.14	0.24	0.03	.07	0.02	.55
gs4	0.87	.20	0.50	0.46	.13	0.27	-0.02	.08	-0.01	0.26	.16	0.15	0.01	.06	0.00	.67
pc2	0.10	.12	0.05	1.56	.34	0.79	0.08	.11	0.04	-0.01	.06	0.00	0.04	.08	0.02	.74
pc3	0.00	.07	0.00	1.44	.30	0.78	0.06	.09	0.03	0.05	.07	0.03	0.04	.08	0.02	.71
m1	0.05	.10	0.03	-0.10	.07	-0.06	0.18	.18	0.11	0.79	.17	0.50	0.43	.15	0.27	.60
m2	0.24	.14	0.17	0.18	.09	0.13	0.05	.08	0.03	0.48	.13	0.34	0.19	.10	0.14	.49
m3	-0.06	.10	-0.03	0.03	.04	0.02	0.16	.16	0.10	1.08	.22	0.65	0.22	.16	0.14	.64
m4	0.08	.11	0.05	0.13	.11	0.07	-0.18	.15	-0.09	1.59	.23	0.85	-0.05	.05	-0.03	.71
t1	-0.02	.08	-0.01	0.05	.08	0.03	1.59	.18	0.84	0.08	.08	0.04	-0.07	.08	-0.04	.73
t2	0.15	.12	0.10	0.20	.11	0.13	0.93	.13	0.61	-0.09	.10	-0.06	0.03	.07	0.02	.58
t3	0.05	.10	0.03	-0.05	.08	-0.02	1.60	.22	0.82	0.02	.08	0.01	0.10	.08	0.05	.74
t4	0.16	.11	0.10	0.09	.12	0.05	1.00	.16	0.60	0.10	.07	0.06	0.08	.08	0.05	.64
cb1	0.46	.21	0.25	-0.02	.05	-0.01	-0.13	.11	-0.07	-0.02	.06	-0.01	1.36	.21	0.74	.70
cb2	-0.01	.07	-0.01	0.18	.12	0.11	0.34	.19	0.20	0.16	.14	0.10	0.89	.19	0.52	.65
cb3	-0.01	.08	-0.01	0.07	.08	0.05	0.18	.19	0.12	0.06	.11	0.04	0.94	.18	0.62	.56

Note. Statistically significant coefficients were bolded. GS = game strategy; PC = physical conditioning; T = technique; M = motivation; CB = character building.

Deriving Measures from the APCCS II-HST: Question 2

Target rotation was then applied to Model 5 (i.e., Model 7). Selection of targets for the APCCS II-HST will be briefly and non-technically summarized here (but a fuller review of related issues, including rotation identification more generally, is available in Appendix B_1 of the supplemental electronic-only materials). Targets within B were selected based on both content knowledge and previous empirical information. From a content perspective, gs2, make effective strategic decisions in pressure situations during competition, was expected to have trivially sized pattern coefficients on all factors except game strategy within the measurement model. Each of the other items that were involved in the targets (pc3, accurately assess players’ physical conditioning; m4, motivate players for competition against a weak opponent; t1, teach players the complex technical skills of your sport during practice; cb3, effectively promote good sportsmanship in players) could be interpreted in a similar form. Note that unlike in CFA, the pattern targets were not fixed to zero. Rather, B simply informed the rotation criterion as to the structure that Λ should be rotated towards. It should be noted that although a sufficient number and configuration of targets were specified, simulation research suggests that the factors may be defined more consistent with a well-developed a priori theory with an increasing number of targets (Myers, Ahn, & Jin, 2013).

The measurement model depicted in Figure 2 (i.e., Model 8) exhibited statistically significant worse fit than Model 7, $\Delta {\chi }_R^2\left(47\right)=75$, p = .006. Model 8 estimated 47 fewer parameters than Model 7. For this reason, in addition to the relatively similar fit of the two models, limited and conceptually defensible post hoc alterations to Model 8 were considered. One defensible post hoc alteration allowed g3, make effective player substitutions during competition, to load on M in addition to GS (Model 9). Simply, making a player substitution during competition can serve as a motivational intervention in addition to a tactical strategy. Model 8 exhibited statistically significant worse fit than Model 9, $\Delta {\chi }_R^2\left(1\right)=8$, p = .005. Model 9 exhibited only marginally statistically significant worse fit than Model 7, $\Delta {\chi }_R^2\left(46\right)=67$, p = .024. None of the modification indices for Model 9 suggested statistical significance if freely estimated and the model exhibited close fit to the data: ${\chi }_R^2\left(107\right)=146$, p = .008. RMSEA = .02, CFI = .99, and TLI = .99. For these reasons, in addition to estimating 46 fewer parameters than Model 7, Model 9 was accepted (see Table 2). Given the narrow scope of this approach to post hoc modification of the a priori measurement model, a reasonable answer to Question 2 was: a more parsimonious CFA model, based on the relevant literature plus one post hoc modification, offered a viable alternative to a much more complex ESEM model. For didactic considerations, however, the ESEM approach from Model 5 will be expanded upon in the subsequent multiple-group EFA section. Table 2s in Appendix C provides interfactor correlation matrices for Model 5, Model 7, and Model 9. Interfactor correlations were somewhat similar across the three models.

Table 2.

Confirmatory Factor Analytic Pattern Coefficients (Λ), Standard Errors (SE), Standardized Pattern Coefficients (Λ⁰), and Percentage of Variance Accounted For (R²)

	Factor 1 = GS			Factor 2 = PC			Factor 3 = T			Factor 4 = M			Factor 5 = CB
Item	λ p1	SE	λ p1 0	λ p2	SE	λ p2 0	λ p3	SE	λ p3 0	λ p4	SE	λ p4 0	λ p5	SE	λ p5 0	R2
gs1	1.32	.11	0.80	----	----	----	----	----	----	----	----	----	----	----	----	.64
gs2	1.31	.11	0.80	----	----	----	----	----	----	----	----	----	----	----	----	.63
gs3	0.79	.13	0.54	----	----	----	----	----	----	0.33	.11	0.23	----	----	----	.53
gs4	1.48	.12	0.83	----	----	----	----	----	----	----	----	----	----	----	----	.69
pc2	----	----	----	1.72	.16	0.86	----	----	----	----	----	----	----	----	----	.75
pc3	----	----	----	1.54	.15	0.84	----	----	----	----	----	----	----	----	----	.70
t1	----	----	----	----	----	----	1.49	.10	0.83	----	----	----	----	----	----	.69
t2	----	----	----	----	----	----	1.16	.10	0.76	----	----	----	----	----	----	.58
t3	----	----	----	----	----	----	1.61	.13	0.85	----	----	----	----	----	----	.72
t4	----	----	----	----	----	----	1.43	.10	0.82	----	----	----	----	----	----	.67
m1	----	----	----	----	----	----	----	----	----	1.28	.12	0.79	----	----	----	.62
m2	0.42	.12	0.29	----	----	----	----	----	----	0.65	.11	0.46	----	----	----	.51
m3	----	----	----	----	----	----	----	----	----	1.34	.12	0.80	----	----	----	.64
m4	----	----	----	----	----	----	----	----	----	1.25	.12	0.78	----	----	----	.61
cb1	----	----	----	----	----	----	----	----	----	----	----	----	1.29	.12	0.79	.62
cb2	----	----	----	----	----	----	----	----	----	----	----	----	1.58	.12	0.85	.71
cb3	----	----	----	----	----	----	----	----	----	----	----	----	1.06	.10	0.73	.53

Note. Statistically significant coefficients were bolded. GS = game strategy; PC = physical conditioning; T = technique; M = motivation; CB = character building.

Deriving Measures from the CCS: Question 1

The null hypothesis for exact fit was rejected through seven factor extraction (for fuller results see Table 3s in Appendix C). A model with eight factors produced inadmissible estimates. Model 5 (five factors) through Model 7 (seven factors), however, were judged as not interpretable and likely the result of over-factoring due to reasons similar to those in the previous section. The four factor solution (i.e., Model 4) was accepted despite exhibiting statistically significant worse fit than the five factor solution, $\Delta {\chi }_R^2\left(20\right)=213$, p < .001. There was evidence for approximate fit of Model 4: ${\chi }_R^2\left(184\right)=617$, p < .001. RMSEA = .06, SRMR = .02, CFI = .99, and TLI = .99. Elements within ${\widehat{\Lambda }}^{\ast }$ were somewhat inconsistent with expectations (compare Table 3 to Figure 1). Note that 15 of the 71 cross-loadings that were estimated in the ESEM approach, and inconsistent with Figure 1 (e.g., m1 loads on GS), were statistically significant (standardized loadings ranged from -.08 to .42). A reasonable answer to Question 1 was: at least four factors explained responses to the CCS.

Table 3.

Geomin-Rotated Pattern Coefficients (Λ*), Standard Errors (SE), Geomin-Rotated Standardized Pattern Coefficients (Λ*⁰), and Percentage of Variance Accounted For (R²)

	Factor 1 = GS			Factor 2 = M			Factor 3 = T			Factor 4 = CB
Item	λ*p1	SE	λ*p10	λ*p2	SE	λ*p20	λ*p3	SE	λ*p30	λ*p4	SE	λ*p40	R2
gs2	1.28	.22	0.83	0.02	.05	0.01	-0.02	.07	-0.01	0.07	.07	0.05	.73
gs4	1.33	.22	0.81	0.04	.05	0.03	0.14	.15	0.08	-0.01	.06	-0.01	.79
gs8	1.39	.24	0.83	0.07	.07	0.04	0.06	.13	0.04	0.00	.07	0.00	.79
gs9	1.21	.21	0.77	-0.11	.06	-0.07	0.15	.09	0.09	0.09	.06	0.06	.72
gs11	1.03	.26	0.58	0.24	.09	0.13	0.27	.19	0.15	0.13	.09	0.07	.73
gs17	0.70	.21	0.41	0.15	.12	0.08	0.73	.21	0.42	0.12	.09	0.07	.79
gs21	0.82	.24	0.47	-0.12	.08	-0.07	0.69	.23	0.40	0.20	.12	0.12	.76
ml	0.57	.15	0.31	1.26	.17	0.69	-0.04	.19	-0.02	-0.05	.08	-0.03	.76
m3	1.07	.25	0.61	0.71	.11	0.40	-0.04	.10	-0.03	-0.14	.11	-0.08	.68
m6	-0.01	.07	0.00	1.66	.21	0.82	0.15	.21	0.08	0.18	.11	0.09	.85
m10	0.60	.30	0.31	1.14	.16	0.59	0.01	.18	0.01	0.18	.12	0.09	.77
m12	0.43	.24	0.23	0.83	.19	0.44	0.08	.16	0.04	0.46	.18	0.24	.67
m15	-0.26	.14	-0.13	1.48	.20	0.73	0.71	.19	0.35	0.07	.05	0.04	.87
m23	0.20	.20	0.10	1.17	.15	0.59	0.23	.15	0.12	0.43	.12	0.22	.81
t7	0.62	.28	0.34	0.28	.19	0.15	0.74	.37	0.41	-0.25	.14	-0.14	.52
t14	0.01	.08	0.01	0.32	.18	0.18	1.42	.26	0.80	-0.15	.06	-0.08	.76
t16	0.05	.09	0.03	0.31	.15	0.18	1.32	.20	0.76	-0.01	.07	-0.01	.81
t18	0.54	.22	0.28	0.23	.18	0.12	0.71	.26	0.37	0.30	.15	0.16	.67
t20	0.42	.22	0.24	-0.12	.08	-0.07	1.01	.24	0.58	0.24	.13	0.14	.71
t22	0.30	.20	0.18	-0.02	.12	-0.01	1.20	.28	0.71	0.07	.07	0.04	.77
cb5	0.17	.13	0.09	0.64	.16	0.32	-0.10	.14	-0.05	1.23	.22	0.62	.78
cb13	0.16	.16	0.09	0.34	.19	0.18	0.04	.10	0.02	1.18	.21	0.63	.71
cb19	-0.07	.08	-0.04	0.03	.10	0.02	0.13	.15	0.07	1.63	.25	0.88	.84
cb24	0.01	.09	0.00	0.53	.18	0.27	0.10	.12	0.05	1.27	.19	0.65	.78

Note. Statistically significant coefficients were bolded. GS = game strategy; M = motivation; T = technique; CB = character building.

Deriving Measures from the CCS: Question 2

Target rotation was the applied to Model 4 (i.e., Model 8). The measurement model depicted in Figure 1 (i.e., Model 9 – see Table 5s) exhibited statistically significant worse fit than Model 8, $\Delta {\chi }_R^2\left(59\right)=273$, p < .001. Neither model, however, exhibited especially close fit to the data. Many of the modification indices for Model 9 suggested statistical significance if freely estimated, which was consistent with the many statistically significant cross-loadings observed in Table 3. Given the extent of this potential post hoc exploration for a well-fitting measurement model, a reasonable answer to Question 2 was: a more parsimonious CFA model, based on the relevant literature (see Figure 1), did not offer a viable alternative to a more complex ESEM model (see Figure 4s in Appendix D).

Model 8 (target rotation) had nearly as many statistically significant cross-loadings (14 of 71) as did Model 4 (geomin rotation – compare Table 3 to Table 4s in Appendix C). Interfactor correlations under Model 8 ranged from r_GS,M = .62 to r_GS,T = .90 and from r_GS,M = .57 to r_GS,T = .80 under Model 4. Problems attributed to multicollinearity have caused particular CCS measures to be dropped in substantive coaching research (e.g., Myers, Wolfe, Maier, Feltz, & Reckase, 2006). Given these two pieces of non-exhaustive pieces of information, plus the mathematical equivalence of the solution under both rotation techniques, a reasonable (though certainly not the only and perhaps not the best) answer to the follow-up question to Question 2 was: geomin rotation was preferred. Table 6s in Appendix C provides interfactor correlation matrices for Model 4, Model 8, and Model 9. Interfactor correlations were somewhat higher in Model 9.

Multiple-Group EFA in ESEM

An important question for the emerging line of research involving coaching competency within coaching effectiveness models going forward is: are measures comparable across groups for which the CCS and APCCS II-HST are intended? Borrowing from the multiple-group CFA approach to measurement invariance, multiple-group EFA in ESEM allows researchers to fully test for measurement invariance across groups of substantive interest while generally imposing fewer restrictions than in the CFA framework. For textual parsimony as well as sample size and model-data fit considerations (Yuan & Bentler, 2004), an illustration will be provided based on data from the APCCS II-HST only. The study design in Myers et al. (2010) assumed factorial invariance by country and this variable served as the grouping variable (i.e., United States, U.S. = reference group, and the United Kingdom, U.K. = focal group). Model 5 from Table 1s in Appendix C (i.e., 5 ESEM factors with Geomin rotation) served as the starting point.

Under the theta parameterization, data were fit to four increasingly restrictive multiple-group models for ordinal data (Millsap & Yun-Tien, 2004). Before testing for factorial invariance, the model was imposed separately in each group: Model 1a (U.S. only) and Model 1b (U.K. only). Model 2 through Model 5 tested for factorial invariance. Model 2 (baseline) imposed constraints (detailed in Appendix B_2 of the supplemental electronic-only materials) for identification purposes. Model 3 added the constraint of invariant pattern coefficients (invariant Λ) to Model 2. Model 4 added the constraint of invariant thresholds (invariant Λ and τ) to Model 3. Model 5 added the constraint of an invariant residual covariance matrix (invariant Λ, τ, and Θ) to Model 4. Nested models were compared as described in the EFA in ESEM section.

Countries separately

There was evidence for close fit in the U.S. sample, Model 1a: ${\chi }_R^2\left(61\right)=97$, p = .002, RMSEA = .03, CFI = .99, and TLI = .97. There was evidence for exact fit in the U.K. sample, Model 1b: ${\chi }_R^2\left(61\right)=53$, p = .761, RMSEA = .00, CFI = 1.00, and TLI = 1.01. At least part of the difference between the model-data fit by country was likely due to the difference in sample size: n_U.S. = 491 and n_U.K. = 257.

Model 2 through Model 5

Model 2 (baseline) provided evidence for exact fit: ${\chi }_R^2\left(122\right)=140$, p = .132, RMSEA = .02, CFI = 1.00, and TLI = .99. Model 3 (invariant Λ) fit the data as well as Model 2, $\Delta {\chi }_R^2\left(60\right)=72$, p = .142, and provided evidence for exact fit: ${\chi }_R^2\left(182\right)=203$, p = .139, RMSEA = .02, CFI = 1.00, and TLI = 1.00. Model 4 (invariant Λ and τ) fit the data as well as Model 3 (invariant Λ), $\Delta {\chi }_R^2\left(29\right)=41$, p = .066, and provided evidence for exact fit: ${\chi }_R^2\left(211\right)=237$, p = .105, RMSEA = .02, CFI = 1.00, and TLI = .99. Model 5 (invariant Λ, τ, and Θ) fit the data as well as Model 4 (invariant Λ and τ), $\Delta {\chi }_R^2\left(17\right)=23$, p = .166, and provided evidence for exact fit: ${\chi }_R^2\left(228\right)=254$, p = .117, RMSEA = .02, CFI = 1.00, and TLI = 1.00. Thus, a reasonable conclusion was that there was evidence for factorial invariance by country (i.e., U.S. and U.K.) with regard to responses to the APCCS II-HST.

From a mathematical perspective, “measurement invariance does not require invariance in the factor covariance matrices or factor means” (Millsap & Yun-Tien, 2004, p. 484). From a conceptual perspective, however, (non-)invariance of these parameters (ψ and α, respectively) can be informative with regard to substantive theory (Marsh et al., 2009), and therefore, both of these input files are available in Appendix E of the supplemental electronic-only materials. Briefly, Model 6 (invariant Λ, τ, Θ, and ψ) fit the data as well as Model 5, $\Delta {\chi }_R^2\left(15\right)=21$, p = .128, while Model 7 (invariant Λ, τ, Θ, ψ, and α) fit the data significantly worse than Model 6, $\Delta {\chi }_R^2\left(5\right)=38$, p < .001, with evidence for significantly lower latent means in the UK sample as compared to the US sample with regard to game strategy, technique, and character building.

Summary and Conclusions

This substantive-methodological synergy attempted to merge an extant conceptual model, coaching competency, and a new methodological framework, ESEM, as compared to a more familiar methodological framework, CFA, for the next generation of research in the psychology of sport and exercise to consider. The synergy was a demonstration of how (E)SEM may be used guided by content knowledge to develop better, or confirm existing, measurement models for coaching competency by re-analyzing existing data. A key consideration for deciding between ESEM and the accompanying rotation criterion and CFA in future validity studies within the psychology of sport and exercise should be level of a priori measurement theory.

It should be reiterated that there is no right or wrong rotation criterion from a mathematical perspective in regard to model-data fit. That said, it has been known for some time that mathematically equivalent solutions do not necessarily do an equivalent job of recovering particular parameter values of interest under complex structures (e.g., Thurstone, 1947). Oblique versions of two rotation criterion, geomin and target, were used in this manuscript and a brief case for their inclusion was put forth in the rotation section. Others may prefer different rotation criteria or even one of the selected rotation criterion but with the f(Λ) specified slightly differently (e.g., non-default values for ε under geomin rotation – see Morin & Maïano, 2011, for an example) for the CCS and, perhaps, more generally. Selecting a particular rotation criterion is a multi-faceted post estimation decision that cannot be proven to be “correct” when population values are unknown. For example, in the previous section geomin rotation was preferred for the CCS, in part, because interfactor correlations were somewhat smaller than under target rotation. Clearly, lowering the interfactor correlations was not a sufficient condition for selecting the “right” rotated solution for the CCS. If it were a sufficient condition then the “right” rotation criterion presumably would be one that forced an orthogonal solution, doing so however, would have been inconsistent with a priori substantive theory depicted in both Figure 1 and Figure 2.

It is important to note that statistical models often can be used for exploratory or confirmatory purposes regardless of the semantics used (e.g., exploratory/confirmatory factor analysis). For example, if an a priori theory justified that each indicator was influenced by each factor then confirmatory evidence may be provided for such a theory (within theoretical identification limits) under either CFA or ESEM approach. A similar issue arises in the determination of the number of factors, m, to specify/retain in ESEM. The approach taken in this manuscript: a series of nested model comparisons manipulating the number of factors, m, while considering the interpretability of the solution with regard to a priori theory, and, possible empirical limitations of the nested model comparisons is consistent with a less than strictly confirmatory approach taken in Myers, Chase, Pierce, and Martin, 2011: “comparing_ms”. A fixed number of factors based on theory alone, “theory_m”, can be specified in ESEM consistent with a more strictly confirmatory approach. The author of this manuscript generally prefers some version of the comparing_ms approach when ESEM is used because it empirically subsumes the theory_m approach (i.e., the theory_m solution is fitted). That said, as in the current manuscript, even under the comparing_ms approach the analyst may not strictly adhere to model-data fit information alone – although a reasonable expectation in such cases may be to provide this information in a manuscript. Clearly there may be instances (e.g., very strong a priori theory and previous empirical information consistent with this theory) where theory_m may be justifiable. A “golden rule” mandating one approach over the other in all instances seems unreasonable.

Coaching competency occupies a central role in models of coaching effectiveness, which makes measurement of this construct an important area of research. The CCS and the APCCS II-HST were designed to measure coaching competency. The initial athlete-level measurement model for responses to the CCS and the APCCS II-HST both were put forth prior to the emergence of ESEM (i.e., fitted to CFA). ESEM analysis on extant datasets suggests that for responses to the APCCS II-HST, a CFA model based on the relevant literature plus one post hoc modification (see Figure 2), offered a viable alternative to a more complex ESEM model. For responses to the CCS, a CFA model based on the relevant literature (see Figure 1) did not offer a viable alternative to a more complex ESEM model (see Figure 3s). The author of this manuscript recommends that the measurement models advocated (Figure 2 and Figure 3s) serve as a starting place for subsequent research. The author of this manuscript also recommends that the ESEM framework should be considered in subsequent studies validity studies - for new and/or existing instruments in the psychology of sport and exercise. That said, there is preliminary evidence that ESEM, as compared to CFA, may in some circumstances be more susceptible to non-convergence or convergence to an improper solution when N ≤ 250 (Myers, Ahn, et al., 2011b). In cases where ESEM encounters such problems (and when they are intractable), and when more data are not possible, other practical solutions (e.g., summed scores) may be reasonable.

While the substantive part and the methodological part of this manuscript both were focused primarily on measurement, the fuller ESEM provides a broader methodological framework (that includes but is not limited to the EFA and Multiple-Group EFA examples within this manuscript) within which the next generation of effective coaching research may evaluate fuller models of effective coaching. Many latent variable models that could be imposed within the SEM framework could also be imposed within ESEM framework (Asparouhov & Muthén, 2009). An advantage of the ESEM framework, in instances of insufficient a priori measurement model(s), is reduced likelihood of biased estimates wrought by my misspecification of the measurement model(s). Simply, studies not focused on measurement can still be adversely affected by misspecification of the measurement model(s) because misspecification of the measurement model(s) can produce biased path coefficients (Kaplan, 1988).

There is much work yet to be done to investigate the utility of coaching competency within broader models of coaching effectiveness. While a few studies have explored the ability of coaching competency to predict satisfaction with the head coach (e.g., Myers, Wolfe, et al., 2006) and role ambiguity (Bosselut et al., 2012), many other key relations implied within Horn's (2002) model await investigation. For example, coaching competency is specified to at least partially mediate the effect of coaching behavior on three sets of variables: (a) athletes’ self-perceptions, beliefs, and attitudes, (b) athletes’ level and type of motivation, and (c) athletes’ performance and behavior. Future research that explores these (or other) important implied relations is encouraged. More broadly, the author of this manuscript believes that it may be time for research on coaching competency to evolve beyond such a strong focus on measurement alone because it has long been suspected that “the ultimate effects that coaching behavior exerts are mediated by the meaning that players attribute to them” (Smoll & Smith, 1989, p. 1527) – effects measurement models do not test. Finally, a theory-based investigation for why, on average, UK high school athletes may rate their head coach's game strategy, technique, and character building competency lower than US high school athletes rate their head coach's game strategy, technique, and character building competency could advance the literature.

• ESEM should be strongly considered in subsequent validity studies.

• Level of a priori measurement theory is a key for deciding between ESEM and CFA.

• Figure 2 and Figure 3s provide measurement models for use in future research.