Submillisecond Elastic Recoil Reveals Molecular Origins of Fibrin Fiber Mechanics

Abstract

Fibrin fibers form the structural scaffold of blood clots. Thus, their mechanical properties are of central importance to understanding hemostasis and thrombotic disease. Recent studies have revealed that fibrin fibers are elastomeric despite their high degree of molecular ordering. These results have inspired a variety of molecular models for fibrin’s elasticity, ranging from reversible protein unfolding to rubber-like elasticity. An important property that has not been explored is the timescale of elastic recoil, a parameter that is critical for fibrin’s mechanical function and places a temporal constraint on molecular models of fiber elasticity. Using high-frame-rate imaging and atomic force microscopy-based nanomanipulation, we measured the recoil dynamics of individual fibrin fibers and found that the recoil was orders of magnitude faster than anticipated from models involving protein refolding. We also performed steered discrete molecular-dynamics simulations to investigate the molecular origins of the observed recoil. Our results point to the unstructured αC regions of the otherwise structured fibrin molecule as being responsible for the elastic recoil of the fibers.

Introduction

The mechanical properties of biopolymers are finely tuned to the specific task they perform and the environment in which they perform it (1). Fibrin fibers form within the vasculature, where the pulsatile shear stresses generated by the heartbeat must be accommodated. Within this environment, fibrin fibers undergo cycles of extension followed by elastic recoil while performing the mechanical job of stemming the flow of blood at the sites of vascular injury. On the other hand, the fate of clots that form at sites of plaque buildup, or altered blood flow (stasis), is determined in part by how strongly the clot attaches to the vessel walls, as well as the structural integrity of the clot itself. Thus, the level of catastrophic injury due to embolism, whether in the heart, lung, or brain, is strongly impacted by the physical properties of fibrin (2). Investigators have studied the mechanical properties of fibrin extensively using techniques such as cone-and-plate rheometry (3), atomic force microscopy (AFM) (4–6), and optical tweezers (7). Fibrin fibers exhibit strain stiffening behavior (5,8) and, unlike other semiflexible biopolymers, such as microtubules or actin (9,10), they are elastomeric (i.e., very extensible (>300% maximum strain) (4) and relatively soft (Young’s modulus of 1–10 MPa)). They also have been shown to be viscoelastic (8). Structural studies have shown that in contrast to elastomers such as rubber, whose stretchy properties rely on disordered randomly coiled chains, fibrin fibers have a high degree of molecular order (11,12) (Fig. 1, A and B). How these two contradictory properties—molecular order and stretchiness—are resolved in the structure and molecular arrangements within the fiber is currently the subject of debate (5,13–15) (Fig. 1).

Figure 1.

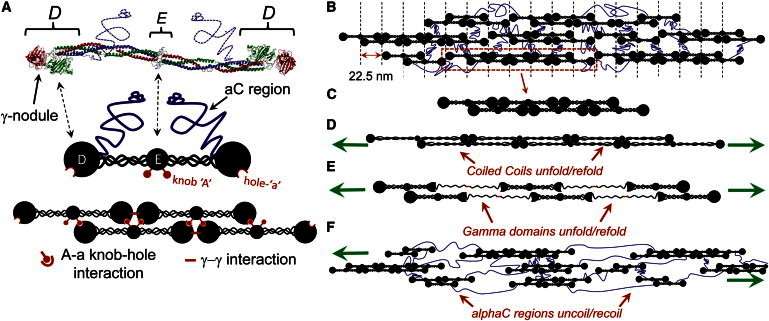
Fibrinogen molecule, polymerization into fibrin fibers, and models of fibrin extension. (A) The crystal structure of the human fibrinogen molecule is shown on top (blue dotted lines drawn in to depict the loose αC region not captured in the crystal structure) and a cartoon representation of the molecule and its polymerization contacts is shown at the bottom. The molecule consists of two sets of three peptide chains linked in the middle E region via disulfide bonds. A triple-helical coiled coil links the center of the molecule to the end D regions and the unstructured αC region. Fibrinogen is converted to insoluble fibrin during hemostasis when thrombin cleaves ∼12 N-terminal residues from the α and β chains near the central E region, revealing knobs A and B (for simplicity, only knob A is shown). These knobs bind to specific holes within the β and γ-nodules in the D region (holes a and b; for simplicity, only hole a is shown), allowing the molecules to polymerize into half-staggered protofibrils and eventually full fibrin fibers. (B) A structural model for the fibrin fiber, consisting of protofibrils C linked together by the unstructured αC regions. The protofibrils align to give a 22.5 nm banding pattern to the fiber. The red dashes between adjacent molecules indicate the site of γ-γ interaction and FXIIIa ligation (for clarity, A-a knob interactions are not shown in B–F). (D–F) Cartoon models depicting extension of the fiber arising from stretching of the coiled-coil region (D), the γ-nodule within the D region (E), and stretching the αC regions between protofibrils (F).

The basic building unit of the fiber, the fibrin molecule, is a large 340 kDa protein consisting of two mirror image subunits, each of which is made of three polypeptide chains (α, β, and γ) linked in a central region of the molecule via disulfide bonds (16). From both sides of the central region, the three chains extend as coiled coils that terminate in two compact, globular nodules (β and γ chains) and a long, partially unstructured segment called the αC region (see Fig. 1 A). According to the standard view, fibrin molecules polymerize in a half-staggered manner via specific, noncovalent interactions between knobs in the central nodule of one molecule and holes in the β and γ-nodules of two other molecules (Fig. 1, A and B), allowing longitudinal growth into a double-stranded protofibril (16–18). The protofibrils then aggregate laterally to form fibrin fibers, in part due to the action of the αC regions (19). Electron-microscope structural studies of fibrin fibers show a distinct banding pattern of 22.5 nm periodicity (half the length of the fibrin molecule) (17,20,21), suggesting that lateral contacts between protofibrils keep them in a registered, paracrystalline packing within the fiber (Fig. 1 B).

Based on this architecture, several models have been proposed to describe the molecular origins of fibrin’s elasticity: 1), unfolding of the coiled-coil region of the molecule (13) (Fig. 1 D; 2), unfolding of the globular γ nodules (Fig. 1 E) (22); and 3), stretching of the αC regions between protofibrils in the fiber (5,23,24), or some combination of these mechanisms (24,25). These models have primarily been derived to account for fibrin’s remarkable elasticity and extensibility as demonstrated in quasistatic force-extension studies, but have not been tested against measurements of dynamics. Given that models 1 and 2 involve protein refolding, whereas model 3 involves the relaxation of stretched polymer chains, the models predict very different dynamic properties for the fiber.

Using AFM-based nanomanipulation, we measured the elastic recoil of fibrin fibers using high-frame-rate fluorescent imaging. We found that they recoiled from high strain on timescales of ∼300 μs and relaxed back into taut conformations within 4 ms, reproducibly, over several load cycles. In addition, we report results from the first (to our knowledge) all-atom, steered molecular-dynamics (MD) simulations of each region of the fibrinogen molecule. Using constant-force discrete MD (DMD) simulations, we determined a critical unfolding force and an unfolded length for the coiled-coil, γ-nodule, and αC regions. Our measurements and modeling demonstrate that reversible protein unfolding cannot explain the rapid recoil observed in fibrin, but extension and entropic recoil of unstructured regions can.

Materials and Methods

Optical microscopy and nanomanipulation

Experiments were performed with the use of a combined inverted optical microscope/atomic force microscope as described previously (5). Fluorescently labeled fibers were suspended between ridges with a 20 μm pitch and then stretched from the center with an atomic force microscope tip. We used nanoManipulator software (3rdTech, Durham, NC) to collect data and control the atomic force microscope (Explorer; Veeco Instruments, Woodbury, NY). We used AppNano HYDRA2R-100NG AFM cantilevers (resonance frequency = 21 KHz, spring constant = 0.011 N/m; Applied NanoStructures, Santa Clara, CA). The atomic force microscope tip was carefully positioned next to a suspended fiber (several microns above the channel floor) and moved at a constant height in a trajectory perpendicular to the fiber axis at a speed of 4 μm/s. All experiments were done in ambient conditions (∼21°C) in an open fluid cell arrangement. Fibers were allowed to slip off the tip, and fiber relaxation was measured optically using an Evolve 128 camera (Photometrics, Tucson, AZ). We measured the frame rate of the camera to be 120–150 frames per second (fps) in full frame mode, and up to 4000 fps in region of interest (ROI) mode, which only measures the photon counts in a subset of the pixels in the detector.

DMD simulations

DMD simulations were carried out on the Biomedical Analysis and Simulation Supercomputer (BASS) at the University of North Carolina at Chapel Hill. A detailed description of the DMD algorithm is presented elsewhere (26–28). Briefly, interatomic interactions are modeled as square-well potential functions. During a simulation, an atom’s velocity remains constant until a potential step is encountered, at which point the velocity changes instantaneously according to the ballistic equations of motion (29). The all-atom DMD method uses a united atom protein model in which heavy atoms and polar hydrogen atoms are explicitly modeled. Bonded interactions (such as bonds, bond angles, and dihedrals) between neighboring atoms/amino acids are modeled by infinitely deep square-well potentials. Nonbonded interactions include van der Waals, solvation, and environment-dependent hydrogen-bond interactions (28). For solvation, the Lazaridis-Karplus solvation model was used and the fully solvated conformation served as the reference state (28,30). Constant temperature simulations were maintained with an Anderson thermostat (31). We performed the constant-force pulling simulations at 300 K and achieved constant force by applying a discretized step function with a constant energy drop, dE, at the distance step of dR (0.1 Å). By simulating the protein dynamics under a range of forces, we could identify the critical force for unfolding as the intersection of barrierless and hindered unfolding force regimes.

The coiled-coil structure was extracted from the crystallography structure (PDB ID: 3GHG) (32). Specifically, amino acids α27-200, β58-198, and γ14-130 from 3GHG were used to generate the initial structure for the simulation (where α, β, and γ denote the three polypeptide chains of the fibrinogen molecule). Each chain of the coiled-coil structure consists of 111 amino acids bookended by cysteine residues at both the N- and C-termini. Disulfide bonds between αCys161-γCys135, αCys165-βCys193, and γCys139-βCys197 on the C-terminal end and αCys45-γCys23, αCys49-βCys76, and βCys80-γCys19 on the N-terminal end were incorporated as described previously (28). The simulations were performed in a rectangular box of dimensions 100 Å × 100 Å × 2000 Å with periodic boundary conditions, with the pulling force applied along the longest dimension.

The original structure for the γ-nodule simulation was taken from the crystal structure (PDB ID: 2FFD) (33). Disulfide bonds in the structure and Zn²⁺ (substituted for Ca²⁺) binding pockets were parameterized with square well potentials as described previously (26). Binding of the A-knob mimic GPRV to the hole-A binding pocket was modeled by constraints using an infinite square well potential. Force was applied to the C_α carbon of Val-4 in GPRP. The simulations were performed in a rectangular box of dimensions 300 Å × 300 Å × 1200 Å with periodic boundary conditions.

The structure for the αC region (amino acids 196–160 of the α-chain) was derived from homology modeling using the I-TASSER online resource and DMD energy minimization (34). To apply force, the C_α carbon of Ser-196 in the N-terminal region was fixed in space and the C_α atom of the C-terminal residue was pulled at constant force toward a fixed point 1200 Å away. The simulations were performed in a rectangular box of dimensions 200 Å × 200 Å × 3000 Å with periodic boundary conditions.

Fibrin polymerization

Fibrin fibers were assembled in situ onto Norland Optical cured structured surfaces (SSs) as described previously (4). A polydimethylsiloxane (PDMS) stamp with 20 μm wide and 10 μm deep channels was placed on a small drop of Norland Optical #81 (an ultraviolet-light-curable optical adhesive) in the middle of a 24 × 50 mm 1.5 coverglass (Corning, Lowell, MA). The adhesive was polymerized with long-wavelength ultraviolet light for 2 min and the stamp was peeled off, leaving a cured SS. Fibrinogen stored at 0.6 mg/mL, thrombin (human α-thrombin, Enzyme Research Laboratories, Indianapolis, IN) stored at 222 U/mL, and Factor XIII (human plasma FXIII; Enzyme Research Laboratories) stored at 68 μg/mL (or equivalently 146 Loey U/mL) at −80°C were thawed rapidly and placed on ice. Fibrinogen and FXIII were diluted to 0.04 mg/mL and 24 μg/mL, respectively, in 20 mM HEPES, 150 mM NaCl, pH 7.4 (HBS), and half the final volume needed to cover the SS (usually 8–10 μL) was pipetted onto the surface. Thrombin was diluted just before use to 2 U/mL in HBS with 10 mM CaCl₂, and an equal volume was added to each SS and mixed by gently pipetting up and down several times. The final concentrations of reagents were 0.02 mg/mL fibrinogen, 1.0 U/mL thrombin, 12 μg/mL Factor XIII (25 Loey U/mL) in HBS, 5 mM calcium. Additional experiments were performed in the presence of 5 mM EDTA to test the effects of calcium on fibrin’s dynamic behavior. In this case, fibers were polymerized in the presence of HBS containing 5 mM CaCl₂ and then subsequently washed four times with HBS without 5 mM CaCl₂ and with the addition of 5 mM EDTA.

Results and Discussion

Fibrin fibers recoil within milliseconds

Suspended fiber samples were prepared by polymerizing fibrin onto micropatterned ridge/channel structures fabricated on glass coverslips (see Materials and Methods for details). Fibrin assembly was initiated directly on the ridges with 0.02 mg/mL purified fibrinogen from human plasma (Peak 1; Enzyme Research Laboratories) by addition of purified human thrombin (final concentration of 1 U/mL). The assembled fibers were visualized using 24 nm fluorescent microbeads on an inverted epifluorescence microscope. This preparation generated many single fibers suspended from plateau to plateau across the 10 μm deep channels, as shown previously (5,35). The atomic force microscope tip was carefully positioned next to a suspended fiber at its midpoint (several microns above the channel floor), brought into adhesive contact with the fiber, and then moved perpendicular to the fiber axis to stretch the fiber until release (Fig. 2). The recoil of the fiber was then captured with high-frame-rate fluorescence imaging at up to 4000 fps in the ROI (see Movie S1 and Movie S2 in the Supporting Material).

Figure 2.

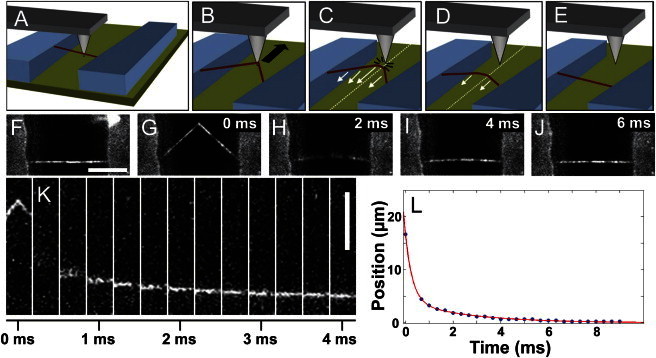
Measurement of dynamic fibrin recoil. (A–E) Cartoon of the AFM manipulation setup. (A) Fibrin fibers suspended between microcontact-printed ridges on a glass coverslip. An AFM tip is brought into contact with the fiber. (B) Once the fiber is attached via nonspecific interactions, the AFM tip is moved parallel to the channel axis to stretch it. (C) When the fiber’s elastic restoring force exceeds the tip-fiber adhesion, the fiber detaches from tip and begins to recoil elastically back to its original straight configuration. (D) The fiber recoils. The white dotted line in panels C and D depicts the axis along which position data are collected for position-versus-time data. (E) The fiber regains its original conformation. (F–J) Full-frame (500 fps) fluorescence data for fibrin relaxation (Movie S1). (F) The fiber is suspended across the channel between two ridges in its original state before stretching. (G) The fiber is stretched by an AFM tip and is shown in frame before the fiber deadheres from the AFM tip and recoils. (H) The first frame after the fiber releases from the tip. (I and J) Subsequent images show the fiber regaining a taut conformation. (K) Imaging only an ROI (a narrow subset of the total image area) allowed frame rates of 3000 fps (Movie S2). Image data depict the center of the fiber as it relaxes back to a straight conformation over 4 ms. (L) The center position-versus-time data are plotted. The center of the fiber at each time was found by applying a Gaussian fit to the image pixel intensity. For each determined position, the σ-value of the Gaussian fit is smaller than the points depicted on the plot. The position-versus-time data were best fit by a double exponential (red line), indicating two distinct time constants for fiber recoil (scale bars: 10 μm).

The position, x(t), of the fiber center along a coordinate perpendicular to the original fiber axis was measured by fitting a 1D Gaussian curve to a cross section of the fluorescence optical image intensity (x(t) is related to fiber strain as described in the Supporting Material and Fig. S1). The position was then plotted as a function of time, and the data were fit with a double exponential decay (Eq. 1; Fig. 2 L) when initial analysis revealed that the data were not well described by a single exponential:

$$x\left(t\right)=x_1{e}^{\left(-\frac{t}{{\tau }_1}\right)}+x_2{e}^{\left(-\frac{t}{{\tau }_2}\right)}$$ (1)

The two decay time constants τ₁ and τ₂ were defined as the fast and slow recoil times respectively, with x₁ and x₂ determined by initial conditions (x(0) = x₁ + x₂), and the proportion of the recoil dominated by the fast versus slow mode. We found τ₁ = 0.33 ± 0.02 ms and τ₂ = 3.4 ± 0.1 ms (N = 60 in both cases, uncertainty = SE) with ∼85% of the total fiber strain recovered in <1 ms.

The recoil decay time is reproducible and independent of strain and load cycle

The most strained fibers observed in this set of experiments reached strains of 100% (with strain defined as the change in length divided by the original length). All fibers exhibited elastic recovery upon repeated stretching cycles, as indicated by consistent recoil times, recovered straight conformation, and AFM-based force measurements (Fig. S2). The elastic response in the strain range observed here is also consistent with previous reports (4,24). Within experimental error, τ was independent of fiber strain at the point of detachment (up to 100% strain) and load cycle (Fig. 3 A; Fig. S3). In previous experiments (4), plastic deformation of fibers was observed at strains above 120%. Due to nonspecific interactions between the fiber and tip in those experiments, the fibers did not reach the point of plastic deformation before detachment occurred (4). We never saw any evidence of plastic damage to the fiber (irreversible elongation). Within the strain regime we tested, we observed consistent elastic behavior. We also note that fibers prepared as described in Materials and Methods produce predominantly taut fibers with no indication of slack. This suggests that they are under some degree of prestrain before manipulation. Observations of broken fibers, where the relaxed length can be gauged, provide a means of estimating the prestrain. The prestrain is on the order of a few percent based on these observations. For the load-cycle dependence, data were collected for 60 independent recoil trials performed on 15 individual fibers. For each fiber for which several stretches were performed and time constants were obtained, a change in τ₂ per load cycle was determined by linear regression (a line was fit to the τ₂ versus load cycle data). The change in τ₂ per load cycle averaged over all fibers was an increase of 0.1 ± 0.5 ms (the mean value of τ₂ was 3 ms). We conclude that no significant load-cycle dependence is evident in the data. We similarly found no load-cycle trend in the fast recoil τ₁ (see Fig. S3). The attrition in the number of data points at high pull count was caused by the higher chance of a release event of the fiber from the ridge edge as we pulled multiple times. The linear regression that determined the trend in τ₂ versus load cycle was weighted to account for the number of data points at each load cycle.

Figure 3.

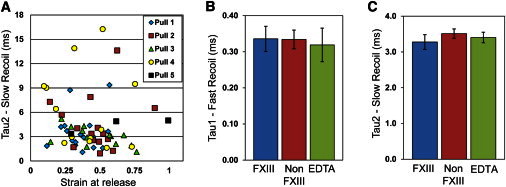
The recoil timescale is independent of strain and fiber treatment with FXIIIa and EDTA. (A) The plot depicts the slow recoil time constant, τ₂, for 60 recoil trials performed on 15 different fibers (no FXIIIa ligation) versus the fiber strain at recoil. Different data symbols indicate the pull number, which indicates how many times a particular fiber has been pulled back and released (load-cycle number). The recoil time constants were reproducible over many load cycles. (B and C) The timescales of the fast and slow recoil time constants (τ₁ and τ₂, respectively) were plotted for samples prepared with and without FXIIIa ligation, and prepared in the presence of the calcium chelator EDTA. Both time constants were found to be unaffected by either FXIIIa ligation or EDTA treatment. No differences were statistically significant (p > 0.25 for all comparisons in B and C; error bars indicate mean ± SE).

Recoil time constants do not depend upon ligation or Ca²⁺

We measured the recoil time constants for fibers under various conditions known to affect fibrin mechanics and polymerization. Specifically, fibers were prepared with and without the presence of the transglutaminase FXIIIa, which ligates the γ-nodules and is known to increase fiber stiffness (7). In addition, fibers were stretched in the presence of 5 mM EDTA, a chelator of calcium that has been shown to affect fibrin network structure (36) as well as the mechanical strength of fibrin polymerization knob-hole interactions (37,38). For all fiber preparations, the data show two separate regimes of relaxation. We did not observe any statistically significant differences in these recoil time constants across our range of conditions (Fig. 3).

Probing the molecular origins of fibrin elasticity using DMD simulations

The recoil results place temporal constraints on the models that have been proposed for the molecular origins of fibrin fiber elasticity. Models involving the coiled-coil or γ-nodule regions of the molecule require protein unfolding and refolding, whereas another model involves the entropic recoil of stretched unstructured polypeptides in the αC region. To compare models quantitatively, we performed independent DMD simulations on the coiled-coil region, the γ-nodule, and the αC region, which yielded force extension and, in some cases, recoil data. In contrast to previous all-atom and coarse-grained fibrin(ogen) MD studies (39,40), we used constant force rather than constant velocity constraint, which enabled us to determine physiologically relevant critical unfolding forces. The critical force, F_c, is defined as the force at which the energy barrier opposing unfolding vanishes (41) (see Fig. S5). We also probed unfolding pathways that up to now have not been studied with MD: the γ-nodule with force applied at the A-a knob-hole interface, and the αC region. The A-a knob-hole interface is of particular interest because it is considered to be the primary interaction between fibrin molecules that drives polymerization (17,42).

To estimate F_c for coiled-coil unfolding, we ran simulations for 50 ns for a range of forces. Fig. 4 A depicts the force versus protein stretching behavior. The plot indicates that the protein remains folded at 100 pN (extension of 1.5 nm, strain of <10%), but at 125 pN the coiled-coil region has gained a 9 nm extension (strain of 53%), and at 150 pN it has gained a 12 nm extension (strain of 75%). This provides an estimate for F_c of the coiled coil of 100–125 pN, in good agreement with previous AFM data (6). More importantly, we found that as the three helices of the coiled-coil regions unfolded, they gradually formed hydrogen bonds with adjacent chains and generated a stable β-sheet structure (Fig. 5, D and E; Movie S3). When the unfolding force was turned off and the structure was allowed to relax, the β-sheets locked the chains into an energetically stable conformation that prevented refolding for the remaining duration of the 100 ns simulation. As a comparison, another simulation involving only the γ-chain of the coiled coil showed an immediate collapse and subsequent reformation of helical structure within the 100 ns simulation (Fig. S4). The high critical unfolding force (125 pN) and the irreversible α-helix to β-sheet transition make the coiled coil a very unlikely candidate for rapid elastic recoil. Biomaterials whose extensibility is known to be mediated by coiled-coil unfolding, such as keratin (43), have relatively high elastic moduli (GPa) as compared with the low modulus of fibrin fibers (MPa). Fig. 4 B depicts the DMD coiled-coil unfolding data as a stress versus strain plot. The elastic modulus of a material is determined by the slope of the stress versus strain curve. Note that the slope is quite steep at strains below 10% corresponding to an elastic modulus of 0.35 GPa. This value depends on estimates of molecular diameter; in this case, we conservatively estimated a 2 nm effective diameter for the coiled coil. Smaller values of effective diameter result in much higher moduli values (1.4 GPa for 1 nm diameter). The irreversible α-helix to β-sheet transition is also consistent with previous experimental results (43,44). Recent computational (45) and experimental (46) reports argued that unfolding of the coiled-coil region with accompanying α-helix to β-sheet transitions is a primary mechanism of extension. The evidence in these studies indicates that the α-β transition occurs mostly above 100% strain and not strongly until 200–300% strain is reached, which is well beyond the elastic regime of fibrin. These studies also indicate, as we have demonstrated in this study, that the α-β transition is, at best, only partially reversible. Therefore, the α-β mechanism may explain extension at very high strain (and correspondingly very high stress), but is not consistent with elastic deformation below 100% strain and the recoil we observe here.

Figure 4.

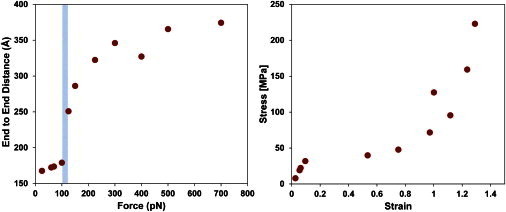
Force-induced unfolding of the coiled-coil. (A) Resulting end-to-end distances for steered DMD simulations stretching the coiled coil region of the molecule. The end-to-end distance (calculated as the distance between γCys19 and αCys161) after 50 ns of simulation was plotted at each force. The critical force is estimated to lie between 100 pN and 125 pN at the sudden jump in protein length (as indicated by the shaded blue area). At 150 pN, the triple helix of the coiled coil was unfolded, but the fourth coil remained folded. At higher forces, the fourth coil unraveled as well. (B) The same force versus end-to-end distance simulation data depicted in A is represented as a stress-versus-strain plot. Strain was calculated by taking the extension (end-to-end distance minus rest length) and dividing by the rest length (16.4 Å). The stress was calculated by taking the applied force and dividing by an estimated molecular cross-sectional area. A circular cross section of radius 1 nm was assumed for the coiled coil to determine stress. Note the dramatic change in slope at the ∼30 MPa stress level.

Figure 5.

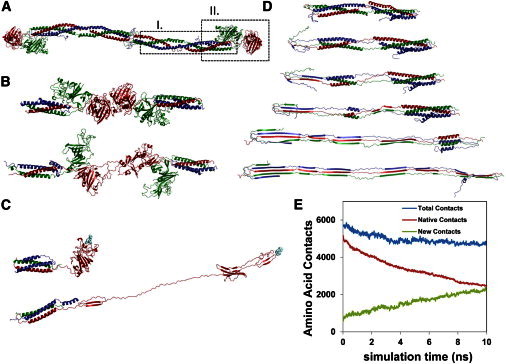
Unfolding of the fibrin molecule. (A) Crystal structure of a human fibrin molecule, with dashed outlines indicating two regions investigated with MD unfolding simulations: I), the coiled-coil region; and II), the γ-nodule within the D end region. (B) Initial and final states of γ-nodule unfolding in the γ-γ interaction simulation. (C) Initial and unfolded states in the γ-nodule unfolding experiment. A GPRV knob-a (pale cyan), which is interacting with the γ-nodule hole a, is pulled. (D) Coiled-coil unfolding. The αhelices in the coiled coil make a continuous transition to β-sheet form. (E) Amino-acid contacts associated with secondary structure. The total number (blue), the native contacts representing the α-helix hydrogen bonds (red), and the new contacts representing the number of amino acid contacts that participate in interstrand β-sheet structure (green) are shown. The plot illustrates that the total number of contacts remains relatively constant and the α-helix to β-sheet transition is gradual rather than abrupt.

For the γ-nodule, forces were applied both at the interface between fibrinogen molecules (γ-γ interface) and at the site of the A-a knob-hole interaction (Figs. 1 A and 5, B and C, respectively). Our simulations showed that the γ-γ interface is weakly interacting, with an F_c of <25 pN. When it was further constrained by knob-hole polymerization interactions, the total potential extension was estimated to be ∼4 nm. In contrast, with force applied at the A-a interface, the γ-nodule underwent two sequential unfolding events with F_c of 74 ± 7 pN and 89 ± 21 pN, and an extension of ∼17 nm (Fig. S5; Movie S4). The critical unfolding forces for the γ-nodule were significantly lower than those for the coiled coil, in agreement with recent AFM and coarse-grained MD studies (22,40). This makes the γ-nodule a more promising candidate for fibrin’s reversible extension. However, the refolding of a complex globular protein domain such as the γ-nodule is very unlikely to occur on the millisecond timescale (47). Folding-rate calculations and known rates for globular proteins of similar complexity yield refolding times on the order of seconds for the γ-nodule (48). We estimated the refolding time of the fibrinogen γ-nodule to be tens of seconds using folding rate calculators (FOLD-RATE and SFoldRate) that have accurately predicted the folding rates of other globular proteins (47,48). Estimates ranged from 20 s (ln(k_f) = −2.99) from FOLD-RATE (48) to 2.3 × 10¹⁰ s (essentially never refolding) from SFoldRate (ln(kf) = −23.88) (47). These estimates need to be verified experimentally, but they agree with the general observation that large globular proteins do not refold on timescales of a few milliseconds, if they refold at all (48–50).

It could be argued that the observed submillisecond recoil could come from the collapse of unfolded γ-nodules, followed by a partial refolding during the slower millisecond relaxation. Although that mechanism cannot be ruled out at this point, it is unlikely, for several reasons. First, after a few milliseconds, the fibers are observed to be completely straight, suggesting full mechanical recovery. Second, the stretching and relaxing are repeatable over several load cycles within tens of seconds. It is unlikely that the fiber would behave reversibly if the γ-nodule were properly folded in the first stretch and then unfolded in subsequent cycles. The AFM-based force versus extension data depicted in Fig. S2 show that fibers are elastic in the strain range studied here, in agreement with prior work (<100%) (4,24).

The αC region is comprised of a natively unstructured segment (amino acids 196–391) called the connector region and a loose β-sheet-containing segment termed the αC domain (51) (Fig. 1 A). Because the exact structure of the αC domain remains elusive, we used I-TASSER (34) to develop a homology model for the entire αC region. Consistent with earlier work (51), the model showed a disordered connector region and a loose β-sheet-containing αC domain. Simulations stretching the αC region showed that the connector region stretched first, allowing ∼50 nm of extension. This is essentially stretching of a random-coil polymer chain, and therefore there was no critical force, and extension occurred continuously (as in the case of a linear spring) for forces between 0 and 25 pN. Unraveling of the β-sheet region occurred with F_c ∼25 pN, yielding an additional 50 nm of extension. We estimated the expected forces required to uncoil the connector region based on simple polymer models (worm-like chain model (52)). For low strain, the entropic force of stretching can be approximated as

$$F=\frac{3k_{B}T}{N{l}^2}\Delta x$$ (2)

Where N is the number of polymeric units (here amino acids), l is the length of the unit, and k_BT is the thermal energy scale. Using numbers for the αC region of k_BT = 4.1 pN/nm, N = 300, and l = 0.34 nm yields a spring constant of 0.4 pN/nm. Thus, stretching the αC region by 50 nm would require 20 pN of force, which is consistent with our simulation. This value for the spring constant of the αC region also matches well with the full fiber AFM-stretching data. Using this spring constant, we can treat the single molecule as a uniform cylinder with an effective Young’s modulus and then compare it with the experimental modulus value. The effective longitudinal spring constant for a cylinder of length L, cross-sectional area A, and Young’s modulus E is given by k = EA/L. An effective molecular diameter range of 3–6 nm yields a range of Young’s moduli of 1–3 MPa. This is in reasonably good agreement with the experimental values found with whole-fiber measurements of 1–10 MPa. In stark contrast, the effective spring constant of the coiled coil at low strain in our simulations is ∼60 pN/nm, >100 times the stiffness of the αC. This value was found by taking the inverse of the slope at low strain of the data depicted in Fig. 4 A.

Single-fiber stress versus strain

Previously reported single-fiber stress-versus-strain measurements (5,24) provide context for the magnitudes of the single-molecule unfolding forces determined here using DMD. From the measured Young’s modulus of a fibrin fiber and the estimate of the lateral packing of fibrin monomers within the fiber, an estimate of the force per molecule can be obtained for a given fiber strain (5). These analyses show that the forces required to unfold the γ-nodule or coiled-coil (forces > 75 pN) require at least 100% strain (5). This suggests that at lower strains below 100% (for which all recoil data were collected), we expect the αC connector region to dominate contribution to strain. Prior studies have also determined the elastic and failure strain limits of fibrin fibers. The elastic limits have been shown to be as high as 180% (8), and the failure strain has been found to occur at >200% (in some cases >300%) (4,8). These results put into context the total potential strain each region is capable of providing to accommodate the total fiber strain. As is clear in Table 1, the αC region is capable of accommodating very high strains, whereas the coiled-coil and γ regions can only accommodate lower strains. Therefore, the αC region is likely to be a key player in enabling the fiber to accommodate reversible strains of well over 100%.

Table 1.

Summary of molecular dynamics results and refolding time estimates

Molecular region	Critical force (pN)	Potential extension per region (nm)	Potential molecular strain	Timescale of reversibility (s)
Coiled-coil	125	21	90%	10°–∞
γ-Nodule	74	3–6	15–30%	101–∞
	89	∼17	80%
αC Domain	20–25	50	220%	unknown
αC Connector (unstructured region)	entropic: 0–25	50–65	220–290%	10−9–10−6
γγ Interface	<25	4	20%	unknown

The table presents the critical force, F_c, the potential extension, and corresponding strain for each portion of the fibrinogen molecule stretched in MD simulations. The coiled-coil region had the highest F_c for unfolding, followed by the γ-nodule and the αC domain. Timescales of reversibility data come from simulation results of the coiled-coil region and estimates from refolding-rate calculators. Potential extension is per molecular region. Potential molecular strain takes into account two units of each type of molecular region (one on each end of the molecule) and is determined by taking the potential extension, multiplying by two, and dividing by the molecular rest length (45 nm).

Prior stress-versus-strain measurements of fibrin fibers also show consensus on several other points relevant to this discussion. First, the stress-versus-strain curve for a fibrin fiber is linear for strains below 100%. A linear curve suggests a consistent or single mode of extension. Although this does not rule out a dramatic change in the mode of extension (from stretching of folded to stretching of unfolded domains), it is not clear how it gives rise to a linear force-versus-extension curve. Second, the stress-versus-strain curve is reproducible over several extensions (<100% strain). Mechanical reversibility (to within 90% recovery at worst) suggests that if any irreversible structural changes in the fiber are occurring, they would have to be relatively minor changes. A transition from a folded protein domain or complex of domains, stabilized through many hydrogen bonds, to an unfolded random-coil polypeptide is a very dramatic change in the context of force-versus-extension behavior (stiffness). Third, the slope of the stress-versus-strain curve at strains below 100% is relatively shallow, corresponding to an elastic modulus (Young’s modulus) of a few megapascals. A material’s stiffness is determined by the nature of the interactions that hold the material together, and therefore folded protein domains that are stabilized through hydrogen bonds have a characteristic stiffness range. Protein assemblies as diverse as actin, microtubules, keratin (43), collagen (53,54), and amyloid fibrils (55) all have stiffness in a relatively narrow range—a few gigapascals (56). The single-molecule unfolding forces observed in experiment and in computations for the γ domain and the coiled coil are consistent with this stiffness (5). Note that the low strain slope in Fig. 4 B corresponds to an elastic modulus of ∼0.5 GPa for the coiled coil. On other hand, protein assemblies whose mechanical properties are determined by unfolded random-coil polymer chains (e.g., elastin, resilin, and capture spider silk) have elastic moduli roughly 2 orders of magnitude lower, in the few-megapascals range (1). Thus, for a biofiber that undergoes a transition from mostly folded to mostly unfolded domains under stretching, we would expect a very dramatic drop in stiffness at the unfolding threshold. This is in fact seen in materials where this transition is known to occur (57). In keratin, a material that shares the coiled-coil structure with fibrin, the initial stiffness is of order GPa and drops dramatically at a few percent strain at the point of the α-helix unfolding (43). This is also what is clearly depicted in Fig. 4 B. The stress-versus-strain curve for the coiled coil undergoes a dramatic change in slope (from ∼0.5 GPa to ∼0.02 GPa) when unfolding occurs. This is in stark contrast to the linear single-fiber curve.

It is important to note that the protein domains that are predominantly responsible for the extension of the fiber must be the same domains that bear the majority of the load. If the extensibility is being borne primarily by the coiled coil or the γ domain, the initial stiffness of the fiber at low strain for the first pull must be comparable to the stiffness of the coiled coil or the γ domain. This is not consistent with the observed behavior. One way to reconcile the ∼GPa stiffness of the coiled-coil and γ regions with the MPa scale for fibrin fibers is a zipper-type mechanism in which the stress is concentrated rather than distributed throughout the fiber. Only a small fraction of the coiled coils would bear the total load, and as they unfold would pass the concentrated load to the next isolated cohort of coiled coils. The global stiffness of the fiber would then appear to be much lower than expected if the load were distributed uniformly. Because there are no structural data consistent with a nonuniform distribution of the applied load, this zipper mechanism is unlikely. The zipper model is also inconsistent with the observed mechanical reversibility.

Low-strain fiber (<100%) extension and relaxation likely arises through the αC region

The accumulated evidence indicates that αC is of central importance for both fibrin’s extensibility and recoil. It will extend at much lower forces than any of the molecular regions that require unfolding, making it the most likely region to stretch during initial stages of fiber extension. It also provides the most potential extension consistent with fibrin’s high extensibility. Most importantly, it is the only region capable of restoring strain on the submillisecond timescale. Rouse’s theory (58) predicts relaxation times of an isolated unentangled polypeptide of the length of the connector region to be ∼1 μs (see Supporting Material), which provides a lower bound (fastest recoil) estimate given the crowded environment within a fiber. We constructed a mechanical model to predict recoil rate by treating the fiber as an overdamped harmonic oscillator. We used fiber geometry in estimating viscous drag, and estimated the spring constant using a network worm-like chain model (5). For fibers with diameters ∼100 nm, the predicted recoil is on the order of 1 ms (see Supporting Material), in reasonable agreement with our experimental timescales. However, this model does not capture the two regimes of recoil observed in experiment. We speculate that the increasing molecular crowding within the fiber as it relaxes from high strain impedes the recoil of individual extended molecules and slows the overall fiber recoil. This question will be the focus of further modeling efforts.

Our model resolves the apparent contradiction between molecular order and elastomeric properties in fibrin: the protein unit itself has both structured and unstructured regions, with the structured regions engendering intermolecular ordering in fibers through specific interactions, and the unstructured regions giving rise to the elastic properties. As the fiber is stretched, the αC regions connecting the structured parts of the molecules extend, allowing protofibril sliding. When the force is removed, the entropic recoil of the αCs results in rapid fiber relaxation (Fig. 1 F). Within this model, extension is supported by strain that occurs between protofibrils rather than within the protofibrils themselves (which would require protein unfolding). As we have described in more detail elsewhere (5), a model that relies on this type of interprotofibril strain puts constraints on the average length of protofibrils within the fiber. For the observed extensibility (>200%) to come from strain between protofibrils, the protofibrils must be relatively short: the average length would have to be of the same order of magnitude as the maximum extension of an interconnection. Previous studies (59–61) have shown that protofibrils are composed of a few monomers (up to 20) under standard polymerization conditions, which is consistent with the αCs supporting the majority of fiber strain. This helps us build a clearer picture of the interrelation of molecular structure, mechanical properties, and physiological function for fibrin. The functional requirement that fibrin fibers must be elastomeric while also supporting multiple specific biochemical interactions that require well-defined tertiary structure may help explain the dual structural nature of fibrin fibers.

The elastomeric properties of fibrin (i.e., extensible and elastic, with rapid recoil) also provide insight into the specific mechanical function for which it is optimized. Like elastin, which provides the elasticity of arterial walls, fibrin is optimized mechanically for elastic energy storage, which enables repeated stretching and contraction at Hz frequencies. This is in contrast to other highly extensible biopolymers such as viscid spider silk (capture silk), which is mechanically optimized for energy dissipation during once-off prey capture, rather than for elastic energy storage (1). Successful mapping of the structure-property-function nexus for fibrin may also have important biomedical implications. Tracing the molecular origins of fibrin’s mechanical properties to the αC region provides a target for fibrin therapeutics. Certain dysfibrinogenemias, such as Fibrinogen Guarenas, have mutations in the αC region, resulting in stiffer clots (62). Experiments investigating the mechanical effect of peptides that target particular locations within the αC could provide higher-resolution insight into the role of the αC region in fibrin fiber mechanics.

Conclusions

We have shown that individual fibrin fibers, comprising tens of thousands of molecules, exhibit submillisecond elastic recoil from high strain. This timescale is striking when compared with the refolding dynamics of large individual proteins that often can take thousands of times longer to refold. Additionally, the recoil is reproducible over several load cycles and independent of the presence of calcium or FXIIIa ligation. We have also shown through DMD simulations that mechanisms for extension and recoil involving reversible unfolding of the coiled-coil or γ domains are unlikely to occur on millisecond timescales. Our experiments and simulations call into question models of fibrin mechanics that rely only on the unfolding and refolding of protein domains to account for fibrin’s elastomeric behavior, particularly at strains below 100%. Instead, the αC region, extending and recoiling as an entropic spring, is the likely origin of fibrin’s low strain extensibility and rapid recoil.