In their comment in this issue of the Biophysical Journal, Münster and Fabry (1) propose a simple and elegant implementation of our bubble method (2) based on the Euclidean distance map (EDM) (3). This EDM bubble method is quite efficient in boosting the performance of our original method because it is fast and at the same time provides the optimal (maximal) coverage of the image, ensuring high accuracy in the parameters recovery (3). Thus, the implementation proposed by Münster and Fabry (1) appears to overcome simultaneously the main two limitations of our original method.
However, as outlined in the comment by Münster and Fabry (1), the EDM bubble method presents some practical applicability problems. Indeed, due to the pixilation of the image, the EDM maxima contains many fake bubbles that are not trapped by the fibers of the networks because they are tangent to only two fibers. To suppress these artifacts, the authors suggest convolving the EDM with a small Gaussian kernel (σ = 1 pixel) before their maxima are determined. This procedure helps, but is not sufficient to remove all the fake bubbles.
To cope with this problem, we here propose an a posteriori analysis of the data, where each raw bubble found with the EDM maxima is processed by comparing the distances Rk (k = 1, 2, 3) of its center from the first three nearest-neighbors fibers. Whenever one of the three Rk values differs >±5% of their average value 〈R〉 = (R1 + R2 + R3)/3, the bubble is considered to be tangent to only two fibers and is filtered out. For small bubbles, for which 0.05 × 〈R〉 is <1 pixel, the filtering threshold is set to 1 pixel. To avoid boundary effects, the bubbles whose centers fall within an edge equal to 5% of the image side are filtered out. All the remaining ones are considered true bubbles (i.e., trapped by the network fibers) with their center given by the EDM maxima and radius equal to 〈R〉.
In Fig. 1, we report an example of the EDM bubble analysis with and without the filtering procedure described above, carried out on an in silico fibrin network characterized by a volume fraction ϕ = 1.14×10−2 with fibers of diameter d=200nm, so that it closely resembles the structure of a real fibrin gel (4–7). In panel A, we report all the raw EDM bubbles found after a convolution of the EDM with a σ = 1 pixel Gaussian kernel, whereas in panel B we show the bubbles that survived the filtering procedure and are tangent to (at least) three fibers. Then, by applying the discarding procedure (2) for selecting the bubbles that are non- or only slightly overlapped, we obtain panels C and D, which correspond to panels A and B, respectively. Finally, in panel E we report, for comparison, the bubbles found with our original algorithm. One can appreciate the similarities between panels D and E, whose covering bubbles are almost the same. Conversely, panels C and E are substantially different, with panel C showing more bubbles than panel E, and, in particular, containing fake bubbles that are not present in panel E.
Figure 1.
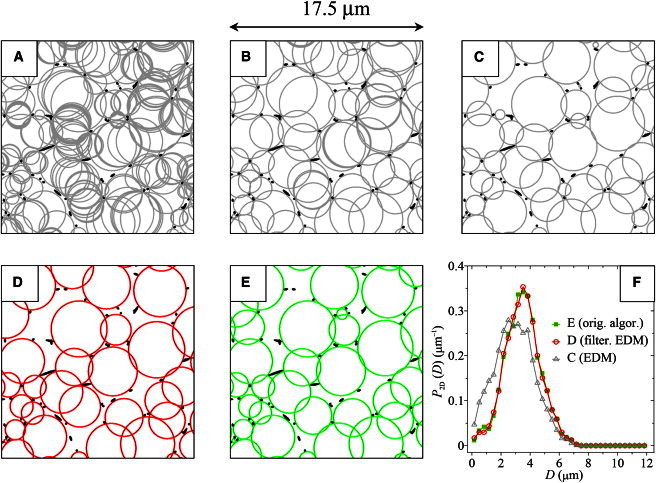
Comparison between the EDM, filtered EDM, and iterative bubble methods for an in silico fibrin network realized at a volume fraction ϕ = 1.14 × 10−2 and characterized by fibers of diameter d = 200 nm. (A) Raw bubbles found with the EDM method after a convolution of the EDM with a σ = 1 pixel Gaussian kernel. (B) Bubbles of panel A survived from the filtering procedure, in which fake bubbles tangent to only two fibers have been filtered out. (C) Non- or slightly overlapped bubbles selected from bubbles of panel A. (D) Non- or slightly overlapped bubbles selected from bubbles of panel B. (E) Non- or slightly overlapped bubbles found with the original iterative algorithm. Note the similarities between panels D and E, whose bubble diameter distributions are perfectly superimposed as shown in panel F.
A statistical analysis of the two-dimensional bubble diameters distribution P2D(D) associated to panels C–E is reported in panel F, which was obtained by averaging many statistical independent sections of the gel. The distributions recovered with our algorithm (solid green squares) and the filtered EDM method (open red circles) are excellently matched to each other, but remarkably different from the distribution recovered with the unfiltered EDM method (open gray triangles). Quantitatively, ours and the filtered EDM method recover average diameters and standard deviations that differ <1%, i.e., 〈D〉2D = 3.47 μm and σ2D = 1.22 μm, while the parameters recovered with the unfiltered EDM method are highly inaccurate, being 〈D〉2D = 2.93 μm and σ2D = 1.35 μm. It is worth pointing out that, in this comparison, our (iterative) method was not stopped at a coverage area of 0.70 (as proposed in Molteni et al. (2)), but run until convergence (see the supplementary materials of Molteni et al. (2)), at which stage the average covering area was ∼0.85. The latter requirement makes the iterative method even slower than what reported in Molteni et al. (2), i.e., ∼4 min/slice on a standard PC (Intel Quadcore-i7 3.07 GHz, 8 GB RAM). At variance, the filtered EDM method takes ∼10 s/slice.
In conclusion, the EDM implementation of our bubble method, as suggested by Münster and Fabry (1), when properly filtered as described in this response, provides a correct recovery of the bubble diameter distribution with processing times much faster (orders of magnitude) compared to our original method.
An executable version of the LABVIEW code running the EDM filtered bubble analysis is available upon request from F.F.
References
- 1.Münster S., Fabry B. Comment to the editor. A simplified implementation of the bubble analysis of biopolymer network pores. Biophys. J. 2013;104:2774–2775. doi: 10.1016/j.bpj.2013.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Molteni M., Magatti D., Ferri F. Fast two-dimensional bubble analysis of biopolymer filamentous networks pore size from confocal microscopy thin data stacks. Biophys. J. 2013;104:1160–1169. doi: 10.1016/j.bpj.2013.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mickel W., Munster S., Schroder-Turk G. Robust pore size analysis of filamentous networks from three-dimensional confocal microscopy. Biophys. J. 2008;95:6072–6080. doi: 10.1529/biophysj.108.135939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Magatti D., Molteni M., Ferri F. Modeling of fibrin gels based on confocal microscopy and light-scattering data. Biophys. J. 2013;104:1151–1159. doi: 10.1016/j.bpj.2013.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ferri F., Greco M., Rocco M. Growth kinetics and structure of fibrin gels. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2001;63:031401. doi: 10.1103/PhysRevE.63.031401. [DOI] [PubMed] [Google Scholar]
- 6.Ferri F., Greco M., Rocco M. Structure of fibrin gels studied by elastic light scattering techniques: dependence of fractal dimension, gel crossover length, fiber diameter, and fiber density on monomer concentration. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;66:011913. doi: 10.1103/PhysRevE.66.011913. [DOI] [PubMed] [Google Scholar]
- 7.De Spirito M., Arcóvito G., Ferri F. Small and wide angle elastic light scattering study of fibrin structure. J. Appl. Cryst. 2003;36:636–641. [Google Scholar]


