Raman signal enhancement via elastic light scattering

Abstract

The enhanced generation of a spontaneous Raman signal by way of elastic scattering is demonstrated. Using Monte Carlo simulations, we show that elastic scattering, by increasing the path length of light through the medium, enhances the generation of a Raman signal. This is investigated over a large parameter space, demonstrating that this effect is robust, and providing additional physical insight into the dynamics of light propagation in a turbid medium. Both the temporal and spatial profiles of the Raman signal are shown to depend heavily on the amount of scattering present.

1. Introduction

Raman spectroscopy has been widely used to obtain detailed chemical information about a system without the need for chemical markers. It has been used for a wide variety of applications including cancer diagnosis [1, 2], the detection of hazardous materials [3], and industrial quality control. Raman spectroscopy has previously been carried out in turbid media [4, 5]; however, the effect elastic scattering has on the process has yet to be investigated. In other words, is there a way to use elastic scattering to optimize Raman generation? Experimentally, colloidal solutions and metamaterials [6] offer the possibility of tuning elastic scattering to maximize the generation of a Raman signal.

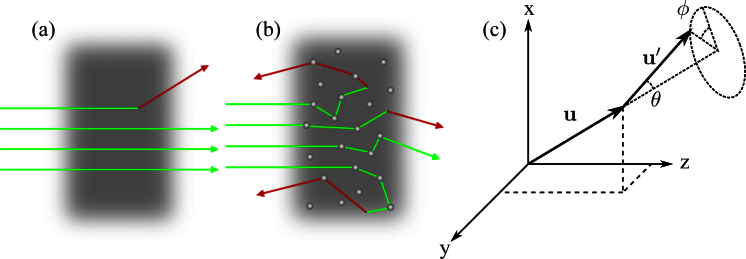
As light propagates through an optically thick turbid medium, photons are elastically scattered multiple times, resulting in an increase in the distance a photon travels inside the medium. This gives the photon more opportunities to interact with the surrounding medium and generate a Raman photon, carrying with it spectroscopic information about the medium. Figs. 1(a) and 1(b) conceptually illustrate the idea of increased path length in the presence of elastic scattering.

Fig. 1.

Conceptual figure illustrating how scattering increases the path length traveled inside a turbid medium: a) without scattering, b) with scattering, c) coordinate system used to describe scattering. Where u is the direction vector before a scattering event, and u′ is the direction vector after a scattering event.

Monte Carlo methods have become the gold standard for modeling light propagation in turbid media. They have previously been used to investigate the effects of elastic scattering, spontaneous Raman scattering [7–10], polarization [11], fluorescence [12, 13], and amplified spontaneous emission [14]. However, elastic scattering has not been included in the parameter space of any of these investigations.

We first discuss our Monte Carlo model for light propagation through a turbid medium. It takes into account elastic scattering, linear absorption, and spontaneous Raman scattering. This differs from previous models, in that we use a small fixed step size allowing us to look at both the low scattering and high scattering regimes [15]. We demonstrate that increased elastic scattering leads to an enhancement of the Raman signal in both, the forward (transmission) and backward (reflection) directions. The spatial and temporal profiles of the Raman signal in the reflection geometry are shown to depend heavily on elastic scattering and closely mimic the distributions of the elastically scattered light.

2. Model

Consider a medium of small spherical particles with radii on the order of the wavelength of light suspended in an active Raman medium. This colloidal suspension allows the scattering mean free path to be variably controlled. Due to the small size of the scatterers and assumed large Raman cross section of the liquid, we assume all the Raman signal is generated entirely in the liquid.

For simplicity, consider a short (1 ps full-width at half-maximum) Gaussian pump pulse with a Gaussian spatial profile normally incident on this medium. We assume the turbid medium is surrounded by vacuum and neglect reflections and refractions at the interfaces, since these will do little to change the effects we are interested in observing [16].

We are particularly interested in investigating the effects in both the low and high scattering regimes. Using the same model, we would like to accurately model the physics even when mean free paths are larger than the physical sample. To accomplish this, we use a fixed step size, Δr, significantly smaller than the shortest mean free path used in the simulation. This differs from traditional Monte Carlo simulations where each photon is propagated with a randomly distributed step size corresponding to the distance between successive scattering events.

To describe elastic scattering, linear absorption, or spontaneous Raman scattering, we define a mean free path, l_s, l_a, or l_R, respectively. During each step, there is a probability of an event given by

$$P_i=1-e^{-\mathrm{\Delta }r/l_i},$$ (1)

where i represents elastic scattering, absorption, or Raman scattering. Each mean free path represents the average distance a photon travels between a particular event.

Anisotropic elastic scattering is taken into account via the anisotropy parameter, g = 〈cos(θ)〉, and the Henyey-Greenstein probability distribution for the scattering angle, θ[17]. Elastic scattering is assumed symmetric around the original propagation axis, hence, ϕ is uniform. Both θ and ϕ are defined by the coordinate system illustrated in Fig. 1(c).

Raman scattering is more commonly discussed in terms of the Raman cross section. The Raman cross section relates to l_R by, 1/l_R = σ_RN, where σ_R is the Raman cross section, and N is the number density of Raman scatterers. Spontaneous Raman scattering is typically very weak (σ_RN ∼ 10⁻⁷ mm⁻¹) for most condensed matter [18]. In order to obtain a usable signal to noise ratio, we would need to propagate about 10⁹ photons per pulse. Due to computational limitations, we choose this effective cross section to be artificially large, σ_RN ∼ 10⁻² mm⁻¹. Until pump depletion becomes non-negligible, this modification manifests itself as simply an overall multiplicative constant in the Raman signal. The parameters used in this paper did not result in pump depletion. Hence, we conclude that for the effects we are interested in, this artificially high Raman cross section does not effect the validity of our conclusions. This analysis is in agreement with previous investigations [7].

3. Discussion and results

For each simulation below, the number of photons per pulse was set to 10⁵ photons. We average over 25 independent pulses. The baseline parameters consist of a sample width, w = 0.5 mm, an anisotropy parameter, g = 0.6, a step size, Δr = 0.001 mm, an index of refraction, n = 1.5, and an effective Raman cross section of σ_RN = 0.01 mm⁻¹. We consider a full-width half-maximum temporal pulse width, δτ = 1 ps, a full-width half-maximum beam diameter, δρ = 0.01 mm, and a temporal pulse delay, Δτ = 5.0 ps, for our incident pulse.

The volume concentration of scatterers is related to the scattering mean free path of the solution by Φ = 2d/(3l_sQ_s) [19], where Φ is the volume concentration, d is the diameter of the scattering particle, and Q_s is the ratio of the particles scattering cross section to its physical cross sectional area known as the scattering efficiency factor. The scattering efficiency factor was set to 2.5. This agrees with the value computed from Mie scattering calculations for a ∼ 1 μm diameter boron nitride particle, suspended in dimethyl sulfoxide (DMSO). DMSO was selected as the prototypical Raman active liquid due to its large Raman cross section. Because of its low absorption, available particle size, ability to suspend in DMSO, and large index mismatch with DMSO (n_BN ∼ 2 vs. n_DMSO ∼ 1.5), boron nitride was chosen to be the scatterer.

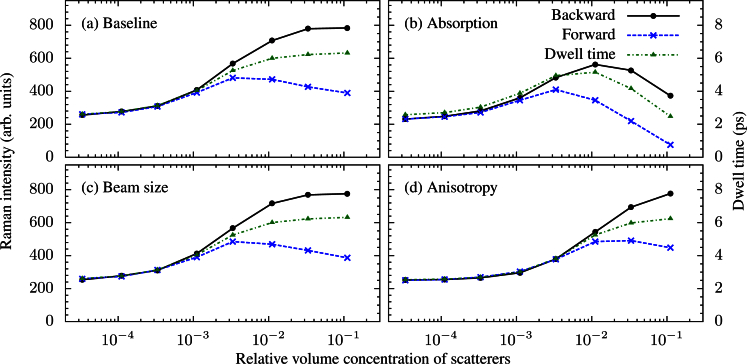
Figure 2 demonstrates the results of several runs using varying parameters. In each case, we observe an enhancement of the Raman signal due to elastic scattering. The increase in the average time a photon spends inside the sample, known as the dwell time, is responsible for this enhancement. In the high scattering regime, a large portion of the incident pulse is scattered out of the sample near the surface. These photons do not travel a long distance in the sample, thus do not contribute significantly to the Raman signal. On the other hand, photons that penetrate into the sample tend to have long path lengths, contributing greatly to the Raman signal. These two competing effects eventually compensate each other, and no additional enhancement is seen with a further increase in scattering.

Fig. 2.

Intensity of the Raman signal and dwell time as a function of scatterer concentration: a) the set of baseline parameters (see the text) are used, b) a weak absorption (l_a = 10 mm) is included, c) a larger diameter incident beam (δρ = 0.1 mm) is used, d) a larger anisotropy parameter (g = 0.9) is used.

In a completely transparent medium, one would expect half the Raman photons to be emitted in the forward direction and half in the backward direction due to the isotropic nature of spontaneous Raman scattering. This results in the Raman signals in the reflection and transmission geometry to be identical until the transport mean free path, l_t = l_s/(1−g), becomes comparable to the thickness of the sample. At this point, reflections become dominant over transmission, leading to a preference in the backward direction.

By varying several parameters, the enhancement of the Raman signal is shown to be robust over a wide parameter space. The most significant change is due to absorption. In the low scattering regime, absorption has little effect because the path lengths traveled by the photons are small compared to l_a. However, in the high scattering regime, even a small absorption has a large effect. In a highly scattering non-absorbing medium some photons spend a very long time in the medium (illustrated by Figs. 3(c) and 3(d)). In the absence of absorption, these photons contribute significantly to the Raman signal because they experience the longest interaction distance. However, many of these photons will be absorbed before they exit the sample when a small amount of absorption is introduced.

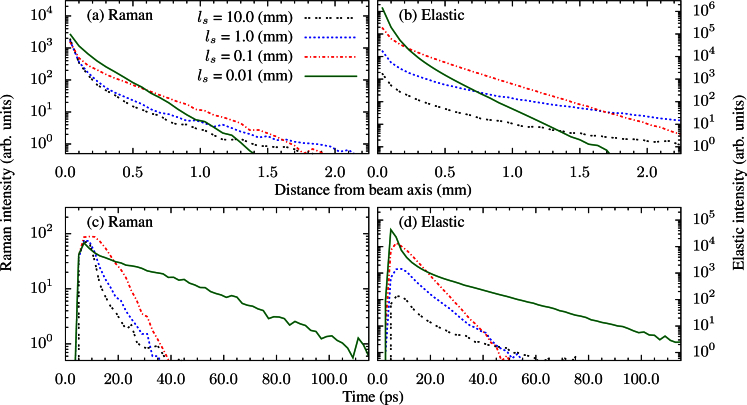
Fig. 3.

Backward spatial distribution of the: a) Raman scattered light, b) elastically scattered light. Backward temporal distribution of the: c) Raman scattered light, d) elastically scattered light.

Furthermore, the incident beam size has no effect on the total intensity of the spontaneous Raman signal. Equivalently, the pulse length will have no effect on this signal. The spatial and temporal Raman signals will, however, depend on the spatial and temporal behavior of the pump. Integrated over space and time, these effects average out. This will no longer be the case if stimulated effects are present and could serve as a potential tool for analyzing whether nonlinear effects are present in a turbid medium.

When we increase the anisotropy, we see an effective shift towards lower scattering. This is because the meaningful length scale of a linear scattering problem is l_t, not l_s[20]. Hence, for a larger g, l_t is longer and the system behaves as if we have less scattering. This argument is valid for discussing linear effects, such as spontaneous Raman scattering, because such effects depend only on the average distance light travels inside the medium. We run into a problem if we try to apply this argument to a system which exhibits non-linear effects. These phenomena depend on the distribution of light inside the sample, which, in turn, depend on both l_s, and g independently.

Figure 3 shows the spatial and temporal distributions of the light that exits the sample in the reflection geometry using the same baseline parameters discussed previously. Here, for simplicity, we have assumed an infinite size detector that is in direct contact with the sample. Multiple values of l_s are shown to illustrate how the system varies with increased scattering. The first thing to notice is the spatial and temporal distributions of the Raman photons closely mimic those of the elastically scattered photons. This is not surprising because we have assumed that our sample has similar optical properties at both the fundamental and the Raman shifted wavelength. Figure 3 illustrates that a technique such as spatially offset Raman spectroscopy (SORS) [21] is best suited for analyzing low scattering media. However, time resolved Raman spectroscopy [22] would be best suited for highly scattering media.

For low scattering (large l_s), the spatial distribution of the light initially broadens. This can been seen by the l_s = 10 mm curve decaying slightly faster than the l_s = 1 mm curve. Heuristically, this is because photons that emerge from the sample a significant distance from their initial location are the photons that, on average, penetrate the deepest into the sample [7]. Thus, in the case of a finite thickness sample whose thickness is small compared to l_t, these deep photons simply exit the sample as transmission photons. As scattering increases (l_s decreases) slightly, l_t correspondingly decreases, making the sample more optically thick and allowing more of these wide scattering photons to emerge as reflected photons. Once scattering increases to the point where l_t is small in comparison to the width of the sample, the sample behaves as a semi-infinite sample and the spatial distribution becomes more narrow. This can be seen by the much faster decay of the l_s = 0.01 mm line compared to the l_s = 0.1 mm line.

The temporal distribution of the backwards signal behaves in essentially the opposite way of the spatial distribution. The argument for why this is the case is the same as above. The most striking feature in the temporal distributions is the appearance of a short spike in the ls = 0.01 mm line. This is a result of the photons that get reflected out of the sample in only a few bounces. The opposite effect of this is the long tail that is present in the same graph. This is generated by the photons that penetrate deep enough into the sample to where l_t is large compared to the distance to either surface, essentially trapping the photon in the medium generating the long tail.

4. Conclusion

A Monte Carlo model with a clear, simple physical picture has been implemented. Elastic scattering, linear absorption, and spontaneous Raman scattering are considered to demonstrate that increased elastic scattering enhances the generation of a spontaneous Raman signal in both the reflection and transmission geometries over a large parameter space. A strong dependence on elastic scattering is observed in both the backward spatial and temporal profiles of the detected light. Preliminary experiments currently under way using colloidal suspensions of boron nitride particles in DMSO show a good agreement with these predicted results.