Stress Analysis at the Molecular Level: A Forced Cucurbituril-Guest Dissociation Pathway

Abstract

Changes in mechanical stresses in a tight-binding host-guest system were computed and visualized as the cationic was computationally pulled out of the cucurbituril host in a series of steps. A sharp conformational transition was observed as one of the guest's ammonium groups jumped through the center of the host to the opposite portal. The conformation immediately prior to this transition was found to possess high levels of Lennard-Jones and electrostatic stress. This observation, along with the specific distribution of Lennard-Jones stress around the portals, suggested that the conformational transition resulted from steric constriction, which had been expected, and electrostatics, which was not expected. An important role for electrostatics, at least at the level of these calculations, was confirmed by a comparative computational pulling study of another guest molecule lacking the critical ammonium group. These calculations suggest that the binding kinetics of diammonium guests that position an ammonium at each cucurbituril portal will be found to be slower than the kinetics of monoammonium guests. More generally, the results suggest that computational stress analysis can provide mechanistic insight into supramolecular systems. It will be of considerable interest to extend such applications to biomolecules, for which the mechanisms of conformational change are of great scientific and practical interest.

Introduction

The concepts of mechanical stress and strain are widely used. For example, engineers rely on them when designing structures, and geophysicists study stress waves propagating through the earth. Materials scientists have, furthermore, developed computational methods of extracting measures of stress from atomistic simulations^1,2,3,4,5,6, and such approaches have recently begun to find application at the level of single molecules. Thus, Rafii-Tabar has discussed stress and strain in carbon nanotubes⁷, and Yamato and coworkers used simulations to observe the propagation of stress in photoactive yellow protein during the “protein quake” generated by photoisomerization of the chromophore⁸. In related earlier work, Yamato and Go computed molecular strain in proteins under hydrostatic pressure⁹; and Beuhler and coworkers have recently computed stress in connective tissue proteins¹⁰. Such applications suggest that atomistic stress theory can contribute to our understanding of molecular mechanisms, and perhaps even guide molecular design. However, stress calculations have not, so far, been applied in the context of supramolecular chemistry.

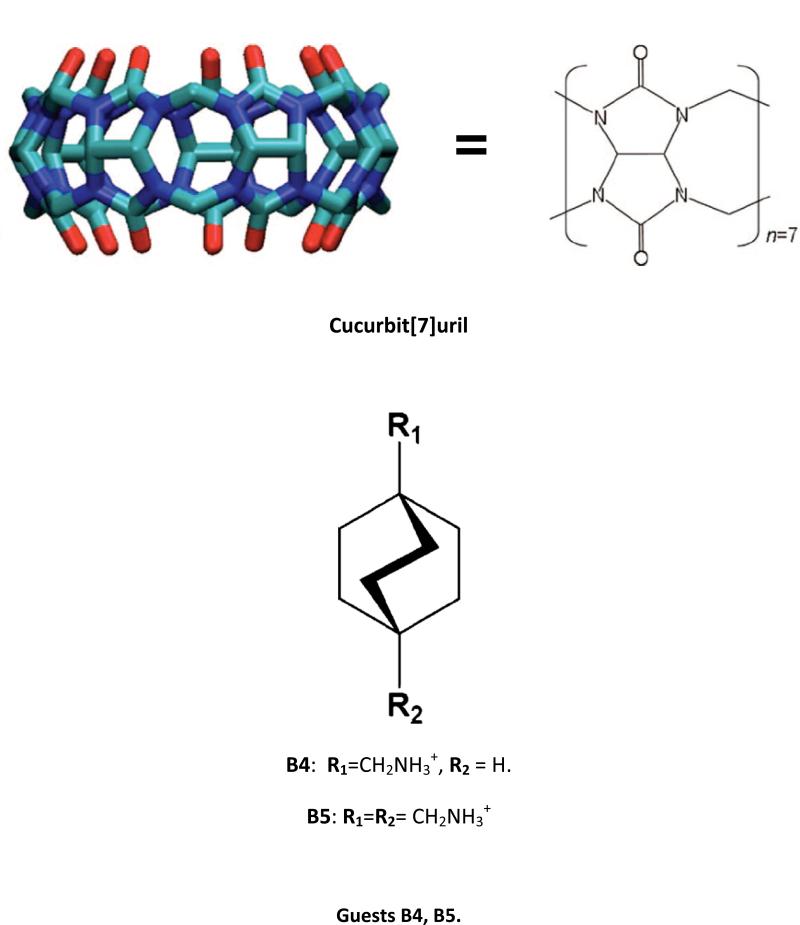
The cucurbiturils^11,12, chemical hosts constructed as rings of glycouril monomers (Figure 1), have been the subject of increasing interest in recent years, as they are relatively easy to synthesize and display distinctive molecular recognition properties, including the ability to bind dicationic guests from aqueous solution¹³, sometimes with affinities rivaling the tightest protein-ligand systems^14,15,16. The cucurbiturils have a rich range of properties and potential applications, as recently reviewed^17,18,19. Examples include formation of polyrotaxanes^20,21, modulation of the fluorescence of guest dye molecules²², chemical catalysis²³, and, for specialized variants, two-site allosteric binding²⁴. The mechanisms and kinetics of cucurbituril-guest binding are thus of considerable interest. It is already known that the size of the guest molecule can strongly influence binding kinetics for cucurbit[6]uril (CB6) in a manner that is essentially independent of binding thermodynamics^25,26. This is presumably because its portals are of smaller diameter than its internal cavity. Such constrictive binding^27,28 highlights the importance of steric interactions as determinants of binding kinetics for these systems, but the pH-dependence of binding kinetics for titratable guests with CB6 indicates that electrostatic interactions also can influence the stability of the transition state^29,26.

Figure 1.

Host cucurbit[7]uril host (CB7) and guests B4 (monoammonium) and B5 (diammonium).

Here, we use computer modeling to study the causes and distributions of atomistic stress in a host and guest when they are forced apart, as if in an atomic force microscopy (AFM) single-molecule experiment. The system consists of cucurbit[7]uril (CB7)^11,12 with a dicationic compound (B5) predicted³⁰ and proven (Inoue, Rekharsky and Yang, to be published) to bind CB7 with an ultra-high affinity similar to that previously observed for a dicationic ferrocene derivative¹⁵. We also carry out comparative calculations for a monocationic guest (B4) predicted³⁰ to bind CB7 less tightly by 3 kcal/mol than B5. (See Figure 1.) Novel methods of computing and visualizing changes in atomistic stress are used to evaluate the relative roles of steric constriction and electrostatics as kinetic determinants in these systems, and reveal informative and unexpected distributions of molecular stress as the complexes dissociate.

Methods and Concepts

Molecular modeling of a forced host-guest dissociation

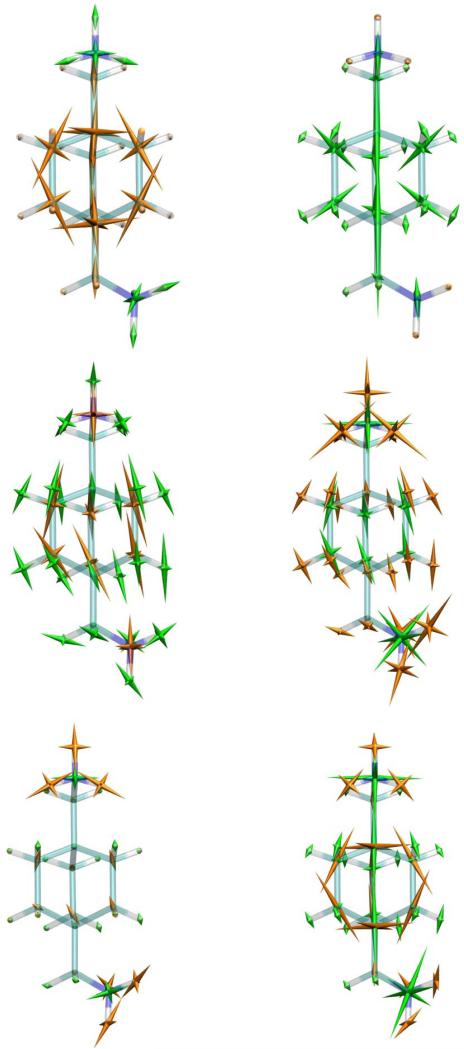
The calculations started with the most stable conformation of the host-guest complex identified with the M2 free energy method^31,32, based on previously described force-field and implicit solvation parameters³⁰. We judged a nitrogen of the guest and an equatorial carbon of the host to be chemically plausible points for added linkages to an AFM tip and a fixed substrate, and assigned pulling forces to these atoms in a computationally simple fashion by adding an artificial harmonic bond between them as illustrated in Figure 2. The N-C distance was about 5.5 Å in the initial conformation of the complex. The equilibrium length B_o of the artificial bond, with force constant 100 kcal/mol/Ų, was increased in increments, and gradient-based energy-minimization was carried out so that the artificial bond would drive the guest molecule partly or fully through and out of the host cavity. The length of the artificial bond after minimization, B, was recorded, and was also used to compute the magnitude of the force, F, exerted by the artificial bond at its N and C attachment points, where F=100(B-B₀). This procedure was repeated for various equilibrium lengths of the artificial bond, and stresses were calculated for the resulting conformations. These stresses were compared with the stresses computed for the most stable conformations of the free host and guest with the M2 method. The stress calculations are described below. Hydration effects were treated approximately by a generalized Born model^33,34,35. Because the present calculations do not account for thermal motion, barrier-crossing results only from the conformational forcing of the artificial bond, rather than from random thermal motion, and the calculations model only one dissociation pathway. They thus model a fast pulling process, and the forces and stresses are expected to be larger than those seen at the lower pulling speeds of typical AFM experiments. A similar forcing process has been used in a prior computational examination of cucurbituril-guest dissociation²⁶.

Figure 2.

Stable bound conformation of CB7 (cyan) with B5 (red), with artificial forcing bond (green dotted line). Hydrogen atoms omitted.

Mechanical stress and its calculation and visualization at the atomistic level

The stress as a function of position within an object is a tensor field that describes the action of local forces. Tensile stress occurs when a volume element of material is pulled in opposite directions from opposite sides, compressive stress when it is pressed on from opposite sides, and shear stress when opposite sides are subjected to oppositely directed tangential forces. A volume element can be under stress yet experience zero net force. Accordingly, an object can be in mechanical equilibrium, yet internally stressed. For example, the cables of a suspension bridge are under tensile stress, and its towers are under compressive stress. Furthermore, a local force on a body can place the whole under stress, with long-ranged consequences. The transmission of torsional stress and its consequences for global DNA supercoiling provides an example at the molecular level. The stress on a volume element generates a deformation, i.e., to strain, which is also a tensor field. For elastic materials, stress and strain are linearly related to each other, and the energy of elastic deformation is directly related to the product of stress and strain. Such a linear relationship is not expected to hold in general for molecules, although it may be a good approximation for ones that are relatively stiff. Note that strain in this mechanical sense is not identical with “chemical strain”: mechanical strain is defined as a spatial deformation induced by stress³⁶, as just described, whereas chemical strain is the enthalpy of a molecule relative to an unstrained reference structure³⁷.

Here, we computed atomistic stresses for individual energy-minimized conformers of the host, the guests, and their complexes. Following Zimmerman and coworkers⁶, we use Hardy's expression for the local stress tensor³⁸. The stress tensor σ_i at each atom i was thus computed as

$${\sigma }_i=\frac{1}{v}\sum _{local}{r}_{ij}\otimes f_{ij}$$

where j indexes atoms within a spherical region of volume v_loc local to atom i, r_ij is the vector from atom i to atom j, and f_ij is the force exerted by atom j on atom i. This formula is most straightforwardly applied to center-to-center forces, so attention here is limited to bonded, Lennard-Jones, Coulombic, and Generalized Born (GB) forces, the latter excluding the force contributions from variation in the effective Born radii. We found it informative to compute and visualize the stresses associated with each separate force term, combining the Coulombic and GB stresses to determine net electrostatic stress. The radius of the spherical region was set to 5 Å and all noncovalent force calculations were cut off at this range. Covalent bond stresses accounted for only atoms j bonded directly to atom i. Here negative and positive values of σ_i imply tensile and compressive stresses, respectively. For constrictive host-guest binding, one may anticipate that forcing a bulky guest out through a narrow portal will generate compressive Lennard-Jones stresses between the guest and the portal, along with tensile bond stresses around the portal itself.

Initial calculations indicated that the free molecules possessed significant baseline stress. We were interested in stress changes on binding, and therefore wished to subtract the stresses of the free molecules from the stresses of their complexes. However, a naïve initial approach to evaluating these differences – simply subtracting the stress tensors – was unhelpful because changes in the lab-frame orientation of the molecules caused matching tensors in the bound and free states not to cancel. We therefore subtract the stress tensors in local molecular coordinate systems, as follows. We transform each atom's lab-frame principal stresses before and after binding into local Cartesian coordinates, subtract free from bound stresses in these local coordinates, then convert back to lab coordinates for analysis and display. Separate local Cartesian coordinates were set up for each atom i by choosing two atoms j, and k, such that i is bonded to j and j to k. Then the local x-axis was aligned with the ij vector, the local y-axis was placed in the ijk plane and orthogonal to the x-axis, and the z-axis was oriented along the cross-product of the x and y unit vectors. The same atom triplets were used for the free and bound states, in order to establish consistent local coordinates.

Stresses, or stress differences, at each atom i were visualized by diagonalizing the tensor S_i to provide the magnitudes and directions of its 3 principal stresses. The program VMD³⁹ was then used to render each principal stress as a spindle-shaped glyph made of two thin cones based at atom i, extending in the positive and negative directions along the direction of the principal stress and having a length proportional to the magnitude of the principal stress. Tensile (negative) and compressive (positive) stress components were distinguished by coloring their corresponding spindles green and orange, respectively. The length of each cone (Å) was set to the magnitude of the corresponding principal stress (kcal/mol/Å), scaled by the factor 0.2 v_loc. This visualization approach differs from previously reported tensor glyphs designed for visualization of stresses in continuous media^40,41,42,43.

Results

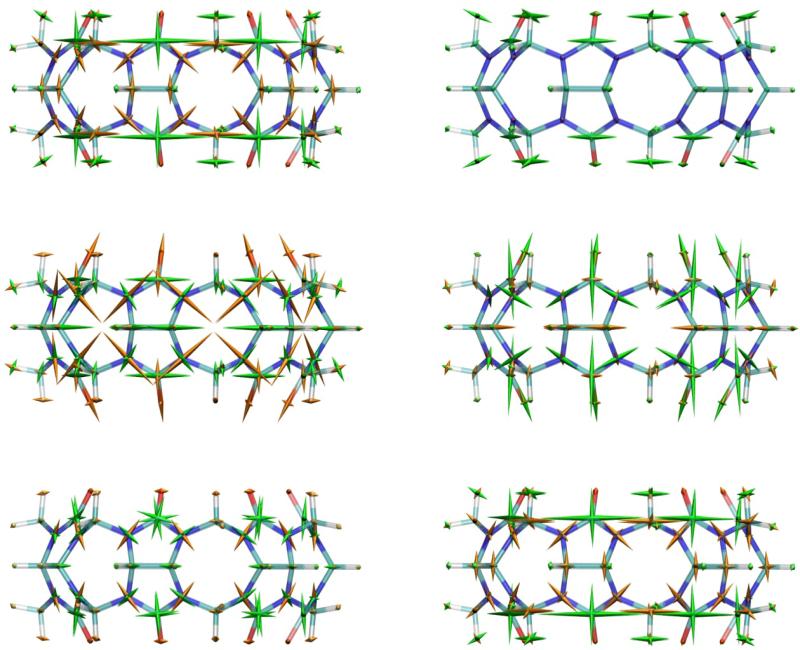
Stresses in the unbound host, CB7, and guest, B5

Figure 3 displays the stresses computed for the most stable conformation found for the free guest B5. Bond-stretch stresses (top left) are tensile (orange spindles) in the bicyclooctane moiety and weakly compressive in the ammonium groups. The Lennard-Jones forces (top right) show compression (green spindles) in the bicyclooctane moiety, reflecting steric repulsion within this compact ring system and accounting for the tensile bond stresses. The Coulombic stresses (middle left) reflect chiefly the influence of the two ammonium groups, which repel the aliphatic hydrogens of the bicyclooctane moiety because of their weakly positive charge and therefore place them under compressive electrostatic stress. The weakly negative bicyclooctanes are correspondingly placed under tensile electrostatic stress. The GB stresses (middle right) largely cancel the Coulombic stresses when summed (bottom left), leaving mainly tensile stress on the ammonium groups, presumably due to unbalanced GB forces drawing them toward the high dielectric solvent. The summed bond-stretch, Lennard-Jones, Coulombic and GB stresses (bottom right) do not fully cancel, indicating that this molecule is stressed in even this energy-minimized conformation.

Figure 3.

a. Stresses in free guest B5. Bonded: top left. Lennard-Jones: top right. Coulombic: middle left. Generalized Born: middle right; Electrostatic (Coulombic + GB): lower left. Total: lower right.

Figures 4A and B display, respectively, top and side views of the stresses computed for the most stable conformation found for the free host, CB7. The bond stresses (top left), which are mainly tensile (orange) appear to result largely from local forces intrinsic to the system of linked glycuril rings. The Lennard-Jones forces (top right), which are mainly compressive and circumferentially oriented, chiefly reflect side-to-side repulsions between neighboring carbonyl moieties. The Coulombic (middle left) and GB stresses (middle right) appear more complicated and display larger radial components than the bonded and Lennard-Jones stresses, but, as for the free guest (above), they largely cancel when summed (lower left). The sum of all computed stresses (lower right) shows considerable overall stress, including compression of the carbonyl carbons and tension of most other atoms in the glycouril units.

Figure 4 A.

Stresses in free host, CB7, top view. Bonded: top left. Lennard-Jones: top right. Coulombic: middle left. Generalized Born: middle right; Electrostatic (Coulombic + GB): lower left. Total: lower right.

Figure 4 B.

Same as Figure 4A in side view.

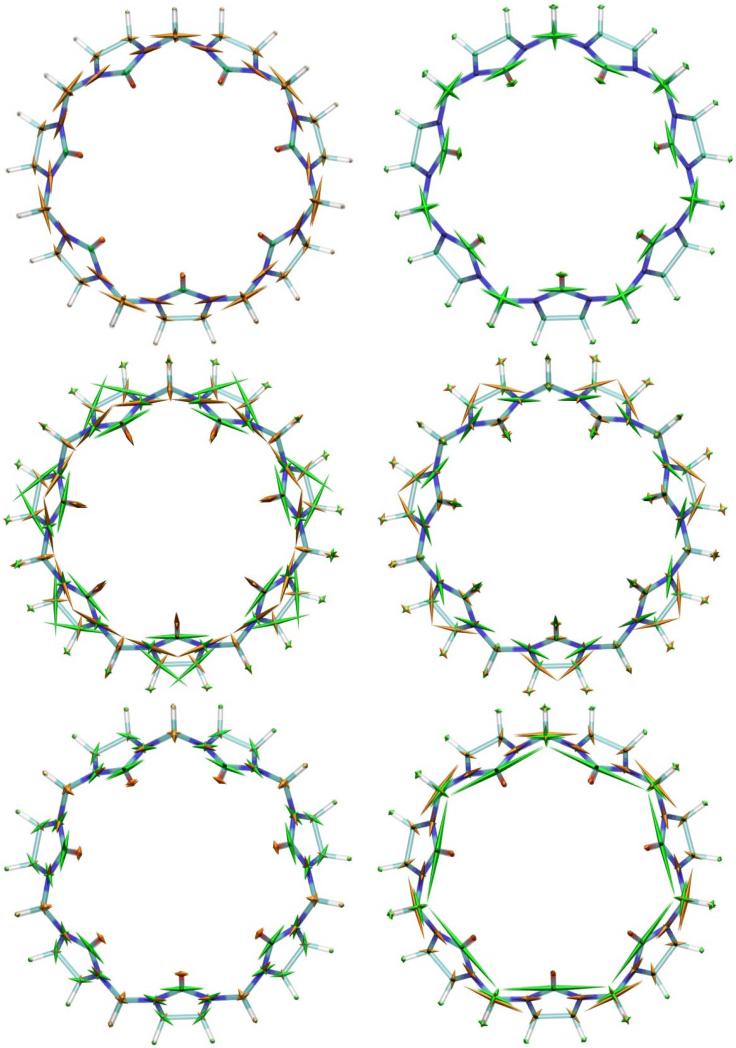
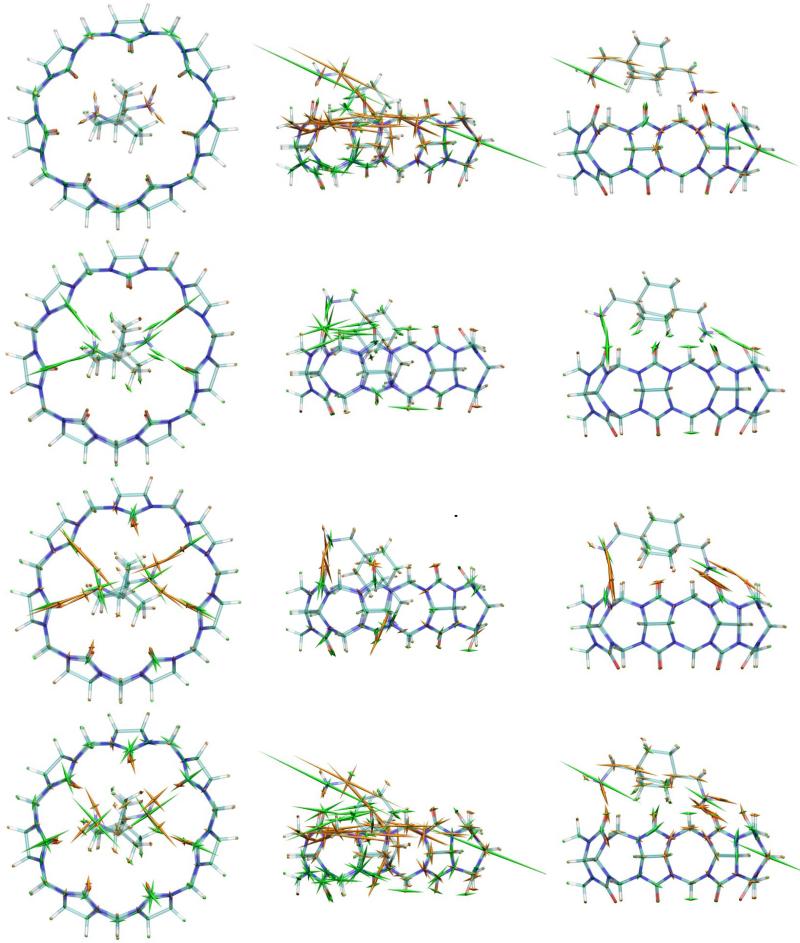
Stress in the relaxed starting conformation of the complex

The starting conformation of the CB7-B5 host-guest complex was generated by conformational search and energy-minimization in the absence of the artificial forcing bond. The guest's bicyclooctane moiety lies in the middle of the CB7 cavity, while its two ammonium groups sit at opposite portals of the host and donate hydrogen bonds to its carbonyl oxygens. The three panels in the left-hand column of Figure 5 visualize differences in stress, relative to the free host and guest, for this unforced, energy-minimized complex. The bond-stresses (top left) have become less tensile and more compressive, relative to the free molecules, as indicated by the ring of green spindles around each of the portals of the host, with some variation of stress around the ring. These observations are consistent with the fact that binding has reduced the diameter of the portals slightly and made the host less round and more oval in shape. One can also see an increase in the tensile bond-stress on the ammonium groups (orange spindles), presumably due to their hydrogen bonding to the host's carbonyl oxygens. The Lennard-Jones stresses (middle left) change little relative to the free molecules except for striking new compressive stresses involving the ammonium groups and the carbonyl oxygens to which they are hydrogen-bonded in the complex. These result from steric compression of the atoms involved in the hydrogen bonds. The same hydrogen bonds are also associated with strong electrostatic stresses (lower left): the attractive interactions of oppositely charged atoms involved in the hydrogen bonds (e.g., ammonium hydrogen and carbonyl oxygen) cause tensile stresses (orange), while the associated repulsions (e.g. ammonium nitrogen and carbonyl oxygen) lead to compressive electrostatic stresses (green).

Figure 5.

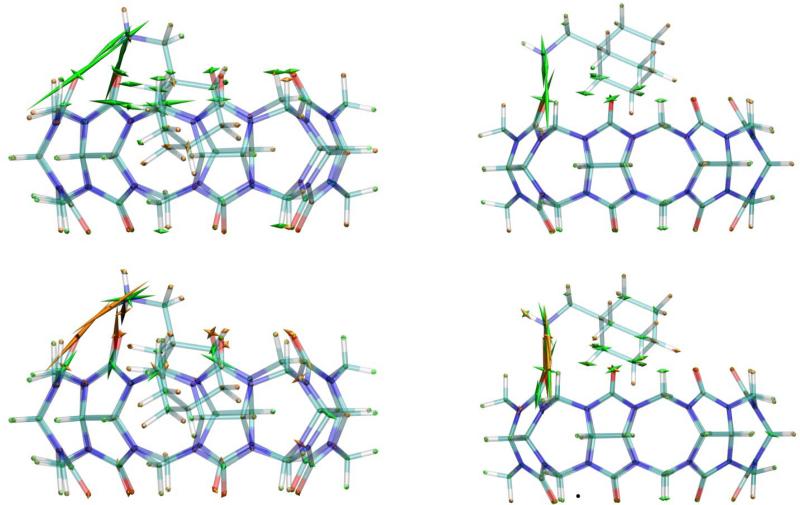
Stresses in three different conformations of the CB7 complex with diammonium guest B5. Left column: unforced starting structure (B=5.5Å), top view. Middle column: conformation with largest force imposed by the artificial bond (B=12.3Å), side view. Right column: conformation immediately after the conformational transition (B=12.4Å), side view. Bond stresses: top row. Lennard-Jones stresses: center row. Electrostatic (Coulombic + GB) stresses: bottom row. The lengths of the bond stress symbols on the two atoms involved in the artificial bond (Figure 2) were scaled down by an additional factor of 0.2.

A sharp conformational transition

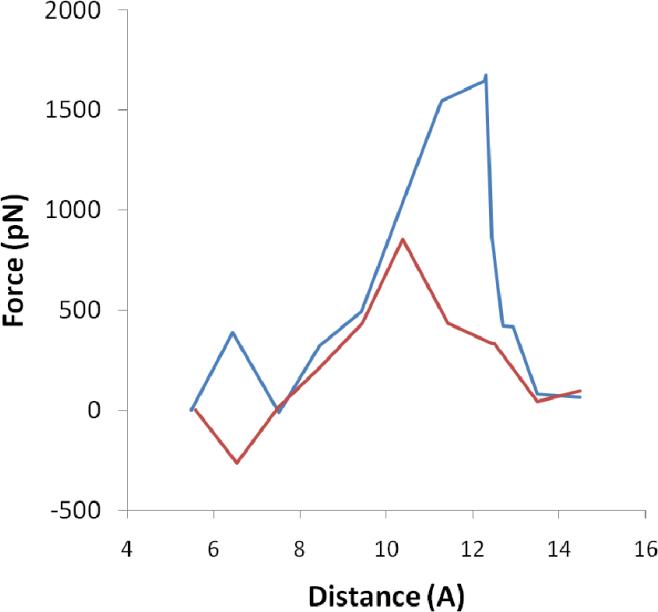
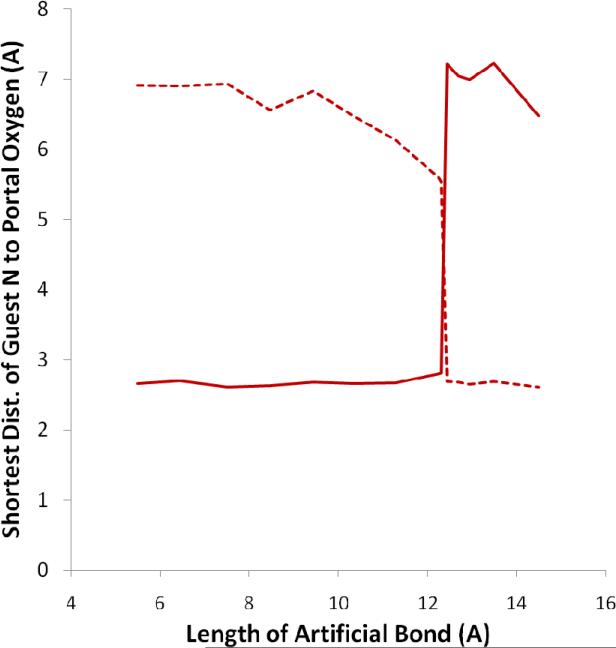
The guest is forced out of the host by incremental increases in the equilibrium length of the artificial bond, B₀ (Figure 2). The bottom ammonium moves to the top portal, while the top ammonium group remains on top. The resistance of the guest to exiting the host is manifested by the magnitude of the force, F, exerted by the artificial bond as a function of its length, B. As graphed in Figure 6A (blue), this force peaks at B=12.3 Å and then drops sharply at 12.4 Å. The drop corresponds to a conformational transition in which the guest's bottom ammonium cationic group jumps from the bottom portal of the host to the top one. This jump is illustrated in Figure 6B, which shows a sudden increase in the distance of the bottom ammonium group from the bottom portal and a simultaneous drop in its distance to the top portal. The conformations immediately before and after this transition are shown in the middle and right-hand columns of Figure 5, respectively.

Figure 6A.

Computed forces exerted by the artificial bond vs the bond length, for guests B5 (blue) and B4 (red).

Figure 6B.

Closest distance of bottom ammonium nitrogen to bottom portal (solid) and top portal (dashed), as a function of the length, B, of the forcing bond.

When the pulling force is at its maximum (B=12.3Å), the complex is highly stressed (Figure 5, middle column). The graphical visualization of bonded stress (top middle) includes two large, diagonal green spindles (rendered at reduced scale) at the N and C atoms used as attachment points for the artificial bond. These indicate that the artificial bond is compressed, because it is pushing the N and C atoms apart. There is also a large buildup of tensile bonded stress (top middle) around the top portal. The stress is greatest at the left of the top portal, toward which the guest is being pushed. In addition, and rather unexpectedly, the left side of the lower portal is under compressive, rather than tensile, stress (green). There is also tensile bonded stress along the long axis of the guest, consistent with the fact that its top ammonium is being pushed up and to the left while the rest of the guest is stuck partway through the host. The Lennard-Jones stresses (center middle) are also focused at the left-hand side of the top portal, since the artificial bond is pushing the guest against the host in this region. The electrostatic stresses (bottom middle) reflect hydrogen-bonding of the top ammonium with the top portal and also show tension between the bottom ammonium and the bottom portal.

After the conformational transition (B=12.4Å), when the bottom ammonium has jumped through the host and is now hydrogen-bonded with the top portal (Figure 5, right-hand column), the stresses have become markedly smaller. This is particularly evident in the bonded stresses (top right vs. top middle). It is interesting to note a persistent spine of modest tensile stress along the axis of the guest molecule, presumably due to the interplay of the imposed pulling force and the restraining H-bonds of the ammonium groups with the carbonyls. The Lennard-Jones stresses also have fallen markedly (center right), and show mainly compressive steric stresses, once again involving ammonium-carbonyl hydrogen-bonds. The electrostatic stresses (bottom right) also are consistent with this pattern of hydrogen-bonding.

Physical basis for the conformational transition

We had initially conjectured that the sharp conformational transition resulted from a build-up and release of compressive Lennard-Jones stress as the bulky bicylooctane group passed through a constrictive exit portal, much as previously argued for a host-guest system involving cucurbit[6]uril (CB6)²⁶. However, this view was not fully supported by the stress analysis, because the compressive Lennard-Jones stress prior to the transition (Figure 5, top middle) does not extend around the whole portal, but is localized on the left-hand side, where the artificial bond is driving the guest. In addition, the bicyclooctane group appears to have already passed most of the way through the top portal by time the forcing bond has reached the length of 12.3 Å. An alternative view is suggested by the observation of tensile electrostatic stresses between the bottom ammonium and the bottom portal (Figure 5, bottom middle). Both Coulombic attractions between the bottom ammonium and the bottom portal carbonyls and GB forces resisting desolvation of the ammonium group could contribute to the resistance of the bottom ammonium to passing through the host, and the view that electrostatics make a major contribution to the dissociation barrier would be broadly congruent with prior observations regarding the role of the guest molecule's pH-dependent charge in the binding kinetics of CB6²⁹.

We tested this idea by repeating the calculations with guest B4 (Figure 1), which is the same as B5 except that it lacks one methylammonium group. The computational pulling experiment was arranged so that the single ammonium group would lie at the top portal and only the bulky but electrically neutral bicyclooctane moiety would need to clear the exit portal. The peak of the new length-force curve (Figure 6a, red) is only half as high as the original and is shifted from 12.3 Å to 10.4 Å. This change indicates that the original electrostatic impediment to dissociation has been removed and its place taken by a different interaction. Visualization of the B4 complexes reveals that this guest, too, undergoes a sharp conformational transition in which the bicyclooctane moiety jumps from an intermediate location (Figure 7, left column) to the top portal (Figure 7, right column) as the peak in the length-force curve is passed. The pattern of Lennard-Jones stresses (Figure 7, top row) is similar to that for B5 at the peak of its force curve (Figure 5 top), but less intense. The same is true for the bond stresses (not shown). The electrostatic stresses (Figure 7, bottom row) are very similar to those for B5 (Figure 5, bottom), except for the absence of stresses on the deleted ammonium group. Comparison of these results with those for guest B5 support the view that electrostatics plays a major role in the conformational transition of the latter.

Figure 7.

Lennard-Jones (top) and electrostatic (Coulombic + GB, bottom) stresses in two conformations of the CB7 complex with monoammonium guest B4. Left: conformation with peak force. Right: conformation immediately after peak force, with guest shifted to top portal.

Discussion

This computational stress analysis yields mechanistic insights into the forced dissociation of a high affinity cucurbituril-guest complex. We had initially expected to observe a classic constrictive binding process; i.e., one in which a peak in the length-force curve resulted from steric hindrance as the bulky bicyclooctane moiety passed through a relatively narrow CB7 portal^27,28. However, the pattern of Lennard-Jones stress at the peak of the length-force curve did not appear fully consistent with this expectation, and we observed, furthermore, that the ammonium being pulled through the host was under tensile electrostatic stress. These observations suggested that electrostatics might play an important role in establishing the peak in the force curve. Such an explanation would be physically reasonable because the hydrogen bond of the bottom ammonium to the bottom portal must be broken for the forced dissociation to occur. Moreover, the work of dehydrating the ionized ammonium on entering the host's cavity should be substantial. Comparative calculations for another guest molecule lacking the bottom ammonium group supported the importance of electrostatics, because the force maximum was reduced and shifted. These results suggest that the association kinetics of CB[7] guests will tend to be faster for monocationic guests than for diammonium guests that position on ammonium at each portal. Both binding and dissociation are expected to be slowed by the requirement of driving one of the ammonium groups through the middle of the host for either process. It is reasonable that electrostatics should be of central importance for diammonium guests, given that even monocationic guests have kinetics that are sensitive to charge²⁹.

It was also interesting to observe a complex distribution of bond stresses around the portals of the host in the highly stressed conformation immediately before the conformational transition involving the diammonium guest, B5. The tensile forces at the top portal could have been anticipated, but the appearance of compression around the bottom portal was more surprising. Such results are reminiscent of stress patterns computed for engineered structures and could be useful as a basis for molecular engineering aimed at tailoring energy barriers or molecular processes and pathways.

The present treatment of the forced dissociation process is preliminary in the sense that, like a prior study²⁶, it does not account for thermal motion. The calculations thus are inconsistent with the quasi-adiabatic assumption that the system equilibrates rapidly with respect to the time-constant for barrier crossing⁴⁴. Therefore, we have in effect studied only a single dissociation pathway for the CB7-B5 complex. One way to arrive at a more comprehensive description might be to carry out a molecular dynamics simulation for each equilibrium length of the artificial forcing bond and use the resulting trajectory snapshots to compute time-averaged stresses at each atom. This would effectively sample multiple pathways for the dissociation process, leading to lower computed forces and stresses. Such a result would be more consistent with the lower forces observed in single-molecule AFM measurements for related host-guest systems^45,46. It is also important to note that the bimolecular rupture (unbinding) force measured by AFM is not an intrinsic property of the molecular system, but instead depends upon the rate at which the two molecules are pulled apart, with higher rates leading to greater forces^47,48,44. Thus, an even better, though more challenging, calculation would be to model the dynamic pulling process itself.

This paper also describes two methodological contributions to the application of stress calculations at the molecular level. One is the calculation of changes in stress in internal molecular coordinates, rather than in lab-frame coordinates, in order to enable meaningful comparisons of stresses among different conformational states and molecular orientations. The second is the method of displaying atomistic stress tensors. This is not trivial challenge, given that the stress on each atom is a symmetric 3×3 stress tensor with 6 distinct components.

The present study supports and advances the usefulness of computational stress analysis at the molecular level. It proves to be remarkably straightforward and informative to compute, compare and visualize the stresses associated with various force components for host-guest systems. It will be interesting in the future to explore broader applications, especially to biomolecules, for which studies of static and dynamic stress can bear on atomistic mechanisms of conformational change that are of enormous scientific and practical importance.