Multiple models to capture the variability in biological neurons and networks

Abstract

How tightly tuned are the synaptic and intrinsic properties that give rise to neuron and circuit function? Experimental work shows that these properties vary considerably across identified neurons in different animals. Given this variability in experimental data, this review describes some of the complications of building computational models to aid in understanding how system dynamics arise from the interaction of system components. We argue that instead of trying to build a single model that captures the generic behavior of a neuron or circuit, it is beneficial to construct a population of models that captures the behavior of the population that provided the experimental data. Studying a population of models with different underlying structure and similar behaviors provides opportunities to discover unsuspected compensatory mechanisms that contribute to neuron and network function.

Almost 60 years ago, Hodgkin and Huxley constructed their classic model of the action potential, starting from voltage-clamp measurements in the squid giant axon¹. Hodgkin and Huxley’s work established a paradigm: to describe the contribution of each conductance to the dynamics of a neuron or network, the investigator (i) isolates each conductance found in the cell and determines its maximal conductance and activation/inactivation properties, (ii) assembles the conductances with the cell’s capacitance, and then (iii) numerically integrates the resulting differential equations to produce traces of voltage versus time. When a model is successfully constructed, then the effects of changing any of the parameters on the ensuing dynamics can be easily studied. This procedure is deceptively simple in concept, and many investigators have tried to use this paradigm to construct models that capture the dynamics of a large variety of neurons^2–4.

Despite the apparent simplicity of the Hodgkin-Huxley program, its implementation is fraught with a number of difficulties, many of which have been either ignored or minimized as investigators have tried to build models that describe the behavior of the neurons they study. In this review, we will discuss some of these issues and then present a new paradigm, in which large populations of model neurons are constructed. This newer approach solves some, but not all, of the problems encountered in the past when trying to construct conductance- based models of neurons.

Problem 1: biological data are variable

Even genetically identical single-cell organisms display variability in their responses to environmental stimuli and in the expression of mRNA and protein⁵. This can be attributed to the accrued influence of the stochastic nature of every molecular biological process⁶ as well as activity-dependent and environmentally influenced changes in channel, neurotransmitter or receptor expression⁷. Consequently, genetically identical animals, be they Caenorhabditis elegans, flies or human identical twins, are nonetheless individuals, who often generate substantially different behaviors in response to similar conditions. If we were magically able to look into each of those nervous systems and measure the numbers and properties of the synapses, ion channels, receptors and enzymes in all of the individuals across the population, we would find real biological variation in most, if not all, of these parameters. And, presumably, this variation would be even larger in genetically diverse natural populations.

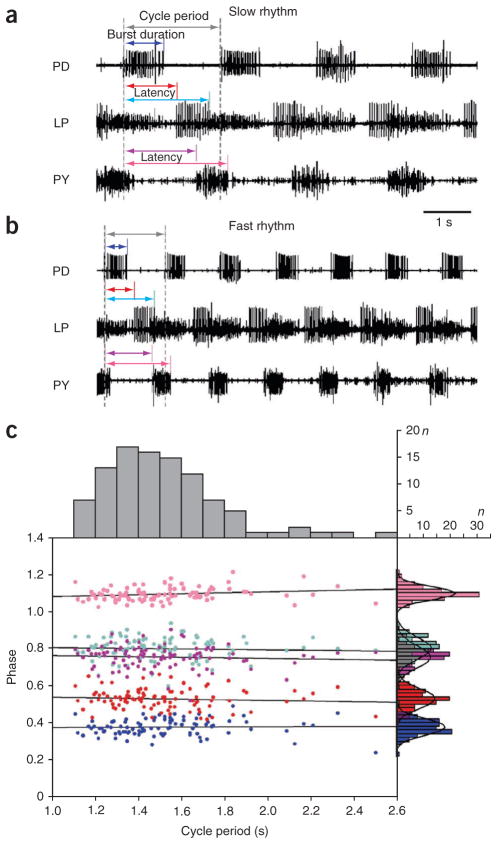
How consistent is a given behavior across individuals of the same species? Some of the most stereotyped behaviors are those produced by central pattern generators, networks that produce rhythmic motor patterns⁸. The pyloric rhythm of the crustacean stomatogastric ganglion is highly robust and reliable. One study examined the range of pyloric motor patterns of the lobster stomatogastric ganglion recorded from 99 preparations under the same conditions (Fig. 1)⁹. Although each of these animals produced characteristic triphasic rhythms in which the lateral pyloric (LP), pyloric (PY) and pyloric dilator (PD) neurons fired in sequence (Fig. 1a, b), the frequency varied over a twofold range (Fig. 1c). Although the phase relationships were, on average, constant as a function of frequency across the population⁹, individual animals showed variability in the extent to which they were phase constant over a range of frequencies. Additionally, the number of LP and PD neuron spikes per burst varied two- to threefold over the population⁹.

Figure 1.

The pyloric rhythm has a variable period but phase relationships are held invariant. (a) Extracellular recordings from a slow pyloric rhythm showing its characteristic repeating pattern of PD, LP and PY neuron activity (on the LP and PY traces, only the largest spikes correspond to spikes from the LP and PY neurons respectively). Arrows indicate measurements made on each pyloric cycle. Gray arrow indicates pyloric period, measured as the latency from the onset of one PD neuron burst to the next. Colored arrows indicate latencies measured from the onset of the PD neuron burst. The dark blue arrow indicates the latency of PD neuron offset. The red arrow indicates the latency of LP neuron onset. The light blue arrow indicates the latency of LP neuron offset. The purple arrow indicates the latency of PY neuron onset. The pink arrow indicates the latency of PY neuron offset. These latencies were then divided by the period to give the phase relationships shown in c. (b) Extracellular recordings from a fast pyloric rhythm. Data are presented as in a. (c) Phase of burst onset/offset versus pyloric period. Each point represents one of 99 animals. Period is a mean period calculated over many cycles, as are phases. Dark blue points, phase of PD neuron offset; red points, phase of LP neuron onset; light blue points, phase of LP neuron offset; purple points, phase of PY neuron onset; pink points, phase of PY neuron offset. The histograms on top of the plot show the distribution of pyloric rhythm periods. The histograms on the right show the distributions of each of the phases, coded in color as for the data points. Adapted from ref. 9.

A series of recent studies has shown that individual stomatogastric ganglion neurons of the same cell type show considerable neuron-to-neuron variability (characteristically two- to sixfold) in the mRNA expression for ion-channel genes and in their maximal conductances measured in voltage clamp^10–15. Interestingly, there are significant correlations in the expression of some of these ion channels^12–14 and between some of these underlying parameters of the neurons in the pyloric network and properties of pyloric motor patterns themselves¹⁰.

The variability across animals seen in the stomatogastric ganglion data is similar to that seen in many other preparations^16,17, although this is often hidden when data are presented as means and standard errors. This sort of variability will be familiar to any experimental biologist, but until recently, most investigators in neuroscience have used a single model to describe the ‘typical’ behavior of the system being studied. Obviously, a single model will be unable to capture the variability of a natural population. Furthermore, neglecting biological variability has several other deleterious effects, described below. Of course, there is a component of measurement error in all experimental studies, and it can be difficult in many cases to estimate the extent to which it contributes to apparent variability.

Problem 2: should one use ‘best’ data or mean data?

It is not uncommon for an electrophysiologist to measure the properties of one voltage-dependent conductance in 10–20 neurons, a second conductance in another 10–20 neurons, and so on. What values should be fit to describe the conductance in a model? In the past, some investigators chose their fastest and largest currents to fit, as most voltage-clamp measurement errors would tend to make the currents appear smaller and slower than they are. Alternatively, some investigators were uncomfortable with using a single measurement and instead fit the mean currents. Both decisions are problematic. The first is problematic because it ignores the possibility of correlated variability between measured quantities. If two maximal conductances are variable but negatively correlated, then making a model that has large values of both will not yield a realistic model. The second is troublesome because it makes the tacit assumption that a neuron with all parameters equal to their mean values would be typical. But in fact a neuron with mean parameters can fail to have properties shared by all of the neurons in the population¹⁸.

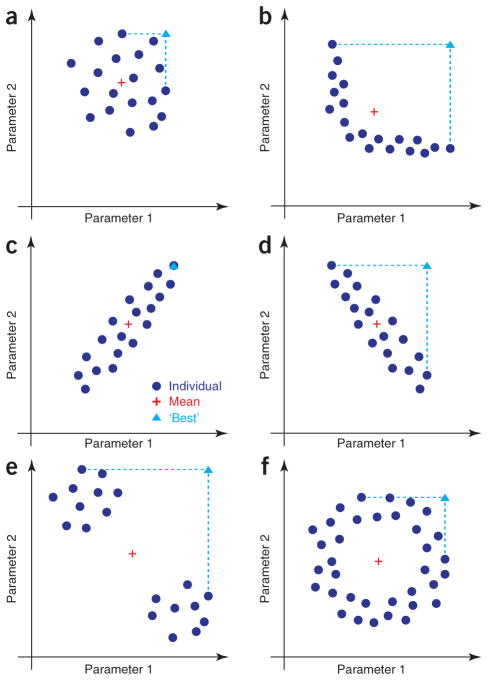
To illustrate these ideas, one can imagine a population of neurons with a given target behavior, with each neuron described by two parameters (Fig. 2). One can then consider the properties of a model with mean parameters or with ‘best’ (that is, largest) parameters. In some cases, the mean neuron will fall within the regime of typical neuron behavior (Fig. 2a). Even in such a case, however, a neuron that had the largest observed values for each parameter would not necessarily be representative of the population (Fig. 2a). In other cases, the mean neuron may not be a typical neuron but rather may lie outside the population itself (Fig. 2b)¹⁸. In still other cases, the mean may be a typical neuron, but the ‘best’ model may fall at the boundary of the population (Fig. 2c) or outside of the population of the typical neurons (Fig. 2d). In more fanciful but still possible scenarios, the mean neuron may not be a typical neuron at all (Fig. 2e, f).

Figure 2.

Example distributions of neuron parameters for neurons that all share a common behavior or set of behaviors. In all panels, dark blue dots represent individual neurons, the red cross represents the mean of the distribution and the light blue triangle represents the hypothetical neuron with all parameters set to their largest, or ‘best’, values. (a) A population with statistically independent parameters. (b) A population in which the mean is not representative. (c) A population with a strong positive correlation between parameters. (d) A population with a strong negative correlation between parameters. (e) A population with two very different subpopulations. (f) A population with a donut-shaped distribution.

Even in well-studied systems, there are some conductances that have not been experimentally well characterized. Some of the common tactics for dealing with this are (i) to use the properties of the same conductance measured in a different system, or (ii) to incorporate any available data into a model of the conductance, and then to adjust the unknown parameters such that the emergent behavior of the model is reasonable. Because models are never made with full knowledge of all the relevant parameters, good biological intuition is invaluable in guiding decisions about how to handle or ignore missing data.

That insights into how systems of neurons, conductances or molecules work may not necessarily come from studying the properties of system components one by one is important, not only for modelers, but for experimentalists wishing to understand how system performance depends on the interaction of the system’s components¹⁰.

Problem 3: what behavior to model?

One begins any modeling effort with a long list of behaviors one would like a model to capture. But as one realizes how difficult it is to build a model that exhibits all of these behaviors, inevitably one pares down the list to those that are most interesting, at least at that moment.

Even the Hodgkin-Huxley model¹ is only a good description of the squid axon within a limited domain. Although it explains many features of the action potential (including making an accurate quantitative prediction of its velocity), it fails to exhibit the spike-frequency adaptation seen in recordings from real squid axons¹⁹. In theory, of course, it should be possible to build models that capture all of a neuron’s behaviors, but given the variability across individuals, this may require constructing a model for each individual neuron.

A population of models can mimic biological variability

To capture the range of pyloric rhythm behaviors (Fig. 1), a population of more than 20,000,000 model networks was created²⁰ and then searched for those that produced outputs that fit within the ranges of the biological data. This process produced about 400,000 pyloric-network models that varied considerably in the maximal conductances of the intrinsic and synaptic currents. This variability is similar to the ranges seen in experimental measurements of these same properties^10–15,21. One important part of this process was that it sidestepped any potential complications of choosing ‘typical’ data or concerns associated with the use of mean data to constrain the model. The resultant population of models can be studied to determine how the intrinsic and synaptic currents in the models contribute to its behaviors²².

Degeneracy: multiple solutions produce similar outputs

An increasing number of studies have shown that the relationship between the parameters of a model and its output can be degenerate; that is, there can be multiple sets of parameters that give rise to the same (or similar) behaviors^{5,11,18,20,23–29}. (Note that we are using this term in the biological but not the mathematical sense⁵; Fig. 3.) Figure 3a, b shows two model LP neurons, drawn from a large population, that are producing very similar firing patterns in response to rhythmic inhibition²⁷. Nonetheless, the maximal conductances in these two models are quite different (Fig. 3c). For example, the axonal Na⁺ conductance is large in model A and small in model B, while the reverse is true of the axonal leak conductance²⁷.

Figure 3.

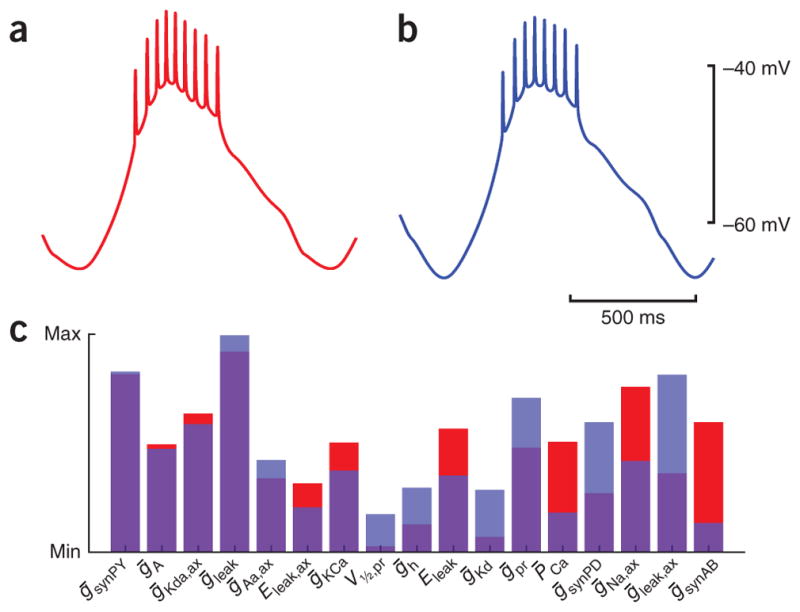
Model LP neurons with similar behavior but substantially different parameters. (a, b) Traces from two randomly generated model LP neurons receiving ongoing pyloriclike synaptic input. (c) The parameters for the two models, which are quite different. Red and blue bars show the parameters of the model that generated the red/blue trace in a. For each parameter, a red and blue bar are superimposed, with their region of overlap shown as purple. Parameters are sorted by the absolute difference between them in the two models. ḡ parameters are maximal conductances of different currents, E parameters are reversal potentials, P̄_Ca is the maximal permeability of the Ca²⁺ current and V_{½, pr} is the half-activation voltage of a modulatory inward current. Max, maximum; min, minimum. The model is described in ref. 27.

There are many possible relationships between system parameters and system output (Fig. 4). If the spike rate of a neuron is a function of one of its maximal conductances, and the spike rate has a range of tolerated values, this implies a range of acceptable values of the maximal conductance (Fig. 4a). The shallower the slope of this relationship, the wider the range of acceptable values of the maximal conductance (Fig. 4b). In the limit of a zero slope, the maximal conductance can take on any value (Fig. 4c). This is one kind of degeneracy: an unconstrained parameter that does not contribute to the behavior of the studied system.

Figure 4.

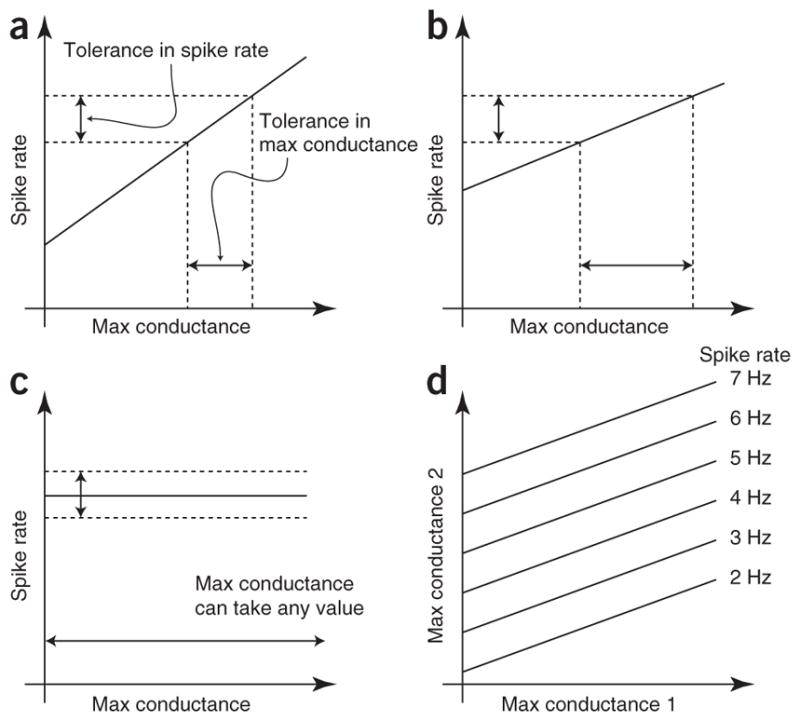
Tolerance and degeneracy. (a) Plot of the map between maximal (max) conductance and firing rate for a hypothetical neuron with only a single variable conductance. Tolerance in the spike rate translates into tolerance in the maximal conductance, with the maximal conductance tolerance determined by the slope of the line. (b) As in a, but here the relationship between spike rate and maximal conductance has a lower slope, leading to a larger tolerance in the maximal conductance for the same spike-rate tolerance. (c) As in a and b, but with a slope of zero. In this case, the firing rate is completely insensitive to the maximal conductance, and thus the maximal conductance can take on any value. (d) Contour plot of the map between maximal conductances and spike rate for a hypothetical neuron with two variable maximal conductances. Each line denotes the set of maximal conductances that yield the given spike rate. Although each conductance affects the spike rate, there are many combinations of maximal conductances that yield the same spike rate.

If multiple parameters affect a given neuronal output, another form of degeneracy is possible (Fig. 4d)³⁰. In this case, each firing rate can be achieved by a large range of parameters, and one could observe constant spike rate in a population despite high variability of both conductance 1 and conductance 2 as long as they compensate for one another. For the functional relationship illustrated (Fig. 4d), this might be apparent as a strong positive correlation between the two conductances when measured across the population. (This form of degeneracy is not mutually exclusive of the zero-slope degeneracy discussed above.) Likewise, constant function in a population can arise from compensatory mechanisms that are seen as negative correlations between processes that are important for system function¹⁶. Within an individual neuron or individual animal, alterations in one conductance (or other parameter) may produce little change in system behavior if there are mechanisms that cause changes in another conductance that compensates for the first change.

Some of the most interesting examples of compensation come from studies of genetic knockouts of ion-channel genes that show little or no phenotype although acute blockade of the same channel does show strong effects^16,21,31. Another example of compensation is seen in experiments in which the mRNA encoding the fast transient potassium current (I_A) was overexpressed in single stomatogastric ganglion neurons, with no obvious change in function because it was accompanied by an increase in the hyperpolarization-activated inward current (I_h)15,32.

Robustness of degenerate solutions

The measured variability in synaptic and intrinsic conductances in individual animals with similar outputs^{10–13,17,21} argues that biological nervous systems have degenerate solutions to producing similar behaviors⁵. The advantage of this is obvious: it is not necessary to specify the exact number of ion channels or receptors that each neuron should express, either during development or over the lifetime of the neuron and animal. Instead, ongoing activity-dependent rules of various kinds can be used to modify channel and receptor numbers and distributions to maintain target-circuit performance despite ongoing channel and receptor turnover^33–37.

At the same time, it is clear that although there may be degenerate solutions to the production of a given circuit output, animals with these different solutions will not respond identically to all perturbations. Nonetheless, biological networks can be far more reliable in response to perturbations than might be expected^38,39. This may indicate that the set of degenerate solutions found in a given biological population may be enriched for those with the ability to respond reliably to the normal environmental perturbations seen by animals³⁹ but not necessarily included during model selection. Moreover, homeostatic and other compensatory mechanisms are likely to be continuously at work, allowing a variety of adaptations to environmental and activity perturbations^7,14,40.

More global forms of sensitivity analysis

Sensitivity analysis is often used to determine how changes in one parameter influence a model’s behavior^41–44. A population of models can illuminate other aspects of the relationship between parameters and behavior. In traditional sensitivity analysis, one takes a single model, varies one parameter at a time, and examines how that changes the model’s output^41–44. But with a large population of models, one can perform a more global sensitivity analysis, in which the variation in parameters, and the resulting variation in behavior, is described over the full population. This was done in the LP neuron population described above²⁷, and this generated a compact description of how strongly each parameter influenced each behavior of the model (Fig. 5). The take-home lesson from this study is that almost every behavior of the neuron arises from the contribution of many conductances, and that each behavior is determined by a different subset of the underlying conductances²⁷. Additionally, this global sensitivity analysis describes these influences for the entire population, not just in the vicinity of a single model²⁷.

Figure 5.

Quantification of the effect of each model parameter on each model property for a population of LP models. The area of each circle represents the average amount of variance explained by that parameter as a fraction of the variance explained by the complete fit. The areas of the circles in each row sum to 1. Most properties show contributions from many conductances. Parameters are the same as those in Figure 3. Adapted from ref. 27.

Although it is possible for models of similar behavior to be found in separate islands of parameter space (Fig. 2e), in several large populations of models we have found that models with similar behavior are found in connected regions of parameter space^11,26,27,45. It seems plausible that as the number of conductances in a model increases, so does the likelihood that there will be some path that can connect models with the same behavior in a high-dimensional parameter space. If neurons with a particular type of behavior are in a connected region of parameter space, this may allow relatively simple homeostatic tuning rules to work to maintain stable neuronal and network function despite ongoing turnover of receptors and channels^33–37.

Generating many models to capture the individual

As the computational power available to all of us has increased, it has become possible to generate large populations of models relatively easily. A number of different methods are available to generate a population of models with a target set of behaviors, without resorting to handtuning. Evolutionary algorithms have been used extensively and successfully to generate conductance-based models by investigators wishing to avoid handtuning^23,46,47. Evolutionary algorithms can converge onto very specific target-activity patterns but have the potential disadvantage that, in general, they do not uniformly sample the region of parameter space where acceptable models lie.

As an alternative to evolutionary algorithms, a number of investigators have instead generated populations of models either by sampling large volumes of parameter space on a multidimensional grid^20,26,48 or by randomly sampling large volumes of parameter space^11,27. These methods have the advantage that they uniformly sample the region of parameter space in which acceptable models lie. However, they have the disadvantage that if the acceptable models lie in a very small volume of parameter space, finding them may require a prohibitive number of samples. This problem grows exponentially worse as the number of parameters increases.

In addition to the methods described above, there is a large body of established Monte Carlo techniques for sampling from an arbitrary distribution when only the probability density at an arbitrary point is easy to calculate⁴⁹. This body of techniques could profitably be used to generate populations of models that conform to a probability distribution that mimics chosen aspects of the biological distribution. The random-sampling technique above could be seen as an example of the rejection-sampling technique⁴⁹ with a probability density that is flat over the region of acceptable models. Applying Monte Carlo techniques to generate populations of neuronal models has promise for future work.

The ideal solution to many of the concerns addressed above would be to build a model of every individual neuron or circuit studied, rather than building a population of models with statistics that are similar to those of the biological population. This would presumably involve subjecting each neuron or circuit to a battery of stimuli, varied and numerous enough that the preparation’s response to them would provide enough information to determine all of the parameters of the model. Some initial attempts along these lines have been made⁴⁶, but achieving these goals requires much additional work, both experimentally and computationally. Recent results have shown that given accurate descriptions of channel kinetics, one can use wideband stimuli to determine the maximal conductances of isopotential model neurons⁴⁶. However, the method seems to be sensitive to errors in the channel kinetics and to the presence of unanticipated conductances. Thus, this kind of method will need to be generalized to account for cell-specific differences in both channel density and other channel properties.

Conclusions

Molecular techniques will soon enable us to determine routinely the genomic sequences of individual flies, crabs and humans. Therefore, it is time to ask how much the brains of normal, healthy animals differ. There are excellent historical reasons why experimentalists have typically focused on mean data and neglected to some extent the ranges and variances of their data. Nonetheless, there are newer studies that argue that variation in neuronal function might be computationally advantageous⁵⁰.

In the past, limited computational resources significantly constrained the kinds of models that could be built. Today, we are entering an era in which we should attempt to collect as much data as possible on each individual¹⁰, to attempt to see the correlations between underlying mechanisms and system behavior. At the same time, as the computational power available increases, it is now possible to construct and study large populations of models, to understand better the ranges of synaptic and intrinsic parameters consistent with healthy brain function, and in turn, to understand where the boundaries between health and disease are found.