Abstract
Compound identification in gas chromatography–mass spectrometry (GC-MS) is usually achieved by matching query spectra to spectra present in a reference library. Although several spectral similarity measures have been developed and compared using a small reference library, it still remains unknown how the relationship between the spectral similarity measure and the size of reference library affects on the identification accuracy as well as the optimal weight factor. We used three reference libraries to investigate the dependency of the optimal weight factor, spectral similarity measure and the size of reference library. Our study demonstrated that the optimal weight factor depends on not only spectral similarity measure but also the size of reference library. The mixture semi-partial correlation measure outperforms all existing spectral similarity measures in all tested reference libraries, in spite of the computational expense. Furthermore, the accuracy of compound identification using a larger reference library in future is estimated by varying the size of reference library. Simulation study indicates that the mixture semi-partial correlation measure will have the best performance with the increase of reference library in future.
Keywords: GC-MS, spectral matching, compound identification, weight factor
1. Introduction
Gas chromatography–mass spectrometry (GC-MS) is widely used to analyze chemical compounds in complex samples, where the compounds are first separated on a GC system and further measured on a mass spectrometer that is usually equipped with an electron ionization (EI) ion source. Compound identification in analysis of the GC-MS data is usually achieved by matching the experimental mass spectra to the mass spectra present in a reference library, i.e., mass spectral matching. To improve the accuracy of compound identification, several mass spectral similarity measures have been developed, including Stein and Scott's composite similarity [1], Hertz similarity index [2], probability-based matching system [3], normalized Euclidean distance (L2 -norm) [1,4,5], and absolute value distance (L1 -norm) [1,5], Most recently, Koo et al. introduced Fourier and wavelet transform-based composite (DFT/DWT) measures [6], and Kim et al. proposed mixture semi-partial and partial correlation-based measures [7].
The intensity of fragment ions in an EI MS spectrum tends to be smaller with the increase of the m/z value. Such a tendency reduces the contribution of large fragment ions to the spectral similarity score. To increase the weight of peak intensities of fragment ions with large m/z values, the intensities and m/z values are usually transformed with a set of weight factors for the computation of spectral similarity. Stein and Scott [1] suggested weight factor (0.5, 3) for power transformation of fragment ion intensity and m/z value, respectively. They also pointed out that weight factor (0.5, 2) was equally effective. Horai et al. reported weight factor (0.5, 2) using the MassBank database [8]. Recently, Kim et al. suggested weight factor (0.53, 1.3) using the weighted cosine similarity as a spectral similarity measure and the main EI MS library of the NIST/EPA/NIH Mass Spectral Library 2011 (NIST11) as the reference library [9].
Kim et al. also compared the performance of compound identification of multiple mass spectral similarity measures, including weighted cosine, Stein and Scott's composite, DFT/DWT-based composite and mixture partial/semi-partial correlation similarity scores using a small reference library, NIST Chemistry WebBook library (WebBook) [7]. Although they addressed that the optimal weight factor is dependent on the mass spectral library, it still remains unknown whether the optimal weight factor depends on spectral similarity measure and the size of reference library.
With the rapid development of EI MS library, more similar EI MS spectra are added to the reference library, making it more challenging for high accuracy compound identification. The size of reference library will continuously increase in future. It is important to foresee the compound identification accuracy of mass spectral matching with the increasing size of reference library. It's still unknown which spectral similarity measure is the best in an even larger mass spectral database.
The objectives of this study are first to compare the performance of the literature reported spectral similarity measures using the NIST11 library and investigate the dependence among the optimal weight factor, spectral similarity measure and the size of reference library. We further estimate the performance of existing spectral similarity measures in a larger reference library to be developed in future.
2. Materials and Methods
2.1. NIST EI mass spectral databases
The latest version of NIST/EPA/NIH Mass Spectral Library 2011 contains two EI mass spectral libraries, the main EI MS library (NIST11) and the replicate EI MS spectra. The main library and the replicate EI MS spectra have 212,961 and 30,932 mass spectra, respectively. The main EI MS library of NIST/EPA/NIH Mass Spectral Library 2005 (NIST05) has 163,198 mass spectra. The NIST Chemistry WebBook library (WebBook) extracted on November 28, 2011 consists of 23,721 mass spectra.
In this study, the replicate EI MS spectra of the NIST/EPA/NIH Mass Spectral Library 2011 are used as a query spectral library, while the WebBook, NIST05 and NIST11 are used as reference library, respectively. The query spectral library has 30,932 mass spectra for 19,788 unique compounds. To ensure that all compounds given the query spectra are present in each of the three reference libraries, the replicate library is filtered as follows: the interception of the three reference libraries is first calculated based on compound CAS (Chemical Abstracts Service) registry numbers; any compound in the replicate library that does not have a corresponding CAS number in the interception of the three reference libraries is removed from the replicate library. This results in a set of filtered query spectra with 23,001 mass spectra for 13,154 unique compounds. Only 43 mass spectra in the NIST11 reference library have fragment ion m/z values larger than 1000 and therefore, the fragment ions with m/z > 1000 in the reference library are further removed to minimize computation burden.
2.2. Weighted cosine similarity
Let us consider the two spectral signals X = (x1, x2,…, xn) and Y =(y1,y2,…,yn), which are the query and reference mass spectra, respectively. In order to calculate the spectral similarity of these two mass spectra, one of the simple mathematical ways is to use cosine correlation formula defined as follows:
| (1) |
where the inner product and the norm . Stein and Scott demonstrated the importance of weight for intensity and m/z value [1]. The weighted spectra X,Y are considered as follows:
| (2) |
where mi, = 1…,n is m/z value of the ith fragment ion, and a, b are the weight factors for peak intensity and m/z value, respectively. The weighted cosine similarity SWC(X,Y) is then defined as follows:
| (3) |
2.3. Stein and Scott's composite similarity
Stein and Scott firstly defined a ratio of peak pair SR as follows [1]:
| (4) |
where n = −1 or 1 if the term in parentheses is less than or greater than unity, respectively, xi,yi are all non-zero intensities having common m/z value, and the value NX^Y is the number of non-zero peaks in both the reference and the query spectra. The composite similarity is then calculated by
| (5) |
where NX is the number of non-zero peak intensities existing in the query spectra. As for a part of weighted cosine similarity, they set weight factor to (a,b) = (0.5,3).
2.4. Discrete Fourier- and wavelet- transform composite similarity
Discrete Fourier transform (DFT) converts an original spectral signal X =(x1,…,xn) into a new signal as follows [10]:
| (6) |
where the notation i is the imaginary unit and is a a primitive n th root of unity. By Euler's formula, exp(iϕ) = cosϕ + i sinϕ, the original equation becomes
| (7) |
We have a new transformed signal XFR consisting of real part of xkF as follows:
| (8) |
with
| (9) |
where a function Re(·) is the real part of imaginary number or function
The discrete wavelet transform of a signal X =(x1,…,xn) is calculated by passing it through a low-pass filter g and a high-pass filter h, resulting in two subsets of signals: approximations and details [11]. The coefficients of approximations and details are defined as follows:
| (10) |
| (11) |
where g and h are the low-pass filter and the high-pass filter, respectively. This study used Daubechies' scaling functions with an order of 4 as for low-pass filters [11]. Then the approximation and detail DWTs of an original signal X are as follows, respectively:
| (12) |
The DFT with real and DWT with detail composite similarity are defined as follows [6]:
| (13) |
and
| (14) |
2.5. Mixture semi-partial composite similarity
The mixture semi-partial correlation ρX(Y|Z) between X and Y with controlling variables Z = {Z1,…,Zn} is the correlation between the random variable X and residuals RY|Z of Y on Z, and is represented by
| (15) |
where the residuals RY|Z of Y on Z is the difference between observed and estimated output data, and is calculated from the linear regression of Y on Z corresponding to an ordinary least square solution of linear system as follows:
| (16) |
Suppose that X is a query mass spectrum and Y = {Y1,Y2,…,YN} is a set of N mass spectra in the reference library. The semi-partial correlation between X and Yi given Y(i) is calculated by
| (17) |
where a set Y(i) = Y\{Yi} = {Y1,…,Yi−1,Yi+1,YN} and \ denotes the set minus operator. Note that X,Yi and Y(i) in the previous equations have the identical roles as X,Y and Z, respectively. Given the rank k, the semi-partial correlation is defined by
| (18) |
where Y(i,k) = {Yj ∈ Y(i) | Rank(SWC(X, Yj)) ≤ k} and Rank(SWC(X,Yj)) is the rank of the similarity score SWC(X,Yj) in descending order. Then the mixture semi-partial correlation is defined by [7]
| (19) |
where w is a coefficient ranging from 0 to 1 (w is set as 0.1 in this study based on [7]).
2.6. Performance measure
The performance of each mass spectral similarity measure for compound identification is evaluated as follows:
| (20) |
If a spectrum in reference library having the largest mass spectral similarity score is considered as the identification result of a query mass spectrum, a correct identification refers that the query spectrum and the spectrum from the reference library have the same CAS registry number. In case that the top k ranked mass spectral similarity scores are considered, an identification is considered as a correct identification as long as one of the top k ranked reference spectra has the same CAS number as the query spectrum.
3. Results and Discussion
We evaluated the performance of compound identification methods, including weighted cosine (WC), Stein and Scott's composite (SS), discrete Fourier- and wavelet- transforms composite (DFT and DWT), and mixture semi-partial similarities (SP). To find the optimal weight factor w = (a, b) of power transformation for peak intensity and m/z value, we considered {0.1, 0.2, 0.3, 0.4, 0.45, 0.47, 0.49, 0.51, 0.53, 0.55, 0.57, 0.59, 0.61, 0.65, 0.7, 0.8, 0.9, 1, 2, 3} as intensity weight factors and {0.1, 0.5, 0.8, 0.9,1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 2, 3, 4, 5} as m/z weight factors, respectively. The optimal weight factor is a pair of peak intensity and m/z weight factors that provides the best accuracy for compound identification. A total of 280 pairs of weight factors (20 intensity factors and 14 m/z factors) were tested. Our previous study showed that the optimal weight factor for WC similarity and the SP similarity is w = (0.53, 1.3). Therefore, a dense interval was used near the optimal values, while a sparse interval was used in the other region.
3.1 Optimal weight factors
Table 1 lists the optimal weight factor and the corresponding identification accuracy obtained for each combination of spectral similarity measure and reference library. It can be see that the value of optimal weight factor is dependent on both the reference library and the method of mass spectral similarity measure. In case of WC, the optimal weight factors discovered in this work for NIST11 are not identical to any literature reported values, but these discovered weight factors are within the top 10% of the weight factors (i.e., 0.5 ≤ a ≤ 0.55 and 1.1 ≤ b ≤ 1.4) discovered by Kim et al. [9], which used the same spectral database NIST11 as the reference library. It should be noted that the query library of this study is different from that of Kim et al. [9]. That is, the query library spectra used in this study was extracted from NIST11 replicate library and was filtered to fit to all three reference libraries, i.e., WebBook, NIST05 and NIST11 libraries, while those query spectra used by Kim et al. [9] were extracted from NIST08 spectral database. The optimal weight factors of WC measure are mostly within the range of 0.5 ≤ a ≤ 0.55 and 1.1 ≤ b ≤ 1.4, while the other spectral similarity measures tend to be outside these ranges. The optimal weight factors for SS, DFT, and DWT found in this study are very different from their values reported in the original literatures [1,6], which used the weight factor (0.5, 3). This was caused most likely by the difference of the mass spectral library. Another possibility for the difference is that the optimal weight factor can be biased on input query spectra, although NIST replicate library is the best possible data set on hand for performance evaluation.
Table 1.
The optimal weight factors and identification accuracy of different mass spectral similarity measures.
| Method | WebBook | NIST05 | NIST11 | |
|---|---|---|---|---|
| WC | Weight factor | (0.55, 1.3) | (0.53, 1.1) | (0.51, 1.1) |
| Accuracy | 0.845 | 0.824 | 0.801 | |
| SS | Weight factor | (0.4, 1.2) | (0.3, 0.9) | (0.3, 0.9) |
| Accuracy | 0.834 | 0.805 | 0.785 | |
| DFT | Weight factor | (0.49, 1.5) | (0.45, 1.5) | (0.49, 2) |
| Accuracy | 0.833 | 0.812 | 0.785 | |
| DWT | Weight factor | (0.47, 2) | (0.49, 1.4) | (0.49, 1.4) |
| Accuracy | 0.836 | 0.815 | 0.789 | |
| SP | Weight factor | (0.55, 0.1) | (0.57, 1.4) | (0.57, 1.4) |
| Accuracy | 0.848 | 0.829 | 0.806 |
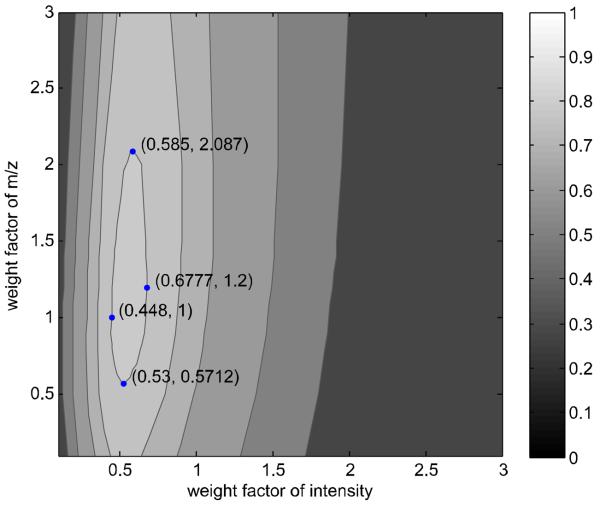
The weight factor of m/z value of each method has a wider range than the intensity weight factor (Figure S-1 to S-5 in Supplementary Information), which is similar to the observation by Kim et al. [9]. For example, considering elevation label at identification accuracy of 79.9% in the WC similarity measure with NIST11 as reference library, Figure 1 displays the locations of four pairs of intensity and m/z weight factors (0.59, 2.09), (0.68, 1.20), (0.53, 0.57) and (0.45, 1.00) clockwise. The up-and-down (the dimension of m/z weight factor) distance is 1.52, while the distance from side to side (the dimension of intensity weight factor) is 0.2. This indicates that the compound identification accuracy is more sensitive to intensity weight factor than the m/z weight factor as discussed by Kim et al. [9]. Interestingly, the identification accuracy of SP measure is almost independent on the weight factor of m/z in all three reference libraries (the contours of Figure S-5). This is because all weighted mass spectra have the exactly same weight factor of m/z regardless of intensities so that the common effect of m/z weight factor is removed by the SP measure.
Figure 1. Contour plot of compound identification accuracy calculated using the WC similarity measure and NIST11 as reference library.
The four points in the plot show the minimum and the maximum of weight factors for intensity and m/z, respectively, for identification accuracy of 79.9%.
3.2 Performance of different spectral similarity measures
Figure S-6 in Supplementary Information (as well as Table 1) depicts the performance of each spectral similarity measure at its optimal weight factor. The SP method outperforms other spectral similarity measures in all three reference libraries, with an identification accuracy of 84.8%, 82.9%, and 80.6% corresponding to WebBook, NIST05 and NIST11, respectively. Figure S-6 also shows that the accuracy of compound identification decreases with the increase of library size. The average accuracy of all spectral similarity measures decreases by 2.2% and 2.4% when the size of reference library is increased from WebBook to NIST05 and from NIST05 to NIST11, respectively. Interestingly, the accuracy of SS improved in the literature [7] by about 3%, but the SS method with the optimal weight factor found in this study also improves the accuracy by about 1.7% against literature [7]. The total improvement of the SS method between weight factors (0.5, 3) and (0.4, 1.2) using WebBook library as the reference library is 5.1% and its performance is the same as DFT.
3.3 Effect of the size of reference library
To investigate the trend of compound identification accuracy corresponding to the size of reference library, a total of 100 pairs of subset query spectra and subset reference spectra were randomly generated from the replicate query library and the NIST11 reference library, respectively, subjected to that all compounds in each sub-query library (subset query spectra) present in the corresponding sub-reference library (subset reference spectra). Each sub-query library has 2000 spectra. For each sub-query library, five sub-reference libraries were created with 25000, 50000, 100000, 150000 and 200000 compounds in each library, respectively.
To get the statistics of the compound identification accuracy on the randomly generated pair of sub-query library and sub-reference library, a total of 100 sampling pairs of sub-query library and corresponding sub-reference library were created. The mean and standard deviation of compound identification accuracy were then calculated based on the 100 sampling pairs. Figure S-7 in Supplementary Information depicts the error bar plot of mean and standard deviation of the 100 random sampling. It can be seen that the identification accuracy of using all five spectral similarity measures decreases with the increase of the size of reference library, and these spectral similarity measures provides different mean of identification accuracy when the same reference library is used.
Student t-test was performed to assess the statistical significance of the mean difference of the identification accuracy obtained from these five spectral similarity measures. The null hypothesis of t-test is that the means of compound identification accuracy of two spectral similarity measures are the same if the same reference library is used. To each of the five sub-reference libraries, the 100 sub-query libraries generate 100 identification accuracy values for each of the five spectral similarity measures. A t-test was performed on two sets of the 100 identification accuracy values, generated by two spectral similarity measures. A p-value of the t-test indicates the statistical significance of the difference between the mean values of the two sets of 100 accuracy values. Table 2 summarizes the p-values of all t-tests. It can be seen that the compound identification accuracy of the five spectral similarity measures are statistically different from each other at 95% of confidence level, except the identification accuracy between SP and WC in case of reference library containing 25000 and 50000 compounds, and DFT and DWT in all five reference libraries. The non-significant mean difference between SP and WC is mostly likely caused by the small size of the reference library, while the non-significant difference between DFT and DWT may be induced by the use of frequency information for compound identification. It is interesting to note that the p-value decreases with the increase of the size of the reference library. That is, the difference of average identification accuracy between spectral similarity measures becomes more statistically significant when a larger reference database is used.
Table 2.
The p-values of student t-tests for purpose of assessing the statistical significance of identification accuracy difference obtained using the six spectral similarity measures. The null hypothesis of each test is that mean values of identification accuracies of two mass spectral similarity measures are the same if the same reference library is used. The two sets of 100 identification accuracies in a t-test are the identification accuracy of 100 sub-query libraries and a corresponding sub-reference library.
| Reference size | Similarity Mesure | SS | DFT | DWT | SP |
|---|---|---|---|---|---|
| 25000 | WC | 1.01E–17 | 3.93E–03 | 8.20E–04 | 0.1029 |
| SS | 1.06E-09 | 3.35E-08 | 1.25E-24 | ||
| DFT | 0.5964 | 3.65E-06 | |||
| DWT | 4.08E-07 | ||||
|
| |||||
| 50000 | WC | 6.54E-23 | 5.48E-04 | 3.22E-04 | 0.0575 |
| SS | 2.45E-11 | 1.10E-10 | 3.38E-31 | ||
| DFT | 0.8613 | 8.40E-08 | |||
| DWT | 4.23E-08 | ||||
|
| |||||
| 100000 | WC | 1.33E-30 | 3.35E-06 | 1.46E-05 | 0.0143 |
| SS | 1.22E-12 | 9.91E-15 | 3.81E-41 | ||
| DFT | 0.6443 | 4.44E-12 | |||
| DWT | 2.24E-11 | ||||
|
| |||||
| 150000 | WC | 2.22E-32 | 3.35E-07 | 1.83E-05 | 0.0085 |
| SS | 8.64E-12 | 1.17E-15 | 1.40E-44 | ||
| DFT | 0.3253 | 4.79E-14 | |||
| DWT | 8.70E-12 | ||||
|
| |||||
| 200000 | WC | 9.19E-36 | 5.72E-08 | 9.95E-06 | 0.0046 |
| SS | 9.23E-12 | 7.27E-18 | 1.28E-51 | ||
| DFT | 0.1877 | 4.89E-16 | |||
| DWT | 3.08E-13 | ||||
By comparing the results displayed in Figure S-7 and Table 2, we can conclude that the compound identification accuracy of spectral similarity measures in descending order is SP > WC > DWT, DFT > SS. This agrees with the simulation results using the entire NIST replicate library as query library and WebBook, NIST05 and NIST11 as the three reference libraries (Figure S-6 and Table 1). Table 1 shows that SS has a slightly better performance than DFT when the WebBook is used as reference library, and SS has the same identification accuracy as DFT in case that the NIST11 is used as the reference library. Figure S-7 shows that DFT has a much improved mean value of identification accuracy than SS across all sub-reference libraries. The average mean difference between SS and DFT is greater than 1.15%. Such a simulated result depicted in Figure S-7 actually agrees with the results listed in Table 1 because the error bars in Figure S-7 show that there is a certain degree of overlap in identification accuracy between the five spectral similarity measures when the same reference library is used. It is possible the SS may have an equal or even better performance than DFT, as demonstrated in Table 1. Such a performance difference is caused by the query spectra and the reference spectra.
To predict the identification accuracy of each spectral similarity measure on a large reference library in future, the compound identification accuracy and size of reference library is fitted by linear regression with the second order polynomial as follows:
| (21) |
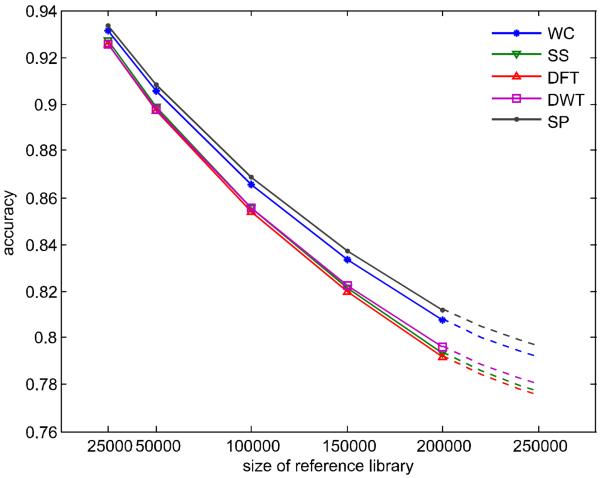
where n is the number of reference library and regression coefficients βi, i = 0,1,2 are estimated by ordinary least square method. Figure 2 depicts the results of regression. As expected, the accuracy of each spectral similarity measure decreases with increase of the reference library size. The SP method has the best accuracy in the large reference library in future (dotted lines in Figure 2). Interestingly, since the slop of SP method is smaller, the difference of compound identification accuracy between SP and the other spectral similarity measures at 250000 reference library size becomes larger than that in the 200000 reference size. For example, with increase of the size of reference library from 50000, 100000, 150000 to 200000, the identification accuracy difference between SP (the best spectral similarity measure) and WC (the second best spectral similarity measure) is 0.23%, 0.31%, 0.37% and 0.43%, respectively. For the future reference library containing EI MS spectra of 220000, 240000 and 250000 compounds, the estimated accuracy differences are 0.46%, 0.48% and 0.49%, respectively. For this reason, we predict that the proposed SP measure should have the best performance in the future.
Figure 2. Accuracy of compound identification by random sampling.
The solid lines stand for results of 100 time random sampling. The dash lines represent the predicted identification accuracy of each spectral similarity measure using large reference library to be developed in future.
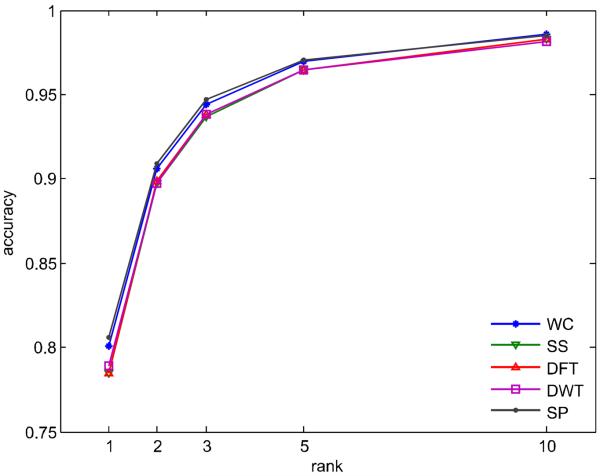
Figure 3 shows the compound identification accuracy when the true compound has one of the top ranked spectral similarity scores, where NIST11 is used as the reference library. Compared with finding the true compounds using the best spectral similarity score, the identification accuracy is increased, on average, 10.9%, 14.8%, 17.4%, and 19.1% when the top 2, 3, 5, and 10 ranked compounds are considered, respectively. It, however, should be noted that the accuracy of mass spectral matching levels off at 98.5% when the top 10 matches are considered, indicating there is a limitation of compound identification accuracy using mass spectrum only. The reason is that the EI MS spectrum just contains partial information of molecular structure. Therefore, the other compound information such as retention index is needed for high accuracy compound identification [12–14].
Figure 3. Accuracy of compound identification.
An identification result is considered as correct if the correct reference spectrum is one of the multiple top ranked reference spectra.
A significant challenge of using the retention index to aid compound identification is the incompleteness of existing retention index database. The NIST11 retention index database has 73,379 Kovats retention index values for only 19,970 compounds, and 111,778 linear retention index values for 49,374 compounds. Even though retention index is normalized retention time for the purpose of minimizing the effects of experimental conditions on the magnitude of retention index, it is still affected by several experimental conditions, including column stationary phase, elution mode, etc. [14]. This worsens the situation of the incompleteness of the current retention index database, and makes it challenging to use the retention index acquired under different experimental conditions for retention index matching. Another challenge is the accuracy of the existing retention index values in the database. For example, compound sabinene has a total of 87 literature reported linear retention index values on the non-polar column with a span of 955–992 retention index units in the NIST11 retention index database (mean = 966, standard deviation = 6.4), while compound citronellyl acetate have 46 retention index values with a span of 1330–1347 retention index units (mean = 1336, standard deviation = 3.5). These indicate the variation of retention index from its mean value is compound dependent in the current retention index database. This makes it challenging to find an optimal retention index deviation window for a compound that has just one or a few number of retention index values in the retention index database. A large retention index deviation window reduces the effectiveness of retention index matching, while a small retention index deviation window increases the chance of filtering a true identification. Furthermore, the retention index information is currently used to filter the identification results after mass spectral matching. In this analysis strategy, the mass spectral matching and the retention index matching are treated as two separate analysis steps. It is necessary to investigate how to effectively use the retention index information for compound identification. For example, applying retention index filtering before the mass spectral matching can reduce the mass spectral matching space, i.e., a small size of reference library is used for identification. Therefore, an improved identification can be expected by using such a small reference library. Another approach of simultaneously evaluating the closeness of the mass spectrum and the retention index may further improve the identification accuracy.
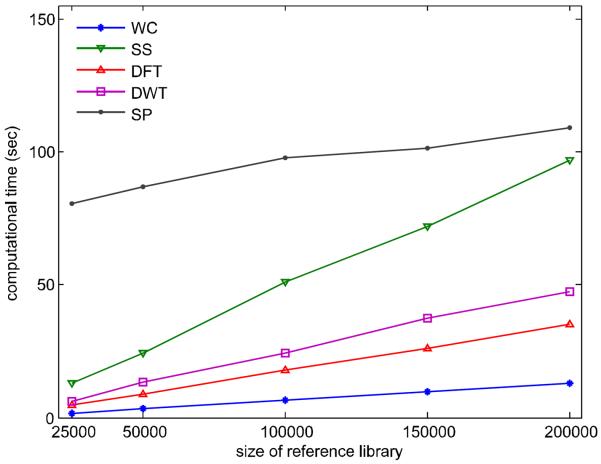
As the size of query and reference library increases, the burden of computation is rapidly increased as shown in Figure 4. All calculations are performed on an Intel Core i7 – 3960X CPU @ 3.30GHz with 16 GB main memory and all similarity scores are calculated in Matlab R2010b (The Mathworks, Natick, MA). WC is the most efficient method while the SP method is the most expensive one. The SS method is very sensitive on the size of reference library. The other methods are more expensive than WC because they all are composite/mixture models based on the WC.
Figure 4.
Computational time of each spectral similarity measure.
It should be noted that the computation time of a similarity measure can be affected by many factors, including the computer hardware, the implementation of the algorithms, and the particular values of weight factor a and b. For instance, compared with the weight factor (0.5, 1), the computational time is increased by 30.1% if the optimal weight factor (0.51, 1.1) is used to identify compounds for the spectra in the replicate library from the NIST11 reference library. Therefore, the absolute values of computation time calculated here holds true only to the conditions used in this study.
In this study, an identification is considered as a correct identification if the matched two spectra, one from the query library and the other from the reference library, have identical CAS register numbers. Using the CAS numbers in the NIST database does not introduce any error in assessing the correctness of an identification result. It, however, may introduce a certain level of variation in the calculation of identification accuracy, in which the number of query spectra is used (see Eq. 20). For example, 1,2-dimethyl-cyclohexane has a CAS number of 2207-01-4 for the cis and 6876-23-9 for the trans, respectively. There is also an entry for cis/trans with a CAS number of 583-57-3. These three CAS numbers were treated as three different compounds during the calculation. We believe that a small portion of the compounds in the NIST database have such complication of CAS numbers and therefore, their effects on assessing the overall compound identification accuracy is very limited.
The focus of this study is to compare the performance of literature reported five mass spectral similarity measures on the accuracy of compound identification using different query and reference libraries. Compound identification accuracy can be affected by many other factors, including experimental conditions, the method of reducing the instrument data to mass spectra, and the completeness of the reference spectral library. For example, the purity of the chromatographic peaks entering the ionization source plays a significant role in the quality of the mass spectra. To reduce the chance of co-eluting chromatographic peaks, a comprehensive two-dimensional gas chromatograph time-of-flight mass spectrometry (GC×GC-TOF MS) can provide improved GC separation and high quality mass spectra for compound identification. The other experimental conditions such as the slop of temperature gradient, the selection of column, mass spectrum acquisition frequency, etc. can also contribute to the quality of mass spectra and therefore, can significantly affect the accuracy of compound identification.
4. Conclusions
In order to investigate relationship among accuracy of compound identification and reference mass spectral database, we evaluated five literature-reported spectral similarity measures such as weighted cosine, Stein and Scott's composite, Fourier/wavelet transform-based composite, and the mixture semi-partial correlation measures. The performances of those five spectral similarity measures were studied using different reference libraries, including WebBook, NIST05 and NIST11, by varying weight factors for intensity and m/z value. The SP spectral similarity measure always outperforms other spectral similarity measures in all testing reference libraries, with the highest identification accuracy of 84.8% in WebBook and 80.6% in NIST11. Considering multiple spectra with the top-ranked spectral similarity scores rather than the compound candidate that has the best spectral similarity score, the compound identification accuracy is increased, but levels off at 98.5% when the top 10 matches are considered. This indicates that there is a limitation of compound identification accuracy using mass spectrum only. The other compound information such as retention index is needed for high accuracy compound identification.
The study of compound identification accuracy using different spectral similarity measures and reference libraries demonstrates that the values of optimal weight factor for peak intensities and m/z depend on both the spectral similarity measure and the size of reference library. With the increase of the size of reference library, the optimal weight factor for each spectral measure varies and the identification accuracy is decreased. By varying the size of reference library, simulation study indicates that the SP will have the best performance in future and the computation challenge of SP is the worst. The development of efficient version of SP to reduce computational time and have higher accuracy is left a future work.
Supplementary Material
Compared performance of 5 literature-reported compound identification measures.
Estimated dependency of identification accuracy on the size of reference library.
Weight factors dependent on both reference library and spectral similarity measures.
The semi-partial correlation mixture measure performs the best.
ACKNOWLEDGMENT
This work was supported by National Institute of Health (NIH) grant 1RO1GM087735 through the National Institute of General Medical Sciences (NIGMS) and R21ES021311 through the National Institute of Environmental Health Sciences (NIEHS).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- [1].Stein SE, Scott DR. Journal of the American Society for Mass Spectrometry. 1994;5:859. doi: 10.1016/1044-0305(94)87009-8. [DOI] [PubMed] [Google Scholar]
- [2].Hertz HS, Hites RA, Biemann K. Analytical Chemistry. 1971;43:681. [Google Scholar]
- [3].Atwater BL, Stauffer DB, Mclafferty FW, Peterson DW. Analytical Chemistry. 1985;57:899. [Google Scholar]
- [4].Julian RK, Higgs RE, Gygi JD, Hilton MD. Analytical Chemistry. 1998;70:3249. doi: 10.1021/ac971055v. [DOI] [PubMed] [Google Scholar]
- [5].Rasmussen GT, Isenhour TL. Journal of Chemical Information and Computer Sciences. 1979;19:179. [Google Scholar]
- [6].Koo I, Zhang X, Kim S. Analytical Chemistry. 2011;83:5631. doi: 10.1021/ac200740w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Kim S, Koo I, Jeong J, Wu SW, Shi X, Zhang X. Analytical Chemistry. 2012;84:6477. doi: 10.1021/ac301350n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Horai H, Arita M, Nishioka T. BioMedical Engineering and Informatics, 2008. BMEI 2008. International Conference on.2008. p. 853. [Google Scholar]
- [9].Kim S, Koo I, Wei XL, Zhang X. Bioinformatics. 2012;28:1158. doi: 10.1093/bioinformatics/bts083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Brigham EO. The fast Fourier transform. Prentice-Hall; Englewood Cliffs, N.J.: 1974. [Google Scholar]
- [11].Daubechies I. Ten lectures on wavelets. Society for Industrial and Applied Mathematics; Philadelphia, Pa.: 1992. [Google Scholar]
- [12].Koo I, Zhao YP, Zhang J, Kim S, Zhang X. Journal of Chromatography A. 2012;1260:193. doi: 10.1016/j.chroma.2012.08.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Zhao YP, Zhang J, Wang B, Kim SH, Fang AQ, Bogdanov B, Zhou ZX, McClain C, Zhang X. Journal of Chromatography A. 2011;1218:2577. doi: 10.1016/j.chroma.2011.02.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Zhang J, Fang AQ, Wang B, Kim SH, Bogdanov B, Zhou ZX, McClain C, Zhang X. Journal of Chromatography A. 2011;1218:6522. doi: 10.1016/j.chroma.2011.07.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.