Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jul 1.
Published in final edited form as: Gait Posture. 2013 Jan 20;38(3):537–540. doi: 10.1016/j.gaitpost.2012.12.018

Executive function orchestrates regulation of task-relevant gait fluctuations

Leslie M Decker 1,2,*, Fabien Cignetti 1,3, Nicholas Stergiou 1,4
PMCID: PMC3686983  NIHMSID: NIHMS437808  PMID: 23337732

Abstract

Humans apply a minimum intervention principle to regulate treadmill walking, rapidly correcting fluctuations in the task-relevant variable (step speed: SS) while ignoring fluctuations in the task-irrelevant variables (step time: ST; step length: SL). We examined whether the regulation of fluctuations in SS and not in ST and SL depends on high-level, executive function, processes. Young adults walked on a treadmill without a cognitive requirement and while performing the cognitive task of dichotic listening. SS fluctuations became less anti-persistent when performing dichotic listening, meaning that taxing executive function impaired the ability to rapidly correct speed deviations on subsequent steps. Conversely, performing dichotic listening had no effect on SL and ST persistent fluctuations. Findings suggest that high-level brain processes are involved only in regulating gait task-relevant variables.

Keywords: Walking, Variability, Minimum Intervention Principle, Executive Function, Detrended Fluctuation Analysis

1. Introduction

In a wide range of tasks, humans apply a minimum intervention principle to regulate movement, correcting fluctuations only if they interfere with task performance [1,2]. This control holds because correcting task-irrelevant fluctuations in addition to task-relevant fluctuations has detrimental effects on the central nervous system (CNS), increasing noise and computational effort.

In gait, such a principle has been demonstrated by examining the statistical persistence/anti-persistence of the stride-to-stride fluctuations during treadmill walking [3,4]. Specifically, fluctuations in stride time and stride length were found to be persistent, meaning that their values continued increasing or decreasing over several subsequent strides before reversing. Conversely, fluctuations in stride speed were anti-persistent, rapidly reversing direction on subsequent strides. Given that the treadmill walking task requires maintaining (on average) the same walking speed (to avoid walking off the treadmill) and that many combinations of stride length and stride time equally achieve that speed, only task-relevant fluctuations therefore were immediately corrected.

However, the question remains as to whether persistent and anti-persistent fluctuations stem from similar or different control processes of the CNS. Interestingly, only anti-persistence in step speed is needed to achieve the treadmill walking goal (to maintain constant walking speed [3,4]). Accordingly, high-level executive function processes, which are involved in handling goal-directed actions [5], may play a role only in shaping anti-persistent behavior. If so, taxing these processes with a concurrent cognitive task during treadmill walking would alter anti-persistence in step speed while persistence in step time and step length would remain unchanged.

2. Methods

Twenty healthy adults (12♀/8♂, 24.45±0.87 years, 1.73±0.02 m, 70.41±2.63 kg) participated in two experimental sessions after providing written informed consent. The session order was counterbalenced between subjects. In one session, subjects performed the cognitive task of dichotic listening while seated to establish baseline performance [6,7]. They had to listen and report consonant-vowel syllables (phonologically salient, but semantically meaningless) presented dichotically under three attention conditions: non-forced (NF) consisted in reporting the syllable heard best, and forced-right (FR) and forced-left (FL) the syllable heard in the right and left ear, respectively. The conditions increased the need for executive control, from NF to FL. In the other session, subjects walked on a treadmill at preferred speed (1.06±0.03 m/s) with markers attached at anatomical landmarks [8], first without a cognitive requirement (walking: W) and afterwards while performing dichotic listening in NF (W+NF), FR (W+FR) and FL (W+FL) (Fig. 1). In both sessions, NF was presented first and FR and FL were counterbalanced between subjects. Each condition lasted for three minutes, involving 36 different syllable pairs. E-prime® was used for syllable presentation and report collection. The marker movements were recorded (60 Hz) with an 8-camera Motion Analysis Eagle Digital system and low-pass filtered at 10 Hz with a zero-lag Butterworth filter.

Fig 1.

Fig 1

Open in a new tab

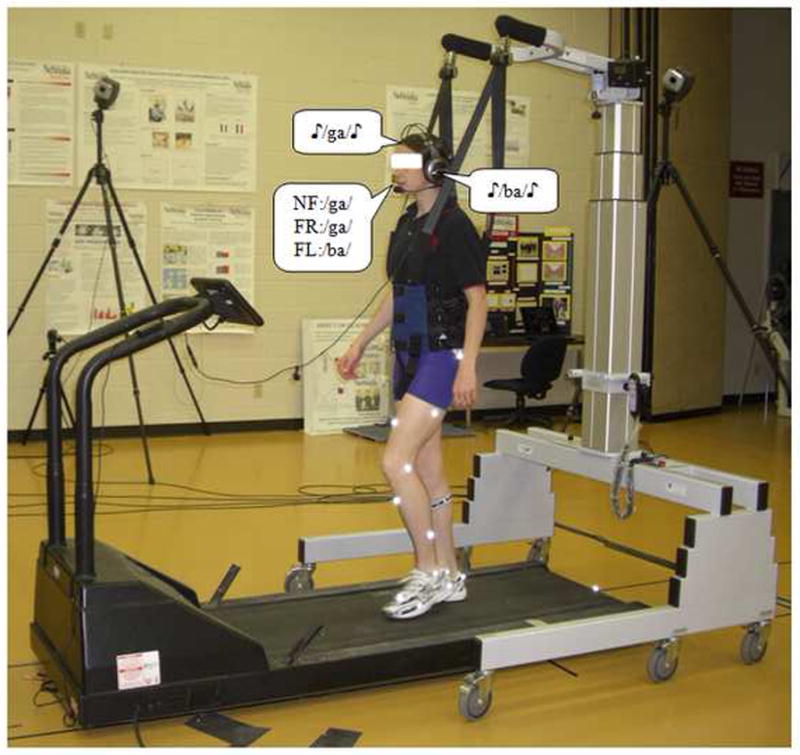
Experimental setup with a subject walking on the treadmill while performing the dichotic listening test. Consonant-vowel syllables /ba/, /da/, /ga/, /pa/, /ta/, and /ka/ were presented as stimulus-pairs (e.g., /ga/-/ba/) using a headphone, one syllable to the right ear (e.g., /ga/) and simultaneously the other syllable to the left ear (e.g., /ba/). The subjects were asked to freely report the consonant-vowel syllable they heard best from the dichotic syllable pair in the non-forced (NF) condition (e.g., /ga/, assuming a right ear advantage). On the other hand, they were instructed to report only the syllable presented to the right ear in the forced-right (FR) condition (e.g., /ga/) and to the left ear in the forced-left (FL) condition (e.g., /ba/). The subjects were secured in the LiteGait® harness system for safety purposes. Reflective markers were attached to specific anatomical landmarks, including the anterior and posterior superior iliac spine, lumbosacral joint, greater trochanter of the femur, lateral mid-thigh, front lower thigh, lateral and medial epicondyles of the femur, front mid-shank, lateral lower shank, lateral and medial malleoli, lateral border of the fifth metatarsal head, medial border of the first metatarsal head, lateral and medial processes of the calcaneal tuberosity, heel, and between the second and third metatarsal phalangeal joints.

Dichotic listening was scored through the laterality index (LI), which is the ratio of the difference between correct reports for the right ear and those for the left ear to the total number of correct reports, expressed as a percentage. Step time (ST) and step length (SL) were defined as the time interval and horizontal distance between consecutive toe-off events, with the toe-off defined from the maximum backward displacement of the marker located between the second and third metatarsal phalangeal joints during each step. Step speed (SS) was defined as SS=SL/ST. The time series were shortened to 272 data points (the number of steps of the slowest subject). Persistence/anti-persistence in ST, SL and SS was examined using Detrended Fluctuation Analysis (DFA) [9,10]. DFA computed mean square roots of detrended residuals, F(n), of the integrated time series over a range of interval lengths, n. The scaling exponent α was then estimated from the slope of the linear relationship between log[F(n)] and log(n). A restricted range of interval lengths was used, from n=17 steps to n=45 steps, where the slope was the most stable as determined by the DFBETA statistics [10] (Fig. 2). α<0.5 indicates anti-persistence, with fluctuations in one direction immediately followed by corrections in the opposite direction. α>0.5 indicates persistence, with fluctuations in one direction followed by fluctuations in the same direction. LI and α were subjected to two-way (session×condition) and one-way (condition) within-subjects analyses of variance (ANOVAs), respectively.

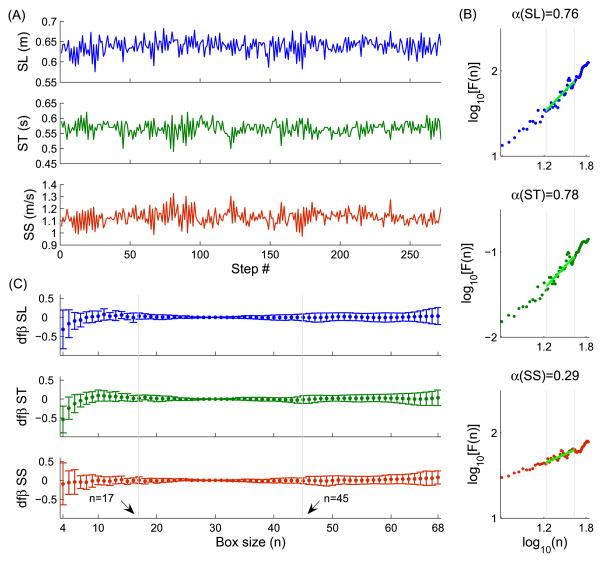
Fig 2.

Fig 2

Open in a new tab

(A) Step length (SL), step time (ST) and step speed (SS) time series (N=272 steps) obtained from a representative subject walking at preferred speed. (B) Corresponding log-log plots of average fluctuations F(n) vs. interval lengths n, obtained using the Detrended Fluctuation Analysis. The log10[F(n)] vs. log10(n) plots were fitted with linear functions and the scaling exponents α were obtained from the slopes of these lines over the range of interval lengths n=17 to n=45. This range provided the most stable estimates of α for SL, ST, and SS. As illustrated, step-to-step fluctuations of both SL and ST time series were persistent (α>0.5) while those of SS time series were anti-persistent (α<0.5). (C) The stable interval length fitting range was determined from the distribution of the diagnostic measure DFBETA, which reflects how much the exponent α changes when sequentially removing the intervals of length n. The values presented here are means ± standard deviations of the population. For small interval lengths (n<17data points), the DFBETA values exhibited bias away from zero and were importantly dispersed, reflecting estimations of α over- or under-estimated and poorly stable, respectively. Indeed, small intervals contain few data points for fitting the trends, which likely render the α estimates inaccurate and variable. For large interval lengths (n>45 data points), the DFBETA values did not exhibit bias but were highly dispersed. These interval lengths provide sufficient data to fit the trend but the average fluctuations around the trends are more variable, making the α estimates less stable. Therefore, the restricted range of lengths 17≤n≤45 was considered for estimating α.

3. Results

Cognition

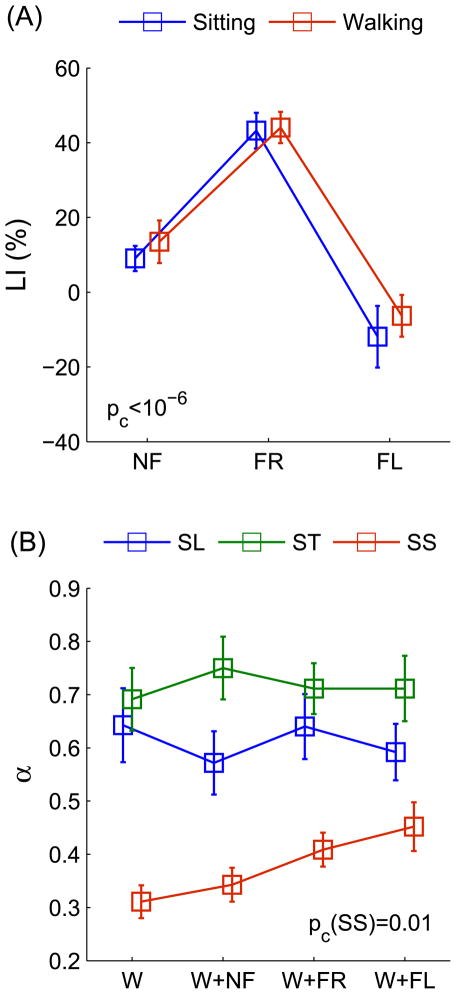
There was a condition effect for LI (F2,38=32.91, p<10−9, η2 =0.44), which increased from NF (11.27±3.29%) to FR (43.65±3.13%; p=0.003) and decreased from FR to FL (−9.08±4.93 %; p<0.001) (Fig. 3A). As previously found, subjects reported more correct answers for the right ear in NF and FR, and inversely reported more correct answers for the left ear in FL [7]. The ANOVA did not reveal a session effect for LI, meaning that cognitive performance was maintained during walking.

Fig 3.

Fig 3

Open in a new tab

(A) Laterality indexes (LI) obtained in the dichotic listening conditions (NF: non-forced, FR: forced-right, FL: forced-left) during the sitting and walking sessions. Results from the two-way within-subjects ANOVAs (Condition×Session) indicated a significant main effect of condition for LI, with the p-value for the effect - pc - reported on the graph. (B) Exponents α obtained from step length (SL), step time (ST), and step speed (SS) time series as a function of the experimental conditions (walking: W, walking when performing dichotic listening: W+NF, W+FR, and W+FL). Results from the one-way within-subjects ANOVAs indicated a significant main effect of condition for α(SS), with the p-value for the effect - pc(SS) - reported on the graph. LI and α values are means ± standard errors of the population.

Gait

DFA revealed anti-persistence in SS (α<0.5) and persistence in ST and SL (α>0.5). The ANOVA yielded a condition effect for α(SS) (F2,44=4.71, p=0.01, η2=0.12). Fluctuations were less anti-persistent in W+FL (α=0.45±0.04) than in W (α=0.31±0.03, p=0.006) and W+NF (α=0.34±0.03, p=0.041). There were no significant resultsfor α(ST) and α(SL) (Fig. 3B).

4. Discussion

This study examined the origins of persistent/anti-persistent fluctuations in gait. As expected, taxing the executive function processes with dichotic listening led to less anti-persistent SS, which reflected an impaired ability to rapidly correct speed deviations on subsequent steps. Therefore, executive function was involved in regulating anti-persistence in the variable relevant for achieving the treadmill walking goal (to maintain constant speed [3,4]). Interestingly, a previous model of gait dynamics reproduced anti-persistent fluctuations in ST (the task-relevant variable) during metronomically paced walking [11,12]. The authors suggested that anti-persistence resulted from the “human consciousness” of being constrained to walk at a controlled pace by following external timing cues. Accordingly, our finding supports the proposal that anti-persistence in gait results from high-level brain processes.

Conversely, decreasing the cognitive resources available had no effect on the persistence of the task-irrelevant variables for treadmill walking (ST and SL). Accordingly, the persistent fluctuations likely stem from low-level processes of the CNS and the inherent biomechanics of the locomotor system. This interpretation is in agreement with modeling studies that reproduced persistent fluctuations in ST using either an intra-spinal network of neurons coupled, or not, to a mechanical oscillator [9,11–14] or a biomechanical model of walking operating under minimal feedback (spinal reflex) [15].

In summary, high-level brain processes were only involved in regulating anti-persistent speed fluctuations. This finding suggests that the minimum intervention principle minimizes the cognitive cost of locomotion by tightly regulating only step speed, the variable that is directly relevant to achieving the task goal.

Highlights.

  • We examined the origins of task-relevant and task-irrelevant fluctuations in gait

  • Decreasing cognitive resources altered regulation of task-relevant fluctuations only

  • Task-irrelevant fluctuations come from low-level processes and biomechanical factors

  • Task-relevant fluctuations depend also on high-level brain processes

Acknowledgments

This research was supported by the National Institute on Aging, part of the National Institutes of Health (1K99AG033684), and the Nebraska Research Initiative.

Footnotes

Conflict of interest statement

The authors have no financial and personal relationships to disclose with other people or organizations that could have inappropriately influenced this work.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5(11):1226–35. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
  • 2.Liu D, Todorov E. Evidence for the flexible sensorimotor strategies predicted by optimal feedback control. J Neurosci. 2007;27(35):9354–68. doi: 10.1523/JNEUROSCI.1110-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Dingwell JB, Cusumano JP. Re-interpreting detrended fluctuation analyses of stride-to-stride variability in human walking. Gait Posture. 2010;32(3):348–53. doi: 10.1016/j.gaitpost.2010.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Dingwell JB, John J, Cusumano JP. Do humans optimally exploit redundancy to control step variability in walking? PLoS Comput Biol. 2010;6(7):e1000856. doi: 10.1371/journal.pcbi.1000856. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Yogev-Seligmann G, Hausdorff JM, Giladi N. The role of executive function and attention in gait. Mov Disord. 2008;23(3):329–42. doi: 10.1002/mds.21720. quiz 472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Jäncke L, Shah NJ. Does dichotic listening probe temporal lobe functions? Neurology. 2002;58(5):736–43. doi: 10.1212/wnl.58.5.736. [DOI] [PubMed] [Google Scholar]
  • 7.Hugdahl K, Westerhausen R, Alho K, Medvedev S, Laine M, Hämäläinen H. Attention and cognitive control: unfolding the dichotic listening story. Scand J Psychol. 2009;50(1):11–22. doi: 10.1111/j.1467-9450.2008.00676.x. [DOI] [PubMed] [Google Scholar]
  • 8.Vaughan C, Davis B, O’Connor J. Dynamics of human gait. Cape Town, South Africa: Kiboho Publishers; 1999. [Google Scholar]
  • 9.Hausdorff JM, Peng CK, Ladin Z, Wei JY, Goldberger AL. Is walking a random walk? Evidence for long-range correlations in stride interval of human gait. J Appl Physiol. 1995;78(1):349–58. doi: 10.1152/jappl.1995.78.1.349. [DOI] [PubMed] [Google Scholar]
  • 10.Damouras S, Chang MD, Sejdić E, Chau T. An empirical examination of detrended fluctuation analysis for gait data. Gait Posture. 2010;31(3):336–40. doi: 10.1016/j.gaitpost.2009.12.002. [DOI] [PubMed] [Google Scholar]
  • 11.West BJ, Scafetta N. Nonlinear dynamical model of human gait. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;67(5 Pt 1):051917. doi: 10.1103/PhysRevE.67.051917. [DOI] [PubMed] [Google Scholar]
  • 12.Scafetta N, Marchi D, West BJ. Understanding the complexity of human gait dynamics. Chaos. 2009;19(2):026108. doi: 10.1063/1.3143035. [DOI] [PubMed] [Google Scholar]
  • 13.Hausdorff JM, Ashkenazy Y, Peng CK, Ivanov PC, Stanley HE, Goldberger AL. When human walking becomes random walking: fractal analysis and modeling of gait rhythm fluctuations. Physica A. 2001;302(1–4):138–47. doi: 10.1016/s0378-4371(01)00460-5. [DOI] [PubMed] [Google Scholar]
  • 14.Ashkenazy Y, Hausdorff JM, Ivanov PC, Stanley HE. A stochastic model of human gait dynamics. Physica A. 2002;316 (1–4):662–70. [Google Scholar]
  • 15.Gates DH, Su JL, Dingwell JB. Possible Biomechanical Origins of the Long-Range Correlations in Stride Intervals of Walking. Physica A. 2007;380:259–270. doi: 10.1016/j.physa.2007.02.061. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES