Motion-Robust MRI through Real-Time Motion Tracking and Retrospective Super-Resolution Volume Reconstruction

Abstract

Magnetic Resonance Imaging (MRI) is highly sensitive to motion; hence current practice is based on the prevention of motion during scan. In newborns, young children, and patients with limited cooperation, this commonly requires full sedation or general anesthesia, which is time consuming, costly, and is associated with significant risks. Despite progress in prospective motion correction in MRI, the use of motion compensation techniques is limited by the type and amount of motion that can be compensated for, the dependency on the scanner platform, the need for pulse sequence modifications, and/or difficult setup. In this paper we introduce a novel platform-independent motion-robust MRI technique based on prospective real-time motion tracking through a miniature magnetic field sensor and retrospective super-resolution volume reconstruction. The technique is based on fast 2D scans that maintain high-quality of slices in the presence of motion but are degraded in 3D due to inter-slice motion artifacts. The sensor, conveniently attached to the subject forehead, provides real-time estimation of the motion, which in turn gives the relative location of the slice acquisitions. These location parameters are used to compensate the inter-slice motion to reconstruct an isotropic high-resolution volumetric image from slices in a super-resolution reconstruction framework. The quantitative results obtained for phantom and volunteer subject experiments in this study show the efficacy of the developed technique, which is particularly useful for motion-robust high-resolution T2-weighted imaging of newborns and pediatric subjects.

I. Introduction

The relative phase evolution of the MR signal induced as a result of the nuclear spin motion between the phase encode steps, presents as ghosting, blurring, and smearing of signal intensity to incorrect locations in the image space [1]. Inter-scan motion and small ranges of within-scan motion may be corrected by retrospective techniques, e.g. [2], but these techniques cannot correct the ghost and blurring artifacts due to within-scan and within-plane motion.

It is evident that a complete and efficient estimation and correction of motion artifacts is possible through fast real-time motion estimation ideally implemented with prospective acquisition planning [3]-[5]. Various prospective techniques have been proposed in the literature, including (1) orbital Navigator Echo (ONAV) techniques, e.g. [3]-[5], (2) motion reducing K-space encoding/reconstruction, such as motion compensated projection reconstruction [6], and Periodically Rotated Overlapping ParallEL Lines with Enhanced Reconstruction (PROPELLER) [7], [8], (3) optical motion tracking techniques, e.g. [9]-[11] (4) Prospective Acquisition Correction (PACE) [12], and (5) prospective real-time correction using active markers [13]. Promising results have been reported with some of these techniques; however their routine implementation is limited as they require significant changes in the scanner; many of these techniques, especially the ONAV, require substantial modification of pulse sequences, which complicates the optimization of the sequences to achieve the required imaging performance, increases the duration of the scan, and makes the design platform-dependent [14].

The techniques in group (2) only provide partial reduction in motion artifacts and have disadvantages such as reduced scanning efficiency due to oversampling. The optical motion tracking techniques in group (3) have difficulties such as the installation of the optical system in the scanner and maintaining an unobstructed line of sight between the reflectors and the detectors, as well as a necessary calibration and coordinate system registration. Three-dimensional PACE is slow with typical update times of a few seconds. It has appeared to be useful for inter-volume motion correction in functional MRI, but is not used for within-volume and within-plane motion artifacts. Finally, prospective correction based on active markers also requires significant pulse sequence programming.

The compensation of motion in fast imaging protocols is especially difficult due to pulse sequence timing limits. Our main contribution is to compensate the motion and enhance the resolution of these fast scans simultaneously. Our novel motion-robust technique is based on prospective real-time motion tracking using a miniature magnetic field sensor and retrospective volume reconstruction using a model-based approach developed in [15]. Our technique is efficient, platform independent, and is simple and convenient as it only requires the attachment of a miniature sensor to the subject. We will discuss the methodology in the next section and the results for phantom and volunteer experiments in section III.

II. Methodology

A. Image Acquisition and Motion Tracking

Our motion-robust MRI technique is specifically designed based on fast 2D imaging protocols. The focus in this article will be on half-Fourier acquisition single shot turbo spin echo (HASTE) MRI, but the technique can be generalized to fast 2D scans. The 2D slice acquisitions in HASTE are robust to motion; high-resolution high-quality slices are normally obtained using HASTE in the presence of motion; however, occasionally fast spike like motion may deteriorate a few slices. The idea is that the subjects do not move fast continually; therefore with multiple orthogonal HASTE scans a sufficient number of high-quality 2D slices are obtained that allow the reconstruction of a uniformly sampled volume from motion corrected slice acquisitions.

We use a miniature three-dimensional magnetic field sensor to track the motion of the subject, which allows us to estimate the relative location of the slices for retrospective volume reconstruction. The sensor, shown in Figure 1, is made by three orthogonal pairs of pickup coils. The location and orientation of the sensor in three dimensions (six parameters) are calculated in real-time using the native gradient fields of the MRI scanner. The time required for position update can be as short as 5msec. The motion information is then processed and incorporated in a slice acquisition model for volume reconstruction.

Fig. 1.

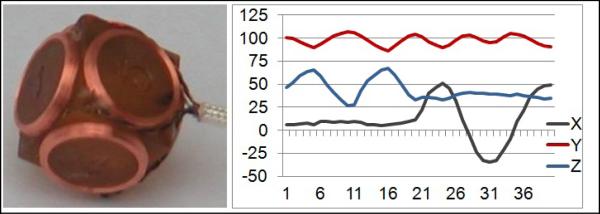
The magnetic field motion tracking sensor, and typical motion tracking results (translations in mm along 3 axes are shown), which give relative location of 40 slices in this scan.

B. Volume Reconstruction

A set of 2D thick slices are obtained by multiple orthogonal HASTE scans. The relative 3D location of each slice is computed through the sensor motion parameters at the time of slice acquisition. Our approach for reconstructing a volumetric image from these slices is based on a slice acquisition model [15]. The slice acquisition model describes how the acquired slices are obtained from the imaged object during the HASTE acquisition process:

$${\mathbf{y}}_k={\mathbf{W}}_k\mathbf{x}+{\mathbf{v}}_k,k=1,\dots ,n$$ (1)

where y_k is the vector of the voxels of the k^th 2D slice, x is a vector of the desired uniformly-sampled volumetric image voxels in the lexicographical order; v_k is a Gaussian noise vector, n is the number of slices obtained from N scans, and W_k = D_kB_kS_kM_k, where M_k is a matrix modelling the motion of the imaged subject, S_k is a matrix representing the slice selection profile, B_k is a blur matrix representing the point spread function of the MRI signal acquisition process, and D_k is a down-sampling matrix.

Volume reconstruction is mathematically formulated as the inverse problem of finding x in equation (1) given the acquired slices y_k. This inverse problem can be solved through maximum a posteriori (MAP) estimation based on the approach presented in [16]:

$$\widehat{\mathbf{x}}=\underset{\mathbf{x}}{ArgMin}\left[\sum _{k=1}^n{\Vert {\mathbf{W}}_k\mathbf{x}-{\mathbf{y}}_k\Vert }_2^2+\lambda {\Vert \mathbf{Cx}\Vert }_2^2\right]$$ (2)

Where ∥∥.∥∥ is the l₂ norm, C is a positive definite matrix, and λ is a weighting coefficient. The cost function in this formulation involves two terms, the first term is a summation of slice error vector norm over all slices, and the second term is obtained from a quadratic image prior model which penalizes the high frequency components in the estimated volumetric image. Equation (2) involves very large matrices and its pseudo-inverse solution is prohibitive. Instead, we utilize the numerically stable steepest descent approach to iteratively calculate the volumetric image. By substituting W_k with matrix image operators and differentiating, the following iterative formula is obtained

$${\widehat{\mathbf{x}}}^{n+1}={\widehat{\mathbf{x}}}^n+\alpha \left[\sum _{k=1}^N{\mathbf{M}}_k^{\mathbf{T}}{\mathbf{S}}_k^{\mathbf{T}}{\mathbf{B}}_k^{\mathbf{T}}{\mathbf{D}}_k^{\mathbf{T}}\left({\mathbf{y}}_k-{\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{S}}_k{\mathbf{M}}_k{\widehat{\mathbf{x}}}^n\right)-\lambda {\mathbf{C}}^{\mathbf{T}}\mathbf{C}{\widehat{\mathbf{x}}}^n\right]$$ (3)

The matrices C, D_k, B_k, S_k, and M_k and their transposes are exactly interpreted as corresponding image operators. C is the image derivatives operation. For simplicity the desired reconstructed image spacing is considered to be equal to the in-plane spacing thus D_k=I. B_k is defined as the convolution with a Gaussian kernel. S_k is defined for each slice based on the slice selection profile and the direction cosines matrix which defines the geometry of the slice acquisition. Finally, M_k is a matrix of 3D rigid transformation defined for each slice reflecting the relative location of the slices based on estimated motion parameters from the sensor.

Our reconstruction algorithm involves two stages: first, the motion parameters from the sensor are used to estimate the M_k matrix for an initial reconstruction using scattered data interpolation (SDI). Note that SDI is used as a fast non-model based technique to reconstruct a high-resolution volume from scattered data obtained from motion-corrected slices (see [15] for illustration). This reconstruction is then refined through model-based super-resolution reconstruction based on Equation (3). In the second stage, retrospective slice-to-volume registration is used to compensate the sensor motion estimation errors in M_k. The reconstructed volume is thus refined in the second stage through iterations of slice-to-volume registration and super-resolution reconstruction.

III. Results

A. Data Acquisition

HASTE scans for human subjects as well as pineapple and water phantoms were acquired on Siemens Trio 3-Tesla scanners. HASTE imaging was performed for the human subjects with TR=1500 ms, TE=83 ms, slice thickness of 4 mm, and in-plane resolution of 1 mm. One entire scan of 40 slices was about 60 seconds. Six scans (two in each slice select direction) were collected in all experiments. A half-slice shift was planned between the two scans with the same slice select direction, aiming at shifted sampling in the image space. HASTE imaging parameters for the phantoms were TR=254 ms, TE=83 ms, slice thickness of 4 mm, and in-plane resolution of 1.25 mm. High-resolution sagittal MPRAGE scans were also acquired in phantom experiments. A mechanical platform was used to generate phantom motion. The volunteer subjects were asked to move during some scans and stay still during some others for validation.

B. Moving Phantom Experiments

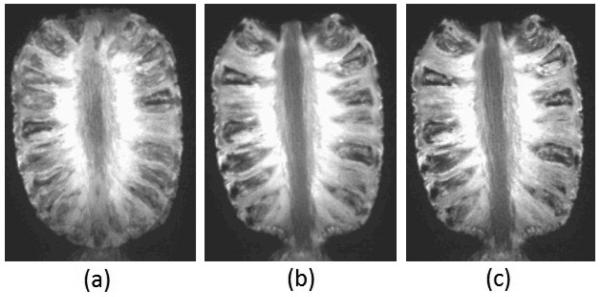
Figure 2 shows the results of a pineapple phantom experiment; (a) is an image obtained without motion correction and by averaging the acquired MPRAGE scans of the phantom in two positions; (b) shows the reconstructed image with our novel sensor based motion correction and volume reconstruction technique, and (c) shows a reference MPRAGE image of the phantom without motion. Same experiments were performed with HASTE scans.

Fig. 2.

Results of phantom experiments with through-plane motion between two positions: images obtained (a) by averaging two input scans without motion correction, (b) by motion correction and retrospective reconstruction as discussed in section II; and (c) reference image acquired without motion.

Quantitative evaluation was performed by computing performance metrics and sharpness measures. Performance metrics involved mean square error (MSE) of intensity values and peak signal to noise ratio (PSNR) computed between the reconstructed and reference images of the same sequences; and mutual information (MI) and normalized mutual information (NMI) computed as similarity between the reconstructed and reference images of different sequences (e.g. between HASTE and a reference MPRAGE image). Sharpness measures included the intensity variance measure (M1) and the energy of the image gradient (M2). The details of the computation and the meaning of these measures can be found in [15].

The average metrics and measures for the phantom experiments have been reported in Tables 1 and 2 for images obtained from three techniques: (1) averaging: simple averaging of the acquired scans without motion correction, (2) MC-SDI: motion-corrected reconstruction with sensor-based motion correction followed by scattered data interpolation (SDI), and (3) MC-MAP: reconstruction with motion correction and MAP estimation as illustrated in section 2. The bold numbers in the Tables show the best values in each comparison (in each column). These quantitative evaluation results along with visual inspection of all phantom experiments indicate that the developed technique in this study (MC-MAP) generates accurate and sharp volumetric images in the presence of motion and eliminates the motion-induced blurring artifacts that were apparent in the images obtained by averaging.

Table 1.

Performance metrics for phantom experiments computed as the difference and similarity of the reconstructed images to the reference images acquired without motion.

	MPRAGE		HASTE
metric	MSE	PSNR	MI	NMI
Averaging	145.16	20.50	0.517	1.11
MC-SDI	81.83	25.71	0.607	1.13
MC-MAP	58.83	28.24	0.618	1.14

Table 2.

Sharpness measures for phantom experiments.

	MPRAGE		HASTE
metric	M1	M2	M1	M2
Averaging	1.46×106	7.71×1011	24950	4.20×109
MC-SDI	1.52×106	5.07×1011	27340	4.88×109
MC-MAP	1.57×106	9.85×1011	30040	2.1×1010
Reference	1.60×106	1.49×1012	30457	2.2×1010

C. Volunteer Subject Experiments

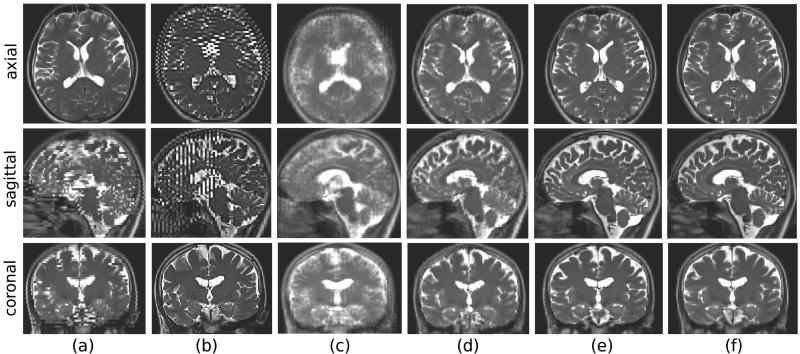
The averaging, MC-SDI, and MC-MAP techniques were applied to HASTE scans acquired for volunteer subjects. Each experiment was carried out one time with motion, and another time without motion for comparison and validation. Figure 3 shows a sample result of these experiments. For each image in this figure, three slice views (axial, coronal, and sagittal views) are shown. (a) and (b) show samples of acquired axial and coronal HASTE scans, respectively; (c) is the image obtained by averaging seven acquired HASTE scans in this experiment; (d) is the image obtained after sensor based motion correction and SDI reconstruction, and (e) is the image obtained by MC-MAP reconstruction. The image in (e) is obtained from MC-MAP applied to HASTE scans acquired without motion. This image was used as the reference for evaluation of the technique.

Fig.3.

Results of a volunteer subject experiment. Three slice views (axial, coronal, and sagittal) are shown for each image from top to bottom. (a) and (b) axial and coronal HASTE scans during motion; (c) volumetric image obtained by averaging without motion correction; (d) reconstructed volumetric image obtained after sensor-based motion correction; (e) reconstructed volume after sensor-based and registration-based motion correction and MC-MAP super-resolution volume reconstruction; (f) reference super-resolution volumetric image reconstructed from three orthogonal HASTE scans acquired when the subject did not move in the scanner. This image was used as the reference for quantitative evaluation.

It is observed in (a) and (b) that although the slice plane views in HASTE scans reflect the details of the anatomy in 2D, severe inter-slice motion artifacts appear in out-of-plane views, thus the acquired HASTE scans do not reflect coherent anatomic boundaries in 3D. These motion artifacts appear as blurring in the image obtained by averaging in (c). The image reconstructed using MC-MAP in (e) is a refined version of (d) using iterations of retrospective registration and reconstruction, is sharp, and reflects the details of the anatomy in all three planes. The quantitative results averaged for three experiments are shown in Table 3. The MC-MAP technique generated the best metrics for all experiments.

Table 3.

Average metrics for volunteer experiments.

	MSE	PSNR	Ml	M2
Averaging	86.49	26.13	161138	6.30×1010
MC-SDI	54.48	29.20	179826	8.72×1010
MC-MAP	53.14	29.50	189721	1.99×1011

IV. Conclusion

We have developed a motion-robust MRI technique that utilizes (1) multiple orthogonal fast slice acquisitions, (2) motion tracking parameters from a magnetic field sensor, and (3) an advanced model-based volume reconstruction technique to generate high-resolution volumetric images in the presence of motion. Quantitative and qualitative evaluation results obtained from phantom and volunteer subject experiments have shown the efficacy of this technique. The developed technique does not involve a complicated setup and is platform independent. The entire scan time is less than 6 minutes. This technique is particularly useful for T2-weighted imaging of newborns and children thus may help in reducing sedation rate.