Evaluation of methods for modeling transcription-factor sequence specificity

Abstract

Genomic analyses often involve scanning for potential transcription-factor (TF) binding sites using models of the sequence specificity of DNA binding proteins. Many approaches have been developed to model and learn a protein’s binding specificity, but these methods have not been systematically compared. Here we applied 26 such approaches to in vitro protein binding microarray data for 66 mouse TFs belonging to various families. For 9 TFs, we also scored the resulting motif models on in vivo data, and found that the best in vitro–derived motifs performed similarly to motifs derived from in vivo data. Our results indicate that simple models based on mononucleotide position weight matrices learned by the best methods perform similarly to more complex models for most TFs examined, but fall short in specific cases (<10%). In addition, the best-performing motifs typically have relatively low information content, consistent with widespread degeneracy in eukaryotic TF sequence preferences.

Accurate modeling of the sequence specificities of TFs is a central problem in understanding the function and evolution of genomes. Ideally, sequence specificity models should predict the relative affinity (or dissociation constant) for different individual sequences, and/or the probability of occupancy at any position in the genome. The major paradigm in modeling TF sequence specificity is the position weight matrix (PWM) model^1-3. PWMs represent the DNA sequence preference of a TF as an N by B matrix, where N is the length of the site bound by the TF, and B is the number of possible nucleotide bases (i.e. A, C, G or T). Each position provides a score for each nucleotide representing the relative preference for the given base. PWM models provide an intuitive representation of the sequence preferences of a TF, including the exact position it would bind the DNA, and involve relatively few parameters. However, recent studies suggest that shortcomings of PWMs, including their inability to model variable gaps, capture dependencies between the residues in the binding site or account for the fact that TFs can have more than one DNA-binding interface, can make them inaccurate^4-9. Alternative models have been developed that extend the PWM model by considering the contribution of combinations of nucleotides, e.g. dinucleotides or combinations of multiple motifs^{4, 6, 7, 10}. As another alternative, k-mer–based approaches^{7, 11} assign a score to every possible sequence of length k, and hence make no assumptions about position dependence, variable gap lengths or multiple binding motifs. To our knowledge, the relative efficacies of these approaches have not been systematically compared.

A major difficulty in studying TF-DNA binding specificity, and therefore in the evaluation of models for representing this specificity, has been scarcity of data. The process of training and testing models benefits from a large number of unbiased data points. In the case of TF DNA-binding models, the required data are the relative preference of a TF for a large number of individual sequences. Ideally, such data should be obtained in an in vitro setting, as many confounding factors can influence the binding of a transcription factor in vivo (e.g. chromatin state, TF concentration or interactions with cofactors). Methods for measuring in vitro binding specificity include (HT)-SELEX/SELEX-seq^12-15, HiTS-FLIP⁸, mechanically induced trapping of molecular interactions (MITOMI)^{9, 16}, cognate site identifier¹⁷, bacterial one-hybrid¹⁸ and protein binding microarrays (PBMs)¹⁹.

PBMs have enjoyed increasingly widespread use owing to the ease, accessibility and relatively high information content of the assay. Raw PBM data consists of a score (i.e. fluorescence signal intensity) representing the relative preference of a given TF to the sequence of each probe contained on the array. PBM data represents specificity (i.e. how strongly a given TF binds to a given sequence, relative to all other sequences), as opposed to binding affinity (i.e. how strongly a TF binds to a single sequence); as argued by Stormo and Zhao²⁰, specificity is the more important measure, because in vivo, the TF must be able to distinguish its functional sites from all accessible sequences in the genome. A typical universal PBM is designed using a de Bruijn sequence, such that all possible 10-mers, and 32 copies of every non-palindromic 8-mer are contained within ~40,000 60-base probe sequences (each containing either 35 or 36 unique bases) on each array, offering an unbiased survey of TF sequence specificities¹⁹. Constructing arrays with different de Bruijn sequences, each capturing the sequence specificities of the same TF to entirely different sets of sequences, provides a means to test the relative performance of various algorithms for modeling and predicting TF sequence specificities, because models can be learned from one array and tested on the other^{7, 19}. Here we present an evaluation of 26 different algorithms for modeling the DNA sequence specificity of a diversity of TFs, using two PBM array designs for each TF.

RESULTS

The DREAM5 challenge

The DREAM5 TF challenge^21-23 formed the original basis for the analyses presented here. The challenge used PBM data to test the ability of different algorithms to represent the sequence preferences of TFs (here, ‘algorithm’ refers to the combination of data pre-processing, TF sequence specificity model, training and scoring). Briefly, we generated PBM data measuring the DNA sequence preferences of 86 mouse TFs, taken from 15 diverse TF families (Supplementary Table 1). All TFs were assayed in duplicate on two arrays with independent de Bruijn sequences (denoted ‘ME’ and ‘HK’). In the DREAM5 challenge, the sequences of both arrays were made known, but only a subset of the PBM data was provided to participants, and the teams submitted predictions on the held-out array data. For 20 TFs, array intensity data was provided from both array types, in order for the participants to calibrate and test their algorithms. For 33 TFs, intensity data were provided only from the ME type of array; data for the remaining 33 TFs were only provided for HK type of array. Given the output of probe intensities of one PBM array type, the challenge consisted of predicting the probe intensities of the second array type.

The probe intensity predictions from each participant were then evaluated using five criteria (i.e. scores) that assess the ability of an algorithm to either predict probe sequence intensities or assign high ranks to preferred 8-mer sequences. These criteria, and a combined score that summarizes the performance of each algorithm, are described in Supplementary Note 1. Briefly, the k-mer-based method of Team_D¹¹ outperformed all other algorithms, with algorithms ranked two through five performing similarly to each other (Supplementary Table 2). Of note, the top five teams represent a wide range of sequence specificity models (Table 1), suggesting that the algorithm, its implementation and its scoring system might be of greater importance than the type of model employed.

Table 1.

Summary of evaluated algorithms.

Name and reference	Model type	Description of algorithm
Team_D (1)11	k-mers	Constructs a matrix indexing the presence of contiguous k-mers (size 4-8) on each probe. Estimates an affinity vector by applying a conjugate gradient method, and uses it to predict intensities11.
Team_F (2) / Dispom41	Markov model	Constructs a probabilistic classifier based on foreground and background Markov models. Weighted extension of the Dispom algorithm.
Team_E (3)	PWM + HMMs	Learns PWMs using MEME42, retrains by Expectation-Maximization using a Hidden Markov Model43, and combines it with a probe-specific bias using a linear model.
Team_G (4)	k-mers	Models probe affinities as a product of an occurrence matrix of motif sequences (contiguous or gapped 6-mers) and a vector of unknown motif affinities. Estimates motif affinities using a multiple linear model.
Team_J (5)44, 45	Dinucleotides	Learns binding energy linear models with nearest-neighbor dinucleotide contributions, and combines them with probe sequence-dependent bias under an information theory-based framework44, 45.
Team_I (6)	k-mers	Uses top 1000 and bottom 250 8-mers for specific binding, and nucleotide triplet background frequencies for non-specific binding. Performs linear regression between these features and the observed binding intensities using Lasso46.
Team_C (7)	PWM + k-mers + Random forests	Constructs blended predictions from random forests of contiguous k-mers (length 4 through 6) and RankMotif++27 PWMs.
Team_H (7)10	k-mers + dinucleotides	Trains support vector regression models to directly learn the mapping from probe sequences (using inexact matches to dinucleotide k-mers of length 10 to 15) to the measured binding intensity10.
Team_A (10) / Amadeus47	k-mers + PWM	Identifies and scores 20 de novo PWM models using Amadeus47. Combines the PWM with maximum probe sequence contiguous 6-mer AUC scores, and performs linear regression against the probe intensities.
Team_K (11)	k-mers	Identifies informative contiguous k-mers (length 1 to 8) using feature selection (allowing mismatches), learns their weights using regression against the probe intensities.
Team_B (13)	PWM	Uses top and bottom 1000 probes as positive and negative sets for discriminative motif discovery using eTFBS48. Uses PWM scores as features for constructing regression models.
BEEML-PBM24, 25	PWM or dinucleotides	Obtains maximum likelihood estimates of parameters to a biophysical PWM24 or dinucleotide25 model, including the TF’s chemical potential, non-specific binding affinity, and probe position-specific effects.
FeatureREDUCE	PWM, Dinucleotides and/or k-mers	Combines a biophysical free energy model (PWM or dinucleotide) with a contiguous k-mer background model (length 4 to 8) in a robust regression framework. Throughout, we use ‘FeatureREDUCE’ to denote the combined dinucleotide and k-mer model, FeatureREDUCE_PWM to denote the PWM-only model, and FeatureREDUCE_dinuc to denote the dinucleotide-only model.
MatrixREDUCE26	PWM	Performs a least-squares fit to a statistical-mechanical PWM model to discover the relative contributions to the free energy of binding for each nucleotide at each position26.
RankMotif++27	PWM	Learns PWMs by maximizing the likelihood of a set of binding preferences under a probabilistic model of how sequence binding affinity translates into binary binding preference observations27.
Seed-and-Wobble19	PWM	Uses the 8-mer with the highest E-score as a seed, and inspects all single-mismatch variants (and positions flanking the seed sequence) to identify the relative contribution of each base at each position to the binding specificity19.
8mer_max	k-mers	Calculates the median probe score of all contiguous 8-mers. Prediction is the maximum 8-mer score on each probe.
8mer_pos	k-mers	Similar to 8mer_sum, but takes into account probe position effect in a manner similar to BEEML-PBM.
8mer_sum	k-mers	Calculates the median probe score of all contiguous 8-mers. Prediction is the sum of all 8-mer scores on each probe.
PWM_align	PWM	Aligns all contiguous 8-mers with E-score > 0.45 to create a PWM.
PWM_align_E	PWM	Aligns all contiguous 8-mers with E-score > 0.45, weighting each sequence by its E-score, to create a PWM.

The type of sequence specificity model used by each algorithm is indicated, along with a brief description of the algorithm (more information about the algorithms can be found in Supplementary Note 9). The final rank in the original DREAM challenge is indicated in parenthesis after the algorithm’s name, where applicable.

The DREAM5 outcome, and feedback from participants and others, led us to revisit and investigate several aspects of the results. First, we wanted to revisit the evaluation criteria. Second, we wanted to account for the possibility that microarray data pre-processing might have an effect on the final performance of a model or algorithm, as it clearly did for Team D¹¹. Third, we wanted to incorporate published algorithms that were not represented in the challenge, including three biophysical energy-based algorithms, BEEML-PBM^{24, 25}, FeatureREDUCE (TRR and HJB, manuscript in preparation) and MatrixREDUCE²⁶, as well as two statistical algorithms, RankMotif++²⁷ and Seed-and-Wobble¹⁹. We also wanted to examine the impact of dinucleotide-based PWM models and ‘secondary motifs’, which can model proteins with multiple modes of binding DNA⁷. Here, we include 15 published and unpublished algorithms, in addition to 11 algorithms submitted as part of the original challenge (Table 1). Fourth, we wished to examine whether the results we obtained for in vitro data were supported by in vivo analyses and alternative in vitro assays.

Revised evaluation criteria

We considered two general issues in revisiting the evaluation criteria. The first is that, ideally, a representation of DNA sequence preference (e.g. a PWM) should output a number that reflects relative preference to a given sequence²⁰. Most of the algorithms we considered aim to do this. In such cases it is reasonable to score using Pearson correlation. We note, however, that other models are intended to discriminate bound from unbound sets of sequences, or to represent the best binding sequences. In addition, microarray data can be subject to noise and saturation effects. In such cases it is appropriate to ask whether highly bound sequences can be discriminated from unbound sequences, which can be measured by the area under the receiver operating characteristic (AUROC).

The second issue is whether scoring should be based on predicting the 35-mer probe intensities, or their transformations into 8-mer values (we refer to full probe sequences as 35-mers, since each 60 base probe sequence contains 35 unique bases). The original DREAM competition included both. There are arguments for and against both^{7, 19, 24} and our comparisons to independent data did not support either as being superior overall (Supplementary Note 2). In addition, the 8-mer values can be derived by different means; one previous study⁷ directly predicted values for the test 8-mers with PWMs, whereas another²⁴ first scored the test 35-mer scores and then converted these to 8-mer scores. We found that the latter approach²⁴ results in dramatically improved correlations to the measured test 8-mer Z-scores (Supplementary Note 2), suggesting that previous conclusions regarding secondary motifs, which were derived using the former approach⁷, should be revisited (see below). Using the latter procedure²⁴, the correlations obtained for 8-mers and for 35-mers on the same array scale with each other almost perfectly, whether the 35-mers are scored with PWMs or with 8-mers (Supplementary Note 2). The only significant difference we have observed between scoring 35-mers or 8-mers is that ‘secondary motifs’ appear to confer a slight advantage when scoring 8-mers, but not 35-mers (see below).

In the evaluations below, we use two criteria that are based on prediction of 35-mer intensities (which was the original DREAM5 challenge), but acknowledge that the data may be noisy and semi-quantitative: (i) Pearson correlation between predicted and actual probe intensities (in the linear domain), and (ii) the AUROC of the set of positive probes, where positive probes are defined as those with actual intensities greater than 4 standard deviations above the mean probe intensity for the given experiment (average of 350 probes per experiment, out of ~40,000 probes total) (Fig. 1). We calculate a normalized score in which the top performing algorithm for the given evaluation criterion receives a 1, and all other algorithms receive scores proportional to the top algorithm. The final score for an algorithm is the average of its two normalized scores. We also report the Pearson correlation between measured and predicted 8-mer scores, and the AUROC of positive 8-mers, where positive 8-mers are defined as those with associated E-scores > 0.45 in the actual experiment, following Berger et al.²⁸, although these are not used to gauge the efficacy of algorithms or models.

Figure 1.

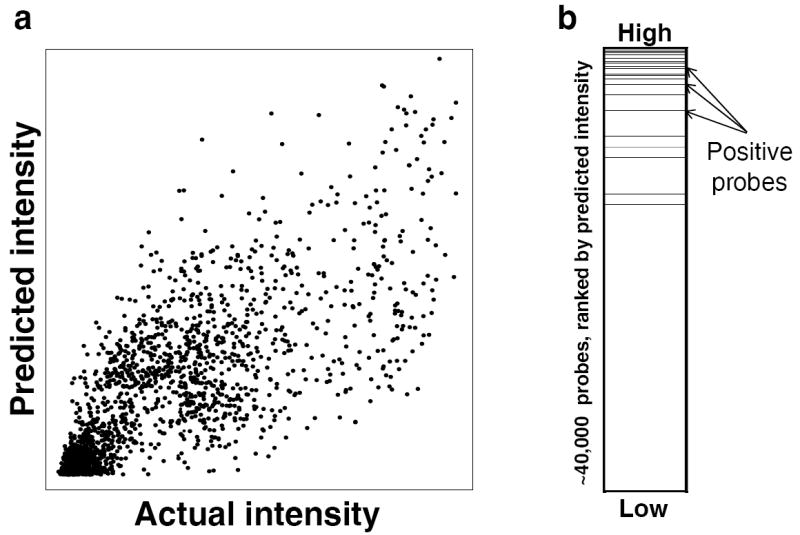
Evaluation criteria used in this study. For each TF, we scored an algorithm’s probe intensity predictions using two evaluation criteria, which are illustrated here for TF_16 (Prdm11), using the predictions of BEEML-PBM on the raw array intensity data. (a) Pearson correlation between predicted and actual probe intensities across all ~40,000 probes. (b) Area under the receiver operating characteristic curve (AUROC) of the set of positive probes. Positive probes (black dashed lines) were defined as all probes on the test array with intensities greater than four standard deviations above the mean probe intensity for the given array.

Results of new evaluations

In the revised evaluations, we used the 35-mer scores from the DREAM challenge directly for eight of the algorithms. For the top three algorithms in the initial DREAM challenge that take less than 24 CPU hours to run per experiment (originally ranked 1, 3 and 4), as well as the algorithms BEEML-PBM²⁴, FeatureREDUCE (manuscript in prep), RankMotif++²⁷ Seed-and-Wobble¹⁹ and five simple algorithms we implemented to provide a baseline (PWM_align, PWM_align_E, 8mer_max, 8mer_sum and 8mer_pos), we constructed a training dataset from the combination of pre-processing steps that resulted in the best final score for the given algorithm (Supplementary Note 3). Algorithms that were not subjected to the pre-processing analysis may perform better in practice. We scored all 26 algorithms across our panel of 66 mouse TFs (see Supplementary Table 3 for all evaluation scores of each algorithm on each TF).

The results of our revised evaluation scheme produce similar rankings to those of the DREAM challenge, with the algorithm of Team_D again performing best among the original challenge participants (Table 2). Final performance was robust to the choice of evaluation criteria (Supplementary Fig. 1). Overall, the highest scoring algorithm is FeatureREDUCE, which combines a dinucleotide model in a biophysical framework with a background k-mer model explicitly intended to capture PBM-specific biases. In general, k-mer and dinucleotide-based algorithms scored highest, although some PWM-based algorithms produced competitive results. Overall, it is notable that the specific algorithm is still more important than the type of sequence specificity model used by the algorithm. For example, BEEML-PBM, a published PWM-based algorithm, receives a better final score than three k-mer based algorithms. Furthermore, algorithms based on the same sequence specificity model type (e.g., PWM, dinucleotides or k-mers) do not necessarily produce similar probe intensity predictions (Supplementary Fig. 2).

Table 2.

Final evaluation results.

Rank	Algorithm	Model	Final score	Corr (probes)	AUROC (-0.5) (probes)	Corr (8-mers)	AUROC (-0.5) (8-mers)
1	FeatureREDUCE	Dinuc+ k-mer	0.997	0.693	0.449	0.786	0.497
2	Team_D	k-mer	0.984	0.691	0.438	0.820	0.496
3	Team_E	PWM	0.952	0.696	0.406	0.761	0.447
4	Team_G	k-mer	0.950	0.652	0.433	0.767	0.494
5	FeatureREDUCE_dinuc	Dinuc	0.924	0.624	0.428	0.694	0.490
6	BEEML-PBM_dinuc	Dinuc	0.919	0.623	0.424	0.738	0.488
7	Team_F*	Other	0.901	0.610	0.416	0.764	0.476
8	8mer_pos	k-mer	0.899	0.603	0.419	0.765	0.490
9	BEEML-PBM	PWM	0.898	0.607	0.415	0.722	0.479
10	8mer_sum	k-mer	0.896	0.598	0.419	0.766	0.490
11	Team_J*	Other	0.895	0.611	0.410	0.740	0.465
12	FeatureREDUCE_PWM	PWM	0.880	0.586	0.413	0.647	0.485
13	8mer_max	k-mer	0.846	0.541	0.411	0.688	0.494
14	Team_I*	Other	0.813	0.581	0.356	0.683	0.439
15	BEEML-PBM_sec	2 PWMs	0.812	0.539	0.382	0.671	0.477
16	Team_C*	Other	0.812	0.517	0.396	0.664	0.476
17	MatrixREDUCE	PWM	0.791	0.526	0.371	0.669	0.455
18	FeatureREDUCE_sec	2 PWMs	0.790	0.508	0.382	0.610	0.482
19	Team_A*	k-mer	0.789	0.533	0.365	0.671	0.414
20	Team_H*	Other	0.778	0.468	0.397	0.625	0.491
21	PWM_align	PWM	0.768	0.493	0.372	0.641	0.462
22	PWM_align_E	PWM	0.757	0.511	0.351	0.666	0.468
23	Team_K*	k-mer	0.702	0.461	0.333	0.561	0.430
24	Seed-and-Wobble	PWM	0.647	0.324	0.372	0.303	0.460
25	RankMotif++	PWM	0.582	0.275	0.346	0.408	0.460
26	Team_B*	PWM	0.509	0.266	0.286	0.354	0.393

Algorithms are ranked by their final score, which is a combination of the evaluation criteria indicated in the first two columns (Online Methods). Original DREAM challenge participants are indicated with their challenge ‘Team’ IDs. Algorithms indicated with an asterisk ‘*’ were not subjected to data pre-processing improvement attempts either because they did not finish in the top four of the original DREAM challenge, are not fully automated or take greater than one CPU week to run on a single experiment. The highest score obtained for each evaluation criterion is indicated in underlined italics. Corr, Pearson correlation; AUROC (-0.5), area under the receiver operating characteristic curve (after subtracting 0.5).

Algorithm performance varied substantially across the 66 TFs (Fig. 2a). The quality of the underlying experimental data appears to be the major factor in the overall ease of predicting probe intensities for a given TF, as opposed to inherent differences between TF families in the difficulty of modeling DNA sequence preferences (Fig. 2b and Supplementary Note 4). For example, TFs that were harder for most algorithms to model tended to have lower correlation between the 8-mer Z-scores of their training and test arrays, and fewer 8-mer E-scores > 0.45 on their training arrays.

Figure 2.

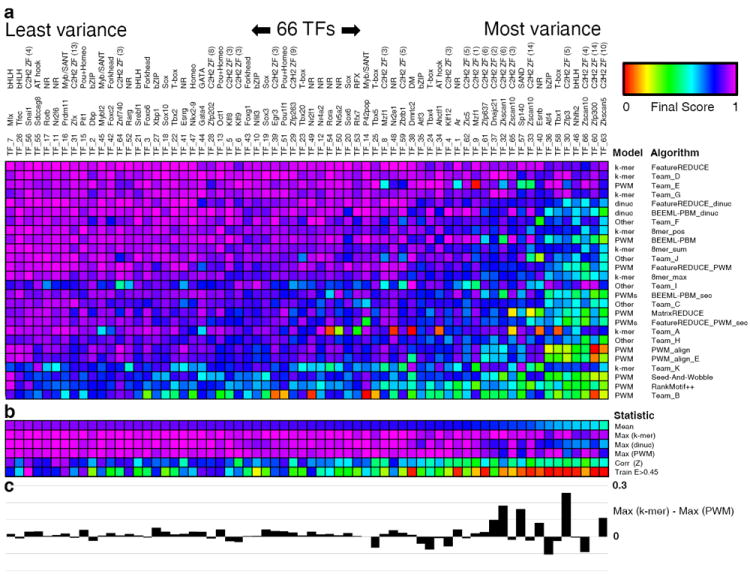
Comparison of algorithm performance by transcription factor. (a) Final score of each algorithm for each TF. TF name, ID and family are depicted across the columns, and sequence specificity model type and name are depicted across the rows. Color scale is indicated at the upper right. Algorithms are sorted in decreasing order of final performance across all TFs. TFs are sorted in decreasing order of mean final score across all algorithms. (b) Summary statistics for each TF across all algorithms: mean final score, maximum final score achieved by any k-mer, dinucleotide or PWM-based algorithm, Pearson correlation of 8-mer Z-scores between replicate arrays, and the number of 8-mers with E-scores > 0.45 on the training array (normalized by the maximum such value across all TFs). (c) Difference between the best score achieved by any k-mer based algorithm and the best score achieved by any PWM-based algorithm for each TF.

To further examine the relative performance of the k-mer, dinucleotide and PWM models, we compared the final scores produced by the single algorithm from each model category that performed best for each TF. On average, the best k-mer-based algorithm outperformed the best dinucleotide or PWM algorithm, but this is largely due to large differences in a handful of specific TFs (Fig. 2b, c and see below). Algorithms based on dinucleotides performed substantially worse on these harder to model TFs, suggesting that they might be overfitting to array-specific noise. The best PWM-based algorithm performs comparably to the best k-mer-based algorithm for the majority of TFs (Fig. 2c), with a median difference of only 0.014. PWM algorithms, in fact, performed slightly better than k-mer based algorithms for 18 TFs (Fig. 2c). However, of the five cases in which the final score for the best of one model type beats the best of the other type by greater than 0.10, all but one favor k-mer algorithms (Fig. 2c). The majority of TFs showing substantial improvement with the k-mer model contain C₂H₂ zinc finger arrays, which, depending on which C₂H₂ fingers are engaged, may have different binding modes; there is previous evidence for such phenomena both in vivo and in vitro^{7, 29}. However, some of these C₂H₂ zinc fingers present a challenge for all sequence specificity models, perhaps owing to the small number of sequences they preferentially bind (Fig. 2 and Supplementary Note 4).

Despite the fact that more complicated algorithms produce higher scores, the results of these analyses suggest that the PWM model can accurately capture the sequence preferences for most TFs. Nevertheless, we observed a wide range in PWM-based algorithm performance across the 66 TFs (Fig. 2a). The fact that the two highest-scoring PWM-based algorithms, Team_E and BEEML-PBM (Table 2), both model PBM-specific effects suggests that their high scores might not be solely due to superior PWMs. We performed a series of analyses aimed at isolating the predictive ability of the PWMs produced by all of the PWM-based algorithms. Those produced by BEEML-PBM were the most accurate of all of the algorithms; the high performance of Team_E is due to its extensive modeling of PBM background effects, and not due to the quality of its PWMs (Supplementary Note 5). We also found this to be the case for predicting in vivo TF binding (see below).

Analysis of dinucleotide matrices and secondary motifs

Numerous studies have called into question the accuracy of the assumption inherent to the PWM model that bases are independent, and instead propose the use of dinucleotide dependencies to model TF binding. To quantify the relative accuracies of the dinucleotide and PWM models, we compared the performance of two of the top algorithms, FeatureREDUCE and BEEML-PBM, both of which can be run using either type of model. Both performed better overall when using the dinucleotide model (Table 2), although the difference was not dramatic, and certain TFs benefit more than others (Supplementary Table 4; median improvement of 0.019 and 0.006, respectively). In general, an overall improvement is not surprising because the dinucleotide model has more parameters. Importantly, we note that the degree of improvement is poorly correlated between FeatureREDUCE and BEEML-PBM, and negatively correlated with how well each performs using only a mononucleotide PWM (Supplementary Fig. 3), suggesting that much of the improvement may be due to poorly fit mononucleotide PWMs. Of the six cases in which a dinucleotide model results in an improvement of greater than 5% in the final score for both FeatureREDUCE and BEEML-PBM, five are among the TFs for which it appears to be difficult to learn a PWM (Fig. 2). These observations suggest that there are relatively few cases in which there are bona fide dinucleotide interactions that have a major impact on model performance.

Secondary motifs would represent alternative binding modes for a TF that are also not possible to capture with a single PWM⁷. The previously claimed widespread prevalence of secondary motifs⁷ was recently contested by the finding that a single BEEML-PBM PWM is more predictive than two PWMs derived by Seed-and-Wobble²⁴, using the same data set used to support the original claim⁷. To more directly examine the importance of secondary motifs, we identified secondary motifs in both the PBM data of this study and that of the previous study⁷. We discovered secondary motifs using the residuals of the primary motif probe signal intensity predictions for both BEEML-PBM and FeatureREDUCE, used regression on the training data to assign weights to the two motifs and evaluated their impact on the overall performance of each algorithm (Online Methods). Overall, the performance of both BEEML-PBM and FeatureREDUCE was in fact slightly weakened using this scheme (Table 2).

Because the decreased performance might be due to probe-level noise drowning out the comparatively weaker secondary motif signal, we evaluated the performance of the secondary motifs using 8-mer scores, using the newer 8-mer scoring procedure²⁴ (Online Methods). Under this scoring scheme, secondary motifs provided a slight increase in overall performance (2–8% improvement in average correlation) (Supplementary Table 5). However, examination of secondary motif performance for each TF revealed that secondary motifs substantially increase performance only in specific cases (Supplementary Table 6). Moreover, as in the case of dinucleotide-based models, the degree of improvement is poorly correlated between FeatureREDUCE and BEEML-PBM, and again correlates negatively with how well each algorithm scores using only a mononucleotide PWM (Supplementary Fig. 3). Manual inspection of these examples revealed that improvement can typically be attributed to either the identification of a minor variation on the primary motif, a ‘second chance’ after producing an inaccurate motif on the first attempt, or by the identification of the second half-site for a TF that can bind DNA as a homodimer (Supplementary Note 6). We did identify several instances of what appear to be alternative binding modes, including three examples capturing the classic TAATA and ATGCWWW sequences of Pou+Homeodomain TFs, and extensions of primary motifs (e.g. extending the consensus sequence of Nr5a2 from AAGGTCA to TCAAGGTCA), indicating that our methodology can detect bona fide cases of secondary motifs (Supplementary Note 6). Nonetheless, it appears as if the major benefit of secondary motifs is to make up for shortcomings in the initial motif-finding process.

In vitro–derived PWMs accurately reflect in vivo binding

We next asked whether conclusions reached using in vitro data also apply to TF binding in vivo. The sequence specificity of a TF is only one of several factors that determine where it binds in vivo (others include cofactors and DNA accessibility); nonetheless, motifs consistent with those obtained in vitro can often be derived directly from in vivo data^{7, 30, 31}, indicating that the intrinsic sequence specificity of TFs is a major factor in controlling its DNA binding in vivo. We obtained publicly available ChIP-seq data for five of the mouse TFs whose DNA sequence preferences were measured using PBMs in this study, and ChIP-exo data from four yeast TFs whose preferences have been measured using PBMs in other studies. We then learned PWMs from the PBM data using each algorithm, and gauged their ability to accurately distinguish ChIP-seq and ChIP-exo bound sequences from control sequences. We also learned PWMs from the same in vivo data by running ChIPMunk³² and MEME-Chip³³, methods that have been specifically tailored for motif discovery from ChIP-seq data, in a cross validation setting. We evaluated each algorithm with AUROCs, which here measure the ability of a given algorithm to assign higher scores to positive (bound) sequences relative to control (random) sequences (Online Methods).

All PWM-based algorithms could discriminate ChIP-seq and ChIP-exo peaks from control sequences to some degree, as evidenced by the fact that the average AUROC scores of all algorithms exceed the random expectation of 0.5 (Fig. 3). Conversely, the algorithms that performed best in our in vitro evaluations (FeatureREDUCE and Team_D, which both incorporate k-mer sequence specificity models) perform poorly (Team_D) or substantially worse (FeatureREDUCE) in nearly all cases analyzed (as does the simple 8mer_sum algorithm, see Fig. 3). Likewise, the dinucleotide versions of BEEML-PBM and FeatureREDUCE do not improve upon their PWM-based counterparts. The performance of the k-mer and dinucleotide-based in vitro-learned models on in vivo data could be due to a combination of modeling probe-specific effects such as GC content, and complications arising from biases in genomic nucleotide content relative to PBM probe sequences. Indeed, the 8mer_sum_high algorithm, which only incorporates 8-mers with Z-scores higher than 3 (a cutoff that likely excludes PBM-specific background noise), performs substantially better than the 8mer_sum algorithm, which incorporates scores across the entire range of k-mer values (Fig. 3).

Figure 3.

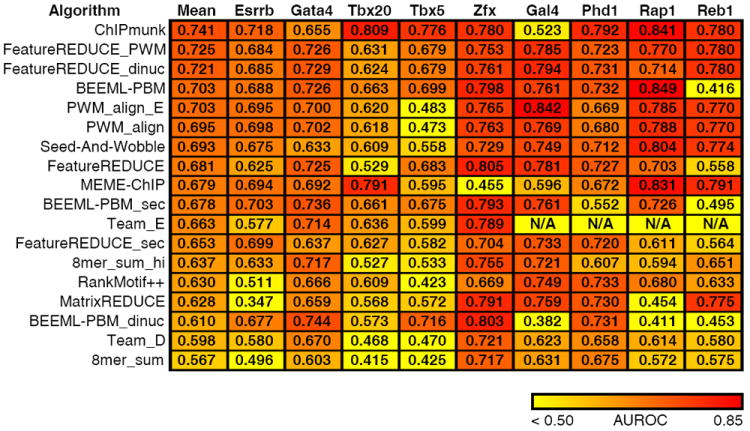
Comparison of algorithm performance on in vivo data. For each algorithm, we learned a model (PMW, k-mer or dinucleotide) using PBM data, and gauged its ability to discriminate real from random ChIP peaks using the AUROC (Online Methods). Data for the first five TFs were taken from mouse ChIP-seq data. The final four are from yeast ChIP-exo data. The color scale is indicated at the bottom. Team_E was not run on the ChIP-exo data, because it requires initialization parameters specific to the individual TF. FeatureREDUCE was run using models of length 8, instead of length 10, owing to the superior performance of this length model on in vivo data (T.R. Riley and H.J. Bussemaker, manuscript in preparation).

Overall, PWMs produced by the FeatureREDUCE_PWM algorithm perform best on in vivo data (Fig. 3). Notably, FeatureREDUCE_PWM performs similarly to ChIPMunk, and out-performs the MEME-Chip algorithm, despite the fact that the latter algorithms learn their PWMs from the ChIP-seq data, and should thus incorporate features unique to in vivo data, such as nucleotide bias. All of our conclusions were robust to a variety of positive and negative sequence settings (Supplementary Table 7). Thus, at least for the nine TFs we examined here, in vitro–derived PWMs are in general better than in vitro–derived k-mer and dinucleotide models, and similar to in vivo-derived PWMs, in terms of predicting bound versus unbound ChIP-seq and ChIP-exo sequences.

Accurate prediction of data from alternative in vitro assays

Finally, we examined how well PBM-derived motifs, with or without dinucleotides, secondary motifs or k-mers, could predict data for 24 TFs that have been assayed using the MITOMI^{9, 16} or HiTS-FLIP technologies⁸, all of which also have PBM data available from other studies^{7, 31, 34}. We trained the best-performing FeatureREDUCE algorithm on the PBM data in each of its possible settings: PWM only, dinucleotides, dinucleotides+k-mers and two PWMs (secondary motifs). We then compared the ability of each model to predict the values produced by the other technology.

The inclusion of features beyond mononucleotide PWMs had limited impact for the majority of these 24 TFs (Supplementary Note 7). We note, however, that we were able to detect specific examples where more complicated models provided an increase in performance across platforms (Supplementary Note 7). For example, k-mers and secondary motifs both improve cross-platform performance for Cbf1. This finding confirms that PBMs are capable of detecting cases where more complicated binding modes exist, and that these models are capable of improving predictive performance on other data sources. Taken together, these results are consistent with our findings that PWMs work well for most TFs, although certain TFs require more complicated models.

DISCUSSION

This study has several major conclusions that have broad implications for the representation of sequence specificity of DNA-binding proteins. We note that the exact conclusions reached depend on both the TFs used for evaluation and the evaluation criteria, a fact that likely accounts for the ongoing controversy in this area. However, our general conclusions are robust to changes in the PBM scoring procedure. In addition, our conclusion that well-implemented PWMs can perform as effectively as more complicated models in most cases is supported by cross-technology analysis of in vitro data and by analysis of in vivo data.

Our first major conclusion is that, when testing on PBM data, k-mer based models score best overall. Other approaches can perform nearly as well, however, and details of implementation, such as parameter estimation techniques, can be as important to the performance of an algorithm as the underlying model. Indeed, the algorithms that produce the most predictive PWMs, FeatureREDUCE_PWM and BEEML-PBM, which both learn PWMs in an energy-based framework (Supplementary Note 8), perform similarly to more complicated models for the majority of TFs, supporting the contention that imperfections in motif derivation (and scoring) underlie most of the apparent superiority of k-mer scoring that we previously reported^{7, 24}. PWMs consistently fared poorly in ~10% of the TFs, relative to k-mer-based sequence specificity models; however, many of these cases are characterized by having few high-scoring 8-mers (Fig. 2b and Supplementary Note 4). Thus, the scarcity of the data itself may limit the ability of algorithms to learn a PWM. Modification of the algorithms may help improve these cases.

The fact that incorporation of dinucleotide interactions improves the performance of both BEEML-PBM and FeatureREDUCE, but for different sets of TFs, suggests that the need for these extensions to mononucleotide PWM is driven more by the algorithm than by a property of the TF. Dinucleotide interactions clearly do exist²⁵ and were highlighted in previous analyses using MITOMI⁹, HiTS-FLIP⁸ and PBM¹⁹ data. However, these studies did not specifically ask how much of the overall variation in the data (e.g. using Pearson correlation) is accounted for by mononucleotide versus dinucleotide PWMs. We also note that more complex models can be more prone to learning platform-specific noise. At present it is not clear what the best approach is for different platforms; resolving the source and relative contribution of complexities in DNA-binding data would benefit from analysis of the same TFs on multiple high-resolution platforms.

One striking outcome of our study is that the appearance and information content of a motif has little bearing on its accuracy: the motifs produced by BEEML-PBM and FeatureREDUCE_PWM—two of the highest-scoring PWM algorithms—are, in general, those with the lowest information content (Box 1 and Supplementary Fig. 4). Conversely, PWMs produced by Seed-and-Wobble and PWM_align appear to be the strongest (i.e. they are wider and have larger letters in the traditional ‘information content’ sequence logos), but they score substantially lower than those of BEEML-PBM and FeatureREDUCE_PWM, on both PBM and ChIP-seq data. We conclude from this analysis that information content has little to do with the accuracy and utility of a motif, underscoring the fact that degeneracy is common among eukaryotic TFs sequence specificities, and that most TFs will bind to many variations of their ‘consensus sequence’, albeit at lower affinity. Indeed, previous studies have demonstrated the importance of low affinity binding sites in vivo^35-38. PWMs that allow for a greater amount of degeneracy (and hence have lower information content) are able to better capture the full range of lower affinity sites.

Box 1. Appearance and information content of a motif may not reflect accuracy.

Sequence logos^{39, 40} provide a simple, intuitive means for conveying information about a TF’s binding preferences. However, several aspects of their interpretation can be misleading. To illustrate, logos produced by the eight PWM-based algorithms evaluated here are depicted for TF_6, the C₂H₂ zinc finger TF Klf9 (Fig. 4). At a glance, the PWMs produced by Seed-and-Wobble and the PWM_align algorithms might be interpreted as being superior to the others, given their high information content. However, based on our evaluations, these PWMs are in fact too stringent, and place too much emphasis on the consensus sequence of this TF (compare the final scores of each algorithm). Rather, the lower information motif produced by BEEML-PBM is a better predictor of Klf9’s sequence preferences. In general, this observation holds for almost all TFs analyzed here—the Seed-and-Wobble and the PWM_align algorithms tend to produce PWMs that are ‘too stringent’ and too long, and energy-based algorithms such as BEEML-PBM produce motifs that represent the correct degree of degeneracy and length (see Supplementary Fig. 4 for logos and Fig. 2 for evaluations).

Figure 4.

Characteristics of Klf9 motifs produced by the eight PWM-based algorithms evaluated in this study. The algorithms are ranked top to bottom in order of the overall score of their PWM for this TF in our evaluation scheme. Two popular visualization methods of the PWMs produced by each algorithm are depicted: on the left are traditional sequence logos^{39, 40}, which display the information content of each nucleotide at each position; the total information content of the PWM is given to the left of this logo. On the right are frequency logos, in which the height of each nucleotide corresponds to its frequency of occurrence at the given position⁴⁰.

Similarly, different interpretations might be made about a TF’s sequence preferences based on which visualization method is used to depict a PWM. For example, the importance of the initial T nucleotide in the TAACGG consensus sequence in the motifs of BEEML-PBM might be considered negligible upon viewing of the information-content-based logo, whereas this nucleotide would likely be considered highly important based on the frequency plot. Indeed, the information specified at this position does play a large role in the overall effectiveness of the motif. When ignoring the frequencies specified at this position (i.e., setting all four nucleotide frequencies to 0.25), the correlation between BEEML-PBM’s predicted and actual probe signal intensities drops from 0.58 to 0.38. Furthermore, the sequence logos for BEEML-PBM, MatrixREDUCE, FeatureREDUCE and Team_E appear nearly indistinguishable based on the sequence logos, despite their drastically differing final evaluation scores. In summary, we find that the appearance of sequence logos has little bearing on their predictive accuracy.

The finding that different algorithms excel (and fail) for different TFs suggests that an algorithm incorporating all of their advantages will likely outperform any individual one. To aid in the continued improvement of algorithms for the modeling of TF binding specificities, we have created a web server that allows users to upload their own probe intensity predictions, and compare them to those of the algorithms evaluated here (http://www.ebi.ac.uk/saezrodriguez-srv/d5c2/cgi-bin/TF_web.pl). We anticipate that the availability of this resource will help encourage future improvements to algorithms for the modeling and predicting of TF binding specificities.

Online methods

Protein binding microarray experiments

Details of the design and use of PBMs has been described elsewhere^{19, 28, 49, 50}. Here, we used two different universal PBM array designs, designated ‘ME’ and ‘HK’, after the initials of their designers. Information about individual plasmids is available in Supplementary Table 8. We identified the DNA Binding Domain (DBD) of each TF by searching for Pfam domains⁵¹ using the HMMER tool⁵². DBD sequences along with 50 amino acid residues on either side of the DBD in the native protein were cloned as SacI–BamHI fragments into pTH5325, a modified T7-driven GST expression vector. Briefly, we used 150 ng of plasmid DNA in a 15 μl in vitro transcription/ translation reaction using a PURExpress In Vitro Protein Synthesis Kit (New England BioLabs) supplemented with RNase inhibitor and 50 μM zinc acetate. After a 2-h incubation at 37°C, 12.5 ml of the mix was added to 137.5 ml of protein-binding solution for a final mix of PBS/2% skim milk/0.2 mg per ml BSA/50 μM zinc acetate/0.1% Tween-20. This mixture was added to an array previously blocked with PBS/2% skim milk and washed once with PBS/0.1% Tween-20 and once with PBS/0.01% Triton-X 100. After a 1-h incubation at room temperature, the array was washed once with PBS/0.5% Tween-20/50 mM zinc acetate and once with PBS/0.01% Triton-X 100/50 mM zinc acetate. Cy5-labeled anti-GST antibody was added, diluted in PBS/2% skim milk/50 mM zinc acetate. After a 1-h incubation at room temperature, the array was washed three times with PBS/0.05% Tween-20/50 mM zinc acetate and once with PBS/50 mMzinc acetate. The array was then imaged using an Agilent microarray scanner at 2 mM resolution. Images were scanned at two power settings: 100% photomultiplier tube (PMT) voltage (high), and 10% PMT (low). The two resulting grid images were then manually examined, and the scan with the fewest number of saturated spots was used. Image spot intensities were quantified using ImaGene software (BioDiscovery). PBM data are available at NCBI GEO under accession GSE42864.

Prediction of array intensities

We evaluated a panel of 26 algorithms, based on their ability to accurately predict array intensities (see Table 1 for descriptions). Parameters used for the published and novel algorithms, and full descriptions of the algorithms submitted as part of the DREAM challenge can be found in Supplementary Note 9.

Evaluation criteria

We evaluated the probe intensity predictions produced by each algorithm for each TF using two evaluation criteria (see Figure 1 for illustrations, and below for descriptions). Before performing our evaluations, we removed all spots manually flagged as bad or suspect from the set of test probe intensities used in the evaluations. Each of the 66 experiments was scored individually using each criterion. The final score for both criteria was calculated as the average across all 66 experiments. To assign a final score to each algorithm, the score distributions of both of the criteria were first converted to relative scores, such that the best performing algorithm for the given criterion received a score of 1, and the scores of all other algorithms were relative to this best score (e.g. 0.90 as good as the top score, 0.80 as good, etc). The final score for each algorithm was then calculated as the average of its two relative scores, and can hence be interpreted as how well the algorithm performed relative to the best algorithm, on average. A similar calculation was performed in order to achieve the final scores of the individual TFs depicted in Figure 2. In this case, the calculations were carried out as described above, but individually for each of the 66 experiments (i.e. skipping the step of averaging across all 66 experiments).

Pearson correlation of probe intensities

We measured the correlation between the predicted probe intensities p and the actual intensities a using the (centered) Pearson correlation, r:

$$r(p,a)=\frac{\sum _{i=1}^N\left(p_i-\overline{p}\right)\left(a_i-\overline{a}\right)}{\sum _{i=1}^N{\left(p_i-\overline{p}\right)}^2\sum _{i=1}^N{\left(a_i-\overline{a}\right)}^2,}$$

where N is the total number of probe sequences on the array, p̄indicates the mean probe intensity across all predicted probe intensities, and ā indicates the mean across all actual probe intensities. We chose not to use the Spearman correlation because its rank transformation results in a loss of resolution in the high probe intensity range, placing greater emphasis on the (majority of) unbound, low intensity probes.

AUROC of probe intensity predictions

As a second measure of an algorithm’s accuracy, we quantified the ability of the given algorithm to assign high ranks to bright probes. We defined bright probes as those whose intensities were 4 standard deviations above the mean in the actual experiment, as in Chen et al. 2007²⁷. This results in an average of 350 bright probes per experiment, with an enforced minimum of 50, and a maximum of 1300. For each algorithm’s predictions for each TF, we ranked the ~40,000 probes based on their predicted intensities and calculated the AUROC of the actual bright probes. We subtracted 0.50 from the final AUROC score, so that a value of 0 corresponds to random expectation.

Identification and evaluation of secondary motifs

We identified primary and secondary PWMs for each TF in this paper and the TFs from Badis et al. 2009⁷ using two of the top algorithms (FeatureREDUCE and BEEML-PBM), and used a combination of both PWMs to predict probe intensities using the following procedure:

1. Run the algorithm to learn a single PFM, PFM₁, on the training array data.

2. Use PFM₁ to predict the probe intensities of the training array (intensities₁).

3. Regress the values of intensities₁ against the actual training array intensities.

4. Calculate the residuals by subtracting the regressed intensities from the actual training array intensities. Set any resulting negative values to 0.

5. Run the algorithm to learn a single PFM, PFM₂, on the residuals.

6. Use PFM₂ to predict the probe sequences of the training array (intensities₂).

7. Regress the two sets of probe scores (intensities₁ and intensities₂) against the training probe intensities to learn the weights of the two PFMs.

8. Use PFM₁ to predict the probe intensities of the test array.

9. Use PFM₂ to predict the probe intensities of the test array.

10. Combine the two sets of predicted probe intensities using the regression coefficients learned on the training array in step 7.

We found that the resulting secondary motif probe intensity predictions decreased performance for both algorithms in our evaluation scheme (Table 2). We therefore tried an alternative scheme (similar to that of Zhao and Stormo²⁴) where we converted the training intensities and probe intensity predictions of PFM₁ and PFM₂ to 8-mers (using the median probe intensity), and then learned the weights of the two PWMs by performing regression on these 8-mer values. The resulting weights were then used to combine the predicted 8-mer scores of PWM₁ and PWM₂ on the test data. Using this strategy, we observed a minor increase in overall performance for both algorithms on both datasets (Supplementary Table 6).

Comparison of algorithm performance on in vivo data

We gauged the ability of each algorithm to predict in vivo TF binding by comparing the ability of their PWMs to accurately predict ChIP-seq and ChIP-exo binding data. We searched for publicly available ChIP-seq data measuring the in vivo binding of any of the 66 mouse TFs evaluated here using a variety of sources, including the hmCHIP database⁵³, ArrayExpress⁵⁴, and the NCBI Gene Expression Omnibus⁵⁵. Some data was unusable because scores were not assigned to individual peak calls. In total, we obtained data for five TFs: Esrrb (hmCHIP accession SRP000217), Zfx (hmCHIP accession SRP000217), Tbx20 (GEO accession GSM734426), Tbx5 (GEO accession GSM558908), and Gata4 (GEO accession GSM558904). We also obtained four yeast ChIP-exo experiments from Rhee and Pugh 2011²⁹.

For each in vivo dataset, we defined a set of positive (bound) sequences and negative (control) sequences. Positive sequences were defined for ChIP-seq data as the 500 highest confidence peaks, using only the middle 100 bases of each peak (similar results were obtained when using the middle 50 bases, see Supplementary Table 7). Full-length sequence reads were used for ChIP-exo data. Random sequences were defined in one of three ways: 1) 500 randomly chosen genomic regions of the same length as the positive sequences, excluding all repeat sequences using RepeatMasker; 2) 500 sequences of length 100 (or 50) randomly chosen from promoter sequences, where promoters were defined as the 5000 base upstream regions upstream of the transcription start site of RefSeq genes, excluding all sequences flagged by RepeatMasker (obtained from the UCSC Genome Browser⁵⁶); 3) 500 randomly shuffled positive sequences, where dinucleotide frequencies were maintained.

We assessed the PWMs produced by each algorithm by scoring the positive and negative sequences, and calculating the AUROC of the sequence scores using the positive and negative probe labels. Positive and negative ChIP sequences were scored using the energy scoring framework of BEEML-PBM (setting mu to 0, and ignoring strand-specific biases). The final score for each algorithm on each TF was calculated as the mean AUROC across the three negative peaks sets. We also scored the probe sequences using the k-mer-based algorithms of Team_D, 8mer_sum, and FeatureREDUCE, and the dinucleotide algorithms of BEEML-PBM_dinuc and FeatureREDUCE_dinuc. We examined the performance of BEEML-PBM and FeatureREDUCE secondary motifs on the in vivo data using the PWMs and PWM weights learned from the in vitro data, as described above. In order to compare the in vitro generated motifs to in vivo-derived ones, we also used PWMs derived by ChIPMunk³² and MEME-Chip³³ when run on the same in vivo data in a cross validation setting. For these analyses, half of the positive probes were randomly chosen for training, and the other half were used for testing. This procedure was applied 10 times, and the final numbers reported are the average evaluation scores across all 10 iterations.

Data availability

PBM data are available at NCBI GEO under accession GSE42864, and on the project website (http://hugheslab.ccbr.utoronto.ca/supplementary-data/DREAM5/). Source code from the top-performing algorithms and the best-performing PWMs for each TF are available as Supplementary Files on the Nature Biotech website, and on the project website.

DREAM5 CONSORTIUM

Phaedra Agius¹, Aaron Arvey¹, Philipp Bucher^2,3, Curtis G. Callan Jr.^4,5, Cheng Wei Chang⁶, Chien-Yu Chen⁷, Yong-Syuan Chen⁷, Yu-Wei Chu^7,8, Jan Grau⁹, Ivo Grosse⁹, Vidhya Jagannathan^2,10, Jens Keilwagen¹¹, Szymon M. Kiełbasa¹², Justin B. Kinney¹³, Holger Klein¹⁴, Miron B. Kursa¹⁵, Harri Lähdesmäki^16,17, Kirsti Laurila¹⁸, Chengwei Lei¹⁹, Christina Leslie¹, Chaim Linhart²⁰, Anand Murugan⁴, Alena Myšičková¹², William Stafford Noble²¹, Matti Nykter¹⁸, Yaron Orenstein²⁰, Stefan Posch⁹, Jianhua Ruan¹⁹, Witold R. Rudnicki¹⁵, Christoph D. Schmid^2,22,23, Ron Shamir²⁰, Wing-Kin Sung^24,6, Martin Vingron¹², Zhizhuo Zhang²⁴

¹ Computational Biology Program, Sloan-Kettering Institute, Memorial Sloan-Kettering Cancer Center, New York, NY, USA

² Swiss Institute of Bioinformatics, Lausanne, Switzerland

³ EPFL (École Polytechnique Fédérale de Lausanne) SV ISREC (The Swiss Institute for Experimental Cancer Research) GR-BUCHER, Lausanne, Switzerland

⁴ Department of Physics, Princeton University, Princeton, NJ, USA

⁵ Lewis-Sigler Institute for Integrative Genomics, Princeton University, Princeton, NJ, USA

⁶ Genome Institute of Singapore, Singapore

⁷ Department of Bio-Industrial Mechatronics Engineering, National Taiwan University, Taipei, Taiwan

⁸ Graduate Institute of Communication Engineering, National Taiwan University, Taipei, Taiwan.

⁹ Institute of Computer Science, Martin Luther University, Halle-Wittenberg, Germany

¹⁰ Institute for Genetics, University of Bern, Bern, Switzerland

¹¹ Leibniz Institute of Plant Genetics and Crop Plant Research, Gatersleben, Germany

¹² Max Planck Institute for Molecular Genetics, Berlin, Germany

¹³ Simons Center for Quantitative Biology, Cold Spring Harbor Laboratory, Cold Spring Harbor, NY, USA

¹⁴ MicroDiscovery GmbH, Berlin, Germany

¹⁵ Interdisciplinary Centre for Mathematical and Computational Modelling, University of Warsaw, Warsaw, Poland

¹⁶ Department of Information and Computer Science, Aalto University School of Science and Technology, Aalto, Finland

¹⁷ Turku Centre for Biotechnology, Turku University, Turku, Finland

¹⁸ Department of Signal Processing, Tampere University of Technology, Tampere, Finland

¹⁹ Department of Computer Science, University of Texas at San Antonio, San Antonio, TX, USA

²⁰ Blavatnik School of Computer Science, Tel Aviv University, Tel Aviv, Israel.

²¹ Department of Genome Sciences, University of Washington, Seattle, WA, USA

²² Swiss Tropical and Public Health Institute (Swiss TPH), Basel, Switzerland

²³ University of Basel, Basel, Switzerland

²⁴ School of Computing, National University of Singapore, Singapore