Cellular modeling of cancer invasion: Integration of in silico and in vitro approaches

Abstract

Cancer invasion is one of the hallmarks of cancer and a prerequisite for cancer metastasis. However, the invasive process is very complex, depending on multiple correlated intrinsic and environmental factors, and thus is difficult to study experimentally in a fully controlled way. Therefore, there is an increased demand for interdisciplinary integrated approaches combining laboratory experiments with multiscale in silico modeling. In this review, we will summarize current computational techniques applicable to model cancer invasion in silico, with a special focus on a class of individual-cell-based models developed in our laboratories. We also discuss their integration with traditional and novel in vitro experimentation, including new invasion assays whose design was inspired by computational modeling.

Cancer invasion is one of the hallmarks of cancer (Hanahan and Weinberg, 2000) and a prerequisite for cancer metastasis, so it is a critical step in tumor progression. However, many aspects of this invasive process and certain features of the invading cells are still not fully understood. How is tumor invasion actually initiated? Is this an individual or collective enterprise? What kind of genetic/epigenetic and/or phenotypic changes are required of the cell to become invasive? Is the tumor microenvironment (mE) merely a barrier that need to be crossed or an active player in the invasion process?

Solid tumors are generally considered as invasive once they start penetrating the surrounding extracellular matrix (ECM) and the multiple layers of mesenchyme. Typically, we can recognize two forms of tumor cell invasion into the surrounding stromal tissue. Tumor cells can either outgrow the normal tissue and stromal cell layers expanding as a bulk mass of cells, or they can intermingle with stromal cells forming migrating cell cohorts. The former case is similar to the growth of subcutaneously implanted tumors that form compact spherical multicellular clusters embedded in soft tissue. The latter case is often characterized by a finger-like morphology (similar in shape to a “crab” from which the word “cancer” was derived) and has been correlated with harsher mEs to which cells with only certain phenotypes can adjust and progress. However, tumor invasiveness cannot be solely attributed to tumor cell growth ability or migratory potential. Computational models developed in our laboratories (Anderson, 2005; Anderson et al., 2009; Quaranta et al., 2008; Rejniak, 2005) indicated that cancer invasion is an emerging property of collective cell response to environmental cues. Similarly, our experimental data acquired by a novel in vitro invasion assay showed that development of irregular margins in a cancer tissue depends on both the microenvironmental conditions and cellular heterogeneity within the growing cell population (Kam et al., 2009). It has also been shown experimentally by others that invasiveness is context-dependent, i.e., the invasive capabilities of certain cell lines grown in one environment can be completely inverted when these cells are exposed to different environmental conditions (Kenny and Bissell, 2003; Nelson and Bissell, 2005; Paszek et al., 2005).

How can cancer cell invasion be studied? Ideally one would like to know how changes in cell phenotype, alterations in the cells immediate environment as well as how modifications to cell-cell interactions impact tumor invasiveness in vivo. However, in animal models any induced change, whether by cell mutations or in tumor mE, may be compensated by other (sometimes multiple) factors that make the overall experiment difficult to both control and interpret. in vitro experiments allow for better control of individual factors, but the complexity of in vivo environment is impossible to reconstruct. To be able to include in a controlled fashion in one experiment multiple processes, such as cell metabolism, cell-cell adhesion, intercellular signaling, remodeling of the cell mE, along with the intra-tumoral heterogeneity, a more interdisciplinary approach, combining laboratory experiments with multiscale in silico modeling is not only required but essential (Anderson and Quaranta, 2008; Sanga et al., 2007). In silico models, especially individual-cell-based models, can bridge these two experimental extremes since they can integrate measurements from different in vitro experiments, reconstruct certain aspects of in vivo environments and allow for a systematic analysis of the influence of individual as well as combined factors on overall tumor behavior. Although, the laboratory experiments are necessary for both computational models parameterization and validation of simulated results.

In this review, we summarize current approaches to model cancer invasion in silico, with a special focus on a class of individual-cell-based models developed in our laboratories. We also discuss their integration with traditional and novel in vitro experiments, including new assays whose design was inspired by computational modeling.

1. In silico modeling of tumor invasion

A key advantage of in silico computational models is their natural ability to handle multiple dynamic interacting variables, such as numerous cell types or various environmental factors. A typical way to investigate how individual components of a system contribute to the emerging properties of the whole is via systematic manipulation of these variables and the parameters that control them within dynamic computational simulations. This is similar to experimental approaches in which the importance and influence of a certain gene or protein is assessed by over-expressing it or knocking-out and comparing the animal or cell with wild-type animals or the healthy parental cell line. However, in computer simulations every parameter can be altered over a broad spectrum of possible values, and multiple parameters can be varied simultaneously, which is often difficult, if not impossible, to achieve experimentally in an accurate controlled fashion. Therefore, computational modeling enables one to track the behavior of a whole multicellular system as well as each of the individual components of the system simultaneously in time and space, allowing one to determine the relative importance and contribution of each factor in achieving the final simulated result. Fundamentally, this allows such models to generate experimentally testable predictions and hypotheses. Moreover, one can also apply various analytical and statistical tools to analyze the multicellular system and its sensitivity to parameter perturbations. Another advantage of computational models is that they naturally integrate multiple traits that define an individual cellular phenotype. Understanding how these traits act in symphony to produce the phenotype is experimentally tricky, but computationally clear.

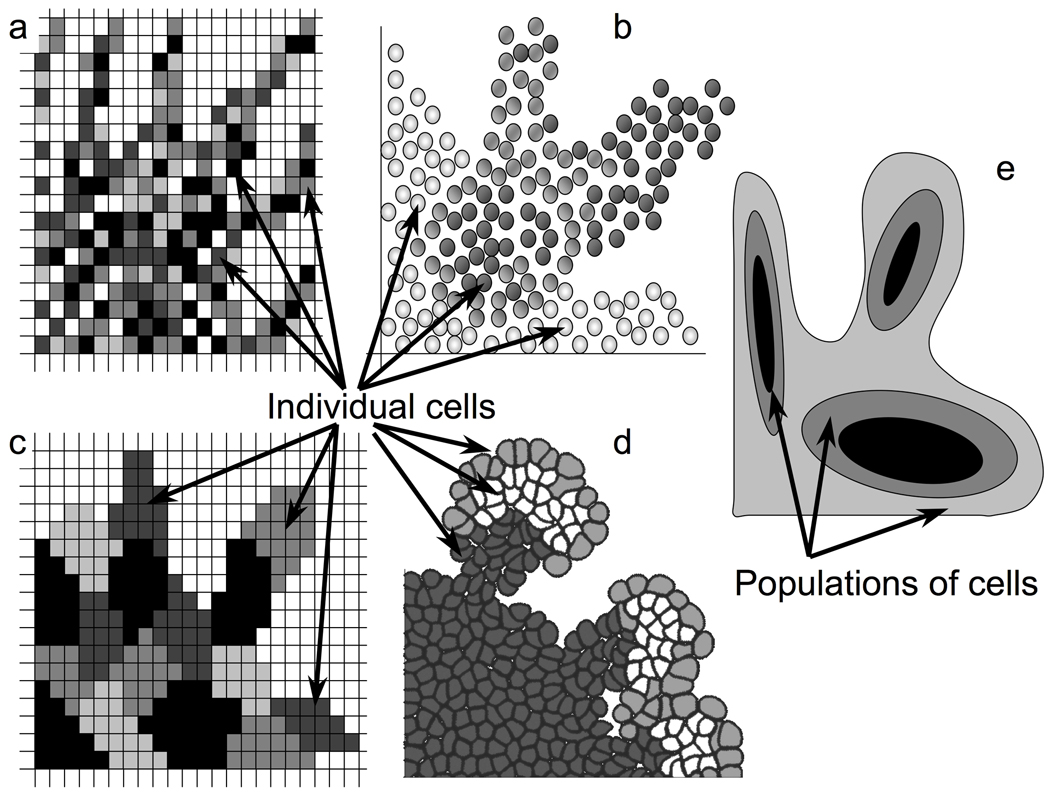
Several different computational models of tumor growth and invasion have been developed and can be broadly divided into two classes (Fig.1): continuous models representing tumors as densities of cells and individual-cell-based (agent-based) models in which each cell is treated as a separate entity (agent). The latter can be subdivided into nuclei-centered models and deformable cell models depending on how much cell structural detail is incorporated into the model. We briefly describe all three approaches below, but the interested reader is encouraged to consult the following reviews for further details (Anderson et al., 2007a; Araujo and McElwain, 2004; Byrne and Drasdo, 2009; Lowengrub et al., 2010; Preziosi, 2003; Rejniak and Anderson, 2011; Rejniak and McCawley, 2010; Rejniak et al., 2010b).

Fig. 1.

Schematic illustrating different computational models of invasive cell cohorts. a) Cellular automata model in which each cell occupies a single grid site; b) Cell-centered grid-free model in which each cell is defined as a points (nucleus); c) Cellular Potts model in which each cell is composed of several grid sites defining cell shape and area; d) IBCell model in which each cell consists of a deformable elastic membrane filled with gel-like cytoplasm; e) Continuous models in which each region represents mass (population, density) of cells of the same type.

1.1. Individual nuclei-centered models

In this class of models, individual cells are represented in space by their nuclei and equipped with a set of cell characteristic features that may include cell age, its current phenotypic state, acquired mutations and individually regulated cell cycle. Cells are located in a computational domain that represents either the culture condition or the stromal tissue surrounding the growing tumor. In the latter case several environmental factors may be incorporated in the model, such as metabolic gradients, various stromal cells, and the heterogeneous structure of the ECM. Each cell can respond to these environmental cues by changing its metabolic state, direction of cell movement, or actively remodeling the surrounding ECM. All cell-cell and cell-ECM interactions are defined locally between individual cells and the overall tumor behavior is an emergent property of the collective behavior of many individual cells. In terms of the scale of the experimental in vitro systems (multicellular clusters of the size up to a few centimeters) there is an obvious fit with nuclei-centered approaches, since these models can handle up to a few million individual cells. Therefore not only are they capable of representing in vitro systems, but also in vivo and even potentially clinically relevant size tumors. All agent-based models have an added advantage as they can connect directly with the in vitro experimental assays at the level of an individual cell. This is particularly useful if we are interested in accounting for heterogeneity across the cellular populations. Examples of this class of models include: grid-based (Fig.1a) (Aubert et al., 2008; Dormann and Deutsch, 2002; Enderling et al., 2009; Kim et al., 2009; Zhang et al., 2009) and lattice-free models (Fig.1b) (Drasdo et al., 2007; Galle et al., 2005; Norton et al., 2010).

1.2. Individual deformable cell models

In this class of models, each cell is an entity characterized by a deformable shape and volume (or area) that can vary in time depending on the cell state (growing, dividing, dying, migrating), interactions with other cells (cell packing due to adhesion) and the cell mE (deformation due to obstacles or ECM fibers alignment). Since individual cells do not need to be identical, i.e. each cell may have a slightly different area and/or membrane surface, this modeling technique captures the natural morphological heterogeneity between cells that in turn allows for a more natural representation of the variation in local cell-cell and cell-ECM interactions. In addition, each individual cell can be equipped with various cell membrane receptors that may be used to define cell cycle, determine underlying cell life processes and intracellular pathways, or physical interactions with other cells and the mE. The variable cell morphology also enables one to distinguish between cytoplasmic and membrane-related events allowing for a more realistic comparison between the simulated and experimental data, from both in vitro cultures and ex vivo tissue slices (especially using fluorescent, immunohistochemical and histological staining). Examples of this class of models include: grid-based (Fig.1c) (Bauer et al., 2009; Shirinifard et al., 2009) and lattice-free models (Fig.1d) (Dillon et al., 2008; Schaller and Meyer-Hermann, 2005)

1.3. Continuous (population) models

In this class of models, tumors are represented as populations (densities, concentrations) of identical indistinguishable cells whose properties (doubling time, death rate, movement speed) are defined as averages for the whole cell population (Fig.1e). These models are by definition deterministic and whilst it is possible to include several cell subpopulations (such as proliferating, quiescent, necrotic, or dead cells), the number of various cell phenotypes must be specified apriori since each subpopulation needs to be handled by a separately defined equation. The advantage of continuous models is in their ability to reproduce clinical size tumors, thus these models can provide a more global view of developing tumors and tumor treatment, and show the potential to match some image-based clinical data. They are also more amenable to analytical investigation which can often highlight key underlying mechanisms. Examples of recently published models in this class can be found in (Bellomo, 2008; Hinow et al., 2009; Lowengrub et al., 2010; Macklin et al., 2009; Painter et al., 2010; Szeto et al., 2009)

1.4. Specific examples of in silico invasion modeling

To illustrate how computational models can be applied to study tumor cell invasion we describe here in more detail two distinct agent-based approaches, the hybrid discrete-continuous (HDC) model and the immersed boundary model of a cell (IBCell) model, both developed in our laboratories.

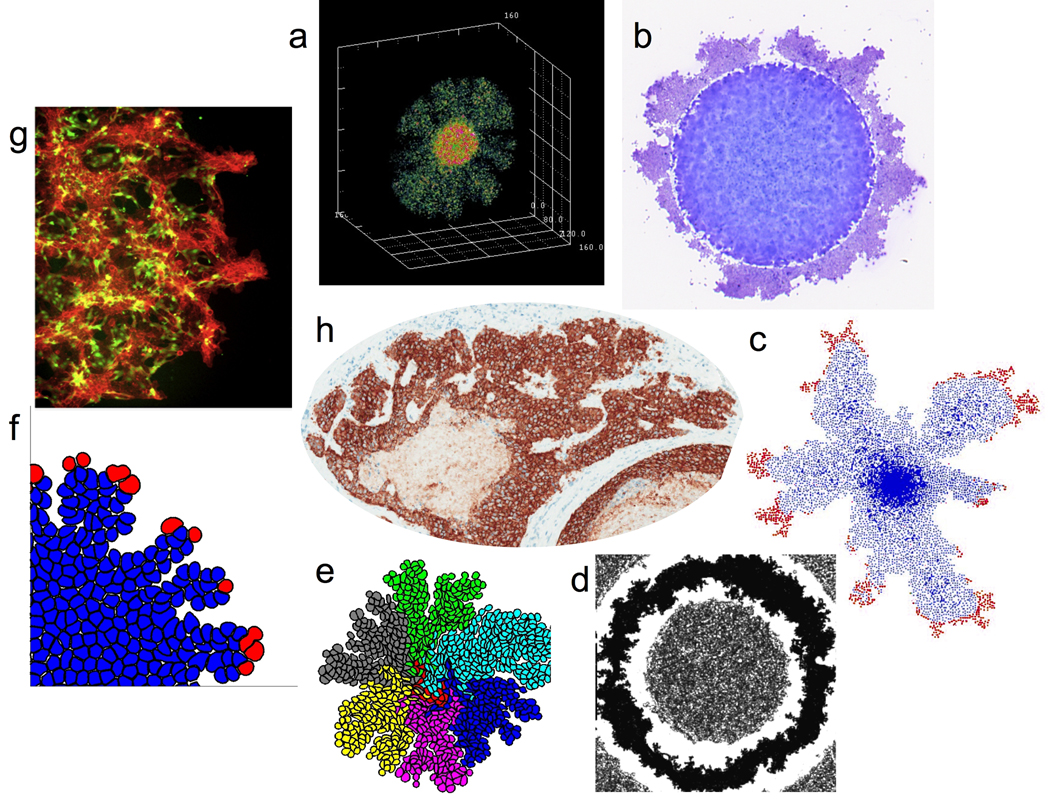
The HDC model of tumor invasion couples a continuum deterministic model of microenvironmental variables (based on a system of reaction-diffusion equations) and a discrete cellular automata-like model of individual tumor cell migration and interaction (based on a biased random-walk model, see (Anderson, 2005) for more details). This model operates at the cell-to-tissue scale and is therefore ideal for examining the tumor mE interactions. It is broadly based on the growth of a generic three-dimensional solid tumor, but, we only consider a one-cell diameter thick two-dimensional slice through it. Translation to 3-D is straightforward (Fig.2c), though somewhat computationally intensive. An important aspect of the HDC model is that individual cells are defined via collection of phenotypic traits including proliferation, death, cell-cell adhesion, mutation, and production/degradation of mE specific components which determines how a cell behaves and interacts with other cells and its mE. The mE consists of concentrations of ECM, oxygen and matrix degrading enzymes. Cells migrate, proliferate, die and potentially mutate depending on their phenotype and the mE. If a cell does mutate during division it is randomly assigned a different phenotype from a predefined pool. The role of mE in aiding or inhibiting tumor progression was one of the key questions we wanted investigate with the HDC model. By considering different mE conditions (uniform ECM, grainy ECM and high/low oxygen) we were able to show that in difficult or harsh mEs the tumor morphology that emerged was distinctly different, being more fingered and asymmetric (Fig.2a). More importantly these fingered tumors were composed of fewer more aggressive phenotypes, defined in terms of low cell-cell adhesion, short proliferation age, and high migration coefficients. These results led to a theoretical publication in Cell (Anderson et al., 2006) and development of multiple modeling approaches to further investigate these results (Anderson et al., 2009; Anderson et al., 2007a; Anderson et al., 2007b; Quaranta et al., 2008).

Fig. 2.

The formation of microinvasions observed in vivo (center) can be investigated by both in vitro (b,d,g) an in silico (a,c,e,f) muticellular assays that allow to research interactions between individual cells, as well as interactions between tumor cells and their mE. Figure a) reprinted from [Anderson & Quaranta, 2008; Fig.5]; b) from Y. Kam [unpublished]; c) from [Quaranta et al., 2008; Fig.5]; d) from [Kam et al., 2009; Fig.4a]; e) from [Rejniak, 2007 ]; f) from [Quaranta et al., 2008; Fig.3]; g) from [Kam et al., 2009; Fig.4c]; h) from M.C. Lloyd, Moffitt Analytic Microscopy Core [unpublished]; with permissions.

The IBCell model is capable of capturing the morphology of fully deformable cells, especially during their individual or collective migration and growth (Fig.2e,f). Each cell is modeled as an elastic membrane enclosing the gel-like cytoplasm and cell cytoskeleton, and can be equipped with various cell membrane receptors. These receptors are used to determine which cell life process will be initiated based on local cues sensed by the host cell from other cells and cell mE. For example, the cell will start growing if it senses (through their membrane receptors) that there is enough free space in its vicinity to expand. Similarly, the cell remains viable as long as it senses (via its receptors) that there are sufficient levels of growth factors or nutrients around its membrane. The cell can move up the gradients of chemo- or hapto-attractants, using its membrane receptors to determine the chemical concentrations in its mE. Since all cells are deformable, the numbers of their membrane receptors exposed to a certain cues may be different in each cell leading to a natural cell-to-cell heterogeneity in cell response. This in turn influences the collective behavior of cell clones or cohorts. This model has been used to investigate how tumor cell competition for space and nutrients, which depends on cell intrinsic metabolic properties, may result in different tumor cluster morphologies, with distinct growth and invasion dynamics. Using this model we have shown that natural cell-to-cell variability in cell shape, cell membrane surface area and the number of cell membrane receptors can result in the formation of invasive cell cohorts in mEs depleted from nutrients, whereas in rich environments cell collective behavior is more homogeneous despite the individual cell variability (Anderson et al., 2009; Quaranta et al., 2008; Rejniak, 2005; Rejniak, 2007)

Computational models give an opportunity to test the outcomes of experiments in which multiple parameters (corresponding to cellular features or environmental conditions) can be varied simultaneously and over a wide range of values, that is often impossible to do experimentally. However, one can ask whether computational outcomes represent biological reality or are simply results specific to a particular choice of model parameter set. One way to address this issue is to design laboratory experiments to verify computational results. Another way is to develop different computational models based on different mathematical assumptions to address the same problem and compare their simulations results in order to dissect both similarities and differences between them. We used this approach in (Anderson et al., 2009) to investigate the formation of cell invasive cohorts as a result of interactions between individual cells and their immediate mE. In this study we applied three different computational models (both HDC and IBCell are discussed above, and the evolutionary hybrid cellular automata model, EHCA, which is not) to simulate growth and movement of a cluster of tumor cells by systematically varying two model parameters: the rate of nutrient consumption by an individual cell and the oxygen threshold below which a cell is considered to be in a hypoxic state. The models were based on different mathematical frameworks, but all three pointed to a correlation between tumor cell competition for space and nutrients and finger-like morphologies of tumor tissue in a nutrient-poor environment, in contrast to round tumor tissue margins in nutrient-rich surroundings. Since the same result naturally emerged from each model one can conclude that we have found a model-independent mechanism that should be biologically relevant and therefore worth pursuing experimentally.

2. In vitro assays for cancer invasion modeling

In mathematical models of cancer invasion, regardless of how complex or how simple the model is, the variables that drive it need to faithfully represent various biological processes, and thus need to be properly parameterized. The real potential of in silico modeling is in its ability to tailor a model on a per patient basis and therefore ideally we want to obtain all model parameters from individual human tumor samples to predict patient specific outcomes. However, access to patient pathology samples that show spatial progression of tumor invasion over more than two time points is extremely limited. It is far easier to use cell culture systems to provide continuous quantitative data over extended periods of time that describe the dynamic response of individual cells to various extrinsic conditions such as nutrient deprived mEs. Furthermore, the parameters from in vitro experiments can be measured under more controlled conditions than in the in vivo setting. This is particularly important for both computational model parameterization and validation, and the individual-cell-based models discussed above are ideal counterparts for in vitro assays as they focus mostly, but not exclusively, on cellular phenotypes such as cellular proliferation or death rates, cell metabolism and/or motility. Numerous in vitro experimental tools are available to gather parameters at various modeling scales, from single-cell unidirectional movement, to multi-cellular clonal growth, to population dynamics in a 3D culture. Here we briefly review a selection of in vitro assays commonly used to collect basic cellular traits which are related to cancer invasion, and compare the more traditional invasion assays with several new assays driven by in silico modeling (Table 1).

Table 1.

Examples of in vitro assays applicable for integration with in silico model

Proliferation Assays

Direct cell number counting

Manual counting using Hemocytometer

Flow Cytometry

Metabolic Activity Measurement

Colorimetric assay of Tetrazolium dye (i.e. MTT, MTS, GTS)

Luminescence assay

Nucleic acid detection

Microscopic detection (i.e. BrdU, Ki-67, PCNA)

Label-free cellular assays

Aopotosis Assays

Microscopic Assay (i.e. TUNEL)

Biochemical Assay (i.e. Caspase-3)

Flow Cytometry (i.e. Annexin V)

Motility Assays

Boyden chamber-based Assay

Wound-healing Assay (CWA)

Live cell imaging

3D Assays

Invasion Assays

Boyden chamber-based Assay

Wound-healing-based assay (CIA and NEA)

3D Assays

2.1. Proliferation

Proliferation rate in vitro is determined by measuring cell number increase in a finite space such as a culture plate. Numerous methods have been developed to measure the proliferation rate ranging from manual counting, using hemocytometer, to automated high throughput measurement. The most popular method used is to measure the metabolic activity representing the quantity of live cells by using colorimetric reaction (Cory et al., 1991; Scudiero et al., 1988), or luminescence (Crouch et al., 1993). Other methods to assess the quantity of living cells include the direct measurement of ATP or nucleic acid contents for live cell titrating. All of these methods provide an efficient measure of the live cell population size, however, more information regarding the spatial and temporal aspects of division is often required for in silico modeling. In addition to traditional microscopic assay using BrdU or proliferation-specific antigens (i.e. Ki-67 or PCNA, (Leonardi et al., 1992; Scholzen and Gerdes, 2000)), many experimentalists also use fluorescent molecules designed to be internalized by live cells and dead cells selectively such that proliferating subpopulations are easily visible (i.e., calcein-AM vs. ethidium homodimer). In addition to these standard assays, there have been efforts to monitor cell proliferation and adhesion using label-free technology (Xi et al., 2008). These label-free cellular assay tools enable more physiological and quantitative analysis of cell proliferation and cytotoxicity as well as providing live cell data instead of end-point readouts.

The counterpart of proliferation, cell death rate, can also be measured directly. Instead of measuring the net proliferation rate or the simple cytotoxicity, the apoptotic active programmed cell death is quantified by flow cytometry (Nicoletti et al., 1991; Vermes et al., 1995) or microscopy (Gavrieli et al., 1992; van Engeland et al., 1998). The flow cytometry-based assay allows for large numbers of cell to be counted and therefore fits well with in silico models focused on population dynamics whereas microscopy provides more detailed spatial and temporal information of cell death in fewer cells.

2.2. Motility

Cell migration on ECM is one of the critical intrinsic cell characteristics which enable cancer cells to escape their initial location and invade into new areas. There is clearly a significant difference between cell migration on a 2D surface and in a 3D matrix as well as between migration in vitro and in vivo. Nevertheless, the relative motility of cells from 2D in vitro systems still provides useful quantification of the intrinsic potential of cells to move along an ECM matrix and is widely used to provide parameters for in silico modeling. The methods generally used for in vitro motility measurements are the (1) Boyden chamber assay, (2) in vitro wound-healing assay, and (3) live cell tracking under a microscope – ideal for monitoring individual cell movement.

The Boyden chamber is a filter device which divides cell culture space into an upper and lower compartment and the filter has many pores through which cells can pass (Boyden, 1962; Shaw, 2005). This is a highly quantitative and efficient way to measure migration toward a more favorable environmental cue, such as serum. Due to its simplicity and efficiency it has turned into the most popular migration/invasion assay platform. However, whilst this method represents the quantity of motile cells very well, it provides no information about migration speed, direction and cell morphological dynamics during the migration process.

To assess the migration speed and other metrics relating to motility, the in vitro wound-healing assay and the live cell imaging assay are the most commonly utilized tools. Although the live cell imaging requires a specially equipped microscope, with a compartment controlled for CO₂ concentration, temperature and humidity, it has the great advantage of providing dynamic information on cell migration speed and direction. A disadvantage of this method is that mostly unbiased migration can be assessed and the effects of cell-cell contact are often ignored. The unbiased movement does give some limited information about the intrinsic amoeboid motility, whereas the wound healing assay can provide additional information about the contribution of cell-cell interactions, cell polarization, as well as proliferation (Liang et al., 2007; Nobes and Hall, 1999). However, despite the advantages, there is an inherent lack of reproducibility for this assay, in generating the wound by scratching, which limits its application. As an alternative approach, the circular wound-healing assay (CWA) (Frey et al., 2004; Kam et al., 2008; Watanabe et al., 1995) was designed, and also developed commercially in a similar format. This assay consists of a reproducible circular cell-free area in the center of the plate and is used to measure the rate at which this space closes.

The 2D motility assay has an innate limitation because it relies on the amoeboid movement on a culture plate which is not the same as migration in a tissue. Recently, a number of in vitro and in vivo methods have been developed which focus on illuminating the various mechanisms of motility in a 3D environment (Condeelis and Segall, 2003; Demou and McIntire, 2002; Friedl, 2004; Voytik-Harbin et al., 2001). The majority of these assays are performed using 3D microscopy and fluorescent markers as well as specially designed 3D matrix structures. Recent advances in microscopy using confocal laser scanning microscope and multiphoton excitation microscope enabled the dynamic 3D imaging. Confocal backscatter/reflection microscopy (Hartmann et al., 2006; Voytik-Harbin et al., 2001) has an advantage in 3D ECM monitoring whereas the conventional confocal microscopy holds general advantages in 3D cell imaging. Multiphoton microscopy is one of the most prominent tools to obtain high resolution images from living biospecimen such as thick tissues in vivo as well as artificial 3D matrices in vitro. Since cell migration in the 3D matrix requires active remodeling of the ECM environment by cells, 3D migration analysis implies the more complex tumor invasion mechanisms than simple 2D motility assays. For example, the tracking of cell-ECM interactions in 3D assays provided an insight to formulate a multistep cancer invasion theory involving both individual and collective migration forms (Friedl and Wolf, 2009; Wolf et al., 2007).

2.3. ECM modulation

The generation and degradation of ECM is one of the most important environmental factors facilitating or limiting cell invasion. The expression level of ECM proteins facilitating cell migration is generally measured biochemically. ECM degradation activity can be predicted by measuring ECM-digesting enzymes such as matrix metalloproteinase (MMP) production which can be measured by immunochemical procedures. However, the majority of MMP or other digesting enzymes require the activation cascades and more quantitative enzymatic assyas are required for the discrimiatation between zymogens and active enzymes. The MMP activity measurement in vitro is achieved by using natural protein substrates or by using synthetic peptide substrate (Lombard et al., 2005). Particularly, the fluorescence liberation from fluophore-conjugated ECM upon the digestion turned to a useful tool to detect local MMP activity around cells migrate and invade in a 3D matrix In addition to the total activity averaged. Similarly, the matrix layer degradation by invadopodia is also used to measure the ECM digesting enzyme(s) linked to individual cells (Enderling et al., 2008; Linder, 2007) The 3D cell tracking technique also can be applied to monitor the ECM dynamics in the cancer invasion process (Condeelis and Segall, 2003; Friedl, 2004; Wolf et al., 2007).

2.4. Invasion

Cancer cell motility in vitro, often referred to as cancer invasiveness index, is an essential factor in cancer invasion. However, it is only a necessary, but not a sufficient factor because the invasion process requires additional processes such as penetration through normal epithelial layer or ECM barrier. Although there has been significant advance in 3D cell tracking in the ECM matrix, most traditional invasion studies still rely on the traditional invasion assays such as the Boyden-chamber based assay in which an ECM gel (i.e. Matrigel™) barrier is built on a filter dividing an upper and lower chamber (Shaw, 2005). This Boyden-chamber technique focuses on the intrinsic invasion potential of cancer cells in culture and is often combined with the migration assay to compare the invasiveness between different cell lines. However, it also faces the same limitations as in the motility assay to provide viable parameters for in silico models.

The circular invasion assay (CIA, Fig.2g) is a novel assay that has been designed to overcome the limitations of traditional methods and is an ideal platform for integrated modeling as it provides cell-scale quantification of invasiveness (Kam et al., 2008). It is based on CWA with the major difference that there is an ECM gel overlay mimicking the physical barrier that cancer would normally encounter. It can be used to quantify the relative invasiveness of a tumor cell line in a variety of ‘controlled conditions’, which mimic real tumor mEs (i.e., growth factor availability). By using live cell imaging it can also provide information regarding single cell migration and cell-cell interactions during the invasion process. Therefore it could serve as an experimental tool for investigating individual vs. collective cancer cell invasion modes (Friedl and Wolf, 2008; Wolf et al., 2007). Similarly to the Boyden chamber-based assay, CIA data can be paired with CWA to distinguish the relative invasiveness from relative motility. Recently, an alternative approach called the nest expansion assay (NEA, Fig.2d) (Kam et al., 2009) was developed as a multi-parametric invasion assay, which enables a better morphological link to tumor cell growth and migration in the HDC and IBCell computational models. The NEA is similar to the CIA but it produces outward tumor invasion and is thus closer to cellular progression in the in vitro invasion process. One advantage of this new method is quantification of the leading margin shape variation using fractal-lacunarity measurements (Plotnick et al., 1996; Smith et al., 1996). Even though cell invasion under ECM gel layer is MMP-dependent however, both CIA and NEA still have the amoeboid movement limitation that all wound-healing assay-based approaches have.

A 3D implementation of the migration and proliferation assays has the potential to be a great invasion assay as it would be highly comparable to the true in vivo processes occurring during invasion and be modulated by factors such as the composition and rigidity of the ECM used. 3D spheroid cultures embedded in ECM are also a useful model system for certain types of cancers (Haass et al., 2008; Lin and Chang, 2008; Stein et al., 2007; Wiercinska et al., 2010). However, even with these assays more technical improvements are required to utilize them for in silico modeling because of limitations in the uniform application and quantification of invasiveness. The image analysis tools currently used in 2D assays could be developed to apply to 3D data and therefore aid in achieving a more uniform and reproducible metrics, e.g. the fractal/lacunarity measurement.

3. Integration of in silico and in vitro modeling

Most in silico models have been developed and parameterized using preexisting data reported in the literature. Often this data was collected from different tumors grown in different experimental conditions, using various cell lines or different animal breeds that, when combined, may not correspond to any single real tumor type. In addition, critical information on the role of cell-cell interactions and microenvironmental cues on local invasion of tumor cells may also be lost. This is in part due the fact that a complete (or even significant) set of parameters and processes that truly represent real tumors are rarely published by any single lab. This is partially due to the fact that standard assays have generally been developed to quantify one specific aspect of the invasion process (i.e., either proliferation or migration, or ECM degradation), which makes it difficult to tease apart the multifactorial interactions that drive true invasive outcomes. It is desirable to measure a full set of parameters that will inform mathematical models, however in some cases in may be difficult (e.g. cell-cell interaction can be difficult to quantify). Certain computational techniques have been developed to integrate individually measured traits in order to dissect ranges of parameters leading to the same cellular behavior (we used this approach to investigate phenotypical changes in breast cell mutants (Rejniak and Anderson, 2011; Rejniak et al., 2010a; Rejniak et al., 2010b)). However, close collaboration between experimentalists and modelers can lead to the development of novel assays influenced by in silico approaches and to novel computational tools than can integrate them.

Since in silico models by definition lack any experimental error, are cheap, accurate and, generally, fast they can provide a rapid means to systematically test the influence of individual and multiple cellular features under a spectrum of environmental conditions on the final multicellular morphologies. However, such computational results need to be verified by laboratory experiments, and if such results are inconsistent with the experimental data then the in silico models need to be modified to achieve consistency. This iterative loop between experiments and theory should ultimately converge on a model that is both validated and predictive and, in our experience, can lead to both experiments and model developments that would never have been considered independently. Thus, there is a real need for new experimental assays designed to meet requirements of computational models and whilst both in silico and in vitro approaches to tumor invasion have been useful in isolation, we believe that their true potential can be realized only upon integration. When both experimental and computational results can be compared in a quantitative way, and used to inform and improve both research approaches we will be directly positioned to make new discoveries not just in cancer invasion but in cancer progression in general. We admit this is not going to be an easy process, however, in our laboratories we have already began this process. By developing together both the computational techniques allowing for integration of various experimental measurements, and in vitro assays inspired by and tailored to the requirements of in silico modeling. In the following paragraphs we shall briefly discuss a couple of examples where we have developed such approaches either experimental assays that were inspired by theoretical models or theoretical tools that were applied to experimental assays.

In order to investigate the emergence of multicellular morphologies when cell sensitivity to microenvironmental hypoxia levels and cell metabolic rates were varied (Anderson et al., 2009; Anderson et al., 2007b) we compared 3 different in silico models. Our simulations indicated that cancer invasion may be a consequence of competition for adaptation between distinct cancer cell phenotypes driven by a tumor microenvironment with scarce resources. These dynamics appeared to be primarily driven by differential proliferation induced by low nutrient conditions, although other factors, such as matrix protein-digesting proteases or cell-cell interactions may also contribute to the observed morphological changes. If tumor invasion is in fact an emergent property of cancer cell populations adapting to selective microenvironmental pressure then this poses a difficult experimental challenge. Since traditional invasion assays were not suitable to address this challenge, novel experimental assays (i.e. NEA and CIA, discussed above) were developed (Kam et al., 2008; Kam et al., 2009). They were specifically designed to recapitulate the in silico simulation by providing high reproducibility and quantitative analysis of morphological variation as well as accommodation for microenvironment modulation. They also allow us to monitor cell scale variation during the invasive process. We are currently in the process of applying these assays in a systematic study of resource-driven tumor cell competition that leads to the emergence of an invasive subpopulation. The limited time but detailed cellular scale data of NEA is better suited to the IBCell model, which is driven by cell-cell interactions (via cell receptor dynamics), using cell viability, cell location, orientation and colony morphology whereas the HDC model, which spans both larger spatial and temporal scales, is better suited to the CIA model as it incorporates the spatial distribution of different clones over time and overall tumor morphology.

One of the important aspects of model integration is quantitative comparison between experimental and simulated data. Typically, the in silico model can be fine-tuned to fit the experimental data, such as growth or death curves, by adjusting the model parameters. However, a more challenging issue is to compare both kinds of results spatially, such as multicellular or clonal morphologies, and distributions of certain cell phenotypes. We have used the fractal dimension as one potentially useful measurement of surface irregularity (a “fingering” morphology) in the NEA assay (Kam et al., 2009).

It is worth noting that many in silico models consider cancer invasion as the outcome of both cell-cell and cell-matrix interactions, and these interactions may be cooperative and/or competitive, more accurate quantification of such interactions needs to be developed. Ultimately this boils down to new cell-scale measures that may need to be established, such as fingering dimension (e.g. length and width), balance between cell proliferation and death at the “finger tips”, or structure lacunarity. However, these cell-scale approaches will require development of higher throughput and higher content image analysis algorithms in order to be fully realized.

4. Conclusions and perspectives

In this review we have presented a range of in silico and in vitro modeling approaches of cancer invasion. We focused on some of our own techniques that attempt to integrate in silico and in vitro modeling in order to more accurately investigate cell-to-cell and cell-to-mE interactions that lead to tumor cell invasion. Specifically, for the in silico models we considered both the HDC and IBCell models and for the in vitro we considered NEA, CIA and CWA assays. We discussed the importance of developing an integrated approach, allowing models to drive experimentation and experiments to drive model development in a more natural manner and how this often results in both approaches taking a path that would not have been taken otherwise.

Rather than summarizing what we have already discussed, it is worth reminding ourselves that cancer is truly a complex multiscale system where changes at the genetic scale propagate through, proteins, pathways, cells, tissues, organs and eventually lead to cancer that can be fatal. These multiple scales feed back on one another but the pivotal scale is the cell scale. The cell-centric view of cancer invasion is where both of the in vitro and in silico models shine and really where we have the best chance of understanding some of the key dynamics of the invasion process. However, cells are defined by a diversity of traits (such cell metabolism, migration, death, and cell-cell adhesion, to name a few) most of which are technically impossible to measure simultaneously in a single experiment. The natural ability of mathematical models to integrate multiple interacting variables, and predict how these variables change both temporary and spatially, means that we can potentially overcome these experimental limitations. By using high throughput simulations with systematically varied multiple parameters, in silico models can inspect the multi-dimensional parameter space and determine parameter ranges that lead to the desired biologically-relevant results, and those that lead to the outcomes that have not been observed neither in experiments nor in patients’ samples. This in turn will determine how separate experimental measurements, acquired from different in vitro experiments, can be integrated in order to reproduce the observed experiments.

It is our perspective that in silico models will become integrated into the fabric of modern cancer research just as in vitro and in vivo models are today, in silico models will be in the future. The iterated dialogue between theory and experiment has already led us to a deeper understanding of the importance of heterogeneity, morphology and interactions with the microenvironment in tumor growth. We firmly believe this dialogue will continue to provide ripe rewards for the cancer research enterprise and whole-heartedly encourage you to join us in this fascinating conversation.