Towards the Use of a Lower Limb Exoskeleton for Locomotion Assistance in Individuals with Neuromuscular Locomotor Deficits

Abstract

The authors intend to utilize a lower limb exoskeleton for gait assistance in individuals with lower limb neuromuscular deficit. The authors suggest that two foundational elements are required to do so effectively. First, the exoskeleton system must be capable of reliable real-time gait phase detection, in order to determine the nature of gait assistance to provide. Second, in gait phases or circumstances in which the exoskeleton provides minimal assistance, the passive dynamics of the exoskeleton should not hinder the individual (i.e., should have the capability to minimally interfere with gait dynamics). As such, the exoskeleton system should be capable of actively compensating for its passive dynamics, namely the inertial, gravitational, and frictional effects it imposes on the user. This paper describes the implementation of these two foundational elements (real-time gait phase detection and active cancellation of passive dynamics) on a prototype lower limb exoskeleton, and provides experimental data demonstrating their respective efficacy.

I. Introduction

A number of neuromuscular impairments result in acute and/or chronic locomotor deficits. Common conditions resulting in gait deficit or impairment include incomplete spinal cord injury (SCI), cerebral palsy (CP), multiple sclerosis (MS), and complications resulting from cerebral vascular accident (stroke). There are approximately 260,000 persons in the US with SCI, approximately one half of which are incomplete injuries [1]; there are approximately 765,000 individuals in the US with CP [2]; and there are approximately 350,000 individuals in the US with MS [3]. Collectively, there are approximately 1.3 million persons in the US living with one of these conditions. Further, there are approximately 7 million persons living in the US who have experienced a cerebral vascular accident (stroke) [4], and a significant portion of these have or have had gait impairment as a result.

The authors are developing a lower limb exoskeleton for gait assistance in individuals with lower limb neuromuscular deficit, such as individuals in those populations previously cited. Some work has been performed on treadmill and over-ground robotic devices, and their control strategies have been characterized [5, 6]. In order to use a lower limb exoskeleton for gait assistance, two foundational capabilities must exist. First, such a system must correctly and accurately detect the phase of the user’s gait, so that it can cooperatively assist the user in an appropriate manner. Second, in order for a device to be useful as an assistive device for persons with lower limb deficit, it must not significantly impair the natural gait of the user in phases of gait, or in locomotion circumstances, in which the user needs minimal assistance from the device. Given the current state of robotic technology, implementation of a device capable of biological levels of torque and speed in the lower limb will likely introduce nonnegligible mass, rotational inertia, and possibly joint friction. As such, the authors have designed and implemented a controller with active compensation for the purpose of mitigating these passive dynamics. This paper describes the implementation of these two foundational capabilities in a lower limb exoskeleton, and evaluates the efficacy of the gait phase detection (GPD) component of the system, as well as the efficacy of the active compensation of passive dynamics (ACPD).

II. Vanderbilt Lower Limb Exoskeleton

The Vanderbilt exoskeleton [7, 8] is shown in Fig. 3(a). The exoskeleton is a fully powered lower limb orthosis with right and left powered hip and knee joints. The exoskeleton has a mass of 12 kg (26.5 lb), incorporates brushless DC motors and backdrivable transmissions at each of the four joints, and is powered by a lithium polymer battery contained within the hip piece of the unit. The exoskeleton can be used with a standard ankle foot orthosis (AFO) if needed.

Figure 3.

a.) Exoskeleton prototype. b.) Experimental setup for EMG recordings. Subjects were asked to raise their dominant leg to an angle of approximately 75 degrees from the vertical position. Real-time readouts of absolute thigh orientation provided subjects with feedback to ensure an appropriate angle was maintained. Subjects grasped a walker to ensure they could easily maintain balance. EMG signal wires and exoskeleton data-tether not pictured.

III. Gait Phase Detection

In order for a system to cooperatively offer assistance to a user, it is necessary for the system to change its behavior at certain critical points in the gait cycle. These points include heel strike, toe off, and reversal of joint direction of motion. For this application, the authors have divided the gait cycle into 4 phases where the behavior of the device is expected to remain relatively consistent during each phase, and change at each phase transition. A state machine with switching conditions for the transitions is shown in Fig. 1. A discussion of the phases and transitions follows.

Figure 1.

Simplified state machine model for phase recognition. Guard conditions are shown in brackets along each transition.

Phase 0 (heel strike through mid-stance)

Enters phase by exceeding a threshold in acceleration along the leg axis, as measured by an accelerometer on the exoskeleton. During this phase the knee remains essentially fully extended, and the hip transitions from flexion to extension. The phase ends in a mid-stance configuration, when the center of mass of the body is essentially over the stance leg.

Phase 1 (mid-stance through toe-off)

Enters phase based on prescribed hip angle, as measured by hip joint angle measurement on the exoskeleton. During Phase 1 the hip continues to extend and the knee begins to flex slightly. This brings the center of mass anterior to the stance leg during double support. Toe off typically occurs at the end of this phase.

Phase 2 (early swing)

Enters phase based on angular velocity of hip reversing direction. Phase 2 is considered the first part of swing phase. In this phase the hip and knee flex to bring the foot upward and forward and allow for toe clearance.

Phase 3 (late swing)

Enters phase based on angular velocity of knee reversing direction. Phase 3 is the second part of swing phase and is characterized by rapid knee extension and maximum extension in the hip. The phase ends at heel strike.

To evaluate the accuracy and consistency of the phase tracking system, a healthy subject was asked to walk on a treadmill while wearing the exoskeleton. The subject was instructed to walk for 3 minutes at a velocity of 0.67 m/s (1.5 MPH), as measured by the treadmill. This speed was estimated to be a representative speed for the intended patient population. Joint angles and estimated phase of gait from the exoskeleton were recorded. The exoskeleton was set in a passive mode so that there was no assistance of any kind. Data for ten consecutive strides were extracted and analyzed (Fig. 2). As indicated by the figure, the gait phase detection approach provides consistent identification of the significant phases of level walking.

Figure 2.

Knee and hip angles recorded for ten consecutive strides walking on a treadmill at 0.67 m/s. Vertical lines indicate transition points between labeled phases for all 10 strides. The Phase 3 to Phase 0 transition occurs at heel strike, and therefore at the 100% mark in all ten strides. Flexion is defined as positive.

Numerous gait phase detection approaches have been characterized for other applications (e.g. the HAL exoskeleton [6]). However, the phase detection algorithms presented here are novel in that they operate without load sensors, electromyogram (EMG), or any under-the-foot hardware.

IV. Active Compensation of Passive Dynamics

The exoskeleton prototype (Fig. 3) imposes undesirable passive dynamics on the user via three primary effects. First, the system has a mass of 12 kg, and therefore adds significant weight to the lower body of the user, potentially increasing the hip torque required to raise the knee by flexing the hip. Second, the links and motors add significant rotational inertia about the joints, primarily resulting from the motor rotor inertia as reflected to the joint through the backdrivable transmission. The reflected inertia is especially apparent at the knee, presumably due to the greater angular accelerations experienced by the knee relative to the hip joint [9]. Third, the system introduces friction at each joint, which again is most apparent at the knee joint, presumably due to the greater angular velocities at the knee joint (relative to the hip) [9]. While complete elimination of these passive dynamic contributions is unlikely, it is possible to reduce the effects of the passive dynamics so that the gait of a healthy subject approaches that of his or her gait without the exoskeleton. In the following two subsections, the results of two experiments demonstrate that the ACPD controller is effective in reducing the effect of the exoskeleton’s passive dynamics on the user.

A. Gravity Compensation

Since the great majority of the exoskeleton mass is located in the respective thigh links (approximately 4.1 kg per thigh link), the primary intention of gravity compensation is to minimize hip joint effort required to flex the hip, and thus raise the thigh segment through the gravitational field. As such, the exoskeleton hip joint torque is supplemented with a compensatory torque,

$${\tau }_g=\frac{\mathit{lmg}sin\alpha }{2}$$ (1)

where m is the mass of the thigh link, l is the length of the thigh segment, m is assumed to be distributed uniformly along l, g is acceleration due to gravity, and α is the angle of the thigh link relative to the vertical. Note that the latter is measured via an accelerometer on the exoskeleton, as described in [8].

To evaluate the efficacy of the gravity compensation algorithms, EMG data from three healthy subjects were collected and analyzed for three conditions corresponding to no exoskeleton, exoskeleton without gravity compensation, and exoskeleton with gravity compensation. Subject ages ranged from 24 to 26 years, and subjects 1, 2, and 3 had masses of 77 kg, 64 kg, and 100 kg respectively. For the experiment each subject was asked to stand upright and elevate their dominant side leg to approximately 75 degrees from the vertical while EMG data were recorded from the rectus femoris muscle in the thigh.

Subjects were instructed to allow their lower leg to remain passive. A real-time estimate of the thigh angle relative to gravity was produced on a monitor so that the subjects could easily adjust to maintain the appropriate angle. Fig. 3 shows the exoskeleton and experimental setup. Subjects were asked to keep their limb elevated for ten seconds before being instructed to relax. In between trials subjects were allowed to rest, and were instructed to alert the experimenter immediately if they felt they were beginning to fatigue. This procedure was carried out 12 times for each of 3 conditions: no exoskeleton, and the exoskeleton with and without compensation for gravity. “No Compensation” refers to a non-assistive setting in which the exoskeleton remains passive. In the “With Compensation” setting, the exoskeleton provides torque equivalent to 100% of its estimated mass. Trials were performed in a semi-randomized order to ensure results were unaffected by trial order.

EMG signals were low-pass filtered at 500 Hz, high-pass filtered at 10 Hz, and sampled at 1000 Hz. These data were rectified and low-pass filtered at 3 Hz to produce an envelope. For each trial a four second window was selected from the middle of the trial, and the EMG signal was averaged over that window. The mean of the four second windows was averaged for ten trials to produce an average EMG magnitude for each of the 3 settings. Fig. 4 shows the difference between the average EMG magnitude for each exoskeleton assistance setting, relative to the case without the exoskeleton. Thus, the values indicate the respective increase in EMG amplitude relative to the normal condition. These results are reiterated quantitatively in Table I. As evident by the results, the presence of gravity compensation substantially reduces the effective weight of the exoskeleton (although it does not return it to the EMG level measured in the absence of the exoskeleton). Note that, in the absence of a subject within the exoskeleton, the gravity compensation fully compensates for the gravitational effects at the hip joint (i.e., the exoskeleton hip joint will remain in a given configuration in the presence of gravity). As such, it is hypothesized that a portion of the elevated EMG seen in the gravity compensation experiment was due to the (sagittal plane) constraints on motion imposed by the exoskeleton. Specifically, slight changes in the plane of movement may increase the level of muscular co-contraction required to flex the hip joint, and therefore the presence of the exoskeleton may slightly increase quadriceps EMG during hip flexion due to secondary factors. Although the exoskeleton is easily capable of providing additional gravity compensation (which can offset the increase in EMG), the authors chose instead to maintain the level of gravity compensation that is appropriate in the absence of a subject, and thus used the settings indicated in Fig. 4 (and Table I) in the level walking experiments described subsequently.

Figure 4.

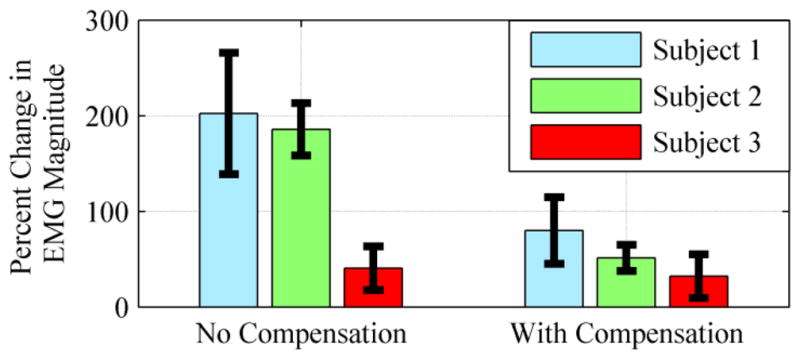
Percent change in average EMG from no-exoskeleton condition. EMG signals were recorded from the rectus femoris while the subjects’ legs were raised to 75 degrees from the vertical. Values indicate an increase in EMG from the no-exoskeleton condition. Each bar indicates an average over ten trials.

TABLE I.

Percent Change in EMG Magnitude for each Assistance Condition

Subject	Average EMG magnitude for “No Exoskeleton”	No gravity compensation	With gravity compensation
1	34 μV	202%	80%
2	32 μV	186%	51%
3	66 μV	41 %	32%

B. Inertia and Friction Compensation

In order to reduce the effects of added inertia, hip and knee joint torques are supplemented in proportion to the respective angular acceleration of the joint,

$${\tau }_i\propto \frac{d^2}{{dt}^2}(\theta )$$ (2)

where θ is the angular position of that joint, and where the constant of proportionality (i.e., the effective rotational inertia) was determined experimentally by iteratively increasing the value. In order to reduce the effects of added friction, hip and knee joint torques are supplemented in proportion to the respective angular velocity of the joint,

$${\tau }_f\propto \frac{d}{dt}(\theta )$$ (3)

where the constant of proportionality (i.e., the damping coefficient) was determined experimentally by iteratively increasing the value. The total passive dynamics compensation therefore consists of the application of equation 1 at the hip joints, and the sum of equations 2 and 3 at the knee joint.

C. ACPD Experiment and Results

To test the efficacy of the ACPD controller, kinematic data from the hip and knee joints during gait were recorded for a single healthy subject, walking under three conditions: no exoskeleton (unaffected walking), passive exoskeleton, and exoskeleton with ACPD. In the passive-exoskeleton condition the subject wore the exoskeleton, but gravity, inertia, and friction compensation were disabled. In these experiments, the subject walked on a treadmill at 0.67 m/s for 3 minutes for each condition. The subject was a 24 year old male with body weight of 100 kg and height of 1.85 m. In these experiments, the subject was instructed to walk naturally in all cases. For the no-exoskeleton condition, hip and knee angle data were collected using a motion capture system (OptiTrack 12-camera motion capture with ARENA software). For the passive-exoskeleton and exoskeleton-with-ACPD conditions, hip and knee joint angle data were recorded from the exoskeleton. Fig. 5 shows averaged knee and hip angle for ten consecutive strides in each condition. It is clear from the data that the joint trajectories with ACPD are much closer to the unaffected walking than those of the exoskeleton without compensation (i.e., the passive exoskeleton). This trend is especially clear in the knee joint, where the average peak in the knee angle is severely reduced for the passive-exoskeleton trajectories compared to the other two sets. Table II summarizes the respective ranges of motion of the knee and hip joint during walking at this speed for the two cases of wearing the exoskeleton, relative to the case of unaffected walking. As indicated in the table, when wearing the exoskeleton without passive dynamics compensation, the knee joint achieved 73% of its normal range of motion, while the hip joint achieved 111%, indicating the passive dynamics had a significant effect on knee joint motion, and relatively little impact on hip joint motion. With the addition of the ACPD controller, the knee joint achieved 96% of its normal range of motion, while the hip joint achieved 108%. As such, the joint range of motion with ACPD is nearly unaffected when walking with the exoskeleton. These results suggest the efficacy of the ACPD, and further suggest that with such compensation, a user is able to perform level walking in the exoskeleton without substantially affecting the user’s natural gait dynamics.

Figure 5.

Averaged knee and hip angles for ten consecutive cycles with standard deviation shown. Shown are no-exoskeleton, exoskeleton-with-ACPD, and passive-exoskeleton conditions. The maximum knee flexion for the passive-exoskeleton condition is significantly reduced in comparison to the other two conditions, and hip kinematics suggest that the ACPD condition matches the no-exoskeleton condition more closely as well.

Table II.

Range of Motion Analysis for Exoskeleton

Condition	Percent Range of Motion
	Knee	Hip
Passive	73%	111%
ACPD	96%	108%

V. Conclusion

The authors present the implementation of two important components of a lower limb exoskeleton for gait assistance in persons with locomotor deficits. The first is gait phase detection, and the second is active compensation for passive dynamics. In this paper, the authors describe an implementation of each, and provide experimental results indicating the respective efficacy of each component. Future work includes adding a gait assistance component to the exoskeleton, and assessing the ability of the exoskeleton to provide appropriate gait assistance to persons with locomotor deficit.