Normalization of mass cytometry data with bead standards

Abstract

Mass cytometry uses atomic mass spectrometry combined with isotopically pure reporter elements to currently measure as many as 40 parameters per single cell. As with any quantitative technology, there is a fundamental need for quality assurance and normalization protocols. In the case of mass cytometry, the signal variation over time due to changes in instrument performance combined with intervals between scheduled maintenance must be accounted for and then normalized. Here, samples were mixed with polystyrene beads embedded with metal lanthanides, allowing monitoring of mass cytometry instrument performance over multiple days of data acquisition. The protocol described here includes simultaneous measurements of beads and cells on the mass cytometer, subsequent extraction of the bead-based signature, and the application of an algorithm enabling correction of both short- and long-term signal fluctuations. The variation in the intensity of the beads that remains after normalization may also be used to determine data quality. Application of the algorithm to a one-month longitudinal analysis of a human peripheral blood sample reduced the range of median signal fluctuation from 4.9-fold to 1.3-fold.

INTRODUCTION

Mass cytometry is a recently developed format for single-cell flow cytometry in which inductively coupled plasma mass spectrometry is used to measure signals from antibodies conjugated to multi-atom metal tags[1, 2]. The high dimensionality of mass cytometry data makes it well suited for the analysis of primary samples, which are often complex mixtures of distinct cell subpopulations. Changes in instrument performance can cause observable fluctuations in signal strength after just a few hours of acquisition, presumably due to a combination of built-up cellular material and variations in plasma ionization efficiency. Additionally, between mass cytometer runs on any given day, further shifts in performance can be caused by manual interventions such as cleaning and calibration. Thus, in order to produce a more accurate interpretation of the biological differences between samples, it is imperative that measurement variations are minimized in the final data.

Recent mass cytometry experiments that analyzed the signaling responses of immune cell subsets in healthy human bone marrow dealt with instrument fluctuations by measuring unstimulated controls several times throughout the course of the experiment and assuming linear decay between these measurements[2]. This approach assumed that median surface marker expression remained constant throughout the experiment, which was appropriate given that the measured samples had overlapping staining panels and were from a single individual. While an assumption of linearity could hold true under certain circumstances, the ability to build more complex (nonlinear) models of signal strength variation across multiple days and patients requires accurate monitoring of short-term fluctuations and other changes that may occur concurrently with data acquisition. Therefore, it is imperative to consider the implementation of such for mass cytometry.

A normalization algorithm based on prominent features or “landmarks” in raw flow cytometry data was recently used to correct for instrument variability[3]. Although use of this algorithm resulted in an improvement in aligning datasets from two sample cohorts, the algorithm was dependent upon the samples having consistent cell subpopulations, which may not be the case in all studies. To assure comparable data on the same instrument over days and weeks, it is also standard practice in polychromatic flow cytometry to calibrate and optimize instrument performance before any sample introduction with beads containing a multi-peak fluorescent dye[4]. The fluorescence intensities from the labeled samples may then be normalized with a linear regression performed on the median fluorescence intensities (MFI) of the bead dye and the molecules of equivalent soluble fluorochrome (MESF) per bead[5]. Importantly, the dyes used in this approach can be excited by a wide range of wavelengths, making calibration possible across multiple fluorescent channels with a single species of bead, but the normalization is only relevant to a single instrument over time. An ideal mass cytometry normalization protocol would be independent of specific cell populations, would capture short-term fluctuations during data acquisition, would be applicable to all channels using a single bead standard, and would not assume linear decay between baseline measurements.

This report describes a method of correcting technical variation in mass cytometry data for all measured elements throughout their dynamic ranges by the use of polystyrene bead standards embedded with a combination of heavy metal isotopes. By adding bead standards to each biological sample and applying a “bead gate” after data acquisition, a time-dependent correction function was generated that is defined uniquely for each event and that accounts for both short- and long-term instrument sensitivity fluctuations. After application of the normalization algorithm to correct for instrument performance, the resulting single-cell data can be analyzed by any user-desired computational or statistical methodology. The normalization procedure described here is fully automated subsequent to bead gating. The output is an .fcs file containing the normalized single-cell data. Software implementing this method is freely available for download from www.cytobank.org/nolanlab.

MATERIALS AND METHODS

Reagents

A single lot of polystyrene bead standards embedded with five different metal isotopes (La 139, Pr 141, Tb 159, Tm 169, and Lu 175) having masses spanning the primary analysis range of the mass cytometer were synthesized as previously described[6, 7] and provided as a kind gift from Scott Tanner’s group at the University of Toronto and Daniel Majonis of DVS Sciences Inc. These polystyrene bead standards were selected such that the median dual counts on each mass channel ranged between 100 and 2000 counts per bead to ensure that there was both sufficient signal over background and that the signal was within the linear measurement range of the instrument. The use of 5 different metal isotopes spanning the mass range was intended to capture ‘mass-specific’ sensitivity variation in this study, however our data indicated that this phenomena was not prevalent and the change in signal was predominantly mass independent (Figure 2C). As such, any combination of isotopes would be appropriate for use in these beads standards as long as the met the aforementioned criteria (as few as two have been tested – data not shown). Use of a higher number of isotopes is recommended because it allows the more efficient removal of bead events and bead/cell doublets because of the unique fingerprint in 5 dimensional space and a more accurate approximation of variation by averaging all of the channels. Ideally, for identification purposes, the beads will contain at least one isotope not used as an antibody reporter; however, the software/algorithmic approach in this study is designed to accept any bead formulation that can be measured on the mass cytometer so as long as the same lot of beads is kept consistent for all files to be compared.

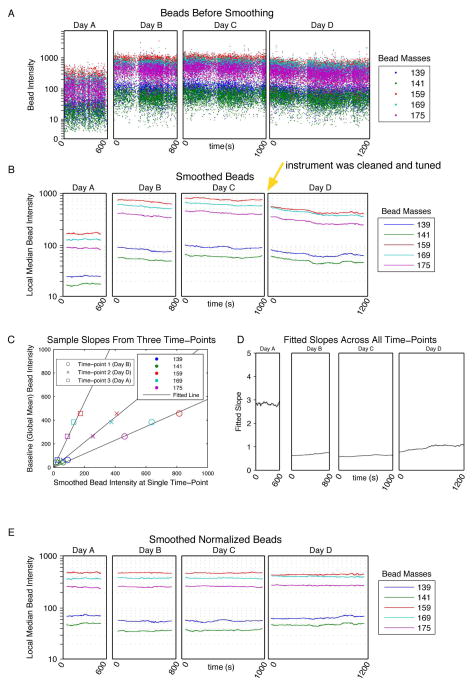
Figure 2. Bead smoothing and normalization.

(A) The raw intensities of the bead events in all of the bead channels were plotted over time for four files acquired on different days. (B) Smoothed intensity values were calculated by computing the median intensities across a sliding window of 500 beads. The smoothed intensities of the bead events in all of the bead channels were then plotted over time in the four files. Between collection of data files 3 and 4 the instrument was cleaned and tuned (yellow arrow), which resulted a shift in the relative bead intensities. (C) At each time-point in the smoothed data, the slope of the line through the origin was determined by minimizing the sum of the squared error between the bead intensities at that time point and the mean smoothed bead intensities across the experiment. The fits at three time points are shown. (D) The fitted slopes for all time points across the experiment. (E) The raw bead intensities were multiplied by the fitted slopes at each time point and then re-smoothed and plotted.

Antibodies against cell human blood cell surface epitopes were purchased from DVS Sciences (Sunnyvale, CA): CD19-Nd142, CD4-Nd145, CD8-Nd146, CD20-Sm147, CD61-Gd150, CD123-Eu151, CD45RA-Eu153, CD45-Sm154, CD33-Gd158, CD11c-159Tb, CD14-Dy160, CD16-Ho165, CD38-Er167, CD3-Yb170. Human peripheral blood mononuclear cells (PBMCs) were isolated using density gradient separation (Ficoll, Sigma-Aldrich) from whole blood obtained from the Stanford Blood Bank as previously described[2]. The blood for this study was obtained with informed consent in accordance with the Declaration of Helsinki. Stanford University’s institutional review board administrative panel on human subjects in medical research approved the collection of the peripheral blood at the Stanford Blood Center and the applications in the study described herein.

Preparation of cellular samples with bead standards

PBMCs were stained as previously described[2]. Briefly, 1.6% paraformaldehyde (PFA) fixed PBMCs were stained simultaneously with metal-conjugated antibodies according to the manufacturer’s recommendation. Cells were then permeabilized and fixed with methanol and incubated with a 1:5000 dilution of the Ir intercalator (2000x formulation, DVS Sciences) in PBS with 1.6% PFA. Cells were stored in this format for up to 1 month at 4°C. Over that period, aliquots of cells were periodically removed and analyzed on the same CyTOF mass cytometer (DVS Sciences). Just prior to analysis, the stained and intercalated cell pellet was re-suspended to a concentration of approximately 10⁶ cells per mL in ddH₂O containing the bead standard at a concentration ranging between 1 and 2 × 10⁴ beads per mL. Ideally, the bead standard acquisition rate should be 3 to 6 beads per second. The bead standards were prepared immediately prior to analysis, and the mixture of beads and cells were filtered through a 35-μm filter cap FACS tubes (BD Biosciences) before analysis.

Data acquisition

Cell events were collected on a CyTOF mass cytometer as previously described[2]. Briefly, cell length was set to range from 10 to 75 with a convolution threshold of 10 with the detection in dual counting mode. A detector stability delay of 20 seconds was used and all samples were diluted such that the acquisition rate was less than 500 cells per second. To ensure maximum consistency across data files, the dual count was set to ‘instrument’ mode rather than ‘data’ mode. The reason for using ‘instrument’ instead of ‘data’ based calibration was for the instrument to utilize the same set of dual count calibration slopes for all of the data acquired (as opposed to ‘data’ which calculates these on a file-by-file basis for each analyte). In doing so, we were able to keep the relative signal for each analyte (mass channel) consistent despite the global change in signal intensity; however, this normalization protocol is applicable regardless of the instrument set-up. Along with standard instrument maintenance and tuning, the instrument dual count slopes were also calibrated weekly according to the manufacturer’s recommended protocol. The instrument was cleaned and tuned between the third and fourth acquisitions. All other data acquisition and fcs conversion parameters were the manufacturer’s default settings. The data were processed using MATLAB (MathWorks).

Software

Executable MATLAB versions of the normalization software along with the original .FCS files analyzed in this manuscript will be available for download at www.cytobank.org/nolanlab.

RESULTS

Use of polystyrene, metal-containing beads as internal standards

Polystyrene bead standards embedded with five different metals meet several criteria allowing them to serve as internal standards for mass cytometry experiments. Each bead contained five virtually monoisotopic metal elements (La 139, Pr 141, Tb 159, Tm 169, and Lu 175) representative of the mass and dynamic ranges of the elements used to label antibodies[1, 2, 8]. The concentration of the beads was optimized to give a subpopulation of single-bead events (“singlets”) minimally compromised by cell-bead or bead-bead doublets - events that result from a bead combined with a cell or another bead, and therefore need to be discarded.

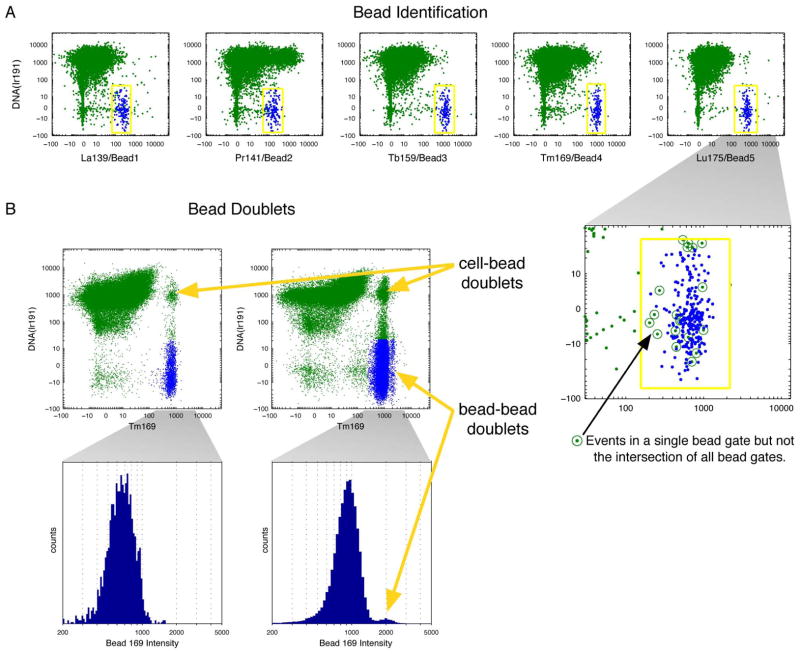
A mass cytometry experiment was performed with a sample of cells spiked with isotope-containing beads where the cells had been stained with antibodies conjugated to isotopic reporters on the same mass channels as the bead metals. A series of biaxial plots were generated to investigate the overlap of beads and cellular events (Figure 1A). To identify the beads, which were the events indicated by the presence of signals from each of the five bead elements and by a lack of DNA signal, five bead-channel vs. DNA gates were tailored to each file separately (Figure 1A). The events in each file that fell into all five gates were designated as beads, and the events that fell in some bead gates but not others were excluded; this filtered out cells and debris (Figure 1A close-up). Overall, the beads were clearly identifiable and separable from cell events; this means that an element can be used both to label a bead and to label an antibody, therefore resulting in no loss of available measurement parameters.

Figure 1. Bead singlet identification.

(A) Beads were identified by manually drawing liberal gates on biaxial plots of DNA by each of the five bead channels, shown in yellow. Events falling in the intersection of the five gates were labeled as beads and colored in blue. As seen in the close-up of the Lu175 plot, some events fall inside single gates but are eliminated because they are not present in the intersection of all five gates. The bead gating was done for each file separately. (B) Biaxial plots of DNA by the Tm169 bead channel in files using 1x and 10x of the standard bead concentrations, respectively, with histogram close-ups of the beads events within those files. Bead-bead doublets can be seen in the higher concentration, and cell-bead doublets are present in both.

To investigate the impact of bead doublets, samples spiked with 10,000 isotope-containing beads/ml (1X) and 100,000 beads/ml (10X) were compared in biaxial plots of DNA vs. Tm169, a metal present on the beads (Figure 1B left and right, respectively). In the sample spiked with the 1X beads, only bead singlets and cell-bead doublets were clearly observed. However, at the 10X concentration of beads, the biaxial plots revealed a subpopulation of the identified beads that had higher Tm169 than the main bead singlet population. A density estimate of Tm169 intensity in the identified beads within this sample yielded modes of the main and sub-peaks at 915 and 1992 counts, respectively (standard deviations σ=275 and σ=263). Measured intensities are expected to scale linearly on this instrument, so this supports the conclusion that the peak with higher Tm169 intensity, consisting of 1.9% of the identified bead events, was formed by bead-bead doublets (Figure 1B histograms). The effect of the bead-bead doublets on the median intensity of Tm169 at the 10X concentration was only a slight shift, from 904 counts in the entire bead population, to 900 counts when only the bead singlets (i.e., events with intensities lower than the saddle between the peaks) were considered. At the 1X bead concentration, bead doublets were estimated as only 0.43% of the identified bead events. The median intensities of the bead-embedded metals were used for normalization, so at the optimized concentration of beads (1X), the effect of bead-bead doublets was negligible.

The bead gates were drawn to select DNA-low events and thus excluded most cells, but some cell-bead doublets were present outside of these gates. In the 1X and 10X examples, cell-bead doublets accounted for 0.50% and 2.9% of all events, respectively. The cell-bead doublets can be gated out by identifying events positive for all five bead-elements without requiring low DNA as in the initial bead identification. More generally, all bead-associated events can be eliminated by removing events within a user-defined distance from the beads identified within the original overlapping five bead gates.

These results indicate that polystyrene beads can be distinguished from cell events even when the bead-embedded metals are also used as reporters for antibodies. The only restriction on panel design is that the composite bead signature must be distinct from that of all cells. In other words, no cell should have metal intensities overlapping the beads on all five bead channels, but four or fewer is permissible. Moreover, these results indicate that bead doublet events (both bead-bead and cell-bead) can be removed from the subsequent analysis using the unique signature of the five-metal bead standards. In cases where absolute separation of bead and cell events is required, the investigator may simply reserve one of the bead-embedded metals solely for the purpose bead identification (i.e. do not use any antibodies labeled with that metal). This approach would make identification of all bead-related events completely unambiguous.

Normalization of bead data

After identification of isotope-containing bead events, the intensities of the elements present on the beads were plotted over time (Figure 2A). To reduce the local variance, the raw intensities were smoothed by conversion to local medians. This smoothing was accomplished by calculating the median intensities within a sliding window of 500 bead-associated events centered at the time-stamp of each bead event (Figure 2B), which increased the mean pairwise correlations over time of the bead elements in a single file from 0.73 to 0.93 (Figure S1). Since the bead elements span the mass range of the CyTOF and their measured intensities vary across the instrument’s dynamic range, the fact that they were well-correlated with each other supported using the fluctuations observed in the smoothed beads to model changes in any intensity on all channels.

The smoothed intensities from each bead element were averaged across all files in the experiment, and these global means were chosen to be the baselines to which the beads would be normalized. For each time point at which a bead was present, a slope was computed for the line through the origin that minimized the residual sum of squares between the smoothed bead intensities at the given time and the baseline levels (Figure 2C). The linearity of the various bead elements as compared to their baselines confirmed that any mass-dependent sensitivity bias was static, i.e., the intensities of all bead elements varied at similar rates. The fitted slope summarized these rates into a single value at each time-point, which in turn formed the basis for a correction function that related the instrument sensitivity at a given time to the baseline normalization level.

Since the minimum intensity recorded by the instrument is always zero, the y-intercepts of the fitted lines were fixed at the origin (Figure 2C). To ensure accuracy of the fits, the slopes of the lines with fixed y-intercepts were compared to slopes fitted with variable y-intercepts. The slopes with an unfixed intercept differed from the zero-fixed slopes by an average of 2.2%, with a maximum difference of 4.2%. These discrepancies were small, and as non-zero intercepts would misalign negative populations, the fixed-intercept slopes were used.

To extend the calculated slopes from bead-associated events to all events, the values of the slopes were linearly interpolated over all time points of the experiment. Slopes were not interpolated across file boundaries; rather, the slopes for the events at the boundaries of the files (i.e., when the window contained fewer than 500 bead-associated events) were extrapolated by assuming that they had equal slopes to the closest bead time-point.

To restore the measured intensities to the global mean, the final normalization step involved multiplying the data in each event by the interpolated slope defined for that particular time point. The values of the slopes were highest in the first file, when the instrument sensitivity was approximately 3-fold lower than the average across the entire experiment (Figure 2D). After this normalization step and subsequent resmoothing, the average range of smoothed bead intensities across the experiment decreased from 4.9-fold to 1.3-fold (Figure 2B and E, respectively).

Bead- versus cell-derived normalization

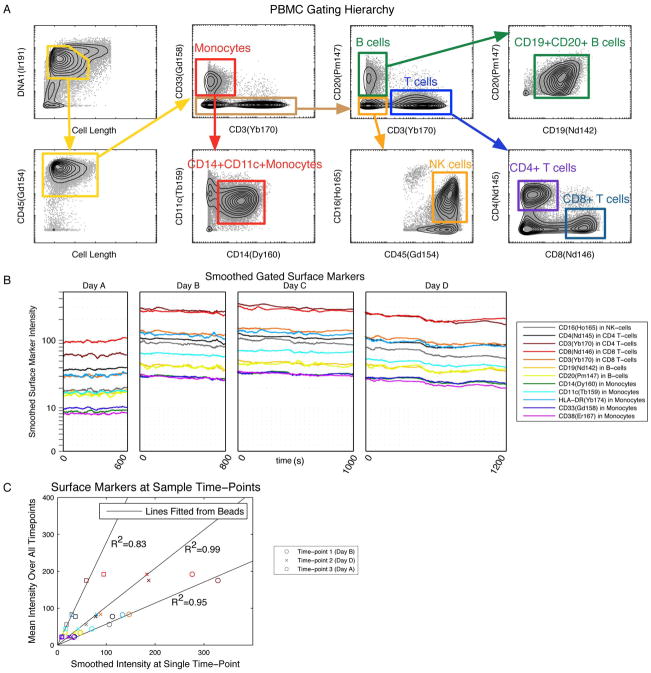
It was important to validate that intensities associated with cell-based events could be accurately normalized using the bead-derived slopes. In the case of data collected over 3 weeks from a single sample of human PBMCs, the signals of the surface markers positive in the gated cell populations were treated analogously to the beads, since they too could be assumed to have constant median intensities over time in the absence of technical variation. The identification strategy for cell populations of interest is shown in Figure 3A; the gates were tailored to each file separately to account for variations in the un-normalized signal intensities. To facilitate comparison between cell-associated and bead-associated metal intensities over time, the surface markers’ counts within these populations were smoothed according to sliding event-number windows (Figure 3B). The same windows were also applied to the beads, allowing association of each event with both median positive surface marker intensities and bead-associated intensities.

Figure 3. Selecting biological signals for validation of bead-based normalization.

(A) Human PBMC from a single healthy donor was stained with a panel of 14 antibodies against surface antigens, then measured repeatedly by mass cytometry on different days over a period of 1 month. The data was gated manually to identify 8 distinct immune subpopulations representing different levels of homogeneously expressed “positive” markers. The gate locations were tailored to each file separately; a representative file is shown. (B) The intensities of surface markers positive in each gated population were smoothed by computing the local medians in equal-sized event number windows and were then plotted over time. (C) The smoothed surface marker values at a given time point were compared to their means. Values are plotted here for three time points against the lines computed from the beads closest in time. The R² values of the markers with respect to the bead lines are shown.

The R² values of the smoothed cell surface marker signals relative to the bead-derived slopes had a mean of 0.95, with all values above 0.71. Examples from three different times are shown in Figure 3C. The agreement between the slopes computed from the beads versus the cells within the same sample confirmed that the beads captured the instrumental artifacts in the measurement of the metal-conjugated antibodies. This supports the general application of this bead normalization procedure to realistic biological experiments, in which measurements of the metal-conjugated antibodies are expected to change under different experimental conditions and therefore cannot be used for normalization.

Normalization of surface marker signals in immune cell subsets

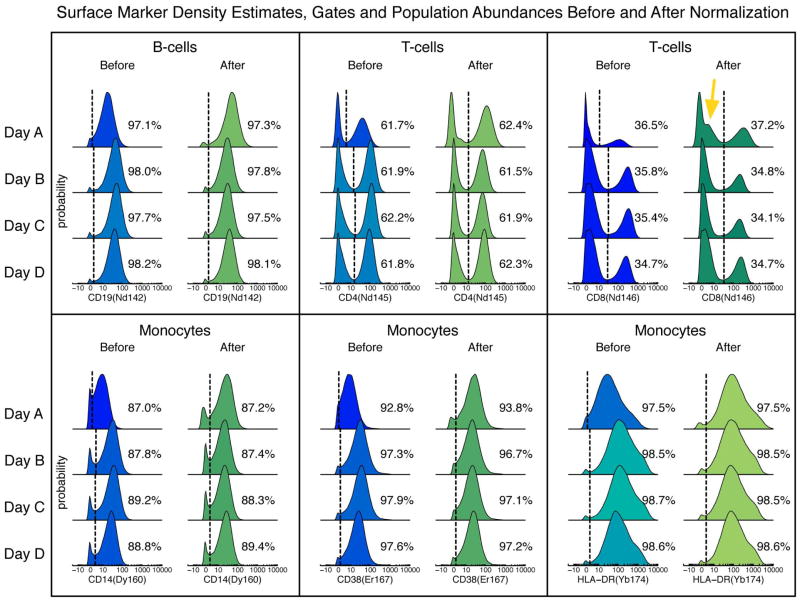
Examining the alignment, abundance, and correlations of the surface markers in the gated immune cell subsets of the PBMC sample before and after normalization corroborated the validity of the algorithm. Without normalization, it was necessary to draw gates manually for each file because variations in signal levels over time shifted the population boundaries. For example, important gates for defining B cells, T cells, and monocytes are shown in Figure 4, along with the percentage of cells falling into each positive gate. If the tailored gate determined by the first file had been applied to all four files without normalization, the abundances of the positive populations in the latter three files would have varied from their tailored values by up to 5.7%, with an average difference of 2.0% (data not shown). In contrast, after normalization, a single gate for each surface marker globally applied to all the files preserved each of the pre-normalization tailored abundances to within 1%.

Figure 4. Distributions of surface markers before and after bead normalization.

Density estimates of selected markers in various populations before and after bead normalization in the same sample measured on four different days. Binary gates (dotted lines) were manually tailored to each of the four files separately before normalization, and global gates were drawn after normalization. The percentages of the cells in the positive gates are shown.

Because the corrections are made with a multiplicative factor, noise amplification can occur when the instrument sensitivity is much lower than the baseline level. An example of this effect is seen in the CD8⁻ cells within the CD3⁺ population (Figure 4, yellow arrow). The raw values were multiplied by slopes of approximately 3, amplifying the noise around the intensity values of 1–2 counts. Even though the abundance within the gate was not changed significantly, the correction altered the negative half of the distribution, and thus caution must be used when drawing conclusions from the profile of low-intensity events after normalization. In this extreme example, the instrument sensitivity was approaching its lower limit of utility when the first file was acquired; the positive and negative subpopulations within the monocytes were just barely separable before normalization (Figure 4). Had the sensitivity been any lower, the positive population would not have been discernible from the negative cells even after normalization. These results underscore that it is imperative that the instrument is cleaned and tuned regularly such that all analytes are at detectable levels, since the normalization procedure cannot correct for this after the fact. Importantly, the choice to use the global mean of the smoothed bead intensities as the baseline, rather than the minimum or maximum levels, limited the noise amplification while maintaining a dynamic range that allowed separation of populations.

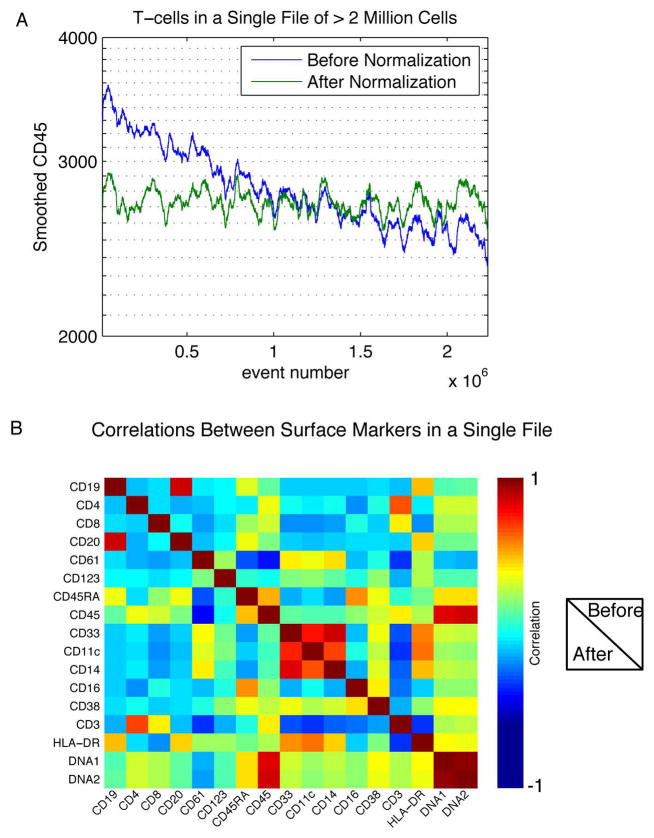
In general, there is a decrease in instrument sensitivity as a function of acquisition time (with the sensitivity restored after routine maintenance), thus decay of signal strength within a single file is most pronounced when data is acquired from large numbers of cells. Such data acquisitions may be necessary when quantifying rare cell-types, or when barcoding different conditions together will result in subdivision of the file into many parts[9]. In an example of a single file containing more than 2 million events collected over approximately 3hrs, the median CD45 intensity of the last 1000 T cells analyzed was 73% of that of the first 1000 T cells analyzed (Figure 5A). After normalization, the median intensity of the last 1000 cells was increased to 98% of the initial 1000 cells. This example reinforces the necessity of using the sliding window approach described herein rather then applying a global correction to each acquired file.

Figure 5. Normalization stabilizes surface marker intensities over time and maintains multivariate correlations between markers.

(A) A sample of > 2 million cells was measured in a single acquisition acquired over a period of >2 hours. The smoothed CD45 intensity of CD3⁺ cells is shown before and after bead normalization. (B) The pairwise correlations between cell surface markers in a single file were calculated and displayed here as a heatmap. The correlations before and after normalization are shown in the upper-right and lower-left triangles of the plot, respectively. The values on the diagonal are the correlations between a single parameter with itself before and after normalization.

To investigate the possibility of systematic artifacts introduced by the normalization procedure, we tested whether multivariate relationships between different measured parameters were preserved. The pairwise correlations between surface markers in the file from Day C are shown in a heat map (Figure 5B). The symmetry across the diagonal demonstrates consistent correlations before and after application of the normalization algorithm, confirming that the application of a single multiplicative factor as a correction for all parameters of each event does not significantly alter the relationships between the parameters measured in each cell in the experiment.

Normalization algorithm applied to different primary samples measured over time

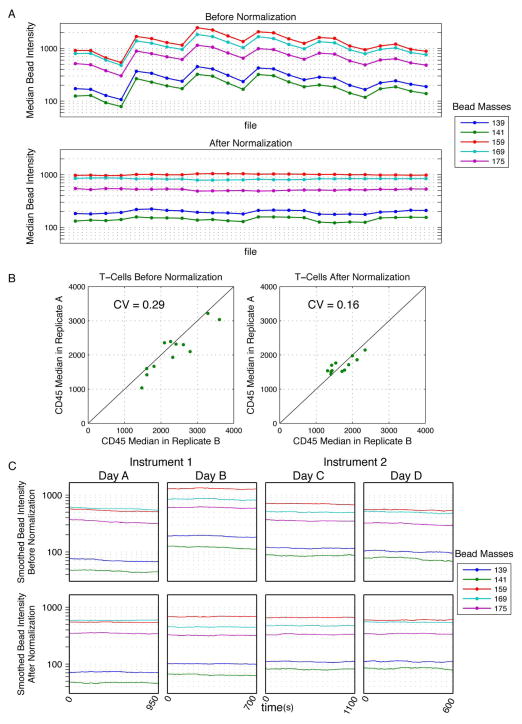
To demonstrate the utility of this algorithm in analysis of a greater number of biological replicates collected over a period of several days, an experiment was performed in which, over the course of two weeks, twelve primary samples representing different individuals were analyzed. Two samples from each of the twelve individuals were collected, generating 24 data files in total. The median bead intensities for all files were plotted before and after normalization; application of the normalization algorithm reduced the fold-change of bead intensity medians over the course of the experiment from 4.1 to 1.2 (Figure 6A). Additionally, the median CD45 intensities from gated CD3⁺ T cells in replicate A and B from each individual were compared for the 12 samples, both before and after normalization (Figure 6B). The coefficients of variation (CV) for the median CD45 values in the each of the files were reduced from 0.29 to 0.16 by normalization. Thus, normalization reduced the variability of CD45 levels both within and across the samples, allowing confident interpretation of the biological differences between samples. In this example, surface marker-based normalization would have been impractical because consistency cannot be assumed across samples from different human donors.

Figure 6. Normalization of data spanning multiple days and instruments.

(A) Pediatric leukemia bone marrow samples (n = 12) were measured with 2 antibody staining panels, totaling 24 .fcs files collected over 6 days. Median intensities of bead events extracted from each file were plotted before and after normalization (each point represents one file). (B) Gated CD3⁺ T cells from each staining panel (Panel A and Panel B) were used as technical replicates to illustrate the improved consistency after normalization. The median CD45 values for T cells from each staining panel were plotted against each other for each of the 12 samples, before and after normalization. The R² values of the data as compared to a line of equality are shown. (C) Metal-embedded beads were acquired on two different days and two different instruments. Bead intensities were smoothed as described and, are plotted over time.

Normalization algorithm applied to data collected on different instruments

Application of this normalization algorithm should also improve the correspondence of data acquired on different instruments. Indeed, an improvement in cross-instrument consistency was observed when this method was applied to data acquired on two different machines over two days (Figure 6C). However, subtle differences in the relative signal strengths of different mass channels between machines compromised the linearity of the relationship between intensities analyzed at different time points and the global mean baseline. This is the same issue that has been occasionally observed when using a single instrument before and after tuning (Figure 2B, yellow arrow). Therefore, while the methodology presented here appears to make data more comparable between analogous instruments, this experimental approach should be avoided if possible, as it falls short of the accuracy that could be obtained by performing the same analysis longitudinally on a single instrument with consistently applied settings.

Bead fluctuations provide a threshold for biologically meaningful signals

A notable benefit to measuring beads simultaneously with cells is that the beads allow the technical variation in instrument measurements to be quantified. In the absence of instrument fluctuations, the smoothed intensities of the beads should remain constant over time. Thus, any deviations that are observed in the bead signals indicate the amount of variation expected in the cellular data due to changes in instrument state. For example, in the PBMCs examined here, the 4.9-fold range in median bead intensity between files A and C meant that up to a 5-fold change in intensity could be due to instrument fluctuations. Application of the normalization algorithm reduced this to 1.3 fold (Figure 2B and E), effectively decreasing the threshold below which observed fold-changes in data were likely to be dominated by technical variation rather than biological differences. In this example, cellular parameters exhibiting a >1.3-fold change have the potential to be biologically meaningful, but appropriate controls are still needed to identify the overall technical variation in the assay (i.e., pipetting error). It is noteworthy that the threshold values can change based on the performance of the bead-based normalization. Factors contributing to such changes include instrument maintenance and tuning, working with data from multiple instruments, and the duration of data acquisition time. This threshold, as well as plots of the smoothed beads over time both before and after normalization, is included as outputs in the normalization software.

DISCUSSION

A normalization algorithm that reduces the contribution of instrument fluctuations to mass cytometry data is presented here. At the core of the algorithm are the signal intensities of metal-embedded beads included in each cellular sample measured by the mass cytometer. The method described employs a multiplicative correction derived from slopes fitted between smoothed bead signals and their global averages, thus minimizing the effects of instrument variation on mass cytometry data. It therefore expands the types of analyses available using mass cytometry by allowing comparisons to be made across data acquired over periods of weeks or longer.

In particular, this type of normalization is crucial for the study of samples from different individuals treated under different conditions. In these cases, samples may be collected over extended time periods, and surface marker expression may differ from person to person and condition to condition. Previously, data from such studies had been corrected using the intensities of metal-conjugated antibodies in technical replicates that were collected throughout the experiment[2]. However, even when a parameter can be expected to remain constant across several samples and a surface marker-based normalization is possible, correction slopes derived from metal-conjugated antibodies will be uncertain due to differences in staining (“batch effects”). Moreover, the small CVs of the bead population as compared to those of the cell surface markers, plus the rarity of bead-bead doublets and the ease of consistent bead gating, make a bead-based approach superior to cell-based normalization. The normalization software is freely available at www.cytobank.org/nolanlab.

In addition to being used for data normalization, the internal bead standards may provide a mechanism for quantification and monitoring instrument performance, assuring the highest quality data. Weaker antibody targets require a certain minimum threshold of instrument performance to be detected, while abundant antibody targets may continue to be detectable after many hours of instrument use. The intensities of the bead-embedded metals can be monitored such that when they drop below a critical threshold, it is an indication that the instrument’s sensitivity has dropped below specification and thus it needs to be cleaned or recalibrated. The definition of this threshold will vary depending on the analytes in each investigator’s experiment. For example, the Pr141 intensity of the beads on Day A approached zero (Figure 2A), which corresponded to an overlap of the CD14⁺ and CD14⁻ subpopulations within the CD33⁺ monocytes. The normalization procedure cannot successfully recoup data in this case, and in fact may introduce artifacts by over-amplifying noise. Thus to achieve the highest data quality, it is advised that each investigator determine the critical sensitivity threshold for their assay, and monitor the bead signal levels frequently (e.g., hourly and at the start of each acquisition), cleaning the instrument as needed.

The increased dimensionality (>40 parameters) of mass cytometry relative to standard fluorescence-based flow cytometry has enabled collection of significantly more information at the single-cell level. Given the depth of the biology revealed, it is critical to account for variations related to instrument performance so that the data is reliable. Experimental design can mitigate these variables to a certain extent. For example, when measuring intracellular signaling profiles of samples treated with different extracellular modulators, samples may be barcoded and data acquired simultaneously to minimize the effect of signal level drift[9]. Using this strategy, fluctuations will increase the variance in the measurements, but will not bias certain conditions to appear higher or lower than others due to their measurement order. For example, by using the IC₅₀ of drug responses, or the fold-change values between treated and untreated conditions, the reliance on absolute signal levels is decreased. Regardless of experimental design, however, normalization that accounts for instrument fluctuations is a desirable and fundamental addition to the mass cytometry workflow. The bead-based approach described here offers a means for correcting inter-experiment as well as minimizing inter-machine variation during various mass cytometry studies.