Abstract
Every sensory event elicits activity in a broad population of cells that is distributed within and across cortical areas. How these neurons function together to represent the sensory environment is a major question in systems neuroscience. A number of proposals have been made, and recent advances in multi-neuronal recording have begun to allow researchers to test the predictions of these population-coding theories. In this review, I provide an introduction to some of the key concepts in population coding and describe several studies in the recent literature. The focus of this review is on sensory representation in the visual cortex and related perceptual decisions. The frameworks used to study population coding include population vectors, linear decoders, and Bayesian inference. Simple examples are provided to illustrate these concepts. Testing theories of population coding is an emerging subject in systems neuroscience, but advances in multi-neuronal recording and analysis suggest that an understanding is within reach.
Keywords: Population code, visual cortex, perceptual decision, linear decoder, Bayesian inference
Introduction
One of the major goals of systems neuroscience is to understand how the nervous system creates complex behavior, such as perception and cognition. A key structure of the brain is the cerebral cortex, where neural circuits convert sensory signals into motor commands. Much of systems neuroscience endeavors to understand the computations that take place in these circuits. One powerful approach is to measure the signals in a given circuit, namely, the spike trains of neurons, and to study their relationship to a sensory stimulus or motor output.
The traditional method of directly measuring spike trains is to insert microelectrodes into the cortical tissue. This method, however, poses a number of challenges. Arguably the most profound is the small number of spike trains that can be measured simultaneously. In traditional experiments, no more than a few neurons are sampled at a time (Alonso et al., 1996; DeAngelis et al., 1999; Gawne et al., 1996; Gochin et al., 1994). This severely limits the range of questions that can be addressed via experiment. Even simple relationships, such as the correlation of a neuron with its neighbors, are difficult to characterize without simplistic assumptions (Zohary et al., 1994). Thus, traditional methods have hindered the progressive chain of building theories and testing predictions of how networks of neurons give rise to the computations underlying complex behavior.
Techniques for multi-neuronal recording have advanced over the past decade. Whereas multi-neuronal recording previously involved measuring the spike trains of pairs of neurons (Alonso et al., 1996; DeAngelis et al., 1999; Gawne et al., 1996), it now involves simultaneously recording from populations of neurons on the order of approximately 70 cells (Churchland et al., 2010; Cohen and Maunsell, 2009; Ecker et al., 2010; Smith and Kohn, 2008). This technological advancement has expanded analyses beyond pairwise relationships of firing patterns, e.g., synchrony or correlation, to information coded in the population activity (Berens et al., 2012; Churchland et al., 2012; Graf et al., 2011). In this review, I cover several areas in which considerable strides have recently been made by neuronal populations, with a focus on the coding of sensory information in the visual cortex.
Population vectors and linear decoders
A pioneering theory of population coding in the visual cortex assumed that each neuron represented a vector (Gilbert and Wiesel, 1990; Vogels, 1990). In this view, the preferred orientation of a neuron defines the direction of a vector and the neuron’s firing rate provides the amplitude. The neuronal population coded the stimulus orientation as the vector sum of all the neurons; hence, this coding scheme is termed the “population vector”. The population vector was originally posited for coding the direction of a reaching arm movement by neurons in the motor cortex (Georgopoulos et al., 1986). In both models of the visual and motor cortices, the population vector utilizes the bell-shaped tuning functions of individual neurons to represent a circular variable. In principle, the value of the encoded variable is completely recoverable with a very small number of neurons in the representation. In the absence of response variability, two neurons are sufficient to represent the full range of orientations (Fig 1A).
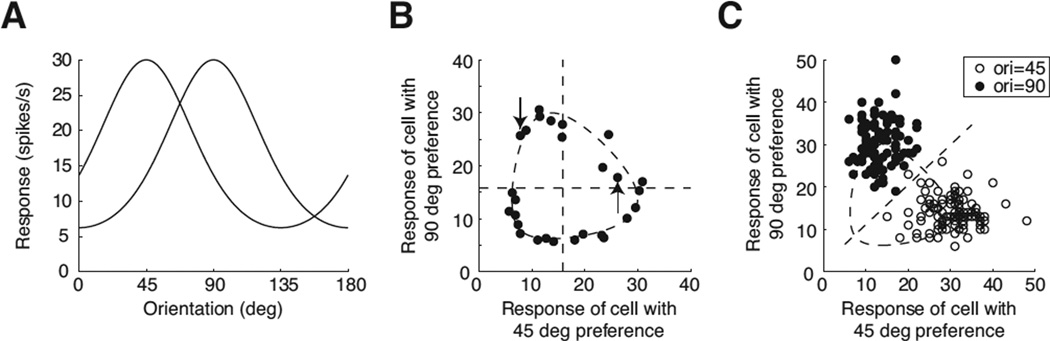
Figure 1.
A demonstration of a population response. A) The population consists of two cells. One cell prefers a 45 deg orientation, while the other prefers a 90 deg orientation. The tuning functions are modeled with a Von Mises function. B) The population response represents a single point on a plane. The dashed ellipse shows the set of points as orientation varies, in the absence of variability. The black dots show how the responses deviate from the ellipse in the presence of Poisson variability. Orientation was varied in 5 deg steps. The upward and downward arrows point to the responses when the orientation was 45 deg and 90 deg, respectively. These points correspond to the right-hand and top corners of the dashed ellipse. C) The two orientations, 45 deg (open dots) and 90 deg (filled dots), were repeated 100 times each. The variability of the responses makes the points scatter around the corresponding point on the dashed ellipse. The diagonal line shows the fitted boundary between the two clouds of dots. Linear discriminant analysis was used for the fit.
The minimum population size of two follows from two simple mathematical facts: A) orientation is a circular variable that can be mapped onto a point on a unit circle and B) the point can be represented in a Cartesian coordinate system with two dimensions. In order for the mapped set to be an exact circle, the orientation tuning of individual neurons must have a sinusoidal shape, and the sinusoids must be orthogonal to each other. For example, let’s assume that there are two neurons with response r1 and r2,. Their responses to an orientation θ are
, where r̄ denotes the average response to all orientations. With elementary trigonometry, we can solve the equations for θ with the following:
.
Thus, the original value θ is completely recoverable from the responses of the two model neurons. Real neurons deviate from the idealized conditions in a number of ways, but subtle deviations in the shape of the tuning functions are relatively trivial. The population vector works as long as neurons have bell-shaped tuning functions.
In reality, small populations of neurons provide poor coding performance because the responses of visual neurons are variable to repeated trials of the same stimulus (Shadlen and Newsome, 1998; Tolhurst et al., 1983; Vogels et al., 1989). The variability acts as noise in the visual system, when we view the function of the system is to represent the stimulus value (Fig 1B). In the above equation, we cannot recover the original θ with perfect accuracy when r1 and r2 are corrupted with noise. However, we can make the population vector robust to such noise by increasing the population size because independent variability is cancelled through the summation. As more neurons are recruited to the population, more of the independent variability is canceled. This follows directly from the central limit theorem, which states that the confidence interval of the mean from N samples is inversely proportional to the square root of N. In the case of the population vector, having neurons with the same tuning function in the visual system is not redundant, but rather is advantageous to the animal for representing the stimulus value.
Pooling over a large population will eliminate noise when the variability is independent across the population. Otherwise, when the variability is not independent between the neurons, the pooling will not eliminate the noise no matter how large the population might be (Shadlen et al., 1996; Zohary et al., 1994). In most areas of the cortex, the variability of neurons is weakly correlated. Values of the measured correlation varies across studies, but the correlation are always non-zero (for a summary across various cortical areas, see (Cohen and Kohn, 2011)). Even a weak correlation will preclude the elimination of noise by pooling.
Theoretical studies predict that the structure of correlated variability can have strong effects on the accuracy of the population code (Abbott and Dayan, 1999; Paradiso, 1988; Shadlen et al., 1996; Vogels, 1990). The equations and simulations show that knowledge of the correlation matrix is critical to estimate the accuracy of the coding. The difficulty in measuring the structure of correlations has been the inadequate size of the sampled population of neurons. Because all the neurons have fluctuations, the correlation matrix of all combinations of neurons in a population must be measured in order to adequately characterize the variability.
An important implication of the theoretical studies was that the population vector is neither an accurate nor plausible way of representing a stimulus variable (Salinas and Abbott, 1994). The population vector is prone to misrepresent the stimulus variable when faced with response variability; the reconstructed stimulus will have a bias unless certain conditions are fulfilled. A generalization of the population vector was proposed (Salinas and Abbott, 1994), which relaxes the fixing of the vector, and retains the weighted summation (also known as the linear combination in mathematical terms) of the population’s response. This generalized model was coined the linear decoder. Under the assumptions of the linear decoder, the challenge is to correctly estimate the weights in order to recover the original stimulus (Fig 1C). The approach of the linear decoder is to use a prerecorded set of trials to fit the weights of each neuron. If the weights are estimated correctly, the original stimulus should be recoverable more accurately from the weighted sum of the population’s response than from the population vector.
To demonstrate the difference in accuracy, we take the example in Fig 1C and modify the model so that a misrepresentation becomes more apparent. This is done by replacing the model cell with a 45 degrees (deg) preference for another one with an 85 deg preference. With the modified model, the clouds of dots with filled and open symbols will overlap substantially. We simulated the modified model and found that the population vector correctly recovered the stimulus in only 90% of trials, while the linear decoder did so in 96% of trials. Thus, the linear decoder was more accurate at reconstructing the stimulus.
The linear decoder has an appealing aspect besides it accuracy. The weighted summation is a plausible model of what actually happens in the visual cortex; the summation of inputs is what neurons compute, to a rough approximation (Shadlen et al., 1996). This allows us to investigate how sensory representations lead to perception. To set the stage for concrete predictions, we must first define perception as a measurable quantity. A powerful approach is sensory discrimination, in which subjects must decide which action to take based on what he/she just perceived. This framework has come to be widely known as perceptual decision making (Newsome et al., 1989) to clarify that the task of the subject involves both perception and decision-making.
Bayesian inference and probabilistic population code
Perceptual decisions are inevitably accompanied by uncertainty. Subjects are aware of the multiple choices that are potentially correct, but the ground truth is undisclosed. Subjects must use the available information in order to infer the truth as accurately as possible. This is an inference process, so it is helpful to formalize the problem in terms of statistical inference (Gold and Shadlen, 2001).
The basis of statistical inference is the Bayes’ theorem, which establishes the precise relationship of the probabilities regarding the sensory stimulus s and the population response r = {r1, r2, …, rN}, as:
.
The denominator P(r) is often omitted because it does not depend on the stimulus s. In an inference process, the value of P(r) is fixed. Its omission from the denominator turns the Bayes’ theorem into a proportional relationship:
.
This relationship has useful implications. The distribution P(s|r) on the left-hand side is the desirable function for the inference (called the posterior probability). Given the population response r, the decision process needs to determine the s that has the highest probability. The problem with this inference is that there is no means for directly estimating P(s|r) in an experiment, as it would take an enormous number of trials to sample every population response multiple times. The above relationship provides a solution to this problem. The two distributions on the right-hand side are in fact measurable. We will follow the nomenclature of statistical inference and call P(r|s) and P(s) the likelihood and the prior probability, respectively.
The ground truth of the prior probability P(s) is predefined in the perceptual-decision task. Typically the prior probability is set to a uniform distribution, in which P(s) is substituted with a constant and absorbed into the proportionality. The above relationship simplifies to P(s|r)∝P(r|s). When the task satisfies this proportionality, the highest peak in the distribution of the posterior probability coincides with the highest peak in the distribution of likelihood (Fig 2). Thus, determining the peak of likelihood is the statistically optimal solution of the inference.
Figure 2.
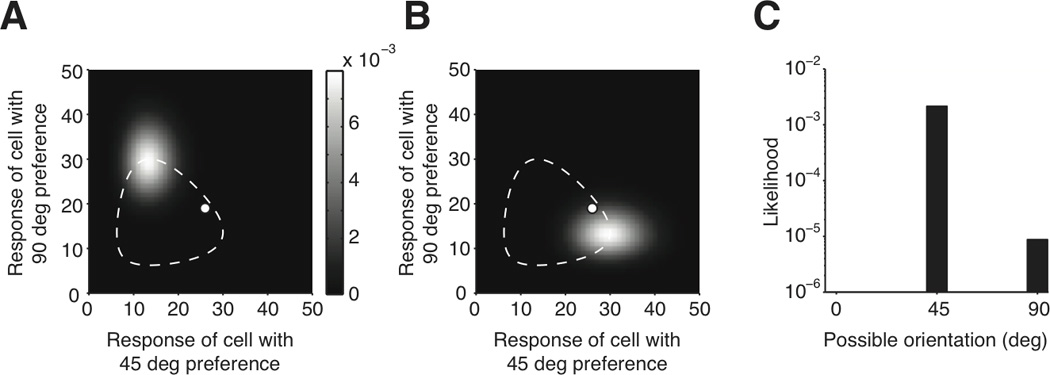
A demonstration of Bayesian inference. A) The values of the likelihood P(r|s=90) are shown as a heat map. Each position represents a population response to a 90 deg orientation. The peak of the heat map is located at the top corner of the dashed ellipse, which corresponds to the response in the absence of variability. The white dot shows the population response on a given trial. B) The values of the likelihood P(r|s=45) are shown. The white dot is plotted again for the same sampled trial. We use the heat maps to look up the likelihoods of 45 and 90 deg orientations on the sampled trial. C) The likelihood values of this trial are plotted against orientation. The likelihood of a 45 deg orientation was higher than 90 deg. The final output of the inference process is an orientation of 45 deg.
An optimal inference is possible with a model as simple as a linear decoder, provided that the variability of individual neurons follows a Poisson distribution (or a distribution with similar properties as a Poisson) and provided that the variability of the neuronal population is independent of each other. Under these conditions, the logarithmic of likelihood P(r|s) is a linear combination of the population response r = {r1, r2, …, rN}. The prediction is that each neuron’s tuning function determines the weights (Jazayeri and Movshon, 2006). The predicted relationship is formally written as:
where the function fi(s) represents the orientation tuning of the i-th neuron. A straightforward way to test this prediction is to compare the accuracy of inference with other linear decoders (e.g., ones that fit the weights). The Bayesian model should infer the orientation more accurately than any other linear decoder.
A recent study tested this prediction with population responses measured in the primary visual cortex (Graf et al., 2011). The authors found that, contrary to the prediction, it was the linear decoder with fitted weights that outperformed the Bayesian model in accurately inferring the orientation. The linear decoder with fitted weights was able to infer two orientations, separated by 5 deg, with ~85% accuracy, whereas the Bayesian model inferred with only ~70% accuracy. The results of this study suggest that the population response in the visual cortex deviates from the assumptions of the model. In particular, the correlated variability of the neuronal population caused the Bayesian model to perform less well. The linear decoder with fitted weights adapted successfully to the existing correlation. It is essential to record the trial-by-trial responses of the population for the fitting, as an accumulation of paired recordings in separate sessions is not sufficient to fit the weights. The superior accuracy of the linear decoder implies that the decision mechanism should take into account the correlations in the visual cortex, rather than be based simply on individual tuning properties, to provide the best performance.
The Bayesian model is a general framework with a wide range of applications. The model applies to cases with more than one population of neurons representing the same sensory stimulus. Two populations might provide separate information to the decision mechanism. The solution to this conflict is to sum the responses of the two corresponding neurons (Ma et al., 2006). The authors propose that the resulting population response, as a whole, implicitly represents the distribution of the posterior probability. They show that the summation is actually advantageous because the peak of the represented posterior probability is closer to the truth than either of the two populations alone. In this model, probabilities are not explicitly calculated with a linear decoder. Ma et al. termed this coding scheme the “probabilistic population code” and distinguished it from linear decoding models. Probabilistic population codes and linear decoders are not mutually exclusive. It is possible that both mechanisms work at different levels in the neural mechanism of perceptual decisions. The probabilistic population code has yet to be tested with experimental data; a direct test would require recordings from three separate populations that have correspondence between their neurons.
Object recognition and dimensionality reduction
The major difference between a linear decoder and the population vector is that a linear decoder detaches neurons from their labels (i.e., the preferred orientation). Without the labels on the neurons, the linear decoder has a wider range of applications than the population vector.Gochin et al. (1994) employed this property of linear decoders to explore the sensory representation in a higher area of the visual cortex. In the inferior temporal cortex (IT cortex), neurons do not have a distinct bell-shaped tuning function to any stimulus variable, although they signal information about the identity of objects. Without a bell-shaped tuning, it is unhelpful to attach a label to the neurons (e.g., the preferred orientation). Instead of varying the orientation, the authors used a variety of images of real and abstract objects. They recorded simultaneously from up to eight neurons in the IT cortex. They fitted a linear decoder to the data and were able to recover the image with 75% accuracy (Gochin et al., 1994). This accuracy is high compared to a chance level accuracy of 20% (the linear decoder must recover one image out of five). The success of a linear decoder suggests that a similar mechanism might underlie the transformation of visual representations in the IT cortex to object recognition.
The linear decoder applied to IT neurons has a property that is intriguingly similar to our daily experience in recognizing objects. We accurately recognize objects from their images even though the images vary to a great degree, depending on variables such as the object’s position in the visual field. Our visual system is thought to learn the association between the object and particular images and generalize the association to new images. Similar to that human ability, a linear decoder fitted to the responses of IT neurons successfully recovers the category and identity of the object even after the image has been altered for translation and expansion (Hung et al., 2005). A mechanism similar to a linear decoder might transform the object representation by IT neurons to object recognition. Such a transformation suggests that any dynamic changes in the population response of IT neurons should be reflected in object recognition.
A graphical visualization of the population response helps us characterize how the response evolves over time. To do this, it will help to return to the inner workings of the linear decoder. At the front end of a linear decoder, the geometrical representation of the sensory representation is a point (or a vector) in an Ndimensional space, where N is the number of neurons in the population. That point is then projected to a point in low dimensional space. This reduction in dimensionality is a powerful approach to make the stimulus reconstruction more straightforward. The previous example in Fig 1C graphically illustrates the dimensionality reduction. The linear decoder projects each dot on a plane (a 2- dimensional space) onto an axis (a 1-dimensional space) which is perpendicular to the boundary. The projection reduces the dimensions from 2 to 1. A similar technique for dimensionality reduction is principal component analysis (PCA). The only difference with linear decoders is that PCA determines the projection solely based on the distribution of the cloud in the original N-dimensional space. PCA identifies the projection onto the axis along which the entire cloud is elongated. Unlike a linear decoder, it does not fit the best projection for stimulus reconstruction.
Using PCA, the population response of IT neurons was shown to evolve in a particular pattern over the course of the response. During the first 50 ms of the response, the cloud of dots is separated by category only (Matsumoto et al., 2005). All the dots corresponding to the same category form a tight cluster of dots. Thus, the population response only differentiates the category of the stimulus, and not the identity. Toward the latter 50 ms of the response, each tight cloud begins to spread. The spreading suggests that the population response is able to differentiate the identity of the stimulus.
The delay of spreading provides an explanation of why object recognition appears to happen in two steps; we recognize the rough category of the object first (e.g., face vs. non-face) and later discern the identity from finer details (e.g., the faces of individuals A vs. B). The population responses are very similar for the various identities in the same category in the early phase of the response. There is no boundary that might separate the tight cloud of dots. Boundaries can only be drawn when the cloud separates in the later phase of the response (Matsumoto et al., 2005). This example of the IT population demonstrates how powerful dimensionality reduction is as a tool for analyzing the dynamics of the population response. Dimensionality reduction has also revealed interesting transitions in the movement signals of the motor cortex, from which the population vector was first conceived (Churchland et al., 2012, 2010). Dimensionality reduction may open new doors into understanding the computations that take place in various other cortical circuits.
Conclusions
This review covered several topics that directly used population codes as a means to represent sensory information in the visual cortex. Some of the concepts, such as the population vector, have been around for over two decades (Georgopoulos et al., 1986), although they are relatively newer to neurophysiology than traditional concepts such as stimulus selectivity and receptive fields (Hubel and Wiesel, 1962). Techniques for multi-neuronal recording have brought population codes from the arena of mathematical modeling to evidence-based testing. The neural circuits that convert sensory representations into perceptual decisions provide a model system for testing population codes. This is not to say that these circuits are the only system. The motor cortex (Churchland et al., 2012, 2010) and the retina (Pillow et al., 2008; Schneidman et al., 2006; Shlens et al., 2006) have also proven to be powerful test-beds, although they were not covered in this review.
Technological advancement of multi-neuronal recording and conceptual advancement in population coding have evolved hand-in-hand. On one hand, ideas on how to test population codes have pushed researchers to take up newly available recording systems. On the other hand, demands from researchers have spurred engineers to develop devices that record ever-larger populations of neurons simultaneously. In addition to testing theories of population codes, another notable drive for developing these devices is the applications to medical engineering, such as neural prostheses (Nirenberg and Pandarinath, 2012; O’Doherty et al., 2011; Velliste et al., 2008). We expect to see more discoveries as more theories of population coding are tested and as even newer concepts are introduced.
Highlights.
Techniques for multi-neuronal recording have advanced in the past decade.
Researchers are now able to test the predictions of population-coding theories.
Several topics on population coding are introduced and reviewed.
We expect to see more discoveries as newer concepts and predictions are introduced.
Acknowledgment
The author thanks Adam Kohn for providing helpful comments on this manuscript.
Abbreviations
- deg
degrees
- IT
Inferior temporal
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abbott LF, Dayant P. The effect of correlated variability on the accuracy of a population code. Neural Comput. 1999;11:91–101. doi: 10.1162/089976699300016827. [DOI] [PubMed] [Google Scholar]
- Alonso JM, Usrey WM, Reid RC. Precisely correlated firing in cells of the lateral geniculate nucleus. Nature. 1996;383:815–819. doi: 10.1038/383815a0. [DOI] [PubMed] [Google Scholar]
- Berens P, Ecker AS, Cotton RJ, Ma WJ, Bethge M, Tolias AS. A fast and simple population code for orientation in primate V1. J. Neurosci. 2012;32:10618–10626. doi: 10.1523/JNEUROSCI.1335-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, Shenoy KV. Neural population dynamics during reaching. Nature. 2012;487:51–56. doi: 10.1038/nature11129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Ryu SI, Shenoy KV. Cortical preparatory activity: representation of movement or first cog in a dynamical machine? Neuron. 2010;68:387–400. doi: 10.1016/j.neuron.2010.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Kohn A. Measuring and interpreting neuronal correlations. Nat. Neurosci. 2011;14:811–819. doi: 10.1038/nn.2842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Maunsell JH. Attention improves performance primarily by reducing interneuronal correlations. Nat Neurosci. 2009;12:1594–1600. doi: 10.1038/nn.2439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAngelis GC, Ghose GM, Ohzawa I, Freeman RD. Functional microorganization of primary visual cortex: receptive field analysis of nearby neurons. J Neurosci. 1999;19:4046–4064. doi: 10.1523/JNEUROSCI.19-10-04046.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ecker AS, Berens P, Keliris GA, Bethge M, Logothetis NK, Tolias AS. Decorrelated neuronal firing in cortical microcircuits. Science. 2010;327:584–587. doi: 10.1126/science.1179867. [DOI] [PubMed] [Google Scholar]
- Gawne TJ, Kjaer TW, Hertz JA, Richmond BJ. Adjacent visual cortical complex cells share about 20% of their stimulus-related information. Cereb Cortex. 1996;6:482–489. doi: 10.1093/cercor/6.3.482. [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science. 1986;233:1416–1419. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Wiesel TN. The influence of contextual stimuli on the orientation selectivity of cells in primary visual cortex of the cat. Vision Res. 1990;30:1689–1701. doi: 10.1016/0042-6989(90)90153-c. [DOI] [PubMed] [Google Scholar]
- Gochin PM, Colombo M, Dorfman GA, Gerstein GL, Gross CG. Neural ensemble coding in inferior temporal cortex. J. Neurophysiol. 1994;71:2325–2337. doi: 10.1152/jn.1994.71.6.2325. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Neural computations that underlie decisions about sensory stimuli. Trends Cogn. Sci. 2001;5:10–16. doi: 10.1016/s1364-6613(00)01567-9. [DOI] [PubMed] [Google Scholar]
- Graf ABA, Kohn A, Jazayeri M, Movshon JA. Decoding the activity of neuronal populations in macaque primary visual cortex. Nat. Neurosci. 2011;14:239–245. doi: 10.1038/nn.2733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hung CP, Kreiman G, Poggio T, DiCarlo JJ. Fast readout of object identity from macaque inferior temporal cortex. Science. 2005;310:863–866. doi: 10.1126/science.1117593. [DOI] [PubMed] [Google Scholar]
- Jazayeri M, Movshon JA. Optimal representation of sensory information by neural populations. Nat. Neurosci. 2006;9:690–696. doi: 10.1038/nn1691. [DOI] [PubMed] [Google Scholar]
- Ma WJ, Beck JM, Latham PE, Pouget A. Bayesian inference with probabilistic population codes. Nat. Neurosci. 2006;9:1432–1438. doi: 10.1038/nn1790. [DOI] [PubMed] [Google Scholar]
- Matsumoto N, Okada M, Sugase-Miyamoto Y, Yamane S, Kawano K. Population dynamics of face-responsive neurons in the inferior temporal cortex. Cereb Cortex. 2005;15:1103–1112. doi: 10.1093/cercor/bhh209. [DOI] [PubMed] [Google Scholar]
- Newsome WT, Britten KH, Movshon JA. Neuronal correlates of a perceptual decision. Nature. 1989;341:52–54. doi: 10.1038/341052a0. [DOI] [PubMed] [Google Scholar]
- Nirenberg S, Pandarinath C. Retinal prosthetic strategy with the capacity to restore normal vision. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:15012–15017. doi: 10.1073/pnas.1207035109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Doherty JE, Lebedev MA, Ifft PJ, Zhuang KZ, Shokur S, Bleuler H, Nicolelis MAL. Active tactile exploration using a brain-machine-brain interface. Nature. 2011;479:228–231. doi: 10.1038/nature10489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paradiso MA. A theory for the use of visual orientation information which exploits the columnar structure of striate cortex. Biol. Cybern. 1988;58:35–49. doi: 10.1007/BF00363954. [DOI] [PubMed] [Google Scholar]
- Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, Simoncelli EP. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature. 2008;454:995–999. doi: 10.1038/nature07140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E, Abbott LF. Vector reconstruction from firing rates. Journal of computational neuroscience. 1994;1:89–107. doi: 10.1007/BF00962720. [DOI] [PubMed] [Google Scholar]
- Schneidman E, Berry MJ, Segev R, Bialek W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature. 2006;440:1007–1012. doi: 10.1038/nature04701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Britten KH, Newsome WT, Movshon JA. A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J Neurosci. 1996;16:1486–1510. doi: 10.1523/JNEUROSCI.16-04-01486.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci. 1998;18:3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shlens J, Field GD, Gauthier JL, Grivich MI, Petrusca D, Sher A, Litke AM, Chichilnisky EJ. The structure of multi-neuron firing patterns in primate retina. J. Neurosci. 2006;26:8254–8266. doi: 10.1523/JNEUROSCI.1282-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Kohn A. Spatial and temporal scales of neuronal correlation in primary visual cortex. J. Neurosci. 2008;28:12591–12603. doi: 10.1523/JNEUROSCI.2929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolhurst DJ, Movshon JA, Dean AF. The statistical reliability of signals in single neurons in cat and monkey visual cortex. Vision Res. 1983;23:775–785. doi: 10.1016/0042-6989(83)90200-6. [DOI] [PubMed] [Google Scholar]
- Velliste M, Perel S, Spalding MC, Whitford AS, Schwartz AB. Cortical control of a prosthetic arm for self-feeding. Nature. 2008;453:1098–1101. doi: 10.1038/nature06996. [DOI] [PubMed] [Google Scholar]
- Vogels R. Population coding of stimulus orientation by striate cortical cells. Biol. Cybern. 1990;64:25–31. doi: 10.1007/BF00203627. [DOI] [PubMed] [Google Scholar]
- Vogels R, Spileers W, Orban GA. The response variability of striate cortical neurons in the behaving monkey. Experimental brain research. Experimentelle Hirnforschung. Expérimentation cérébrale. 1989;77:432–436. doi: 10.1007/BF00275002. [DOI] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, Newsome WT. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature. 1994;370:140–143. doi: 10.1038/370140a0. [DOI] [PubMed] [Google Scholar]