Abstract
We evaluate a theoretical model in which Ru is substituting for Ti at the (100) surface of anatase TiO2. Charge transfer from the photo-excited TiO2 substrate to the catalytic site triggers the photo-catalytic event (such as water oxidation or reduction half-reaction). We perform ab-initio computational modeling of the charge transfer dynamics on the interface of TiO2 nanorod and catalytic site. A slab of TiO2 represents a fragment of TiO2 nanorod in the anatase phase. Titanium to ruthenium replacement is performed in a way to match the symmetry of TiO2 substrate. One molecular layer of adsorbed water is taken into consideration to mimic the experimental conditions. It is found that these adsorbed water molecules saturate dangling surface bonds and drastically affect the electronic properties of systems investigated. The modeling is performed by reduced density matrix method in the basis of Kohn-Sham orbitals. A nano-catalyst modeled through replacement defect contributes energy levels near the bottom of the conduction band of TiO2 nano-structure. An exciton in the nano-rod is dissipating due to interaction with lattice vibrations, treated through non-adiabatic coupling. The electron relaxes to conduction band edge and then to the Ru cite with faster rate than hole relaxes to the Ru cite. These results are of the importance for an optimal design of nano-materials for photo-catalytic water splitting and solar energy harvesting.
Keywords: hot carrier relaxation, photocatalysis, water oxidation, transition metal doping, electron transfer, ruthenium
1 Introduction
Titanium dioxide (TiO2) has received considerable attention due to its numerous applications in many important fields, such as catalysis, sensors, corrosion, coatings, and solar cells.1–7 Among these applications, energy harvesting directly from sunlight is a desirable approach toward fulfilling the need for clean energy with minimal environmental impact. Using TiO2-based materials – functionalized or doped – sunlight energy can be transformed and stored into two different forms (i) electric energy derived by light-induced charge separation with dye-sensitized solar cells2, 6, 8 or (ii) chemical energy as fuel and oxidizer, e.g. molecular hydrogen and oxygen which are products of water splitting reaction.1, 4, 9 Light-induced charge separation is essential for both of these applications.
We focus on solar fuel catalysis that depends on at least three key steps. The first is the light capture – absorption the sunlight by the active material, resulting in an electron-hole pair. The second is the electron transfer – sunlight produced electron and hole diffuse to the catalytic sites, separated in space.10 This process is accompanied by electron and the hole relaxation toward the conduction band (CB) minimum and valence band (VB) maximum, respectively.11–13 During this step electronic excitation energy is partially lost to thermal energy of lattice vibrations via electron-phonon interactions. The last step is catalysis – the efficient making and breaking the chemical bonds using the harvested electron-hole pairs.
Among the various oxide photocatalysts, TiO2 (titania) still remains the most promising photocatalyst owing to its low cost, chemical inertness, low toxicity and high photostability.4 The chemical and physical properties of materials used for solar-energy conversion strongly depend on their size, shape and crystalline structure.6 The variation of surface morphology allows selection of the optimal electronic structure.14 The origin of such difference was recently revealed by experiment where it was shown that the exciton lifetime in anatase phase is much larger than corresponding value for exciton in rutile phase.15, 16 This facilitates the translocation of the photon-excited electrons and holes from the bulk to the surface, where the photochemical reactions take place.17 For small TiO2 nanoparticles (< 50 nm), anatase seemed more stable and transformed to rutile at temperature > 973 K.18, 19 Thus, at room temperature small enough titania nanocrystallites are expected to have anatase structure and be much more effective for sunlight harvesting applications.
Recently there were proposed new approaches to synthesize high-purity anatase TiO2 single crystals with a large percentage of (001) facets.20, 21 These facets are much more reactive for water-dissociation reactions than the (101) surface, which normally forms the majority of the surface area. However, the clean anatase (001) surface reconstructs under ultrahigh vacuum conditions.22 The reconstruction strongly stabilizes the surface23 and at the same time largely reduces its reactivity: calculations indicate that the fraction of active sites for water dissociation is reduced ~25% with respect to the unreconstructed surface.24
The optical band gap of titania in anatase phase is 3.2 eV, much larger than resonance energy of 1.23 eV required for water splitting.25, 26 Therefore use of the bare titania for solar energy harvesting is not efficient. Band gap excitation requires ultraviolet irradiation, however UV light accounts for only 4% of the solar spectrum compared to 45% visible. So, any shift in optical response to visible range will have profound positive effect on photocatalytic efficiencies of the TiO2 materials. Various compounds ranging from anions27, 28 to cations, including wide range of transition metals29–31 such as Fe,32, 33 Pt,34 Co,35 Nb,36 and others37–39 were used for this purpose. A remarkable catalytic effect of RuO2 on powdered TiO2 for hydrogen evolution from an ethanol-water mixture has been observed by Sakata et al.40 To investigate the supporting effect of RuO2 on TiO2, experiments varying the amount of RuO2 on a fixed amount of TiO2 were carried out.40 The hydrogen evolution rate for RuO2/TiO2 was found to be 30 times higher than that for TiO2 alone and sensitive to increasing amounts of RuO2 reaching a maximum at 0.4 × 10−3 molar ratio of RuO2/TiO2. Ruthenia nanoparticles here act as electron pools (reducing sites)41 while titania is an oxidizing electrode, i.e. hydrogen and oxygen evolution takes place on ruthenia nanoparticles and titania, respectively.
As it was found experimentally, at monolayer coverage of water on the rutile TiO2 (110) surface, the ratio OH: H2O ≈ 0.5, while heating yields an increased OH: H2O ratio.42 Theoretical analysis also reveals that molecular and dissociated water can coexist on rutile (110)43 and anatase (100) and (001) surfaces.44, 45
The computational modeling of the hot carrier relaxation in molecules and nanostructures rests on partitioning the total energy between electronic part and nuclear part and allowing for energy flow between them, going beyond Born-Oppenheimer approximation.46 Several successful computational strategies for electronic relaxation are based on the concept of surface hopping between potential energy surfaces.47, 48 Numerical implementations of this strategy can be based on various methods ranging from density functional theory (DFT)49 to high-precision nonadiabatic excited state molecular dynamics approach.50 It has been proved efficient to use molecular dynamics trajectory for determining the electron-to-lattice coupling in semiconductors.51 A computational procedure integrating relaxation of electrons as open system with time dependent density functional theory (TDDFT) treatment of excited states was recently offered.52 Historically, in the limit of long time dynamics, low couplings, and multiple electronic states, one considers multilevel Redfield theory as a common approach for electronic relaxation.53–62 There were recent approaches to combine Redfield theory of electron relaxation with on-the-fly coupling of electrons-to-lattice through a molecular dynamics trajectory in the basis of DFT.63 Energy and charge transfer processes may occur in the ultrafast and/or coherent regime at times shorter than dephasing time. Such regimes are expected, for example, in systems with sparse energy states. In contrast, systems with dense energy states such as semiconductor surfaces, can manifest coherent behavior only at ultrashort time scales due to faster dephasing. However, in present studies of charge transfer for photo-catalysis, one primarily focuses on mechanisms of population relaxation.
Recently we have used computational models to explore charge transfer states introduced to wet anatase (100) and (001) surfaces upon transition metal doping64–66 and proton reduction reaction on the surface of the Pt nanocatalyst.67
In the present paper we investigate relaxation of electronic excitations on the titania anatase (100) crystallographic surface with Ru(IV) sites as a nanocatalyst that dopes electrons into titania. The details of electron-hole relaxation in aqueous conditions is discussed. These results are used to predict the time-resolved spectra and frequency dependent response functions collected from ultrafast nonlinear time-resolved experiments. They are important for optimal design of photo-catalytic water splitting and solar energy harvesting. We found that optically enabled excitations form an electron-hole pair in which the electron relaxes to the CB edge and then to the Ru site while hole relaxes to Ru site at a slower rate.25 explaining the significant increase of water decomposition effectiveness due to the ruthenia doping. At the same time ruthenia doping leads to increasing of the light adsorption effectiveness by anatase phase of titania in the visible range.
2 Methods: Computation Details
While studying photocatalysis in energy materials one can represent the overall catalytic process as a sequence of elementary steps responsible for the total effect. Specifically, interaction of electrons with light corresponds to elementary processes of photon absorption and emission. Interaction of electrons with lattice vibrations corresponds to relaxation of electronic bands populations and reorganization of ionic configuration. The mixing of electronic orbitals is associated with elementary processes of surface charge transfer and appearence of photovoltage. The common feature of all these elementary processes is that electronic degrees of freedom (DOF) cannot be considered as isolated.
In order to model such processes in photocatalytically active energy materials we employ combination of two approaches. First is the computational modeling of electronic structure for the system investigated. The density functional theory (DFT) seems to be the best suited for a class of system with reduced symmetry, where standard analytical methods of solid state theory approaches developed for periodic structures are not well applicable. Among such systems are inhomogeneous systems, surfaces with defects, and interfaces between different substances where chemical reactions take place. Our second approach is a modeling of quantum relaxation dynamics. Here we simulate interaction of non-equlibrium electronic states with light and lattice vibrations. This method has a development potential as it goes beyond basic quantum description of isolated systems. Combination of both DFT electronic structure calculations with further time evolution analysis of electronic subsystem is employed in present investigation.
2.1 Computational modeling of non-adiabatic transitions
Due to the fundamental role of radiationless processes in chemical reactivity, there is abundant literature devoted to extracting non-adiabatic coupling from computer simulations. Theoretical approaches utilized for this purpose fall into two general categories: trajectory based methods and techniques based on direct propagation of the reduced density operator.
The latter set of methods include the mean-field Ehrenfest,68 surface-hopping,47, 69 semi-classical initial value representation,70 linearization,71, 72 and classical mapping73, 74 approaches. The former techniques are based on evolution of the reduced density matrix (RDM) and consider Redfield equations75 and the non-interacting blip approximation,76 which serves as a time-dependent generalization of Förster theory.77 In present paper the reduced density operator formalism is employed for description the non-adiabatic charge dynamics in bare and ruthenia doped anatase (001) titania of anatase phase for practical design material for sunlight harvesting.
2.1.1 Reduced density operator theory
The basic idea in microscopic theory of non-adiabatic charge dynamics is a decomposition of a total system into a system and bath parts. In particular case of present research the former one corresponds to electronic while the latter one is an ionic part. Complete Hamiltonian of a problem under consideration is written as a sum of electronic Hamiltonian Ĥel, an ionic Hamiltonian Ĥion and their interaction Ĥint,
| (1) |
where R and r are ionic and electronic coordinates. The dynamics of electronic subsystem is described by the RDM,78 which is obtained by tracing the density matrix of whole system over the ionic bath DOF. Dependence of Ĥel on the ionic DOF emphasizes the non-adiabatic character of charge dynamics in investigated system.
Hereafter we focus our attention on charge dynamics initiated by incident light beam. Let consider formation of an excited state at surface of interest continuously irradiated by light of frequency Ω, consistent with an experimental setup. Light promotes electrons up in energy from the VB to the CB, while relaxation processes lead to de-excitation of back towards the ground electronic state. These processes are described within a reduced density operator ρ̂ = ∑ij |i〉ρij〈j| and RDM ρij treatment within Born and Markov approximations.78 Born approximation corresponds to the weak electron-ion coupling, so that the back-action of the system onto the bath can be neglected. Within Markov approximation it is assumed that system correlation time is short.
Eather way, one can pose a formal problem of time-dependent evolution in terms of density operator ρ̂ which, in numerical representations, is composed of N2 elements, compare to N elements for wavefunction. Density operator follows the von-Neumann equation of motion (EOM). Density operator is a powerful theoretical tool combining quantum mechanics and thermodynamics. It allows us to describe an open system interacting with the environment: solvent, substrate, lattice vibrations, or quantized radiation.55–61 Density operator provides quantum picture of energy dissipation, photoemission and de-phasing. We focus on EOM for electronic DOF and take into account the influence of thermalized ionic motion in an approximate fashion, similar to Redfield approach.53 The density operator for electronic and ionic DOF ρ̂tot is projected on electronic DOF by integrating out the ionic DOF ρ̂el = Trion{ρ̂tot}. Here we assume that total density operator can be factorized on electronic ρ̂el and ionic ρ̂ion components and that the ionic density operator obeys thermal equilibrium distribution. In this approach the EOM for reduced density operator for electronic DOF gains an additional term representing the approximate infuence of lattice vibrations on the electonic DOF. This term, often referred to as Redfield term, is obtained79 as second order perturbation in respect to electron-phonon interaction Hamiltonian as described belod.
There one applies several approximations: perturbative in electron-to-lattice ion interaction, Markov, convolutionless
| (2) |
Equation (2) provides time increment of the electronic density matrix ρ̂el and linearly depends on its value at specific time ρ̂el(t). First term of the equation is trivial, contains phase increment due to the electronic Hamiltonian, plus an influence of a driving laser field, if any, and corresponds to the elastic, reversible dynamics.
In contrast, second term is very specific. It uses Hamiltonian of interaction of electrons and lattice vibrations Ĥint. This Hamiltonian is small compare to Ĥel. The second term appears as a perturbative correction of the second order since the first order correction vanishes upon average. The second term has prefactor of ħ−2. The dimension of the second term is the same as the dimension of the first term: time−1. The integration limit runs from the instant the interaction was switched on until the time we focus on. The symbol Trion corresponds to an average over states of ionic subsystem, in thermal state, which is characterized by the ion density operator ρ̂ion. The double commutator appears from the second order perturbation. The Hamiltonian of interaction Hint enters there twice: at the initial instant of time t = 0 and at the delayed instant of time t = τ. This corresponds to two elementary events of interaction, separated by the time interval τ. During the interval between these events, there appears an accumulation of phase, corresponding to non-interacting ions and electrons. The density matrix of electronic system enters there as an argument, at time t. Interaction Hamiltonian is often factorized as a bilinar product of relevant operators affecting electronic subsystem and ionic lattice subsystem. The second order perturbation term, upon average over lattice motion contains autocorrelation function for lattice operators.
In case a specific basis {|i〉} is chosen, the density operator converts into density matrix ρij = 〈i|ρ|j〉 for electonic DOF.53, 55–61 RDM obeys Redfield EOM
| (3) |
Elements of the Redfield tensor R are expressed in terms of partial rates Γ±
| (4) |
Here, the partial rates Γ± are expressed in terms of autocorrelation functions M of interaction-Hamiltonian
| (5) |
| (6) |
The phase increment factors exp {−iωljτ} appear from the time evolution of the electronic DOF, and use energy difference ħωij = εj − εi. The autocorrelation function of the interaction Hamiltonian reads
| (7) |
with an assumption M′(τ, 0) = M′(τ + τ′, τ′). Here we define
| (8) |
Note that approximations which we have committed lead to the time-independent coefficients Rijkl for this system of linear differential equations. Later, for the practical implementation of the Redfield Eq. 3 we replace the general Hamiltonian with the Fock operator or one-electron Kohn-Sham operator, in agreement with used computational basis. For the focus on energy relaxation and charge transfer, it is sufficient to include only single excitations of electronic states in the explicit treatment of Hel. In what follows the interaction Hamiltonian is exclusively based upon non-adiabatic coupling elements activated by motion of ions.
In numerical form, based on the derivative of Hamiltonian (Fock operator), in the basis |k〉, |l〉 in n respect to normal modes displacements or to the position of Ith ion the interaction Hamiltonian is composed of the terms including products of gradient matrix elements , α = x, y, z and momentum as follows . Here, for each timestep, the difference between αth Cartesian coordinate of Ith atom at time moments of t and t + Δt can be expressed in term of momentum , where MI is mass of Ith atom. The autocorrelator (7) is composed of the terms including products of matrix elements and momentum-momentum correlation function
| (9) |
In numerical form, based on “on-the-fly” calculation, the autocorrelator (7) is composed of the terms including products of matrix elements of interaction Hamiltonian at different instants of time
| (10) |
plus permutations. Here, the average over bath states Trion is represented by the summation of snapshots of multiple trajectories or one long trajectory. Note that in last two equations, autocorrelation function includes only interaction Hamiltonian and is expected to decay rapidly in systems with broad and dense spectra of lattice vibrations. An autocorrelation of the total Hamiltonian include components, which might decay at longer time scale and contribute to such effects as pure dephasing.80–82
2.2 Practical application of methodology to functionalized titania slabs
The equations below represent implementation of Redfield equation in basis of Kohn-Sham orbitals as explained in Appendices I–III.83, 84
| (11) |
| (12) |
where γjj = ∑k≠j κjk, are population and coherence relaxation rates and is a state-to-state transition rate in the Markoff limit. Here Ωjk = −Djk·ℰ0/ħ, and Δjk = Ω − ħωjk stand for Rabi and detuning frequencies respectively. Also, ħωjk = εj − εk, J, , and T are described in83, 85, 86 and stand for an energy difference, spectral density of bosons, their thermal distribution for vibrational frequencies ω, and temperature, respectively, while stands for a pure dephasing component, obtained through an autocorrelation of time-dependent KSO energy 〈εi(t)εj(τ)〉.80, 82 The initial values for the RDM correspond to the system initially at thermal equilibrium and then excited by light, during a very long time. The thermal equilibrium state in our electron system is specified by the Fermi-Dirac distribution as applies to our system at equilibrium at temperature T before excitation.
2.2.1 Solution in the limit (i) steady state
As soon as we have established formal EOM 11 for the electronic DOF perturbed by light and lattice vibrations we have to solve it. We consider the solution of Eq. 11 in two practically important limits, first, in the limit of continuous photoexcitation at a given frequency. This corresponds to experiment with CW-excitation. In this limit, at a long time after the excitation was switched on the excitation of the model by light and deexcitation due to interaction with lattice vibrations, in average, compensate each other.
In such case, the average of any element of density matrix experiences no change in time. The model comes into so called steady state ρ̂ss. In steady state, the differential EOM for density matrix 11 transforms into linear algebraic equation wich establishes connection between equilibrium density matrix ρ̂eq and steady state density matrix ρ̂ss.
A system driven by steady light of a given frequency shows two competing tendencies that establish a steady state: light promotes electronic population from the valence band to the CB and interaction with the medium returns population back to the valence band. Furthermore, interaction with the medium over long times damps rapidly oscillating coherences. In such case, as long as the intensity of irradiation is kept constant, it is possible to search for solutions of the EOM with steady state values for times , which can be obtained imposing the condition ∂ρ̂ij/∂t = 0. In the limit of weak optical field intensity for which |gjk| << γjj a Taylor series expansion of matrices leads to
| (13) |
| (14) |
with and details given in.84, 87 Interestingly, the off diagonal elements, for k and j in different bands correspond to transition density matrix.
2.2.2 Solution in the limit (ii): evolution of nonequilibrium excitation
Another limit, when Eq. 11 is important to solve is the limit of time evolution of nonequilibrium excited state created by instantaneous ultrafast pulse or by abrupt switching off the steady excitation. In this limit, EOM keeps only terms for phase increment and for lattice induced evolution. The EOM is solved by numerical diagonalization of the matrix equation88
| (15) |
where elastic and inelastic terms in the Redfield equation are transformed into ℒ̂ and ℛ̂ super-matrices, providing the electron density matrix at each time. Here, ρ̂(J) stands for an eigenmatrix of the RDM EOM. The coefficient AJ = Tr [ρ̂(0)† ρ̂(J)] is obtained from the initial conditions, and J = (i, j) stand for a diadic superindex.63
2.2.3 Applying RDO solutions to explore properties of materials
As soon as one has solved the EOM for density matrix one may want to connect this knowledge about electronic system details to a real world, to observables which reflect steady- and time-dependent system properties. We select such observables which are either easy to measure for this class of systems or reflect most important features of the models, see Appendix IV.
For models of functionalized surfaces for energy applications one is interested in the ability of the material to absorb light and to convert the relevant energy into form of charge transfer and later, into chemical form. One can quantify the ability of material to participate in charge transfer event in an average way. A surface of a material can be approximately considered as a double layer capacitor with one layer A representing the inner area of material well below the surface and second layer B representing the outer area of the material, facing the vacuum or other type of environment. A photoexcitation may induces average charge imbalance between such layers. This creates a homogeneous electric field across the capacitor plane and a voltage between layers of double-layer capacitor. The corresponding electric potential difference between charged layers is proportional to their average charge and to the distance between oppositely charged layers, and can be cast for a continuous charge distribution as,89 described in Appendix IV.
Other quantities we follow are very helpful for understanding the mechanism of energy relaxation and charge transfer in the models of titania surfaces, energy distribution of photoexcited carriers as function of energy and time and space distribution of photoexcited carriers as function of position and time. We consider average energy of a carrier as function of time to quantify average features of energy relaxation. We quantify the amount of charge transfer by considering average repartitioning of charge between titania slab and ruthenia nanocatalyst.
A population distribution in the energy domain reads n (ε, t) = ∑i ρii (t) δ (εi − ε), while a relative change of population with respect to the equilibrium distribution reads
| (16) |
and represents an increase of population (electrons, Δn > 0), a decrease (holes, Δn < 0), or unchanged population for Δn = 0.
The ruthenia nanocatalyst and Ru doping of titania surfaces have potential to promote oxidizing half reaction of water splitting. Therefore, one focuses on the details of the hole transfer and on behavior of carriers in the occupied valence band.
The charge density distribution in the VB/CB as function of z reads, with r = (x, y, z),
| (17) |
| (18) |
for the initial nonequilibrium (a, b) photoexcitation, and characterizes the electron density localized at an adsorbate at time t. Below we solve for the RDM and obtain the above distributions to perform a case study of photoinduced evolution in our models of titania slabs, with and without Ru adsorbate.
The relaxation of the hot carrier (hole) energy Δεh given by
| (19) |
The expectation value of the hot carrier (hole) energy Δεh given by
| (20) |
In order to compute the average rate of energy dissipation we convert expectation values 〈Δεe〉(t) and 〈Δεh〉(t) into their dimensionless counterparts
| (21) |
Both of theses functions change between 0 and 1. We try to fit the dissipation of energy in the CB and VB in to a monoexponential decay 〈Ee〉(t) = exp{−ket}, 〈Eh〉(t) = exp{−kht}. Here the decay rate is approximated as inverse of the time integral
| (22) |
Average partitioning of the charge can be quantified as follows
| (23) |
so that charge presence above titania surface z > 0 yields increment proportional to the amount of charge transfer.
2.3 Electronic structure calculations
A set of Kohn-Sham (KS) orbitals is computed using density functional theory (DFT) with the Perdue-Burke-Ernzerhof (PBE) parametrization90 as it implemented in VASP code.91, 92 Obtained set of KS orbitals is used to calculate matrix elements of the relevant density operators.92–94 The Ti3d states in titania were explicitly treated as valence states through the projector augmented wave method95 and cutoff energy value equal to 400 eV. The slab replicated along (100) crystallographic surface contains 8 layers thickness containing totally 96 atoms and was cleaved from the anatase phase structure of titania downloaded from the NRL database.96 The z axis of expected charge transfer is chosen to be orthogonal to the exposed (100) surface.
The periodic boundary conditions a = 7.570Å and b = 9.908Å are imposed along x (010) and y (001) directions. A vacuum layer of 8 Å was added to the simulation cell along z (100) direction to prevent spurious interactions between periodic replicas. The above described model of titania surface was modified to approximately represent surface nanocatalyst. To do so, one Ti atom at top and bottom surfaces covered by water was replaced by Ru atom. These represent “doped” and “undoped” models, which are studied as follows.
Here we restrict ourselves by consideration of water monolayer adsorption on investigated surfaces. Recent theoretical results indicate that the presence of second layer of water molecules causes those in the first water molecules layer to be reoriented and a monolayer model was found of at best limited applicability to understanding the water-TiO2 interface.97 The resulting structure was saturated by H2O molecules to mimic realistic situation of titania nanorod immersed in water. The resulting geometry is shown in Fig. 1(left). The effect of explicit thermal motion of surface layer of water molecules is included into ab-initio molecular dynamics trajectories involved into computation of correlation functions, Redfield tensor elements, and relaxation rates. This can be best visualized based on online movies submitted to supplemental materials.98, 99
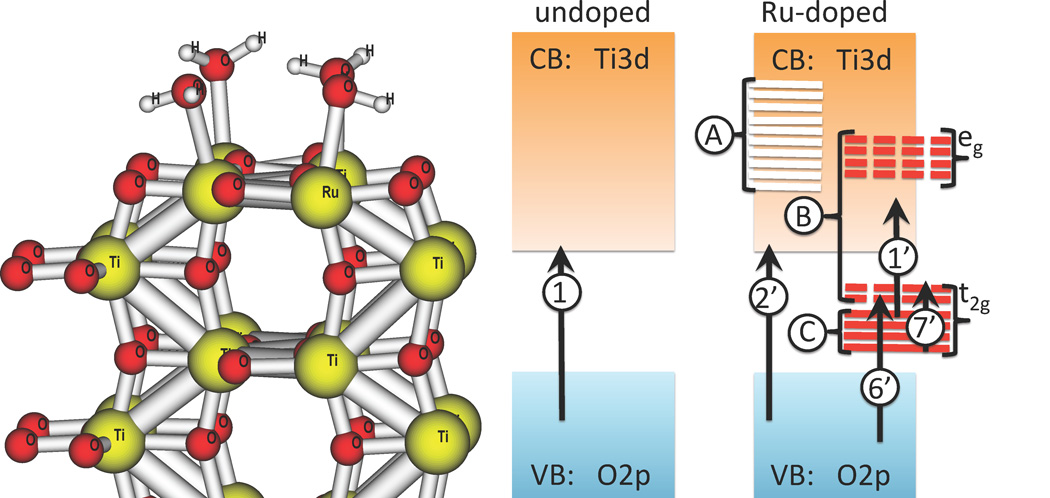
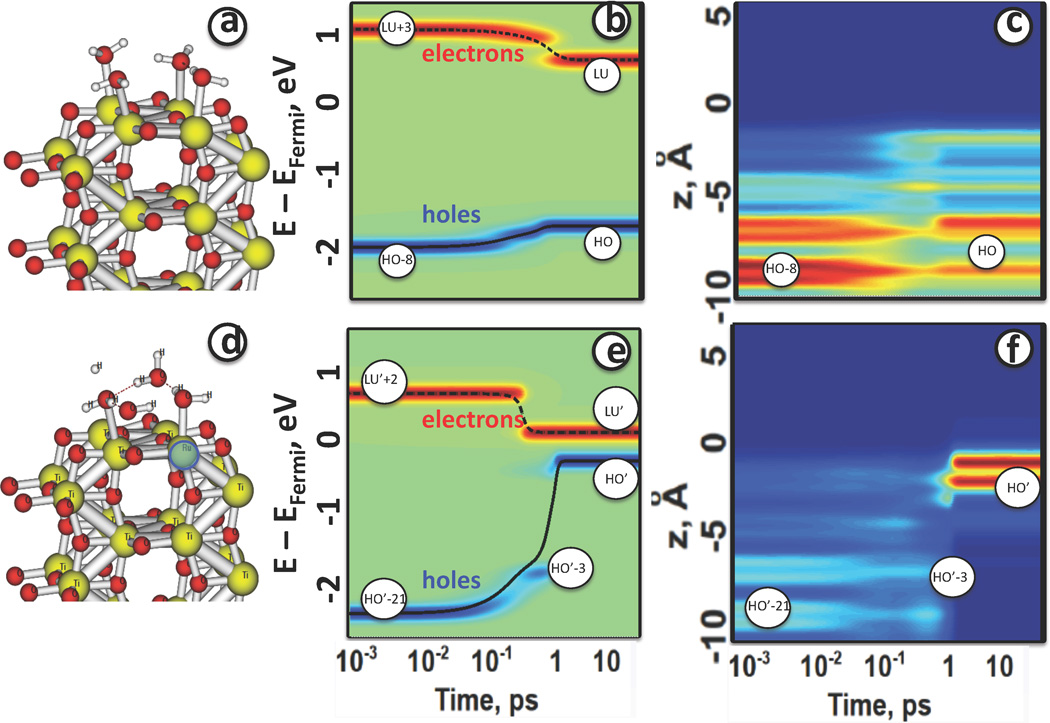
Figure 1.
Atomistic model (left) and schematic representation of electronic structure of anatase (100) surface, undoped (center) and doped (right) by Ru-ion. left Atomic model of doped surface. Atoms are color coded as Yellow, Blue, Red, and white spheres standing for Ti, Ru, O, and H atoms. The figure shows only one half of the structure. Periodic boundary conditions are implied along x〈010〉 and y〈001〉 directions. Dangling surface bonds are compensated by water molecules. center, right Upon replacement doping, ten of Ti3d unfilled orbitals are removed from the conduction band (A) and replaced by ten Ru4d orbitals (B)–(C), with splitting due to octahedral crystal field. Six of these orbitals are unfilled (B, red dashes) and partitioned between CB and bandgap region, while four of those orbitals are filled (C, solid red lines) and contribute to the bandgap energy region. Basic electron-hole excitations in the undoped (1) and doped (1’)–(7’) models are symbolized by vertical arrows and are explained as follows. Notation is chosen in consistency with Table 2. (1) undoped transition is neutral, it oxidizes O and reduces Ti, in a delocalized way. (2’) doped transition is neutral, it oxidizes O and reduces Ti, in delocalized manner. (7’) neutral transition, it promotes an electron from filled to unfilled Ru4d orbital; this excitation easily recombines into ground state. (6’) charged transition, it oxidizes O and reduces Ru ion as follows Ru(4+)+e− → Ru(3+), negative charge migrates to surface. (1’) charged transition, it oxidizes Ru ion and reduces Ti ion. Ru reduction reaction follows as: Ru(4+) → Ru(5+) + e−, positive charge migrates to the surface.
The energies of KS orbitals {εi}, transition dipoles {D⃗ij}, spatial distributions of KS orbitals partial charge density ρi(r⃗), normal modes, ab initio molecular dynamics trajectories, and average nonadiabatic transitions coefficients , and autocorrelation functions Mijkl(τ) were extracted by postprocessing of the output of VASP DFT calculation for each model.63 All coefficints for the Redfield equation are computed based on the ab initio data.
3 Results and Discussion
3.1 Effect of doping on ground state electronic properties
Geometry modification and binding energies
As Ti-O bond length is shorter than Ru-O, replacement of Ti(IV) with Ru(IV) leads to slight distortion of the lattice. The distortion affects the in-surface bonds differently than M-O bonds perpendicular to the surface as shown in Table 1. Calculated by Eq. 24 binding energy of Ru to titania surface is also shown in Table 1.
| (24) |
where the energies of clean and doped surfaces are Eclean = E(Ti32O64 × 8H2O) = −973.58595 eV Edoped = E(Ru2Ti30O64 × 8H2O) = −962.55960 eV. The chemical potentials of Ru and Ti atoms were calculated for hexagonal Ru and α-Ti crystals μdoping atom = E(Ru) = −8.568 eV/atom and μhost atom = E(Ti) = −7.658 eV/atom, respectively. Plugging in these values into Eq. 24 one obtains per Ru atom. The functionalized titania surface is an energetically preferred composition.
Table 1.
Geometry modification of titania surface by ruthenium ion functionalization, doping replacement energy, and water-to-surface binding energy.
| Me=Ti | Me=Ru | |
|---|---|---|
| dMe−O,‖ Å, | 1.977 ± .1 | 1.982 ± .1 |
| dMe−O,⊥ Å, | 1.842 ± .005 | 1.844 ± .003 |
| , eV, | 0 | 6.4237 |
| , eV, | −0.2612 | −0.3365 |
Upon optimization, water molecules are arranged to optimize hydrogen bonding. H atoms of each H2O molecule protrude parallel to the surface plane to the nearest O atom from the neighboring H2O molecule. The average binding energy of H2O molecule to doped and undoped surface equals to
| (25) |
where Nads stands for number of H2O ligands covering the surface, Eslab+ads total energy of a model covered with water, Eslab total energy of a model with bare surface, ENads total energy of all water adsorbants. Numerical values and are also summarized in Table 1.
Density of states
The electronic configuration of titanium, oxygen, and ruthenium are Ti = [Ar] 3d24s2, O = [He] 2s2p4, and Ru = [Kr] 4d75s1. Electronic structure of doped and undoped models is schematically summarized in Fig. 1 and supported by computational results as follows. Symbolically, the K-S effective Hamiltonian operator of pure TiO2 can be labeled as . Introduction of Ru-doping created the several changes of the electronic structure. The model Hamiltonian for the doped slab includes a term for the electronic changes due to a dopant in the host lattice, and a term for the induced distortion of the lattice, so that
| (26) |
Features of electronic structure and K-S eigenenergies of doped and undoped slabs are analyzed using density of states D(ε) = ∑j δ(εj − ε). For better visualization DOS for both models is shifted in energy in respect to for undoped model. Comparison of the DOSs D0 and D for pure and doped slabs helps to identify changes due to electronic contributions from dopants and due to lattice distortion, with
| (27) |
Figure 2(a)–(b) illustrates the effect of doping on the electronic properties of ruthenia-doped TiO2 slab and shows calculated DOS, total and projected on atomic orbitals. The DOSs D0(ε) versus ε shows a null region typical of the gap between VB and CB of the titania crystal, as seen in Fig. 2(a). Based on calculated projected DOS, one notices that for undoped model all orbitals in the valence bands are composed as superposition of O2p-orbitals of oxygen and all orbitals in the CB conduction band are composed as superposition of Ti3d-orbitals of titanium. The density of states for doped model, in Fig. 2(b) approximately reproduce the DOS for undoped model, in Fig. 2(a) in the energy range below −1.5 eV (VB) and above 0.5 eV (CB). Slight change of peak position is attributed to electronic states being perturbed by lattice distortion . The unique changes intoduced by doping are manifested as states within the bandgap.
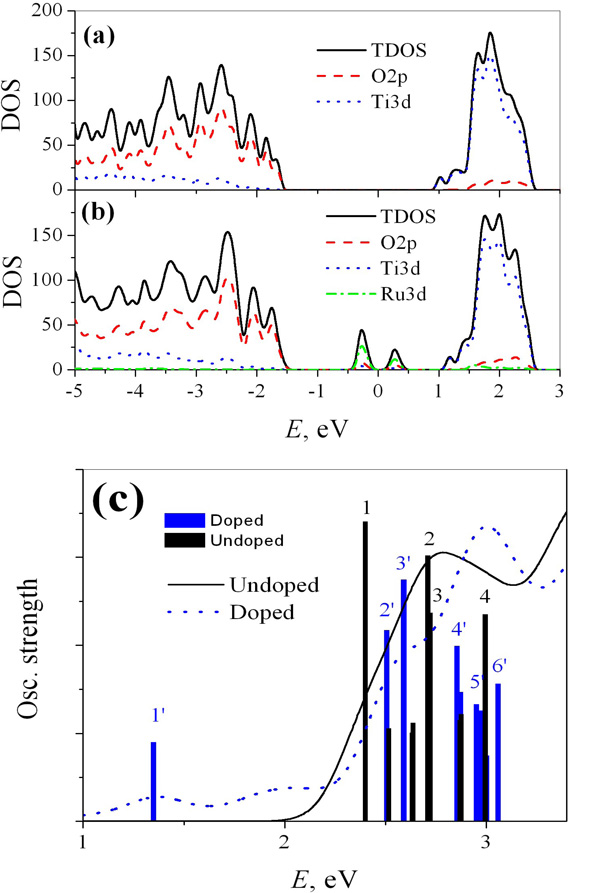
Figure 2.
Basic electronic structure features for doped and undoped TiO2 anatase (100) surface. Panel a, b show comparison of total density of states (lines) and partial density of states components on O2p (long dashes), Ti3d (short dashes), and Ru4d (dot-dashes) for undoped a and doped b models. Undoped surface has a bandgap of over 2 eV. Doped surface shows states contributed by doping in the bandgap area. Part of Ru-doping-related states are populated. Panel c shows absorption spectra of undoped (solid) and doped (dashes) models. Electronic transitions contributing at most to the doped model are represented by vertical stems with heigh equal to their oscillator strength. Labels of individual excitations are consistent with scheme in Fig. 1 and notations in Tables 2, 3.
The equilibrium population of undoped model is trivial: all states in the VB (below 0 eV) are occupied, all states in the CB (above 0 eV) are unoccupied. In the doped model, pseudooctahedral Ru ion contributes t2g orbitals to the bandgap. Their filling is consistent with d4 configuration of Ru(IV). This feature plays a role in understanding charge transfer mechanism. These results may potentially be used as model for more complex Ru-based sites such as clusters or nanoparticles. We expect that the Ru-band in the bandgap range will gain more states and will broaden for the larger ruthenia nanocatalyst, providing similar qualitative trends in the electronic structure.
Electronic absorption spectra of doped and undoped models are presented in Fig. 2(c). Examples of electronic transitions contributing to the spectra are given in Table 2. For both models, bright transitions, appear above the optical bandgap of the undoped model. The absolute values of the optical band gap energies can be systematically improved by employing GW corrections and Bethe-Salpeter equation approach.26
Table 2.
Featured electronic transitions. The featured electronic transitions are presented for undoped and doped models. The criterion for selecting the states is the vicinity of the transition energy to the bandgap, large value oscillator strength, and potential to contribute to the charge transfer. Indices of doped orbitals are indicated with prime sign. Bright excitations are enlabeled in accordance with Fig. 1(c). Cartesian projections are included to identify the transitions of similar symmetry.
| index | description | orbital pairs | main data | cartesian projections | ||||
|---|---|---|---|---|---|---|---|---|
| hole index |
electron index |
oscillator strength |
transition energy, eV |
< 010 > Dx |
< 001 > Dy |
< 100 > Dz |
||
| Undoped (100) TiO2 anatase + H2O, HO = 288 | ||||||||
| 1 | Bright, 1st | HO−7 | LU | 3.40182621 | 2.4003 | −4.3875 | 0.1813 | 0.0025 |
| 2 | Bright, 2nd | HO−8 | LU+3 | 3.01603938 | 2.7111 | −0.0317 | −0.0648 | 3.8899 |
| Ru-doped (100) TiO2 anatase + H2O, HO′ = 292 | ||||||||
| 1′ | Charged, Ru → slab | HO′−2 | LU′+4 | 0.89327673 | 1.3504 | 0.0887 | −0.7205 | −2.9109 |
| 2′ | Bright, 1st analog | HO′−10 | LU′+2 | 2.16722662 | 2.5076 | −3.4274 | −0.0128 | 0.1078 |
| 3′ | Bright, distortion-due | HO′−7 | LU′+3 | 2.74285120 | 2.5915 | 3.7948 | −0.0099 | −0.0044 |
| 4′ | Bright, 3rd analog | HO′−21 | LU′+2 | 1.98818034 | 2.8562 | −0.0275 | −0.3825 | 3.0535 |
| 5′ | Bright, 2nd analog | HO′−11 | LU′+4 | 1.46676219 | 2.8725 | 0.0729 | −0.0262 | 2.6347 |
| 6′ | Charged, slab → Ru | HO′−13 | LU′+1 | 0.18207940 | 2.1087 | −1.0814 | −0.0715 | −0.0169 |
| 7′ | Neutral, Ru → Ru | HO′−2 | LU′+1 | 0.18397963 | 0.5293 | 0.1680 | −0.3840 | 2.1339 |
Ru-doped surface exhibits a significant red-shift in electronic absorption spectrum relative the undoped titania. Ru-doping and relevant lattice distortion effect perturbs position of main absorption peaks above 2.3 eV in comparison to the undoped model. Ru-doping also adds several semi-bright transitions below the optical bandgap. These transitions are involved in the formation of charge separated states and are discussed in what follows. Individual transitions with maximal oscillator strength are shown in Fig. 2(c), for the doped model in a form of vertical stems with heights proportional to the oscillator strength. As expected, KS orbitals localized on adsorbed water do not contraibute to electronic absorption spectrum. Interestingly, two most intense transitions in both doped and unroped models, have the same orientations of transition dipoles, along 〈100〉 and 〈010〉 directions.
Ab initio molecular dynamics trajectories at ambient temperatures were used to compute couplings and Redfield tensor elements.98, 99 Due to contact to thermostat, all ions and fragments included in model, experience quasichaotic motion. Ti, Ru, and O ions of the slab perform motion of oscillatory character, with different phases, while solvent H2O molecules saturating surface dangling bonds perform more complicated motion. These motions include rotation, forming and breaking hydrogen bonds, desorption and re-adsorption back of water from/to the surface. This approach approximately takes solvent effects into account.
One sees two ways to address dynamics solvent reorganization at higher precision: (i) compute multidimensional potential energy surfaces by including vibrational degrees of freedom, all or most important ones, into explicit considerations100–102 and (ii) update the ionic trajectory according to electron dynamics.103, 104 Both approaches will demand substantial computational resources, compare to present approach. Non-adiabatic molecular dynamics implies generation the vibrational forces and trajectorirs for each of possible electronic states or even for each of possible sequence of electronic states taken by the system. This approach works efficiently for lighter elements and smaller systems, such as dendrimers.104 It is an interesting idea to try such approach for class of models considered here. Specifically, Some basis KS orbitals have a portion of charge localized on water. Energies of such orbitals may get modified in a treatment with updated trajectories.
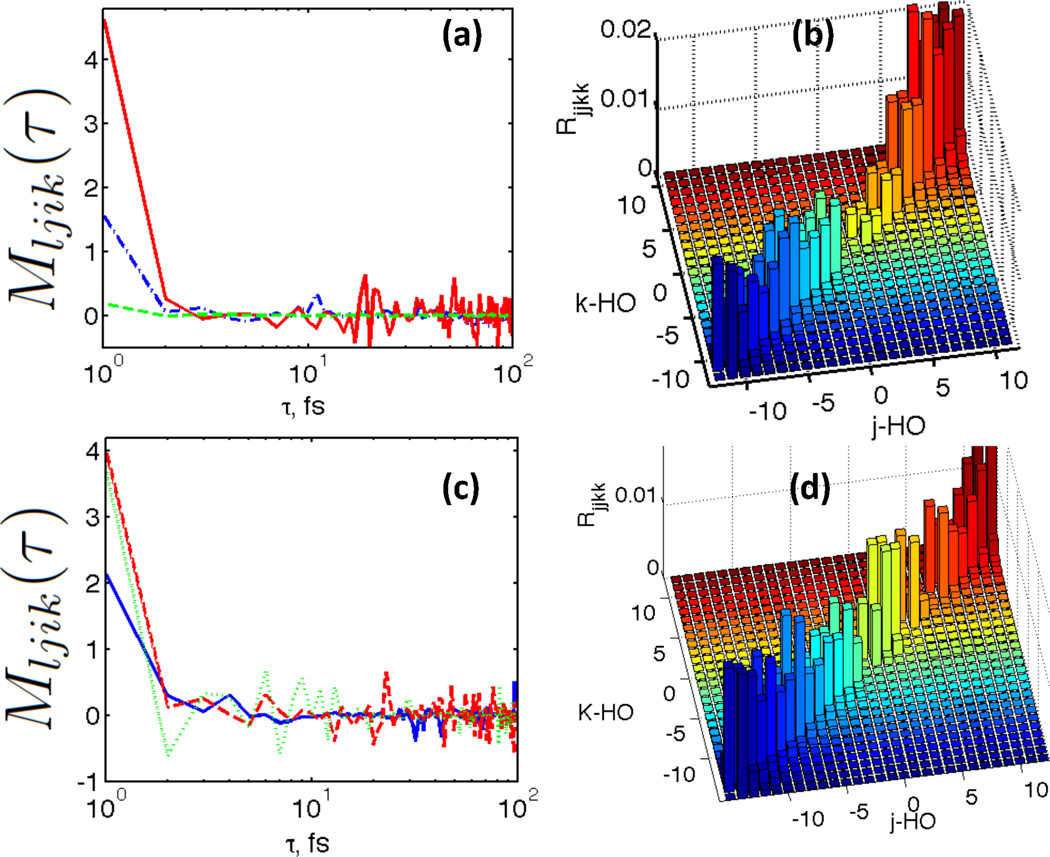
Nonradiative transitions Figure 3 shows representative examples of correlation functions components Mljik(t) Eq. 7 and selected elements of Redfield tensor Eq. 4 for studied atomic models with and without Ru doping. Here we focus on analysis of those elements of autocorrelation function and Redfield tensor, which correspond to population transfer. It is very interesting and important that the autocorrelations function elements Mljik(t)decays rapidly as function of time. This numerical observation provides validation for applying Markoff approximation. The computed Redfield tensor elements responsible for population transfer exhibit a feature: specifically, the maximal absolute values appear for those elements describing relaxation between states with close energies Rj,j,j±1,j±1. Note that, the elements of Redfield tensor connecting states near the bandgap |j − HO| < 2, |k − HO| < 2 are qualitatively different for doped and undoped models. For undoped model, the values of Rjjkk are vanishing and correspond to long non radiative lifetime. For Ru-doped model, the values of Rjjkk are of the order of .01 fs−1. Ru ion contributes states which facilitate the relaxation near the bandgap. The computed atomistic data are used for parametrizing EOM for RDM, solved in the following sections.
Figure 3.
Representative examples of correlation functions Mljik Eq. 7 (a), (c) and selected elements of Redfield tensor (b), (d) for studied atomic models without doping (a),(b) and with Ru doping (c), (d). The units for Redfield tensor elements are inverse femtoseconds. Here we focus on analysis of those elements of autocorrelation function and Redfield tensor, which correspond to population transfer. Interestingly, the maximal absolute values appear for Rj,j,j±1,j±1. Note that, the elements of Redfield tensor connecting states near the bandgap |j − HO| < 2, |k − HO| < 2 are qualitatively different for doped and undoped models. For undoped model, the values of Rjjkk are vanishing. For Ru-doped model, the values of Rjjkk are of the order of .01 fs−1. Ru ion contributes states which facilitate the relaxation near the bandgap.
3.2 surface photovoltage created by cw photoexcitation
We analyze interaction of electromagnetic radiation with doped and undoped titania surfaces. We start analysis by considering continuous wave (cw), low intensity irradiation leading to a steady state excitation of titania surface models. This analysis is helpful for interpreting absorption spectra in Fig. 2(c) and photovoltage spectra in Fig. 4(a). Optical perturbation of a given frequency creates coherence between occupied and unoccupied orbitals, referred to as transition density matrix. At the same time, optical excitation perturbs the equilibrium populations of states in valence and conduction bands. In average, originally occupied orbitals of valence band yield decrement in population and originally unoccupied orbitals of conduction band yield increment of population.105 This corresponds to optical excitation promoting an electron from the VB to the CB. Steady state solutions of the EOM for density matrix for titania surface models provide transition density matrix and steady state populations of orbitals as function of incident light frequency. The absolute value of the relative change of such populations in respect to their equilibrium valies is shown in Fig. 4(b)–(c) for undoped and doped models. An nonequilibrium excited state created by light of a given frequency Ω can be considered as a superposition of multiple electron-hole pairs and perturbs both VB and CB orbitals. Light of lower frequency perturbs only few orbitals in the bandgap area HO−Δ̃ < i < HO + Δ̃, Δ̃ < 5. Light of higher frequency perturbs orbitals further away from the bandgap. At higher frequency, more orbitals become involved into the formation of a nonequilibrium excited state, Δ̃ > 5.
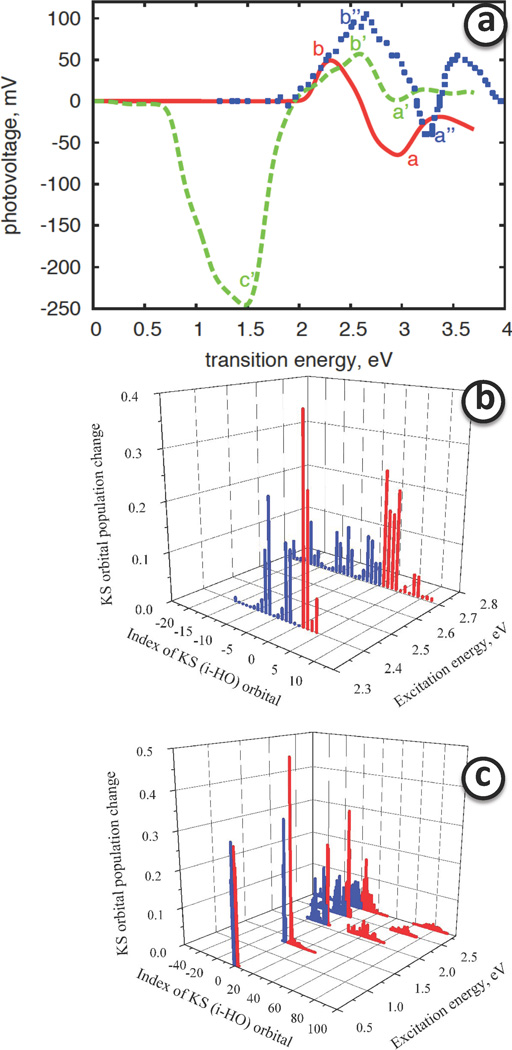
Figure 4.
Panel a Calculated surface photovoltage and corresponding relevant population changes of Kohn-Sham orbitals b–c. Panel a shows calculated Surface photo-voltage as function of photon excitation energy for undoped (solid) and doped surfaces (dashes). Similar features of the spectra are indicated by symbols a, b for undoped and a′, b′ for doped models. The feature c′ for doped model is unique and is appearing due to presence of doping. The blue square symbols correspond to experimental data.107 The features, similar to the calculated ones are labeled as a″ and b″. Panel b Photoinduced change of population of KS orbitals of an undoped titania anatase (100) surface. Orbitals belonging to the CB or VB are drawn as blue and red bars, respectively. Panel c The same for doped titania anatase (100) surface.
For undoped model, the excitation with frequency (transition energy) below bandgap does not perturb populations of orbitals. Starting with frequency matching the optical bandgap (in this calculation 2.1438 eV) light perturbs pairs of orbitals with nonzero transition dipoles, as shown in Fig. 2(b).
For doped model, light of much lower frequency is able to perturb some orbitals since there are Ru4d t2g orbitals contributed by surface Ru-doping. The actual bangap of doped model ( in this calculation) is smaller than the optical bangap of titania anatase. Several band-gap area transitions have small values of transition dipole, therefore, noticeable perturbations of KS orbital populations are calculated at the transition energies of about 1eV, as shown in Fig. 4(c). The transitions in the range of excitation energy between 1eV and 2eV involve orbitals localized on Ru(IV) and contribute to formation of O2p → Ru4d and Ru4d → Ti3d charge separated states as discussed later in this section.
Earlier calculations of SPV for crystalline, amorphous, and doped Si (c-Si)84, 87, 105, 106 provide the correct sign of the photovoltage and qualitatively correct positions of peaks in the dependence on photon energy in comparison to experimental data. This provides a partial justification of the method and a background to expect that the applying the same approach to doped TiO2 surfaces provides reasonable insight on the details of formation of an integrated charge transfer state on the surface. The solution for steady state density matrix is plugged in to equation for surface photovoltage , with details provided in Eq. 55, Appendix IV.
The resulting Vs(Ω) dependences for both doped and undoped models are presented in Fig. 4(a) along the experimental results of SPV for porous anatase film of 16nm in vacuum.107 This is the best relevant data available in the literature. Surface photovoltage spectra of doped (calculated and measured) and undoped models exhibit similar features, at the approximately same frequency, sign, and intensity. These features are labeled as (a), (b) for undoped model and as (a′), (b′) in the doped model, and as (a″), (b″) in the undoped experimental data. In addition to these features, SPV spectrum for doped model exhibits a high intensity negative peak at about 1.5 eV, labeled as (c′). This peak establishes an evidence of formation of charge transfer state on doped titania surface. Negative sign of photovoltage indicates the direction of charge transfer: upon excitation at transition energy of ħΩ = 1.5 eV the surface is getting depleted with electrons and enriched with holes. Note that this information is frequency dependent, not time dependent. The detailed mechanism and nature of this event is analyzed later in this section. SPV calculation has proved the h+ transfer from titania active media to ruthenia nanocatalyst.
3.3 electronic dynamics after instantaneous photoexcitation
Here we consider the solution of the RDM EOM in the time domain. The instantaneous optical pulse creates nonequilibrium state of the model by promoting an electron from occupied orbitals in the valence bands (a) to unoccupied orbitals in the conduction band (b). This event is most probable in case the oscillator strength fab is maximal and transition energy εab = ωab/ħ is in resonance with the central frequency of the exciting laser pulse Ω.
In what follows, we assume that the system is optically excited at t < 0 by steady light of frequency Ω ≈ (εb−εa)/ħ, that promotes an electron from occupied orbital a to unoccupied orbital b, and that at t ≥ 0 its electric field is zero. The initial value of the density matrix is therefore ρij(0) = δij · νj, with orbital occupation numbers νj = 1 for occupied j and zero otherwise, except that νa = 0 and νb = 1. Its change over time is shown as .
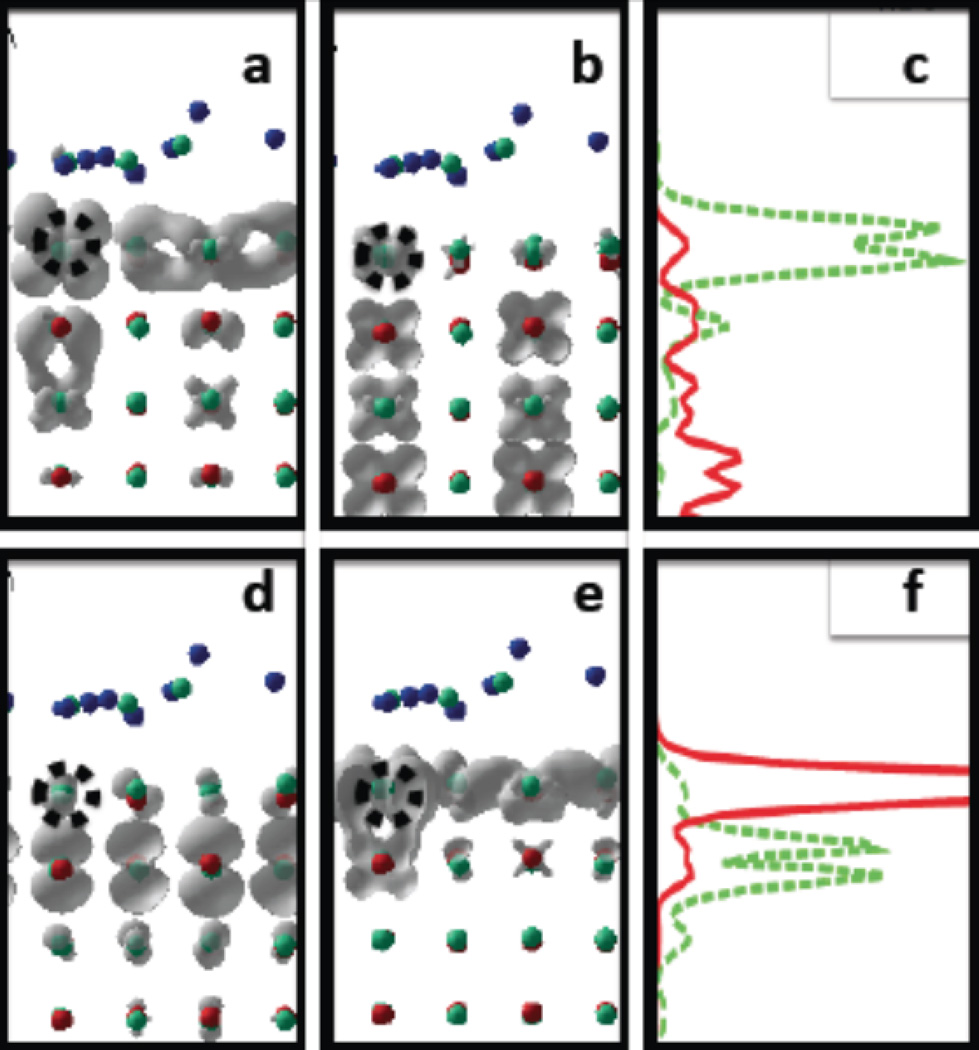
This initial state, specified by indices a, b is evolving in time due to interaction of electronic DOF with lattice vibrations. Figure 5 shows representative examples of photoexcited dynamics in models with and without surface doping for the following initial conditions a = HO−8, b = LU+3, created by pulse of central frequency ħΩ = 2.7111 eV, and a = HO′ − 21, b = LU′ + 3, created by pulse of central frequency ħΩ = 2.8562 eV. We analyze the photoexcited dynamics of the nonequilibrium electron distribution as function of time. Figures 5(b),(e) show isocontours of the population Δn(a,b)(ε, t), Eq. 16 giving the dynamics of similar photoexcitations calculated for the titania surface with and without surface adsorbed Ru-nanocatalyst, with red indicating large gain and blue large loss of electron density in respect to equilibrium distribution. Over time, the maxima are found to relax to a lower excitation energy. It corresponds to the electronic part of excitation (red) approaches CB minimum and hole part of excitation (blue) approaches VB maximum. As the systems relax, the populations of some orbitals change by large amounts, going through maxima before they decrease.
Figure 5.
a, d. Atomic models of thin semiconductor films with and without metal adsorbate. a: Ti32O64 × 8H2O; d: Ti30Ru2O64 × 8H2O. All models contain eight monoatomic layers, with 12 atoms each. The vertical axis z is perpendicular to the surface and is positive above the surface. Periodic boundary conditions are implied along x and y directions. Dangling surface bonds are compensated by water molecules. b, e. Isocontours of the population Δn(a,b)(ε, t) giving the dynamics of similar photoexcitations calculated for the silicon surface with and without surface adsorbed silver cluster. Here, red, green, and blue colored areas label the distribution Δn(a,b)(ε, t) in Eq. 16 for gain, no-change, and loss, respectively, in comparison with the equilibrium distribution; red areas can be understood as relating to electrons, and blue ones to holes. c, f. Spatial distributions as functions of time from Eq. 17. Colors from blue to red symbolize charge density value from 0 to 1. The figure presents the time evolution of electron density distribution in the normal direction to the surface for a silicon surface with and without an adsorbed silver cluster.
In the undoped model, Fig. 5(b), The relaxation of holes takes place at earlier time (10 – 100fs) than the electron relaxation (1 – 10ps). Both electron and hole relax to lowest available excitation for the undoped model. Such excitation, HO → LU, undergoes longer recombination process, kHO,LU = 2.85 × 10−2 ps−1, τHO,LU ≈ 35 ps This is quicker than electron-hole recombination time in water-dissolved titania quantum dots that is reported as equal to 500ps at 12K108 and varies with nanoparticles size from 66 to 405 ps at room temperature.109 The rate of recombination is determined by several key parameters, which should match in the system and in the model: (a) temperature, (b) nuclear fluctuations, (c) value of bandgap, (d) surface-to-volume ratio (e) details of surface functionalization. Influence of each parameter is discussed in Discussion section. In the doped model, Fig. 5(e), the relaxation of electrons occurs earlier in time at about 1ps. The relaxation of holes experiences several subsequent steps. Hole part of excitation subsequently visits several orbitals from the VB. In general, these steps of hole relaxation take longer than in the undoped model since these relaxation events involve new orbitals contributed by Ru-doping. Interestingly, the electron relaxes to the CBM LU′ earlier (.5ps) than the hole relaxes to the VBM HO’ (10ps). The strongest attention is focused on the time interval 1ps < t < 10ps, when one carrier (e−), arrives to the surface earlier than another one (h+). In such regime, the surface is being charged and is ready to facilitate reactions. Finally, both e− and h+ localize on the same surface. However, in a realistic setup with both oxidizing and reducing nanocatalysts the e− carrier is expected to be swept off to the reducing catalyst providing an excess of h+ charges on the surface with oxidizng RuO2 nanocatalyst.
Next, we focus on the time evolution of the valence band (VB) charge distribution in space since evolution of hole part of excitation plays key role in triggering oxidizing reaction on RuO2 nanocatalyst. Spatial distributions as functions of time from Eq. 17 are presented in Figure 5(c),(f).
The dynamics of hole part of excitation for the undoped titania surface, Fig 5(c) shows subsequent maximal occupation of orbitals HO−8, HO−1, HO. This corresponds to spatial charge evolving from being equally distributed between all inner layers of the slab towards semi-delocalized distribution over two atomic layers near the surface.
The dynamics of hole part of excitation for the doped titania surface, Fig 5(f) shows that maximal occupation of orbitals HO′−22, HO′−11, HO′−3, HO′ corresponds to spatial charge evolving from being equally distributed between O2p of all inner layers of the slab towards localization on the Ru4d surface doping. This illustrated the dynamics towards formation of the charge separated state. Possibly, this process can be summarized by an approximate redox reactions involving O and Ru
| (28) |
| (29) |
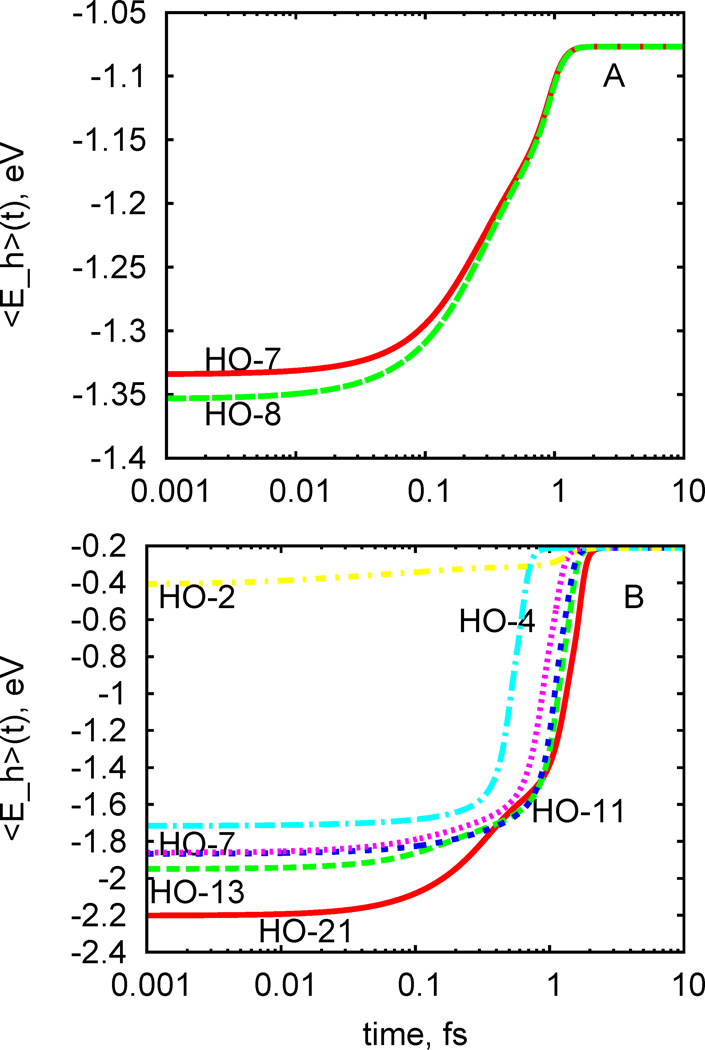
It is noted that these equations are symbolic simplifications. In reality, the electron is getting transferred between orbitals, which are delocalized over multiple oxygen ions. Interestingly, titania thin film surface charge transfer is reflected in the photovoltage observable which slowly decays in time as excited states recombine to the equilibrium110, 111 The information about time evolution of a photoexcited carrier for a given photoexcitation can be, in average, consolidated into a single function, such as evolution of an average energy of the carrier. Figure 6 illustrates the dependence of such average energy of hole as function of time, for different initial photoexcitations, for doped and undoped models. Table 3 summarizes the numerical measure of carrier energy dissipation for various initial excitations as computed according to Eq. 22.
Figure 6.
Dependence of hole relaxation dynamics on the initial excitation. Representative on individual excitations are selected according to electron-hole transitions with maximal oscillator strength. Only the hole dynamics is represented here. The expectation value of the hole energy is calculated by integrating the energy distribution of charge below Fermi energy weighted by relevant energy value. Panel a shows average hole energy dynamics for undoped titania anatase (100) surface, for different initial excitations. Panel b average hole energy dynamics for Ru-doped titania anatase (100) surface, for different initial excitations. The index of VB orbital where initial nonequilibrium population is created is explicitly labeled with the index of the orbital.
Table 3.
Dynamics of featured electronic transitions, for undoped and doped models. This table sumarizes the rates of computed dynamics. The values for 6’ and 7’ are high since these relaxation channels involve nearly degenerate orbitals.
| index | radiative lifetime, τ, ns |
hole relax. rate, kh, ps−1 |
electron relax. rate ke, ps−1 |
energy relax. rate kx, ps−1 |
|---|---|---|---|---|
| Undoped (100) TiO2 anatase + H2O, HO=288 | ||||
| 1 | 7.40 | 2.1394 | NA | 2.1394 |
| 2 | 6.54 | 2.1651 | 0.9138 | 3.0789 |
| Ru-doped (100) TiO2 anatase + H2O, HO′ = 292 | ||||
| 1′ | 89.07 | 1.3726 | 1.3145 | 2.6871 |
| 2′ | 10.64 | 1.2185 | 2.0219 | 3.2404 |
| 3′ | 7.87 | 1.9735 | 1.0590 | 3.0325 |
| 4′ | 8.94 | 0.9708 | 2.0219 | 2.9927 |
| 5′ | 11.98 | 0.9848 | 1.3145 | 2.2993 |
| 6′ | 179.21 | 0.9793 | 48.8368 | 49.8161 |
| 7′ | 2815.10 | 1.3726 | 48.8368 | 50.2094 |
3.4 Analysis of active orbitals
The models are oriented in such way that x, y, and z coordinates correspond to b = (010), c = (001), and a = (100) crystallographic axes, respectively. For undoped model, the two brightest transitions have transition dipoles oriented along (001) and (010) axes. The electronic configuration of titanium and ruthenium are Ti = [Ar] 3d24s2 and Ru = [Kr] 4d75s1. In our simulations, the orbitals near bandgap are contributed by valence electrons only. While doping, we replace two Ti atoms, from the top and bottom surfaces of the slab by Ru atoms, gaining four additional valence electrons per each dopant. HO′ = HO + 4, Here HO = 288, HO′ = 292 correspond to twice the number of valence electrons in the model. Our calculation is not spin polarized. The dopant atoms contribute 4 additional orbitals within the bandgap. Three of them are occupied, one of them is unoccupied. This analysis provides an argument, that the index of VB orbitals of a given symmetry are shifted down by 3 in doped model compare to undoped one. By analogy, the index of unpopulated CB orbitals are shifted up by +1 in doped model compared to undoped one. This expectation is partially fulfilled for two lowest and brightest transitions, their indices are as follows: pair of orbitals (1) = (HO − 7; LU)undoped converts into pair of orbitals (2′) = (HO′ − 10; LU′ + 2)doped. By analogy, pair of orbitals (2) = (HO − 8; LU + 3)undoped converts into pair of orbitals (5′) = (HO′ − 11; LU′ + 4)doped. The difference, if any, is due to perturbation imposed on all orbitals due to presence of the dopant. These four examples of pairs of orbitals are illustrated in Figures 7 and 8 and can be symbolically represented by redox reactions
| (30) |
| (31) |
There is another sequence of transitions involving orbitals contributed by doping. Such orbitals are spatially localized in the vicinity of the doping atom. The host, TiO2 orbitals are typically delocalized over the whole slab. We consider transitons from host to dopant, from dopant to host and Ru d-d transitions. The representative examples of such transitions are mentioned in the last three rows of the Table 2. The mean position of electron orbital distribution 〈i|r⃗|i〉 is localized in the surface region for doping orbitals and localized in the inner area of the slab for host orbitals. This fact is responsible for the specific character of partial contribution of a given pair of orbitals to the formation of charge transfer state and to photovoltage signal at a given transition frequency.
Figure 7.
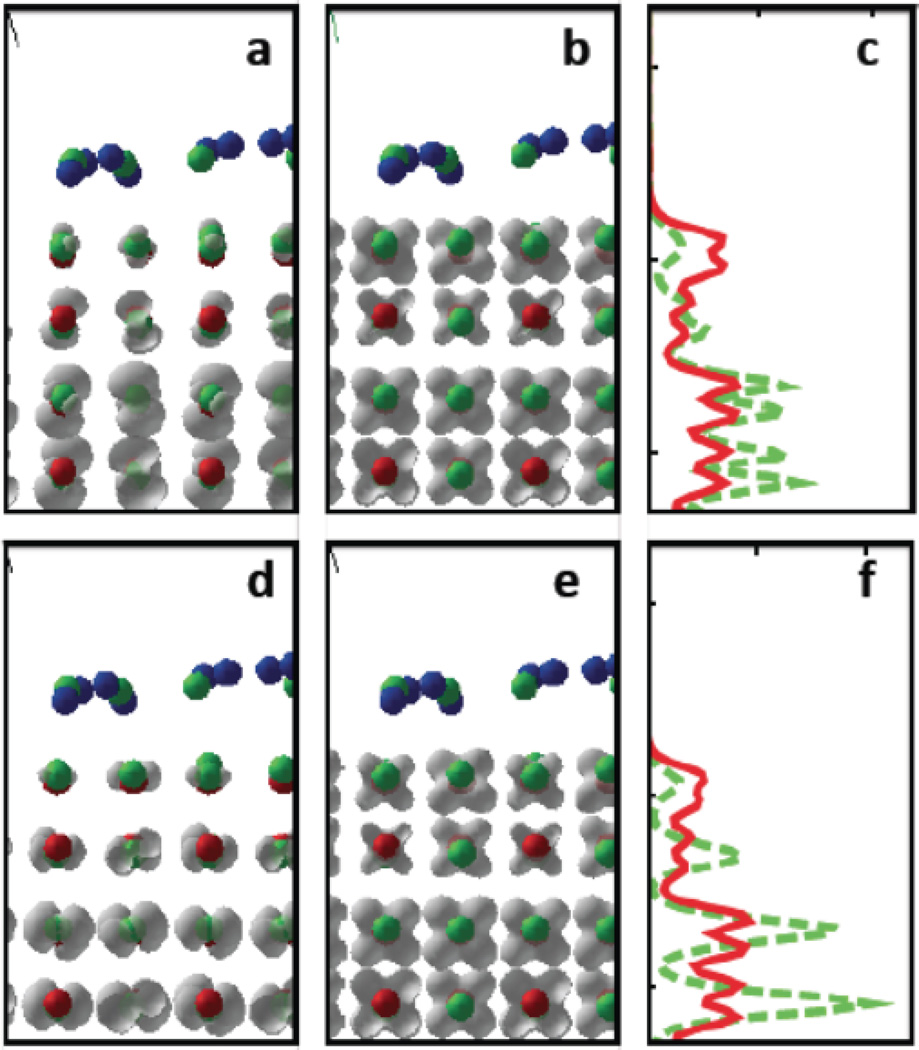
Bright excitations (1) and (2) for undoped TiO2 surface. Pairs of occupied and unoccupied KSOs contributing to low-energy optical transitions, for atomic model of anatase TiO2 with (100) face exposed and covered by a monolayer of water. Red, green, blue, stand for Ti, O, H atoms. Grey clouds symbolize isosurfaces of KSO. Panels a,b,d,e show partial charge density of a given KSO. Panels c, f show partial chagre density integrated over x,y direction, as function of z, < 100 > direction is orthogonal to the plane of the figure. Lowest brightest transition HO−7 to LU at transition energy 2.40 eV with oscillator strength f=3.40 is represented by panels a–c and corrsponds to index (1) in Table 2 and scheme in Fig. 1. Panel a and pabel c, green dashes stand for HO−7. Panel b and panel c, solid red line stand for LU. Second brightest transition HO−8 to LU+3 at transition energy 2.71 eV with oscillator strength f=3.01 is represented by panels d–f and compared to index (2) in Table 2. Panel d and panel f, green dashes stand for HO−8. Panel e and panel f, solid red line stand for LU+2. Interestingly, all occupied orbitals are composed as superposition of p-orbitals of oxygen and clearly exhibit p-character. All unoccupied orbitals are composed as superposition of d-orbitals of titanium. The vision is difficult since the atoms of O and Ti are stacking in the < 001 > view directions.
Figure 8.
Bright excitations (2’) and (5’) for doped TiO2 surface. Pairs of occupied and unoccupied KSOs contributing to low-energy optical transitions, for atomic model of anatase TiO2 with (100), exposed, doped by Ru atom and covered by a monolayer of water. Red, green, blue, stand for Ti, O, H atoms. Position of Ru surface doping atom is indicated by dashed circle. Grey clouds symbolize isosurfaces of KSO. Panels a,b,d,e show partial charge density of a given KSO. Panels c, f show partial chagre density integrated over x,y direction, as function of z. < 001 > direction is orthogonal to the plane of figure. This figure show bright transitions which have similar orbital symmetry with those of undoped titania surface. Lowest brightest transition HO′ − 10 to LU′ + 2 at transition energy 2.50 eV with oscillator strength f = 2.16 is represented by panels a–c and labeled as (2’) in Table 2. Panels a and panel c, green dashes stand for HO′ − 10. Panel b and panel c, solid red line stand for LU’+2. Second bright transition similar to one in the undoped structure is HO′ − 11 to LU′ + 4 at transition energy 2.87 eV with oscillator strength f = 1.46 is represented by panels d–f and labeled as (5’) in Table 2. Panel d and panel f, green dashes stand for HO′ − 11. Panel e and panel f, solid red line stand for LU′ + 4.
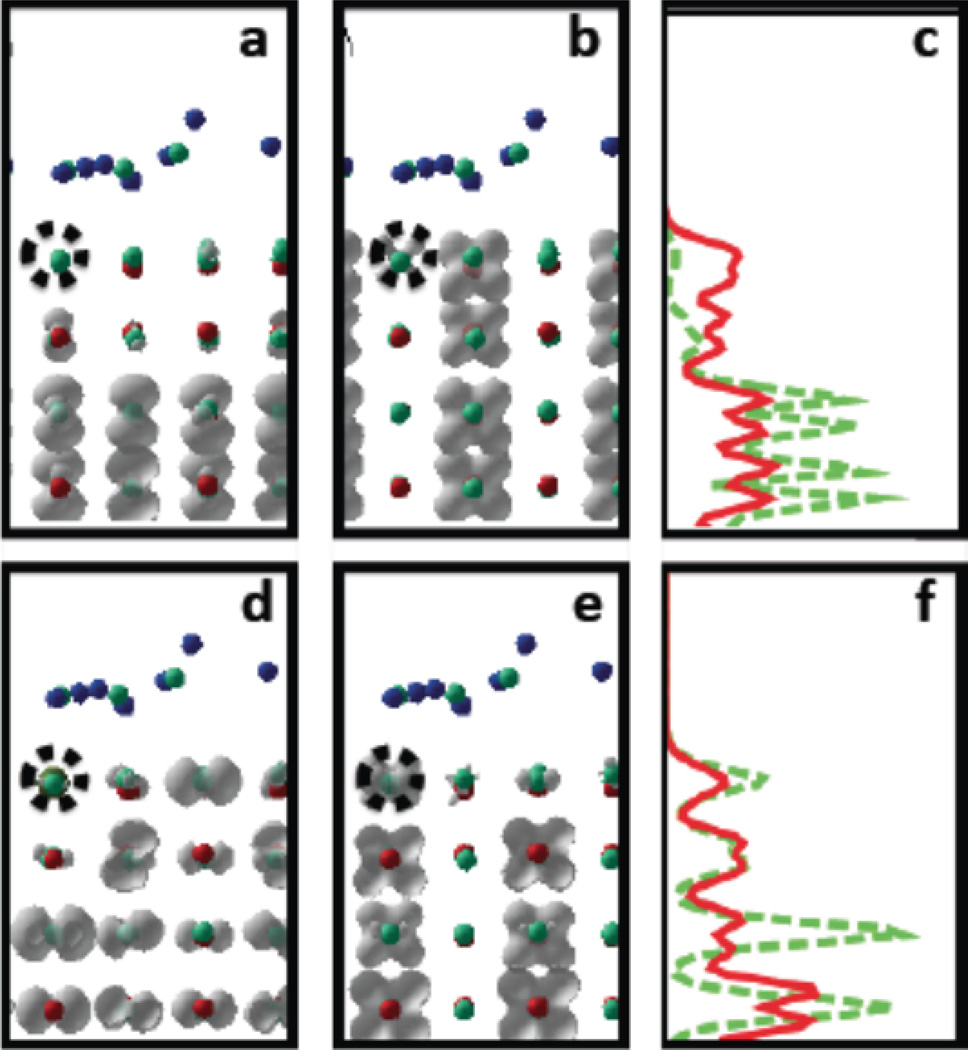
For example, the transition (1′) = (HO′ − 2 → LU′ + 4) corresponds to electron being promoted from the surface dopant to the Ti3d inner area of the slab as summarized by redox equation
| (32) |
| (33) |
Here we hypothesize x = 4, but this must be supported by additional computational data. The electron is transfered from the surface to inside of the slab. Exciting such transition creates electron depletion on the surface. In other words this can be interpreted as hole transfer to the surface. At the same time this transition has nonzero oscillator strength. Therefore, this elementary process of photoexciting this transition contributes to the photovoltage negative peak shown in feature c′ in Figure 2(a). The Kohn-Sham orbitals for this transition are visualized in Figure 7(a)–(c).
Another featured transition, (6′) = HO′ − 13 → LU′ + 1 corresponds to transition from O2p occupied host delocalized orbital to an unoccupied Ru4d localized doping orbital corresponds to electron being promoted from the inner area of the slab to the surface doping as summarized by redox reaction
| (34) |
| (35) |
The electron is transfered from inside of the slab to the surface. Exciting such transition creates electron enriching on the surface. In other words this can be interpreted as an electron transfer to the surface. Therefore, this elementary process of photoexciting this transition could contribute to the photovoltage positive peak. However, due to this transition has low oscillator strength the contribution is negligible and not seen in Figure 2(a). The Kohn-Sham orbitals for this transition are visualized in Figure 8(a)–(c).
We offer a hypothesis that the negative contribution by Ru doping in the photovoltage spectrum can be rationalized as follows: As seen in DOS, Fig.1(a), the number of interband occupied orbitals contributed by Ru-doping is larger than the number of interband unoccupied states contributed by Ru-doping. Therefore, the relative number of transitions with h+ transfer to surface, similar to (1′) = (HO′ − 2 → LU′ + 4), overcomes the number of transitions with e− transfer to the surface, similar to (6′) = (HO′ − 13 → LU′ + 1). By adding together the partial contributions from transitions of both types the h+-transfer transitions overweight and give overall h+ transfer and negative peak in the SPV spectra.
The last type of transitions, from localized doping orbital to another localized doping orbital, such as (7′) = (HO′ − 2 → LU′ + 1) does not contribute neither to optical absorption nor to charge transfer. Such transitions, however, are the lowest available transitions. Any excitation is expected to relax to them. Such excitations are expected to contribute to either Ru-based luminescence, recombination, or for triggering chemical reaction.
4 Discussion
Quantitative description of relaxation in Redfield formalism can be useful for description of broad range of phenomena from (a) hot carrier relaxation to (b) multiple exciton generation and (c) reaction dynamics. Here we focus on (a) energy relaxation and charge transfer. Therefore, it is sufficient to include only single excitations of electronic states in the explicit treatment. For implementing such formalism to (b) and (c) one needs to consider Hamiltonian in bigger basis. For (b) one needs to explicitly include double excitations etc. For (c) one needs to treat few nuclear DOF explicitly.
Pure TiO2 is a wide gap semiconductor. For such material, Multiple Exciton Generation (MEG) would be available at high UV excitation energy. This is probably of limited practical interest. MEG seem to be possible if involving dopant states. Atomistic consideration in basis of Kohn-Sham orbitals was reported for silicon quantum dots.112, 113 Description of multi-exciton generation in density matrix formalism was reported in basis of KP, effective mass theory.114 Combination of both, atomistic and density matrix approaches need to add few modules to the code. Practically, description of MEG would need 2 modules: (i) include multiple excitations into basis, (ii) include Coloumb matrix element computation.
The photoexcitation is inducing several pathways: cooling, trapping, recombination and others, taking place at different time scales from picoseconds to nanoseconds108, 109, 115, 116 In comparing experimental observations and computational modeling there is an issue of careful assigning lifetime of charge trapping versus charge recombination processes. The rate of recombination is determined by several key parameters, which should match in both experimental system and atomistic model: (a) temperature, (b) nuclear fluctuations, (c) value of bandgap, (d) surface-to-volume ratio (e) details of surface functionalization.
Temperature increase is expected to speed up the recombination according to Bose-Einstein distribution fBE, introduced after Eq. (10).
Fluctuations of ionic positions are the key feature promoting electronic transitions. The amplitude of fluctuations may depend on size of the model. Specifically, in larger models, energy is expected to partition as 1/2 kT over each nuclear degree of freedom. In smaller models, away from statistical regime, this partition may be violated for a limited time, leading to higher rates of electronic transitions.
The value of bandgap, and, generally, energy difference between orbitals experiencing transitions has a critical influence on the recombination and relaxation rates. This dependence can be partitioned on three factors: coupling, availability of phonon modes to accommodate energy difference, and phonon occupation function. Coupling is expected to depend on inverse of energy difference, contributing factor |εi − εj|−2 into overall rate. Bandgap of 2ev instead of 3eV will accumulate a factor roughly estimated as , providing computed recombination rate 2.25 times quicker. Correction of the computed bandgap can be achieved by applying GW approach with BSE corrections. A hybrid functionals, eg. HSE06 might work as a quick-fix solution. Another factors, availability of phonon modes, and Bose-Einstein distribution function contain more complicated dependence on energy difference and also affect the recombination rates.
Larger surface-to-volume ratio provides higher concentration of surface recombination sites and, in average, facilitates quicker relaxation. This dependence can be explored by manipulating the thickness of the model slab, leaving the same surface area and changing the volume of the model.
Present work delivers results for water molecules passivating surface active sites. Another options of experimental importance are hydroxyls, carboxyls, amines, etc. Each of them may contribute additional electronic states and vibrational modes, making strong effect on surface charge transfer and electron hole recombination.
5 Conclusions
We have presented theoretical and computational treatment of charge transfer at the Ru doped wet anatase titania surface. The applied theoretical method covers two major challenges at the same time: (i) atomistic details of changes in electronic structure introduced by of defects, surfaces, interfaces and (ii) dynamics of open systems: electrons interacting with lattice vibrations and light. Our method combines density matrix formalism and ab initio electronic structure calculations using an on-the-fly method to compute electron-lattice vibration non-adiabatic couplings. Then, a time average of the autocorrelation function of the electron-to-lattice couplings provides coefficients of electronic transitions that enter into the equation of motion for the electronic degrees of freedom. This approach allows for the description of relaxation phenomena and allows calculation of dynamics of electronic charge redistribution in the model. Optimum results are expected in the following conditions: ions are considered as point charges, lattice vibrations instantaneously equilibrate with a thermostat, coupling autocorrelation function decays abruptly leading to Markov approximation, vibrational reorganization is neglected, and excited state potential energy surfaces are assumed to have the same shape as for the ground state.
This method provides a way for atomistic computation of time-resolved observables, with the only input being a set of atomic positions for the model of reasonable practical size. A wide range of time intervals, from femto- to nanoseconds, could be explored without any additional computational cost. This is due to solution of equation of the motion by diagonalization of Liouville operator with constant coefficients. Applicable systems include rigid solids, whose lattice vibrations are close to harmonic law; void of bond breaking, bond formation, and low-frequency non-linear motion of atoms such as spatially confined semiconductor nanostructures at times longer than vibrational period.
Application of the method to wet titania surface dopants reveals additional pathways for photoinduced surface charge transfer. Dynamics of charge-separation demonstrate subsequent arrival of opposite charges to catalytic site. According to to computed data the direction of charge transfer can be controlled. In the time domain, the surface dopant first gains negative charge that is later neutralized upon arrival of a hole to the same site. In the frequency domain, with CW excitation, the computation shows formation of a stable state with a net positive charge in the surface. We are looking forward to verify this conclusion by experiment or an alternative computational procedure. A more complex system with an additional functional group(s) may serve for capturing an electron and having oxidizing and reducing sites separated in space.
Our results suggest specific surface redox reactions in the system. The computed results support the expectations that oxidizing and reducing nanocatalysts deposited on a semiconductor substrate are expected to exhibit higher catalytic activity upon charge transfer from the substrate to the nanocatalyst.117–121
Specifically, water splitting reducing and oxidizing half-reactions facilitated by charging of surface should be simulated by ab-initio molecular dynamics of charged models. Combining together the simulation of photon absorption,64–66 charge transfer from a substrate to reducing and oxidizing nanocatalysts63, 122–124 and a charge-facilitated surface reaction67 complete the pathway of subsequent elementary processes contributing to the photocatalytic water splitting.
The theoretical and computational modeling help in interpreting available experimental results and predicting an outcome of a possible experiment and in suggesting a design of a novel material with desired optical and electronic characteristics.
Figure 9.
Charged excitations (1’) and (6’) for doped TiO2 surface. Abbreviations and symbols are defined same way as in the previous figure. Panels a,b,d,e show partial charge density of a given KSO. Panels c, f show partial chagre density integrated over x,y directions, as function of z. This figure show charged transitions which are associated with surface Ru-doping and do not have similar orbital symmetry with those of undoped titania surface. Lowest charged, semi-bright transition HO′ − 2 → LU′ + 4 at transition energy εij = 1.35 eV with oscillator strength f = 0.89 is represented by panels a–c, labeled as (1’) in Table 2. Panels a and panel c, green dashes stand for HO′ − 2. Panel b and panel c, solid red line stand for LU′ + 4. Second charged, semi-bright transition is HO′ − 13 → LU′ + 1 at transition energy εij = 2.1087 eV 2.87 eV with oscillator strength f = 0.18 is represented by panels d–f, labeled as (6’) in Table 2. Panel d and panel f, green dashes stand for HO′ − 13. Panel e and panel f, solid red line stand for LU′ + 1.
Figure 10.
Schematic representation of an photoelectrochemical cell converting light into chemical form. Light is efficiently absorbed by active media, such as titania nanorod with absorption enhanced by a photosensitizer. An exciton is broken into free carriers, electrons and holes, each of which are swept off to surface nanocatalysts, adsorbed on opposite sides of the active media. Holes move to the oxidation nanocatalyst, e.g. ruthenia nanoparticle. Electrons move to reducing nanocatalyst, such as platinum nanoparticle. Charge transfer to nanocatalysts triggers the photo-catalytic half reactions, leading to producing fuel compound e.g H2 on the reducing nanocatalyst and oxidizer compound e.g. O2 on the oxidizing nanocatalyst. In case all nano-catalytic cell is immersed in water, the relevant half-reactions look as follows: 2H2O = 4H+ + 4e− + O2 and 2H+ + 2e− = H2. These half reactions are connected by two charge transfer channels: electron transfer across the nano-catalytic cell and proton transfer in surrounding solvent.
ACKNOWLEDGMENTS
This research was supported by South Dakota Governor’s Office of Economic Development, NSF award EPS0903804, and by DOE, BES - Chemical Sciences, NERSC Contract No. DE-AC02-05CH11231, allocation Awards 85213 and 86185 ”Computational Modeling of Photo-catalysis and Photo-induced Charge Transfer Dynamics on Surfaces”. The authors acknowledge computational resources of USD High Performance computational facilities co-sponsored by South Dakota IDeA Networks of Biomedical Research Excellence NIH 2 P20 RR016479 and operated by Douglas Jennewein. DK thanks Sergei Tretiak for hosting the visit at the Los Alamos National Lab during manuscript preparation. DK thanks Svetlana Kilina, David Micha, Oleg Prezhdo, for fruitful discussions. Editorial proofreading by Stephanie Jensen is gratefully acknowledged.
Appendix I
Numerical implementation of RDO in Kohn-Sham basis
Diagonal elements of the density matrix give state populations and off-diagonal elements of density matrix correspond to quantum coherences. The evolution of electronic states of a model system is conveniently described by the EOM in the Schrödinger picture of quantum mechanics81, 125, 126
| (36) |
Equation (36) contains populations ρii and coherences ρij for Kohn-Sham orbitals (KSOs) of a system with periodic boundary conditions, given by and used as a basis set. Here j and k denote KSOs, the vectors G are the reciprocal lattice vectors, Gcutoff is the value of the reciprocal lattice vector for a truncated Fourier expansion, and Cj,G stands for a KSO in the momentum representation.88, 93, 106 These KSOs are eigenfunctions of the Kohn-Sham effective Hamiltonian FKS with energies εj, and they will be shown as |j〉 = |ϕj〉.
The density matrix EOM (36) contains a reversible dynamics term from the operator F̂KS and the potential energy coupling of the dipole vector operator D̂ to the external electric field, and an irreversible dynamics relaxation rate term, both of which are needed to describe transient phenomena. The reversible term describes phase oscillations and interaction with light. It is constructed from KSO energies, transition dipoles, and the explicit form of the electric field. The relevant KSO energies εj satisfying are imported from the electronic structure calculations at fixed atomic positions. The transition dipole operator is obtained from transition dipole matrix elements calculated according to the formula .88, 106 The electric field for a photoexcitation created by steady irradiation with light of frequency Ω and electric field strength given by ℰ (t) = ℰ0(t) (exp{−iΩt} + exp{iΩt}). with ℰ0 = const for t ≥ π/(2Ω), and ℰ0 = 0 for t < π/(2Ω), which is effectively zero in our time scales. An expression for the relaxation rate can be obtained in the absence of light to second order in the interaction energy between the system of electrons and lattice vibrations.
Appendix II
Computational procedure for interaction hamiltonian and its autocorrelation function
Hamiltonian
Let one consider general Hamiltonian operator for electronic system with coordinates r which depend on positions of ions R as a parameter:
| (37) |
If the electronic DOF are the considered as a quantum system surrounded by bath of lattice vibrations the Hamiltonian can be partitioned as
| (38) |
where Ĥint denotes here the electron-ion interaction.
For each specific geometry configuration, such as equilibrium relaxed geometry R = Req one can find the electronic eigenfunctions of the Hamiltonian |n〉eq which are orthogonal to each other.
| (39) |
However, small perturbation of ionic positions R = Req + ΔR perturbs Hamiltonian
| (40) |
For this perturbed Hamiltonian, the equilibrium electronic states |n〉eq are not the eigenstates anymore. The displacement of ions breaks orthogonality of the chosen set of electronic states. This non-orthogonality may lead to electronic transitions. This effect can be quantified by estimating the increment to the matrix element of Hamiltonian:
| (41) |
Here the expression Ĥ|n〉 obeys the eigenstate property (39) and since eigenvectors of non-pertubed Hamiltonian Ĥ0 are orthonormal the Eq. (41) can be re-written as
| (42) |
Here one can notice the equivalence of the two ways to account for lattice vibrations: through increment of Hamiltonian in Eq. (40) and through increment of electronic state in Eq. (42), both reflecting the deviation of ionic configuration from equilibrium.
The method of overlap of displaced orbitals can be efficiently computationally implemented based on “on-the-fly” numeric adiabatic ab-initio molecular dynamics.49, 63, 104 There, a molecular dynamics trajectory is represented by a set of subsequent atomic configurations and momenta. In the framework of molecular dynamics description of lattice DOF, trajectories are represented by a set of subsequent atomic configurations and momenta. For each timestep, the difference between αth Cartesian coordinate of Ith atom at time moments of t and t + Δt can be expressed in term of momentum , where MI is mass of Ith atom. For each atomic configuration, there is a corresponding set of eigenstates. In Eq. (41) the gradient term times displacement ΔR is replaced by time derivative of electronic wavefunction. For a discrete time increment, this all yields discretized time dependent non-diagonal Hamiltonian, which characterize interaction of electrons-to-lattice vibrations, with matrix element
| (43) |
The features of the electrons-to-lattice coupling can be understood by analysis of autocorrelation function of the interaction operator
| (44) |
In numerical form, based on the derivative of Hamiltonian, the autocorrelator (44) is composed of the terms including products of matrix elements and momentum-momentum correlation function
| (45) |
In numerical form, based on “on-the-fly” calculation, the autocorrelator (44) is composed of the terms including products of matrix elements
| (46) |
plus permutations. Here, the average over bath states Trion is represented by the summation of snapshots of multiple trajectories or one long trajectory.
Appendix III
Numeric implementation of RDO EOM in KSO DFT
For long time phenomena as we consider here, the relaxation rate can be expressed in terms of the Redfield coefficients Rijkl which can in turn be calculated from state-to-state rate coefficients.83, 126 In the Schroedinger picture (SP),
| (47) |
which can be used in our treatment insofar adding light would change this rate only to higher order in the strength of the electric field.
To proceed, we transform the EOM for the RDM to the interaction picture (IP) of quantum mechanics to identify terms that are oscillating slowly over time. These are the terms which survive a long time average of the EOM and contribute to the steady state solution we are looking for. In detail, a term in the EOM containing the phase factor exp(iΔ․t), averaged over a long time τ around t gives , for τ >> Δ−1. Therefore we’ll keep in equations only terms which oscillate slowly over time.
In the IP we have that , with ωjk = (εj − εk)/ħ, and similarly for other operators. We consider first oscillatory terms coming from light absorption and emission. Light of frequency Ω activates only transitions allowed by Djk ≠ 0, and after time averaging it involves transitions with detuning Δjk = Ω − (εj − εk)/ħ, smaller than dephasing rates γkj defined in what follows. We consider only interband optical transitions so that i and j belong to different bands: CB, i ≥ LUMO and VB j ≤ HOMO. We decompose the dipole coupling in the IP as
The first two terms in the brackets describe processes where a semiconductor surface gets excited from VB KSO 〈j〉 to CB KSO 〈i〉 by absorbing light, or gets de-excited from CB KSO 〈i〉 to VB KSO 〈j〉 by emitting light. These terms involve slow time dependent contributions oscillating with frequencies Ω − |ωij|. We keep these slow changing terms and omit the other fast ones, as in the Rotating Wave Approximation (RWA)127, 128 for the coupling potential. The resulting EOM can conveniently be expressed in terms of the new density matrix elements
| (48) |
and ρ̃ii(t) = ρii(t). These will be called the rotating frame DM elements.
Turning to oscillating terms in the relaxation rate (ρ̇ij)rel within (36), they are cast in the IP as
| (49) |
The Redfield coefficients are sorted in accordance to whether εi − εk − εj + εl = 0 or not. Keeping only the matching terms one arrives at the secular approximation.128 Specifically, this condition is fullfilled in two specific cases (i) εi = εj, εk = εl providing relaxation (both gain and loss) rates Riijj for populations ρii, and (ii) εi = εk, εj = εl providing dephasing rates Rijij for coherences ρij. The other terms describe coherence transfer, or coupling between populations and coherences. They give smaller contributions upon averaging over long times, and they are neglected in what follows. Furthermore, the electronic transition energies Vjk, mediated by vibrational motion and charge polarization (bosonic excitations) in the medium, are small for the localized phenomena of present interest, and can be assumed small. This justifies an expansion of the solutions to the relaxation equation in powers of the strength of the R-coefficients. The leading population loss rate is then given by Γj = Rjjjj, and the balance of loss minus gain can be written as , using detailed balance at thermal equilibrium for a collection of electrons. Similarly, the relaxation rate for the quantum decoherence of state pair (jk) is written as , with γjk = Rjkjk.
Hence, combining reversible and irreversible dynamics terms and staying within the mentioned approximations, the EOM reads83, 126
| (50) |
| (51) |
| (52) |
| (53) |
Here Ωjk = −Djk · ℰ0/ħ, and Δjk stand for Rabi and detuning frequencies respectively. Also, ħωjk = εj − εk, J, fBE, and T are described in83, 85, 86 and stand for an energy difference, spectral density of bosons, their thermal distribution for frequencies ω, and temperature, respectively, while stands for a pure dephasing component.126 The thermal equilibrium state in our electron system is specified by the Fermi-Dirac distribution for the diagonal elements of the density matrix and by zero values for the off-diagonal density matrix, , i ≠ j, as follows from the relaxation of our system as it interacts with a medium at temperature T.
Appendix IV
Observables
The electronic excitations induced in a slab by a light adsorption lead to creation a photoinduced polarization with a time-dependent component.129 The polarization generates generates an electric field and, if the slab is brought into contact with electric circuit it lead to electrical voltage generation. Measured photovoltage is related the time average of surface electric dipoles, and these in turns could be theoretically derived from a time-dependent density matrix (TDDM) ρ̂ using using the KSO basis set.
Consider the situation when a surface acquires an excess or deficit of electronic charge density with respect to ground state distribution one. The electronic charge density is assumed to be periodically distribute in XY plane. The dependence of the electronic charge density along the Z coordinate perpendicular to the surface leads to inhomogeneity in total surface charge density across the slab , which becomes a source of an electric field εz = ctot(z)/(εrε0), perpendicular to the surface. The corresponding electric potential difference between charged layers is proportional to to their average charge and and the distance between the layers with excess and deficient planar electronic charge distribution as:
| (54) |
where w, z, ctot, ε0, εr stand for the width of a photoactive layer, the distance perpendicular to the surface, the total charge density per unit length across the surface, the dielectric constant of vacuum, and the dielectric coefficient of the photoactive medium, respectively. Note that this universal equation is valid for ctot representing ground or excited state of the semiconductor surface. The total charge density contains both ionic and electronic contributions, so that ctot(z) = cion(z) + cel(z), with and cel(z) = −en(z). Here, Cσ is the ion charge, Ziσ is the z component of of position vector of atom of type σ, e is an elementary charge and n(z) is electronic charge density along z-axis.
Within DFT, the electronic charge density is modeled as the sum of partial charge densities from KS orbitals. The electronic charge follows from the electronic density matrix of the whole system in the coordinate representation at each time moment t as cel(r, t) = −eρ(r, r, t). The electronic density matrix is expressed in a basis st of KS orbitals {ϕi(r)} and the surface photovoltage (SPV) VSPV = Vs(Ω) − Vs(0)106 constructed from
| (55) |
with A the surface area of the simulation supercell, Cσ and Ziσ the atomic core charge and position in the lattice, and 〈i|z|i〉 an average electronic position, so that ṼSPV (Ω) is obtained with respect to the voltage of the non-excited system.87 The density matrix elements ρij(Ω) depend on the frequency of incident light Ω as it is shown below.
Footnotes
Supporting Information
This information is available free of charge via the Internet at http://pubs.acs.org
References
- 1.Fujishima A, Honda K. A Low-Cost, High-Efficiency Solar Cell Based on Dye-Sensitized Colloidal TiO2 films. Nature. 1972;238:37–38. [Google Scholar]
- 2.O'Regan B, Gratzel M. Electrochemical Photolysis of Water at a Semiconductor Electrode. Nature. 1991;353:737–740. doi: 10.1038/238037a0. [DOI] [PubMed] [Google Scholar]
- 3.Bandara J, Kiwi J, Pulgarin C, Peringer P, Pajonk G-M, Elaloui A, Albers P. Novel Cyclic Process Mediated by Copper Oxides Active in the Degradation of Nitrophenols: Implications for the Natural Cycle. Environ. Sci. Technol. 1996;30:1261–1267. [Google Scholar]
- 4.Walter MG, Warren EL, McKone JR, Boettcher SW, Mi Q, Santori EA, Lewis NS. Solar Water Splitting Cells. Chem. Rev. 2010;110:6446–6473. doi: 10.1021/cr1002326. [DOI] [PubMed] [Google Scholar]
- 5.Hagfeldt A, Graetzel M. Light-Induced Redox Reactions in Nanocrystalline Systems. Chem. Rev. 1995;95:49–68. [Google Scholar]
- 6.Chen X, Burda C. The Electronic Origin of the Visible-Light Absorption Properties of C-, N- and S-Doped TiO2 Nanomaterials. J. Am. Chem. Soc. 2008;130:5018–5019. doi: 10.1021/ja711023z. [DOI] [PubMed] [Google Scholar]
- 7.Henderson MA. A Surface Science Perspective on Photocatalysis. Surf. Sci. Rep. 2011;66:185–297. [Google Scholar]
- 8.Kovash CS, Jr, Hoefelmeyer JD, Logue BA. TiO2 Compact Layers Prepared by Low Temperature Colloidal Synthesis and Deposition for High Performance Dye-Sensitized Solar Cells. Electrochim. Acta. 2012;67:18–23. [Google Scholar]
- 9.Nocera DG. Chemistry of Personalized Solar Energy. Inorg. Chem. 2009;48:10001–10017. doi: 10.1021/ic901328v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Asbury JB, Hao E, Wang Y, Ghosh HN, Lian T. Ultrafast Electron Transfer Dynamics from Molecular Adsorbates to Semiconductor Nanocrystalline Thin Films. J. Phys. Chem. B. 2001;105:4545–4557. [Google Scholar]
- 11.Petek H, Zhao J. Ultrafast Interfacial Proton-Coupled Electron Transfer. Chem. Rev. 2010;110:7082–7099. doi: 10.1021/cr1001595. [DOI] [PubMed] [Google Scholar]
- 12.Duncan WR, Prezhdo OV. Theoretical Studies of Photoinduced Electron Transfer in Dye-Sensitized TiO2. Ann. Rev. Phys. Chem. 2007;58:143–184. doi: 10.1146/annurev.physchem.58.052306.144054. [DOI] [PubMed] [Google Scholar]
- 13.Hilgendorff M, Sundstrom V. Dynamics of Electron Injection and Recombination of Dye-Sensitized Tio2 Particles. J. Phys. Chem. B. 1998;102:10505–10514. [Google Scholar]
- 14.Xu T, Yan M, Hoefelmeyer JD, Qiao Q. Exciton Migration and Charge Transfer in Chemically Linked P3HT-TiO2 Nanorod Composite. RSC Adv. 2012;2:854–862. [Google Scholar]
- 15.Park N-G, van de Lagemaat J, Frank AJ. Comparison of Dye-Sensitized Rutile- and Anatase-Based TiO2 Solar Cells. J. Phys. Chem. B. 2000;104:8989–8994. [Google Scholar]
- 16.Grätzel M. Dye-Sensitized Solar Cells. J. Photochem. Photobiol. C. 2003;4:145–153. [Google Scholar]
- 17.Xu M, Gao Y, Moreno EM, Kunst M, Muhler M, Wang Y, Idriss H, Wöll C. Photocatalytic Activity of Bulk TiO2 Anatase and Rutile Single Crystals Using Infrared Absorption Spectroscopy. Phys. Rev. Lett. 2011;106:138302. doi: 10.1103/PhysRevLett.106.138302. [DOI] [PubMed] [Google Scholar]
- 18.Zhang H, Banfield JF. Kinetics of Crystallization and Crystal Growth of Nanocrystalline Anatase in Nanometer-Sized Amorphous Titania. Chem. Mater. 2002;14:4145–4154. [Google Scholar]
- 19.Gribb AA, Banfield JF. Particle Size Effects on Transformation Kinetics and Phase Stability in Nanocrystalline TiO2. Am. Mineral. 1997;82:717–728. [Google Scholar]
- 20.Yang HG, Sun CH, Qiao SZ, Zou J, Liu G, Smith SC, Cheng HM, Lu GQ. Anatase TiO2 Single Crystals with a Large Percentage of Reactive Facets. Nature. 2008;453:638–641. doi: 10.1038/nature06964. [DOI] [PubMed] [Google Scholar]
- 21.Gordon TR, Cargnello M, Paik T, Mangolini F, Weber RT, Fornasiero P, Murray CB. Nonaqueous Synthesis of TiO2 Nanocrystals Using TiF4 to Engineer Morphology, Oxygen Vacancy Concentration, and Photocatalytic Activity. J. Am. Chem. Soc. 2012;134:6751–6761. doi: 10.1021/ja300823a. [DOI] [PubMed] [Google Scholar]
- 22.Herman GS, Sievers MR, Gao Y. Structure Determination of the Two-Domain (1×4) Anatase TiO2(001) Surface. Phys. Rev. Lett. 2000;84:3354–3357. doi: 10.1103/PhysRevLett.84.3354. [DOI] [PubMed] [Google Scholar]
- 23.Lazzeri M, Selloni A. Stress-Driven Reconstruction of an Oxide Surface: the Anatase TiO2(001) − (1 × 4) Surface. Phys. Rev. Lett. 2001;87:266105. doi: 10.1103/PhysRevLett.87.266105. [DOI] [PubMed] [Google Scholar]
- 24.Selloni A. Crystal Growth: Anatase Shows its Reactive Side. Nature Mater. 2008;7:613–615. doi: 10.1038/nmat2241. [DOI] [PubMed] [Google Scholar]
- 25.Nowotny J, Bak T, Nowotny M, Sheppard L. Titanium Dioxide for Solar-Hydrogen I. Functional properties. Int. J. Hydrogen Energy. 2007;32:2609–2629. [Google Scholar]
- 26.Chiodo L, Garcia-Lastra JM, Iacomino A, Ossicini S, Zhao J, Petek H, Rubio A. Self-Energy and Excitonic Effects in the Electronic and Optical Properties of TiO2 crystalline phases. Phys. Rev. B. 2010;82:045207–12. [Google Scholar]
- 27.Asahi R, Morikawa T, Ohwaki T, Aoki K, Taga Y. Visible-Light Photocatalysis in Nitrogen-Doped Titanium Oxides. Science. 2001;293(5528):269–271. doi: 10.1126/science.1061051. [DOI] [PubMed] [Google Scholar]
- 28.Wang H, Lewis J. Second-Generation Photocatalytic Materials: Anion-Doped TiO2. J. Phys. Cond. Matt. 2006;18:421–434. [Google Scholar]
- 29.Choi W, Termin A, Hoffmann MR. The Role of Metal Ion Dopants in Quantum-Sized TiO2: Correlation between Photoreactivity and Charge Carrier Recombination Dynamics. J. Phys. Chem. 1994;98:13669–13679. [Google Scholar]
- 30.Choi J, Park H, Hoffmann MR. Effects of Single Metal-Ion Doping on the Visible-Light Photoreactivity of TiO2. J. Phys. Chem. C. 2010;114:783–792. [Google Scholar]
- 31.Umebayashi T, Yamaki T, Itoh H, Asai K. Analysis of Electronic Structures of 3d Transition Metal-Doped TiO2 Based on Band Calculations. J. Phys. Chem. Solids. 2002;63:1909–1920. [Google Scholar]
- 32.Navio JA, Macias M, Gonzalez-Catalan M, Justo A. Bulk and Surface Characterization of Powder Iron-Doped Titania Photocatalysts. J. Mater. Sci. 1992;27:3036–3042. [Google Scholar]
- 33.Bickley RI, Lees JS, Tilley RJD, Palmisano L, Schiavello M. Characterisation of Iron/Titanium Oxide Photocatalysts. Part 1.-Structural and Magnetic Studies. J. Chem. Soc. Faraday Trans. 1992;88:377–383. [Google Scholar]
- 34.Kominami H, Murakami S, Kohno M, Kera Y, Okada K, Ohtani B. Stoichiometric Decomposition of Water by Titanium(IV) Oxide Photocatalyst Synthesized in Organic Media: Effect of Synthesis and Irradiation Conditions on Photocatalytic Activity. Phys. Chem. Chem. Phys. 2001;3:4102–4106. [Google Scholar]
- 35.Sullivan JM, Erwin SC. Theory of Dopants and Defects in Co-doped TiO2 Anatase. Phys. Rev. B. 2003;67:144415. [Google Scholar]
- 36.Huy HA, Aradi B, Frauenheim T, Deak P. Calculation of Carrier-Concentration-Dependent Effective Mass in Nb-Doped Anatase Crystals of TiO2. Phys. Rev. B. 2011;83:155201. [Google Scholar]
- 37.Nair M, Rao K, Nair C. Investigation of the Mixed Oxide Materials–TiO2–SiO2TiO2–SiO2–Al2O3, TiO2–SiO2–In2O3 and TiO2–SiO2–RuO2–In regard to the Photoelectrolysis of Water. Int. J. Hydrogen Energy. 1991;16:449–459. [Google Scholar]
- 38.Wang MH, Guo RJ, Tso TL, Perng TP. Effects of Sintering on the Photoelectrochemical Properties of Nb-Doped. TiO2 Electrodes. Int. J. Hydrogen Energy. 1995;20:555–560. [Google Scholar]
- 39.de Lara-Castells M, Krause J. Theoretical Study of the Interaction of Molecular Oxygen with a Reduced TiO2 Surface. Chem. Phys. Lett. 2002;354:483–490. [Google Scholar]
- 40.Sakata T, Hashimoto K, Kawai T. Catalytic Properties of Ruthenium Oxide on n-Type Semiconductors under Illumination. J. Phys. Chem. 1984;88:5214–5221. [Google Scholar]
- 41.Vanden Brink M, Peck MA, More KL, Hoefelmeyer JD. Alkylamine Stabilized Ruthenium Nanocrystals: Faceting and Branching. J. Phys. Chem. C. 2008;112:12122–12126. [Google Scholar]
- 42.Walle LE, Borg A, Uvdal P, Sandell A. Experimental Evidence for Mixed Dissociative and Molecular Adsorption of Water on a Rutile TiO2 (110) Surface without Oxygen Vacancies. Phys. Rev. B. 2009;80:235436. [Google Scholar]
- 43.Lindan PJD, Harrison NM, Gillan MJ. Mixed Dissociative and Molecular Adsorption of Water on the Rutile (110) Surface. Phys. Rev. Lett. 1998;80:762–765. [Google Scholar]
- 44.Walle LE, Borg A, Johansson EMJ, Plogmaker S, Rensmo H, Uvdal P, Sandell A. Mixed Dissociative and Molecular Water Adsorption on Anatase TiO2 (101) J. Phys. Chem. C. 2011;115:9545–9550. [Google Scholar]
- 45.Vittadini A, Selloni A, Rotzinger FP, Grätzel M. Structure and Energetics of Water Adsorbed at TiO2 Anatase (101) and (001) Surfaces. Phys. Rev. Lett. 1998;81:2954–2957. [Google Scholar]
- 46.Webb S, Iordanov T, Hammes-Schiffer S. Multiconfigurational Nuclear-Electronic Orbital Approach: Incorporation of Nuclear Quantum Effects in Electronic Structure Calculations. J. Chem. Phys. 2002;117:4106–4118. [Google Scholar]
- 47.Tully JC. Molecular-Dynamics with Electronic-Transitions. J. Chem. Phys. 1990;93:1061–1071. [Google Scholar]
- 48.Tully JC. Perspective: Nonadiabatic Dynamics Theory. J Chem. Phys. 2012;137:22A301. doi: 10.1063/1.4757762. [DOI] [PubMed] [Google Scholar]
- 49.Kilina SV, Craig CF, Kilin DS, Prezhdo OV. Ab Initio Time-Domain Study of Phonon-Assisted Relaxation of Charge Carriers in a PbSe Quantum Dot. J. Phys Chem. C. 2007;111:4871–4878. [Google Scholar]
- 50.Fernandez-Alberti S, Kleiman VD, Tretiak S, Roitberg AE. Nonadiabatic Molecular Dynamics Simulations of the Energy Transfer between Building Blocks in a Phenylene Ethynylene Dendrimer. J. Phys. Chem. A. 2009;113:7535–7542. doi: 10.1021/jp900904q. [DOI] [PubMed] [Google Scholar]
- 51.LGC Rego, Batista VS. Quantum Dynamics Simulations of the Interfacial Electron Transfer in Sensitized TiO2 Semiconductors. J. Am. Chem. Soc. 2003;125:7989–7997. doi: 10.1021/ja0346330. [DOI] [PubMed] [Google Scholar]
- 52.Parkhill JA, Tempel DG, Aspuru-Guzik A. Exciton Coherence Lifetimes from Electronic Structure. J. Chem. Phys. 2012;136:104510. doi: 10.1063/1.3689858. [DOI] [PubMed] [Google Scholar]
- 53.Redfield AG. On the Theory of Relaxation Processes. IBM J. Res. Dev. 1957;1:19–31. [Google Scholar]
- 54.Breuer H, Petruccione F. The Theory of Open Quantum Systems. USA: Oxford University Press; 2007. [Google Scholar]
- 55.Egorova D, Thoss M, Domcke W, Wang H. Modeling of Ultrafast Electron-Transfer Processes: Validity of Multilevel Redfield Theory. J. Chem. Phys. 2003;119:2761–2773. [Google Scholar]
- 56.Pollard W, Friesner R. Solution of the Redfield Equation for the Dissipative Quantum Dynamics of Multilevel Systems. J. Chem. Phys. 1994;100:5054–5065. [Google Scholar]
- 57.Jean JM, Friesner RA, Fleming GR. Application of a Multilevel Redfield Theory to Electron Transfer in Condensed Phases. J. Chem. Phys. 1992;96:5827–5842. [Google Scholar]
- 58.Sundstrom V, Pullerits T, van Grondelle R. Photosynthetic Light-Harvesting: Reconciling Dynamics and Structure of Purple Bacterial LH2 Reveals Function of Photosynthetic Unit. J. Phys. Chem. B. 1999;103(13):2327–2346. [Google Scholar]
- 59.Kuhn O, May V, Schreiber M. Dissipative Vibrational Dynamics in a Curve-Crossing System. J. Chem. Phys. 1994;101:10404–10415. [Google Scholar]
- 60.Venkataraman C, Soudackov AV, Hammes-Schiffer S. Dynamics of Photoinduced Proton-Coupled Electron Transfer at Molecule-Semiconductor Interfaces: A Reduced Density Matrix Approach. J. Phys. Chem. C. 2010;114:487–496. [Google Scholar]
- 61.Shi Q, Geva E. A Semiclassical Generalized Quantum Master Equation for an Arbitrary System-Bath Coupling. J. Chem. Phys. 2004;120:10647–10658. doi: 10.1063/1.1738109. [DOI] [PubMed] [Google Scholar]
- 62.Davis WB, Wasielewski MR, Ratner MA, Mujica V, Nitzan A. Electron Transfer Rates in Bridged Molecular Systems: A Phenomenological Approach to Relaxation. J. Phys. Chem. A. 1997;101:6158–6164. [Google Scholar]
- 63.Kilin DS, Micha DA. Relaxation of Photoexcited Electrons at a Nanostructured Si(111) Surface. J. Phys. Chem. Lett. 2010;1:1073–1077. [Google Scholar]
- 64.Jensen SJ, Kilin DS. Anatase (100) Thin Film Surface Computational Model for Photoelectrochemical Cell. Int. J. Quantum Chem. 2012;112:3874–3878. [Google Scholar]
- 65.Jensen SJ, Kilin DS. Computational Modeling of TiO2 Anatase (100) Thin Film Photoelectrochemical Cell. Prepr. Pap.-Am. Chem. Soc., Div. Energy Fuels Chem. 2012;57:536–536. [Google Scholar]
- 66.Zhang Y, Kilin DS. Computational Modeling of Wet TiO2(001) Anatase Surfaces Functionalized by Transition Metal Doping. Int. J. Quantum Chem. 2012;112:3867–3873. [Google Scholar]
- 67.Meng QG, May PS, Berry MT, Kilin DS. Sequential Hydrogen Dissociation from a Charged Pt13H24Cluster Modeled by Ab Initio Molecular Dynamics. Int. J. Quantum Chem. 2012;112:3896–3903. [Google Scholar]
- 68.Tully JC. Classical and Quantum Dynamics in Condensed Phase Simulations. World Scientific Publishing Company; 1998. [Google Scholar]
- 69.Pechukas P. Time-Dependent Semiclassical Scattering Theory. II. Atomic Collisions. Phys. Rev. 1969;181:174–185. [Google Scholar]
- 70.Miller WH. The Semiclassical Initial Value Representation: A Potentially Practical Way for Adding Quantum Effects to Classical Molecular Dynamics Simulations. J. Phys. Chem. A. 2001;105:2942–2955. [Google Scholar]
- 71.Shi Q, Geva E. A Relationship between Semiclassical and Centroid Correlation Functions. J. Chem. Phys. 2003;118:8173–8184. [Google Scholar]
- 72.Poulsen JA, Nyman G, Rossky PJ. Practical Evaluation of Condensed Phase Quantum Correlation Functions: A Feynman–Kleinert Variational Linearized Path Integral Method. J. Chem. Phys. 2003;119:12179–12193. [Google Scholar]
- 73.Meyera H-D, Miller WH. A Classical Analog for Electronic Degrees of Freedom in Nonadiabatic Collision Processes. J. Chem. Phys. 1979;70:3214–3223. [Google Scholar]
- 74.Stock G, Thoss M. Semiclassical Description of Nonadiabatic Quantum Dynamics. Phys. Rev. Lett. 1997;78:578–581. doi: 10.1103/PhysRevLett.87.140404. [DOI] [PubMed] [Google Scholar]
- 75.Redfield AG. The Theory of Relaxation Processes. Adv. Mag. Reson. 1965;1:1–32. [Google Scholar]
- 76.Leggett AJ, Chakravarty S, Dorsey AT, Fisher MPA, Garg A, Zwerger W. Dynamics of the Dissipative Two-State System. Rev. Mod. Phys. 1987;59:1–85. [Google Scholar]
- 77.Förster T. 10th Spiers Memorial Lecture. Transfer mechanisms of electronic excitation. Discuss. Faraday Soc. 1953;27:7–17. [Google Scholar]
- 78.Nitzan A. Chemical Dynamics in Condensed Phases. New York: Oxford University Press; 2006. [Google Scholar]
- 79.Baiz CR, Kubarych KJ, Geva E. Molecular Theory and Simulation of Coherenct Transfer in Metal Carbonyls and its Signature on Multidimensional Infrared Spectra. J. Phys. Chem. B. 2011;115:5322–5339. doi: 10.1021/jp109357d. [DOI] [PubMed] [Google Scholar]
- 80.Kamisaka H, Kilina SV, Yamashita K, Prezhdo OV. Ultrafast Vibrationally-Induced Dephasing of Electronic Excitations in PbSe Quantum Dot. Nano Lett. 2006;6:2295–2300. doi: 10.1021/nl0617383. [DOI] [PubMed] [Google Scholar]
- 81.Mukamel S. Principles of Nonlinear Optical Spectroscopy. Oxford: Oxford Univ. Press; 1995. [Google Scholar]
- 82.May V, Kühn O. Charge and Energy Transfer Dynamics in Molecular Systems. Berlin: Wiley-VCH; 2000. [Google Scholar]
- 83.Schatz GC, Ratner MA. Quantum Mechanics in Chemistry. Prentice-Hall: Englewood Cliffs; 1993. [Google Scholar]
- 84.Kilin DS, Micha DA. Surface Photovoltage at Nano-structures on Si Surfaces: Ab-initio Results. J. Phys. Chem. C. 2009;113:3530–3542. [Google Scholar]
- 85.Apanasevich PA, Kilin SY, Nizovtsev AP, Onishchenko NS. Statistics of Dephasing Perturbations and Relaxational Processes in a High-Power Optic Field - Application to Free-Induction Decay. J. Opt. Soc. Am. B. 1986;3:587–594. [Google Scholar]
- 86.Kilin D, Kleinekathöfer U, Schreiber M. Electron Transfer in Porphyrin Complexes in Different Solvents. J. Phys. Chem. A. 2000;104:5413–5421. [Google Scholar]
- 87.Kilin DS, Micha DA. Modeling the Photovoltage of Doped Si Surfaces. J. Phys. Chem. C. 2011;113:770–775. [Google Scholar]
- 88.Kilin DS, Tsemekhman K, Prezhdo OV, Zenkevich EI, von Borczyskowski C. Relaxation of Photoexcited Electrons at a Nanostructured Si(111) Surface. J. Photochem. Photobiol. A. 2007;190:342–351. [Google Scholar]
- 89.Kronik L, Shapiro Y. Surface Photovoltage Phenomenon: Theory, Experiment, and Applications. Surf. Sci. Rep. 1999;37:1–206. [Google Scholar]
- 90.Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 91.Kresse G, Hafner J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B. 1994;49:14251–14269. doi: 10.1103/physrevb.49.14251. [DOI] [PubMed] [Google Scholar]
- 92.Kresse G, Furtmüller J. Efficient Iterative Schemes For Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 93.Martin RM. Electronic Structure: Basic Theory and Practical Methods. Cambridge MA: Cambridge University Press; 2004. [Google Scholar]
- 94.Hafner J. Ab Initio Simulations of Materials Using Vasp: Density-Functional Theory and Beyond. J. Computat. Chem. 2008;29:2044–2078. doi: 10.1002/jcc.21057. [DOI] [PubMed] [Google Scholar]
- 95.Blöchl PE. Projector Augmented-Wave Method. Phys. Rev. B. 1994;50(24):17953–17979. doi: 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
- 96. [accessed on 7/11/11];Center for Computational Material Science, N. R. L. http://cst-www.nrl.navy.mil/lattice/struk/c5.html.
- 97.Liu L-M, Zhang C, Thornton G, Michaelides A. Structure and Dynamics of Liquid Water on Rutile TiO2 (110) Phys. Rev. B. 2010;82:161415. [Google Scholar]
- 98. [accessed on 27/12/12];video-sharing website YOUTUBE, L. L. C. http://youtu.be/LmRmP63kmE4.
- 99. [accessed on 27/12/12];video-sharing website YOUTUBE, L. L. C. http://youtu.be/UhnMsBQsAMU.
- 100.Schreiber M, Kilin D, Kleinekathöfer U. Comparison of Two Models for Bridge-Assisted Charge Transfer. J. Lumin. 1999;83:235–240. [Google Scholar]
- 101.Parson WW, Warshel A. Dependence of Photosynthetic Electron-Transfer Kinetics on Temperature and Energy in a Density-Matrix Model. J. Phys. Chem. B. 2004;108:10474–10483. [Google Scholar]
- 102.Parson WW, Warshel A. A Density-Matrix Model of Photosynthetic Electron Transfer with Microscopically Estimated Vibrational Relaxation Times. Chem. Phys. 2004;296:201–216. [Google Scholar]
- 103.Fernandez-Alberti S, Kleiman VD, Tretiak S, Roitberg AE. Unidirectional Energy Transfer in Conjugated Molecules: The Crucial Role of High-Frequency C-C Bonds. J. Phys. Chem. Lett. 2010;1:2699–2704. [Google Scholar]
- 104.Nelson T, Fernandez-Alberti S, Chernyak V, Roitberg AE, Tretiak S. Nonadiabatic Excited-State Molecular Dynamics Modeling of Photoinduced Dynamics in Conjugated Molecules. J. Phys. Chem. B. 2011;115:5402–5414. doi: 10.1021/jp109522g. [DOI] [PubMed] [Google Scholar]
- 105.Vazhappily T, Kilin DS, Micha DA. Photoabsorbance and Photovoltage of Crystalline and Amorphous Silicon Slabs with Silver Adsorbates. J. Phys. Chem. C. 2012;116:25525–25536. [Google Scholar]
- 106.Kilin DS, Micha DA. Atomic Modeling of Surface Photovoltage: Application to Si(111):H. Chem. Phys. Lett. 2008;461:266–270. [Google Scholar]
- 107.Duzhko V, Timoshenko VY, Koch F, Dittrich T. Photovoltage in Nanocrystalline Porous TiO2. Phys. Rev. B. 2001;64:075204. [Google Scholar]
- 108.Cavigli L, Bogani F, Vinattieri A, Cortese L, Colocci M, Faso V, Baldi G. Carrier Recombination Dynamics in Anatase TiO2 Nanoparticles. Solid State Sci. 2010;12:1877–1880. [Google Scholar]
- 109.Serpone N, Lawless D, Khairutdinov R, Pelizzetti E. Subnanosecond Relaxation Dynamics in TiO2 Colloidal Sols (Particle Sizes Rp=1.0-13.4 nm). Relevance to Heterogeneous Photocatalysis. J. Phys. Chem. 1995;99:16655–16661. [Google Scholar]
- 110.Mora-Sero I, Dittrich T, Belaidi A, Garcia-Belmonte G, Bisquert J. Observation of Diffusion and Tunneling Recombination of Dye-Photoinjected Electrons in Ultrathin TiO2 Layers by Surface Photovoltage Transients. J. Phys. Chem. B. 2005;109:14932–14938. doi: 10.1021/jp058128w. [DOI] [PubMed] [Google Scholar]
- 111.Neumann B, Bogdanoff P, Tributsch H, Sakthivel S, Kisch H. Electrochemical Mass Spectroscopic and Surface Photovoltage Studies of Catalytic Water Photooxidation by Undoped and Carbon-Doped Titania. J. Phys. Chem. B. 2005;109:16579–16586. doi: 10.1021/jp051339g. [DOI] [PubMed] [Google Scholar]
- 112.Hyeon-Deuk K, Prezhdo OV. Multiple Exciton Generation and Recombination Dynamics in Small Si and CdSe Quantum Dots: An Ab Initio Time-Domain Study. ACS Nano. 2012;6:1239–1250. doi: 10.1021/nn2038884. [DOI] [PubMed] [Google Scholar]
- 113.Hyeon-Deuk K, Prezhdo OV. Photoexcited Electron and Hole Dynamics in Semiconductor Quantum Dots: Phonon-Induced Relaxation, Dephasing, Multiple Exciton Generation and Recombination. ACS Nano. 2012;24:363201. doi: 10.1088/0953-8984/24/36/363201. [DOI] [PubMed] [Google Scholar]
- 114.Velizhanin KA, Piryatinski A. Numerical Analysis of Carrier Multiplication Mechanisms in Nanocrystalline and Bulk Forms of PbSe and PbS. Phys. Rev. B. 2012;86:165319. [Google Scholar]
- 115.Hoffmann MR, Martin ST, Choi W, Bahnemann DW. Environmental Applications of Semiconductor Photocatalysis. Chem. Rev. 1995;95:69–96. [Google Scholar]
- 116.Yamada Y, Kanemitsu Y. Determination of Electron and Hole Lifetimes of Rutile and Anatase TiO2 Single Crystals. Appl. Phys. Lett. 2012;101:133907. [Google Scholar]
- 117.Kamat PV. Manipulation of Charge Transfer Across Semiconductor Interface. A Criterion That Cannot Be Ignored in Photocatalyst Design. J. Phys. Chem. Lett. 2012;3:663–672. doi: 10.1021/jz201629p. [DOI] [PubMed] [Google Scholar]
- 118.Linic S, Christopher P, Ingram DB. Plasmonic-Metal Nanostructures for Efficient Conversion of Solar to Chemical Energy. Nature Mater. 2011;10:911–921. doi: 10.1038/nmat3151. [DOI] [PubMed] [Google Scholar]
- 119.Vayssilov GN, Petrova GP, Shor EAI, Nasluzov VA, Shor AM, Petkov PS, Rosch N. Reverse Hydrogen Spillover on and Hydrogenation of Supported Metal Clusters: Insights from Computational Model Studies. Phys. Chem. Chem. Phys. 2012;14:5879–5890. doi: 10.1039/c2cp23648f. [DOI] [PubMed] [Google Scholar]
- 120.Boronat M, Illas F, Corma A. Active Sites for H2 Adsorption and Activation in Au/TiO2 and the Role of the Support. J. Phys. Chem. A. 2009;113:3750–3757. doi: 10.1021/jp808271y. [DOI] [PubMed] [Google Scholar]
- 121.Enache DI, Edwards JK, Landon P, Solsona-Espriu B, Carley AF, Herzing AA, Watanabe M, Kiely CJ, Knight DW, Hutchings GJ. Solvent-Free Oxidation of Primary Alcohols to Aldehydes Using Au-Pd/TiO2 Catalysts. Science. 2006;311:362–365. doi: 10.1126/science.1120560. [DOI] [PubMed] [Google Scholar]
- 122.Inerbaev TM, Kilin D, Hoefelmeyer J. Atomistic Simulation of Dissipative Charge Carrier Dynamics for Photocatalysis. MRS Proceedings. 2012;1390:187–192. [Google Scholar]
- 123.Inerbaev TM, Kilin D, Hoefelmeyer J. Dissipative Charge Carrier Dynamics for Photocatalysis. Prepr. Pap.-Am. Chem. Soc., Div. Energy Fuels Chem. 2012;57:429–430. [Google Scholar]
- 124.Chen JC, Schmitz A, Kilin DS. Computational Simulation of the p-n Doped Silicon Quantum Dot. Int. J. Quantum Chem. 2012;112:3879–3888. [Google Scholar]
- 125.Micha DA, Santana A, Salam A. Nonlinear Optical Response and Yield in the Femtosecond Desorption of CO from the Cu(001) Surface: a Density Matrix Treatment. J. Chem. Phys. 2002;116:5173–5185. [Google Scholar]
- 126.Ramakrishna S, Willig F, May V. Photoinduced Ultrafast Electron Injection from a Surface Attached Molecule: Control of Electronic and Vibronic Distributions via Vibrational Wave Packets. Phys. Rev. B. 2000;62:R16330–R16333. [Google Scholar]
- 127.Sargent M, III, Scully MO, Lamb WE. Laser Physics. London, England: Addison-Wesley; 1974. [Google Scholar]
- 128.Cohen-Tannoudji C, Dupont-Roc J, Grynberg G. Atom-Photon Interactions. New York: Wiley; 1992. [Google Scholar]
- 129.Krasnoslobodtsev AV, Smirnov SN. Surface-Assisted Transient Displacement Charge Technique. I. Photoinduced Charge Transfer in Self-Assembled Monolayers. J. Phys. Chem. B. 2006;110:17931–17940. doi: 10.1021/jp060757y. [DOI] [PMC free article] [PubMed] [Google Scholar]