Static vs. mobile sink: The influence of basic parameters on energy efficiency in wireless sensor networks

Abstract

Over the last decade a large number of routing protocols has been designed for achieving energy efficiency in data collecting wireless sensor networks. The drawbacks of using a static sink are well known. It has been argued in the literature that a mobile sink may improve the energy dissipation compared to a static one. Some authors focus on minimizing Emax, the maximum energy dissipation of any single node in the network, while others aim at minimizing Ebar, the average energy dissipation over all nodes. In our paper we take a more holistic view, considering both Emax and Ebar.

The main contribution of this paper is to provide a simulation-based analysis of the energy efficiency of WSNs with static and mobile sinks. The focus is on two important configuration parameters: mobility path of the sink and duty cycling value of the nodes. On the one hand, it is well known that in the case of a mobile sink with fixed trajectory the choice of the mobility path influences energy efficiency. On the other hand, in some types of applications sensor nodes spend a rather large fraction of their total lifetime in idle mode, and therefore higher energy efficiency can be achieved by using the concept of reduced duty cycles. In particular, we quantitatively analyze the influence of duty cycling and the mobility radius of the sink as well as their interrelationship in terms of energy consumption for a well-defined model scenario. The analysis starts from general load considerations and is refined into a geometrical model. This model is validated by simulations which are more realistic in terms of duty cycling than previous work.

It is illustrated that over all possible configuration scenarios in terms of duty cycle and mobility radius of the sink the energy dissipation in the WSN can vary up to a factor of nine in terms of Emax and up to a factor of 17 in terms of Ebar. It turns out that in general the choice of the duty cycle value is more important for achieving energy efficiency than the choice of the mobility radius of the sink. Moreover, for small values of the duty cycle, a static sink turns out to be optimal in terms of both Emax and Ebar. For larger values of the duty cycle, a mobile sink has advantages over a static sink, especially in terms of Emax. These insights into the basic interrelationship between duty cycle value and mobility radius of a mobile sink are relevant for energy efficient operation of homogeneous WSNs beyond our model scenario.

1. Introduction

Recent advances in the development of low cost sensing devices and microminiaturization have further advanced the scope of applications of wireless sensor networks (WSNs). WSN based solutions have been designed and implemented in diverse areas, including environment and habitat monitoring, building automation, disaster and waste management, infrastructure monitoring, etc. [1]. Sensor nodes used in these applications are characterized by limited resources in terms of memory, computation power, and energy [2]. In particular, WSNs deployed for remote area monitoring usually comprise a large number of tiny static sensing devices, which are deployed in an ad hoc manner over a geographically wide area to sense parameters of interest. Such a random and uncontrolled deployment results in unknown network topology which, along with dynamic environment, low bandwidth, limited battery power and constrained storage capacity of the nodes, necessitates that each node always knows an energy efficient routing path to the sink with low congestion. Since ad hoc deployment of the nodes restricts programmers from pre-configuring routing tables at the sensor nodes, various techniques have been developed to maintain up-to-date routing paths to the sink. In the case of slowly changing topologies a proactive routing approach can provide an efficient solution where network topology discovery is based on the periodic broadcast of a beacon signal from the sink to the entire network [3]. In addition to maintaining energy efficient routing paths to the sink two other techniques often used for achieving energy efficiency are sink mobility [4,5] and duty cycling of the nodes [6].

In this paper we consider a WSN comprising homogeneous static sensor nodes. The sink can be static or mobile (for details see Section 2), and can be placed at different locations in the WSN. In the case of a static sink, nodes located in the vicinity of the sink deplete their energy (and die) much earlier compared to the nodes located farther away from the sink due to higher data relaying load. In order to address this issue, sink mobilization has been introduced, where the sink moves along a certain path through the network (see Section 2.2). It has also been shown that in most cases sink mobility helps in balancing the routing load and hence energy dissipation of the nodes [7,8].

Although it is clear that sink mobility improves load balancing among the nodes, it is an open question whether this also leads to improvements in the energy efficiency of a WSN. In order to address this question, we first need to define suitable metrics for quantitatively measuring energy efficiency.

One possible approach for comparing different sink mobility strategies is to compare the total energy consumption of the nodes in the WSN for the same total work(load) processed by the WSN. Consequently, our primary focus in this paper is on the average energy dissipation per node Ebar, i.e., the average over the accumulated energy dissipations of all nodes in the WSN during the observation period: $\mathit{Ebar}={\sum }_{i=1}^N\frac{e_i}{N}$, where N denotes the total number of nodes in the WSN and e_i is the accumulated energy dissipation of node i during the observation period.

However, it is well known that in the case of a static sink the energy consumption of individual nodes varies strongly across the WSN, since the nodes close to the sink are much more heavily burdened due to relay operations than those farther away from the sink. For this reason, we additionally investigate the maximum energy dissipation per node $\mathit{Emax}={\max }_{i=1\text{,}2\text{,}\dots \text{,}N}{e}_i$.

For load balancing reasons, a static sink is usually located at the center of the WSN. If too many nodes in the area surrounding a static sink fail since they have used up their energy resources, the sink might become disconnected from the rest of the WSN. Therefore, Emax is definitely one of many possible relevant indicators for the lifetime of the WSN [27,31] in a generic abstract model for a WSN, which is the focus of this paper. Most of the existing work in the literature (see, e.g. [4,9,10]) discusses either the lifetime of a WSN or the average energy dissipation per node (either Emax or on Ebar). Contrary to that, in this paper we evaluate different protocols in terms of metrics for both of these aspects and pinpoint in which situations they yield different information. More importantly, in most cases the effects of duty cycling of the nodes, a very important feature in the practical application of modern WSNs, are not taken into account in quantitative evaluations.

In this paper, we quantitatively model and investigate the influence of duty cycling of static sensor nodes and of the mobility path of a mobile sink on the energy consumption in a simplified model scenario of a WSN. We quantitatively compare the energy efficiency of this model WSN with a static and a mobile sink in terms Emax and Ebar. We illustrate that for certain network configurations sink mobilization alone is not enough to improve Emax and Ebar compared to a static sink. We also show that for other configurations a mobile sink can significantly improve both Emax and Ebar by reducing data relaying load on the sensor nodes and congestion in the network. Ebar can vary up to a factor of 17 and Emax up to a factor of nine across all possible combinations of duty cycle value and mobility path of the sink. We explain the reasons for these observations on the basis of a geometrical model and validate this model by simulations. The basic understanding gained by the analysis presented in this paper can serve as a first step for the development of configuration guidelines for WSNs with homogeneous nodes which are valid beyond the simplified model setup analyzed in this paper.

The rest of the paper is organized as follows: Section 2 summarizes current state-of-the-art routing schemes for WSNs with a static or a mobile sink. Section 3 summarizes the considered mobility model, WSN model, energy model and the simulation methodology. Section 4 analyzes the effect of sink mobility and duty cycling on the energy efficiency of a WSN, and Section 5 concludes the paper.

2. Related work

In the following, we review state-of-the-art routing schemes for WSNs with static or mobile sinks.

2.1. WSNs with a static sink

In the early days, a typical WSN was composed of static sensor nodes and a static sink placed inside the observed region. In such a setup, the major energy consumer is the communication module of each node. In practice, multi-hop communication is required for sending data from sources to sink nodes. Consequently, the energy consumption depends on the communication distance. One way to reduce the communication distance is to deploy multiple static sinks [11] and to program each sensor node such that it routes data to the closest sink. This reduces the average path length from source to sink and hence results in smaller Ebar compared to the case of single static sink. On the other hand, reduction in Emax is also observed because routing load on the nodes located in the vicinity of a single sink also gets distributed among all the nodes located in the vicinity of multiple static sinks. The authors of [11,12] propose to deploy multiple static sinks. These static sinks partition the WSN into small sub-fields each with one static sink. By simulation it was shown that the proposed scheme leads to energy efficiency and better data delivery ratio compared to schemes based on a single sink.

However, a major problem with multiple static sinks is that one has to decide where to deploy them inside the monitored region so that the data relaying load can be balanced amongst the nodes. Vincze et al. consider this problem in [13] as an instance of the well-known “facility location problem” where for a given number of facilities and customers the optimal position for the placement of the facilities has to be identified so that all facilities are evenly burdened. If the positions of the static sinks are given, then the solution of this problem can be used for finding the optimal partitioning of the field. However, even if we assume location-optimal deployment of static sinks, the nodes close to a sink will deplete their energy rather rapidly. Adding some mobile sinks to a set of static sinks has been shown to improve the data delivery rate and to reduce energy dissipation of the sensor nodes [14].

2.1.1. Improvements for the static sink case

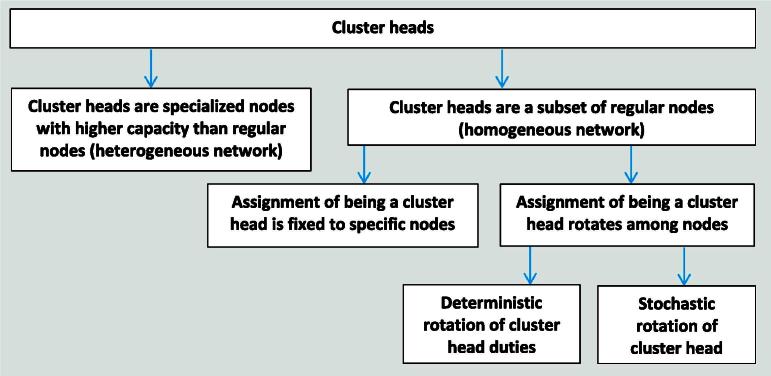
Some of the benefits of multiple static sinks for energy efficiency can also be realized with a single static sink by logically partitioning the sensor field at a single level or hierarchically. Such a partitioning can be either static or dynamic, and it can be predetermined or self-organized within the network. Besides the field partitioning, the selection of a cluster head in each partition is an important issue (see Fig. 1).

Fig. 1.

Basic cluster head strategies for sensor networks with a single static sink.

In order to avoid the “dying” of nodes close to the sink, partitioning of the field into subareas (clusters) has been investigated (e.g. [15,16]). Within each cluster, a cluster head is determined to which local nodes send their data. Cluster heads tend to have higher capacity than regular nodes and are responsible for forwarding collected data to the sink over single or multiple hops. Both the cluster formation and the selection of the cluster head is done in such a way that the energy dissipation during routing can be minimized [17]. This approach can also be extended to multilevel hierarchies [18]. Clusters and the hierarchical structures can either be determined once (statically) or can be changed dynamically [19]. To define a cluster, either a self-organizing algorithm can be used where each sensor independently determines whether it would like to be a cluster head or not, or a fixed regular structure of the clusters is given at the beginning of the entire process [20]. In the latter scenario, the clustering and routing overhead is reduced, but it has limited applicability. Using the concept of multilevel hierarchies, the lifetime of the WSN can be optimized as shown in [20], using an optimal number of master aggregators. Additionally, (application dependent) data aggregation (data fusion) can be performed at each cluster head before data is transferred to the sink in order to reduce the amount of data to be transmitted to the sink [16]. Potential interference of neighboring clusters can be eliminated by using CSMA-like protocols [21].

In order to extend the lifetime of the cluster head node, the task of being a cluster head can be rotated within a cluster [20]. The cluster head can be chosen either stochastically (e.g. [16]) or based on deterministic strategies [15].

Summarizing, existing approaches for WSNs with a single static sink differ primarily in the strategies for the partitioning of the sensor field and in the cluster head selection method.

2.2. WSNs with a mobile sink

Another approach for extending the lifetime of the nodes close to the sink is the utilization of a mobile sink. In some aspects, this is similar to using several static sinks – however, using several static sinks requires additional global communication for collecting all data at a single final point [12].

In order to overcome the shortcomings observed for a static sink, the use of a mobile sink has been proposed [4]. A mobile sink can follow different types of mobility patterns in the sensor field, such as random mobility, predictable/fixed path mobility, or controlled mobility, which has consequences with respect to energy efficiency and data collection strategies. In the following we summarize some proposed solutions for each type of mobility.

Random mobility. In this class, the sink follows a random path in the sensor field and important questions relate to the data collection strategy (see Fig. 2). Usually, the sink uses a pull strategy for collecting data from the sensor nodes. In a pull strategy, a node forwards its data only when the sink initiates a request for it, whereas in a push strategy a node proactively sends its data towards the sink. Chatzigiannakis et al. have shown in [22] that random sink mobility can be used to reduce Emax and Ebar compared to the case of a static sink. Single hop data collection leads to the strongest reduction of energy consumption, because no data relaying load on the sensor nodes exists. However, it can also result in incomplete data collection from the WSN, because with a random mobility pattern there is no guarantee that the sink will reach all nodes in the sensor field or it might take too much time to do so. If the time required for complete coverage of the field has to be even lower, then the sink can be programmed to collect data from all nodes which are within a maximum number of hops larger than one. This results in increased relaying load on the sensor nodes, and hence increases Emax and Ebar compared to the case of single hop data collection [22].

Fig. 2.

Basic approaches for data collection with random sink mobility.

Obviously, there is an important trade-off between coverage time of the WSN and energy dissipation. The coverage time can be further reduced if multiple mobile sinks move randomly in the sensor field in an efficient way (see, e.g. [5,23]). In this case, Kinalis et al. proposed in [9] the path coordination of the mobile sinks in the sense that each sink leaves a trail on its mobility path. When other sinks encounter this trail they change their mobility direction, which improves the coverage of the sensor field. However, the extra coordination effort needed for these strategies results in additional overhead and additional energy dissipation from the nodes.

If the data collection is not triggered by the sink, but follows a push strategy, another major overhead in the case of random sink mobility occurs because of the difficulty of tracking the current position of the sink and adapting the routing paths to the sink in the case of multi-hop communications (see Fig. 3), which leads to increased energy dissipation. In order to address this issue, Yu et al. [24] proposed to use the overhearing feature of the wireless networks to track the position of the randomly moving sink. They propose that the mobile sink periodically transmit a beacon message containing its position. Whenever a neighboring node of the sink hears this message, it updates the sink location in subsequently transmitted packets accordingly. Every node that overhears the packet from neighboring nodes of the sink will also update the location coordinates of the sink thus eventually all nodes will have updated the location coordinates of the sink for geographic routing. Yu et al. [25] proposed a multi agent based data routing and mobile sink tracking scheme. They propose to select multiple intermediate nodes between a source node and the sink, which are called agents. These agents (especially the one closest to the sink) are responsible of tracking the location of the mobile sink thus minimizing the path updating cost that eventually reduces the overhead in tracking the location of the randomly moving sink. Yun et al. [26] proposed a mobile sink based data collection scheme for delay tolerant networks by formulating an optimization problem that maximizes the lifetime of the WSN given delay and flow conservation constraints. The formulated model enables the node to identify the best time to route data to the sink so that all constraints regarding energy and delay can be met.

Fig. 3.

Basic approaches for tracking the position of a sink with random mobility.

Fixed mobility. In this class of schemes the sink is programmed to follow a fixed path in a round robin fashion. This fixed path is predetermined and is not influenced by the behavior of the WSN at runtime. Coverage of the sensor field has to be guaranteed by an appropriate strategy for determining the routing paths for the data packets. An important distinction is whether the sink can predict its future positions or not (see Fig. 4). In [7], Giannakos et al. propose a reactive data forwarding mechanism using a pull strategy based on request messages broadcasted by the sink. Moreover, sink mobility is planned such that the complete sensor field can be traversed in minimum possible time. As a result, energy dissipation (Emax and Ebar) can be very low. In case the sink is able to predict its future positions it can communicate this information to a node located in the vicinity of its future position. This node is responsible for collecting the sensor data in its vicinity so that when the sink actually arrives at this position, it should not have to wait for the data. Wu et al. [27] implemented this idea for a sink with directional antenna, claiming that their scheme results in increased packet delivery rate and reduced energy dissipation of the nodes.

Fig. 4.

Basic approaches for data collection with fixed sink mobility.

The problem of finding the optimum fixed path in terms of network lifetime has been investigated theoretically by Luo et al. [8]. For a simple network model they showed that if nodes in a WSN are programmed to report data towards the sink within a certain fixed time interval, then minimum Emax can only be achieved if the mobility trajectory of the sink is set close to the periphery of the sensor field. The authors noted that due to the simplified system model their results may be misleading. In [4] they designed a practical routing protocol that not only balances the energy dissipation of the nodes but also tries to reduce data losses. Based on simulations, they illustrate the advantages of a mobile sink over a static one. Their scheme is based on discrete mobility of the sink, where the sink sojourn time at predetermined locations is greater than its mobility time (total time that the sink spends in motion) which helps to avoid frequent route updates in the WSN, hence leading to energy efficiency both in terms of Emax and Ebar compared to other mobile sink based routing schemes.

So far, it was assumed that the data rate is identical for all sensor nodes. In the case of varying data rates across sensors, energy dissipation can be balanced by partitioning the nodes in groups (clusters) such that each group has approximately the same total data rate. Based on this assumption Xu et al. [28] proposed to divide the sensor field in small portions equal to the number of available data collector nodes, which they call “gateway nodes”. The gateway nodes have similar duties as the cluster heads mentioned earlier. The authors have also proposed heuristic algorithms for the selection of packet nodes and assigning them to gateway nodes. This way, each portion of the field has a set of packet nodes that route their data to the corresponding gateway node. Then the trajectory of the sink is fixed and it is defined such that in each cycle it must pass by each gateway for data collection. A similar approach has been proposed by Gao et al. [29]. They denote the cluster heads as “sub sinks”, which are deployed in the sensor field. Each sensor node is then associated with one of the sub sinks. The association criterion is based on how much time the sink spends with each sub sink. If a sub sink has the mobile sink in its vicinity for a longer time, then more sensor nodes are associated with it and vice versa, which improves the throughput of the sensor field.

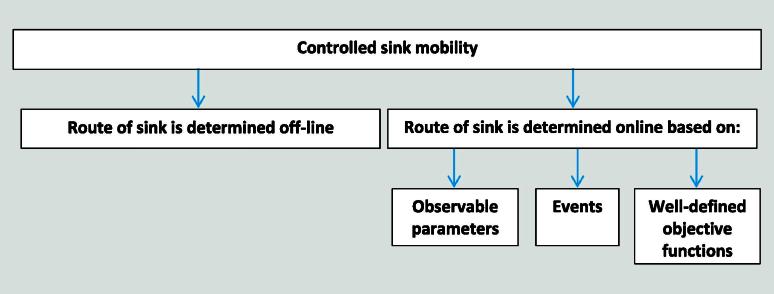
Controlled mobility (see Fig. 5) refers to schemes where sink mobility is controlled or guided based on a parameter of interest, such as residual energy of the nodes, or on a predefined objective function, or on predefined observable events. Bi et al. argued that an energy-unconscious mobility of the sink results in uneven energy dissipation from the nodes [30]. To address this particular problem, the authors presented a mobile sink based approach, where the sink tries to stay away from the nodes with less residual energy and tries to be in the vicinity of those nodes that have high residual energy. This helps balancing the energy dissipation from the nodes, and hence reduces Emax.

Fig. 5.

Basic approaches for controlled sink mobility.

The idea of using controlled mobility in WSNs for reducing Emax was also discussed by Basagni et al. in [31]. In order to determine sink movements, the authors define a mixed integer linear programming (MILP) model for maximizing sojourn times at the sites the sink can visit subject to constraints in terms of energy dissipation and other parameters. An off-line solution of this analytical model provides those sink routes that minimize Emax (similar to the approach pursued in [30]). Moreover, in [31] a greedy maximum residual energy (GMRE) heuristic moves the sink only to those sites where the residual energy of the node is maximum. However, the communication required for retrieving the residual energies of the nodes adds extra overhead.

More general, Mudigonda et al. [32] proposed a framework for real time calculation of the sink mobility path based on a given objective function. Various metrics were used for defining the objective function, such as residual energy of the nodes, network congestion and average distance between nodes and the sink. In their concept, the sink is mobilized to a new location whenever degradation in the objective function is observed. Liang et al. [33] proposed to improve the lifetime of a WSN using multiple mobile sinks. They presented a heuristic algorithm that computes the mobility trajectory as well as the sojourn time for each mobile sink such that network lifetime is maximized.

In event-driven networks, adaptive mobility strategies can be used where the sink adapts its location based on current events in the field [34].

In this paper, we focus on the generic model situation of a WSN with circular shape and a mobile sink which moves along a fixed concentric circle around the center. We compare this scenario to a static sink at the center of the WSN. In addition to the influence of radius of this circular sink trajectory, we investigate the influence of the duty cycling of the sensor nodes on the energy consumption of the WSN.

3. Assumptions and simulation methodology

The performance of a routing protocol in a WSN strongly depends on the network and energy model considered. Therefore, we discuss our WSN model in terms of the underlying mobility model of the sink, the duty cycling strategy and the energy model in the following. Moreover, we also explain how we performed the simulations discussed in Section 4.

3.1. Mobility model

Two basic types of state-of-the-art routing protocols will be discussed in this paper:

• (i)the SS protocol for a WSN based on a static sink placed at the center of the sensor field and on shortest path routing of data from the nodes towards the sink [8]; and
• (ii)the MS protocol for a WSN based on a mobile sink which moves along a fixed concentric circle around the center of the WSN in a stop-and-go fashion [4,8] and on shortest path routing of data from the nodes towards the current location of the sink.

During the early days of WSNs only static sinks were used and it was recognized that the strategically best position for a static sink in a WSN is the center of the field, as this leads to minimum Ebar (details will be discussed in Section 4). On the other hand, it is also known from our discussion in Section 2 that a mobile sink can adapt different types of mobility patterns in a WSN, such as random mobility, fixed mobility or controlled mobility. The question arises which type of mobility scheme performs best. In [8,31,35], this question has been investigated for a simpler network model than the one we are considering. The authors of [8,31,35] concluded that if the deployment region of a WSN is of circular shape, then the maximum lifetime of a WSN (minimum Emax) can be achieved if the radius of a circular mobility trajectory of the sink is set to $\frac{\sqrt{2}R}{2}$, where R is the radius of the WSN area. However, the authors of [31,35] do not provide much information regarding the effect of changing the radius of the mobility trajectory of the sink on Ebar. We will investigate this aspect in Section 4.

For the MS protocol it is assumed that the sink sojourn time at predetermined locations is greater than the time that it spends in motion. This helps to avoid frequent route updates in the WSN; hence increasing energy efficiency both in terms of Emax and Ebar compared to other mobile sink based routing schemes, as mentioned in Section 2.2. One method of accomplishing such a decrease in the cost for updating routing information is by programming the sink to move only when the energy level of the nodes positioned in the vicinity of the sink falls below a certain pre-defined threshold. This threshold can be adapted dynamically every time the sink arrives in order to allow for repeated round trips of the sink. This scheme could be implemented by periodically reporting residual energy levels from these nodes to the sink. As a result, the energy spent by each node for updating the routing path will be very small compared to the sum of the energy spent by each node for relaying the data packets from upstream nodes towards the sink, for idle listening and for sensing parameters of interest. In our performance analysis we neglect the energy dissipation due to routing path updates for the MS protocol, and consequently the analysis we provide gives upper bounds for the lifetime achieved with this protocol.

3.2. Network model

We consider a network composed of N stationary, identical sensor nodes that are uniformly distributed over a disk of a given radius R. We assume a two-dimensional and stationary topology for the nodes. The sink is located within the sensor field. In order to ensure end-to-end connectivity for each node (from source to sink) during the simulation run, our simulation model assumes (for practical reasons of the simulation only) that nodes have unlimited battery and buffer capacity in order to avoid node failures or packet loss due to buffer overflow during a simulation run. It is further assumed that sensor nodes do not have any location information, but that the sink can obtain its position coordinates when desired using state-of-the-art GPS equipment.

The nodes are responsible for sensing and reporting the parameters of interest with constant time intervals. We assume low cost energy constrained sensor nodes that have simple and identical transceiver sub-systems and are equipped with omni-directional antennae having common fixed communication range. The communication range of the nodes is assumed to be (very) small compared to the radius R of the WSN. As a result, data propagation from source to sink can only be achieved via multi-hop routing, i.e., the best routing paths in terms of hop counts for each node are determined during the initialization phase which comprises the construction of routing tables, etc. The initialization costs are not accounted for.

3.3. Duty cycling

In our simulation model, (abstract) time is divided into slots of constant length, corresponding to the time between two ticks of the simulation clock. In reality, the distributed nodes need to be resynchronized from time to time in order to account for clock drifts. In the simulation we do not consider the overhead caused by necessary resynchronization [36]. The length of the time slots is defined in the simulator and is not representative for the real time. In a real world scenario the time taken by a node to transmit or receive a message can vary from a few microseconds to tens of milliseconds depending on the size of a packet, the MAC protocol, etc. In our simulation we assume that the length of a time slot is determined by the maximum amount of time needed by any of these actions, i.e., any action can be performed in a single time slot.

In some types of applications (which also motivate the investigations in this paper) sensor nodes spend a big fraction of their total lifetime in idle mode (doing nothing), for example, in sensing applications where sensing does not happen very frequently. Therefore, the concept of low duty cycling has been introduced, which achieves higher energy efficiency (i.e., reduces Emax and Ebar). In this case, particular modules of the sensor are turned off when not needed, i.e., energy can be saved by reducing the active time (or duty cycles) of various components of the node. This defines various operational modes for the sensor nodes. For example, Wang et al. proposed [6] four different operating modes for a sensor node: node on-duty (the node is in active state), sensing unit on-duty (only sensing and processing unit are on), transceiver unit on-duty (only transceiver and processing unit are on), and off-duty (sensing, processing unit and transceiver units are off, only a timer is running to switch on the node after some time interval).

In our simulation, we distinguish two operational modes for a node in every time slot: sleep (off-duty) and active (on-duty). In sleep mode a sensor node is in the state with the lowest energy consumption and does not carry out any task – it neither senses or processes any data nor transmits or receives data packets. After the sleep period, the node is woken up by a timer and changes into active mode, where it may either actively participate in data routing (transmitting or receiving a message) or it may be idle.

The scheduled periods of activity and sleep are modeled deterministically according to the parameters p and q (0 < p, q < 1), respectively. For floor(1/q + 0.5) time slots the node is active, and this active phase is followed by a period of floor(1/p + 0.5) time slots that the node is asleep. In general, p and q can take any value between 0 and 1 independently of each other. The higher p and q, the more frequently the node transits from active to sleep mode and vice versa. In our simulations we always choose these parameters such that p + q = 1, i.e., the value of p (the “duty cycle value”) determines the fraction of time during which the node is active. For example, to achieve 10% duty cycling, i.e., the node is 10% of the time active, p and q are set to 0.1 and 0.9, respectively.

In order to handle heavy routing load, sensor nodes sometimes need to extend their active phase beyond the scheduled duration. This is accomplished by implementing the following condition: a node can transit from active to sleep mode only if its data buffer is empty. Thus, a sensor node extends its scheduled active phase (specified number of time slots) until all the data has been forwarded to one of the next-hop neighboring nodes (extended active phase). Thus, each actual active phase of a sensor can be divided into two parts: the scheduled part and the extended active phase. The number of time slots in extended active mode depends on the number of packets in the buffer and on how long it takes until a channel to a suitable forwarding node becomes available. As a result, even with low duty cycling of the nodes, data eventually gets forwarded towards the sink. However, in order to achieve energy efficiency and to switch to sleep mode as quickly as possible, a sensor node turns its sensing unit off during the extended active phase and neither senses data nor accepts relaying data. Depending on the sampling frequency, this may cause data loss in reality.

3.4. Energy model

In scheduled active mode or in extended active mode a sensor node can only be in one of the following operational modes: transmit, receive or idle. In transmitting/receiving mode the energy dissipation is due to transceiver electronics. In idle mode the energy dissipation of the node is only due to local data processing activity. In extended active mode, a node is only idle if it cannot forward any data packet from its buffer since all its neighbors are busy. In each active time slot, exactly one data packet can be transmitted or received, and we assume that sending and receiving a data packet takes the same amount of time. In summary, in a single (extended) active time slot the following actions can happen: (i) in active mode: generating/sensing plus forwarding a packet OR (ii) in active mode: receiving a packet to be relayed from a different node OR (iii) in active or extended active mode: forwarding a packet from the local buffer which has been received from a different node or from the own sensing unit in a previous time slot during the current active period.

We model the CSMA/CA (carrier sense multiple access/collision avoidance) protocol [21] at the MAC layer with the assumption that each task can be finished within a fixed time slot. Therefore, in any given time slot a pair of nodes can perform a successful communication only if none of their neighboring nodes are allowed to transmit. This MAC protocol is simulated as follows: At the start of each active time slot all the sensors can potentially transmit or receive or they are idle. In order to resolve channel contention issues, random permutations of the indices 1, 2 …, N associated with the sensor nodes are generated. Each sensor node is then examined based on the order resulting from the permutation. If a sensor node is able to transmit its data in the current time slot it is allowed to do so. However, no other node within the communication range of the transmitting/receiving node is allowed to transmit in the current time slot. Thus, at the start of each time slot transmissions are chosen randomly and fairly.

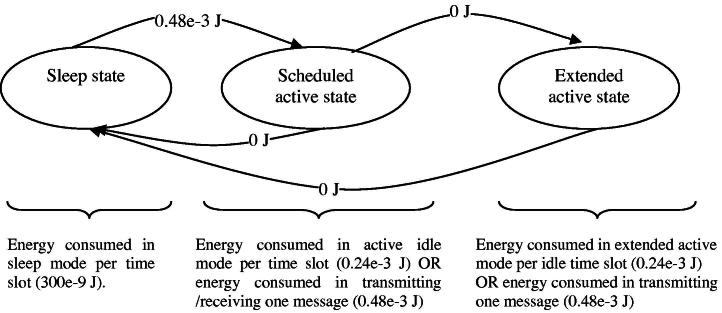
In a duty cycled sensor field many factors play a crucial role in identifying the total energy dissipation by any node in a WSN. Our model distinguishes four major energy consuming tasks as shown in Fig. 6. The energy consumed by the node to stay in idle active mode for one time slot (Eidle), the energy consumed by the node for transmitting/receiving one message (Etx/rx), the energy consumed in sleep mode per time slot (Esleep), and the energy consumed by a node to transit from sleep to active mode (Etrans). Since we assume that sensor nodes have a fixed communication range and exchange messages with fixed size, the energy dissipation during each message transmission and reception by a node is also fixed. The energy consumed in the transition from active to sleep mode is assumed to be zero. Since the energy cost of sensing the environment (sensor) is negligible compared to Etx/rx and Eidle we have ignored it in our simulations. Moreover, we do not consider the energy consumption of any local processing activities in our model. Depending on channel availability a node can generate and transmit its own packet in a single time slot. However, as mentioned above there is no sensing in sleep mode and in extended active mode. The total energy dissipation of a node is the sum of Eidle, Etx/rx, Etrans and Esleep.

Fig. 6.

Energy dissipation map of a node.

3.5. Execution of the simulation

For a simulation-based analysis of energy consumption and comparison of SS and MS, we adapted a custom-built discrete-time simulator written in C++ by Michele Garetto et al. [37].

The throughput G of the WSN, i.e., the total number of data packets generated in the WSN per time slot, is defined as G = Ngp/(p + q) [37]. g is the data generation rate per node (measured in packets per time slot) and p and q are the above mentioned parameters for the transition from sleep to active state and vice versa. Since in our simulations we chose p + q = 1, we get G = Ngp. Note that G represents the sum of the throughputs of all sensor nodes and is determined by parameters which are input to our model. All nodes use the same frequency for communication. As a result, at any given time the sink can communicate to only one node and exchange only one data packet per time slot. Therefore, the theoretical network throughput G is limited to a value in the interval (0, 1], i.e., the sink cannot receive more than one data unit per time slot. In the simulation g, N and p cannot be chosen independently of each other.

For simulating sink mobility in the SS protocol, the sink is placed at the center of the deployment area. In the case of the MS protocol sink mobility is simulated by placing the sink at different uniformly distributed locations along its cyclic mobility trajectory such that the sink completes one round trip. For the MS protocol, the sink makes k stops along its cyclic trajectory, and thus k simulation runs are performed independently from each other. Each of them is terminated when L packets have been received by the sink, determining the length of the simulation run. Our model assumes that all nodes send their data towards the position where the sink currently stops. The routing information needs to be updated at every node in the network for each new position of the mobile sink. After k simulation runs, the k accumulated energy values per node are added. For the SS protocol, the simulation terminates when kL packets have been received by the sink. Consequently, in both cases (SS and MS) the same total number of packets arrives at the sink during the simulation. In order to produce comparable results with sufficiently small confidence intervals, L has to be chosen sufficiently large.

Simulation parameters. For the simulations discussed in Section 4, the parameters of the simulation model were set as shown in Table 1. The value of r was chosen such that the combination of R, r and N represents a practically relevant WSN scenario with reasonable connectivity. Note that contemporary sensor nodes have typical communication ranges up to 100 m, and therefore our choice of r = 0.1 in a unit disk for the sensor field corresponds to a WSN radius up to 1000 m in reality. The throughput G of the WSN is an application-dependent parameter. The concrete values for the energy consumption are the same as used in [37] (see Fig. 6). In reality, Etx is usually higher than Erx, but we set them equal for simplicity. L determines the duration of a simulation run. Our choice ensures that the load handled in each simulation run is large enough to observe the system beyond the transient phase.

Table 1.

Parameters used in the simulation.

Parameter	Value
Radius R of the circular sensor field	1
Transmission range r of a sensor node	0.1
Number N of nodes in the sensor field	2000
Throughput G	0.8 [packets/time slot]
Eidle	0.24e−3 [J/time slot]
Etx = Erx	0.48e−3 [J/message]
Esleep	300e−9 [J/time slot]
Etrans	0.48e−3 [J/transition]
Number of stops k of the mobile sink per round trip	4
Number of data packets L received by the sink during one simulation run	10000

4. Effects of duty cycling and sink mobility on the energy efficiency of a WSN

Our central objective is to quantitatively investigate the effects of duty cycling of the nodes and of sink mobility on the energy consumption of the WSN. We start with some general observations about the process of data transmission from sensor nodes to the sink in a WSN. We consider a fixed multihop routing strategy along the shortest path. In such a setup, congestion can occur at nodes in the WSN if several transmission paths to the sink meet at a single relaying node and if the traffic load to be relayed by this node becomes too high. If the duty cycle is too short for the load to be relayed, nodes fail to handle the data traffic during their normal scheduled active time slot and hence have to extend their active periods (see Section 3.3). In extended active periods the node remains in active mode and it neither receives data from neighboring nodes nor generates data, but it keeps on contending for channels. As long as no channel is available (because neighboring nodes are also trying to relay their load), the node remains in (extended active) idle mode. Once a channel is acquired, the node retains the channel until all the data packets in the buffer using this channel are forwarded. The extended active period ends when the buffer is empty. When congestion builds up in a specific region of the WSN, a high percentage of the nodes in that region will enter extended active mode because they are not able to acquire a transmission channel during their active period. Thus, in the case of congestion, nodes tend to have even more idle time slots in extended active mode due to non-availability of transmission channels. This higher number of idle time slots leads to higher energy dissipation and increases Emax. The higher fraction of the extended active idle mode corresponding to congestion for smaller values of the duty cycle of the nodes is confirmed in our simulations, as Fig. 7 illustrates. The more nodes experience congestion effects, the more Ebar is increased.

Fig. 7.

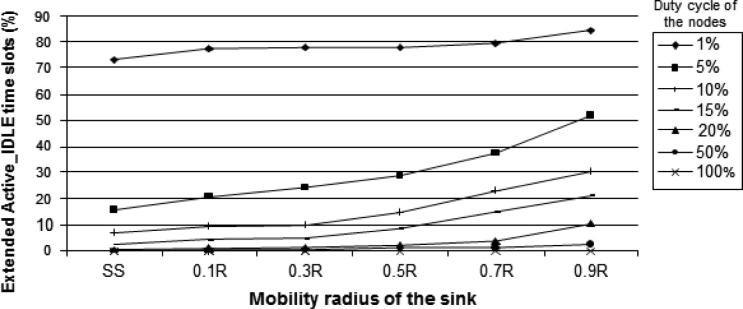
Fraction [%] of total simulation time spent in extended active idle mode.

Note that not only a (too) short duty cycle (duty cycle value too small) increases Emax. If the duty cycle is too long (duty cycle value too large) the active phases of the nodes are unnecessarily long (with unnecessarily many idle time slots in the active phases), which again causes an increase in Emax. Consequently, we conjecture the existence of an optimum duty cycle value in terms of Emax.

The position of the sink in the WSN obviously determines at which nodes many transmission paths to the sink meet. For a static sink at the center of the WSN, the critical area with heavily burdened nodes clearly is around the center of the field. We observed in our simulations that also for a mobile sink (independently of the radius of the mobility trajectory of the sink) the nodes with the highest energy consumption tend to be concentrated in the area around the center of the sensor field. They experience most congestion, because many transmission paths run through the central region. Furthermore, if the sink is at the center of the sensor field, the nodes in the neighborhood of the sink are basically evenly loaded. If the sink is moved away from the center, the load on the nodes surrounding the sink gets unbalanced due to the increase in the number of handled transmission paths and their lengths. This implies that the nodes with higher load have to enter extended active mode more frequently than in the balanced central case. These effects will become more obvious in the following two subsections, where some geometrical considerations help to explain them.

In the following, we quantitatively compare the energy consumption of data collection in terms of Emax and Ebar as motivated in Section 1 in a network with a static sink (SS protocol) to the one of a network with a mobile sink (MS protocol). As explained before, the duty cycle value of the nodes obviously influences their energy consumption. Since our objective is to compare a static with a mobile sink, we also need to investigate the influence of the radius of the mobility trajectory of the sink. In the following, we first outline general considerations which lead to a basic conjecture about how the mobility radius influences the energy consumption of the data transfer from source to sink. Then, we formulate and analyze a geometrical model which substantiates and proves this conjecture. Finally, we discuss simulation results which confirm the behavior predicted by the geometrical model.

4.1. General considerations – a gedankenexperiment

Let us first focus on the influence of the mobility radius of the sink. Since we consider shortest path routing to the sink, all data to be transferred from a certain sector of the field has to pass through a critical area around the center of the sensor field independently of the position of the sink (see Fig. 8). For a fixed critical region at the center, we expect its load to increase when the sink is positioned closer to the center and to decrease when the sink moves away from the center. On the other hand, moving the sink away from the center will increase the load to be handled by some nodes in the vicinity of the sink, as explained in the following.

Fig. 8.

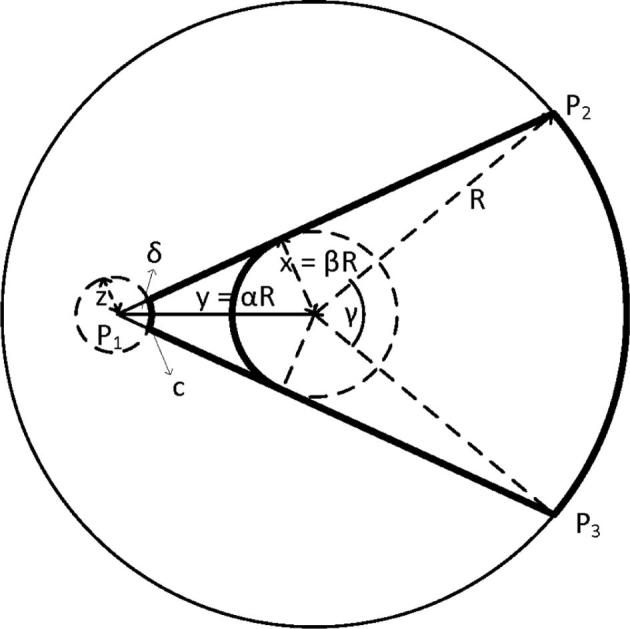
Geometrical model for analyzing the influence of the mobility radius on energy dissipation.

When the sink has a larger mobility radius, the path length which the data has to travel until it reaches the sink varies more – for the data originating from nodes between the sink and the closest boundary the path length decreases, whereas for the data originating from nodes on the other side of the center of the network the path length increases. On a longer path data has a higher probability for encountering congestion, which may cause more extended active periods in the nodes and thus lead to a higher total energy dissipation of the affected nodes. Moreover, a larger mobility radius leads to a stronger funneling effect, i.e., the area in the neighborhood of the sink through which data from far away has to pass becomes smaller for larger mobility radius, because the corresponding angle becomes narrower. Once the sink moves away too far from the center, much more load comes from the central area than from the periphery, which also results in more congestion and increased energy dissipation along the longer paths.

Nevertheless, sink mobility and a larger mobility radius also have a positive influence on the energy dissipation. A mobile sink collects data at several locations, and the increased congestion is effectively divided by the number of stops of the sink since the mobile sink remains at each position for a shorter time than the static sink at the center. Moreover, as mentioned before, the larger the mobility radius, the less relaying load we expect in a fixed region around the center of the WSN.

So far, we have summarized some basic considerations. Next, we investigate the situation more formally with a simple geometrical model in order to verify this basic understanding of the influence of the sink’s mobility radius on the energy consumption.

4.2. Geometrical model

Let us assume that the sink is positioned at a point P₁ at a distance y = αR from the center of the sensor field with radius R. We consider a circle of radius z around the sink representing the neighboring nodes of the sink and a circle of radius x = βR around the center of the sensor field representing the critical central region (see Fig. 8) with α, β $\in$ (0, 1). All data in the corresponding sector from the opposite side of the sensor field has to pass through this circle around the center.

The area A(P₁ P₂ P₃) can be computed by summing the area of the sector with angle $\gamma =360-2\text{arccos}\beta -2\text{arccos}\frac{\beta }{\alpha }$ and twice the area of the triangle formed by P₁, P₃ and the center of the sensor field: $A=R^2\pi \frac{y}{360}+R^2\beta [\sqrt{1-{\beta }^2}+\sqrt{{\alpha }^2-{\beta }^2}]$. The corresponding arc c of the circle around P₁ is given as $c=\frac{2\pi z}{180}\text{arcsin}\frac{\beta }{\alpha }$.

With these quantities, we can quantify the data load which has to pass on average through one node along the arc c as a function of the distance α of the sink from the center of the sensor field:

$$\frac{\mathit{load}}{\mathit{node}}=\frac{A-\mathit{sector}(\delta \text{,}z)}{c}=\frac{R^2\pi \frac{\gamma }{360}+R^2\beta \left[\sqrt{1-{\beta }^2}+\sqrt{{\alpha }^2-{\beta }^2}\right]-z^2\pi \frac{\delta }{360}}{\frac{2\pi z}{180}\text{arcsin}\frac{\beta }{\alpha }}$$

For given R, β, and z this load per node increases monotonically and superlinearly with the distance α of the sink from the center of the sensor field. Moreover, the load $\overline{A}$ going through the critical region around the center of the sensor field is given by summing the area to the right of the critical region and the area of the critical region itself:

$$\overline{A}=R^2\pi \frac{\gamma }{360}+R^2\beta \sqrt{{\alpha }^2-{\beta }^2}+R^2{\beta }^2\frac{\pi }{180}\text{arccos}\frac{\beta }{\alpha }$$

For given R and β, the load $\overline{A}$ going through the critical region decreases monotonically for increasing α. This decrease is stronger for small α and becomes weaker as α increases.

Summarizing, the geometrical model leads to the following observations:

• (i)On the one hand, the load per node in the close neighborhood of the sink increases monotonically with increasing mobility radius of the sink. From this fact, we expect more congestion close to the sink and thus higher Emax for larger mobility radius of the sink.
• (ii)On the other hand, the load to be handled by the region around the center of the sensor field decreases monotonically with increasing mobility radius of the sink. From this fact, we expect less congestion close to the center of the field and thus lower Emax for larger mobility radius of the sink.

The investigations so far clearly demonstrate that the duty cycling value and the mobility radius of the sink have a very strong influence on the contention and thus on the energy dissipation of the WSN. Since some of the effects work in opposite directions, it remains to be explored which of them are stronger. Moreover, we want to quantify the energy dissipation of the WSN for various combinations of duty cycling value and mobility radius of the sink. For this purpose, we summarize and discuss the results of corresponding simulation experiments in the following and compare them to the analytical insights from this section.

4.3. Simulation experiments

For the simulation experiments, we used the model presented in Section 3 and varied the duty cycling value between 1% and 100% and the mobility radius between zero (static sink at the center of the WSN) and 0.9R. We are aware that other model parameters may also influence the energy consumption of the WSN to some extent, but our investigations show that duty cycling value and mobility radius are the most important ones. Therefore, in order to be able to handle the high dimensional parameter space we kept the other simulation parameters fixed as stated in Table 1. The number of repeated simulation experiments has been chosen sufficiently large in order to get acceptably narrow 95% confidence intervals for the results. In most cases, the data shown is averaged over 15 simulation runs. Only in very few cases 20 or 25 simulation runs were needed.

In the following, we compare SS and MS in terms of Emax as well as in terms of Ebar. In each case, we try to follow the same structure: First, we state the central conclusions derived from the simulations, then we discuss the simulation results in more detail, and afterwards we explain the observations and the underlying system behavior.

4.3.1. Overview of simulation results

Our simulation shows that a mobile sink can potentially reduce Emax compared to a static sink at the center of the sensor field, in particular for longer duty cycles. Two parameters strongly influence whether the mobile sink has an advantage: most importantly, the duty cycling of the nodes and, to a lesser extent, the radius of the trajectory of the mobile sink. Overall, the influence of the mobility radius turned out to be stronger for short duty cycles, but negligible for very long duty cycles.

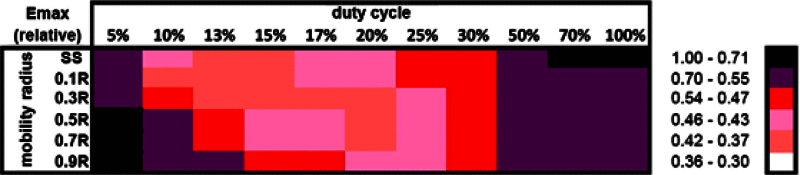
Tables 2 and 3 provide a compact summary of relative Emax and Ebar values for various configurations. In order to quantify the reductions in energy consumption, we divided every Emax and Ebar value by the respective value for a reference configuration with mobility radius of 0.9R and 5% duty cycling of the nodes. Only the Emax and Ebar values for 1% duty cycling are larger than the ones for this reference configuration. However, we decided not to use 1% duty cycling as a reference, since the corresponding Emax and Ebar values are so extreme (much larger than the ones of the reference configuration, see Sections 4.3.2 and 4.3.3) that it would have been much more difficult to distinguish the relative values for a wide range of configurations. Darker colors correspond to a larger ratio and thus to a weaker reduction in energy consumption, and lighter colors correspond to a smaller ratio and thus to a stronger reduction in energy consumption. For example, Table 3 shows that the Emax value resulting from a mobility radius 0.1R and 20% duty cycling is slightly less than half (between 43% and 46%) of the Emax value for the reference configuration.

Table 2.

Relative Ebar values (reference value is Ebar for the sink at 0.9R with 5% duty cycling of the nodes).

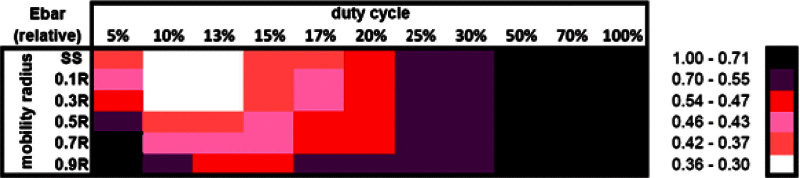Table 3.

Relative Emax values (reference value is Emax for the sink at 0.9R with 5% duty cycling of the nodes).

In Table 2 we see that for Ebar this ratio increases for constant duty cycling value with the mobility radius of the sink. For constant mobility radius, the ratio has a convex shape with a clearly visible optimal range for the duty cycle value. For increasing mobility radius, this optimal range slightly shifts towards higher duty cycle values. Overall, Ebar can be reduced by a factor of three compared to the reference configuration. When compared to the highest Ebar value for 1% duty cycling (see Section 4.3.3), this reduction is even by a factor of 17.

In Table 3 we see that for constant duty cycling the Emax ratios exhibit a convex behavior with varying mobility radius. Exceptions are the extreme duty cycling values, where there is less influence of the mobility radius on the Emax ratios. For constant mobility radius, the Emax ratios also have a convex shape with a clearly visible optimal range for the duty cycle value. For increasing mobility radius, this optimal range again slightly shifts towards longer duty cycles. Overall, Emax can be reduced by a factor of 2.5 compared to the reference configuration. When compared to the highest Emax value for 1% duty cycling (see Section 4.3.2), this reduction is by a factor of 9.

Beyond that, we note the following central observations:

Due to congestion, very short duty cycles can become clearly worse than 100% duty cycling. At very short duty cycles (1%) due to congestion nodes spend many of the time slots in extended active mode (partly idle because there is no available channel for relaying their data) which causes increased energy dissipation. On the other hand, in the case of 100% duty cycles nodes spend all their simulation time in active mode and data quickly reaches the sink. Thus it is quite realistic that at extremely short duty cycles energy dissipation from the nodes is even higher than at 100% duty cycle.

There is a certain critical range of interest for the duty cycle value where Emax hardly depends on the mobility radius. When the duty cycle values of the nodes are set close to 20% (for the chosen network setting and a throughput of 0.8), then the most heavily burdened nodes around the center of the sensor field are operating at the most energy efficient duty cycles for relaying data towards the sink, and a change in the mobility radius of the sink has a negligible impact on Emax. As a result, for these duty cycles we have almost constant Emax independently of the mobility radius of the sink, and thus the best duty cycle value can be determined largely independently of the mobility radius of the sink.

4.3.1.1. Energy-optimal configurations

Based on the simulation results, it is possible to make qualitative statements about energy-optimal configurations of WSNs with a mobile sink (see Figs. 9 and 10). The insights gained from these qualitative statements (e.g., that the duty cycle value should be larger when the mobile sink operates further away from the center of the WSN) are definitely relevant for more general settings of WSNs.

Fig. 9.

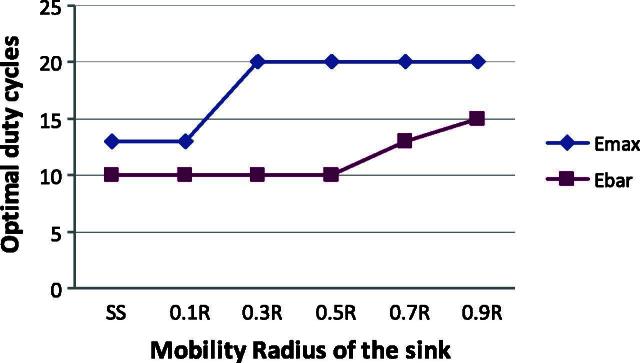
Energy-optimal duty cycle value.

Fig. 10.

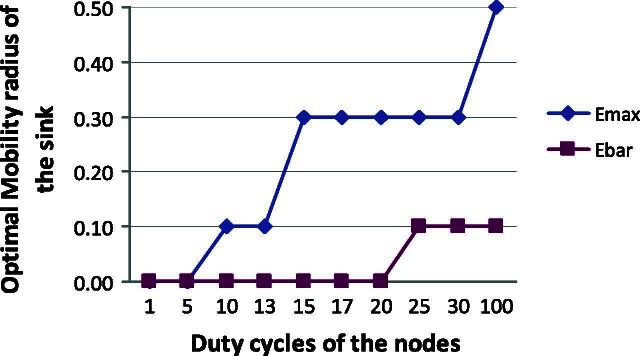
Energy-optimal mobility radius.

Optimal duty cycle for varying mobility radius. Due to the effects discussed before, the optimal duty cycle value of the nodes in general increases monotonically with the mobility radius of the sink. In terms of Emax, the energy-optimal duty cycle value increased from around 13% for a static sink to around 20% for a mobile sink at a mobility radius of 0.9R. In terms of Ebar, the energy-optimal duty cycle value stayed constant at roughly 10% for SS and MS up to a mobility radius around 0.5R. For larger mobility radius, it increased to around 15%.

Optimal mobility radius for varying duty cycle. Due to the effects discussed before, the optimal mobility radius of the sink in general also increases monotonically with the duty cycle value of the nodes. In terms of Emax, the energy-optimal mobility radius increased from 0 (static sink) for duty cycle values 1% and 5% to around 0.5R for a duty cycle value of 100%. In terms of Ebar, the energy-optimal mobility radius stayed constant at 0 (static sink) up to a duty cycle value around 20%. Only for longer duty cycles, it increased to around 0.1R. Consequently, for short duty cycles, the static sink is optimal in terms of both Emax and Ebar. In terms of Emax, the static sink is optimal only for very short duty cycles. Around duty cycle values of 10% a mobile sink yields already lower Emax values.

In the following three subsections, we discuss the simulation results in more detail.

4.3.2. Comparison of SS and MS in terms of Emax

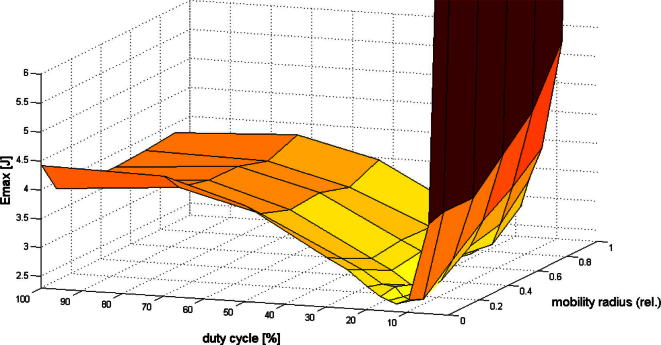
Fig. 11 illustrates the relationship between the duty cycle value, the radius of the mobility trajectory of the sink and Emax. We see that the surface strongly depends on the duty cycling value and varies less with the mobility radius. In detail, the influence of the duty cycle value and of the mobility radius of the sink is as follows.

Fig. 11.

Emax for varying duty cycle values of the nodes and varying mobility radius of the sink. Darker colors represent higher energy consumption.

4.3.2.1. Influence of the duty cycle

For duty cycling values 15% and lower, MS has larger or equal Emax values than SS. The situation gets worse for increasing mobility radius. The shorter the duty cycle, the less attractive is MS compared to SS with increasing mobility radius. For 10% duty cycling and lower, Emax values can even be higher than the corresponding ones for 100% duty cycling. The cross-over point with 100% duty cycling in terms of mobility radius decreases with decreasing duty cycle value. However, for duty cycling values of 20% and higher, MS achieves lower Emax than SS. In this range of duty cycles (20% and higher), the absolute level of Emax increases with increasing duty cycle value.

This behavior can be explained as follows. Considering that the throughput is fixed as in our simulation, reducing the duty cycles below 20% leads to increased congestion because nodes do not have enough time in active mode to identify an available communication partner and to relay the traffic. As a result, nodes have to extend their active mode which leads to increased energy dissipation from the nodes. On the other hand, if the duty cycle of the nodes is larger than 20%, then nodes tend to spend more time in active idle mode (active, but doing nothing, e.g., not relaying data) and sleep less. This also increases energy dissipation compared to 20%. Thus, for the considered network setting, duty cycle values of the nodes around 13% are optimal for SS and around 20% for MS in terms of Emax. Any other duty cycle value leads to increased Emax.

4.3.2.2. Influence of the mobility radius

Only for duty cycles below 15%, there is a clear dependency of Emax on the mobility radius. For very short duty cycles, the increase in Emax with increasing mobility radius is stronger. Between 15% and 20% duty cycling, Emax tends to be hardly influenced by the mobility radius of the sink. For duty cycles of 20% and above, Emax tends to decrease for mobility radius values up to 0.3R. For mobility radius values above 0.3R, there is no clear dependency of Emax on the mobility radius.

This behavior can be explained as follows. When the nodes are operating at duty cycles below 15%, for a static sink (SS) the active periods of the nodes are sufficient for avoiding strong congestion effects. But as we increase the mobility radius of the sink (0.1R and higher), congestion starts to build up for duty cycles below 15%. The active periods of the nodes become insufficient to relay data towards the sink, causing extended active mode of the nodes and hence increased Emax with increasing mobility radius of the sink. Still, even at relatively short duty cycles (10%, 15%, 17%) MS performs better than SS when the sink is close to the center (0.1R).

At longer duty cycles an increase in the mobility radius of the sink does not have a strong influence on Emax, because nodes are already spending enough time in active mode which prevents congestion from kicking in. Even when the mobility radius of the sink is increased, MS is better than SS. When the sink is moved away from the center of the WSN (sink at the center leads to most balanced routing load on the nodes), congestion increases in the field especially at the nodes located in the vicinity of the center of the WSN and around the sink. This indicates another benefit of a mobile sink compared to a static sink at the center of the network – the reduction of the load on the nodes in the vicinity of the sink.

Summarizing, both duty cycle and mobility radius of the sink influence Emax. The effects are partly in opposite directions, and the influence of the duty cycle value tends to be stronger. Shorter duty cycles and (as indicated in the geometrical model in Section 4.1) larger mobility radius lead to more congestion in the vicinity of the sink and hence to higher Emax. Note that more extended active periods with shorter duty cycle are not equivalent in terms of energy consumption to longer active periods due to a longer duty cycle. A node in extended active mode needs to find a neighbor in active mode in order to be able to send its data. If the duty cycling is longer, then there is a higher chance to find a neighbor in active mode which can receive packets. Based on the simulation results it can be inferred that the duty cycle of the nodes has much stronger impact on Emax than the mobility radius of the sink. This is evident from the fact that when the duty cycle of the nodes is set to 15% or longer, then an increase in the mobility radius of the sink has negligible effect on Emax. Overall, we conclude for the network setting considered that for a duty cycle of 20% and longer the position of the sink does not influence energy dissipation significantly as long as the mobility radius is larger than 0.3R.

4.3.3. Comparison of SS and MS in terms of Ebar

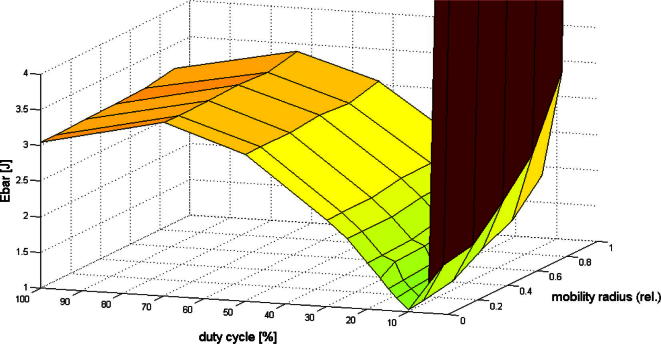
Fig. 12 illustrates the relationship between the duty cycle value, the radius of the mobility trajectory of the mobile sink and Ebar. First of all, we note that there is less variability than in the case of Emax.

Fig. 12.

Ebar for varying duty cycle values of the nodes and varying mobility radius of the sink. Darker colors represent higher energy consumption.

From the details of the simulation results, we can conclude that in terms of Ebar a mobile sink basically has no advantages over a static sink. Ebar increases with increasing mobility radius for all duty cycles. However, for longer duty cycles, this increase with increasing mobility radius becomes less significant, e.g., for 5% and 100% duty cycles of the nodes when the mobility radius of the sink is varied from 0 to 0.9R then the increase in Ebar is 2.06 and 0.11 J, respectively. For 100% duty cycling, there is only a very weak increase. For duty cycling values below 13%, the Ebar values for larger mobility radius are above the Ebar values for longer duty cycles, and the crossover points move to smaller mobility radius values (5% is already completely above 10%). For 100% duty cycling, Ebar decreases slightly compared to 50% and 70% duty cycling.

This behavior can be explained as follows. At shorter duty cycles an increase in the mobility radius of the sink strongly influences Ebar and vice versa. This is due to the fact that whenever the sink moves away from the center of the WSN, an uneven routing load distribution on the nodes located at the same distance from the sink results. This causes congestion on nodes located at heavily loaded routes which increases the energy dissipation of these nodes. With longer duty cycles, nodes can prevent congestion from building up and therefore Ebar is much higher for very short duty cycles (1% and 5%). Similar to the behavior of Emax, for fixed mobility radius of the sink increasing duty cycle values of the nodes first rapidly reduce Ebar due to the reduction of congestion. If the duty cycle value is further increased beyond the optimal value, Ebar starts to increase again due to the increasing number of idle time slots in active mode. For very high duty cycling values, the energy consumption of the transition from sleep to active mode becomes less significant, and this explains that for 100% duty cycling Ebar is slightly lower than for 70% duty cycling.

4.3.4. Discussion with respect to previously published results

Consequently, the simulation also confirmed that duty cycle of the nodes and mobility radius of the sink do not influence Ebar as strongly as Emax. Moreover, we saw that the optimal mobility radius in terms of Emax is smaller than $\frac{\sqrt{2}R}{2}$ for all duty cycle values. Note that this differs from results in the literature which conclude that $\frac{\sqrt{2}R}{2}$ is the energy-optimal radius of the mobility trajectory [8,33,35]. The reasons for this difference are the following: In [33,35] the basic setup is comparable to our setup (the routing is modeled the same way as in this paper), but the authors did not take into account channel contention and the resulting congestion effects. In [8], however, the routing strategy is different from the one we consider: outside the mobility trajectory of the sink, data is routed along concentric circles in order to reduce the load on the central region. Based on simulation, which again does not account for congestion effects due to channel contention, the authors of [8] conclude that the radius of the optimal mobility trajectory of the sink is between $\frac{\sqrt{2}R}{2}$ and 0.9R (slightly larger than in [33,35]). In this paper, we show with our geometrical model and with our simulations, that a larger radius of the mobility trajectory of the sink tends to increase congestion, and consequently the optimum mobility radius is actually smaller than $\frac{\sqrt{2}R}{2}$.

5. Conclusions

In this paper we have extensively compared the energy efficiency of static and mobile sink-based routing protocols in a WSN. In our analysis we have also taken into account channel contention and the resulting congestion effects. Our analysis revealed that it is important to consider both Emax and Ebar in the energy analysis of a routing protocol, as improvement in one can result in degradation of the other and vice versa. It has also been observed that adopting a mobile sink and reducing the duty cycle of the nodes does not necessarily reduce the energy dissipation of the WSN. Instead, a careful selection of duty cycle value of the nodes and of mobility radius of the sink is required in order to achieve higher energy efficiency than with a duty cycle value of 100% and a static sink.

Moreover, we conclude that in comparison to a static sink placed at the center of the WSN, a mobile sink can reduce Emax significantly; however, for a fixed duty cycle value, a static sink placed at the center of the WSN always leads to lower Ebar than any mobile sink. Irrespective of the mobility radius of the sink, extremely short duty cycles (e.g., 1%) lead to very high energy dissipation due to congestion, even higher than a duty cycle value of 100%.

In the future, we plan to extend our impact analysis to other parameters, such as throughput or density of the WSN. Preliminary results indicate that the basic findings of this work, such as the conclusion that the choice of the duty cycle value is more important than the mobility radius of the sink, also remain valid for a range of throughput values. Moreover, it can be expected that the optimal duty cycle value decreases with decreasing throughput of the WSN. Beyond theoretical analysis and simulation, we also plan to complement the investigations summarized in this paper with experiments on real test beds, such as SensLab (http://www.senslab.info/).