Trabecular Bone Strength Predictions of HR-pQCT and Individual Trabeculae Segmentation (ITS)-Based Plate and Rod Finite Element Model Discriminate Postmenopausal Vertebral Fractures

Abstract

While high-resolution peripheral quantitative computed tomography (HR-pQCT) has advanced clinical assessment of trabecular bone microstructure, nonlinear microstructural finite element (μFE) prediction of yield strength by HR-pQCT voxel model is impractical for clinical use due to its prohibitively high computational costs. The goal of this study was to develop an efficient HR-pQCT-based plate and rod (PR) modeling technique to fill the unmet clinical need for fast bone strength estimation. By using individual trabecula segmentation (ITS) technique to segment the trabecular structure into individual plates and rods, a patient-specific PR model was implemented by modeling each trabecular plate with multiple shell elements and each rod with a beam element. To validate this modeling technique, predictions by HR-pQCT PR model were compared with those of the registered high resolution μCT voxel model of 19 trabecular sub-volumes from human cadaveric tibiae samples. Both Young’s modulus and yield strength of HR-pQCT PR models strongly correlated with those of μCT voxel models (r²=0.91 and 0.86). Notably, the HR-pQCT PR models achieved major reductions in element number (>40-fold) and CPU time (>1,200-fold). Then, we applied PR model μFE analysis to HR-pQCT images of 60 postmenopausal women with (n=30) and without (n=30) a history of vertebral fracture. HR-pQCT PR model revealed significantly lower Young’s modulus and yield strength at the radius and tibia in fracture subjects compared to controls. Moreover, these mechanical measurements remained significantly lower in fracture subjects at both sites after adjustment for aBMD T-score at the ultradistal radius or total hip. In conclusion, we validated a novel HR-pQCT PR model of human trabecular bone against μCT voxel models and demonstrated its ability to discriminate vertebral fracture status in postmenopausal women. This accurate nonlinear μFE prediction of HR-pQCT PR model, which requires only seconds of desktop computer time, has tremendous promise for clinical assessment of bone strength.

INTRODUCTION

Osteoporosis is a major metabolic bone disease characterized by low bone mass and microarchitecture deterioration of trabecular and cortical bone that leads to increased bone fragility (1). Mechanical strength of trabecular bone is directly related to bone fragility and is largely determined by trabecular microstructure (2–5). Mechanical testing of ex vivo bone specimens is considered the gold standard method to assess bone strength (5–7). However, this testing cannot be applied in vivo. Microstructural finite element (μFE) analysis based on high-resolution images of bone structure represents an alternative approach to assess bone stiffness (the ability to resist deformation) and bone strength (the breaking capacity) non-invasively (8,9). The recent development of high resolution peripheral QCT (HR-pQCT) and microstructural magnetic resonance imaging (μMRI) has made clinical assessment of trabecular microstructure possible (10–12). Specifically, studies have shown these high-resolution clinical images as suitable for input into μFE models for assessing bone strength (13–16). Currently, the most common μFE modeling strategy is to convert each voxel from an image into a single finite element, creating three dimensional (3D) patient-specific models that can provide an accurate and direct estimate of bone’s mechanical competence such as stiffness or strength. Since the resulting computational models integrate whole bone geometry and the trabecular and cortical microstructure from high-resolution clinical scans, HR-pQCT and μMR image-based μFE analysis promises to become a powerful tool for the clinical assessment of bone strength and fracture risk (13,17–24).

Depending on the range of deformation of bone tissue, the mechanical behavior of trabecular bone structure differs and requires different FE analyses to describe its mechanical properties. When bone is loaded within the elastic limits of the bone tissue, i.e., bone structure deforms due to loading from daily activities and always returns to its original configuration once the loading is released, linear FE analysis is adequate to derive bone’s linear elastic properties such as Young’s modulus or stiffness. On the other hand, once bone is loaded beyond the elastic limits of the bone tissue, i.e., bone structure will not return to its original configuration or shape after tissue deformation that is caused by overload, nonlinear FE analysis is required to derive bone’s nonlinear properties such as bone’s yield strength or failure load. In general, a nonlinear FE analysis is mathematically more complicated and computationally more expensive than a linear FE analysis. Several studies have compared mechanical properties predicted by the voxel model with those predicted by mechanical testing and have demonstrated that the voxel FE model accurately predicts Young’s modulus and yield strength of human trabecular bone (8,15,25). However, the simple voxel-to-element modeling strategy results in a very large model size. Typically there are hundreds of thousands of elements in a voxel model of trabecular bone based on an HR-pQCT scan at 82 μm voxel size. Thus, the computational costs to derive nonlinear mechanical properties of bone, such as yield strength or failure load, for clinical use are prohibitively high (8,25). Linear mechanical properties, such as elastic modulus or stiffness, are often used as alternative surrogates to indicate bone’s resistance to fractures. Nevertheless, it still requires hours of computer central processing unit (CPU) time for a voxel model to assess bone’s linear mechanical properties.

From a biomechanical perspective, the microarchitecture of trabecular bone consists of a collection of trabecular plates and rods (26–30). Recently, a highly efficient plate and rod FE modeling strategy has been proposed (31,32). The plate and rod FE model maintains the advantages of the voxel-based FE models in capturing the major trabecular structural components, plates and rods, while allowing faster computation to fill the unmet clinical need for a fast estimate of bone strength. Using individual trabecula segmentation (ITS) technique to segment the trabecular bone structure into individual plates and rods (27,33), a specimen-specific plate and rod (PR) model was developed by modeling each of these trabecular plates and rods as a single beam/shell element rather than as a collection of hundreds of 8-node brick elements. In our prior study we have applied PR modeling technique to micro computed tomography (μCT, 25 μm voxel size) images of trabecular bone and demonstrated significant and strong correlations between Young’s modulus and yield strength measured by mechanical testing and those predicted by PR models of human trabecular bone at the proximal tibia, femoral neck, and greater trochanter (34). Moreover, the average CPU time for PR model to complete bone strength calculation was within 10 minutes, which represented a 900-fold reduction from CPU time required by a voxel model.

The purpose of this study was to translate the μCT image-based plate and rod FE modeling technique to clinical HR-pQCT images of trabecular bone at the distal radius and tibia. The first objective was to validate the computations of Young’s moduli and yield strength of the HR-pQCT-based PR model by correlation analysis with those of μCT-image-based voxel model, the computation gold standard. The second objective was to test the ability of mechanical properties predicted by PR μFE models of HR-pQCT images at the distal radius and tibia to discriminate between postmenopausal women with and without vertebral fractures. We hypothesized that HR-pQCT image-based PR μFE models can accurately and efficiently assess trabecular bone strength at the distal radius and tibia and distinguish postmenopausal women with vertebral fractures.

Materials and Methods

HR-pQCT and μCT Images of Human Cadaver Tibiae

Nineteen freshly frozen human cadaveric tibiae from thirteen donors (six pairs and seven singles, ten males and three females) were obtained from the International Institute for the Advancement of Medicine (Scranton, PA). The age of subjects ranged from 55 to 84 years with an average of 70.6 years. The subjects’ medical histories were screened to exclude metabolic bone diseases or bone cancer. A soft tissue-equivalent gelatin phantom (35) was built into the shape of human leg and each tibia was scanned inside the phantom first by HR-pQCT (Xtreme CT, Scanco Medical AG, Bassersdorf, Switzerland) according to clinical scan protocol. The HR-pQCT measurement included 110 slices, corresponding to a 9.02 mm section of the distal tibia along the axial direction, with a nominal voxel size of 82 μm. Using a band saw, a 25 mm section centered in the scanned area from each distal tibia was obtained by two cuts along transverse plane of the tibia. The central 10 mm section along the axial direction was then scanned by μCT (μCT 80, Scanco Medical AG, Bassersdorf, Switzerland) to encompass the same region scanned by HR-pQCT at an isotropic 25 μm voxel size.

All the μCT images were then registered to the corresponding HR-pQCT images to encompass the same volume of interest by using a landmark initialized mutual information based registration approach (36–38), μCT images were processed by Gaussian filtering and specimen-specific adaptive thresholding to extract the mineralized phase using the standard protocol of Scanco software for μCT analysis. The mineralized phase of HR-pQCT images was thresholded automatically by using a Laplace-Hamming filter followed by global threshold using a fixed value of 40% of maximal grayscale value of the images, a standard clinical protocol (39). Subsequently, a 70×70×70 voxel cubic sub-volume was extracted from the center of the trabecular bone compartment of the thresholded HR-pQCT image, equivalent to a physical size of 5.74×5.74×5.74 mm³. The corresponding sub-volume was also extracted from each of the thresholded μCT images. The same set of images have been used and described in a previously published study (40).

Patient Population

Thirty vertebral fracture and 30 control subjects from a subset of subjects previously described by Stein et al. (22) were included in this study. Postmenopausal women, over age 60 or more than 10 years post menopause, were recruited at Columbia University Medical Center (CUMC; New York, NY) or Helen Hayes Hospital (HHH; West Haverstraw, NY) by advertisement, self- or physician referral. Subjects were eligible for inclusion as vertebral fracture cases if they had a history of a low trauma vertebral fracture that occurred after menopause or were found to have vertebral fractures by spine x-ray. Low trauma was defined as equivalent to a fall from a standing height or less. Vertebral fractures were classified using spine x-rays according to the semi-quantitative method of Genant et al. (41). Vertebrae were graded as normal, or with mild, moderate or severe deformities, defined as reductions in anterior, middle or posterior height of 20–25%, 25–40%, and >40% respectively. Control subjects had no history of low trauma fractures at any site and no vertebral deformity on lateral radiograph, as dictated by pre-specified exclusion criteria. There were no BMD requirements for inclusion. Potential cases and controls were excluded if they had endocrinopathies (e.g., untreated hyperthyroidism, Cushing’s syndrome, prolactinoma), celiac or other gastrointestinal diseases, abnormal mineral metabolism (e.g., clinical osteomalacia, primary hyperparathyroidism), malignancy except for skin cancer, and drug exposures that could affect bone metabolism (e.g., glucocorticoids, anticonvulsants, anticoagulants, methotrexate, aromatase inhibitors, thiazolidinediones). Women using hormone replacement therapy or raloxifene were permitted to participate. Women who had ever used teriparatide, or who had taken bisphosphonates for more than one year were excluded. All subjects provided written informed consent and the Institutional Review Board of Columbia University Medical Center approved this study. At the study visit, past medical history, reproductive history, and medication use were assessed. A physical exam was performed including height by Harpenden stadiometer and weight. Of 411 women screened, 30 vertebral fracture and 120 control subjects were eligible and agreed to participate. Then, we randomly chose 30 subjects from the 120 control subject pool that were age-matched with the 30 vertebral fracture subjects as the control subjects for the current study.

Areal Bone Mineral Density (aBMD)

Areal BMD was measured by DXA (QDR-4500, Hologic Inc., Walton, MA at CUMC; Lunar Prodigy, GE, Peewaukee, WI at HHH) of the lumbar spine (LS), total hip (TH), femoral neck (FN), 1/3 radius (1/3R), and ultradistal radius (UDR). T scores compared subjects and controls with young-normal populations of the same race and sex, as provided by each manufacturer.

HR-pQCT Images of fracture and non-fracture subjects

HR-pQCT of the non-dominant distal radius and distal tibia was measured at CUMC as previously described (10,13,42). The HR-pQCT measurement included 110 slices, corresponding to a 9.02 mm section along the axial direction, with a nominal voxel size of 82 μm. Quality control was provided by scanning the European Forearm Phantom at the time subjects were scanned. The mineralized phase was thresholded according to the standard patient evaluation protocol (43). Total volumetric BMD (vBMD) and trabecular vBMD of both the radius and tibia were calculated.

A 5.7×5.7×5.7 mm³ cubic sub-volume corresponding to 70×70×70 voxels was extracted from the center of trabecular bone compartment of each image of the distal radius; similarly, a 9.0×9.0×9.0 mm³ sub-volume corresponding to 110×110×110 voxels was extracted from each distal tibia. Due to the size difference of the distal radius and distal tibia segment, the cubic sub-volume of the distal radius was smaller than that of the distal tibia. The rationale for choosing different sized models for the tibia and radius was to maximize the region of interest at each site in order to capture as trabecular bone volume as possible for more accurate assessment.

ITS-based PR Nonlinear Finite Element Analysis

The HR-pQCT images of human cadaveric tibia and the radius and tibia of human subjects were all subjected to PR μFE analysis. To construct the PR model, shell and beam element meshes were created based on the segmented skeleton image of individual trabecular plates and rods through a digital topological analysis (44–46) and individual trabecula segmentation technique (27,33). Briefly, the original trabecular volume was converted to a trabecular skeleton consisting of 1-voxel thick plate skeleton (surface) and rod skeletons (curve) though an iterative thinning process (46). Each rod skeleton was meshed into a 2-node beam and each plate skeleton was meshed into one or several 3-node shell elements by the Delaunay triangulation. Based on the simplified trabecular bone microstructure of individual trabecular plates and rods, a PR microstructural model of each image was generated for FE analysis. A schematic of conversion from voxel model to PR model was shown in Figure 1. Detailed methods describing the generation of PR model can be found in (47).

Figure 1.

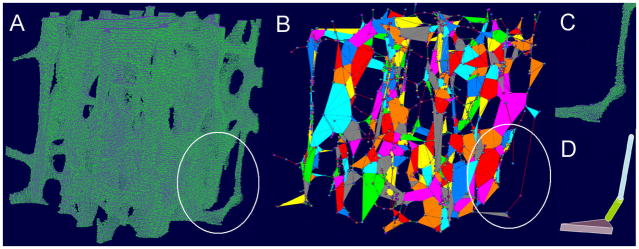
Illustration of convertion of (A) a voxel model to (B) PR model. Nodes are shown as 8-node bricks; element thickness is not shown in (B). (C)–(D) Illustrations of conversion of voxel elements to plate/rod elements with various thickness.

A commercially available finite element software ABAQUS 6.1 (Dassault Systèmes Simulia Corp., Versailles, France) was used to simulate uniaxial compression tests for each model. The previous beam and shell meshing results were written as an input mesh file for ABAQUS. Each trabecular rod was prescribed as a 2-node beam element (B31 in ABAQUS). The beam cross-section of the trabecula was assumed as circular and uniform along the trabecula and the average radius of the trabecular rod determined using the previously described technique was used to describe the dimension of the beam cross-section. Triangular shell elements were used to model the resulting triangular plates (STRI3 in ABAQUS). The average thickness of the plate was used as the thickness of the shell element. Then, an elastic-plastic isotropic material property was used. The plastic model was used when the tissue strain reached 0.81% with a post-yield modulus equal to 5% of the Young’s modulus. After the nonlinear simulations, the apparent modulus was calculated from the slope of the linear curve fit of the 0% to 0.2% strain portion of the stress-strain curve. The yield strength and yield strain were determined using the 0.2% offset method (48). A tissue modulus of 16.59 GPa and Poisson’s ratio of 0.3 was used first to calculate the apparent Young’s modulus. Then based on the linear correlation between the Young’s modulus of PR model and μCT-based voxel model, tissue modulus was adjusted to be 39.62 GPa to match the mean of apparent Young’s modulus predicted by two models. The same tissue modulus was also applied to the HR-pQCT PR models of vertebral fracture and non-fracture subjects.

Voxel-based Nonlinear Finite Element Analysis

Each thresholded μCT image at 25 μm voxel size, corresponding to a 230×230×230 voxel cubic sub-volume, was converted to μFE models by converting each image voxel to an 8-node elastic brick element. Each HR-pQCT image at 82 μm voxel size was also directly converted to μFE voxel models by voxel-to-element conversion. The tissue constitutive law was described by the elasto-plasticity material model that incorporates large deformation (49,50). The tissue-level yield strains were 0.33% strain in tension and 0.81% strain in compression, respectively (51). After the yield point, the post-yield modulus was decreased to approximately 5% of the initial value. An implicit parallel finite element model built on the highly scalable Olympus platform (52) was used to solve the nonlinear FE models on a Sun Constellation Linux Cluster (Texas Advanced Computing Center, The University of Texas at Austin). Apparent modulus and yield strength were calculated using the same method described in the PR model FE analysis. Poisson’s ratio was defined as 0.3 and a 16.59 GPa tissue modulus derived from our previous study (34) was first used for both μCT and HR-pQCT-based voxel model. Then, according to linear correlation between HR-pQCT and μCT-based voxel model, tissue modulus of HR-pQCT was adjusted to be 10.43 GPa to match the mean of apparent Young’s modulus predicted by two models. The same tissue modulus was also applied to the HR-pQCT voxel models of vertebral fracture and non-fracture subjects.

Statistical Analyses

Statistical analyses were performed using NCSS software (NCSS 2007, NCSS Statistical Software, Kaysville, Utah). Descriptive data are presented as mean ± standard deviation (SD). Two-sided p values < 0.05 were considered to indicate statistical significance. Axial Young’s modulus and yield strength of human cadaveric tibiae of HR-pQCT image-based PR models were correlated individually to the corresponding properties derived from μCT image-based voxel models. Pearson correlation coefficients are provided if both parameters were normally distributed and Spearman correlation coefficients are provided if results of one or both parameters were not normally distributed based upon a Shapiro-Wilk test. Element number and CPU time associated with the HR-pQCT-based PR model and μCT-based voxel model were compared by Student’s t-test or Mann-Whitney U test if data was not normally distributed.

For the clinical HR-pQCT study, group comparisons are presented as mean ± standard error of the mean (SEM). Differences between fracture and non-fracture subjects were assessed by Student’s t test or Mann-Whitney U test if data were not normally distributed. ANOVA was used to evaluate differences in μFEA parameters at the radius or tibia after adjustment for aBMD T-score at the ultradistal radius or total hip, respectively. Standard receiver operating characteristic (ROC) curve analysis was performed to determine the ability of DXA, HR-pQCT, and μFEA to discriminate fracture status. In this type of analysis, an area under the curve (AUC) >0.75 is considered compelling evidence for the ability to discriminate an outcome. A diagnostic test with an AUC of 0.5 is considered to perform no better than chance. In addition, a multivariable ROC analysis was performed to calculate AUC by including one parameter from density measurements and another parameter from mechanical measurements for each skeletal site.

Results

Validation of HR-pQCT Image-based PR Model by μCT Image-based Voxel Model of Human Cadaveric Tibia

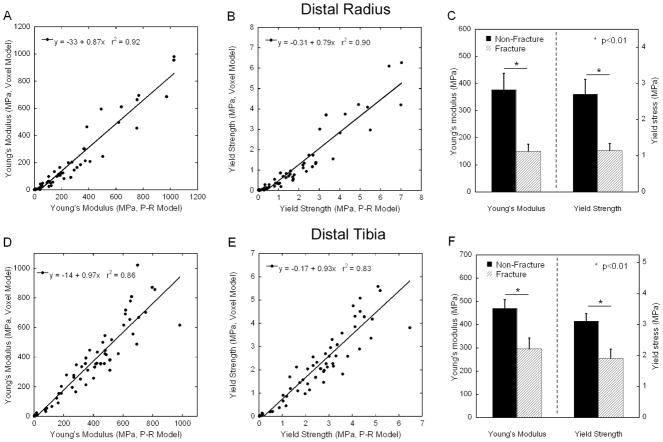
Upon visual inspection of HR-pQCT and the registered μCT images, similar trabecular bone patterns were found (Figure 2). As shown in Figure 2C, plate and rod configuration of the trabecular network was preserved in the HR-pQCT image-based PR model. It was displayed as a simplified view in which plate and rod elements are represented by beam and shell without showing the thickness (Figure 2). Significant correlations were found for both elastic modulus and yield strength of HR-pQCT image-based PR model against those of HR-pQCT (r²=0.97 and 0.95) and μCT image-based voxel models (r²=0.91 and 0.86), respectively (Figure 3). By applying the same bone tissue modulus (16.6 GPa for μCT voxel model), HR-pQCT-based PR model significantly underestimated the mechanical measurements compared to the gold-standard μCT voxel model, while in contrast the HR-pQCT-based voxel model overestimated those measures. Therefore, we performed linear regression to calculate correction factors and then applied them to adjust the HR-pQCT-based PR model and voxel model tissue modulus to be 39.6 GPa and 10.4 GPa, respectively. While all highly correlated, no significant difference was found between the apparent Young’s modulus and yield strength of three models after adjustment of their tissue moduli.

Figure 2.

The 3D reconstruction of a registered (A) μCT and (B) HR-pQCT cubic trabecular bone images of human tibia. Based on (B), a PR model was generated and shown in (C). Color indicates different individual trabecula.

Figure 3.

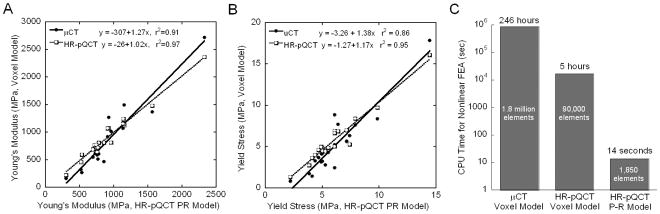
Linear correlations of (A) Young’s modulus and (B) yield strength of HR-pQCT-based PR model with those of HR-pQCT and μCT-based voxel model; Effective tissue modulus 16.6 GPa, 10.4 GPa, and 39.6 GPa were used for μCT-based voxel model, HR-pQCT-based voxel model, and HR-pQCT-based PR model, respectively; (C) CPU time for nonlinear FE analysis using μCT-based voxel model, HR-pQCT-based voxel model, and HR-pQCT-based PR model.

The conversion from the voxel model to PR model resulted in a remarkable reduction in element number from more than 1.8 million for μCT-based voxel models and more than 85,000 for HR-pQCT-based voxel models to less than 2,000 for HR-pQCT-based PR Model. Furthermore, the CPU time for nonlinear analysis was reduced from 246 hours for μCT-based voxel models and 5 hours for HR-pQCT-based model to 14 seconds for HR-pQCT PR model. On average, the reduction in CPU time for assessing trabecular bone yield strength is 1,295±229 fold from HR-pQCT voxel-based model to PR model. In addition, the model generation time for HR-pQCT PR model on average is within a few seconds, which is no more than the time required for generating the voxel model.

Subject Characteristics

Thirty women with a history of postmenopausal vertebral fragility fracture and thirty women with no fracture history were enrolled (Table 2). The majority (64%) of vertebral fractures were asymptomatic. Thirteen subjects (43%) had sustained multiple postmenopausal fractures. Subjects were predominantly Caucasian (90%). More women in vertebral fracture group were Latina. (p<0.01) The groups did not differ according to age, BMI, years since menopause, chronic medical conditions, osteoporosis risk factors, calcium and vitamin D supplementation, exposure to HRT or bisphosphonates. Alcohol consumption was low in both groups, 0–1 beverage daily, but was lower among women with vertebral fractures (p<0.02).

Table 2.

Characteristics of the study population (mean±SEM)

	Vertebral fracture N=30	Control N=30	P-value
Age	69 ± 1	69 ± 1	0.98
Race
% Caucasian	86	93	0.86
% African American	4	3
% Other	10	4
Ethnicity
% Hispanic	28	5	0.01
% Non-Hispanic	72	95
BMI (kg/m2)	27 ± 1	26 ± 1	0.35
Years since menopause	18 ± 2	20 ± 1	0.56
Family history of osteoporosis by BMD (%)	54	45	0.34
Family history of fracture (%)	27	33	0.23
Tobacco use –
Never (%)	55	70	0.10
Former (%)	41	30
Current (%)	4	0
Alcohol use (beverages per day)	0.4 ± 0.1	1.1 ± 0.3	0.02
Calcium supplements – total daily dose (mg)	730 ± 136	1025± 102	0.14
Vitamin D supplements – total daily dose (IU)	632 ± 386	190 ± 40	0.29
Hormone replacement therapy – Past (%)	39	61	0.13
–Current (%)	15	9	0.96
Bisphosphonatesa - Past (%)	7	3	0.55
Current (%)	10	3	0.31
Raloxifene (%)	11	4	0.40
Thyroxine (%)	18	35	0.17
SSRIs (%)	11	13	0.80
Inhaled glucocorticoids (%)	0	4	0.27

^aPrior bisphosphonate use limited to <1 yr

Bone Mineral Density by DXA and HR-pQCT

Mean T scores were above the WHO osteoporosis threshold (T score ≤−2.5) and did not differ between the groups at the LS, FN, TH, 1/3R, or UDR (Table 3). At the FN and UDR, the mean T score tended to be lower in women with fractures (p=0.09; Table 1). In contrast to the aBMD findings, vBMD assessed by HR-pQCT revealed significant differences between fracture and non-fracture subjects (Table 3). vBMD of whole bone and trabecular bone were 15% and 21% lower in fracture vs. control subjects at the radius, and 18% and 20% lower at the tibia.

Table 3.

Comparison of DXA, HR-pQCT and mechanical parameters in subjects with and without vertebral fractures.

Variable (units)	Fracture (Mean ± SEM)	Nonfracture (Mean ± SEM)	p Value	AUC
DXA T-Score
Total Spine	−1.70 ± 0.29	−1.42 ± 0.23	0.33	0.55
Total Hip	−1.44 ± 0.16	−1.09 ± 0.17	0.13	0.62
Femoral Neck	−1.97 ± 0.12	−1.65 ± 0.14	0.09	0.61
1/3 Radius	−1.59 ± 0.24	−1.09 ± 0.20	0.90	0.55
Ultradistal Radius	−1.79 ± 0.19	−1.25 ± 0.25	0.09	0.62
HR-pQCT - Radius
Total Bone Density (mgHA/cm3)	250 ± 9	294 ± 11	0.003b	0.71
Trabecular Bone Density (mgHA/cm3)	104 ± 6	131 ± 6	0.004a	0.69
PR Model FEA – Radius
PR Model – Young’s Modulus (MPa)	150 ± 26	377 ± 61	0.002 b	0.71
PR Model – Yield Strength (MPa)	1.15 ± 0.19	2.71 ± 0.41	0.001 b	0.72
HR-pQCT - Tibia
Total Bone Density (mgHA/cm3)	199 ± 7	243 ± 6	<0.0001c	0.77
Trabecular Bone Density (mgHA/cm3)	120 ± 6	149 ± 6	0.005b	0.71
PR Model FEA – Tibia
PR Model – Young’s Modulus (MPa)	296 ± 46	470 ± 38	0.005 a	0.72
PR Model – Yield Strength (MPa)	1.91 ± 0.29	3.11 ± 0.25	0.003 a	0.73

Significance of comparisons after adjustment for UDR (radius) and TH (tibia) T-score is denoted by

^ap<0.05,

^bp<0.01, and

^cp<0.001.

Table 1.

Comparisons between the HR-pQCT image-based PR model and μCT and HR-pQCT image-based voxel models based on the same human tibia trabecular bone volumes (mean±SD).

	HR-pQCT PR Model	HR-pQCT voxel Model	μCT voxel Model
BV/TV (%)	16.1±3.5 a	25.2±5.6	14.5±4.8
Tissue Modulus (GPa)	39.6	10.4	16.6
Apparent Young’s Modulus (MPa)	923±439	919±457	869±587
Yield Strength (MPa)	4.34±2.01	5.87±3.14	5.18±3.89
Total Number of Elements	1,849±502 a,b	86,261±19,339	1,763,102±586,479
CPU Time (sec)	14±5 a,b	17,128±3,495	886,837±258,387

^aindicates significant difference between HR-pQCT PR model and HR-pQCT voxel model and

^bbetween HR-pQCT PR model and μCT voxel model (p<0.05).

Fracture Status Discrimination by Mechanical Measurements of HR-pQCT-based PR model

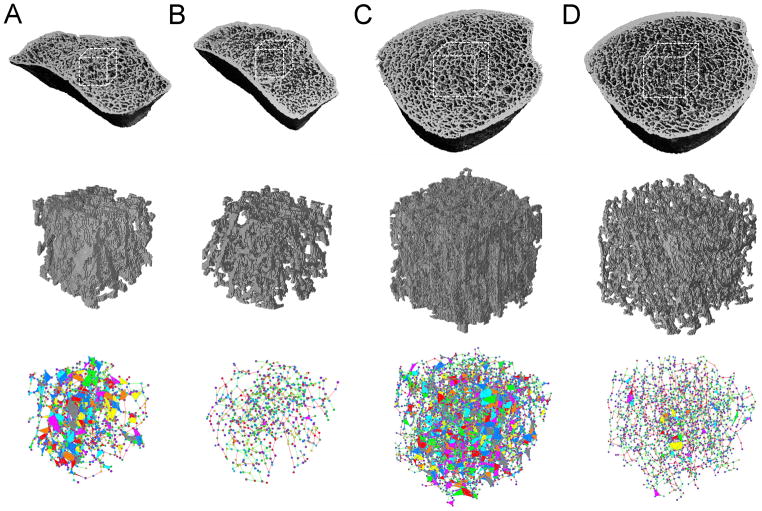
Figure 4 shows representative images of voxel and PR models of fracture and control subjects. Bone volume fraction of PR model was 21% and 25% lower respectively at the radius and tibia of women with a history of fracture. Moreover, plate element number was 47% and 34% lower at the radius and tibia, respectively; rod element number was 24% higher at the tibia and tended to be higher at the radius (19%, p=0.06) in fracture subjects than controls (Table 4). Although there were fewer plate elements in the PR model of fracture subjects, the average thickness of plate element was 2% greater at the radius and tended to be higher (2%, p=0.06) at the tibia in fracture subjects.

Figure 4.

(Top row) HR-pQCT images of distal radius of (A) the control group and (B) the fracture group, and distal tibia of (C) the control group and (D) the fracture group; (Middle row) HR-pQCT-based voxel models of central cubic sub-volumes (70×70×70 at distal radius and 110×110×110 at distal tibia) extracted from corresponding images; (Bottom row) HR-pQCT-based PR models of the corresponding cubic images.

Table 4.

Comparison of PR model parameters (Mean±SEM) in subjects with and without vertebral fractures.

	Distal Radius			Distal Tibia
	Fracture	Nonfracture	P value	Fracture	Nonfracture	P value
HR-pQCT Image BV/TV (%)	13.7±1.1	17.3±1.3	0.04	13.4±1.1	17.9±0.9	0.003
PR Model BV/TV (%)	8.9±0.7	11.3±0.9	0.03	8.8±0.8	11.9±0.6	0.002
% Plate Element Volume	6.3±0.9	9.6±1.7	0.09	13.4±1.4	15.2±1.3	0.4
% Rod Element Volume	93.7±0.9	90.4±1.7	0.09	86.6±1.4	84.8±1.3	0.4
Number of Plate Element	124±25	232±43	0.03	814±112	1238±124	0.01
Number of Rod Element	798±62	987±76	0.06	2588±278	3403±215	0.02
Plate Element Thickness (mm)	0.183±0.002	0.179±0.001	0.04	0.188±0.001	0.185±0.001	0.06
Rod Element Diameter (mm)	0.207±0.001	0.210±0.002	0.3	0.216±0.002	0.219±0.002	0.31
PR Model Generation Time (s)	3.4±0.2	3.1±0.2	0.4	19.7±1.5	17.0±1.0	0.13

Strong correlations were found for Young’s modulus (r²= 0.86–92) and yield strength (r²= 0.83–0.90) between voxel model-based and PR model-based predictions at both the radius and tibia. Plate and rod μFE analysis revealed that trabecular bone elastic modulus and yield strength were lower in women with fractures at both sites (Figure 5 and Table 3). Young’s modulus and yield strength were 60% and 58% lower (p<0.01) at the distal radius, and 37% and 39% lower at the tibia, respectively, in fracture subjects compared to controls. Moreover, these mechanical measurements remained significantly lower in fracture subjects at both sites after adjustment for aBMD T-score at the ultradistal radius or total hip.

Figure 5.

Comparison of Young’s modulus and yield strength predicted by voxel-based model and PR model at distal radius (A–C) and distal tibia (D–E). Effective tissue modulus 10.4 GPa, and 39.6 GPa were used for the HR-pQCT-based voxel model and PR model, respectively. Strong correlations were found for Young’s modulus and yield strength predicted by voxel-based and PR model. Significant difference in mechanical properties was shown between fracture group and control group by FE analysis using HR-pQCT-based PR model.

Logistic Regression Analyses

Except by tibial total vBMD, discrimination of fracture status by DXA, HR-pQCT density measurements, and PR model μFEA parameters was not statistically different (AUC: 0.55–0.62 for DXA T-score, 0.69–0.73 for HR-pQCT density and PR model measures, Table 3). Thus, despite the highly significant between-groups differences, no single trabecular mechanical measurement by the HR-pQCT-based PR model demonstrated adequate sensitivity or specificity by ROC analysis (AUC >0.75) for fracture status classification. However, when trabecular vBMD was combined with a PR model measure, such as yield strength, the prediction of fracture status was significantly improved for the distal radius. For example, a multivariable model that included radial trabecular vBMD and yield strength by PR model increased AUC to 0.75 (Table 5). In contrast, prediction by the tibial total vBMD alone was significant (AUC = 0.77) while combination of tibial trabecular vBMD and mechanical measures did not improve the prediction at the tibia (Table 5).

Table 5.

Area under curve (AUC) of multivariable ROC analysis by including one parameter from density measurements and another parameter from mechanical measurements for each skeletal site.

AUC by including a density and a mechanical measurement	Distal Radius		Distal Tibia
	Young’s Modulus	Yield Strength	Young’s Modulus	Yield Strength
Total Bone Density	0.76	0.77	0.79	0.79
Trabecular Bone Density	0.75	0.75	0.71	0.72

Discussion

In this study, a specimen-specific (subject-specific) plate and rod microstructural model of human trabecular bone based on μCT and HR-pQCT images was interfaced with a μFE analysis software to determine the nonlinear mechanical properties of trabecular bone. The strong correlations found for the predicted apparent Young’s modulus and yield strength between the HR-pQCT-based PR models and the gold standard, μCT-based voxel models, demonstrated the excellent prediction power of the HR-pQCT PR model for assessing mechanical competence of trabecular bone in clinical patients. Moreover, tremendous reductions in element number and processing time were achieved by using the PR model, making the bed-side assessment possible. In our previous study, we demonstrated that microstructure and mechanical competence of peripheral skeletal sites reflects that of central skeletal sites (53). Together with the strong and positive results from the cadaveric validation study of the PR μFE model (34), it led to our first attempt of using the PR μFE predictions based on clinical HR-pQCT images of the distal radius and tibia to discriminate clinical subjects with and without a previous history of vertebral fracture. Not only did the PR model predictions detect a significant reduction in apparent Young’s modulus and yield strength at both the radius and tibia in subjects with a history of fracture, the difference remained significant after adjustment for aBMD T-score by DXA.

Unlike the previously described beam model (54–56) in which trabecular bone structure was simulated as connected rods, the plate and rod model fully appreciated trabecular bone structure as a combination of plate-like and rod-like structure. Our previous studies suggest that plate-like trabecular structure plays a far more important role in determining the mechanical competence of human trabecular bone (27,33,57,58). Therefore, the modeling strategy of including the trabecular plate as a major element type is critical for accurate assessment of mechanical parameters of trabecular bone with a broad range of bone volume fractions from severely osteoporotic to healthy. The feasibility of the PR modeling strategy was tested in our recent studies in both idealized structure (59) and high-resolution μCT images of human trabecular bone (34) and there was excellent agreement between model predictions and mechanical testing results. Independent from our work, a different approach was proposed by Vanderoost et al. to simplify the voxel FE model to a combination of shell and beam elements and linear elastic analysis was implemented in their models for assessing apparent Young’s modulus (60). Compared to Vanderoost et al., a far greater reduction in element number and CPU time was achieved by the modeling technique in the current study due to the different strategy of meshing plate-like trabeculae. For example, the CPU time reduction is more than 1000-fold by our model compared to less than 50-fold reduction in Vanderoost et al. (60). Moreover, to our knowledge, our study is the first in which the PR modeling technique was integrated with HR-pQCT imaging technology for clinical assessment of trabecular bone strength.

Consistent with studies reported by us and others (17,21–24,42), vBMD of the radius and tibia were lower in subjects with a history of vertebral fractures. Due to the tremendous CPU time involved with nonlinear FEA, surrogate measurements of bone strength by linear FEA were often used. Although highly correlated with linear mechanical properties, nonlinear properties of trabecular bone, such as yield strength, are more closely related to fracture resistance of bone. In this study, we extended our findings of the reduction in linear elastic properties of trabecular bone in postmenopausal fragility fracture; by nonlinear FEA of PR model we found that postmenopausal vertebral fractures were associated with a marked reduction in yield strength of radial and tibial trabecular bone. The composition of PR model elements of women with fractures and their non-fracture peers explained the significant differences in the model prediction outcomes. Lower BV/TV and yield strength in women with fractures were associated with fewer plate and rod elements and a reduced percentage of plate elements over all elements. With lower strength at the radius and tibia, these postmenopausal women who had experienced previous vertebral fragility fracture also had fractures at the peripheral skeletal sites. Indeed, 37% of the vertebral fracture subjects who enrolled in the current study also sustained one or more fractures at peripheral sites.

In contrast to the major differences between fractured and non-fractured women detected by HR-pQCT and PR model, by DXA no significant differences were detected at any site. The AUC for HR-pQCT bone density and PR model mechanical measurements (0.69–0.73) were higher than those for DXA (0.55–0.62); however, except for the total vBMD at the tibia, none achieved sufficient sensitivity or specificity for fracture discrimination (AUC>0.75). At the distal radius, any combination of a vBMD measurement and PR model measurement resulted in a significant improvement in AUC (>0.75) than any of these measurements alone. Although many factors are involved with fracture risk, effective prediction of previous vertebral fracture status was possible by accounting for radial bone density and strength. Prospective studies with larger cohorts will be needed to evaluate further the potential of these measurements for prediction of future fractures. Additionally, by combining tibial trabecular vBMD and yield strength, no significant improvement was achieved. In contrast, the total vBMD, which was an integrated density measurement of both cortical and trabecular bone, alone provided sufficient power for discriminating vertebral fracture status. It also suggested that the deterioration in cortical bone compartment at the tibia, which was reflected by total vBMD, might be one of the major factors that effectively discriminate vertebral fracture status (22).

There are several limitations associated with this study. To adjust the mean apparent mechanical properties of HR-pQCT-based PR model to be compatible with that of the μCT-based voxel model, linear correction factors were calculated for the PR model and applied to the trabecular tissue modulus. After the adjustment, mean apparent modulus and strength predictions did not differ between the three model types. However, the adjusted tissue moduli differed significantly among three FE models, ranging from 10 GPa to 40 GPa. Previous studies have used a variety of mechanical testing methods to assess bone tissue mechanical properties. Reported values of bone tissue elastic modulus are highly variable by different investigations, ranging from 3 to 20 GPa (51,61–65). In the current study, the tissue modulus of the μCT-based voxel model (16.6 GPa) was back-calculated to match the apparent elastic modulus from mechanical testing results. The derived effective tissue modulus was in the range of reported values by earlier studies that used a similar approach (51,64). The effective tissue moduli of HR-pQCT voxel and PR models were derived by direct comparison with the μCT-based voxel model prediction. A lower tissue modulus (10.4 GPa) of HR-pQCT voxel model was derived to compensate the overestimation of bone volume due to the partial volume effect associated with its large voxel size. On the other hand, the effective tissue modulus of HR-pQCT PR model (39.6 GPa) was much higher than those of the voxel models and those reported by mechanical testing. This is due to the current limitations of the PR model. First, to reduce the model size and complexity, we implemented coarse meshes for trabecular plates. Moreover, the direct connection between plate and rod elements may induce an underestimation of the bone volume at these junctions. Subsequently the underestimation of bone volume in the PR model caused a much softer mechanical behavior than that of the gold standard μCT-based voxel model. Indeed, PR model behaves much softer than voxel models, especially in the nonlinear loading regime, as reflected by a trend of underestimation in the yield strength prediction even with a prior adjusted tissue modulus by linear voxel models (Table 1). With additional samples lower yield strength of HRpQCT PR model than the other methods might have been detected. In our future studies, we will address the underestimation of bone volume of the PR model possibly by adding the plate to rod junction as a third element type. Nevertheless, the current linearly adjusted predictions by PR model matched well with those by the μCT-based voxel model and demonstrated sufficient power to discriminate between postmenopausal women with and without prior vertebral fractures. In this study, we did not examine the relationship between the HR-pQCT-based PR predictions and experimentally determined mechanical properties, which is another limitation of the current study. However, a more extensive study from our laboratory compared the μCT image-based PR model, μCT image-based voxel model, and mechanical testing outcomes (34). Moreover, studies by us and others showed that the elastic modulus and yield strength derived from FE models is highly correlated with those from mechanical testing (8,25,66).

In this study, for the first time, the clinical potential of a patient-specific plate and rod modeling technique was evaluated in the context of discriminating vertebral fracture status in postmenopausal women. The strong correlation between the mechanical properties determined by HR-pQCT-based PR models and voxel models demonstrated its excellent predictive power for assessing bone strength. Moreover, only seconds of CPU time of a desktop computer were requested for PR model construction and nonlinear FEA analysis. Although additional work is required to implement the cortical compartment from the newest clinical high-resolution imaging tool, the novel PR model shows promise as an important clinical method for direct and real-time assessment of biomechanical functions of the human peripheral skeleton. Furthermore, HR-pQCT-based PR model indicated significant lower modulus and yield strength at both the radius and tibia in women with a history of vertebral fractures, suggesting this accurate and efficient model also has promise to become a clinical tool for assessing vertebral fracture risk.