A Two-Step Penalized Regression Method with Networked Predictors

Abstract

Penalized regression incorporating prior dependency structure of predictors can be effective in high-dimensional data analysis (Li and Li 2008). Pan, Xie and Shen (2010) proposed a penalized regression method for better outcome prediction and variable selection by smoothing parameters over a given predictor network, which can be applied to analysis of microarray data with a given gene network. In this paper, we develop two modifications to their method for further performance enhancement. First, we employ convex programming and show its improved performance over an approximate optimization algorithm implemented in their original proposal. Second, we perform bias reduction after initial variable selection through a new penalty, leading to better parameter estimates and outcome prediction. Simulations have demonstrated substantial performance improvement of the proposed modifications over the original method.

1 Introduction

Penalized regression is a powerful tool for high-dimensional data analysis, especially in situations of “large p, small n”, arising from genomic and proteomic studies. For example, taking advantage of a model’s sparsity, penalized regression with an L₁ penalty, i.e. Lasso (Tibshirani 1996), is capable of performing automatic variable selection, while elastic net (Enet) (Zou and Hastie 2005) in addition implicitly encourages highly correlated predictors to have close parameter estimates (i.e. grouping effects). However, in some applications, in addition to sparsity, there are other sources of prior knowledge. For example, in our motivating example, prediction of survival outcome of cancer patients is a focus in the analysis of microarray gene expression data, where it is known that the genes work coordinately with each other and their relationships can be described by a gene network. A source of prior knowledge is that the genes linked in a network tend to participate together in the same biological process, and their effects on a clinical outcome might be similar. To effectively utilize the prior information of this kind, we need to extend the generic penalized regression methods, such as Lasso and elastic net, to incorporate network information (Li and Li 2008, 2010; Pan et al 2010). In particular, Pan et al (2010) proposed a penalty that realizes simultaneous network-guided group variable selection and network-guided parameter smoothing (i.e. explicit grouping effects), showing its improved performance over several other methods in simulations. Although the method performs consistently well in variable selection, it suffers from biased parameter estimation. Here we propose two modifications to further improve its performance.

2 Methods

2.1 Notation and review

We first review the method of Pan et al (2010), which motivated the current study. Suppose that we are interested in modeling a continuous outcome y_i of subject i using a high-dimensional predictor vector x_i = (x_i1, …, x_ip)′. In addition, a network of the predictors is given to describe their relationships: each node in the network corresponds to a predictor; an undirected edge links two nodes, e.g. i and j, denoted as i ~ j. Our prior knowledge is that the predictors connected in the network are more similar to each other than to other unlinked nodes.

Consider a linear model:

$$y_i=x_i^{\prime }\beta +{\epsilon }_i,$$

where β = (β₁, …, β_p)′ is a vector of unknown regression coefficients to be estimated, and ε_i’s are iid noises with mean E(ε_i) = 0 and variance Var(ε_i) = σ². For parameter estimation, we minimize a penalized loss function

$$\widehat{\beta }=\widehat{\beta }(\lambda )=\text{arg }\underset{\beta }{\text{min }}L(\beta )+p_{\lambda }(\beta ),$$ (1)

where L(β) is a loss function, e.g. minus the log-likelihood, and p_λ(β) is a penalty function of β with tuning parameter λ to be determined. The squared loss is used throughout:

$$L(\beta )={\displaystyle \sum _{k=1}^n}{\left(y_k-{\displaystyle \sum _{i=1}^p}{x}_{\mathit{\text{ki}}}{\beta }_i\right)}^2.$$ (2)

Under the normality assumption on ε_i, we obtain the maximum penalized likelihood estimate (MPLE) β̂.

The most popular penalties, such as Lasso and elastic net, are generic without the use of special structures existing among the predictors. For example, if each the predictor is a gene, thne their relationships can be described by a given gene network, which might help informative in predicting an outcome. For a given predictor network, under the prior of |β_i|/w_i = |β_j |/w_j for two neighboring nodes i and j in the network, Pan et al (2010) proposed a network-based penalty:

$$p_{\lambda }(\beta )=\lambda {\displaystyle \sum _{i~j}}{\left[{\left(\frac{|{\beta }_i|}{w_i}\right)}^{\gamma }+{\left(\frac{|{\beta }_j|}{w_j}\right)}^{\gamma }\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.},$$ (3)

where γ > 1 and λ > 0 are two parameters to be specified. Note that each term of the penalty is an L_γ-norm, and is thus convex in β. As γ → ∞, the penalty becomes

$$p_{\lambda }(\beta )=\lambda {\displaystyle \sum _{i~j}}\text{max }\left(\frac{|{\beta }_i|}{w_i},\frac{|{\beta }_j|}{w_j}\right).$$ (4)

The penalty is used to achieve two goals, variable selection and grouping effects, simultaneously. Specifically, for nodes i ~ j, the penalty pushes for group variable selection (Yuan and Lin 2006) by encouraging both β̂_i = 0 and β̂_j = 0 simultaneously when β_i = β_j = 0, and realizes grouping effects in shrinking the (absolute values of) two estimates towards each other, i.e. |β̂_i|/w_i = |β̂_j |/w_j (Pan et al 2010). In particular, if γ = 2 and w_i = w_j = 1, then the above penalty reduces to the group Lasso penalty (Yuan and Lin 2006), which has been shown to be more effective for variable selection than the standard Lasso. The choice of weights w_i depends on the targeted shrinkage or smoothing of β_j ’s over the network (Pan et al 2010). A good choice motivated by the graph Laplacian is $w_i=\sqrt{d_i}$, where d_i is the degree of node i (i.e. number of edges connecting node i), as proposed by Li and Li (2008, 2010). As shown by Pan et al (2010), under a simple scenario (as to be used in our later simulations), in which node i is only connected to node j and node j may be connected to other nodes, using $w_i=\sqrt{d_i}$ will shrink |β_i| and $|{\beta }_j|/\sqrt{d_i}$ towards each other. If each node corresponds to a gene in a gene network, this choice of weights favors so-called hub genes with large degrees; it is believed that hub genes are biologically more important. Nevertheless, the choice of weights is not a settled problem. In this paper, by default we use $w_i=\sqrt{d_i}$ unless specified otherwise.

For implementation, Pan et al (2010) applied a generalized Boosted Lasso (GBL) algorithm (Zhao and Yu 2004), which was fast in constructing a solution path β̂ = β̂(λ) as a function of λ. They demonstrated the utility of the method via simulations. However, there are a few puzzles left. First, since the GBL is only an approximate algorithm in finding the MPLE, it is not clear whether a more sophisticated optimization algorithm can further improve the performance. Second, since a larger γ poses stronger grouping effects (Bondell and Reich 2008; Pan et al 2010), if the smoothness assumption implied by grouping effects indeed holds, it is expected that γ = ∞ should perform better than other smaller γ < ∞; however, the method with γ = ∞ did not consistently perform better than that with a smaller γ = 2 or γ = 8 in the simulation study of Pan et al (2010). Third, in agreement with its group variable selection, the method performed consistently well in variable selection, but its performance in outcome prediction might be less impressive. Below we propose two modifications to address the above issues.

2.2 Modification I: an alternative algorithm

The penalized estimation problem can be formulated equivalently as a constrained minimization problem:

$$\begin{array}{c}\hfill \underset{\beta }{\text{min}}{\displaystyle \sum _{k=1}^n}{\left(y_k-{\displaystyle \sum _{i=1}^p}{x}_{\mathit{\text{ki}}}{\beta }_i\right)}^2\hfill \\ \hfill s.t.{\displaystyle \sum _{i~j}}{\left[{\left(\frac{|{\beta }_i|}{w_i}\right)}^{\gamma }+{\left(\frac{|{\beta }_j|}{w_j}\right)}^{\gamma }\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.}\le C,\hfill \end{array}$$ (5)

where there is a one-to-one correspondence between the tuning parameter C and the original Lagrange multiplier λ. This is a convex programming problem because both the loss function and the constraint function are convex in β. Note that when γ = ∞, this problem reduces to a quadratic programming problem with a linear constraint

$${\displaystyle \sum _{i~j}}\text{max }\left(\frac{|{\beta }_i|}{w_i},\frac{|{\beta }_j|}{w_j}\right)\le C,$$

which, however, has its Hessian matrix singular for high-dimensional data, leading to numerical instability in the “quadprog” package of R and the “quadprog” package of Matlab. More generally, with γ ∈ (1, ∞), optimization problem (5) is not a quadratic programming problem, but it is convex. Pan et al (2010) used a GBL algorithm, which however gives only an approximate solution. Importantly, it is in general unknown how GBL performs against other more “exact” convex programming algorithms, which is our task here. Specifically, we solve the above constrained minimization problem (5) using a more popular and sophisticated CVX package (Grant et al 2010), which is an easy-to-use Matlab package for solving general convex programming problems with an approach called disciplined convex programming (DCP). DCP imposes some conventions for the user to follow, fully automating the conversion of DCPs to solvable forms while the problem structure in DCPs is exploited to improve performance.

To estimate an optimal value for tuning parameter C, we obtain the parameter estimates over a domain of candidate values of C, say C₁ ≤ C₂ ≤ ⋯ ≤ C_k, then use an independent tuning dataset (or cross-validation) to choose the Ĉ = C_i that minimizes the prediction mean squared error (PMSE) of the outcome.

2.3 Modification II: a two-step approach

As to be shown, the use of CVX improves the performance over that using GBL; in particular, the penalty with γ = ∞ works best. Hence we will focus on the case with γ = ∞. Nevertheless, while the method performs well in variable selection, its parameter estimates may be severely biased, leading to less impressive performance in prediction. The problem is likely caused by the same penalty function being used for both variable selection and grouping: as can be seen from max(|β_i|, |β_j|), in order to realize the grouping effects, the penalty shrinks the parameter estimates towards |β_i| = |β_j|, which at the same time leads to shrinking both |β_i| and |β_j| towards 0, resulting possibly severely biased parameter estimates. Hence, there is a conflict between the two goals, variable selection and grouping. For better grouping, rather than using the L_∞-norm, we propose using a fused-Lasso type penalty:

$$p_{\lambda ,\mathit{\text{FLA}}}(\beta )=\lambda {\displaystyle \sum _{i~j}}\left|\frac{|{\beta }_i|}{w_i}-\frac{|{\beta }_j|}{w_j}\right|$$

Note that p_λ,FLA differs from the fused Lasso penalty (Tibshirani et al 2005) since the former shrinks the absolute values of the (weighted) parameters, not just the values of the (weighted) parameters, towards each other. However, p_λ,FLA is not convex. As an approximation, as proposed by Li and Li (2010), we propose a penalty that depends on an initial estimate β̃:

$$p_{\lambda ,2}(\beta )=\lambda {\displaystyle \sum _{i~j}}\left|\frac{\mathit{\text{sgn}}({\tilde{\beta }}_i){\beta }_i}{w_i}-\frac{\mathit{\text{sgn}}({\tilde{\beta }}_j){\beta }_j}{w_j}\right|.$$

Since our original network-based penalty performs well for variable selection (due to its group variable selection guided by a network), we use it to obtain an initial estimate β̃. Then to improve parameter estimation and/or outcome prediction, we use p_λ,2 to realize grouping effects over a network. Specifically, our 2-step algorithm is as follows:

• Step 1. As discussed in Modification I, use p_λ and CVX to obtain an initial estimate β⁽⁰⁾ with a selected tuning parameter C. Remove all the edges with corresponding ${\beta }_i^{(0)}={\beta }_j^{(0)}=0$ from the original network to yield a new network G′. Mark all the nodes of the deleted edges as non-informative, and let S be the set of non-informative nodes. For all remaining edges i ~ j, calculate

  $${\alpha }_{\mathit{\text{ij}}}^{(0)}=\{\begin{array}{cc}1\hfill & \text{if }{\beta }_i^{(0)}{\beta }_j^{(0)}>0\hfill \\ -1\hfill & \text{otherwise}.\hfill \end{array}$$
• Step 2. For a given E, find the solution to the following problem via CVX:

  $$\begin{array}{c}\hfill \underset{\beta }{\text{min}}{\displaystyle \sum _{k=1}^n}{\left(y_k-{\displaystyle \sum _{i=1}^p}{x}_{\mathit{\text{ki}}}{\beta }_i\right)}^2\hfill \\ \hfill s.t.{\displaystyle \sum _{i~j\text{ in }G\prime }}\left|\frac{{\beta }_i}{w_i}-{\alpha }_{\mathit{\text{ij}}}^{(0)}\frac{{\beta }_j}{w_j}\right|\le E\hfill \\ \hfill {\beta }_i=0\text{ if }i\in S.\hfill \end{array}$$

In Step 2, again we use an independent tuning dataset (or cross-validation) to select the tuning parameter value E from a set of candidate values that minimizes the PMSE of the outcome. In each step, one may use either the CVX or another optimization algorithm.

3 Simulations

3.1 Simulation set-ups

As in Li and Li (2008), we used simulations to evaluate performance of various methods. The simulation set-ups were exactly the same as those in Pan et al (2010). Specifically, the simulated data were generated from a linear model with iid noises $\epsilon ~N(0,{\sigma }^2),{\sigma }^2={\displaystyle {\sum }_i}{\beta }_i^2/2$. There were nTF subnetworks in each set-up. In each subnetwork, there were one transcription factor (TF) and nTarget regulatory target genes of the TF; each TF was connected to each of its target genes, while there was no direct connection between any two target genes, between any two TFs, or between any two subnetworks. For each set-up, we considered both the “small p, small n” situation with nTF = 3 and nTarget = 10, and the “large p, small n” situation with nTF = 10 and nTarget = 10. In the “small p, small n” case we had p = 33, in the “medium p, small n” case we had p = 110, while in the “large p, small n” case we had p = 1100.

Each predictor was marginally distributed as N(0, 1). The joint distribution of each target gene and the TF was bivariate normal with correlation ρ = 0.7; conditional on the TF, the target genes were independent. In set-up 1, we considered the case satisfying the following prior assumption: ${\beta }_i/\sqrt{d_i}={\beta }_j/\sqrt{d_j}$ for any genes i ~ j, where d_i was the number of edges for gene i. Specifically for p = 33, we had

$$\beta =\left(5,\frac{5}{\sqrt{10}},\cdots ,\frac{5}{\sqrt{10}},-3,-\frac{3}{\sqrt{10}},\cdots ,-\frac{3}{\sqrt{10}},0,0,\cdots ,0\right)\prime$$

and for p = 110 or p = 1100, we had

$$\beta =\left(5,\frac{5}{\sqrt{10}},\cdots ,\frac{5}{\sqrt{10}},-5,-\frac{5}{\sqrt{10}},\cdots ,-\frac{5}{\sqrt{10}},3,\frac{3}{\sqrt{10}},\cdots ,\frac{3}{\sqrt{10}},-3,-\frac{3}{\sqrt{10}},\cdots ,-\frac{3}{\sqrt{10}},0,0,\cdots ,0\right)\prime$$

The remaining set-ups perturbed the equality of the weighted coefficients for two neighboring genes. Set-up 2 was the same as set-up 1 except that the signs of β_i’s of the first three target genes in each informative subnetwork were flipped to be opposite to those of their TFs and other genes. Set-up 3 was the same as set-up 1 except that in the second (for p = 33), or in the second and fourth (for p = 110 or 1100) subnetworks, the $\sqrt{10}$ in the target genes’ coefficients was replaced by 10, thus the used weight $w_i=\sqrt{d_i}$ was not optimal in the case. Set-up 4 was the same as set-up 3 except that the signs of the coefficients of the first three target genes in each informative subnetwork were flipped, as in set-ups 1 vs 2. Set-up 5 was similar to set-up 1 except that five out of 10 target genes of each informative TF had β_i = 0, hence the prior belief of co-appearance of a TF and its targets as all informative was not completely correct.

There were n=50, 50 and 200 cases in each training, tuning and test datasets, respectively. The training data were used to fit the model, while the tuning data were used to calculate the PMSE of the outcome for a fitted model, which was used to select the tuning parameter C or E. The test data were used to assess the predictive performance by calculating the PMSE for the outcome. In addition, we also calculated the incorrect number (q₁) of zero estimates of the non-zero β_i’s for the informative genes and the correct number (q₀) of zero estimates of the zero β_i’s for the non-informative genes. q₁ and q₀ are closely related to the numbers of true positives (TP) and false positives: if the numbers of the informative and non-informative genes are p₁ and p₀ respectively, then we have TP=p₁ −q₁ and FP=p₀ −q₀. Hence, a method performs best if it gives the smallest q₁ and largest q₀. For each set-up, 100 independent replicates were generated, from which the means, standard deviations (SDs) and sometimes medians, were calculated for each PMSE, q₁ and q₀.

We decided the candidate values of C in the following way. We first calculated

$$C_{\mathit{\text{max}}}={\displaystyle \sum _{i~j}}(|{\beta }_i^{*}|/w_i,|{\beta }_j^{*}|/w_j),$$

where β^* was the solution corresponding to C = 1000 (virtually no constraint). Then we searched 0 ≤ C ≤ C_max with step size 0.5. We used 10⁻⁶ as the cut-off point to calculate q₁ and q₀; that is, any |β̂_i| < 10⁻⁶ was treated as a zero estimate.

For the 2-step procedure, in the first step, we searched 0.5 ≤ C ≤ C_max with step size 0.5 and C_max as determined before. In the second step, we did a grid-search of 0 ≤ E ≤ 30 with step size 0.5 for the p = 33 situation and with step size 0.3 for the p = 110 situation. We have used 10⁻⁶ as the cut-off point in determining both non-informative nodes (for calculating q₁, and q₀) and non-informative edges (for edge removal).

3.2 Simulation Results: Modification I

Table 1 lists the simulation results for various methods. For comparison, in addition to the new algorithm based on CVX, we show the results from some generic penalized regression methods, including Lasso (Tibshirani 1996) and Enet (Zou and Hastie 2005), and a networkor graph-constrained penalized regression method, called Grace (Li and Li 2008), and that based on the GBL algorithm with parameter γ = 2, γ = 8 and γ = ∞, all taken from Pan et al (2010). From Table 1, we can see that in all cases, the new algorithm with γ = ∞ consistently attained the smallest PMSE values, thus giving the best predictive performance. In contrast, even the new algorithm with a smaller γ = 2 might not perform so well, while the results with γ = 8 were close to that of γ = ∞. For variable selection, the new algorithm performed similarly to the GBL, though the latter gave more sparse models. For the new algorithm with the three values of γ, the one with γ = ∞ seemed to have a slight edge in selecting more sparse models.

Table 1.

The means (SDs) of PMSE values, number of removed informative variables (q₁), and number of removed non-informative variables (q₀) from 100 simulated datasets. The minimal PMSEs for each set-up are bold-faced.

		p1 = 22, p0 = 11			p1 = 44, p0 = 66
Set-up	Methods	PMSE	q1	q0	PMSE	q1	q0
1	Lasso	54.0 (9.0)	5.2 (2.1)	6.9 (2.7)	166.6 (32.9)	20.1 (2.5)	53.9 (6.4)
	Enet	54.8 (10.3)	5.4 (2.3)	7.1 (2.7)	164.3 (29.3)	10.6 (9.2)	31.4 (24.0)
	Grace	54.6 (9.7)	5.4 (2.3)	7.1 (2.7)	154.6 (28.3)	5.0 (7.6)	15.1 (21.2)
	GBL, γ = 2	46.7 (7.6)	0.2 (0.5)	10.1 (1.2)	138.1 (32.3)	3.2 (3.7)	60.0 (5.4)
	GBL, γ = 8	43.6 (6.8)	0.0 (0.0)	10.2 (1.0)	132.0 (35.8)	3.2 (4.3)	60.0 (4.8)
	GBL, γ = ∞	46.3 (8.0)	0.1 (0.8)	9.8 (1.2)	162.9 (46.6)	7.3 (5.9)	56.6 (6.8)
	CVX, γ = 2	51.5 (8.2)	0.2 (1.0)	8.3 (2.8)	166.6 (32.9)	6.3 (4.5)	51.3 (14.9)
	CVX, γ = 8	44.0 (7.0)	0.1 (0.6)	9.5 (2.1)	132.7 (30.0)	2.2 (3.4)	56.7 (8.0)
	CVX, γ = ∞	43.0 (6.9)	0.1 (0.6)	9.5 (2.3)	125.8 (29.2)	1.2 (2.6)	57.5 (7.2)
2	Lasso	59.2 (12.7)	11.6 (3.1)	9.6 (2.1)	160.8 (39.0)	30.2 (4.0)	61.1 (4.2)
	Enet	58.2 (12.6)	12.4 (3.5)	9.8 (2.0)	161.1 (45.5)	29.0 (8.5)	57.8 (15.1)
	Grace	58.2 (12.8)	12.3 (3.3)	9.8 (2.0)	161.7 (44.7)	26.0 (11.7)	52.1 (22.3)
	GBL, γ = 2	57.2 (11.9)	2.8 (3.1)	9.0 (2.7)	161.2 (44.3)	16.8 (8.2)	61.3 (5.1)
	GBL, γ = 8	55.5 (11.4)	2.1 (3.2)	8.1 (3.2)	169.9 (57.4)	19.6 (10.1)	60.2 (7.5)
	GBL, γ = ∞	59.1 (21.6)	2.9 (4.1)	7.3 (3.4)	186.0 (67.6)	23.6 (10.0)	61.0 (7.4)
	CVX, γ = 2	53.9 (7.8)	3.3 (3.7)	7.6 (3.0)	151.3 (25.4)	18.1 (7.2)	54.4 (10.9)
	CVX, γ = 8	51.3 (7.3)	1.5 (2.8)	7.6 (3.1)	145.0 (27.0)	11.8 (7.0)	53.8 (11.2)
	CVX, γ = ∞	50.9 (7.4)	1.1 (2.6)	7.4 (3.4)	142.6 (27.6)	9.9 (6.8)	54.2 (9.2)
3	Lasso	45.4 (8.3)	6.6 (2.4)	7.1 (2.8)	115.3 (24.2)	23.2 (3.2)	56.5 (6.1)
	Enet	45.7 (8.1)	6.7 (2.5)	7.3 (2.8)	118.0 (27.8)	18.2 (9.5)	45.0 (22.2)
	Grace	45.6 (7.8)	6.7 (2.4)	7.3 (2.8)	116.5 (22.5)	11.6 (11.1)	29.6 (27.1)
	GBL, γ = 2	41.7 (7.2)	1.8 (2.4)	10.2 (1.1)	107.5 (25.9)	7.6 (5.3)	61.0 (4.4)
	GBL, γ = 8	39.9 (7.4)	1.0 (2.6)	10.2 (1.2)	107.5 (37.2)	8.8 (6.6)	61.4 (3.9)
	GBL, γ = ∞	42.6 (7.7)	2.9 (3.5)	9.9 (1.4)	129.6 (41.9)	13.2 (7.6)	59.2 (6.3)
	CVX, γ = 2	43.7 (6.5)	2.5 (3.1)	8.5 (2.4)	119.4 (21.2)	9.8 (5.0)	53.5 (12.0)
	CVX, γ = 8	38.7 (5.8)	0.6 (1.8)	9.5 (1.9)	99.8 (20.5)	4.9 (4.8)	55.7 (11.3)
	CVX, γ = ∞	37.8 (5.7)	0.3 (1.3)	9.5 (2.3)	95.3 (20.4)	3.4 (4.5)	56.5 (10.2)
4	Lasso	50.6 (11.4)	12.5 (3.7)	9.5 (2.4)	117.5 (31.6)	31.7 (3.9)	61.6 (4.2)
	Enet	49.2 (9.7)	13.4 (3.7)	9.7 (2.3)	115.8 (30.9)	31.5 (7.1)	60.5 (12.0)
	Grace	49.2 (9.9)	13.3 (3.6)	9.8 (2.3)	113.6 (28.6)	29.1 (10.0)	56.8 (18.5)
	GBL, γ = 2	50.3 (12.0)	4.7 (4.0)	8.8 (2.9)	122.4 (34.3)	18.4 (8.6)	61.9 (5.4)
	GBL, γ = 8	48.5 (10.1)	3.6 (4.1)	8.4 (3.0)	135.6 (51.2)	22.7 (11.1)	61.7 (6.1)
	GBL, γ = ∞	51.2 (18.8)	4.1 (4.5)	7.4 (3.5)	148.6 (56.1)	26.7 (10.5)	62.0 (6.3)
	CVX, γ = 2	45.6 (6.6)	4.3 (3.9)	8.2 (2.6)	111.6 (18.1)	18.5 (7.4)	54.3 (11.3)
	CVX, γ = 8	43.6 (6.4)	3.0 (3.6)	7.7 (3.0)	105.8 (19.0)	11.7 (7.2)	53.9 (12.9)
	CVX, γ = ∞	43.2 (6.4)	2.4 (3.6)	7.7 (3.2)	102.0 (20.1)	11.0 (11.6)	53.3 (12.0)
		p1 = 12, p0 = 21			p1 = 24, p0 = 86
Set-up	Methods	PMSE	q1	q0	PMSE	q1	q0
5	Lasso	38.8 (9.5)	3.1 (1.5)	15.5 (3.4)	112.7 (29.8)	11.4 (2.6)	75.5 (5.8)
	Enet	38.0 (9.7)	3.3 (1.7)	15.7 (3.5)	112.9 (29.0)	10.8 (3.8)	71.1 (17.4)
	Grace	37.6 (8.4)	3.2 (1.6)	15.7 (3.5)	111.8 (27.9)	9.4 (5.0)	61.7 (29.3)
	GBL, γ = 2	37.9 (7.4)	0.2 (0.5)	10.7 (1.8)	110.3 (28.4)	4.2 (3.1)	66.6 (5.8)
	GBL, γ = 8	38.1 (6.8)	0.1 (0.5)	10.0 (2.1)	113.3 (29.4)	5.7 (3.6)	67.1 (7.0)
	GBL, γ = ∞	40.7 (9.6)	0.5 (1.1)	9.3 (3.8)	131.1 (38.1)	7.8 (4.3)	68.2 (9.2)
	CVX, γ = 2	38.6 (5.6)	1.2 (2.3)	8.2 (2.6)	116.1 (21.6)	10.6 (6.3)	52.4 (13.2)
	CVX, γ = 8	36.0 (4.8)	0.3 (1.3)	8.8 (2.7)	103.3 (21.8)	5.2 (5.2)	52.9 (13.8)
	CVX, γ = ∞	35.7 (4.6)	0.3 (1.2)	8.8 (2.9)	99.5 (21.0)	4.1(5.0)	55.5 (8.7)

It is noted that the performance differences among the Lasso, Enet and Grace were quite small for p = 33, perhaps due to the relatively low dimension of p = 33 for a less challenging problem. However, for a higher dimension of p = 110, they performed quite differently, especially in terms of variable selection, for set-ups 1 and 3; on the other hand, their performance differences for set-ups 2 and 4 were smaller. One possible reason could be due to non-optimal choices of the tuning parameter for the grouping (ridge-type) penalty for Enet and Grace. To explore this, we doubled the search range of the tuning parameter (and also doubled the number of the grid points for the other tuning parameter for the L₁ penalty) in set-up 2 for Enet and Grace; we also increased the number of simulations from 100 to 500. The means (SDs) of PMSE, q₁ and q₀ for Enet were 161.0 (40.6), 30.1 (7.3) and 60.2 (12.4), while those for Grace were 160.8 (39.5), 27.2 (11.0) and 54.5 (20.7), showing a similar pattern as in Table 1. Furthermore, to be robust to some possibly extreme simulations, we also calculated the median PMSE, q₁ and q₀: they were 152.5, 31, 64 for Enet, and 152.0, 30 and 63 for Grace, respectively, again suggesting the same conclusion. We notice that the coefficient signs of the genes in the same subnetwork could be different in set-ups 2 and 4, which turned out to negatively influence the performance of Enet and Grace. For Enet, as shown by Theorem 1 in Zou and Hastie (2005), the difference of the estimated coefficients for any two variables tends to 0 if their correlation goes to 1; in the above set-ups, while any two connected genes had a large positive correlation, their true regression coefficients had opposite signs, which was not in agreement with the intended grouping effects of Enet. Since Grace shrinks the regression coefficients of any neighboring genes towards each other, its grouping effect is also against differing coefficient signs of neighboring genes. Finally, we note that, as shown in the simulation study of Li and Li (2010), if the neighboring genes had different coefficient signs, as the correlation among the genes increased, the performance of Enet and Grace became closer, which is in agreement with our results here.

Table 2 summarizes the performance of the various methods for parameter estimation. With either the GBL or CVX algorithm, and with any of the three values of γ, the network-based method gave biased estimates that were over-shrunk towards 0. For γ = ∞, the CVX algorithm did give less biased estimates than that of the GBL algorithm, though the CVX algorithm might not improve over the GBL for other two smaller values of γ. We also note that among the three values of γ in the new algorithm, the one with γ = ∞ appeared to give the best performance.

Table 2.

Mean, variance and MSE of regression coefficient estimate from 100 simulated datasets.

			β1 = 5			β2 = 1.58			β11 = 1.58
Set-up	p	Methods	Mean	Var	MSE	Mean	Var	MSE	Mean	Var	MSE
1	33	Lasso	6.07	4.72	5.81	1.33	1.35	1.40	1.38	1.36	1.39
		Enet	6.42	4.05	6.03	1.36	1.54	1.57	1.40	1.37	1.38
		Grace	6.43	4.03	6.02	1.36	1.53	1.56	1.39	1.36	1.38
		GBL, γ = 2	4.76	0.68	0.51	1.03	0.72	0.78	1.63	0.86	0.58
		GBL, γ = 8	4.29	0.29	0.80	1.48	0.35	0.36	1.48	0.34	0.35
		GBL, γ = ∞	3.63	0.44	2.32	1.60	0.60	0.60	1.56	0.64	0.63
		CVX, γ = 2	2.18	0.44	8.34	1.73	1.35	1.36	1.86	1.19	1.26
		CVX, γ = 8	3.71	0.34	2.00	1.57	0.50	0.50	1.58	0.49	0.49
		CVX, γ = ∞	4.08	0.44	1.28	1.52	0.37	0.37	1.53	0.38	0.38
1	110	Lasso	5.28	8.69	8.69	1.43	2.43	2.42	1.26	2.53	2.61
		Enet	3.79	4.86	6.18	1.82	1.86	1.90	1.47	1.71	1.71
		Grace	5.00	1.69	1.67	1.74	1.33	1.34	1.51	1.31	1.31
		GBL, γ = 2	3.82	1.02	2.41	1.51	1.29	1.28	1.53	1.66	1.64
		GBL, γ = 8	3.47	0.79	3.12	1.50	1.02	1.02	1.60	1.24	1.23
		GBL, γ = ∞	2.13	1.33	9.57	1.64	2.08	2.06	1.75	2.34	2.35
		CVX, γ = 2	1.22	0.53	14.81	2.03	2.67	2.85	1.88	2.40	2.47
		CVX, γ = 8	2.93	0.58	4.86	1.69	1.32	1.32	1.70	1.39	1.39
		CVX, γ = ∞	3.36	0.69	3.38	1.59	1.06	1.06	1.66	1.17	1.17
			β1 = 5			β2 = −1.58			β11 = 1.58
Set-up	p	Methods	Mean	Var	MSE	Mean	Var	MSE	Mean	Var	MSE
2	33	Lasso	3.65	2.39	4.19	−0.09	0.23	2.44	0.83	0.99	1.54
		Enet	4.36	2.14	2.53	−0.08	0.22	2.47	0.84	1.18	1.72
		Grace	4.23	2.19	2.75	−0.08	0.22	2.47	0.83	1.14	1.69
		GBL, γ = 2	2.56	1.38	7.30	−0.17	0.54	2.52	1.17	0.85	1.01
		GBL, γ = 8	2.47	1.37	7.75	−0.28	0.96	2.63	1.28	0.90	0.98
		GBL, γ = ∞	2.18	1.95	9.88	−0.43	1.07	2.38	1.44	1.15	1.16
		CVX, γ = 2	0.95	0.79	17.18	−0.17	0.64	2.62	1.66	1.49	1.48
		CVX, γ = 8	1.90	1.10	10.70	−0.24	0.69	2.48	1.48	1.17	1.17
		CVX, γ = ∞	2.14	1.19	9.37	−0.28	0.71	2.40	1.44	1.12	1.14
2	110	Lasso	2.54	4.31	10.31	0.13	0.34	3.25	0.94	1.92	2.32
		Enet	2.87	4.85	9.32	0.16	0.41	3.44	0.95	1.96	2.34
		Grace	2.88	3.97	8.43	0.16	0.43	3.45	0.93	1.72	2.13
		GBL, γ = 2	1.37	0.79	14.00	0.22	0.28	3.53	1.12	1.56	1.76
		GBL, γ = 8	1.07	0.80	16.22	0.24	0.36	3.67	1.05	1.53	1.80
		GBL, γ = ∞	0.47	0.46	20.98	0.23	0.39	3.65	1.06	2.05	2.30
		CVX, γ = 2	0.25	0.14	22.70	0.28	0.61	4.06	1.54	2.53	2.51
		CVX, γ = 8	1.02	0.56	16.40	0.31	0.59	4.16	1.45	1.96	1.96
		CVX, γ = ∞	1.25	0.76	14.82	0.32	0.61	4.22	1.37	1.74	1.79

As shown in Table 3 of Pan et al (2010), while the GBL algorithm for γ = ∞ did not always give the smallest PMSEs with the default weight $w_i=\sqrt{d_i}$, it did give the smallest PMSEs if a larger weight w_i = d_i was used, even though the simulated data were generated to favor weight $w_i=\sqrt{d_i}$. In Table 3, we present the simulation results for the new algorithm with weights w_i = d_i. We can see that with w_i = d_i, the new algorithm with γ = ∞ still performed best, consistently giving smaller PMSEs than that of the GBL algorithm and than those of the new algorithm with γ < ∞. As expected, the results of the new algorithm with γ = 8 were close to that of γ = ∞.

Table 3.

Means (SDs) of PMSE values, number of removed informative variables (q₁) and number of removed non-informative variables (q₀) with an additional L₁ penalty for only target genes (L₁ − T) or all the genes (L₁ − A), or with different weights from 100 simulated datasets. The minimal PMSEs for each set-up are boldfaced.

		p1 = 44, p0 = 66
Set-up	Methods	PMSE	q1	q0
1	GBL, γ = ∞, wi = di	114.1 (22.5)	0.1 (0.8)	55.3 (10.7)
	CVX, γ = 2, wi = di	114.6 (21.1)	0.3 (1.6)	52.8 (9.3)
	CVX, γ = 8, wi = di	102.6 (16.4)	0.1 (0.8)	48.1 (10.5)
	CVX, γ = ∞, wi = di	101.6 (16.0)	0.2 (1.1)	46.2 (11.8)
2	GBL, γ = ∞, wi = di	127.2 (24.3)	3.0 (4.9)	56.4 (8.5)
	CVX, γ = 2, wi = di	126.3 (23.2)	2.3 (4.2)	49.2 (12.1)
	CVX, γ = 8, wi = di	120.3 (20.3)	1.3 (3.2)	44.7 (12.9)
	CVX, γ = ∞, wi = di	119.7 (19.4)	1.0 (2.8)	41.9 (14.9)
3	GBL, γ = ∞, wi = di	86.2 (18.9)	0.7 (2.2)	56.7 (9.3)
	CVX, γ = 2, wi = di	84.7 (15.0)	0.4 (1.8)	52.9 (8.6)
	CVX, γ = 8, wi = di	77.4 (13.0)	0.3 (1.6)	48.0 (11.5)
	CVX, γ = ∞, wi = di	76.7 (12.6)	0.2 (1.4)	45.9 (11.9)
4	GBL, γ = ∞, wi = di	92.6 (18.5)	4.8 (6.2)	57.9 (7.2)
	CVX, γ = 2, wi = di	91.7 (16.7)	2.9 (4.4)	49.7 (11.8)
	CVX, γ = 8, wi = di	86.9 (14.9)	1.1 (3.0)	45.7 (12.0)
	CVX, γ = ∞, wi = di	86.5 (14.5)	1.1 (3.0)	43.5 (13.7)
		p1 = 24, p0 = 86
Set-up	Methods	PMSE	q1	q0
5	GBL, γ = ∞, wi = di	83.2 (15.1)	0.3 (1.1)	59.7 (8.1)
	CVX, γ = 2, wi = di	85.4 (16.5)	0.7 (2.2)	52.0 (9.3)
	CVX, γ = 8, wi = di	79.4 (13.6)	0.1 (0.7)	47.6 (11.0)
	CVX, γ = ∞, wi = di	79.2 (13.4)	0.1 (0.8)	45.2 (11.8)

3.3 Simulation Results: Modification II

As shown earlier, although the new algorithm with γ = ∞ performed better than the other methods, it still gave possibly severely downward biased estimates. Table 4 compares the results between the one-step (i.e. with only Step 1) and the 2-step procedures, both with γ = ∞. To facilitate comparison, we also included a two-step procedure of Li and Li (2010), called adaptive Grace (aGrace): in the first step, depending on whether p < n, the ordinary least squares or Enet was used to obtain a set of initial estimates; in the second step, the initial estimates were used to determine the signs of the regression coefficients in the ridge penalty of Grace.

Table 4.

Means (SDs) [medians] of PMSEs, number of removed informative variables (q₁) and number of removed non-informative variables (q₀) for 100 simulated datasets. The minimal PMSEs are boldfaced.

Set-up	Dim	Methods	PMSE	q1	q0
1	p1 = 22	aGrace	48.1 (8.4) [47.0]	4.0 (2.4) [4.0]	6.7 (2.8) [7.0]
	p0 = 11	1-step	43.0 (6.9) [42.3]	0.1 (0.6) [0.0]	9.5 (2.3) [10.0]
		2-step	37.6 (5.4) [36.9]	0.1 (0.6) [0.0]	10.2 (2.3) [11.0]
1	p1 = 44	aGrace	103.5 (22.6) [97.4]	3.7 (6.4) [0.0]	30.4 (19.4) [30.0]
	p0 = 66	1-step	125.8 (29.2) [121.3]	1.2 (2.6) [0.0]	57.5 (7.2) [60.0]
		2-step	87.9 (18.7) [82.5]	1.3 (2.8) [0.0]	62.2 (5.4) [64.0]
1	p1 = 44	aGrace	209.5 (68.0) [195.1]	22.0 (8.8) [24.0]	972.7 (137.5) [1022.5]
	p0 = 1056	1-step	174.6 (62.8) [159.4]	1.0 (3.1) [0.0]	752.7 (460.1) [1026.5]
		2-step	136.0 (83.4) [92.6]	1.0 (3.1) [0.0]	761.0 (465.3) [1026.5]
2	p1 = 22	aGrace	49.0 (7.2) [48.3]	4.4 (3.7) [4.0]	5.5 (3.0) [5.5]
	p0 = 11	1-step	50.9 (7.3) [50.2]	1.1 (2.6) [0.0]	7.4 (3.4) [8.0]
		2-step	47.2 (7.6) [46.5]	1.2 (2.6) [0.0]	8.4 (3.7) [10.0]
2	p1 = 44	aGrace	121.6 (24.2) [115.8]	7.0 (9.3) [2.0]	30.2 (18.8) [31.0]
	p0 = 66	1-step	142.6 (27.6) [138.2]	9.9 (6.8) [8.0]	54.2 (9.2) [56.0]
		2-step	129.4 (28.2) [123.4]	10.7 (7.3) [9.0]	59.1 (8.7) [61.5]
2	p1 = 44	aGrace	182.3 (35.9) [178.5]	23.5 (11.8) [28.0]	916.5 (185.8) [1010.5]
	p0 = 1056	1-step	194.8 (40.9) [189.4]	6.6 (8.9) [0.0]	578.9 (515.8) [1015.0]
		2-step	186.5 (60.0) [171.7]	6.7 (9.1) [0.0]	583.4 (519.8) [1026.0]
3	p1 = 22	aGrace	40.4 (6.4) [39.3]	4.9 (2.8) [5.0]	6.5 (3.1) [7.0]
	p0 = 11	1-step	37.8 (5.7) [37.1]	0.3 (1.3) [0.0]	9.5 (2.3) [10.0]
		2-step	33.6 (4.8) [33.0]	0.3 (1.4) [0.0]	10.1 (2.3) [11.0]
3	p1 = 44	aGrace	81.7 (17.0) [80.1]	6.7 (8.7) [3.0]	33.6 (19.1) [35.0]
	p0 = 66	1-step	95.3 (20.4) [92.8]	3.4 (4.5) [0.0]	56.5 (10.2) [59.0]
		2-step	71.3 (14.8) [68.4]	3.6 (4.7) [0.0]	60.7 (9.9) [63.0]
3	p1 = 44	aGrace	143.7 (42.8) [140.0]	25.9 (6.4) [26.5]	1020.3 (24.6) [1022.5]
	p0 = 1056	1-step	128.5 (36.0) [122.0]	2.6 (4.6) [0.0]	702.2 (484.1) [1027.0]
		2-step	106.8 (53.5) [85.3]	2.6 (4.6) [0.0]	708.8 (488.7) [1039.0]
4	p1 = 22	aGrace	41.5 (6.0) [40.8]	5.3 (3.8) [5.0]	5.6 (3.1) [6.0]
	p0 = 11	1-step	43.2 (6.4) [42.7]	2.4 (3.6) [0.0]	7.7 (3.2) [9.0]
		2-step	40.1 (7.0) [39.1]	2.6 (3.7) [0.0]	8.7 (3.4) [10.0]
4	p1 = 44	aGrace	89.7 (15.5) [86.4]	9.2 (10.3) [6.0]	32.1 (18.7) [33.5]
	p0 = 66	1-step	102.0 (20.1) [100.2]	11.0 (11.6) [9.0]	53.3 (12.0) [56.0]
		2-step	92.1 (19.4) [89.5]	11.8 (12.4) [10.0]	57.5 (12.3) [61.0]
4	p1 = 44	aGrace	129.7 (26.1) [126.3]	23.7 (12.5) [29.0]	890.1 (226.0) [1017.5]
	p0 = 1056	1-step	139.3 (28.2) [136.6]	6.9 (8.6) [0.0]	568.3 (516.5) [1012.0]
		2-step	132.4 (39.5) [126.1]	6.9 (8.6) [0.0]	572.8 (520.8) [1024.0]
5	p1 = 12	aGrace	34.9 (5.1) [34.8]	6.2 (3.5) [6.0]	6.9 (3.0) [7.0]
	p0 = 21	1-step	35.7 (4.6) [35.5]	0.3 (1.2) [0.0]	8.8 (2.9) [10.0]
		2-step	33.7 (4.7) [32.9]	0.3 (1.3) [0.0]	9.5 (2.9) [11.0]
5	p1 = 24	aGrace	85.3 (15.6) [84.2]	8.8 (9.6) [5.5]	36.5 (18.0) [40.0]
	p0 = 86	1-step	99.5 (21.0) [96.4]	4.1 (5.0) [0.0]	55.5 (8.7) [58.0]
		2-step	80.2 (16.1) [77.3]	4.5 (5.4) [0.0]	60.3 (8.2) [63.0]
5	p1 = 24	aGrace	139.2 (38.4) [130.5]	24.9 (9.6) [29.0]	970.2 (133.0) [1021.0]
	p0 = 1076	1-step	137.2 (41.2) [129.6]	3.5 (6.0) [0.0]	741.2 (464.6) [1022.0]
		2-step	111.8 (47.0) [97.2]	3.6 (6.1) [0.0]	749.6 (469.9) [1038.0]

In all situations, the new two-step procedure was better than the one-step procedure with smaller PMSEs for test data, though they performed similarly in variable selection. For outcome prediction, in set-ups 1, 3 and 5, our 2-step procedure seemed to perform better than aGrace, though their performance differences in the other two set-ups were in general small. For variable selection, our two-step procedure seemed to give a larger true positive number (i.e. smaller q₁) while maintaining a slightly smaller or comparable false positive number (i.e. slightly larger or comparable q₀).

Table 5 provides an explanation: the 2-step procedure gave the estimates much less biased than those obtained from only Step 1. In set-up 1, the improvement was particularly striking: the estimates from the new two-step procedure were nearly unbiased. In set-up 2, the estimates from the 2-step procedure were still biased, but only to a much lesser degree than that of the one-step procedures with either the GBL or CVX. Between our 2-step procedure and aGrace, their parameter means tended to be close, though thsoe from aGrace might have larger variances.

Table 5.

Mean, variance and MSE of regression coefficient estimate from 100 simulated datasets.

			β1 = 5			β2 = 1.58			β11 = 1.58
Set-up	p	Methods	Mean	Var	MSE	Mean	Var	MSE	Mean	Var	MSE
1	33	aGrace	5.28	6.92	7.00	1.36	1.08	1.13	1.48	0.74	0.75
		1-step	4.08	0.44	1.28	1.52	0.37	0.37	1.53	0.38	0.38
		2-step	5.01	0.23	0.23	1.51	0.18	0.18	1.63	0.14	0.14
1	110	aGrace	4.94	0.90	0.90	1.55	0.52	0.52	1.45	0.50	0.52
		1-step	3.36	0.69	3.38	1.59	1.06	1.06	1.66	1.17	1.17
		2-step	5.02	0.32	0.32	1.50	0.36	0.37	1.56	0.20	0.20
1	1100	aGrace	5.77	7.51	8.10	0.98	1.90	2.26	0.99	1.25	1.60
		1-step	3.26	0.88	3.91	1.28	0.79	0.88	1.29	0.48	0.56
		2-step	4.46	1.00	1.29	1.41	0.10	0.13	1.41	0.10	0.13
			β1 = 5			β2 = −1.58			β11 = 1.58
Set-up	p	Methods	Mean	Var	MSE	Mean	Var	MSE	Mean	Var	MSE
2	33	aGrace	3.40	3.65	6.21	−0.51	0.77	1.94	1.30	0.67	0.75
		1-step	2.14	1.19	9.37	−0.28	0.71	2.40	1.44	1.12	1.14
		2-step	4.06	1.90	2.61	−0.65	1.82	2.69	1.36	0.41	0.46
2	110	aGrace	3.19	1.10	4.38	0.13	0.67	3.59	1.02	0.53	0.85
		1-step	1.25	0.76	14.82	0.32	0.61	4.22	1.37	1.74	1.79
		2-step	3.01	1.93	5.89	0.31	1.08	4.65	1.11	0.61	0.83
2	1100	aGrace	2.55	2.53	8.53	0.10	0.31	3.13	0.71	0.61	1.37
		1-step	1.04	0.55	16.23	0.33	0.14	3.79	0.70	0.58	1.35
		2-step	2.02	1.06	9.94	0.51	0.32	4.69	0.68	0.17	0.98

4 Example

We applied the methods to a microarray gene expression dataset (Horvath et al 2006). The goal was to predict the log survival time (in years) of glioblastoma patients using their gene expression levels. As analyzed in Pan et al (2010), we took the data from one study with the sample size of n = 50 glioblastoma patients. The gene expression levels were profiled on Affymetrix HG-U133A arrays. We used a gene network of 1668 genes compiled from 33 KEGG pathways by Wei and Li (2007). After taking the common set of the genes present in both the gene network and the expression profiles, we ended up with p = 1523 genes. As in Pan et al (2010), due to the small sample size, we focused on gene selection. After removing one outlier, the dataset was randomly split into a training and a tuning datasets with n = 30 and n = 19 respectively.

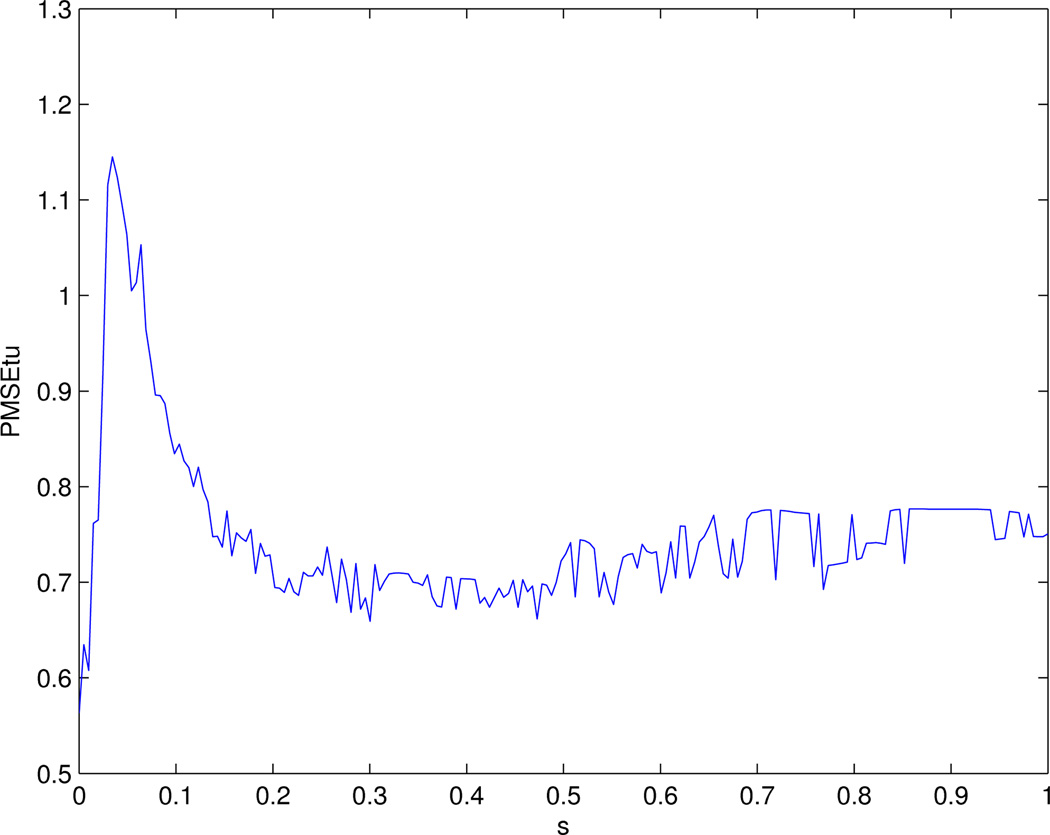
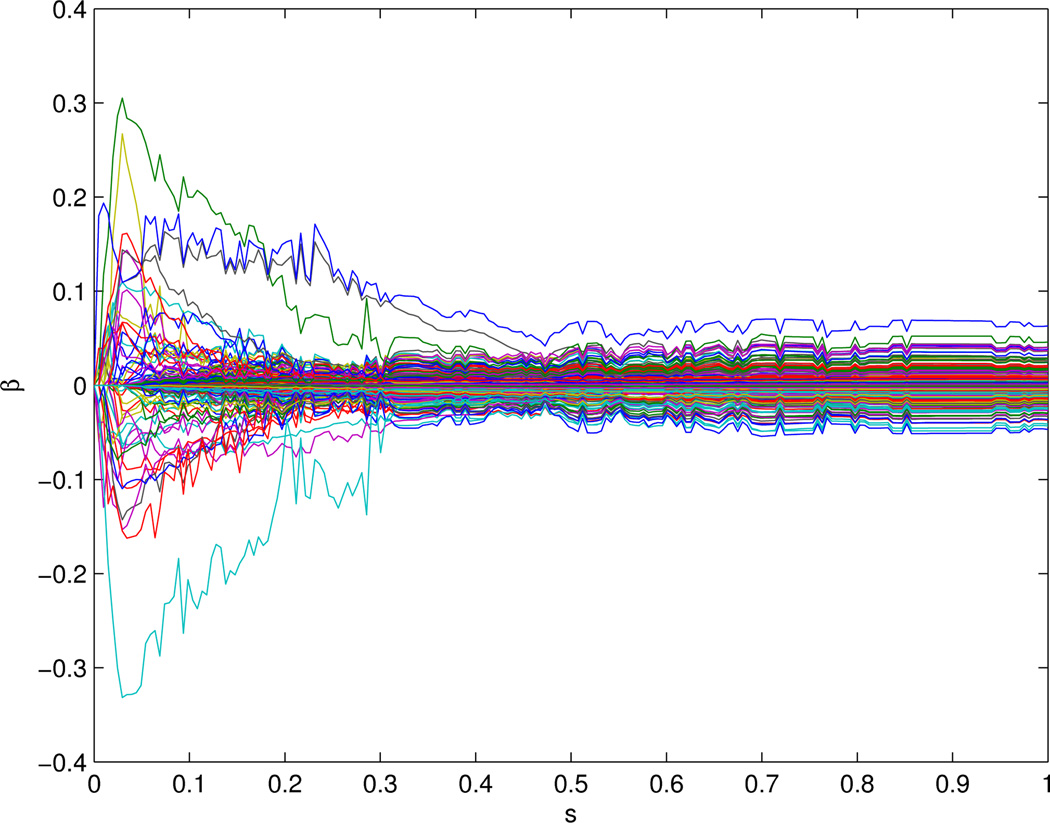
We first applied the Modification I the CVX algorithm. We searched grids of 0 ≤ C ≤ 250 with step size 1. Since the solution did not change much for C ≥ 203, we reparametrized the tuning parameter as s = C/203, 0 ≤ s ≤ 1 to facilitate comparisons with Pan et al (2010). Figure 1 shows how the PMSE of the tuning data (denoted as PMSEtu) depended on the tuning parameter s. We can see that the PMSEtu first increased, then decreased, then increased again and finally leveled off. In agreement with some previous results (Binder and Schumacher et al 2008), the global minimum was attained at s = 0, corresponding to β̂ = 0. The next minimum PMSEtu=0.66 for s ≥ 0.05 was attained around s = 0.3; since this minimum was not so different from that obtained at s = 0, we took the solution at s = 0.3 as our final estimates. Note that this solution matched the result in Pan et al (2010), in which the minimum was also attained at s = 0.3. However, compared to Figure 1 of Pan et al (2010), the solution path here (Figure 2) was different from that of Lasso and that of the network-based method with the GBL algorithm.

Figure 1.

PMSE of the tuning data for the 1-step procedure with CVX.

Figure 2.

The solution path by the 1-step procedure with CVX.

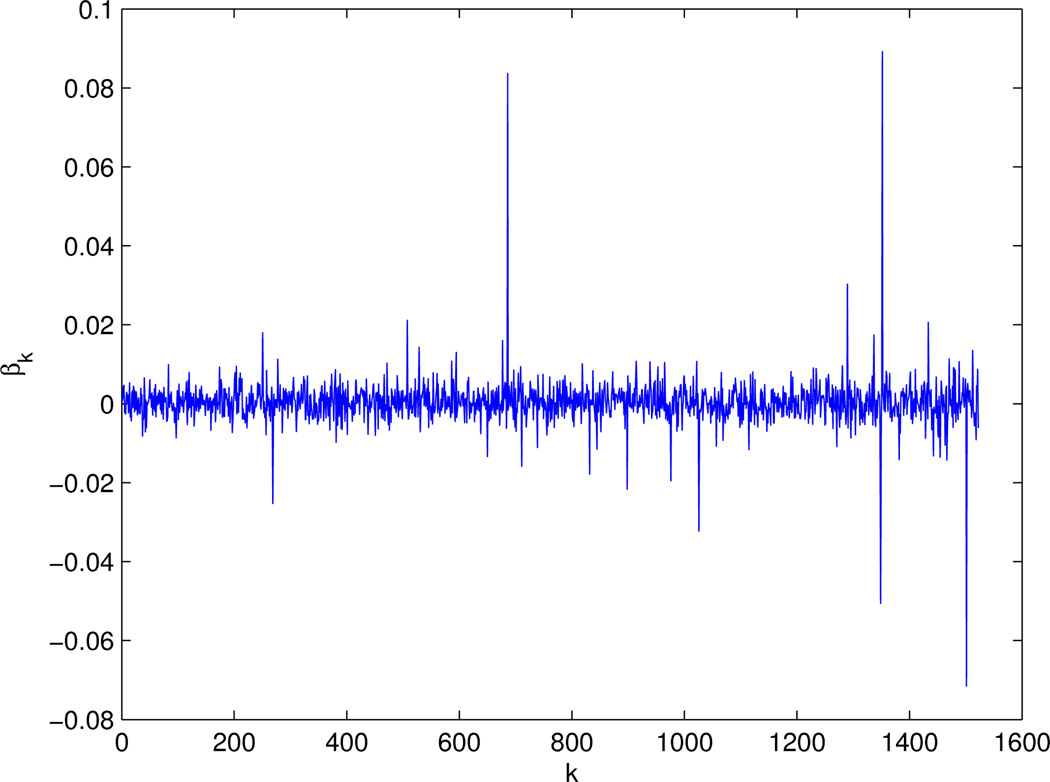
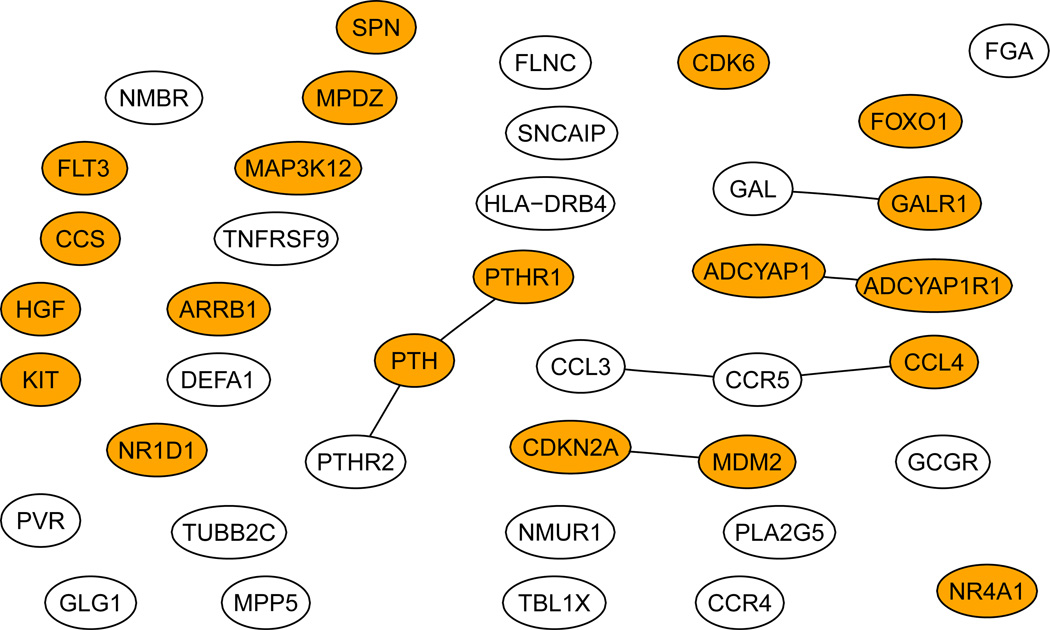
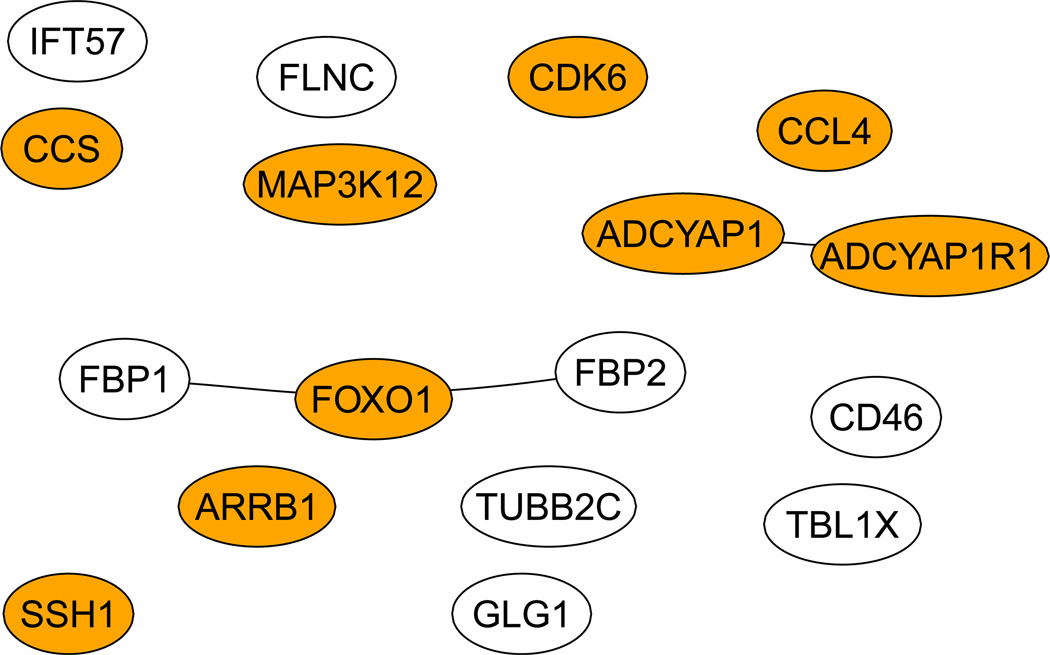
Figure 3 shows our final estimates β₍₀₎ at s = 0.3, in which most of the components were close to 0, but not exactly 0. We took ε = 10⁻² as the cut-off to determine whether an estimate was zero or not: any |β̂_i| < 10⁻² was regarded as 0. Consequently, we obtained 40 informative genes as shown in Figure 5. As a comparison, Figure 4 shows the 17 genes selected by the GBL algorithm of Pan et al (2010). Among the 40 genes selected by CVX, 12 genes were also selected by the GBL algorithm. Among the 40 genes selected here, there were 7 edges connecting 12 genes, in comparison with 3 edges connecting 5 genes by the GBL algorithm. We also searched the Cancer Gene database (Higgins et al 2007): among the 40 and 17 genes selected by the CVX and GBL algorithms, there were 20 and 9 Cancer Genes respectively.

Figure 3.

The estimates β⁽⁰⁾ from CVX.

Figure 5.

The genes selected by the CVX algorithm. Dark ones are the Cancer Genes.

Figure 4.

The genes selected by the GBL algorithm. Dark ones are the Cancer Genes.

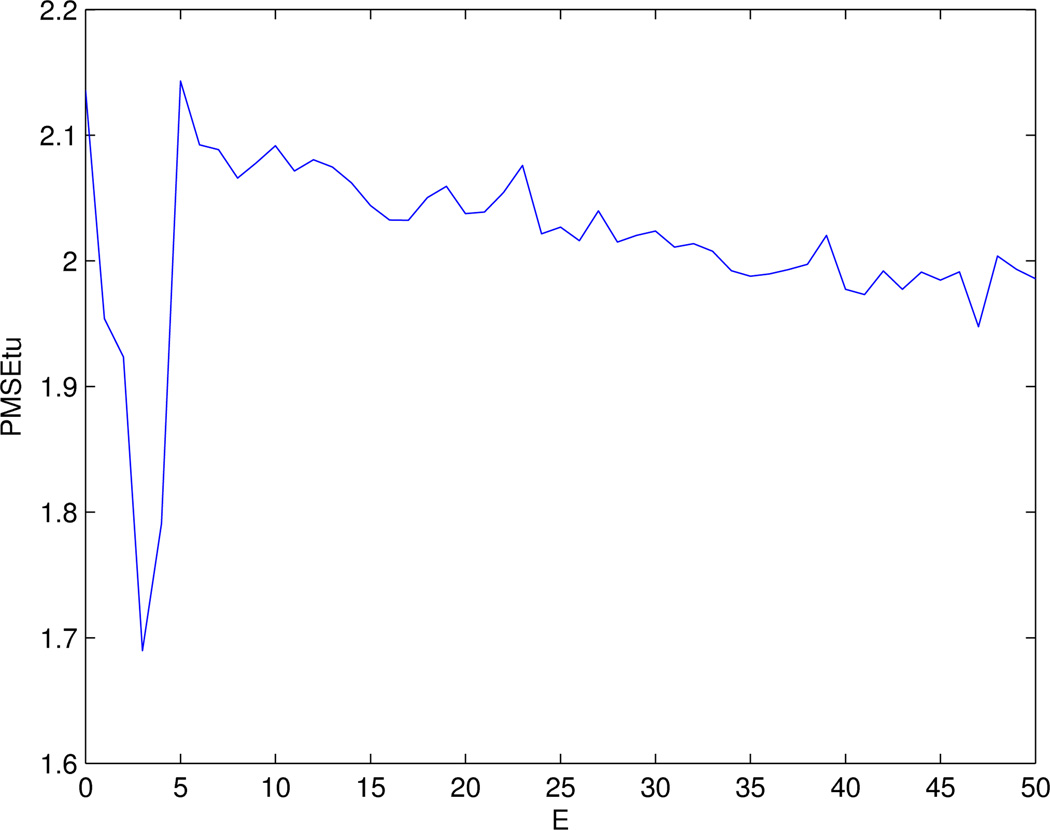
Next, we applied the 2-step procedure with the β⁽⁰⁾ as the initial estimates in Step 2. We took the following strategy to remove edges from the original network: an edge was removed if both its nodes were labeled as non-informative in β⁽⁰⁾ (i.e. zero estimates), which resulted in only 144 edges remaining in the network. These 144 edges connected 53 genes, including the 40 genes selected in Step 1. We did a grid-search of 0 ≤ E ≤ 50 with step size 1 in Step 2. Figure 6 shows the relationship between PMSEtu and E. The minimum PMSEtu=1.69 was attained at E = 3. We selected the solution at E = 3 as the final estimates, denoted as β⁽¹⁾, shown in Figure 7. Unlike β⁽⁰⁾, most components of β⁽¹⁾ were exactly zero, mainly because in Step 2 we imposed that only 53 (out of the total 1523) genes might have a nonzero estimate. Also, comparing Figure 3 and Figure 7, we can see that the absolute values of the non-zero components of β⁽¹⁾ were larger than those of β⁽⁰⁾, which could be attenuated towards 0 as observed in the simulations.

Figure 6.

PMSE of the tuning data for the 2-step procedure.

Figure 7.

The solution β⁽¹⁾ from the 2-step procedure.

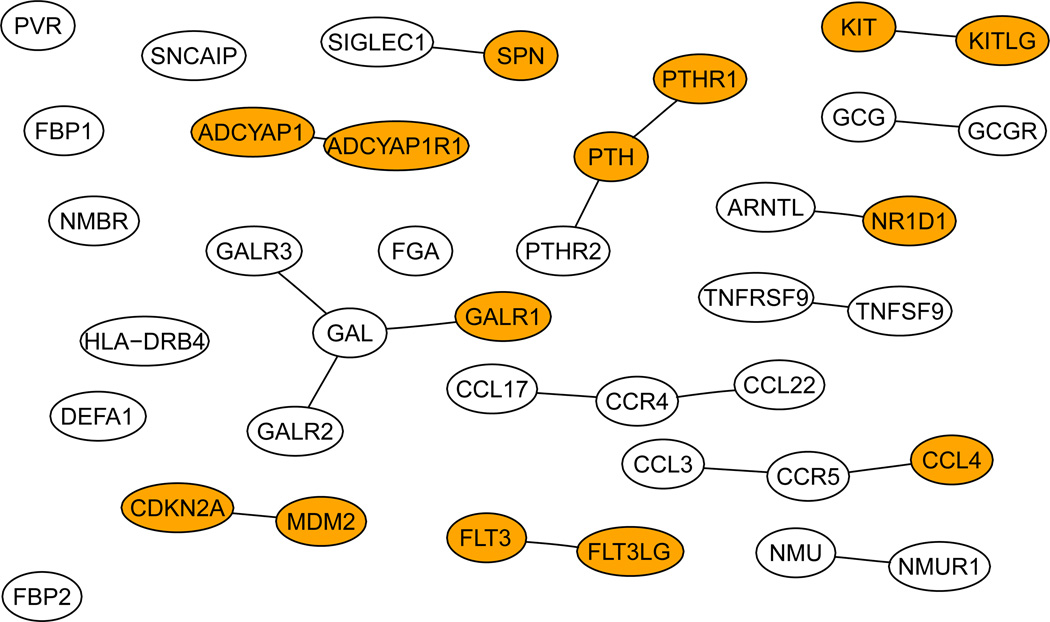
We found that 39 components of β⁽¹⁾ had an absolute value greater than 10⁻², and they were selected as informative genes, as shown in Fig 8. Among the 39 genes, only 5 genes were among the 17 genes selected by Pan et al (2010), and 14 were in the Cancer Gene database. On the other hand, it is interesting to note that there were 18 edges connecting 31 genes.

Figure 8.

The genes selected by the 2-step procedure. Dark ones are the Cancer Genes.

Since the result of any penalized regression method critically depends on the choice of its tuning parameter, especially when an independent tuning dataset (or more generally, cross-validation) is used, which is known to be unstable with a small sample size as encountered here. To investigate this issue, we ran our two-step procedure for nine more times, each with a random splitting of the whole dataset into a training and a tuning datasets. Across the 10 runs, the two-step procedure selected a total of 61 genes, 30 of which appeared only once while 17 appeared twice. Two genes, ADCYAP1 and ADCYAP1R1, included in Figure 8, were selected most frequently at eight times; two and three other genes were selected six and five times respectively. Among the 7 genes selected for 4 times, CCR4, CCL17 and CCL22 are shown in Figure 8. In summary, for a small sample size, its is confirmed that choosing tuning parameters based on independent tuning data is not stable; a promising alternative is to use some stability selection criteria (Meinshausen and Buehlmann 2010), which is beyond the scope here.

5 Discussion

There are a few interesting, mostly not new, observations from this study. First, in penalized regression, in addition to the loss and penalty functions, the computational algorithm being used to solve the optimization problem does matter. As shown here, a convex optimization algorithm (based on the CVX package) not only substantially improves the performance over an approximate (GBL) algorithm, but also gives more sensible conclusions on the relative performance of the network-based L_γ-norm penalty with various values of γ. In particular, in agreement with a theoretical analysis (Pan et al 2010), γ = ∞(i.e. L_∞-norm) maximizes grouping effects over a predictor network and thus performs best. Second, there is some conflict between the two aims of using a single penalty to achieve both (group) variable selection and grouping effects: realizing grouping effects may overly shrink the parameter estimates towards 0, resulting possibly severely biased parameter estimates and downgraded predictive performance. As a remedy, we have proposed using a fused-Lasso-type penalty as a second step for better (i.e. less biased) parameter estimates and thus improved outcome prediction. We note that the above second step is not necessary if one is only interested in variable selection, rather than in parameter estimation or outcome prediction.

The idea of bias correction or reduction following penalized regression has appeared before, such as in relaxed Lasso and thresholded Lasso (Efron et al 2004; Meinshausen 2007; Zhou 2010). In particular, Li and Li (2010) adapted the idea in penalized regression with networked predictors. Although our proposed 2-step procedure shares some similarity with that of Li and Li (2010), they differ in one key aspect: our first step uses a network-guided penalty based on the L_γ-norm for group variable selection, rather than the least squares or elastic net that does not possess the capability of group variable selection; as shown in our simulations, since our method is equipped with group variable selection, it performs better in variable selection with larger true positives and fewer false positives. The penalty adopted in the second step of our method also differs from that of Li and Li (2010): ours is an L₁-norm on the difference of two coefficients (in their estimated absolute values), while a squared L₁- norm (or ridge penalty) is used in Li and Li (2010). Hence, the parameter estimates obtained under our penalty can be exactly equal (in absolute values), while they cannot under with the other penalty. On the other hand, since the ridge penalty is smooth, it is easier to implement it computationally. As in Li and Li (2010), since our desired penalty p_λ,FLA in the second step is not convex, we approximate it with a convex penalty that depends on some initial parameter estimates. In some difficult situations, the initial estimates may not work well, which will lead to deteriorated performance of the final estimates, as shown in our simulations. It will be worthwhile to develop new algorithms for non-convex penalties like p_λ,FLA, possibly following the line of Shen et al (2011), and extend the methods to other nonlinear models or classifiers, such as network-based SVM (Zhu et al 2009).

Matlab code will be posted on our web site at http://www.biostat.umn.edu/~weip/prog.html.