Heterogeneity Even at the Speed Limit of Folding: Large-Scale Molecular Dynamics Study of a Fast-Folding Variant of the Villin Headpiece

Abstract

We have performed molecular dynamics (MD) simulations on a set of 9 unfolded conformations of the fastest-folding protein yet discovered, a variant of the villin headpiece subdomain (HP-35 NleNle). The simulations were generated using a new distributed computing method, yielding hundreds of trajectories each on a timescale comparable to the experimental folding time, despite the large (10,000-atom) size of the simulation system. This strategy eliminates the need to assume a two-state kinetic model or to build a Markov state model. The relaxation to the folded state at 300 K from the unfolded configurations (generated by simulation at 373 K) was monitored by a method intended to reflect the experimental observable (quenching of tryptophan by histidine). We also monitored the relaxation to the native state by directly comparing structural snapshots with the native state. The rate of relaxation to the native state and the number of resolvable kinetic timescales both depend upon starting structure. Moreover, starting structures with folding rates most similar to experiment show some native-like structure in the N-terminal helix (helix 1) and the phenylalanine residues constituting the hydrophobic core, suggesting that these elements may exist in the experimentally relevant unfolded state. Our large-scale simulation data reveal kinetic complexity not resolved in the experimental data. Based on these findings, we propose additional experiments to further probe the kinetics of villin folding.

Introduction

The quest to determine how proteins can fold quickly, despite a vast number of possible conformations, has driven the search for ever faster-folding proteins. This pursuit has produced many notable examples of microsecond and submicrosecond folders whose kinetics have been characterized both experimentally^{1; 2; 3; 4; 5; 6; 7; 8; 9} and computationally.^{4; 10; 11; 12; 13; 14; 15; 16; 17} These studies attempt to address such issues as the existence of a “speed limit” to folding^{3; 6; 8} and the proposition of barrierless folding.^{7; 18; 19}

Fast-folding proteins are a prime target for computational study, as the engineered folding time scales begin to overlap with time scales easily studied with molecular simulation. However, in order for simulation to capture the complexity of microsecond-scale folding kinetics, many microsecond-long simulation trajectories are desired. Simulation of a statistically significant number of protein-folding events on these timescales requires an enormous amount of computational effort. Because of computational restrictions, previous studies have limited either the number of simulations,²⁰ the timescales of the individual trajectories simulated,^{11; 13; 21; 22} or the physical detail of the models.^{10; 12; 15; 16; 17}

Recently, the submicrosecond folding of a mutant form of the chicken villin headpiece subdomain² has been described.²³ The swift folding of this protein (HP-35 NleNle) is the result of replacing lysine at sites 24 and 29 with norleucine residues. Folding was found to be remarkably fast, with a characteristic time faster than one microsecond. An accurate computational prediction of HP-35 NleNle folding could complement experimental observations in a number of ways, not least in the ability to examine folding in greater detail and under a more flexible set of conditions.

The fast folding of HP-35 NleNle opens the door to new possibilities computationally, as the experimental folding timescale found is now in reach even for individual trajectories. Recently, we have released high-performance, multiprocessor client software to our distributed computing project, Folding@home.²⁴ This innovation allows us to obtain trajectories much longer than achieved by a typical single-processor client, in the same amount of wall clock time. This increase is achieved by using a message-passing interface (MPI) version of GROMACS^{25; 26} to use multiple cores within a given machine to speed a single molecular dynamics simulation by about three times. Additionally, the processors in the subset of the Folding@home client pool utilized for such calculations are roughly three times faster than typical processors in the client pool. This leads to an approximate order-of-magnitude longer simulations than were previously possible. Thus, hundreds of microsecond-length trajectories can now be routinely obtained. With such data, protein folding kinetics may be modeled without the need to assume two-state thermodynamics^{11; 13; 21; 22} and without the construction of Markov state models (MSMs).^{27; 28; 29; 30; 31; 32}

In the past few years, discrete-state master equation or Markov chain models have had some success at modeling the long-time statistical dynamics of proteins. In these models, a number of metastable conformational states are identified. The intrastate dynamics are much faster than interstate dynamics such that the states visited by a system over time form a discrete Markov chain. Transition rates between the states are estimated from molecular dynamics simulations. If the model is shown to self-consistently recapitulate the statistical dynamics of the trajectories it was constructed from, and if it obeys the Markov property, it can be used to simulate the statistical evolution of conformational dynamics over much longer times than the lengths of the individual trajectories from which it is constructed. Spectroscopic signals can be computed directly from linear combinations of the “spectroscopic signatures” of each state, and so direct comparisons of relaxation in simulation with experimental spectra can be made.

In this paper, we describe the results from several hundred individual molecular dynamics trajectories, hundreds of which exceed 1 μs in length. Because of the length of these trajectories, we are not forced to assume two-state thermodynamics. Furthermore, because we collect dozens of trajectories from each of 9 starting configurations, we are able to show heterogeneous kinetic behavior without building computationally expensive models such as MSMs in order to address the general kinetic characteristics of the simulations. The trajectories described here each started from one of nine unfolded conformations (generated with 373-K simulations) or from the experimental crystal structure; we follow the relaxation of the unfolded structures towards nativelike structures at 300 K. The relaxation was characterized separately for trajectories generated from particular starting configurations. The results have allowed us to make several predictions as to the key structural elements necessary for the folding of HP-35 NleNle, as well as comment on the apparent low barrier to folding observed in experiments.

Results and Discussion

Simulation statistics

For this report, we generated 410 separate trajectories started from 9 unfolded conformations (shown in Figure 1; their structural characteristics are summarized in Tables 1 and 2) generated by simulation at 373 K, and 120 separate trajectories started from the experimental crystal structure. The trajectories started unfolded consist of 354 μs of simulation (average trajectory length 863 ns) and those of the folded state consist of 121 μs of simulation (average about 1 μs). In total, these data represent about 54 machine-years of wall-clock computation. Each unfolded configuration generated at least 44 individual trajectories. The lengths of trajectories from each unfolded configuration were averaged; the shortest average length was 752.6 ns. Of the trajectories generated from unfolded states, 171 reached at least 1 μs; of trajectories generated from the folded configuration, 48 reached at least 1 μs. Trajectories started from the unfolded and folded configurations reached 2 μs 16 times and 10 times, respectively. Each starting structure except one generated at least two trajectories which reached the folded state; the exception did not produce folding trajectories despite producing 46 trajectories. (We consider a structure to be “folded” according to a sixfold definition involving simultaneous presence of the three helices and the three contacts between the Phe residues; see Methods.)

Figure 1.

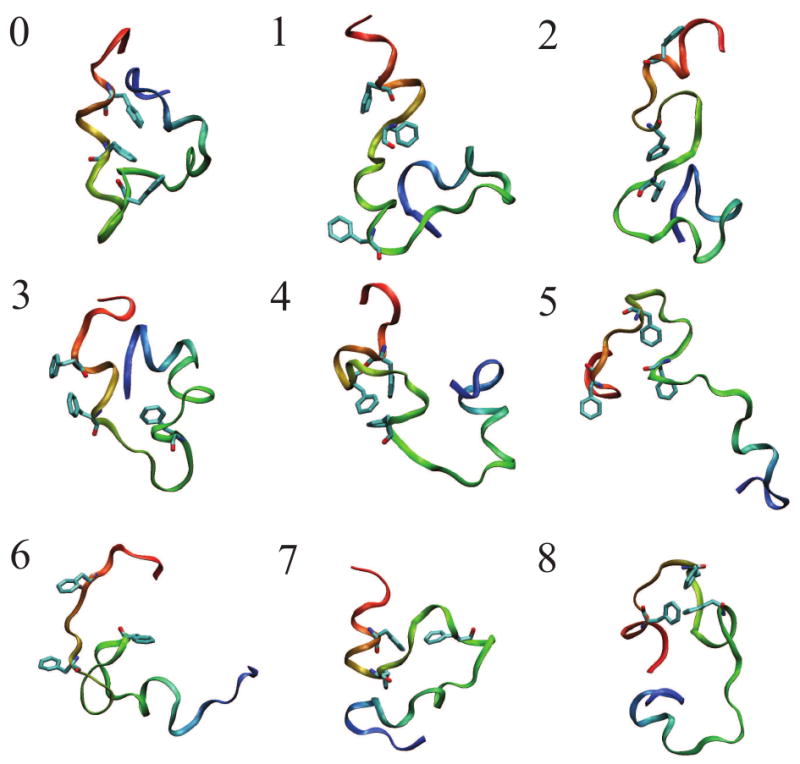
Starting structures for simulations of HP 35 NleNle, generated by thermal denaturation at 373 K. The backbone ribbon is colored from red at the N-terminus to blue at the C-terminus, and the core hydrophobic residues F6, F10, and F17 are shown in light blue licorice. Note the presence of nativelike elements in the starting structures: contact of the core hydrophobic residues in structures 4, 7, and 8, and the turns of helix 1 in structures 0, 1, 2, 4, and 7.The images were generated using VMD.⁵³

Table 1.

Selected characteristics of starting structures and simulations of the native state. ^a C-α root mean square atom displacements from the energy-minimized native structure, Å. ^b Number of native contacts. Two residues were considered to be in contact if their α-carbons were within 7 Å; two nearest neighbors along the chain were excluded. The reference native configuration was the energy-minimized crystallographic structure (see text). ^c Distances between ring centroids, Å. ^d Values from simulation of the native structure. Standard deviation is shown in parentheses.

Starting Structure	C-α rmsda	N.N.C.b	C-α rmsd helix1a	C-α rmsd helix2a	C-α rmsd helix3a	F6-F10 distancec	F6-F17 distancec	F10-F17 distancec
0	7.90	16	1.23	3.23	3.08	5.53	8.81	5.92
1	7.83	26	0.81	0.74	3.21	6.40	18.61	16.88
2	6.86	19	2.35	3.03	2.85	15.62	20.38	4.87
3	7.88	20	1.97	2.85	3.34	7.01	14.11	10.46
4	6.30	28	1.27	1.29	2.87	7.77	5.30	5.96
5	10.14	8	3.79	2.58	3.52	14.03	15.63	10.19
6	7.86	19	3.85	1.82	3.62	11.26	13.35	13.93
7	4.84	23	0.40	1.42	3.86	5.26	5.53	9.05
8	6.83	19	3.33	1.26	3.77	6.09	4.83	4.52
Simulated natived	2.54 (0.71)	47.3 (3.1)	1.07 (0.49)	0.20 (0.13)	0.46 (0.38)	5.35 (1.82)	5.49 (1.27)	5.31 (1.24)

Table 2.

Selected characteristics of the starting structures. The each structural characteristic is compared to the native state in order to determine whether the starting configuration is nativelike. A configuration is nativelike if it compares to the native state within one standard deviation of each metric in the native state simulations (see Table 1). The symbol “√” is used to indicate the presence of the structural characteristic in the starting structure; the symbol “-” indicates that it is not. ^a C-α root mean-square deviation from the energy-minimized native structure. ^b Number of native contacts. Two residues were considered to be in contact if their α-carbons lay within 7 Å; two nearest neighbors along the chain were excluded. The reference native configuration was the energy-minimized crystallographic structure (see text). ^c Distances between ring centroids.

Starting structure	C-α rmsda	N.N.C.b	C-α rmsd helix1a	C-α rmsd helix2a	C-α rmsd helix3a	F6-F10 distancec	F6-F17 distancec	F10-F17 distancec
0	-	-	√	-	-	√	-	√
1	-	-	√	-	-	√	-	-
2	-	-	-	-	-	-	-	√
3	-	-	-	-	-	√	-	-
4	-	-	√	-	-	-	√	√
5	-	-	-	-	-	-	-	-
6	-	-	-	-	-	-	-	-
7	-	-	√	-	-	√	√	-
8	-	-	-	-	-	√	√	√

Heterogeneity in folding based on starting structure

Two of the starting structures (4 and 7) folded much faster than the others. Only one other starting structure, structure 8, was observed to fold to a significant extent. Five of the remaining structures generated trajectories which briefly visited configurations deemed to be folded by our structural metric. Starting structure 1 did not generate trajectories observed to visit this state at all. In light of this, we have decided to examine the kinetics of structures 4, 7, and 8 separately from the other starting structures. We analyze the others (0, 1, 2, 3, 5, and 6) as a distinct group, henceforth denoted as Γ for brevity.

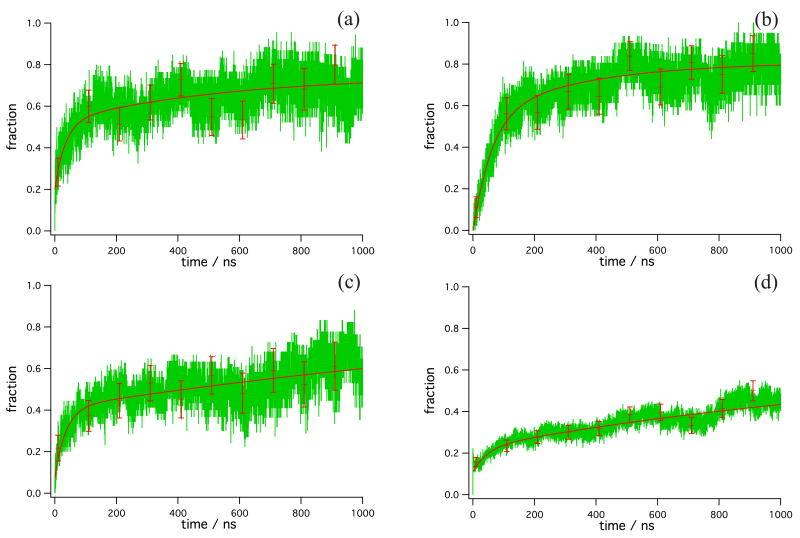
In the spirit of experiments on HP-35 NleNle, we first assessed folding by a surrogate spectroscopic method: the distance between W23 and H27 (Figures 2a-d). In each case, the kinetic traces fit better to double exponential functions than to single exponential functions (the results of the curve fits are summarized in Table 3, along with 95 % confidence intervals for the predicted rates). The rates from these fits are similar for starting structures 4 and 7; structure 4 (Figure 2a) generates trajectories for which the W-H distance relaxes with timescales of 543 and 34 ns, whereas structure 7 trajectories (Figure 2b) display W-H distance relaxation rates of 351 ns and 60 ns. On the other hand, structure 8 (Figure 2c) and the slow-folding group Γ (Figure 2d) have W-H distance relaxation rates roughly an order of magnitude longer in the long time scales, at 2,272 ns and 1,589 ns, respectively. However, the fast time scale of W-H distance relaxation for these starting structures is similar to those observed in trajectories generated from starting structures 4 and 7, at 36 ns for structure 8 and 47 ns for the structures Γ.

Figure 2.

Trp23-His27 distance relaxation (surrogate spectroscopic signal) for trajectories started in (a) structure 4, (b) structure 7, (c) structure 8, and (d) the grouped structures Γ (i.e., all other structures, 0, 1, 2, 3, 5, and 6). A configuration was considered to have a nativelike W-H distance if the W23-H27 distance was less than 7.5 Å. Green-data, solid line-exponential fits. Error bars representing the reweighted standard deviation of the data (see text) are drawn at 10 ns and every 100 ns thereafter.

Table 3.

Results of curve fitting of simulations started in various starting structures. In the “Group” column we list entries of the form “X, structural metric,” where X stands for trajectories started in structures 4, 7, 8, or the remaining structures Γ. “Folding metric” refers to the characteristics displayed in the Figures. “Structural” is folding as assessed by the requirement that all three helices and all three core phenylalanine contacts be present. “W-H dist” refers to the formation of nativelike (<7.25 Å) distances between Trp23 and His27, the spectroscopic probe used in experiments. “Total amplitude” refers to the zeroth-order term in the exponential fit, and “A” is the amplitude of each exponential. The rates k are reported with values defining the 95 % confidence intervals reported by the fitting procedure.

Group	Figure	Total amplitude	A	(k ± ki) / μs-1	τ/ns
4, W-H dist	5(a)	0.748	-0.227	1.84±0.31	543
			-0.320	29.63±2.34	34
4, structural	6(a)	0.658	-0.639	1.34±0.06	746
7, W-H dist	5(b)	0.810	-0.266	2.85±0.42	351
			-0.557	16.63±0.90	60
7, structural	6(b)	0.756	-0.487	2.40±0.16	417
			-0.309	24.31±1.71	41
8, W-H dist	5(c)	0.950	-0.541	0.44±0.27	2272
			-0.335	28.17 ± 1.72	36
8, structural	6(c)	0.578	-0.589	0.22±0.15	4618
Γ, W-H dist	5(d)	0.674	-0.450	0.63±0.11	1589
			-0.113	21.26 ± 1.58	47
Γ, structural	6(d)	0.025	-0.025	0.24±0.47	4167

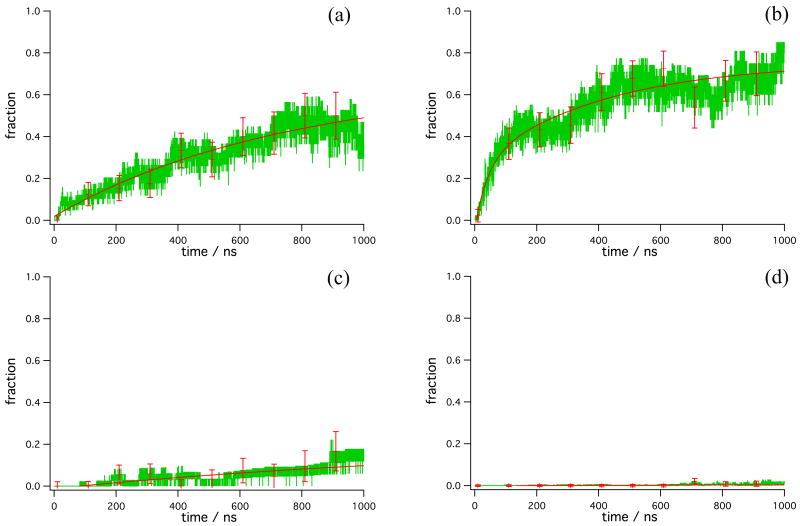
The relaxation of the starting configurations to nativelike structures is shown in Figures 3a-d. Starting structures 4 and 7 generate trajectories in which folding is fast, although the nature of the folding kinetics is different for each. Folding in trajectories started from structure 4 (Figure 3a) exhibits single rather than double exponential kinetics, with a 746-ns time scale. (Indeed, a double exponential fit of these data out to 1 μs yields two identical time scales [within error] with similar amplitudes.) On the other hand, structure 7 has the expected double exponential behavior (Figure 3b), with a long time scale of 417 ns and a short time scale of 41 ns. The two long folding time scales of structures 4 and 7 (746 ns and 417 ns, respectively) cannot be distinguished when curve fitting the trajectories from structures 4 and 7 together, suggesting that structure 7 can either relax to the native state in 46 ns, or relax to a state like which folds, like structure 4, on a submicrosecond time scale.

Figure 3.

Folding according to structural metric for trajectories started in (a) structure 4, (b) structure 7, (c) structure 8, and (d) the grouped structures Γ (i.e., all other structures, 0, 1, 2, 3, 5, and 6). A configuration was considered to be folded if it contained all three helices and all three core hydrophobic contacts to within nativelike fluctuations (see text). Green-data, solid line-exponential fits. Error bars representing the reweighted standard deviation of the data (see text) are drawn at 10 ns and every 100 ns thereafter.

The folding from structure 8 (Figure 3c) and from the group of structures Γ (Figure 3d) is dramatically different from the folding from structures 4 and 7. There were few folding events sampled in these trajectories, indicating the presence of long (multi-microsecond) folding times of 4,618 ns for structure 8 trajectories and 4,167 ns for trajectories generated by group Γ structures (Table 3) according to single exponential fits. Linear fitting has been used in the past^{21; 22} to estimate the folding rate from trajectories as much as 100 × shorter than the folding time scale, as a good first-order approximation to the exponential function is 1 – exp(–kt) ≈ kt for small kt. In the present case, the data fit better to a straight line than to single exponential functions; the linear fits indicated relaxation times of 8,102 ns for structure 8 trajectories and 17,130 ns for group Γ trajectories. For comparison, we calculated a maximum likelihood estimator (MLE) ^{11; 13} for the folding rates of structure 8 and of structures Γ. The MLE yielded a folding time of 7,365 (± 3,294) ns for structure 8, in reasonable agreement with the rate from the curve fit. However, for structures Γ, this method predicted the folding time to be 45,181 (± 11,666) ns, much slower than the ∼4 μs time scale from the curve fit. We regard the MLE as a more reliable means to estimate a folding rate than the curve fitting, but this procedure assumes a two-state (single exponential) model so was not used for the rest of the data.

The rates we report here must be considered in light of the physical limitations of the model. For example, the viscosity of TIP3P water is anomalous^{33; 34} such that rates obtained using this model may be too fast compared to experiment.³⁵ Despite this problem, the apparent double exponential relaxation of the surrogate spectroscopic signal is in qualitative agreement with experiment.

To what degree does box size influence the results?

These simulations were designed to mimic those from the landmark Duan-Kollman trajectory of the villin headpiece subdomain.²⁰ However, while the simulation box (including the protein and 3,036 water molecules) is slightly larger than that publication, we observed the presence of unphysical extended states in 3 % of the conformations in our simulations in which the protein molecule interacts with its periodic image. To assess the degree of impact of these unphysical extended states, we resolvated our starting structures in larger boxes of ∼20,000 atoms total. These new systems were equilibrated and used to generate folding trajectories as described above. This generated ∼400 trajectories of 200 ns. From these simulations and the simulations in the ∼10,000-atom system we computed the probability of reaching the folded state within the first 200 ns. We have calculated the mutual information between the probability of folding in the first 200 ns (random variable X), and either box size (random variable S) or starting configuration (random variable C). The mutual information between two random variables is a measure of the information contained in each about the other³⁶ and is defined as the difference of informational entropy H(X) of the first random variable (in this case X) and the conditional informational entropy H(X|Y) of the first random variable given the value of the second:

$$H(X)=-\sum p(x){log}_{2}p(x)$$

$$H(X|Y)=-\sum p(y)H(X|Y=y)$$

$$I(X;Y)=H(X)-H(X|Y)$$

Treating each starting state as equally likely ( $p=\frac{1}{9}$ for each) and each box size as equally likely ( $\mathit{\text{p}}=\frac{1}{2}$ for each), we compute the mutual information values as being

$$I(X;S)=0.0004\text{bits}$$

$$I(X;C)=0.3206\text{bits}$$

This is to be compared with the mutual information between folding in the first 200 ns and a hypothetical random variable K that completely determines X, such that

$$I(X;K)=H(X)-H(X|K)=H(X)=0.6085\text{bits}$$

as estimated from this data. Therefore, the starting configuration is influential in determining whether a given trajectory will fold in the first 200 ns, while the box size plays essentially no role. Kinetic plots for the 20,000-atom system, equivalent to those presented in this paper, are available in the Supplementary Materials.

Possible discrepancies between folding and surrogate spectroscopic relaxation

For starting structures 4 and 7, the rates of W-H distance relaxation and the rate of folding agree to within a factor of two. For starting structure 8 and the grouped structures Γ, the 95 % confidence intervals for W-H distance relaxation and folding overlap. While this is an overly conservative measure of statistical significance,³⁷ the error estimates that we report for our curve fits (Table 3) underestimate the error because they do not consider the time correlation structure of the data. Despite the lack of a statistically demonstrable difference, in every case the estimated W-H distance relaxation rate is faster than the corresponding folding relaxation. One possible explanation for this finding is that helix 3 (the helix containing W23 and H27) folds faster than the remainder of the protein. If this were true, the W-H distance (and corresponding experimental measurements of quenching of tryptophan fluorescence) would report on the folding of this helix alone, independently of the folding of the entire protein.

Most strikingly, in trajectories starting with structures 8 and Γ the estimated rate of W-H distance relaxation is about 2-3 × faster than the estimated rate of folding. In structure 8, the W-H distance relaxes with a time constant of 2,272 ns, but folding occurs in ∼4 μs by the structural metric. For the group Γ of slowly folding starting structures (0, 1, 2, 3, 5, and 6), the difference is even more pronounced, with a 1,589-ns relaxation time for the surrogate spectroscopic signal and a ∼4 μs time scale for folding. On the other hand, trajectories from the two fast-folding starting structures 4 and 7, the surrogate spectroscopic signal relaxes at a rate similar to the folding rate (Table 3).

There is also a very fast (<100 ns) time scale associated with folding for starting structure 7, and not merely the folding of helix 3. The folding of structure 7 on time scales faster than 100 ns indicates that experimentally observed fast time scales could correspond to folding, rather than merely a helix-coil transition.

Several experimental observables indicate that collapsed, unfolded states are not confused with the native state in these experiments. In particular, tryptophan fluorescence in equilibrium unfolding studies of HP-35 NleNle coincides thermodynamically with the fluorescence frequency shift and circular dichroism data.³⁸ Even so, we believe that the existence of unfolded states spectroscopically indistinguishable from the folded state is still a legitimate concern deserving of a more detailed treatment using both computational and experimental techniques. Building a Markov state model^{27; 28; 29; 30; 31; 32} from our simulation data may help to decide whether folding rather than helix 3 formation is fast. Experiments probing the nature of the equilibrium unfolded states would address the problem directly. We would be interested to learn the results of kinetic experiments using additional probes, or locating the same spectroscopic probe on a different portion of the protein.

On the existence of multiple long timescales in HP-35 NleNle folding

The longer time scales of multiple microseconds that we observe in the 10,000-atom simulations generated from starting structures 8 and Γ are not reported in experiments on HP-35 NleNle. Because the folding rates for structures 4 and 7 are more similar to the experimentally measured folding rate than are the folding rates for structures 8 and Γ, we surmise that experiments may be observing transitions between the native state and unfolded states similar to our structures 4 and 7, distinct from unfolded states similar to structure 8 and structures Γ. We propose that starting configurations 4 and 7 contain significant structure similar to the unfolded state observed in experiments, whereas the remaining structures do not. On the other hand, transitions between the native state and unfolded states similar to structures 8 and Γ are not observed.

What structure is present in starting configurations 4 and 7 leading them to fold more quickly than the others? Both of these structures contain helix 1, which contains some structure in the unfolded state of wild-type HP-35.^{39; 40} Structure in the unfolded state has been implicated as being conducive to fast folding in other proteins, including engrailed homeodomain.^{41; 42} In contrast to structures 4 and 7, structures 0 and 1 contain helix 1 but do not fold rapidly (indeed, structure 1 trajectories do not visit the native state at all); that structures 0 and 1 contain helix 1 but fold slowly indicate that our understanding of the importance of helix 1 is incomplete.

The characteristics of structure 8 may provide an important clue to explain fast folding in structures 4 and 7. Although structure 8 folds slowly, the number of folding trajectories it generates distinguishes it from group Γ. Structure 8 contains nativelike distances for all three core phenylalanine residues (Table 2), a characteristic lacking in the other starting structures. Still, structures 4 and 7 both contain the longest-range core contact, F6-F17, which is absent in structures 0 and 1. Indeed, this is the only one of the three core contacts that slow-folding structure 0 does not contain. In addition, the F10-F17 contact appears in structure 4, and the F6-F10 contact appears in structure 7. The phenylalanine residues of the hydrophobic core of the folded protein have been shown to be vital for the formation of the native structure of wild-type villin.⁴³ Our results indicate that these three contacts are important not only for structure but for the fast folding of this system.

Thus we propose that experiments are probing transitions between the native state and structures that contain helix 1 and the F6-F17 core contact, and probably at least one of the other core phenylalanine contacts. The 5-K laser T-jump does not significantly perturb states which are more unfolded (for example, those lacking helix 1 and with a disassembled hydrophobic core) from equilibrium so that the slow, multi-microsecond transitions between these unfolded states and the native state are not observed. Fast folding of HP-35 NleNle would then predominantly consist of folding helices 2 and 3 and completing the hydrophobic core.

In contrast, our 373 K simulations have generated a high proportion of unfolded configurations separated from the native state by multi-microsecond time scales because they do not contain helix 1 and because they lack a sufficient number or type of core hydrophobic contacts. In addition, the 373-K simulations were run at the constant volume generated by pressure equilibration at 300 K, so it is possible that high-pressure effects are contributing to additional unfolding relative to the unfolded state probed in experiments. We have generated only two configurations containing helix 1 and the F6-F17 contact and which therefore relax to the native state on submicrosecond time scales. This picture suggests further simulations and experiments designed to speed the folding of this protein, namely by generating stabilizing mutations to helix 1 and by replacing the F6-F17 contact with a more stable structure such as a disulfide link. Furthermore, we believe that folding time scales on the order of 10 μs should be detectable in appropriately designed experiments on this system.

Conclusions

In spite of rapid folding of HP-35 NleNle, we have detected a great degree of kinetic heterogeneity in these simulations. In the past, simulations with atomic detail and explicit solvent have, at best, been able to generate trajectories one-tenth the length of the timescales probed.^{11; 13; 21; 22} An early approach for understanding the kinetics in these sorts of simulations was to assume a two-state kinetic model. With short trajectories, this allowed us to make the approximation f(t) = 1 – exp[–kt] ≈ kt to estimate one rate, which supposedly dominates the kinetics at these short times. It may be tempting to suppose a two-state kinetic model for the fast folding of HP-35 NleNle from the outset, but this predetermines the kinetic behavior that one can observe. Because HP-35 NleNle folds so rapidly, and because we may now trivially obtain hundreds of trajectories longer than 1 μs, we opt for direct examination of the folding kinetics on the microsecond timescale. Observing the system this way, we note extremely fast time scales (<100 ns) for folding, which had previously been supposed to be merely helix-coil transitions.²³ There are also folding processes (and other relaxations) occurring on roughly a 1 μs time scale, consistent with the experimental report of submicrosecond folding in this protein. Last, we have observed long time scales for folding in our simulations that have not previously been detected in experiments. The presence of these long time scales not only underscores the need of simulation studies to identify the unfolded states similar to those in experiment, but also suggests a useful direction for future experiments on this system.

While we have attempted to compare our simulation results with experiment through a comparison of relaxation timescales, signal-to-noise limitations prevent us from reproducing the laser T-jump protocol directly. In principle, one could reproduce the laser-induced temperature jump protocol exactly, by equilibrating at the initial temperature and heating the solvent to the final temperature. However, the limited length and number of the trajectories we can produce from such an initial equilibrated system would generate a net change in the number of folded trajectories (upon temperature jump) on the order of, or smaller than, the stochastic fluctuations of the native population.

Finally, the issues raised here suggest that care may be needed in the interpretation of experimental data. For example, data with apparent single-exponential kinetics could conceal a complex heterogeneity in dynamics, masked by the nature of the experimental observables or the timescales examined. These matters are more naturally decomposed with simulation; however, simulation methods are still maturing and a quantitative comparison with experiment is still vital in this area. Thus, it remains clear that a tight coupling of simulation with experimental validation will be critical for discerning the complex nature of how proteins fold.

Methods

Comparison between experimental and computational conditions

In the experimental studies on HP-35 NleNle²³, a laser-induced 5-K temperature jump was applied to a solution of protein in buffer at 343 K. Then, transport between folded and unfolded states was assessed spectroscopically through the quenching of a native tryptophan (W23) by an engineered histidine residue (N27H). To enable this quenching assay, experiments were performed at low pH, so that His27 was protonated. The authors reported a remarkable 730 (±50)-ns folding time for this protein at 361 K and predicted a folding time of ∼720 ns at 300 K.

The high melting temperature of HP-35 NleNle makes laser T-jump experiments challenging at 300 K; on the other hand, this regime is trivial to simulate. In addition, the detail available from computer simulations obviates the need for spectroscopic probes, so that the folding process may be examined at neutral pH. Directly reproducing the T-jump experiment would present several challenges for simulation, the first of which is that the expected number of folding events, even in microsecond-long trajectories, is smaller than the expected fluctuations in the population of the folded state. Instead, we generated for this study unfolded structures of villin HP-35 NleNle during 2-ns simulations at 373 K. We then simulated these thermally denatured structures at 300 K in order to observe many folding events (in addition, the chosen force fields were parameterized for simulations near this temperature). We also chose not to protonate the histidine residue. Additional simulations closer to the conditions studied experimentally are in progress.

System Setup

The crystallographic structure of HP-35 NleNle²³ (PDB structure 2F4K) was used as the starting point for this study. Multiple coordinates had been given for some atoms in the structure, but the first coordinate for each atom was utilized in all cases. The pdb was converted to GROMACS^{25; 26} coordinate and topology files with the GROMACS utility pdb2gmx (version 3.3). Hydrogen atoms in the structure were ignored; new protons were added by pdb2gmx. The AMBER2003 force field,⁴⁴ ported for use with GROMACS, was used. For norleucine, most parameters were assigned in analogy to AMBER2003 parameters for lysine and leucine; previously reported values⁴⁵ were used for the charges. The structure was subjected to a preliminary energy minimization step using the steepest descents method, with 1.5 nm cutoffs for neighborlists, Coulombic interactions, and Van der Waals interactions, until achievement of a maximum force of less than 100 kJ mol^-1 nm^-1. The structure was solvated in an octahedral box of dimensions 4.240 nm × 4.969 nm × 4.662 nm with 1,306 TIP3P water molecules, bringing the total system size to 9,684 atoms. An additional energy minimization step was performed on the system after solvation.

Simulation parameters

For molecular dynamics simulations, the SHAKE⁴⁶ and SETTLE⁴⁷ algorithms were used with the default GROMACS 3.3 parameters to constrain bond lengths. Periodic boundary conditions were employed. To control temperature, protein and solvent were coupled separately to a Nosé-Hoover thermostat^{48; 49} with an oscillation period of 0.5 ps. The system was coupled to a Parrinello-Rahman barostat^{50; 51} at 1 bar, with a time constant of 10 ps, assuming a compressibility of 4.5 × 10^-5 bar^-1.

Preliminary equilibration

The solvated system was equilibrated at 300 K through 1 ns of molecular dynamics, using 2-fs time steps, with the protein coordinates frozen (i.e., not updated) and water bond lengths constrained. Initial velocities were assigned randomly from a Maxwell-Boltzmann distribution. A grid-based neighborsearch to 0.8 nm was conducted every 10 steps. The linear center-of-mass motion of the protein and solvent groups were removed every 10 steps. A cutoff at 0.8 nm was employed for both the Coulombic and Van der Waals interactions.

Starting states

The equilibrated native state was used both as the starting point of native state simulations and as the starting point of simulations at 373 K to generate thermally denatured structures. The latter were nine 10-ns simulations of 1-fs time steps, starting with the native structure, at 373 K, with velocities assigned randomly from a Maxwell-Boltzmann distribution, and constant system volume. All bond lengths were constrained. Otherwise, the parameters were as described for the 300-K equilibration described above. The final structures from these 373-K simulations were used as the starting point for folding studies (at 300 K). These structures were equilibrated at 300 K for 10 ns (using 2-fs time steps) at constant volume, with the protein coordinates fixed. During these simulations, the long-range electrostatic forces were treated with a reaction field assuming a continuum dielectric of 78, and the Van der Waals was treated with a switch from 0.7 to 0.8 nm. The neighborlist was shortened to 0.7 nm in order to improve the computational performance of the system.

The thermally denatured structures generated by simulation at 373 K are shown in Figure 1. A great deal of the native structure was lost during the 373 K simulations, although a surprising degree of nativelike structure remains in the initial structures (Tables 1 and 2). For instance, unfolded structures 0, 1, 4, and 7 had C-α RMSD measures for helix 1 consistent with the native state simulations. Two unfolded configurations, 5 and 6, contained none of the structure we assess in Tables 1 and 2. None of the unfolded structures had a C-α RMSD or a number of native contacts consistent with the folded simulations. The characteristics of the unfolded structures, compared to fluctuations observed in the native simulations, are summarized in Table 2.

Simulation of native and unfolded states

Molecular dynamics simulations at 300 K were run on an MPI-enabled version of the GROMACS molecular dynamics engine ported for the Folding@home distributed computing platform. Random initial velocities were assigned to the atoms from a Maxwell-Boltzmann distribution at 300 K. Otherwise, the parameters were as described for the second 300-K equilibration described above.

Analysis of trajectories

The apparent time scales of “folding” should depend on what observables we choose to follow. Here, we chose to follow both the evolution of a surrogate spectroscopic metric and the fraction of trajectories in the folded state. First, we generated a surrogate for the spectroscopically observable quenching of tryptophan 23 by histidine 27. (We count the N-terminal leucine as residue 1, as do Kubelka et al., in contrast with the pdb structure file counting this as residue 42.) If the distance between W23 and H27 was less than 7.25 Å (the average distance in native state simulations, plus one standard deviation), then a configuration was considered to contain this contact such that tryptophan fluorescence would be quenched.

Second, we analyzed folding by monitoring the collective relaxation of a set of structural elements to nativelike configurations. We computed the root mean-square displacement (RMSD) of each helical α-carbon in the snapshot from an energy-minimized native state structure. We also computed the distances between the three phenylalanine residues, F6, F10, and F17, which comprise the hydrophobic core in the folded structure. A structure was considered to be folded by the structural metric if it met the following criteria:

1. C-α RMSD of helix 1 less than 1.56 Å

2. C-α RMSD of helix 2 less than 0.33 Å

3. C-α RMSD of helix 3 less than 0.85 Å

4. F6-F10 ring centroid distance less than 7.17 Å

5. F6-F17 ring centroid distance less than 6.76 Å

6. F10-F17 ring centroid distance less than 6.55 Å.

The values listed in (1)-(6) are the average over native state simulations, plus one standard deviation, such that each criterion is consistent with fluctuations of the native state. The helical residues were considered to be residues 4-10 for helix 1, residues 15-19 for helix 2, and residues 23-32 for helix 3. We also followed the folding of the helices through criteria (1), (2), and (3); this data is presented in the Supplement. The criteria used here for the folded state definition differ from some of our previous studies which use C-α RMSD metrics of the entire protein.¹⁴ We chose a different set of criteria in order to capture the formation of both secondary and tertiary structure. However, the average C-α RMSD of conformations considered to be folded by the sixfold definition is about 3.4 Å, consistent not only with fluctuations of the C-α RMSD in the native state simulations (3.5 Å average, standard deviation 0.8 Å) but also with previous simulations which used nativelike values for the C-α RMSD of 3-4 Å.⁵²

To understand the dynamics in our trajectories, we determined the fraction of trajectories at each time point satisfying criteria related to the Trp-His distance or the structural metric. For example, for the structural definition of the folded state, we determined the fraction of trajectories satisfying all of criteria (1)-(6) as a function of time. The fraction of trajectories satisfying each definition was fit to single or double exponential equations using the software package Igor Pro (WaveMetrics, Inc., Lake Oswego, OR). The fitting procedure was weighted by the inverse of a reweighted standard deviation, given by:

$$s_t^2=\frac{n_t+1}{{(n_t^{\text{total}}+2)}^2}\left(1-\frac{n_t+1}{n_t^{\text{total}}+2}\right)$$

where s_t is the reweighted standard deviation at time t, n_t is the number of trajectories satisfying the relevant definition at time t, and n_t^total is the total number of trajectories reaching at least t. The software reported 95 % confidence intervals for each fitting parameter. Iterative fits were performed using a convergence criterion of Δχ² ≤ 0.001. In order to ensure that our curve fitting procedures were robust, we only fit the first microsecond of simulation data.

Supplementary Material

01. Supplementary Figure 1.

Comparison of the tryptophan 23-histidine 27 distance relaxation for system sizes of 10,000 atoms (the data presented in the manuscript) and of 20,000 atoms, started in (a) structure 4, (b) structure 7, (c) structure 8, and (d) the grouped structures Γ (i.e., all other structures, 0, 1, 2, 3, 5, and 6). The fraction of trajectories with a nativelike W-H distance is shown in green for the 10,000-atom system and in red for the 20,000-atom system.

02. Supplementary Figure 2.

Comparison of folding for system sizes of 10,000 atoms (the data presented in the manuscript) and of 20,000 atoms, started in (a) structure 4, (b) structure 7, (c) structure 8, and (d) the grouped structures Γ (i.e., all other structures, 0, 1, 2, 3, 5, and 6). The fraction folded is shown in green for the 10,000-atom system and in red for the 20,000-atom system.

03. Supplementary Figure 3.

Folding of helix 1 for trajectories started in (a) structure 8 and (b) structures 2, 3, 5, and 6. (Other starting structures had helix 1 preformed.) Helix 1 was considered to be folded in a configuration if its C-α RMSD was consistent with native state fluctuations (see text). Green-data, solid line-exponential fit. Error bars representing the reweighted standard deviation of the data (see text) are drawn at 10 ns and every 100 ns thereafter.

04. Supplementary Figure 4.

Folding of helix 2 for trajectories started in (a) structure 4, (b) structure 7, (c) structure 8, and (d) the grouped structures Γ (i.e., all other structures, 0, 1, 2, 3, 5, and 6). Helix 2 was considered to be folded in a configuration if its C-α RMSD was consistent with native state fluctuations (see text). Green-data, solid line-exponential fit. Error bars representing the reweighted standard deviation of the data (see text) are drawn at 10 ns and every 100 ns thereafter.

05. Supplementary Figure 5.

Folding of helix 3 for trajectories started in (a) structure 4, (b) structure 7, (c) structure 8, and (d) the grouped structures Γ (i.e., all other structures, 0, 1, 2, 3, 5, and 6). Helix 3 was considered to be folded if its C-α RMSD was consistent with native state fluctuations (see text). Green-fraction folded, red solid line-exponential fit. Error bars representing the reweighted standard deviation of the data (see text) are drawn at 10 ns and every 100 ns thereafter.

06. Supplementary Table 1.

Results of curve fitting helix folding of simulations started in various starting structures. In the “Group” column we list entries of the form “X, structural metric,” where X stands for trajectories started in structures 4, 7, 8, or the remaining structures Γ. The structural metrics are those described in the Table 3 caption. “Total amplitude” refers to the zeroth-order term in the exponential fit, and “A” is the amplitude of each exponential. The rates k are reported with values defining the 95 % confidence intervals reported by the fitting procedure.