Abstract
Despite the recent surge in the development of powerful modeling strategies to test questions about individual differences in stability and change over time, these methods are not currently widely used in psychopathology research. In an attempt to further the dissemination of these new methods, the authors present a pedagogical introduction to the structural equation modeling based latent trajectory model, or LTM. They review several different types of LTMs, discuss matching an optimal LTM to a given question of interest, and highlight several issues that might be particularly salient for research in psychopathology. The authors augment each section with a review of published applications of these methods in psychopathology-related research to demonstrate the implementation and interpretation of LTMs in practice.
As described in the masthead, the Journal of Abnormal Psychology is dedicated to the publication of articles that explore the correlates and determinants of abnormal behavior. Among other aspects of study, it is stated that “Each article should represent an addition to knowledge and understanding of abnormal behavior in its etiology, description, or change.” One powerful method that can be used to pursue this important goal is the collection and evaluation of longitudinal data. Longitudinal methods permit the systematic study of stability and change over time and thus can provide critically needed empirical evaluations of the course, causes, and consequences of abnormal behavior. Because of this, longitudinal design and data analysis play a critical role in many empirical studies of psychopathology.
The incorporation of longitudinal data into empirical research brings with it many advantages but also invites a host of new challenges. One challenge is the selection of an appropriate statistical method given the many options that exist for analyzing repeated measures data. Although the history of longitudinal data analysis in the social sciences can be traced back a century or more, the past decade has witnessed a particularly rapid rise in the development of new and powerful longitudinal methods. This explosion in analytical development is partly attributable to key breakthroughs in mathematical statistics and to the recent advances in high-speed computing. Taken together, there are now a wide variety of new and exciting statistical methods that are available to evaluate research questions in ways that were not previously possible. However, despite many potential advantages, there is only limited evidence that these new techniques are being widely used within the field of psychopathology.
We reviewed the past 5 years of the Journal of Abnormal Psychology and found that the majority of published articles did not incorporate longitudinal data. Of those that did, the majority primarily used more traditional analytic techniques such as fixed-effects regression and repeated measures analysis of variance (ANOVA) and multivariate analysis of variance (MANOVA). Although there were several published applications of more recently developed analytical methods, these were clearly in the minority. Often, our theoretical models do not closely correspond to more traditional statistical models, and this may limit the strength of inferences that can be drawn back to theory (Curran, 2000; Raudenbush, 2001). Furthermore, many of the new analytic techniques can be applied to exactly the same data as were used with more traditional models, thus making these methods a viable alternative strategy for existing measures and data.
Although a variety of impediments may account for the slow integration of this new generation of analytic methods into psychopathology research, one factor might be that there are not many pedagogically focused papers that explore these new methods with the explicit link to real theoretical questions evaluated with real empirical data (though we highlight several applications of these methods later). Because the study of psychopathology introduces unique data analytic challenges, pedagogical tools that are tied to the use of such methods in the study of psychopathology might be of interest to many readers of the journal and facilitate their use. Our hope is to provide such a pedagogical introduction here.
Because our motivating goal is to present an introduction to recently developed analytic methods for longitudinal data, we do not present new quantitative developments here; our article is intended to serve as a review and demonstration accompanied with recommendations for applied researchers. Further, to maintain a reasonable scope of our article, we focus only on one specific data-analytic approach, namely the structural equation modeling (SEM)-based latent trajectory model (LTM). Finally, instead of presenting a fully worked empirical example throughout the article, we have chosen to review previously published applications of LTMs in psychopathology-related research to demonstrate these various models. We chose this strategy so that interested readers may obtain more comprehensive discussions of model estimation and interpretation than would otherwise be possible. Although we highlight much of our own work for ease of presentation and reanalysis of data when needed, we reference applications of these techniques by other researchers as well. Finally, extensive empirical examples including raw data, computer code for a variety of software packages, and resulting computer output can be downloaded directly from www.unc.edu/~curran/example.html.
We open our article with a brief review of more traditional longitudinal data analytic techniques and then introduce the basic LTM. We start with the unconditional trajectory model, and we extend this to consider alternative nonlinear functional forms of growth. We then include one or more predictors of the trajectories, and we explore ways of evaluating both mediating and moderating relations. Next we present multivariate trajectory models for both single-change processes and multiple-change processes. Finally, we conclude with a discussion of several topics of particular importance to psychopathology research and finish with a summary of potential limitations and future directions.
Latent Trajectory Modeling (LTM)
There is a long and rich history in the development and application of statistical methods for analyzing repeated measures data taken over time. It is beyond the scope of our article to provide a full review of these methods, but see Menard (2002), Dwyer (1983), and Crowder and Hand (1996) for further details. The majority of these techniques are related to applications of the general linear model (GLM) to continuously distributed repeated measures (although well-developed techniques can be applied to discrete data as well; see Long, 1997). These GLMs can take the form of repeated measures t tests, ANOVA, analysis of covariance (ANCOVA), MANOVA, multivariate analysis of covariance (MANCOVA), and multiple regression. A commonality among all of these GLMs is that they tend to be considered fixed-effects models; that is, systematic relations are evaluated pooling across individuals, and the only source of random variation is in the residual. For example, we might use a two-timepoint regression to study positive symptoms in schizophrenia, and we might find that emotional expressiveness at Time 1 uniquely predicts symptomatology at Time 2 beyond symptomatology at Time 1. This unique prediction of Time 2 symptoms from Time 1 expressiveness represents this relation pooling over all individuals in the sample. Further, theory may posit an underlying trajectory of symptomatology that unfolds over time, but empirically we are only examining a two-timepoint “snapshot” of this process. Because of these limitations, and many others not described here (see, e.g., Rogosa & Willett, 1985, for further details), we turn our interests to the empirical estimation of developmental trajectories that vary over individuals.
Although there are several statistical methods available for analyzing individual trajectories and related processes of change over time, an often noted distinction is between models estimated within an SEM framework (e.g., Bollen, 1989) and models estimated within a hierarchical linear modeling (HLM) framework (e.g., Raudenbush & Bryk, 2002). HLM was originally designed to properly account for nested data structures, such as children nested within classrooms or patients nested within therapist. However, Bryk and Raudenbush (1987) demonstrated that this nesting could take the form of repeated measures nested within individual, and thus the HLM framework could be applied to study individual trajectories. Several authors have recently compared these two techniques and have demonstrated that under certain conditions the HLM and the SEM provide equivalent results whereas in other conditions they do not (see, e.g., MacCallum, Kim, Malarkey, & Kiecolt-Glaser, 1997; Raudenbush, 2001; Willett & Sayer, 1994). A full exploration of these issues is beyond the scope of our article. However, it is important to understand that despite much overlap, the SEM approach may be better suited for tests of some types of research questions under some types of experimental designs, whereas the HLM approach may be better suited for other types of questions under other types of designs. To retain focus in the current article we will consider only the SEM-based LTM. (See Bryk & Raudenbush, 1987; Raudenbush, 2001; Raudenbush & Bryk, 2002; Willett & Sayer, 1994, for excellent discussions of the HLM approach to trajectory modeling.)
To confuse matters further, even the SEM approach to longitudinal data analysis is denoted in the literature by a number of alternative terms including growth models, latent growth models, LTMs, and latent curve analysis, among others. Here, we adopt the term latent trajectory model to underscore the emphasis on individual patterns of trajectories of behavior over time while avoiding the implication that such trajectories must include systematic increases or decreases (i.e., growth) to be estimated within this framework. As we discuss later, these techniques can often be applied to great advantage even in situations where the repeated measures show no evidence of systematic positive or monotonic growth whatsoever.
The idea of estimating and predicting individual trajectories dates back many years (Gompertz, 1825; Palmer, Kawakami, & Reed, 1937; Wishart, 1938). However, it was not until the seminal work of Meredith and Tisak (1984, 1990), drawing on the earlier developments of Tucker (1958) and Rao (1958), that the analysis of trajectories was embedded within the latent variable framework. The LTM is based on the premise that a set of observed repeated measures taken on a given individual over time can be used to estimate an unobserved underlying trajectory that gives rise to the repeated measures. When thought of in this way, the estimation of individual trajectories falls nicely into the framework of confirmatory factor analysis (CFA). In CFA, the interest is not so much in the characteristics of the set of observed measures but instead in the underlying unobserved latent constructs that explain the relations among the observed measures. This is precisely the approach of the LTM. We begin by first describing the basic within- and between-person trajectory equations and then describe how these equations can be estimated within the SEM framework.
Linear LTMs
The basic LTM begins with the premise that a set of repeated measures are functionally related to the passage of time. This can more formally be expressed as
| (1) |
where yit is measure y for individual i at time t, λt is the value of time1 at t, f(λt) reflects the functional relation between time and the outcome of interest, and εit is the residual for individual i at time t. As we explore further in a moment, the function that relates the repeated measures of our outcome and time can be linear, quadratic, or exponential or take on a variety of other forms. A common trajectory function is linear. Here, f(λt) is defined as
| (2) |
where yit, λt, and εit are defined as above; αi is the intercept of the underlying trajectory for individual i; βi is the linear slope of the underlying trajectory for individual i; and εit is the residual for individual i at time t.
Of key importance is that the intercepts and slopes are allowed to vary over individual; that is, some individuals may report higher initial levels of the outcome relative to other individuals, and some individuals may report greater changes in the outcome over time relative to other individuals. This is highlighted in Figure 1, in which the left panel shows a fitted trajectory for four repeated observations of reading ability for a single child and the right panel shows fitted trajectories for 75 children. (We describe these empirical data in more detail later.) As can be seen in the right panel, there appears to be individual variability in both starting point and rate of change over time.
Figure 1.
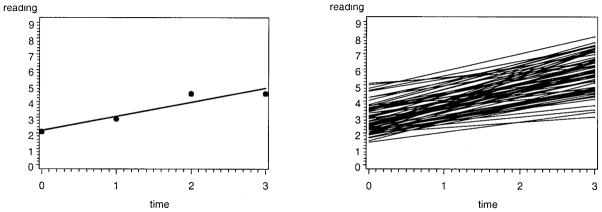
Fitted trajectories discussed in Curran and Hussong (2001) for four repeated measures of reading ability assessed on a single child (left panel) and on 75 children (right panel).
To express this individual variability in statistical terms, we treat the parameters of the trajectories as random variables, which permits us to write equations for the trajectories such that
| (3a) |
| (3b) |
where μα and μβ are the mean intercept and slope pooling over all individuals, and ζαi and ζβi are the deviations of each individual from the group mean. For this linear model, we would like to estimate several key parameters from our sample data. These include the mean starting point and mean rate of change over time, the variance in the starting point and the variance in the rate of change, the covariance between starting point and rate of change, and the time-specific residual variances.
Drawing on the work of Meredith and Tisak (1984, 1990), along with important contributions by McArdle (1988, 1989, 1991), Muthén (1991, 2001a, 2001b), and others, we can estimate these parameters using the standard SEM framework. Specifically, for our linear trajectory example, the repeated measures are used as multiple indicators on two correlated latent factors. The first factor represents the intercept of the trajectory, and the second factor represents the linear slope of the trajectory. Whereas the standard HLM trajectory model considers time as a predictor variable (e.g., Bryk & Raudenbush, 1987), in the LTM framework the passage of time is parameterized via the factor loadings that relate the repeated measures to the latent factors (Meredith & Tisak, 1990). It is through varying the fixed and freely estimated factor loadings that we may define different functional forms of growth.
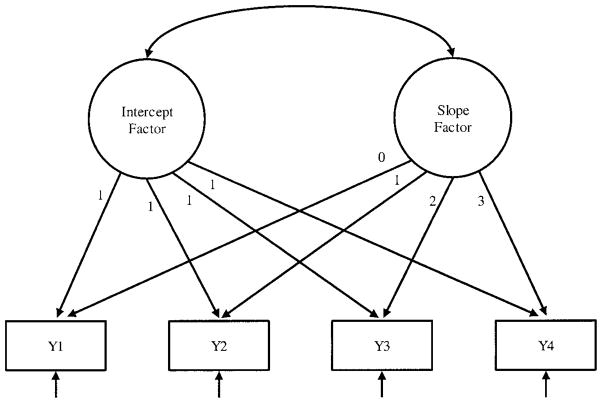
For example, say that we had collected four equally spaced repeated measures2 of our construct over time so that T = 4. We would then define the LTM by setting the four factor loadings on the intercept factor equal to 1.0 and the four factor loadings on the slope factor equal to λt = t − 1, where t = 1, 2, 3, 4. This model is presented in Figure 2. Because we have coded time to begin with zero, the intercept reflects the model-implied value of the outcome measure at the initial period of measure; however, alternative codings of time can be used to define other meanings of the intercept term (see, e.g., Biesanz, Deeb-Sosa, Aubrecht, Bollen, & Curran, 2003).
Figure 2.
Unconditional linear trajectory model for four repeated measures assessed at equal intervals. Y = year.
For the sample case of T = 4 repeated measures and a linear trajectory, the standard LTM will result in nine parameters to be estimated from the data. For the linear trajectory model, the two fixed effects are the means of each latent factor (i.e., μα and μβ); these values represent the mean intercept and the mean slope of the trajectory pooling over all cases in the sample. The random effects are represented by four parameters: a variance for each latent factor reflecting the degree of individual variability in intercepts and in slopes across all cases in the sample (i.e., ψα and ψβ), a covariance3 between the two latent factors that reflects the degree of association between the individually varying intercepts and individually varying slopes (i.e., ψαβ), and a residual variance for each repeated measure that reflects the unexplained variance in the measure net of that associated with the underlying factor (i.e., ). Taken together, these parameters capture the mean trajectory for the overall group, the degree of variability across individual trajectories around these mean values, and the amount of time-specific variance in the repeated measures not explained by the underlying trajectory process.
Nonlinear LTMs
Thus far, we have assumed that the repeated measures are linearly related to the passage of time. That is, a one-unit change in time is associated with a β-unit change in the outcome, and the magnitude of this relation is constant over all points in time. Although this may be a reasonable function to describe stability and change in a behavior over time, there may be either theoretical or empirical reasons to believe that the repeated measures are related to time in some nonlinear fashion where change in y is not constant between equally spaced assessments. Although there are many alternative ways to test for such relations within the LTM, here we discuss three specific techniques: the quadratic function, the exponential function, and functions that are estimated based on the characteristics of the sample data.
The quadratic function
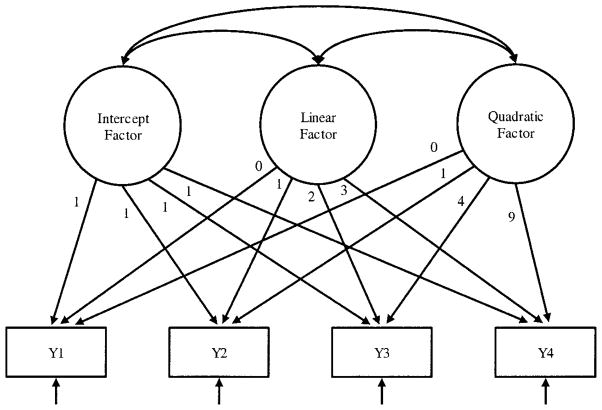
One way that the LTM can be extended to capture nonlinear relations over time is through the quadratic model. Whereas the linear model is defined by an intercept factor and a slope factor, the quadratic model includes a third latent factor to capture any curvature that might be present in the individual trajectories (see Duncan, Duncan, Strycker, Li, & Alpert, 1999, and McArdle, 1991, for further details). The individual trajectory equation for a quadratic model is
| (4) |
where αi remains the intercept of the trajectory, βLi is the linear component of the trajectory, and βQi is the quadratic component of the trajectory. To define the third latent factor, factor loadings reflecting the relations between the latent quadratic factor and the repeated measures are set to the squared values of those on the linear factor. This model is presented in Figure 3.
Figure 3.
Unconditional quadratic trajectory model for four repeated measures assessed at equal intervals. Y = year.
Whereas the linear model implied constant change in y between equally spaced time assessments, the quadratic model implies differential change in y between equally spaced time assessments. For example, there may be large positive changes early in the trajectory that begin to diminish with the passage of time. Similarly, there might be small initial changes that accelerate with the passage of time. One important aspect of the quadratic model is that the trajectory is considered to be unbounded with respect to time. That is, just like the linear model, the quadratic model tends toward plus and minus infinity. In many (if not most) empirical applications, we may not theoretically believe that our measure y tends toward infinity, although a linear or quadratic model might be sufficient to characterize the dependent measure within our window of observation. An alternative trajectory that is bounded, and thus does not tend toward positive or negative infinity, is the exponential function.
The exponential function
It has long been known that exponential functions can be used to model growth or decay that tends toward some asymptote. These models are based on the general premise that future gains (or losses) are proportional to prior gains (or losses). A common exponential function is
| (5) |
where yit is our usual outcome measure, αi is again the intercept of the trajectory, βi represents the total amount of change at the final observation relative to the initial level, e represents the well-known constant, and γ is the rate of change in y over time. Thanks to the work of Browne and du Toit (1991) and du Toit and Cudeck (2000), methods have been developed for estimating this function within the LTM framework (although certain restrictions on the random components are necessary for estimation). Given space constraints, we do not explore this model in greater detail here, but see Browne and du Toit (1991) and du Toit and Cudeck (2000) for further technical details and applied examples.
The completely latent function
The linear, quadratic, and exponential trajectories define known functional forms that relate the repeated measures to the passage of time. That is, a specific functional form is defined and then fit to the observed data. In some situations these trajectory functions might be excessively restrictive or might not optimally capture the pattern of change observed in the data over time. An alternative approach is to estimate the functional form directly from the data. This requires the estimation of an intercept factor and a single latent change factor where a subset of the loadings on the latent slope (or shape) factor are freely estimated from the data instead of being fixed to predetermined values. This approach was first proposed by Meredith and Tisak (1990) and further elaborated by McArdle (1989, 1991).
Consider our hypothetical linear trajectory model from above (i.e., Equation 2). Instead of fixing the factor loadings to 0, 1, 2, and 3, we could instead set the first loading on the linear factor to 0, set the second to 1 (to set the metric of the latent variable), and then freely estimate the third and fourth loading. Alternatively, we could set the first loading to 0 and the last loading to 1, and estimate the second and third loadings. Both of these parameterizations would result in the same overall model fit, but the factor loadings would have a different interpretation (see Aber & McArdle, 1991, for an excellent discussion of these distinctions). The key characteristic of this model is that instead of fixing the factor loadings to values that define a known functional form, one or more factor loadings are freely estimated from the data. This is analogous to fitting a nonlinear spline that best fits the observed data. Freely estimating the loadings has the effect of “stretching” or “shrinking” time to best characterize the pattern of the observed data over time (e.g., Aber & McArdle, 1991). Now instead of having three factors (e.g., intercept, linear, and quadratic), we have two factors where the first remains the intercept but the second is a shape factor that captures the nonlinear propensity to change over time.
Selection of Functional Form: Sample Applications of Unconditional LTMs
It is critically important that the proper functional form of the trajectory be identified prior to analyzing more complicated models. Because several alternative models defining these functional forms are formally nested (e.g., the linear is nested within the completely latent, and the linear is nested within the quadratic), chi-square difference tests can be calculated to estimate the degree of improvement in the fit of one model relative to another. Other functional forms are not formally nested (e.g., the exponential is not nested within the quadratic), but less formal methods may still be used to evaluate the relative fit of these models (e.g., AIC or BIC; Tanaka, 1993).
Often the process of defining the functional forms of latent trajectories requires examining the data graphically as well as analytically through fitting a series of models. We used such an approach to define individual trajectories in reading ability over time (see Curran & Hussong, 2001, for further details). Using a sample of 405 children from the National Longitudinal Study of Youth, we modeled individual trajectories of reading scores on the basis of four annual assessments using the Peabody Individual Achievement Test.4 A linear model was first estimated and demonstrated extremely poor fit to the data, χ2(5, N = 405) = 175.04, p < .001; root-mean-square error of approximation (RMSEA) = .29, confidence interval (CI)90 = .25, .33. Inspection of mean scores on reading achievement showed that although children seemed to increase in their skills over time, the increment of increase was not equal across all intervals (e.g., the means for times 1, 2, 3, and 4 were 25.2, 40.8, 50.1, and 57.7, respectively). To capture this nonlinearity, we contrasted the linear unconditional model with a quadratic unconditional model. Although a chi-square difference test of these two nested models indicated that the quadratic model was a better fit to the data than the linear model, , p <.001, the quadratic model still provided a poor overall fit to the data, χ2(1, N = 405) = 10.65, p < .001; RMSEA = .15, CI90 = .08, .17.
In an attempt to better capture this nonlinearity over time, we next utilized the less restrictive completely latent function in which we set the first two loadings on the slope factor to be 0 and 1 and freely estimated the third and fourth loadings. This model fit the observed data well, χ2(3, N = 405) = 4.4, p = .22; RMSEA = .03, CI90 = 0, .10. The linear model is nested within the completely latent model with the two differing only by the freeing of factor loadings to define a completely latent function. The chi-square difference test demonstrated the superior fit of the completely latent model relative to the linear model, . The first two loadings on the shape factor were set to 0 and 1 to define the metric of the latent variable, but the third and fourth factor loadings were estimated to be 1.6 and 2.1, respectively. Taken together, the results suggest that reading achievement in this sample was characterized by positive changes over time that diminished in magnitude as a function of time, with significant variability across individual children in initial reading skills and in rates of change over time. Other published examples of modeling nonlinearity include Andrews and Duncan’s (1998) study of attitudes and cigarette use, Stoolmiller’s (1994) study of boys’ antisocial behavior, and Windle and Windle’s (2001) study of depression symptoms and smoking.
In sum, we cannot emphasize strongly enough that a properly fitting functional form be identified prior to moving on to more complex models. The unconditional LTM allows for an examination of the fixed and random effects that might underlie a set of repeated measures over time. In many applications, it is then of key interest to predict individual differences in these trajectories over time, and this is the focus of the conditional LTM.
Conditional LTM
Although unconditional LTMs permit us to chart the course of psychopathology over time, many core questions in this field concern the factors that contribute to the development and growth of abnormal behavior. Building on the unconditional LTM, the conditional LTM addresses many such questions (e.g., Tisak & Meredith, 1990; Willett & Sayer, 1994). Recall that in the unconditional LTM the random intercepts and random slopes are characterized by an overall mean and an individual deviation from this mean (see Equations 3a and 3b). However, these equations can be extended to incorporate one or more correlated predictors to better understand the conditional distributions of the random trajectories, much like how we consider predictors in a typical regression model.
For example, say that we had estimated a latent trajectory process for a repeated measure of depressive symptoms over time, and we had also assessed two correlated predictor variables at the initial time of measurement denoted z1 and z2 (say, e.g., gender and diagnostic status). We would expand our trajectory equations such that
| (6a) |
| (6b) |
where the four gammas (i.e., γs) represent the fixed effect prediction of the random intercepts and slopes as a function of the two correlated predictors z. Given the presence of the predictors, μα and μβ now represent regression intercepts and ζαi and ζβi represents regression disturbances. This model is thus evaluating whether individual variability in intercepts and slopes can be predicted by our set of explanatory variables. For example, a one-unit increase on z1 would be associated with a γ1-unit increase on the intercept of the trajectory.
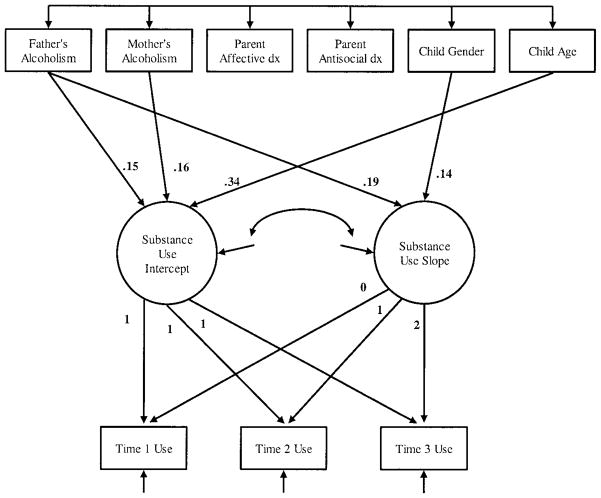
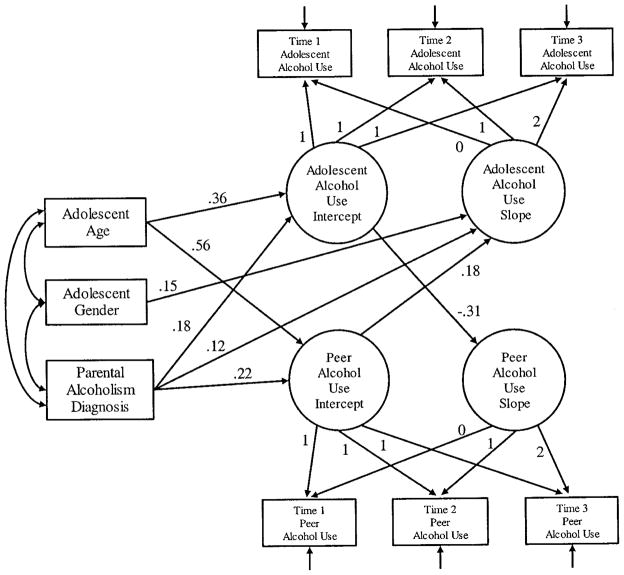
One example of a conditional model appears in Chassin, Curran, Hussong, and Colder (1996) and is presented in Figure 4. Using an unconditional LTM, we first defined the functional form of change in substance use to be characterized by a linear trajectory over the three annual assessments completed by 316 adolescents and their parents. To better understand the impact of parent alcoholism on adolescent substance use over time, we next examined whether parent alcoholism uniquely predicted higher initial levels of adolescent substance use and steeper accelerations in adolescent substance use over time above and beyond the effects of comorbid parent disorder (i.e., affective and antisocial personality disorders). The corresponding conditional model included child age, child gender, and parental diagnoses (father’s alcoholism, mother’s alcoholism, either parent’s affective disorder, and either parent’s antisocial personality disorder) as predictors of the latent factors representing the intercept and the slope of the trajectories for adolescent substance use. All predictor variables were correlated with one another (parallel to the conditions of multiple regression necessary for testing unique effects).
Figure 4.
Conditional linear trajectory model adapted from Chassin et al. (1996). Factor loadings are fixed to predefined values. Only significant effects are shown in the diagram, and all coefficients are standardized and significant (p < .05). dx = disorders.
The final model provided an excellent fit to the data, χ2(13, N = 316) = 24.5, p =.03, Tucker–Lewis index (TLI) = .95, comparative fit index (CFI) = .98. Significant parameter estimates indicated that adolescents who were older or who had an alcoholic biological mother or father reported greater initial levels of substance use than did their peers. Moreover, boys and adolescents of alcoholic fathers also increased more sharply in their substance use over time than did girls or adolescents of nonalcoholic parents.
These results demonstrate the power of the conditional LTM to evaluate prospective hypotheses about predictors of change over time in psychopathology or problem behavior. Other examples of similar types of LTMs in studies of psychopathology include Andrews and Duncan’s (1998) study of cigarette use, Kraatz-Keiley, Bates, Dodge, and Pettit’s (2000) study of internalizing and externalizing symptoms in children, Muthén and Muthén’s (2000) study of adult alcohol use, and Windle and Windle’s (2001) study of depression and smoking. In such conditional LTMs, exogenous predictors serve the same purpose as those that might be used in a standard regression model, although the specific interpretations are often more complex (Curran, Bauer, & Willoughby, 2003). The predictors may be any mix of categorical or continuous measures given that no assumptions are made about the distributions of the predictor variables, and multinomial predictors can similarly be included using effect or dummy coding. The motivating goal of these conditional LTMs is to better understand what factors might predict the individual developmental trajectories over time.
Extensions of the Basic LTMs
The unconditional and conditional LTMs provide the basic building blocks from which more complex models may be estimated. Although certainly not exhaustive, the five modeling extensions we focus on are particularly salient with regard to the types of questions that are typically of interest in psychopathology research. These five extensions allow for testing hypotheses about (a) the mechanisms that explain why certain factors predict change in psychopathology over time (i.e., mediation), (b) the conditions under which a given factor predicts change in psychopathology over time (i.e., moderation), (c) whether time-specific fluctuations in a trajectory of psychopathology are related to intervening factors (i.e., time-varying covariate models), (d) whether change in one measure of psychopathology is systematically related to change in a second measure of psychopathology (i.e., multivariate LTMs), and (e) whether time-specific associations within two growth processes or trajectories are related to one another (i.e., autoregressive latent trajectory models).
Mediation in LTMs
In psychopathology research, we are often interested in mediational processes that predict change over time indexed by our latent trajectory factors in which the distal predictor and potential mediator are both time-invariant variables. Earlier we summarized results from Chassin et al. (1996) indicating that children with an alcoholic parent were more likely to show higher initial levels and steeper accelerations in substance use over time compared with children without an alcoholic parent. We would next like to extend this model to test whether certain factors underlie or account for these effects. Fortunately, when both the predictors and the mediators are time invariant, standard methods for testing indirect effects in SEM can be used for this purpose. It is less straightforward to test predictors and mediators that themselves are changing over time (i.e., time-varying variables), and we consider this topic later in the article.
In the standard SEM, methods for decomposing total effects are used to calculate point estimates and standard errors for direct effects and total indirect effects (Bollen, 1987; Sobel, 1982). Total indirect effects characterize the impact of a predictor variable on an outcome as mediated through all estimated pathways linking the two variables. In other words, these tests evaluate whether there is a significant effect of the predictor on the outcome as mediated by all possible mediating pathways. However, total indirect effects do not reflect the significance of each individual pathway linking the predictor and outcome variable in cases in which two or more pathways are estimated; each of these individual pathways is referred to as a specific indirect effect. Bollen (1987) provides methods for specifying and testing both total indirect effects and specific indirect effects, and his methods can be directly extended to the LTM with one or more mediators.
For an example of tests of total indirect effects, we return to Chassin et al. (1996). After establishing that a significant relation existed between paternal alcoholism and individual differences in starting point and rate of change in adolescent substance use over time, we next examined whether three potential etiological mechanisms explained why children of alcoholic parents started higher and accelerated faster in their substance use than did children without an alcoholic parent. Specifically, we tested whether parenting factors (e.g., mother’s and father’s monitoring of the child’s behavior), the adolescent’s temperament (e.g., emotionality and sociability), and elevated rates of stress and deviant peer associations each accounted for risk of accelerated substance use among children of alcoholic fathers. An excellent fit of this model to the data was found, χ2(62, N = 316) = 88.6, p < .01; TLI = .95; CFI = .98. The total indirect effects were tested, and it was found that together these mediators significantly explained part of the variance in the relation between paternal alcoholism and initial levels of adolescent substance use (z = 2.17, p = .03). These pathways were also marginally significant mediators of the relation between paternal alcoholism and change in adolescents’ substance use over time (z = 1.85, p = .06).
To summarize, we estimated a series of LTMs to demonstrate that (a) there were significant fixed and random components underlying the developmental trajectories of substance use over time, (b) individual differences in both starting point of substance use and rate of change of substance use were reliably associated with parental alcoholism status, and (c) the parental alcoholism effect was partially explained by the three posited mediating mechanisms. Additional examples of LTMs that test mediation hypotheses include Barnes, Reifman, Farrell, and Dintcheff’s (2000) study of parenting and substance use, Colder, Chassin, Stice, and Curran’s (1997) study of expectancies and alcohol use, and Lorentz, Simons, Conger, and Elder’s (1997) study of distress in divorced mothers.
Moderation in LTMs
Whereas tests of mediation consider why a relation between a predictor and an outcome might exist, tests of moderation consider under what conditions such a relation might exist (Baron & Kenny, 1986). There are two ways in which moderation might be considered in LTMs. The first is whether two or more exogenous predictors (that are discrete or continuous) interact with one another in the prediction of the latent trajectory factors. The second is whether one or more parameters that define a trajectory model vary as a function of an observed discrete group membership (e.g., males vs. females, diagnosed vs. nondiagnosed, treatment vs. control). We begin with a brief discussion of interactions among exogenous predictors and extend this to the multiple groups framework.
Recall that the conditional LTM evaluates the relation between one or more predictors of the underlying trajectories (e.g., see Equations 6a and 6b). This model allowed for the evaluation of the unique main-effect prediction of the trajectory factors by each exogenous predictor above and beyond all other predictors. However, this framework is easily extended to consider higher order interactions such that
| (7a) |
| (7b) |
where we model the intercepts and slopes of the trajectory as a function of the main effect of z1, the main effect of z2, and the interaction between z1 and z2. Whereas the prior conditional LTM assessed whether there is a significant relation between z1 and the trajectory factors, the conditional LTM that includes interaction terms assesses whether the magnitude of the relation between z1 and the trajectory factors varies across levels of z2. For example, instead of testing whether there is a difference in slopes as a function of symptom severity, the inclusion of the interaction tests whether the relation between slopes and symptom severity varies as a function of gender. (See Aiken & West, 1991, and Baron & Kenny, 1986, for more details about moderation in general and Curran, Bauer, & Willoughby, 2003, in press, for moderation in growth models.)
The testing of higher order interaction terms in LTM is relatively straightforward and follows the same strategy as that used in a standard regression model (e.g., Aiken & West, 1991). Specifically, an interaction term is computed as the product of the two predictors, and this product term is then entered as an additional predictor variable within the conditional LTM. The test of the regression coefficients for the product terms (e.g., γ3 and γ6 in Equations 7a and 7b) is a direct test of the moderating relation between the two predictors. Probing and plotting of the moderated relations requires us to recall the role of time as a predictor of the repeated measures within the LTM framework. The net result is that if we are testing an interaction between two predictors, this interaction itself interacts with time and must thus be treated as a three-way interaction. We describe this in detail for both HLM and LTM growth models in Curran et al. (2003) and Curran et al. (in press).
An example of testing and probing higher order interactions among exogenous predictors in a conditional LTM was presented in Curran et al. (2003). Data were drawn from a sample of 405 children of the National Longitudinal Study of Youth (see Curran, 1997, for complete details of sample and measures). Children ranged in age from 6 years to 8 years at Time 1 and were interviewed every other year for up to four assessments. All children were interviewed at Time 1, 374 were interviewed at Time 2, 297 were interviewed at Time 3, 294 were interviewed at Time 4, and 221 were interviewed at all four time periods. A cohort–sequential design with missing data was used that resulted in nine assessments ranging in age from 6 years to 14 years (in which each child was evaluated from one to four times). A linear trajectory model was fitted to the nine repeated assessments of child aggressive behavior, and residual moment structures and LaGrange multipliers indicated a good fit to the data (traditional fit indexes are not available given the missing data estimation). A quadratic factor was added to evaluate the presence of any nonlinearity, but this did not significantly improve model fit and was not retained. Significant effects were found for both fixed effects and random effects in the intercept and slope, indicating that on average, the sample was increasing in aggressive behavior over time but that there was substantial individual variability around both starting point and rate of change.
We then regressed the intercept and slope on a dichotomous measure of gender, a continuous measure of parental emotional support of the child at Time 1, and the multiplicative interaction between gender and support. The two-way interaction between gender and support was found to be significant (p < .05). Using the methods described in Curran et al. (2003), we probed this interaction to better understand the nature of the effect. We found that within boys, although simple trajectories of aggressive behavior evaluated at low, medium, and high levels of support were all increasing over time, the magnitude of this increase was significantly greater at lower levels of emotional support in the home. In contrast, whereas the simple trajectories were diverging for males over time, they were converging for girls. That is, the ranking of the simple trajectories of aggressive behavior taken across different levels of support was similar over gender (e.g., low emotional support is associated with the greatest antisocial behavior over time); however, the simple trajectories are significantly increasing for girls at medium and high levels of support but are not significantly different from zero at low levels of support. See Curran et al. (2003) for further details.
The methods described above allow for powerful and insightful tests of the magnitude of the relation between one predictor and the trajectory factors as a function of one or more other predictors. However, an important assumption that we are making here is that all parameters that define the trajectory model are invariant across levels of the predictors. Consider the example above in which the relation between emotional support and trajectories of aggressive behavior varies as a function of gender. In this model we are implicitly assuming that all of the other model parameters are equal for boys and girls. This is often a reasonable assumption, but we can use the strength of the multiple groups framework in SEM to empirically evaluate this in LTMs. Using such an approach, we could estimate either an unconditional or a conditional LTM simultaneously for boys and girls and specifically test the extent to which one or more model parameters are equal across gender (e.g., factor loadings, factor variances, residual variances, etc). Given space constraints, we do not explore multiple group LTMs in detail here. See Curran and Muthén (1999), McArdle (1991), and Muthén and Curran (1997) for further details and Ge, Lorenz, Conger, Elder, and Simons (1994) and Hussong, Curran, and Chassin (1998) for applied examples.
Multivariate LTMs
Up to this point we have focused solely on the situation in which we have repeated measures taken on a single construct over time; this model is often referred to as a univariate LTM. Although it is multivariate in the sense that multiple repeated measures were assessed, it is univariate in that there is only one repeated measures construct under study. Further, we have considered main effects, mediated effects, and moderated effects among predictors of the latent trajectory factors, but these predictors were time-invariant given that they were assessed at a single point in time. However, there are many instances in which we might be interested in trajectories of two related constructs over time. This is often referred to as a multivariate LTM, and these models have many potential applications in studies of psychopathology. We explore three variations of these here. The first incorporates the repeated measures of a second construct as time-varying covariates (TVCs) without estimating a trajectory process for the TVCs. The second model estimates a trajectory process for both constructs over time and relates the two processes solely at the level of the latent trajectories. The third model combines features of the first two approaches and allows for the simultaneous estimation of the trajectories that underlie each construct and the relations among time-specific measures.
TVC LTM
An implicit but critically important assumption that we have made with the LTMs thus far is that the repeated measures on our constructs of interest are completely governed by the underlying trajectory process and any deviations of the repeated measures from this trajectory are treated as error. This assumption allows us to logically move to the conditional LTMs, in which we attempt to predict individual variability in the various trajectory parameters. That is, we used the repeated measures to estimate the trajectory parameters, and these parameters then become the sole outcomes of interest. However, there are situations in which we do not necessarily anticipate that the repeated measures are completely governed by the underlying trajectory process. Instead, we might hypothesize that the repeated measures are in part related to the trajectory process but are also influenced by other time-specific or time-lagged constructs. We can extend the LTM to allow for these types of influences.
Recall that our initial trajectory equation for the linear model was expressed as
| (8) |
Note that the only predictor of the repeated measures in this equation is time (which is parameterized in the LTM via the factor loading matrix). In the TVC model, we allow for the direct prediction of the repeated measures from other measures above and beyond the underlying trajectory process. To accomplish this, we extend the above equation such that
| (9) |
where zit represents our measure of covariate z for individual i at time t, and γt is the fixed regression parameter relating y to z at time t.
It is important to note that although the intercept and slope parameters continue to vary randomly over individual, the regression parameter γt does not. This represents the relation between y and z at time t pooled over all individuals net the influence of the underlying trajectory process. These relations can also be time lagged if so desired (see, e.g., Curran, Muthén, & Harford, 1998). This approach implies that we are not modeling a random trajectory process for the TVCs z, but we are explicitly estimating the simultaneous effects of the TVCs and the underlying random trajectory components for y in the prediction of the time-specific repeated measures outcome yit.
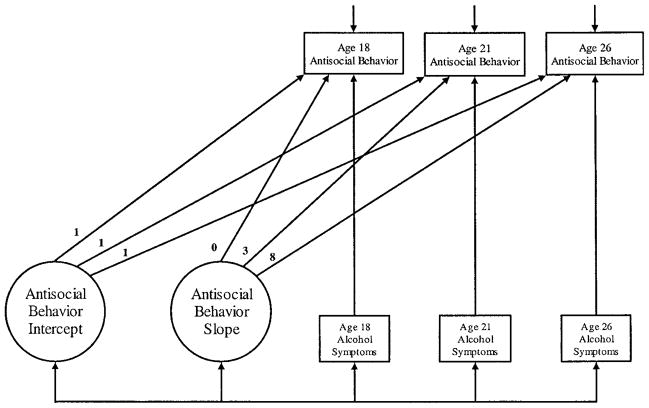
An application of this technique appears in Hussong, Curran, Moffitt, Caspi, and Carrig (2003), in which repeated measures of alcohol abuse in males at ages 18, 21, and 26 were examined as predictors of time-specific deviations from expected individual trajectories in antisocial behavior over time. This model is presented in Figure 5. Testing what Moffitt (1993) has termed a snares hypothesis, the proposed model examined whether the commonly supported pattern of desistance in individual trajectories of antisocial behavior over young adulthood would fail to account for time-specific elevations in antisocial behavior during time periods when these men were involved more heavily in alcohol use. The sample consisted of participants in the Dunedin Multidisciplinary Health and Development Study, a longitudinal investigation of health and behavior in a complete birth cohort (Silva & Stanton, 1996). For the Hussong et al. study, data from 461 male participants were analyzed, though not all participants provided complete data at every assessment period. (The ability of the LTM procedures to incorporate participants with missing data into model estimation is a strength of the technique that we return to later.)
Figure 5.
Unconditional linear latent trajectory model with time-varying covariates from Hussong et al. (2003). See Hussong et al. (2003) for results from more complex models of this type.
To first establish the pattern of change over time in the measures of antisocial behavior from ages 18 to 26, a linear, unconditional growth model was estimated. The resulting model provided a good fit to the data, χ2(1, N = 461) = 9.31, p =.002, incremental fit index (IFI) = .98, CFI = .98. The parameter estimates reflected a significant amount of antisocial behavior at Time 1 and a significant decrement in antisocial behavior over time. Further, there was evidence of significant individual variability in both the starting point and the rate of change. Repeated measures of alcohol abuse were added to this unconditional LTM of antisocial behavior to test whether time-specific measures of antisocial behavior were related to time-specific measures of alcohol abuse above and beyond the influence of the trajectory process underlying antisocial behavior.
In accordance with this hypothesis, we added to the basic unconditional LTM for antisocial behavior the three repeated measures of alcohol abuse as exogenous predictors of the time-specific indicators of antisocial behavior.5 The resulting model fit the data well, χ2(1, N = 461) = 10.59, p = .001, IFI = .99, CFI = 1.0. At age 18, men with greater alcohol abuse showed elevated antisocial behavior compared with expected behavior based on their individual trajectories alone. A similar pattern was found for these men at age 21, but alcohol abuse was only a marginal predictor of antisocial behavior at age 26. These results suggest that during the periods when these young men experience more symptoms of alcohol abuse, they do not decline in their antisocial behavior to the extent that we would expect on the basis of their antisocial behavior throughout young adulthood. Rather, alcohol abuse appears to ensnare these young men within elevated patterns of antisocial behavior, and this effect becomes weaker as men age through this period of desistance. Other examples of TVC models that also address the issue of substance use include Curran et al. (1998) and Harford and Muthén (2001).
In sum, a key characteristic of the TVC trajectory model was that although repeated measures on a second construct are considered, a trajectory process is not estimated for these measures. However, there are situations in which we would like to evaluate whether there is a latent trajectory process that underlies the TVCs as well. To incorporate this second process, we move to the fully multivariate LTM.
Fully multivariate LTM
To include the repeated measures of our time-varying covariates in the univariate LTM, we expanded the individual trajectory equation to include the time-specific measures of z. In contrast, we will now simultaneously estimate a trajectory equation for the repeated measures of y and another trajectory equation for the repeated measures of z. This is expressed as
| (10a) |
| (10b) |
indicating that we now have an individually varying intercept and slope for our repeated measures of y, but we also have an individually varying intercept and slope for our repeated measures of z. This is in contrast to our TVC model, in which we incorporated our repeated measures of z as direct predictors of y, whereas here we are estimating trajectory parameters for both of our constructs, y and z.
As before, we can write an equation for both sets of trajectory parameters such that
| (11a) |
| (11b) |
and
| (12a) |
| (12b) |
where each trajectory process is again characterized by a mean intercept and slope, and by variances and covariances among the intercepts and slopes both within construct and across construct. Thus, the covariance structure among the random trajectory factors reflects the extent to which two constructs “travel together” through time; that is, the covariance between two slope factors represents the correspondence between rates of change in the two constructs over time. Also of interest in these models are the predictions of rates of change in one construct as a function of initial levels of the second construct; this reflects the degree to which change in one construct is in part propelled by the initial level of the other construct. (See Aber & McArdle, 1991, and McArdle, 1989, 1991, for further details on model parameterization and estimation.)
An example of a multivariate LTM was used to test the prospective relations between adolescent alcohol use and that of their peers (Curran, Stice, & Chassin, 1997), and this model is presented in Figure 6. Three annual assessments were taken on a sample of 363 adolescents who ranged in age from 11 to 15 at Time 1. A linear unconditional LTM was found to represent change over time within each construct. For the multivariate LTM, these two unconditional LTMs were combined such that covariances were added among all latent factors (both within constructs and across constructs) and between the residuals of repeated measures (within time and between construct). Cross-lagged predictions were also added from the intercept factor for adolescent alcohol use to the slope factor for peer alcohol use as well as from the intercept factor for peer alcohol use to the slope factor for adolescent alcohol use. Three predictor variables, indexing the adolescent’s age, gender, and parent’s alcoholism status, were related to all latent trajectory variables in the model.
Figure 6.
Fully multivariate unconditional latent trajectory model from Curran et al. (1997). Factor loadings are fixed to predefined values. Only significant effects are shown in the diagram, and all coefficients are standardized and significant (p < .05).
The final model fit the data well, χ2(14, N = 363) = 25.4, p = .03, TLI = .98, CFI = .99. Significant covariances among the latent factors indicated that greater initial rates of alcohol use were associated with greater accelerations in peer alcohol use. Within construct, however, higher initial rates of alcohol use (whether among adolescents or peers) were associated with slower accelerations in alcohol use over time (potentially indicating a realistic ceiling effect in drinking behavior over time). Plotting of the model-implied trajectories showed that growth in adolescent alcohol use was positive and accelerating as a function of peer alcohol use whereas growth in peer alcohol use was positive but decelerating as a function of adolescent alcohol use. Thus, the initial status of both peer alcohol use and adolescent alcohol use was predictive of later changes in the other construct, but the magnitude of the rate of positive change differed within each construct. Other published examples of these types of LTMs in psychopathology-related research include Curran, Harford, and Muthén’s (1996) study of adult drinking, Ge et al.’s (1994) study of adolescent depression, Stoolmiller’s (1994) study of antisocial behavior in boys, Wickrama, Lorenz, Conger, and Elder’s (1997) study of marital quality and physical illness, and Wills, Sandy, Yaeger, Cleary, and Shinar’s (2001) study of family influences on substance use.
The fully multivariate LTM allows for an evaluation of the relation between two or more constructs over time at the level of the random trajectories. One limitation of this model is that, similar to the univariate LTM, an implicit assumption is made that the set of repeated measures is completely governed by the underlying trajectory process. This focus solely at the level of the trajectories might overlook important time-specific relations among the repeated measures, either within construct or across construct, such as those reflected in the time-varying covariate LTM. To address this issue, we can incorporate aspects of the TVC model with those of the fully multivariate model to create a hybrid model sometimes called the autoregressive latent trajectory, or ALT, model.
ALT model
Several methodologists have recognized the need to model dynamic systems that involve interrelations among change processes that occur simultaneously at both the random trajectory and the time-specific levels of analysis. Examples of these alternative approaches include the latent state–trait model (Schmitt & Steyer, 1993; Sher & Wood, 1997; Windle, 1997), the state–trait–error model (Kenny & Zautra, 1995), and the latent difference score model (McArdle, 2001; McArdle & Hamagami, 2001). Here, we focus on a related model, termed the ALT model, that utilizes the strengths of LTM and traditional autoregressive cross-lagged analyses within the SEM framework to address similar questions (Bollen & Curran, 2003; Curran & Bollen, 2001).
The equations for the ALT model become rather complex and are not presented here (see Bollen & Curran, 2003, and Curran & Bollen, 2001, for more details). Like the fully multivariate LTM, the ALT model estimates latent trajectory factors for two sets of repeated measures. Like the TVC model, the ALT model also estimates time-specific bidirectional relations between each of two constructs at the level of the repeated measure indicators. This simultaneous estimation of relations between the two constructs at the level of the latent trajectories and at the level of the time-specific repeated measures appropriately tests theories for which both processes are important in understanding the relation between the two constructs over time.
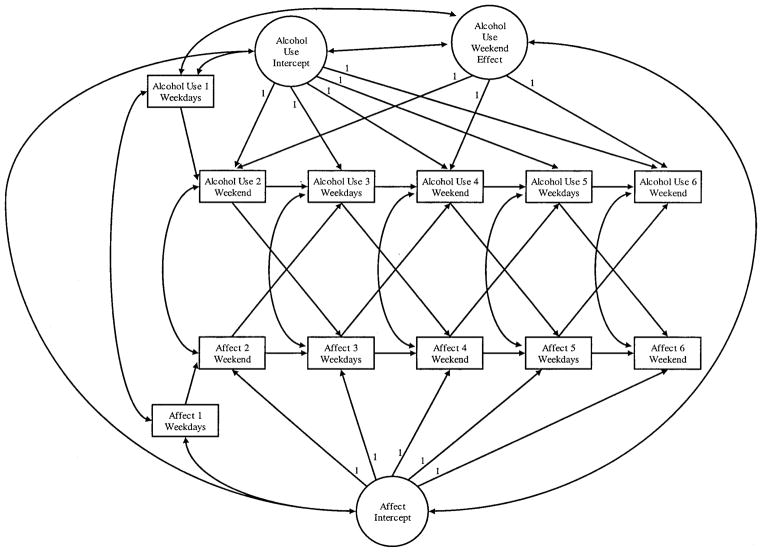
This model was applied to the study of relations among emotional affect and heavy alcohol use by Hussong, Hicks, Levy, and Curran (2001) and is presented in Figure 7. Illustrating dynamic relations between two changing processes over time, we presented a model in which six repeated measures of alcohol use and hostility were examined simultaneously.6 The motivating question was whether time-specific elevations in hostility (above and beyond an individual’s average level of hostility) predicted subsequent time-specific elevations in drinking (above and beyond an individual’s average level of drinking), and vice versa. This prospective cyclical relation between hostility and drinking behavior was tested over alternating weekends and weekdays (e.g., weekend hostility predicting subsequent weekday drinking and weekday drinking predicting subsequent weekend hostility).
Figure 7.
Autoregressive latent trajectory model from Hussong et al. (2001). Path coefficients are presented in Table 2 of Hussong et al. (2001).
Data for these analyses were drawn from 74 college freshman and sophomores who completed up to 21 daily reports of alcohol use and mood, which were subsequently collapsed to form indexes of average alcohol use and mood within each of three weekends and two series of weekdays assessed. Preliminary unconditional LTMs indicated that no systematic growth was evident in the repeated assessments of either alcohol use or hostility. However, systematic fluctuations in drinking behavior were associated with time such that heavier drinking was evident over weekends than during weekdays. To accommodate this systematic trend within the drinking trajectories, a second latent factor was added to the unconditional LTM for drinking behavior. Trajectories for hostility showed no systematic rise related to weekends, so the resulting unconditional LTM included only an overall intercept factor. The ALT model then included both the general intercept factor and the weekend intercept factor from the unconditional LTM for drinking as well as the general intercept-only factor from the unconditional LTM for hostility. Cross-lagged relations between time-specific measures of drinking and hostility were then added to this model, and this final model provided an excellent fit to the data, χ2(6, N = 74) = 72.71, p = .13, IFI = .94, CFI = .93.
Significant covariances were found between the latent factors defining the alcohol trajectories (such that those who drank more overall also elevated their drinking the most on weekends) and between the weekend latent factor on the drinking trajectory and the intercept factor for the hostility trajectory (such that greater changes associated with weekend drinking were negatively related to overall hostility). Perhaps of greatest interest for us in learning about the time-specific associations between hostility and drinking were the cross-lagged pathways reflecting a true prospective prediction above and beyond the underlying trajectory factors. Significant pathways indicate that hostility during the weekend predicted more drinking during the subsequent week, and weekday drinking predicted subsequent weekend hostility. These results highlight the ability of the ALT model to simultaneously consider relations both at the level of the trajectories and at the level of the time-specific repeated observations. The ALT model was used in Rodebaugh, Curran, and Chambless’s (2002) study of day-to-day variation between fear of having a panic attack and the experience of an actual panic attack and in Curran and Bollen’s (2001) study of the relation between child depression and aggressive behavior.
Summary
The TVC model, the fully multivariate model, and the ALT model are three examples of available strategies that might be considered when examining two or more constructs that are both assessed repeatedly over time. As with all LTMs, the optimal modeling strategy must be identified in large part by the underlying substantive theory and associated research hypothesis as well as by the constraints of the available data. Given primary interest in how time-varying events predict time-specific measures of an outcome net of the change process underlying this outcome, the TVC model might be optimal. If the association between the underlying random change process in two constructs is the central question of interest, then the fully multivariate model might be ideal. Finally, if the motivating question concerns both of these levels of analysis simultaneously, then the ALT model might be the best option. In short, the selection of a modeling strategy, as always, depends on theory, but in the case of LTM more refined hypotheses about how change occurs are needed to guide appropriate model selection.
Special Topics in LTM
We have presented a sampling of available modeling strategies that might be of interest to applied researchers studying individual differences in trajectories of psychopathology and abnormal behavior over time. However, the actual estimation of a particular model often presents a number of additional challenges that are common to both LTMs and other analytic methods when applied to empirical data in psychopathology research. We would like to conclude with a brief review of several issues that are particularly salient in these types of studies. These challenges include the role of missing data, assumptions about the distributions of the repeated measures, and the evaluation of model fit. As with other sections of our article, we present only a summary of these issues and recommend more detailed resources for the interested reader.
Missing data
The presence of missing data is a ubiquitous problem in all areas of longitudinal research, but this can be particularly vexing in studies of abnormal behavior over time. Up to even a few years ago, the primary tool for handling missing data was to use listwise deletion and to consider only complete case analysis. It has long been known that this is a highly restrictive approach that can result in multiple sources of bias (see Allison, 2001, and 2003 [this issue], for an excellent review on missing data analysis). Fortunately, several powerful approaches are now available that permit the inclusion of partially missing cases in many types of LTM applications. Although these methods also make important assumptions about the mechanism of missingness, evidence suggests that there is far less risk of bias with the retention of partially missing cases using these new methods compared with the use of listwise deletion with complete case analysis.
The two primary methods for incorporating missing data within the LTM framework are multiple imputation (MI) and full information maximum likelihood (FIML). Again, a detailed exploration of these two methods is beyond the scope of this article. However, Allison (2001) provides an excellent review of recent developments in missing data analysis; FIML is described in greater detail in Allison (1987, 2000) and Arbuckle (1996), and MI is described in Rubin (1976, 1987) and Schafer (1997, 1999). Although MI and FIML approaches to missing data analysis are characterized by similar goals, the actual execution of these methods is quite different. MI generates a complete data set using a model to impute missing cases based on information drawn from present cases. To account for sampling variability in these imputed cases, this process is repeated multiple times (typically from 5 to 10), and the LTM is fit to each of these imputed data sets. Finally, the parameter estimates are pooled across all of the models, and standard errors and fit statistics are bootstrapped to allow for inference testing. In contrast, the FIML approach fits a likelihood to each individual case in the sample using whatever data that case has to offer. These likelihoods are then weighted and summed over all cases to result in a final likelihood, parameter estimates, and standard errors. Regardless of which approach is adopted, we strongly recommend that one of these methods be closely considered when using LTMs in the presence of missing data.
Distributional assumptions
Normal theory maximum likelihood is by far the most common method of estimation used in practice, and this explicitly assumes that the residuals (or disturbances) of the endogenous (or dependent) measures are multivariately normally distributed. In many empirical studies of psychopathology, this is an extremely difficult assumption to meet. That is, we are often interested in behavior that is dichotomous (e.g., diagnostic status, hospital admission, suicide attempt), ordinal (e.g., a symptom is definitely absent, may be present, or is definitely present), or continuous but not normally distributed (e.g., number of alcohol use dependency symptoms, frequency of obsessive–compulsive disorder checking behaviors). However, as with the analysis of missing data, great strides have recently been made in methods of estimation that do not assume that the residuals of the endogenous measures are multivariately normally distributed. (See West, Finch, & Curran, 1995, for a general review.)
Although several options are available for modeling categorical dependent measures, a frequently used approach is weighted least squares estimation, which is based on a polychoric–polyserial correlation matrix and appropriate asymptotic weight matrix. There is a broad literature in this area, and we will not detail this here. (See Muthén, 1979, 1983, 1984, 1993; Olsson, 1979; and Olsson, Drasgow, & Dorans, 1982, for further details.) Briefly, these approaches to categorical data analysis assume that the observed variables are discrete categorizations of truly continuous underlying counterparts. For example, it might be hypothesized that a dichotomous measure of the presence or absence of a particular psychiatric symptom is due to an underlying continuously distributed propensity to express the symptom in which the symptom is observed given the crossing of some threshold on the propensity continuum. The analytic goal is thus to estimate the relations among a set of dichotomous measures at the level of this underlying continuum. Procedurally, the correlational structure among the underlying continuous measures is estimated from the observed categorical measures, and the hypothesized model is then fit to this estimated correlational structure. An example of this technique applied within the LTM framework is presented in Muthén’s (1996) study of the relation between neuroticism and depression.
The second distributional challenge that arises in psychopathology research is nonnormality in continuous repeated measures. These measures cannot be used as dependent variables under normal theory maximum-likelihood estimation, and alternative methods are needed. Fortunately, several viable alternatives exist, such as Browne’s (1984) asymptotic distribution free estimator, that do not assume multivariate normality. Although ADF is asymptotically elegant, it is optimal with large sample sizes and may be analytically challenging when used in the small to moderate sample sizes often encountered in psychopathology research. Muthén, du Toit, and Spisic (in press) recently proposed a robust version of ADF that is designed to perform better in small sample sizes. This is a promising method, and initial simulation results are optimistic (Flora & Curran, 2003). Finally, Satorra (1990), Satorra and Bentler (1988) and others have proposed a robust maximum-likelihood and scaled chi-square test statistic. These robust methods use the normal theory maximum-likelihood parameter estimates (which are unbiased) but adjust the associated standard errors and test statistic for the presence of nonnormality. Simulation studies suggest that these robust methods are well behaved in small to moderate sample sizes (e.g., Curran, West, & Finch, 1996; West et al., 1995), and these methods should be closely considered whenever studying repeated measures that do not meet the assumptions of multivariate normality imposed by standard maximum likelihood estimation.
Model evaluation
How to best evaluate overall model fit is a matter of some ongoing controversy, especially in the use of LTM. In a standard SEM, the goal of the analysis is to parameterize the hypothesized model so that the covariance matrix that is implied by the model closely approximates the covariance matrix that was observed in the sample. The omnibus chi-square test evaluates the null hypothesis that the model-implied covariance matrix is equal to the population covariance matrix. However, because the LTM evaluates both the covariance matrix and the mean vector of all of the variables in the model, the omnibus chi-square test simultaneously evaluates the equality of the model imposed and population covariance and mean structures. It can be argued that because the LTM is evaluating both covariance and mean structures and is imposing a highly restrictive factor loading matrix, standard criteria for evaluating model fit should be loosened (e.g., less stringent chi-square values and fit indexes should indicate adequate model fit).
This is an area in much need of further research, so we only offer our informed opinion on this matter here. Given this, we feel that a conservative approach to model evaluation is optimal. Thus, even though the LTM is indeed imposing a restrictive parameterization on the model structure and is also considering both covariance and mean structures, it is important that the adequacy of model fit be evaluated in precisely the same way as we would any other SEM. This is because we must gain confidence in the degree to which our hypothesized model adequately reproduces the characteristics of the data observed in our sample. The extent to which the hypothesized model fails to correspond to the sample data implies some model misspecification that likely results in parameter bias in some or all parts of the model. The LTM is a restrictive parameterization, but this restrictive structure is precisely what we want to test. If we pass this test, then we have confidence in the underlying process that gave rise to our set of repeated observations; if we fail, then some alternative process is likely responsible and we must consider ways of optimally capturing this prior to substantively interpreting the model results.
Because of space constraints, we do not provide a detailed review of current strategies for evaluating the adequacy of model fit in SEM. (See Bollen & Long, 1993; Hu & Bentler, 1995, 1999; MacCallum, Roznowski, & Necowitz, 1992; and Tanaka, 1993, for further details.) These various resources draw on information based on statistical theory, simulation studies, and applied experience. In general, it is recommended that model evaluation include the model chi-square test statistic, degrees of freedom, and probability value; one or more incremental fit indexes (e.g., CFI, IFI, or TLI); one or more stand-alone indexes (e.g., RMSEA with associated confidence intervals and standardized root mean residuals); evaluation of significant modification indexes or LaGrange multipliers; and examination of residuals between the observed and model-implied covariance and mean structure. Taken together, it is critical that all available evidence support an acceptable fit of the hypothesized model to the observed data prior to interpreting the resulting parameters with regard to substantive theory.
Additional topics to consider
There are a variety of interesting topics relating to the use of LTMs in psychopathology research that we did not explore, given space constraints. First, all of the models we have discussed assume that the sample is drawn from a homogeneous population. However, there may be situations in which subjects were drawn from a heterogeneous population in which group membership is not observed. Statistical methods are available for estimating growth mixture models that attempt to recover these unobserved classes and estimate models within each discrete class. (See Arminger, Stein, & Wittenberg, 1999; Bauer & Curran, 2003; Jedidi, Jagpal, & DeSarbo, 1997; Muthén, 2001a, 2001b; and Nagin, 1999, for further details on this.) Second, it might be of interest to researchers to obtain point estimates for individual trajectories in the sample to be used for model checking or graphical techniques (like those presented in Figure 1). Biesanz, Curran, and Bollen (2003) explore various approaches for estimating individual trajectories for the SEM trajectory model, Raudenbush and Bryk (2002) describe methods for the HLM trajectory model, and Carrig, Wirth, and Curran (in press) present a computer program for graphing trajectories in practice.7 A third topic that is of great importance to applied researchers is how to optimally code and interpret the measure of time. Throughout this article we have used a time-coding strategy that begins with zero so that the intercept is defined as the model-implied value at the initial time period. However, there are other methods for coding time that should be fully understood when using these in practice. (See Biesanz et al., 2003, for further details.) Finally, we considered only manifest measures for all of our LTMs discussed here. However, the full strength of the SEM framework could be invoked to allow for the use of multiple indicator latent factors for exogenous variables, mediators, or even repeated measures. (See McArdle, 1988, 1989, and Sayer & Cumsille, 2001, for further details.)
Potential Limitations
As with any data analytic technique, there are conditions under which the LTM may not be optimal for testing a set of questions of interest. First, a minimum of three repeated measures are needed to overidentify a linear trajectory model, and a minimum of four are needed for a quadratic model. In our own experience we have found that although three-time-point models can be quite useful, at least four time points provide much greater flexibility in model fitting and testing. Second, currently the LTM is primarily restricted to multiple time points nested within individual, and it is difficult to extend this to a higher order of nesting, such as multiple children nested within classroom. Approaches for these types of models have been explored in LTM (e.g., Khoo & Muthén, 2000; McArdle & Hamagami, 1996; Muthén, 1997a, 1997b), but the HLM framework may be currently best suited for these higher order nested structures. Third, both the LTM and HLM approaches implicitly assume that the same measure is used to assess the construct of interest over time. Although there are methods for handling changes in instruments over time (e.g., Burchinal et al., 2000), it is ideal if the same instrument can be retained over all time points (see Curran & Willoughby, 2003, for further discussion of this issue). Finally, we have found in our own work that great care must be taken to not move too far beyond one’s data when estimating more complex models. We recommend that data be carefully screened and that graphical and numerical diagnostics be used to identify potential outlying observations to decrease the probability of drawing erroneous conclusions from complex trajectory models.
Conclusions
Our goal here was to provide an introduction to the statistical underpinnings of the LTM combined with a discussion of how these models might optimally be used in psychopathology research. We have only touched on the many fascinating and complex issues associated with these models, and we encourage the interested reader to consult additional resources in this area for more detailed information. Taken together, the variety of models we have discussed allow for a myriad of theoretical questions to be empirically examined in ways not previously possible. We have found in our own work that the application of these new analytic strategies has pushed us to more carefully consider our hypotheses about stability and change over time and has given us a language for defining longitudinal processes more concretely. As always, the true strength of these techniques rests on the wisdom of researchers to select appropriate models to optimally test their theories of interest.
Acknowledgments
This work was supported in part by National Institute on Drug Abuse (NIDA) Grant DA13148 awarded to Patrick J. Curran and NIDA Grant DA12912 awarded to Andrea M. Hussong. Selected sample data sets and computer code used in this article can be directly downloaded from www.unc.edu/~curran. We thank the valuable input provided by Ken Bollen, R. J. Wirth, and the Carolina Structural Equation Modeling Group at the University of North Carolina.
Footnotes
Note that it is possible to incorporate individually varying measures of time denoted as λit indicating that the value of time can vary over individual. We do not explore this in detail here given space constraints, but see Mehta and West (2000) and Raudenbush (2001) for further details.
Note that equal spacing of assessments is not a requirement, and differential spacing of assessments can easily be incorporated (e.g., factor loadings set to 0, 1, 3, and 6 represent 1-month, 2-month and 3-month observation lags).
Technically the covariance term is itself not considered a random effect but a covariance between two random effects (i.e., ζαiand ζβi).
These are the same data from which the sample trajectories were drawn in Figure 1.
Our presentation here is a slight simplification of the model presented in Hussong et al. (2003), in which marijuana use was also included as a time-varying covariate.
For sake of clarity, this is a simplification of the model in Hussong et al. (2001).
The SAS program and associated documentation can be freely downloaded from www.unc.edu/~curran/olstraj.htm.
References
- Aber MS, McArdle JJ. Latent growth curve approaches to modeling the development of competence. In: Chandler M, Chapman M, editors. Criteria for competence. Hillsdale, NJ: Erlbaum; 1991. pp. 231–258. [Google Scholar]
- Aiken LS, West SG. Multiple regression: Testing and interpreting interactions. Newbury Park, CA: Sage; 1991. [Google Scholar]
- Allison PD. Estimation of linear models with incomplete data. In: Clogg C, editor. Sociological methodology 1987. Washington, DC: American Sociological Association; 1987. pp. 71–103. [Google Scholar]
- Allison PD. Multiple imputation for missing data. Sociological Methods & Research. 2000;28:301–309. [Google Scholar]
- Allison PD. Missing data. Newbury Park, CA: Sage; 2001. [Google Scholar]
- Andrews JA, Duncan SC. The effect of attitude on the development of adolescent cigarette use. Journal of Substance Abuse. 1998;10:1–7. doi: 10.1016/s0899-3289(99)80135-7. [DOI] [PubMed] [Google Scholar]
- Arbuckle JL. Full information estimation in the presence of incomplete data. In: Marcoulides GA, Schumaker RE, editors. Advanced structural equation modeling: Issues and techniques. Mahwah, NJ: Erlbaum; 1996. pp. 243–278. [Google Scholar]
- Arminger G, Stein P, Wittenberg J. Mixtures of conditional mean- and covariance-structure models. Psychometrika. 1999;64:475–494. [Google Scholar]
- Barnes GM, Reifman AS, Farrell MP, Dintcheff BA. The effects of parenting in the development of adolescent alcohol misuse: A six-wave latent growth model. Journal of Marriage and the Family. 2000;62:175–186. [Google Scholar]
- Baron RM, Kenny DA. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bauer DJ, Curran PJ. Distributional assumptions of growth mixture models: Implications for over-extraction of latent trajectory classes. Psychological Methods. 2003;8:338–363. doi: 10.1037/1082-989X.8.3.338. [DOI] [PubMed] [Google Scholar]
- Biesanz JC, Curran PJ, Bollen KA. Estimating individual trajectories in latent trajectory models. 2003 Manuscript submitted for publication. [Google Scholar]
- Biesanz JC, Deeb-Sosa N, Aubrecht AM, Bollen KA, Curran PJ. The role of coding time in estimating and interpreting growth curve models. 2003 doi: 10.1037/1082-989X.9.1.30. Manuscript submitted for publication. [DOI] [PubMed] [Google Scholar]
- Bollen KA. Total, direct, and indirect effects in structural equation models. In: Clogg C, editor. Sociological Methodology 1987. Washington, DC: American Sociological Association; 1987. pp. 37–69. [Google Scholar]
- Bollen KA. Structural equations with latent variables. New York: Wiley; 1989. [Google Scholar]
- Bollen KA, Curran PJ. Autoregressive latent trajectory (ALT) models: A synthesis of two traditions. 2003 Manuscript submitted for publication. [Google Scholar]
- Bollen KA, Long JS. Testing structural equation models. Newbury Park, CA: Sage; 1993. [Google Scholar]
- Browne MW. Asymptotically distribution-free methods for the analysis of covariance structures. British Journal of Mathematical & Statistical Psychology. 1984;37(1):62–83. doi: 10.1111/j.2044-8317.1984.tb00789.x. [DOI] [PubMed] [Google Scholar]
- Browne MW, du Toit SHC. Models for learning data. In: Collins L, Horn J, editors. Best methods for the analysis of change: Recent advances, unanswered questions, future directions. Washington, DC: American Psychological Association; 1991. pp. 47–68. [Google Scholar]
- Bryk AS, Raudenbush SW. Application of hierarchical linear models to assessing change. Psychological Bulletin. 1987;101:147–158. [Google Scholar]
- Carrig M, Wirth RJ, Curran PJ. A SAS Macro for Estimating and Visualizing Individual Growth Curves. Structural Equation Modeling in press. [Google Scholar]
- Chassin L, Curran PJ, Hussong AM, Colder CR. The relation of parent alcoholism to adolescent substance use: A longitudinal follow-up study. Journal of Abnormal Psychology. 1996;105:70–80. doi: 10.1037//0021-843x.105.1.70. [DOI] [PubMed] [Google Scholar]
- Colder CR, Chassin L, Stice EM, Curran PJ. Alcohol expectancies as potential mediators of parent alcoholism effects on the development of adolescent heavy drinking. Journal of Research on Adolescence. 1997;7:349–374. [Google Scholar]
- Crowder D, Hand M. Practical longitudinal data analysis. London: Chapman and Hall; 1996. [Google Scholar]
- Curran PJ. Comparing three modern approaches to longitudinal data analysis: An examination of a single developmental sample. 1997 Retrieved from www.unc.edu/~curran/srcd-docs/srcdmeth.pdf.
- Curran PJ. A latent curve framework for studying developmental trajectories of adolescent substance use. In: Rose J, Chassin L, Presson C, Sherman J, editors. Multivariate applications in substance use research. Hillsdale, NJ: Erlbaum; 2000. pp. 1–42. [Google Scholar]
- Curran PJ, Bauer DJ, Willoughby MT. Testing and probing main effects and interactions in latent trajectory models. 2003 doi: 10.1037/1082-989X.9.2.220. Manuscript submitted for publication. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Bauer DJ, Willoughby MT. Within-level and across-level interactions in hierarchical linear growth models. In: Bergeman CS, Boker SM, editors. The Notre Dame series on quantitative methodology: Vol. 1. Methodological issues in aging research. Mahwah, NJ: Erlbaum; in press. [Google Scholar]
- Curran PJ, Bollen KA. The best of both worlds: Combining autoregressive and latent curve models. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 105–136. [Google Scholar]
- Curran PJ, Harford TC, Muthén BO. The relation between heavy alcohol use and bar patronage: A latent growth model. Journal of Studies on Alcohol. 1996;57:410–418. doi: 10.15288/jsa.1996.57.410. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Hussong AM. Structural equation modeling of repeated measures data. In: Moskowitz D, Hershberger S, editors. Modeling intraindividual variability with repeated measures data: Methods and applications. New York: Erlbaum; 2001. [Google Scholar]
- Curran PJ, Muthén BO. The application of latent curve analysis to testing developmental theories in intervention research. American Journal of Community Psychology. 1999;27:567–595. doi: 10.1023/A:1022137429115. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Muthén BO, Harford TC. The influence of changes in marital status on developmental trajectories of alcohol use in young adults. Journal of Studies on Alcohol. 1998;59:647–658. doi: 10.15288/jsa.1998.59.647. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Stice E, Chassin L. The relation between adolescent and peer alcohol use: A longitudinal random coefficients model. Journal of Consulting and Clinical Psychology. 1997;65:130–140. doi: 10.1037//0022-006x.65.1.130. [DOI] [PubMed] [Google Scholar]
- Curran PJ, West SG, Finch J. The robustness of test statistics to non-normality and specification error in confirmatory factor analysis. Psychological Methods. 1996;1:16–29. [Google Scholar]
- Curran PJ, Willoughby MJ. Reconciling theoretical and statistical models of developmental processes. Development and Psychopathology. 2003;15:581–612. doi: 10.1017/s0954579403000300. [DOI] [PubMed] [Google Scholar]
- du Toit SHC, Cudeck R. The analysis of nonlinear random coefficient regression models with LISREL using constraints. In: Cudeck R, du Toit S, Sorbom D, editors. Structural equation modeling: Present and future. Lincolnwood, IL: Scientific Software International; 2000. pp. 259–278. [Google Scholar]
- Duncan TE, Duncan SC, Strycker LA, Li F, Alpert A. An introduction to latent variable growth curve modeling: Concepts, issues, and applications. Mahwah, NJ: Erlbaum; 1999. [Google Scholar]
- Dwyer J. Statistical models for the social and behavioral sciences. Oxford, England: Oxford University Press; 1983. [Google Scholar]
- Flora DB, Curran PJ. Evaluation of categorical variable methodology for confirmatory factor analysis with Likert-type data. 2003 Manuscript submitted for publication. [Google Scholar]
- Ge X, Lorenz FO, Conger RD, Elder GH, Simons RL. Trajectories of stressful life events and depressive symptoms during adolescence. Developmental Psychology. 1994;30:467–483. [Google Scholar]
- Gompertz B. On the nature of the function expressive of the law of human mortality. Philosophical Transactions of the Royal Society. 1825;115:513–583. [Google Scholar]
- Harford TC, Muthén BO. Alcohol use among college students: The effects of prior problem behaviors and change of residence. Journal of Studies on Alcohol. 2001;62:306–312. doi: 10.15288/jsa.2001.62.306. [DOI] [PubMed] [Google Scholar]
- Hu L-T, Bentler P. Evaluating model fit. In: Hoyle RH, editor. Structural equation modeling: Concepts, issues, and applications. London: Sage; 1995. pp. 76–99. [Google Scholar]
- Hu LT, Bentler P. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
- Hussong AM, Curran PJ, Chassin L. Pathways of risk for children of alcoholics’ accelerated heavy alcohol use. Journal of Abnormal Child Psychology. 1998;26:453–466. doi: 10.1023/a:1022699701996. [DOI] [PubMed] [Google Scholar]
- Hussong AM, Curran PJ, Moffitt TE, Caspi A, Carrig MM. Substance abuse ensnares young adults in trajectories of antisocial behavior. 2003 doi: 10.1017/s095457940404012x. Manuscript submitted for publication. [DOI] [PubMed] [Google Scholar]
- Hussong AM, Hicks RE, Levy SA, Curran PJ. Specifying the relations between affect and heavy alcohol use among young adults. Journal of Abnormal Psychology. 2001;110:449–461. doi: 10.1037//0021-843x.110.3.449. [DOI] [PubMed] [Google Scholar]
- Jedidi K, Jagpal HS, DeSarbo WS. Finite-mixture structural equation models for response-based segmentation and unobserved heterogeneity. Marketing Science. 1997;16:39–59. [Google Scholar]
- Kenny DA, Zautra A. The trait-state-error model for multi-wave data. Journal of Consulting and Clinical Psychology. 1995;63:52–59. doi: 10.1037//0022-006x.63.1.52. [DOI] [PubMed] [Google Scholar]
- Khoo ST, Muthén B. Longitudinal data on families: Growth modeling alternatives. In: Rose J, Chassin L, Presson C, Sherman J, editors. Multivariate applications in substance use research. Hillsdale, NJ: Erlbaum; 2000. pp. 43–78. [Google Scholar]
- Kraatz-Keiley M, Bates JE, Dodge KA, Pettit GS. A cross-domain growth analysis: Externalizing and internalizing behaviors during eight years of childhood. Journal of Abnormal Child Psychology. 2000;28:161–179. doi: 10.1023/a:1005122814723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long JS. Regression models for categorical and limited dependent variables: Analysis and interpretation. Newbury Park, CA: Sage; 1997. [Google Scholar]
- Lorentz FO, Simons RL, Conger RD, Elder GH. Married and recently divorced mothers’ stressful events and distress: Tracing change across time. Journal of Marriage and the Family. 1997;59:219–232. [Google Scholar]
- MacCallum RC, Kim C, Malarkey W, Kiecolt-Glaser J. Studying multivariate change using multilevel models and latent curve models. Multivariate Behavioral Research. 1997;32:215–253. doi: 10.1207/s15327906mbr3203_1. [DOI] [PubMed] [Google Scholar]
- MacCallum RC, Roznowski M, Necowitz LB. Model modifications in covariance structure analysis: The problem of capitalization on chance. Psychological Bulletin. 1992;111:490–504. doi: 10.1037/0033-2909.111.3.490. [DOI] [PubMed] [Google Scholar]
- McArdle JJ. Dynamic but structural equation modeling of repeated measures data. In: Nesselroade JR, Cattell RB, editors. Handbook of multivariate experimental psychology. 2. New York: Plenum Press; 1988. pp. 561–614. [Google Scholar]
- McArdle JJ. Structural modeling experiments using multiple growth functions. In: Ackerman P, Kanfer R, Cudeck R, editors. Learning and individual differences: Abilities, motivation and methodology. Hillsdale, NJ: Erlbaum; 1989. pp. 71–117. [Google Scholar]
- McArdle JJ. Structural models of developmental theory in psychology. In: Van Geert P, Mos LP, editors. Annals of theoretical psychology. Vol. 7. New York: Plenum Press; 1991. pp. 139–160. [Google Scholar]
- McArdle JJ. A latent difference score approach to longitudinal dynamic structural analyses. In: Cudeck R, du Toit S, Sorbom D, editors. Structural equation modeling: Present and future. Lincolnwood, IL: Scientific Software International; 2001. pp. 342–380. [Google Scholar]
- McArdle JJ, Hamagami . Multilevel models from a multiple group structural equation perspective. In: Marcoulides G, Schumacker R, editors. Advanced structural equation modeling techniques. Hillsdale, NJ: Erlbaum; 1996. pp. 89–124. [Google Scholar]
- McArdle JJ, Hamagami F. Latent difference score structural models for linear dynamic analyses with incomplete longitudinal data. In: Collins L, Sayer A, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 139–175. [Google Scholar]
- Mehta PD, West SG. Putting the individual back in individual growth curves. Psychological Methods. 2000;5:23–43. doi: 10.1037/1082-989x.5.1.23. [DOI] [PubMed] [Google Scholar]
- Menard S. Longitudinal research, second edition. Newbury Park, CA: Sage; 2002. [Google Scholar]
- Meredith W, Tisak J. “Tuckerizing” curves. Paper presented at the annual meeting of the Psychometric Society; Santa Barbara, CA. 1984. Jun, [Google Scholar]
- Meredith W, Tisak J. Latent curve analysis. Psychometrika. 1990;55:107–122. [Google Scholar]
- Moffitt TE. Adolescence-limited and life-course-persistent antisocial behavior: A developmental taxonomy. Psychological Review. 1993;100:674–701. [PubMed] [Google Scholar]
- Muthén BO. A structural probit model with latent variables. Journal of the American Statistical Association. 1979;74:807–811. [Google Scholar]
- Muthén BO. Latent variable structural equation modeling with categorical data. Journal of Econometrics. 1983;22:48–65. [Google Scholar]
- Muthén BO. A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika. 1984;49:115–132. [Google Scholar]
- Muthén B. Analysis of longitudinal data using latent variable models with varying parameters. In: Collins LM, Horn JL, editors. Best methods for the analysis of change: Recent advances, unanswered questions, future directions. Washington, DC: American Psychological Association; 1991. pp. 1–17. [Google Scholar]
- Muthén B. Goodness of fit with categorical and other non-normal variables. In: Bollen KA, Long JS, editors. Testing structural equation models. Newbury Park, CA: Sage; 1993. pp. 205–243. [Google Scholar]
- Muthén BO. Growth modeling with binary responses. In: Eye AV, Clogg C, editors. Categorical variables in developmental research: Methods of analysis. San Diego, CA: Academic Press; 1996. pp. 37–54. [Google Scholar]
- Muthén BO. Latent variable growth modeling with multilevel data. In: Berkane M, editor. Latent variable modeling with application to causality. New York: Springer-Verlag; 1997a. pp. 149–161. [Google Scholar]
- Muthén BO. Latent variable modeling with longitudinal and multilevel data. In: Raftery A, editor. Sociological methodology. Boston: Blackwell; 1997b. pp. 453–480. [Google Scholar]
- Muthén BO. Latent variable mixture modeling. In: Marcoulides GA, Schumacker RE, editors. New developments and techniques in structural equation modeling. Hillsdale, NJ: Erlbaum; 2001a. pp. 1–33. [Google Scholar]
- Muthén BO. Second-generation structural equation modeling with a combination of categorical and continuous latent variables: New opportunities for latent class/latent growth modeling. In: Collins LM, Sayer A, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001b. pp. 291–322. [Google Scholar]
- Muthén BO, Curran PJ. General longitudinal modeling of individual differences in experimental designs: A latent variable framework for analysis and power estimation. Psychological Methods. 1997;2:371–402. [Google Scholar]
- Muthén BO, du Toit SHC, Spisic D. Robust inference using weighted least squares and quadratic estimating equations in latent variable modeling with categorical and continuous outcomes. Psychometrika in press. [Google Scholar]
- Muthén BO, Muthén LK. The development of heavy drinking and alcohol-related problems from ages 18 to 37 in a U.S. national sample. Journal of Studies on Alcohol. 2000;61:290–300. doi: 10.15288/jsa.2000.61.290. [DOI] [PubMed] [Google Scholar]
- Nagin D. Analyzing developmental trajectories: A semi-parametric, group-based approach. Psychological Methods. 1999;4:139–177. doi: 10.1037/1082-989x.6.1.18. [DOI] [PubMed] [Google Scholar]
- Olsson U. Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika. 1979;44:443–460. [Google Scholar]
- Olsson U, Drasgow F, Dorans NJ. The polyserial correlation coefficient. Psychometrika. 1982;47:337–347. [Google Scholar]
- Palmer CE, Kawakami R, Reed LJ. Anthropometric studies of individual growth: II. Age, weight, and rate of growth in weight, elementary school children. Child Development. 1937;8:47–61. [Google Scholar]
- Rao CR. Some statistical methods for comparison of growth curves. Biometrika. 1958;51:83–90. [Google Scholar]
- Raudenbush SW. Toward a coherent framework for comparing trajectories of change. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 33–64. [Google Scholar]
- Raudenbush SW, Bryk AS. Hierarchical linear models: Applications and data analysis methods, second edition. Newbury Park, CA: Sage; 2002. [Google Scholar]
- Rodebaugh TL, Curran PJ, Chambless DL. Expectancy of panic in the maintenance of daily anxiety in panic disorder with agoraphobia: A longitudinal test of competing models. Behavior Therapy. 2002;33:315–336. [Google Scholar]
- Rogosa D, Willett JB. Understanding correlates of change by modeling individual differences in growth. Psychometrika. 1985;50:203–228. [Google Scholar]
- Rubin DB. Inference and missing data. Biometrika. 1976;63:581–592. [Google Scholar]
- Rubin DB. Multiple imputation for nonresponse in surveys. New York: Wiley; 1987. [Google Scholar]
- Satorra A. Robustness issues in structural equation modeling: A review of recent developments. Quality and Quantity. 1990;24:367–386. [Google Scholar]
- Satorra A, Bentler PM. Scaling corrections for chi-square statistics in covariance structure analysis. ASA Proceedings of the Business and Economic Section. 1988:308–313. [Google Scholar]
- Sayer A, Cumsille P. Second-order latent growth models. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 179–200. [Google Scholar]
- Schafer JL. Analysis of incomplete multivariate data. London: Chapman & Hall/CRC; 1997. [Google Scholar]
- Schafer JL. Multiple imputation: A primer. Statistical Methods in Medical Research. 1999;8:3–15. doi: 10.1177/096228029900800102. [DOI] [PubMed] [Google Scholar]
- Schmitt MJ, Steyer R. A latent state-trait model (not only) for social desirability. Personality and Individual Differences. 1993;14:519–529. [Google Scholar]
- Sher KJ, Wood PK. Methodological issues in conducting prospective research on alcohol-related behavior: A report from the field. In: Bryant KJ, West SG, Windle M, editors. The science of prevention: Methodological advances from alcohol and substance abuse research. Washington, DC: American Psychological Association; 1997. pp. 3–41. [Google Scholar]
- Silva PA, Stanton WR, editors. From child to adult: The Dunedin Multidisciplinary Health and Development Study. Auckland, New Zealand: Oxford University Press; 1996. [Google Scholar]
- Sobel M. Asymptotic confidence intervals for indirect effects in structural equation models. In: Leinhardt S, editor. Sociological methodology, 1982. San Francisco: Jossey-Bass; 1982. pp. 290–312. [Google Scholar]
- Stoolmiller M. Antisocial behavior, delinquent peer association, and unsupervised wandering for boys: Growth and change from childhood to early adolescence. Multivariate Behavioral Research. 1994;29:263–288. doi: 10.1207/s15327906mbr2903_4. [DOI] [PubMed] [Google Scholar]
- Tanaka JS. Multifaceted conceptions of fit in structural equation models. In: Bollen K, Long S, editors. Testing structural equation models. Newbury Park, CA: Sage; 1993. pp. 10–39. [Google Scholar]
- Tisak J, Meredith W. Descriptive and associative developmental models. In: von Eye A, editor. New statistical methods in developmental research. New York: Academic Press; 1990. pp. 125–149. [Google Scholar]
- Tucker LR. Determination of parameters of a functional relation by factor analysis. Psychometrika. 1958;23:19–23. [Google Scholar]
- West SG, Finch JF, Curran PJ. Structural equation models with non-normal variables: Problems and remedies. In: Hoyle R, editor. Structural equation modeling: Concepts, issues and applications. Newbury Park, CA: Sage; 1995. pp. 56–75. [Google Scholar]
- Wickrama KAS, Lorenz FO, Conger RD, Elder GH. Marital quality and physical illness: A latent growth curve analysis. Journal of Marriage and the Family. 1997;59:143–155. [Google Scholar]
- Will TA, Sandy JM, Yaeger AM, Cleary SD, Shinar O. Coping dimensions, life stress, and adolescent substance use: A latent growth analysis. Journal of Abnormal Psychology. 2001;110:309–323. doi: 10.1037//0021-843x.110.2.309. [DOI] [PubMed] [Google Scholar]
- Willett JB, Sayer AG. Using covariance structure analysis to detect correlates and predictors of individual change over time. Psychological Bulletin. 1994;116:363–381. [Google Scholar]
- Windle M. Alternative latent-variable approaches to modeling change in adolescent alcohol involvement. In: Bryant KJ, West SG, Windle M, editors. The science of prevention: Methodological advances from alcohol and substance abuse research. Washington, DC: American Psychological Association; 1997. pp. 43–78. [Google Scholar]
- Windle M, Windle RC. Depressive symptoms and cigarette smoking among middle adolescents: Prospective associations and intra-personal and interpersonal influences. Journal of Consulting and Clinical Psychology. 2001;69:215–226. [PubMed] [Google Scholar]
- Wishart J. Growth rate determination in nutrition studies with bacon pig and their analysis. Biometrika. 1938;30:16–28. [Google Scholar]