Blur-resistant Perimetric Stimuli

Abstract

Purpose

To develop perimetric stimuli which are resistant to the effects of peripheral defocus.

Methods

One eye each was tested on subjects free of eye disease. Experiment 1 assessed spatial frequency, testing 12 subjects at eccentricities from 2° to 7°, using blur levels from 0 D to 3 D for two (Gabor) stimuli (spatial standard deviation (SD) = 0.5°, spatial frequencies of 0.5 and 1.0 cpd). Experiment 2 assessed stimulus size, testing 12 subjects at eccentricities from 4° to 7°, using blur levels 0 D to 6 D, for two Gaussians with SDs of 0.5° and 0.25° and a 0.5 cpd Gabor with SD of 0.5°. Experiment 3 tested 13 subjects at eccentricities from fixation to 27°, using blur levels 0 D to 6 D, for Gabor stimuli at 56 locations; the spatial frequency ranged from 0.14 to 0.50 cpd with location, and SD was scaled accordingly.

Results

In experiment 1, blur by 3 D caused a small decline in log contrast sensitivity (CS) for the 0.5 cpd stimulus (mean ± SE = −0.09 ± 0.08 log unit) and a larger (t = 7.7, p <0.0001) decline for the 1.0 cpd stimulus (0.37 ± 0.13 log unit). In experiment 2, blur by 6 D caused minimal decline for the larger Gaussian, by −0.17 ± 0.16 log unit, and larger (t >4.5, p < 0.001) declines for the smaller Gaussian (−0.33 ± 0.16 log unit) and the Gabor (−0.36 ± 0.18 log unit). In experiment 3, blur by 6 D caused declines by 0.27 ± 0.05 log unit for eccentricities from 0° to 10°, by 0.20 ± 0.04 log unit for eccentricities from 10° to 20° and 0.13 ± 0.03 log unit for eccentricities from 20°–27°.

Conclusions

Experiments 1 & 2 allowed us to design stimuli for Experiment 3 that were resistant to effects of peripheral defocus.

Automated perimetric testing is an integral part of 21^st-century clinical practice, yet relies on stimuli developed 70 years ago. The most commonly used perimetric stimulus is a sharp-edged circular luminance increment with diameter of 26 minutes of arc, the “size III” stimulus developed by Goldmann¹. For the central visual field (within 30° of fixation), sensitivity to this stimulus is reduced by modest amounts of optical defocus,^2–7 so trial lenses are used to refract for the test distance. However, it is now well documented that there is the potential for significant shifts in the refraction of an eye at locations within 30° of fixation, with substantial variation in peripheral refraction across individuals.⁸ Defocus at 20° from fixation ranges from −2 D to +2D across individuals,⁸ and 2 D of defocus has been found to reduce sensitivity to size III by 0.3 log unit ². Individual variations in peripheral defocus may be one reason that between-subject variability for size III perimetry increases with eccentricity⁹.

Effects of optical blur can be greatly reduced by use of grating stimuli at 0.25 cycle/degree, as in frequency-doubling perimetry, where normal between-subject variability does not increase with eccentricity^{10, 11}. These grating stimuli are quite large, 100 deg², with the same contrast across the entire stimulus, making them poorly suited for localizing visual field defects. By comparison, the conventional size III stimulus covers less than 0.2% of the area covered by these frequency-doubling stimuli. The goal of the current study was to use Gaussian windows to produce stimuli substantially smaller than 100 deg² that retained much of the relative immunity to effects of blur of 0.25 cpd gratings.

Gaussian windows allow smaller and more localized stimuli than hard-edged gratings, and provide a central location at maximum contrast rather than the same contrast across the stimulus as in frequency-doubling perimetry and Pulsar perimetry¹². The use of Gaussian-windowed sinusoids in perimetry has been termed “contrast sensitivity perimetry” (CSP)¹³. We have found that CSP with spatial frequencies from 0.38 to 1.0 cycles per degree (cpd) is as effective as size III perimetry, frequency-doubling perimetry and area of neuroretinal rim in assessing depth of defect^{14, 15}. The current study assessed the relative depth of field for potential CSP stimuli with peak spatial frequencies from 0.1 to 1.0 cpd, in order to reduce the potential effects of peripheral defocus¹⁶. The first two experiments were performed in the macula, where blur conditions could be manipulated without concern for peripheral defocus. The first experiment varied spatial frequency at a fixed size and the second experiment varied size. These results were used to design CSP stimuli that should be similar to 0.25 cpd gratings in terms of resistance to effects of peripheral defocus. The third experiment tested this prediction.

Oriented grating stimuli are affected by astigmatic error, for which blur effect is maximum when the angle of the astigmatism is perpendicular to the orientation of the grating. The J₀ astigmatism component¹⁷ approaches 1D at 30° eccentricity¹⁶, so oriented stimuli could have as much as 3D of peripheral defocus. Therefore this study aimed to develop stimuli for which a blur level of 3 D has only minor impact on perimetric sensitivity, and effect of blur does not increase with eccentricity.

METHODS

Expt 1 assessed effects of blur vs peak spatial frequency in the macula for a fixed size stimulus with no change in mean luminance. Expt 2 assessed effects of blur vs size in the macula with a change in mean luminance. Results of these two experiments were used to design stimuli that should be minimally affected by 3 D of optical blur, with small stimuli in the macula and larger (more blur-resistant) stimuli at more eccentric locations in the central visual field. This prediction was tested in Expt 3.

Participants

Expt 1 was conducted at Indiana University (IU) where 10 subjects were recruited out of the larger pool of control subjects in a longitudinal study of contrast sensitivity perimetry (CSP) at the IU School of Optometry. These subjects had previously participated in this perimetric research project and were experienced. Their ages ranged from 45 to 64 (mean ± SD, 54.5 ± 5.9 years).

Expts 2 & 3 were conducted at the State University of New York (SUNY) School of Optometry, where subjects were recruited from optometry students who had prior experience with perimetry. Experiment 2 recruited 12 people ages 24 to 26 years (25.1 ± 1.1 years), and Experiment 3 recruited people ages 23 to 27 years (24.5 ± 1.1 years). The only overlap between experiments is that two people who participated in Experiment 3 also participated in Experiment 2.

For all three experiments, subjects were recruited who were free of eye disease on a recent comprehensive evaluation within 2 years, including a detailed personal and family history, assessment of visual acuity, refraction, extra-ocular muscle function and binocular vision, as well as evaluation of anterior segment, screening visual fields and dilated fundus exam. Additional inclusion criteria were: best corrected visual acuity of 20/20 or better, spherical correction within −6 to + 2 D, cylinder correction < 3D, clear ocular media, and IOP < 22 mm Hg. Exclusion criteria were an ocular or systemic disease known to affect the visual field, a first-degree relative with glaucoma, usage of medications known to affect visual function. The preferred eye of each person was tested, and data collected from the left eyes were converted to right-eye format by multiplying x-values for all locations by −1. The other eye was occluded with a translucent white patch.

The research for this study adhered to the tenets of the Declaration of Helsinki and was approved by the institutional review boards at Indiana University (Expt 1) and SUNY College of Optometry (Expts 2 & 3). Informed consent was obtained from each participant after explanation of the procedures and goals of the study, before testing began.

Equipment

Custom testing stations were built using cathode-ray-tube (CRT) displays driven by a 14-bit visual stimulus generator that allowed precise control of contrast (ViSaGe; Cambridge Research Systems, Ltd., Cambridge, UK). A photometer with calibration software (Opti-Cal; Cambridge Research Systems Ltd.) was used to measure luminance versus voltage values for each phosphor, calculate transfer functions, and produce red-green-blue (RGB) gamma correction look-up tables. The resolution of the monitor was 800 X 600 pixels, subtending 42°X 35° of visual angle at 40 cm (Expts 1 & 2) and 51°X 42° at 33 cm (Expt 3). A webcam allowed the operator to continuously monitor the subject’s fixation stability.

Expt 1 used a 21-in. monitor (Diamond Pro 2070SB; Mitsubishi Digital Electronics America Inc. Irvine, CA) with a frame rate of 140 Hz. Expts 2 & 3 used a 21-in. monitor (Radius PressView 21SR, Miro Displays, Inc., Germany) with a frame rate of 152 Hz.

For Experiments 1 & 2, testing was in the macula and a 40 cm test distance was used. Each subject was asked to place his or her head in a chin rest (UHCOTech HeadSpot) with the forehead against a bar so that the eye was 40 cm from a fixation target. Trial frames were used to refract the subject for the 40 cm test distance, and accuracy of refraction was checked by having the subject read the 20/20 line on a near chart placed on the monitor.

For Experiment 3, a 33 cm test distance was used to allow testing of more eccentric locations, using a custom-built motorized headrest and monitor stand that allowed better control of head position, and two adjustable headrests which allowed compensation for prominence of the brow. Custom 50 mm spherical lenses were held in place by magnets, and plain glass was used when no spherical correction was needed, so that the metal rim remained as a cue to head and eye position. The patient's head was placed in the motorized chinrest and positioned so that the patient's pupil was centered in the corrective lens (checked with webcam) that was centered on the fixation target. The custom lenses were in 0.5 D steps, and the appropriate lens was selected based on the spherical equivalent of the subject’s refraction plus 3 D for the 33 cm test distance. Appropriateness of refraction was checked by having the subject read the 20/20 line on a near chart placed on the monitor (equivalent to 20/24 at this distance).

Stimuli

Stimuli were two-dimensional Gaussian windows multiplied by horizontal sinusoidal gratings. Stimulus size was determined by the standard deviation of the Gaussian window, and peak spatial frequency was determined by the spatial frequency of the grating, in cycles per degree (cpd). Luminance profiles are shown in Figure 1.

Figure 1.

Stimuli for Experiments 1 & 2. Grayscale images show the stimuli at maximum contrast, as presented on the display; differences in background luminance across stimuli are reflected in the grayscale in the image. Curves to the right and below show one-dimensional luminance profiles centered on the stimuli – curves on the bottom show luminance profiles for the stimuli above them, and curves on the right show vertical luminance profiles for the stimuli to their left. The peak spatial frequency (cpd) for each Gabor and the SD (°) for each Gaussian is shown with the curve. The top two stimuli are for Experiment 1, where the Gaussian window was fixed and spatial frequency was varied; the bottom three are for Experiment 2, which used two different Gaussian windows.

Experiment 1 used stimuli in sine phase, so there was no change in mean luminance of the window. Two stimuli were used, with the same size Gaussian window (SD = 0.5°), and grating spatial frequencies of 0.5 and 1.0 cpd, presented at twelve locations along the diagonal meridians with eccentricities of 1.6°, 4.2°, 7.1°. Background luminance was 50 cd/m².

Experiment 2 used two sizes for the Gaussian window, with SDs of 0.5° and 0.25°, with an increase in mean luminance of the stimuli. Two of the stimuli were Gaussian blobs (equivalent to Gabor in cosine phase at 0 cpd), an increase in mean luminance without oriented spatial content. The third was a Gabor in cosine phase with a peak spatial frequency of 0.5 cpd. The smaller Gaussian blob had similar width to the central bar in the 0.5 cpd stimulus. These stimuli were presented at eight locations along the diagonal meridians with eccentricities of 4.2° and 7.1°. Background luminance was 20 cd/m² for the Gabor cosine and 10 cd/m² for the Gaussian blobs

The third experiment used stimuli in sine phase, so there was no change in mean luminance of the window. Window size and spatial content varied with visual field location. Based on experiment 1, spatial frequencies did not exceed 0.5 cpd, and based on experiment 2, the smallest stimuli had windows with SD = 0.5°. Larger stimuli were used outside the macula to make contrast sensitivity relatively independent of stimulus location, using the method of Watson¹⁸ to magnify the stimulus, based on empirical magnification factors derived by our lab¹⁹. The product of SD times spatial frequency was held constant at 0.25; the stimuli had spatial frequencies from 0.14 to 0.5 cpd, and SDs from 0.5° to 1.8°. Luminance profiles for the stimuli are shown in Figure 2. Background luminance was 40 cd/m².

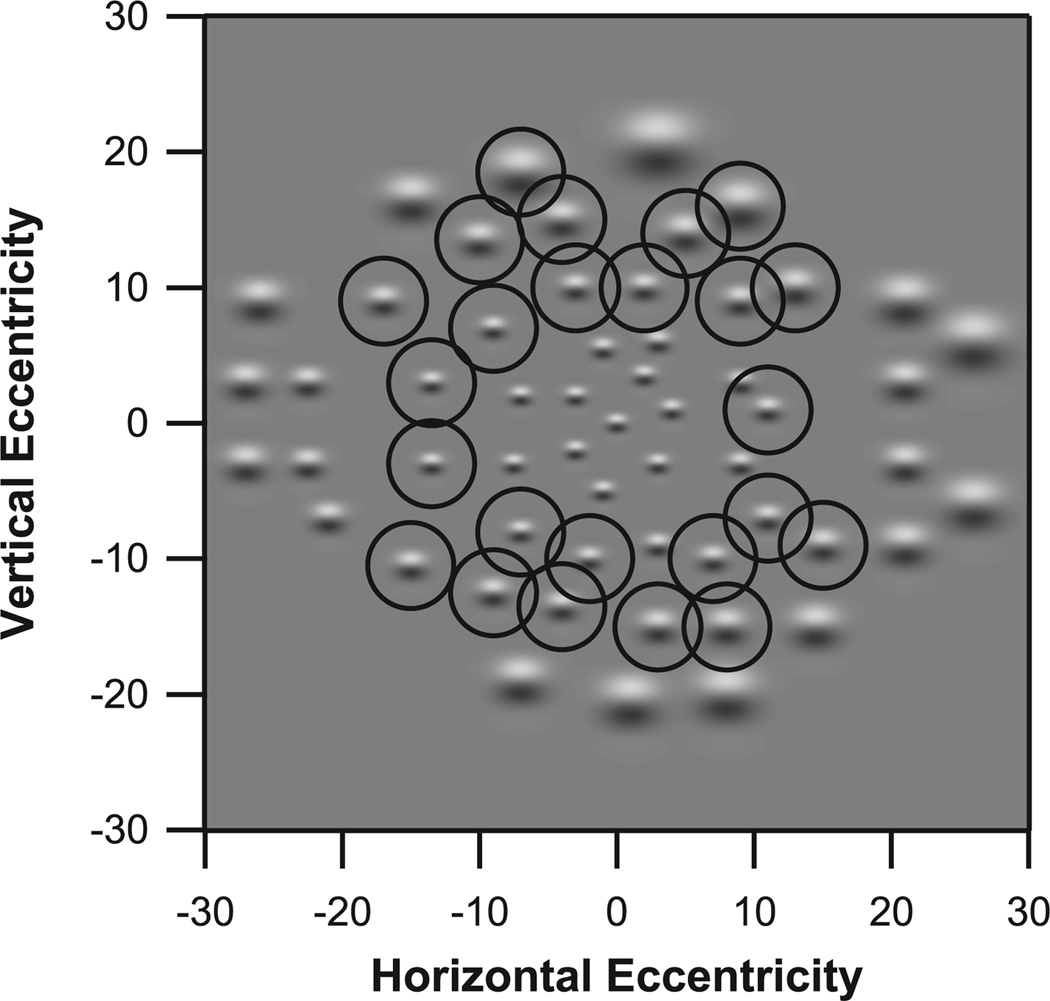
Figure 2.

Stimuli and test locations for the 56 stimuli in Experiment 3, with peak spatial frequencies from 0.14 to 0.5 cpd. The right eye presentation is shown. The stimulus at fixation has a peak spatial frequency of 0.5 cpd, and is identical to the second stimulus from the top in Figure 2. At other locations, stimuli are magnified versions of this stimulus. Circles indicate stimuli contained in Ring 2 (10° to 20°).

Temporal presentation was a 200 msec rectangular pulse for Experiments 1 & 2, and three cycles of 5 Hz counterphase flicker for Experiment 3. In a separate experiment investigating test-retest variability, 5 Hz counterphase flicker was found to be the most stable.

Protocol

Each subject was refracted for the test distance and then had positive blur added. Experiment 1 used eight conditions: two stimuli times four blur levels from 0 D to 3 D in steps of 1 D. Experiment 2 used nine conditions: three stimuli times three blur levels from 0 to 6D in steps of 3 D. Experiment 3 used five conditions, one stimulus at five blur levels from 0 to 6 D in steps of 1.5 D.

For Experiments 1 & 2, log contrast sensitivities were averaged across all locations, to give an average macular log contrast sensitivity for that test. For Experiment 3, log contrast sensitivities were averaged for three rings: Ring 1 included 14 locations at 0 to 9.5° eccentricity, Ring 2 included 25 locations at 10.2° to 19.8° eccentricity, and Ring 3 included 18 locations at 20.0° to 27.5° eccentricity. Figure 2 indicates which stimuli were associated with each ring.

Threshold Algorithm

Contrast sensitivity across the central visual field was measured by having the subject fixate a target in the center of the display and click a button whenever a stimulus was seen. Stimuli were presented at the different visual field locations on a uniform gray background, in a darkened room.

In Experiments 1 & 2 a one-down, one-up staircase method with four reversals was used to determine the subject’s contrast threshold at each location. For each staircase a stimulus with 25% contrast was presented first. Contrast of the stimulus was decreased by 0.3 log units, if responded to, or else increased by 0.3 log units if not responded to, until a reversal occurred. The second reversal was obtained with the same 0.3 log unit steps. For the third and fourth reversals, 0.15 log unit steps were employed. The reciprocal of the “last seen” contrast was the specific measure of contrast sensitivity, the last contrast for which the subject responded was taken as an estimate of contrast threshold. For Experiment 3, the threshold algorithm was a ZEST algorithm,²⁰ which terminated after 6 presentations²¹, and allowed twice as many locations to be tested in the same amount of time as the staircase. The inter-stimulus interval averaged 1700 msec for the staircase and 1200 msec for the ZEST, with a variable foreperiod.

Further detail on strategies for assessing and managing fixation loss, false positives, false negatives and other artifacts are described elsewhere¹⁹

RESULTS

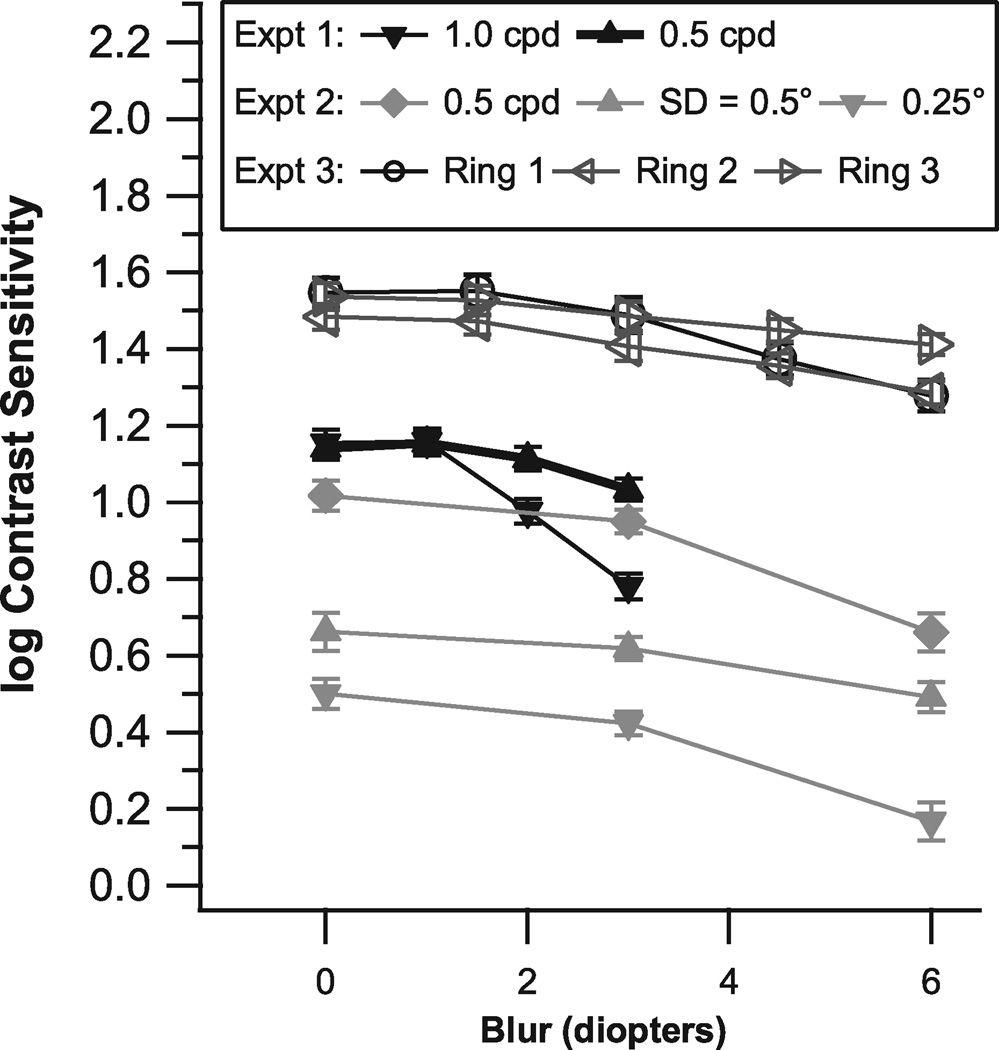
Figure 3 shows mean log contrast sensitivity versus blur condition for the three experiments; error bars show ± 1 standard error of the mean (SEM). In each experiment, SEMs were low and ranged from 0.03 to 0.06 log unit. A blur effect was considered to be significant when the mean log CS declined by more than three times the SEM.

Figure 3.

Mean log contrast sensitivity and standard error across subjects for each of the three experiments, as a function of blur condition. The mean for all locations was computed for each blur condition for experiments 1 & 2, and for Experiment 3 the mean was computed across locations in each ring.

For Experiment 1 (solid symbols in middle of Figure 3) there were significant blur effects at 2 D and 3 D for the 1.0 cpd stimulus, but not for the 0.5 cpd stimulus. The 3 D blur condition caused a greater decline (t = 7.7, p <0.0001) in log contrast sensitivity for the 1 cpd stimulus (−0.37 log unit) than for the 0.5 cpd stimulus (−0.11 log unit).

For Experiment 2 (solid symbols, middle and bottom in Figure 3), for all three stimuli there were significant blur effects for the 6 D condition but not for the 3 D condition. Effects of the 6 D blur condition were similar for the smaller window with SD = 0.25° (−0.33 log unit) and for the 0.5 cpd cosine stimulus (−0.36 log unit). The larger Gaussian (SD = 0.5°) showed less of a decline (t >4.5, p < 0.001), by −0.17 log unit.

For Experiment 3 (open symbols, top in Figure 3), Ring 1 had significant blur effects for the 4 D (−0.17 log unit) and 6 D (−0.27 log unit) conditions, and Ring 2 had a significant effect for the 6 D (−0.20 log unit) condition; there were no significant blur effects for Ring 3. For the 3 D blur condition, all three rings had less than 0.08 log unit decline in sensitivity. For each blur level, the standard deviation was greatest for Ring 1.

DISCUSSION

These experiments explored window size and spatial frequency content to identify stimuli that should be minimally affected by peripheral defocus. For the central visual field, peripheral defocus can be as much as 3 D of blur for an oriented stimulus. Expt 1 found that 3 D of blur had little effect on contrast sensitivity at 0.5 cpd, and had a stronger impact at 1.0 cpd. Expt 2 found that use of even lower spatial frequencies reduced the blur effect at 6 D. This allowed design of CSP stimuli for which the effect of 3 D of blur on contrast sensitivity should be less than 0.1 log unit throughout the central visual field, as confirmed in Exp 3.

Peripheral defocus can be due to either hyperopic or myopic change in peripheral refractive error with eccentricity, and the blur conditions would have opposite effects for these two types of defocus. If in some subjects peripheral refractive error would be compounded by the positive blur of the test lenses and others the effect of the positive test lenses would be corrective then between-subject variability for Rings 2 & 3 would be smallest for Ring 1. However, at all blur levels the standard deviation was largest for Ring 1, which is further evidence that peripheral defocus has minimal effect for these stimuli.

These results are similar to those of a study of blur effects for frequency-doubling stimuli¹⁰, whose 3 D blur condition caused a decline in contrast sensitivity by 0.15 log unit at 0.5 cpd and only 0.05 log unit at 0.25 cpd. Our blur effects at 3 D were similar to theirs for 0.5 cpd: 0.11, 0.07, 0.08 log unit for Experiments 1, 2 ,3, respectively. They also found that between-subject variability did not increase with blur level, and described why this ruled out significant effects of peripheral refractive error. A study of blur effects for 0.25 cpd frequency-doubling stimuli on a clinical device found blur effects of ~0.05 log unit for a 3 D blur condition¹¹. These studies used large stimuli, 100 deg², while our stimuli had areas (at ± 3 SD) as small as 2 deg². For Experiment 3, stimulus areas ranged from 7 deg² to 90 deg². The spatial scaling was intended to make contrast sensitivity constant across the central visual field, and results of Experiment 3 show that this was in the main accomplished, as mean contrast sensitivity for Rings 1 & 3 differed by only 0.01 log unit.

Previous studies have found that grating patches with peak spatial frequencies from 0.25 to 1.0 cpd can provide lower test-retest variability in glaucomatous visual field defects than conventional perimetry, while retaining good ability to assess defects.^{15, 22, 23} The current study finds that caution should be used with spatial frequencies greater than 0.5 cpd, because peripheral defocus could reduce contrast sensitivity. Recently, Harwerth et al.²⁴ found that contrast sensitivity losses at 1–2 cpd preceded losses at 0.25–0.5 cpd in monkeys with experimental glaucoma, which provides a potential support for using 1–2 cpd in CSP. However, the results of the current study show that peripheral defocus may be a potential confounder for these spatial frequencies when used clinically.

To further investigate the potential effects of peripheral defocus, we used geometric optics in three steps of modeling to assess effects of blur. This modeling incorporates the effects of higher-order aberrations, in that the combined effect of all aberrations can be approximated with an equivalent blur circle, which in turn corresponds to spherical blur. The modeling was for spatial frequencies from 0 to 2 cpd, and pupil diameters from 2 to 8 mm. The first step used geometrical optics to calculate the modulation transfer function (MTF) for a given pupil diameter and blur level. The MTF characterizes the reduction of contrast at each spatial frequency for that pupil diameter and blur level (blur effects are greater for larger pupils).

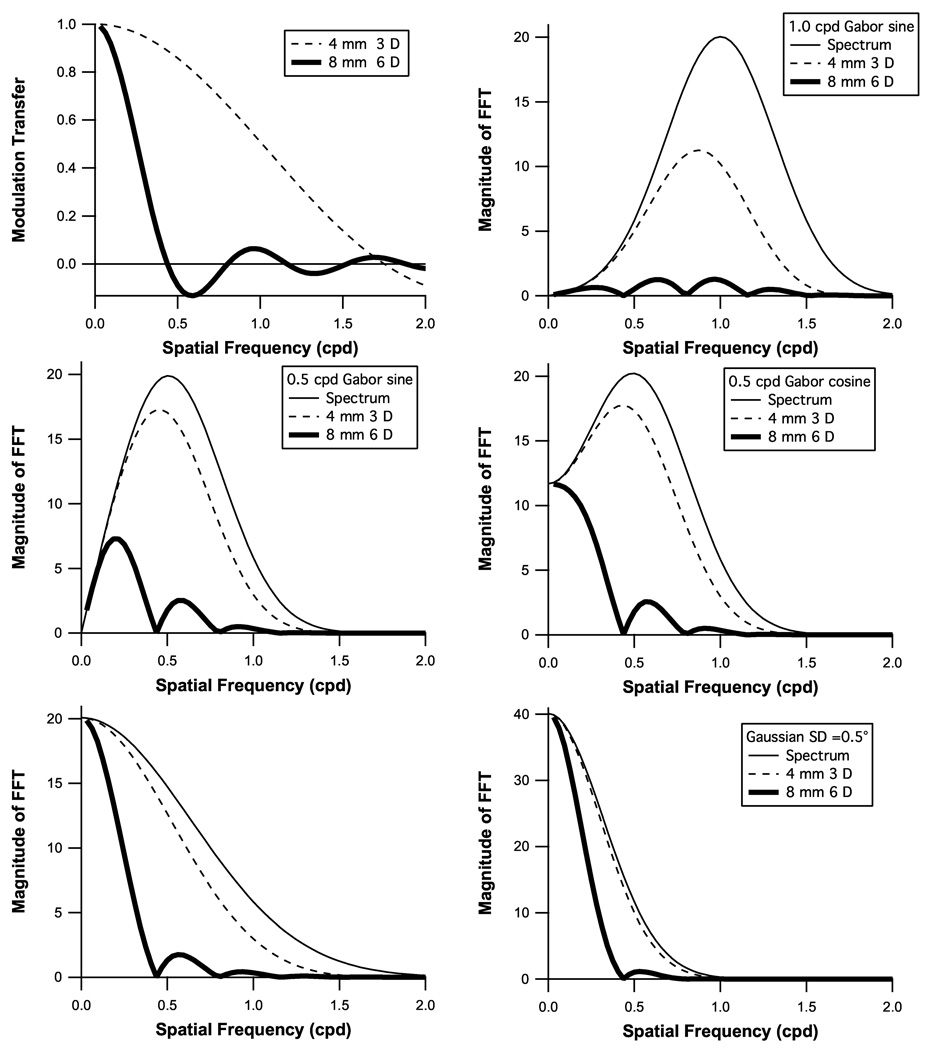
Two examples of MTFs are shown in the upper left panel of Figure 4. The second step calculated changes in the spatial frequency spectrum of the stimulus by multiplying the spectrum by the absolute value of the MTF, as illustrated in the remaining panels. The spatial frequency spectrum of a stimulus is the Fourier transform of the stimulus, and shows how much contrast is present at each spatial frequency. Multiplying the spectrum times the MTF characterizes how blur affects the stimulus. The third step estimated how this change in the stimulus would be expected to affect a subject’s contrast sensitivity. The relative contributions of different spatial frequencies to detection was approximated with a lowpass filter derived from a study of contrast sensitivity using Gabor stimuli¹⁹. The blur effect was computed as the logarithm of the ratio of the mean of the filtered stimulus spectrum and the mean of the filtered stimulus spectrum reduced by the MTF.

Figure 4.

Modulation transfer functions (MTFs) for two examples of pupil diameter and blur level are shown in the upper left panel. The calculated impact of these MTFs on the spatial frequency spectra of the five stimuli in Figure 1 are shown in the remaining panels.

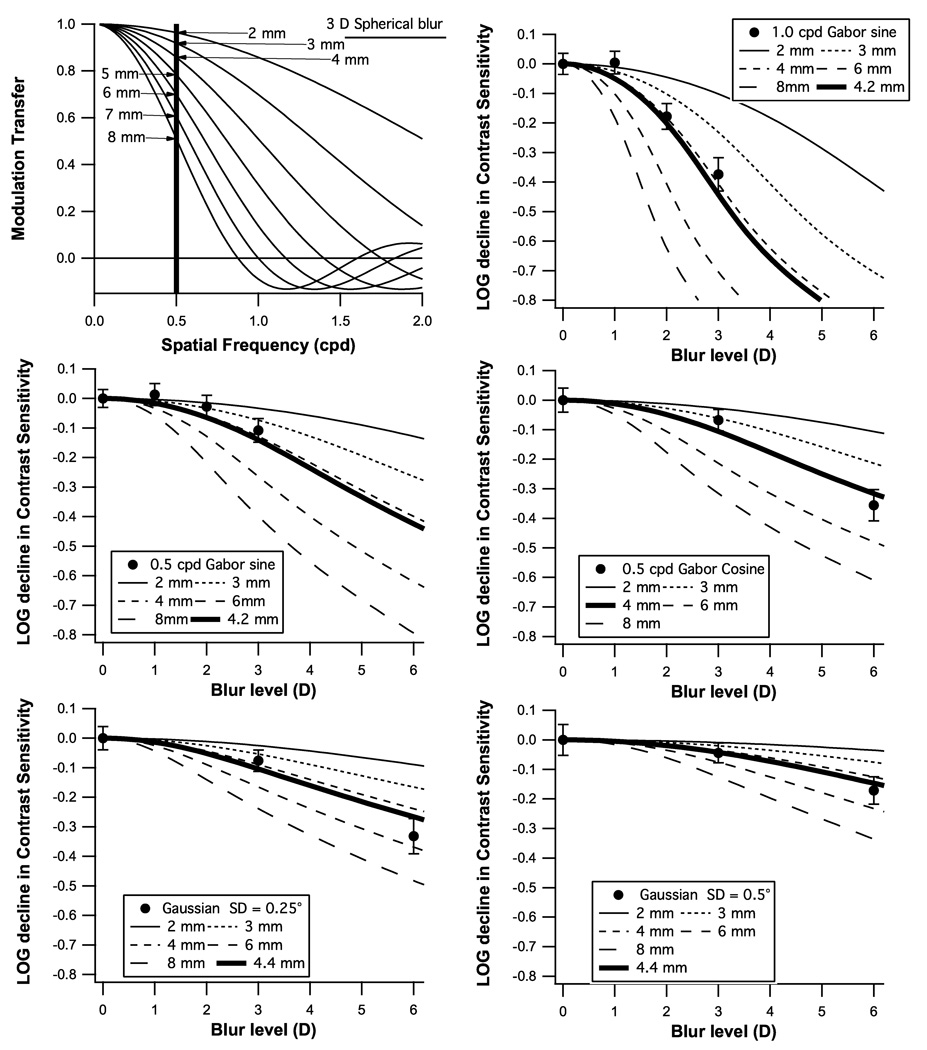
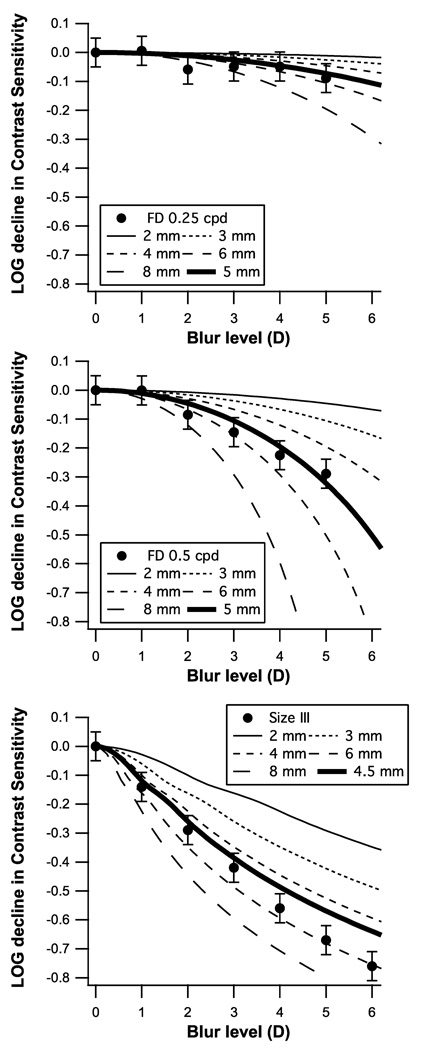
Figure 5 shows the results of step three, the expected reduction in contrast sensitivity as a function of blur for a variety of pupil sizes, along with means from the three experiments. The thick curves are for the mean pupil diameter calculated using a standard model²⁵ for pupil diameter incorporating age, mean luminance and display size for each test. We measured pupil size in a subset of our subjects and obtained results consistent with the standard model. All mean blur effects fell within 1 standard error of the thick curves, although the data tended to fall above the curve for 1–3 D and below the curve for 6 D.

Figure 5.

The expected reduction in contrast sensitivity for the five stimuli from Figure 1 plotted as a function of blur for a variety of pupil sizes, along with the means and standard errors from Experiments 1 & 2.

Figure 6 applies this analysis to data in the literature about blur effects on perimetric sensitivity. The top two panels show blur effects for 0.25 and 0.5 cpd gratings from a study of frequency-doubling stimuli¹⁰, and the bottom panel shows blur effects from a study of size III perimetry². The predicted blur effect for the standard pupil size is shown with a thick curve for each stimulus. Means were within 1 SE of the predicted blur effect for all conditions with grating stimuli, but for the size III data blur effects were greater than expected. The size III stimulus has substantial energy at spatial frequencies greater than 0.5 c/deg, so we removed the lowpass filter and even so the data were more than 1 SE below the predictions at 4–6 D. The ability of the modeling to generate reasonable predictions for most of the stimuli is encouraging, but further work is needed before it can be applied more broadly than the range 0.1 – 1.0 cpd for Gaussian-windowed gratings. The analyses in Figures 5 & 6 provide a basic guideline from geometrical optics: restricting spatial frequency to a maximum of 0.5 cpd provides means that 3 D of blur will cause no more than 0.1 log unit reduction in mean perimetric sensitivity. This is substantially less than the 0.4 log unit reduction reported for size III.

Figure 6.

The expected reduction in contrast sensitivity for the three stimuli from the literature plotted as a function of blur for a variety of pupil sizes, along with the means and standard errors from the studies.^{2, 10}

Experiments 1 & 2 studied effects of blur for variations in spatial frequency and size in the macula, and found the results to be consistent with predictions based on geometrical optics. This allowed us to design CSP stimuli that should be sufficiently resistant to blur throughout the central visual field that perimetric sensitivities will be relatively affected by peripheral refractive error, as confirmed in Experiment 3.