Context-dependent transcriptional interpretation of mitogen activated protein kinase signaling in the Drosophila embryo

Abstract

Terminal regions of the Drosophila embryo are patterned by the localized activation of Mitogen Activated Protein Kinase (MAPK), which induces zygotic genes through relief of their repression by transcriptional repressor Capicua. The levels of MAPK activation at the anterior and posterior termini are close to each other, but the expression patterns of MAPK-target genes, such as zerknüllt (zen) and tailless (tll), display strong anterior-posterior (AP) asymmetry. This region-specific response to MAPK activation provides a clear example of context-dependent interpretation of inductive signaling, a common developmental effect that remains poorly understood. In the past, the AP asymmetry of zen expression was attributed to a mechanism that depends on MAPK substrate competition. We present data suggesting that the asymmetric expression of tll is generated by a different mechanism, based on feedforward control and multiple enhancers of the tll gene. A simple mathematical model of this mechanism correctly predicts how the wild-type expression pattern of tll changes in mutants affecting the anterior, dorsoventral, and terminal patterning systems and some of their direct targets.

Developing tissues are patterned by a small set of signaling pathways that act combinatorially to establish complex patterns of gene expression. Here, we analyze interaction between signaling cues in the early fruit fly embryo, where patterning is initiated by four maternal signals. Traditional view of pattern formation by these systems is essentially one-dimensional: The anterior, posterior, and terminal systems initiate the formation of bands and stripes of gene expression along the long (anteroposterior, AP) axis. In parallel, the orthogonal nuclear localization gradient of Dorsal controls a different set of genes along the short (dorsoventral, DV) axis. The expression patterns of genes that exhibit a combination of AP and DV polarities cannot be explained by just one system and require interactions of multiple spatial signals. Here, we analyze the expression of terminal gap genes tailless (tll) and huckebein (hkb). These genes are expressed in patterns that are nonuniform along both AP and DV axes. Based on the combination of our experiments and published observations, we propose a possible mechanism that can account for complex patterns of tll and hkb. A simple mathematical model of this mechanism predicts how these patterns change when the inductive signals are varied, both alone and in combinations.

INTRODUCTION

The remarkable progression from a fertilized egg to an organism with multiple cell types, tissues, and organs depends on spatiotemporal control of gene expression. This important function can be provided by spatially restricted activation of signal transduction pathways, networks of biochemical reactions that connect ligand-receptor binding at the cell surface to gene expression in the nucleus. Genetic studies of development established that pattern formation across species, from worms to humans, relies on just a handful of signaling pathways that act combinatorially, to generate complex pattern of gene expression and cell fates. Among other things, this means that activation of the same signaling pathway can lead to different transcriptional effects in different cells. While this general concept is firmly accepted, quantitative studies of context dependent cell signaling are still rare, largely because this requires experiments where one must control multiple variables. In this paper, we use the early fruit fly embryo as a flexible experimental system where context-dependent signaling can be studied using a combination of genetic perturbations, quantitative imaging, and mathematical modeling.

Our choice of this experimental system is explained by several factors. First, the early fly embryo has a simple geometry: to a first approximation, it can be modeled by a surface of a spheroid. This geometric simplicity makes imaging of inductive signals and gene expression patterns relatively straightforward. Second, pattern formation in the early fly embryo is initiated by small number of signals. Three of these signals are distributed in graded patterns along the long axis of the spheroid; the fourth signal is distributed along the short axis. Third, each of the signals can be manipulated genetically, resulting in altered inputs to the regulatory regions of target genes that subdivide the embryo into different tissue types. Fourth, the regulatory regions for most of the genes involved in this subdivision have been determined experimentally. Fifth, advances in experimental genomics provide important information about the connection of these regulatory regions to transcription factors that pattern the embryo.

Over the past decade, these experimental advantages have been combined to establish quantitative mathematical models of pattern formation in the early Drosophila embryo. Most of these models are one-dimensional and focus on patterns distributed either along the long or the short axes of the embryo. However, even in the early embryo, most of the experimentally observed gene expression patterns are intrinsically two-dimensional. Explaining these patterns requires explicit modeling of combinatorial signaling. In this paper, we formulate such a model, based on the combination of our experiments and previously published studies by other groups. The resulting mathematical model is rather simple and takes the form of a multivariate algebraic function that maps local levels of inductive signals into level of gene expression. The arguments of this function for a particular gene are chosen on the basis of two types of data: (1) changes in the expression pattern of a gene in response to changes in the levels of inductive signals and (2) information about the sequence of the regulatory DNA of a gene. Below, we provide a more detailed description of our experimental system.

Signaling by the Extracellular Signal Regulated/Mitogen Activated Protein Kinase (ERK/MAPK) pathway controls developmental events in organisms from worms to humans. MAPK signaling is commonly induced by extracellular ligands and alters the activities of transcription factors that serve as connections between inductive signals and their target genes. Transcriptional effects of MAPK are context-dependent, which means that activity of the same enzyme can induce different sets of genes in different cells.^{1, 2} This phenomenon received a lot of attention from biochemists and geneticists, resulting in several models that can potentially account for context-dependent effects of MAPK activation.^{3, 4, 5, 6}

One of these models relies on signal integration at the level of gene enhancers. As a simple example of this model, consider an enhancer of a gene (G) that is controlled by an activator (A) and a repressor (R1). If active MAPK somehow negates the repressive function of R1, then activation of MAPK will induce G, but only if A is present. While the general idea of such mechanisms is well accepted, understanding of endogenous gene expression programs induced by MAPK is far from complete. Here, we analyze context-dependent interpretation of MAPK signaling in the early Drosophila embryo, an experimental system where a symmetric pattern of MAPK activation at the embryonic poles gives rise to a highly asymmetric transcriptional response.⁷ The anatomical simplicity of this system and its amenability to genetic perturbations make it ideally suited for analysis of context-dependent signaling mechanisms.

Terminal regions of the Drosophila embryo are patterned by the localized activation of Torso, a receptor tyrosine kinase (RTK), which establishes a two-peaked pattern of phosphorylated MAPK.⁸ One of MAPK substrates in the early embryo is an HMG-box transcriptional repressor Capicua (Cic).⁹ In the absence of MAPK signaling, Cic is present throughout the embryo. When phosphorylated by MAPK, Cic is excluded from the nuclei at the poles of the embryo,¹⁰ which relieves Cic-dependent repression of zygotic genes,^{9, 11} including nuclear receptor transcription factor tailless (tll) and zinc-finger transcription factor huckebein (hkb) [Fig. 1a].

Figure 1.

Two-domain expression patterns of tll and hkb. (a) Locally activated Torso signaling induces tll and hkb through relief of Cic-mediated repression. (b) and (c) Spatial patterns of tll (b) and hkb (c) mRNAs in wild-type embryos. (d) and (e) Expression patterns of tll (d) and hkb (e) in embryos that lack Bcd (bcd[6]). (f) and (g) Expression patterns of tll (f) and hkb (g) in embryos that lack Trunk (trk[1]), which is a ligand for Torso.

The expression patterns of tll and hkb display pronounced anteroposterior (AP) asymmetry: They overlap at the posterior pole, with the expression domain of hkb fully covered by a broader domain of tll [Figs. 1b, 1c]. In contrast, the expression domains of these two genes do not overlap at the anterior pole. Furthermore, unlike the posterior domain of tll expression, which is uniform along the dorsoventral (DV) axis of the embryo, the anterior domain of tll expression displays a clear DV polarity: it is repressed on the ventral side of the embryo. This asymmetry depends on Bicoid (Bcd), a maternally provided homeodomain transcription factor distributed in anterior-to-posterior concentration gradient that controls the AP pattern of the embryo.^{12, 13} In the absence of Bcd, the expression patterns of tll and hkb become symmetric: the two genes are now expressed in nested domains at both poles of the embryo [Figs. 1d, 1e].¹³

Previous studies identified a number of enhancers responsible for the anterior expression of tll and hkb. These enhancers directly bind Bcd and Cic.¹¹ In the emerging model for the regulation of these enhancers, Bcd is a dose-dependent activator that works “against” the inverse transcriptional repression gradient of Cic [Fig. 2a].¹⁴ This model explains a large number of observations, but several issues are yet to be resolved. For instance, it is unclear why tll, which is activated by MAPK signaling at both poles, is repressed at the anterior-most region. We propose a mechanism that may account for this repression and several other, hitherto unexplained, effects of MAPK signaling. This mechanism is based on the quantitative analysis of pattern formation in mutant genetic backgrounds and can be summarized by a simple mathematical model.

Figure 2.

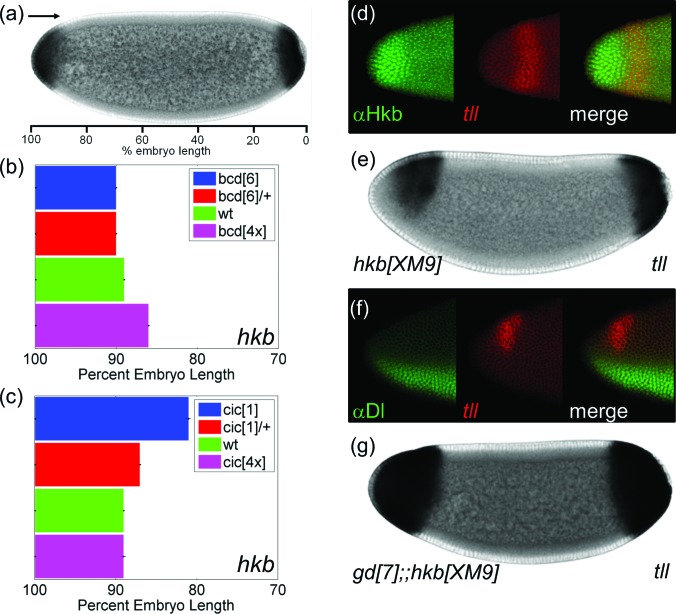
Dose-dependent effects of Bcd and Cic on tll expression. (a) The Bcd activation gradient works against the inverse transcriptional repression gradient of Cic in activating many of its targets. (b) Quantification of the boundaries of anterior tll expression. (c) and (d) Quantified boundaries of the anterior tll in embryos with different levels of Bcd (c) and Cic (d). Averaged boundaries are shown with error bars indicating standard error of the mean (s.e.m). The numbers of embryos used in the analysis are N = 23 (bcd[6]), N = 95 (bcd[6]/+), N = 49 (wt), N = 42 (bcd[4x]), N = 65 (cic[1]), N = 56 (cic[1]/+), and N = 32 (cic[4x]). (e) These results are consistent with incoherent feedforward mechanism, where Bcd and Torso activate both tll and an anterior repressor of tll.

MATERIALS AND METHODS

Fly strains

The following fly strains were used in this study: OreR (wild-type), bcd[6],¹⁵ trk[1],¹⁶ gd[7],¹⁷ cic[1],⁹ Tl[10b],¹⁸ P[Bcd-GFP] (bcd^4x), P[Cic-HA] (cic^4x), hkb[XM9],¹⁹ and kni[9].²⁰ Flies were grown and embryos were collected at 22 °C.

In situ hybridization and immunohistochemistry

Embryos were fixed in 8% formaldehyde for 20 min and treated with 90% xylene for 1 h and 80% acetone for 10 min at −20 °C. Embryos were then hybridized overnight at 60 °C with antisense probes labeled with digoxigenin (DIG), Biotin (BIO), and Fluorescein (FITC). Embryos with labeled probes were visualized using standard immunofluorescence technique. The following primary antibodies were used: sheep anti-DIG (Roche; 1:200), mouse anti-BIO (Jackson ImmunoResearch; 1:200), rabbit anti-FITC (Invitrogen; 1:200), rabbit anti-dpERK (Cell Signaling; 1:100), mouse anti-Dorsal (Developmental Studies Hybridoma Bank, 1:100), rabbit anti-Cic (a gift of C. Berg, 1:2000), and rat anti-Hkb (a gift of J. Jaeger, 1:100).²¹ Alexa fluor conjugated secondary antibodies (Invitrogen; 1:500) were used to label the primary antibodies and DAPI (1:10 000; Vector Laboratories) was used to detect nuclei.

Microscopy and image processing

Imaging was done on a Zeiss LSM510 confocal microscope with Zeiss C-Apo 20× (NA = 0.6). High-resolution images (512 × 512 pixels, 12 bits depth) were obtained from a focal plane in the mid-horizontal cross section of the embryo. Images of individual embryos were automatically extracted from raw confocal files and re-oriented and processed as described elsewhere.²²

Quantification of gene expression boundaries

The expression boundaries of tll and hkb were determined using automated image analysis program in matlab, which finds the boundary of the embryo and then averages staining intensity along the DV axis. This was performed for 1000 points uniformly spaced along the AP axis, generating an AP expression profile of the gene. The locations of the half maximum level were used as boundaries of the expression domains.

Mathematical model

The input gradients of the mathematical model were estimated based on our previous imaging data.^{22, 23, 24, 25, 26, 27} These expressions were used to determine values of Bcd, Dl, and Cic at every point that maps into an ellipsoid with a center (0.5, 0.2, 0.2). Assuming lateral symmetry, we only needed to determine the values of the inputs at every (x,y) which corresponds to AP and DV axes of the embryo, respectively. The radii of the major and minor axis of the ellipsoid are 0.5 and 0.2, respectively. These values reflect the actual proportion of the embryo which has AP length of ∼500 μm and DV length of ∼200 μm. The expression levels of the three maternal inputs at every point in the ellipsoid were then used to determine whether the gene expression was on or off. The values of the constants used in the model were listed in the Table TABLE I..

TABLE I.

Values of the model constants.

Constants	Values
Ahkb,U	0.3
rhkb	1.5
ahkb,B	4
ahkb,DB	2.5
rhkb,C	4
Thkb	0.4
akni,DB	2
rkni,C	4
Tkni	0.3
Atll,U	0.5
rtll	1.5
atll,B	10
atll,D	0.5
atll,C	5
atll,K	8
atll,H	30
Ttll	0.5

The values of the parameters which represent the strength of activation/repression and local threshold levels were estimated based on in-situ hybridization images. Although the absolute levels of these parameters are unknown, their relative values could be estimated from our experimental data. For example, tll extends further toward the midbody of the embryo in comparison with hkb. Thus, we chose uniform barrier of tll activation $(T_{\mathit{t}\mathit{l}\mathit{l}})$ that is smaller than the threshold of hkb ($T_{\mathit{h}\mathit{k}\mathit{b}}$). Similarly, our data showed that the effect of perturbing Cic levels on the anterior tll and hkb are minimal. Hence, the value of the coefficient that model the repression by Cic must be smaller than those of other repressors. Using this approach, we estimated values of the parameters that can reproduce the wild-type patterns of tll and hkb and predict how these patterns change in a large number of mutants presented in Fig. 9. The model was constructed to test whether our mechanism can recapitulate the experimental patterns of tll and hkb. We focus on the qualitative behavior of the model and the relative ratio the parameters rather than their absolute values.

Figure 9.

Modeling of tll and hkb expression patterns in the wild-type and mutant embryos. The model successfully predicts pattern of tll and hkb in multiple mutants corresponding to changes in the levels and spatial distribution of inductive signals and their downstream targets. The spatial distribution of inductive signals is shown as a superposition of theBcd, Cic, and nuclear Dl gradients. Predicted tll and hkb patterns are presented in the 2nd and 3rd columns, and the corresponding experimental patterns are shown in the last two columns.

To model different mutants, the wild-type input gradients were modified accordingly. For instance, to model gd[7] embryo which has no nuclear Dl, $D\left(y\right)$ was set to 0 for all y where y signifies the DV axis of the embryo. Similarly, for Tl[10b], an embryo with Dl inside every nucleus, we set $D\left(y\right)$ to 1 for all y. For changes in the gene dosage, the input gradients were simply multiplied by a constant. Previous studies established that the level of Bcd is proportional to the gene dosage of bcd.²⁸ We further assumed that reducing gene dosage of bcd by half resulted in the gradient with the same shape as that of the wild-type, but with half the amplitude. We found that the same applies to the Cic gradient: changing the gene dosage only affects the amplitude without changing the shape [Fig. 6c].

Figure 6.

Effect of perturbing the Cic gradient. (a) Simultaneous staining of Cic in wild-type and cic[1] embryos reveal very low level of Cic this mutant. (b) Quantified nuclear Cic in the posterior half of the wild-type embryo (red, N = 21) and embryos from cic[1] flies (black, N = 14). Error-bars are s.e.m. (c) Assuming that Cic is downregulated completely at the posterior pole of cic[1] embryos, we obtained normalized Cic gradient in wild-type embryos (red, N = 21), which show that Cic is degraded to approximately 20% of the maximum at the posterior pole. Similar approach was used to determine normalized gradient from cic heterozygous embryos (green, N = 33) and embryos with two extra copies of cic (blue, N = 25). Error bars are s.e.m. (d) Nuclear gradient of Cic in the posterior half of wild-type (red, N = 30) and embryos with two extra copies of cic (blue, N = 32). Filled yellow and green arrows denote the boundaries of tll and hkb, respectively, in wild-type embryos while empty arrows represent the two gene expression boundaries in the mutant embryos.

EXPERIMENTAL RESULTS

Dual control of anterior expression of tll by Bcd and Cic

Previous studies established that the anterior domain of the tll expression pattern is controlled by both Bcd and Cic, which activate and repress tll, respectively.^{11, 29} To examine the quantitative effects of these regulators, we used in situ hybridization to examine how the tll expression domain responds to changes in the levels of Bcd and Cic [Fig. 2b; see Sec. 2]. As expected, the anterior domain of tll expands when the gene dosage of Bcd is increased, which is consistent with the model where Bcd is a dose-dependent activator of tll [Fig. 2c]. Next, we examined the effects of changing the gene dosage of Cic. Consistent with the model where the Bcd gradient acts “against” a gradient of repression by Cic, we found that the posterior extent of the anterior domain of tll expands in embryos with decreased level of Cic [Fig. 2d]. Thus, changes in the posterior border of the tll pattern are consistent with the model where tll is regulated by two opposing gradients.

We found that changes in the level of Cic also affect the size of the anterior-most domain where tll is repressed. Specifically, in the embryos from cic[1] homozygous mothers, the anterior boundary of the anterior expression pattern extends posteriorly [Fig. 2d]. While these observations cannot be explained by direct effects of the activating and repressing morphogen gradients, they are consistent with a modified model, in which the two gradients control tll through an incoherent feedforward loop, a network where an input controls its target genes both directly and through a repressor [Fig. 2e].^{30, 31} In this model, changing the levels of Bcd or Cic would affect the expression domains of both tll and its repressor(s). As a consequence, the size of the anterior repression of tll would be expanded by increasing the levels of Bcd and/or decreasing the levels of Cic.

Hkb as a potential regulator of tll

Another common target of Bcd and Cic, hkb is expressed inside the domain of tll repression [Figs. 1b, 1c]. hkb is expressed as cap-like domains at both poles, reflecting its de-repression by MAPK signaling, which downregulates Cic, which in turn binds to the regulatory region of hkb. At the anterior pole, hkb is also activated by Bcd in combination with Dorsal (Dl), which is evident from the residual hkb expression in the anterior-ventral region in the absence of MAPK signaling³² [Fig. 1g]. Dl is an NF-κb transcription factor that controls the expression of a large number of target genes along the DV axis [Fig. 3f].³³ Importantly, this pattern matches the anterior-ventral repression of tll in the same mutant background [Figs. 1f, 1g]. Furthermore, in response to changes in the levels of Bcd and Cic, the anterior domain of hkb expands and appears to fit almost perfectly into the region where tll is repressed [Figs. 3a, 3b, 3c]. These results suggest that Hkb may repress tll at the anterior pole.

Figure 3.

Anterior repression of tll depends on Hkb and Dl. (a) Quantification of the boundary of anterior hkb. (b) and (c) Quantified boundaries of the anterior hkb in embryos with different levels of Bcd (b) and Cic (c). (d) Averaged boundaries are shown with error bars indicating s.e.m. The numbers of embryos used in the analysis are N = 101 (bcd[6]), N = 64 (bcd[6]/+), N = 52 (wt), N = 67 (bcd[4x]), N = 39 (cic[1]), N = 103 (cic[1]/ +), and N = 41 (cic[4x]). (e) Dorsal view of an embryo stained with Hkb protein (green) and tll transcript (red). The pattern of Hkb closely matches with the repression domain of tll. (e) Pattern of tll in Hkb mutant embryo. (f) Lateral view of an embryo stained for Dl protein and tll mRNA. (g) tll mRNA pattern in an embryo that lacks Dl signaling and Hkb protein.

To test this idea, we co-stained embryos with the anti-Hkb antibody and probes for tll transcripts. We found that the expression of Hkb on the dorsal side of the embryo fits nearly perfectly into the gap in the anterior pattern of tll [Fig. 3d]. This is consistent with the model where Hkb represses tll, either directly or indirectly. As another test of this model, we examined tll expression in embryos that lack Hkb. In these embryos, the anterior repression of tll is alleviated, but the effect is incomplete, with tll still repressed in the ventral and the anterior-most region [Fig. 3e]. Thus, Hkb can repress tll at the anterior pole, but it is not the only repressor.

Dorsoventral control of tll expression

tll is also repressed on the ventral side of the embryo, outside the domain where Hkb is expressed. This suggests that tll is regulated by factors that are distributed nonuniformly along the DV axis. A natural candidate for such a factor is Dl, which is present throughout the embryo, but its nuclear import and transcriptional activity are distributed in a ventral-to-dorsal gradient.

Nuclear Dl is required for the ventral-anterior repression of tll.¹³ To test whether Dl is responsible for the lack of tll expression in hkb mutant embryos, we generated a mutant that lacks both Hkb and nuclear Dl. In these embryos, tll expression expands both anteriorly and ventrally, covering nearly the entire anterior pole [Fig. 3g]. Based on this, we conclude that the anterior repression of tll depends on both Dl and Hkb.

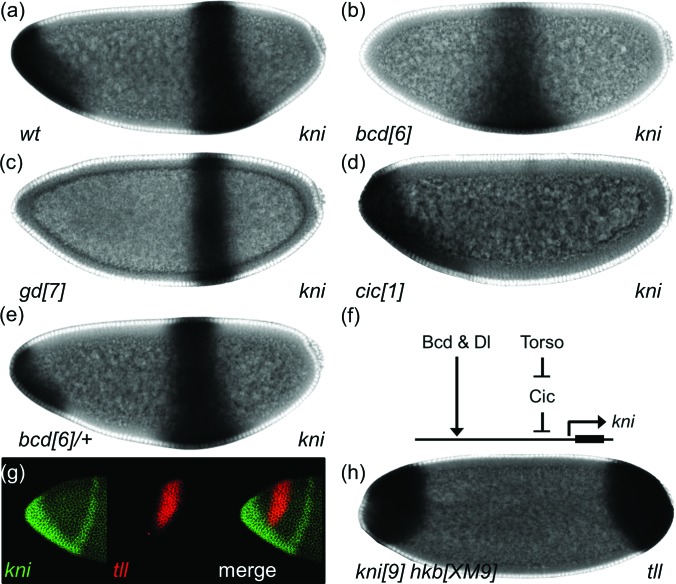
Negative regulation of gene expression by Dl can be either direct or mediated by intermediate repressors that are activated by Dl such as Hkb. Another candidate for such intermediate factor that can mediate Dl-dependent repression of tll is Knirps (Kni), a zinc finger transcriptional repressor expressed in the anterior-ventral region, reflecting its activation by both Bcd and Dl³⁴ [Fig. 4a]. This expression of kni is abolished in the absence of either Bcd or Dl [Figs. 4b, 4c]. kni is also controlled by the terminal system [Fig. 4d]: Specifically, kni domain expands when cic is removed and contracts in embryos from bcd heterozygous females [Figs. 4d, 4e, 4f].

Figure 4.

Kni is an additional repressor of anterior tll. (a)–(d) Expression pattern of kni in wild-type embryos (a), embryos that lack Bcd (b), Dl signaling (c), or Cic (d). (e) Expression pattern of kni in embryos with one copy of bcd. (f) A model for the regulation of anterior-ventral stripe pattern of kni by Bcd, Dl, and Torso signaling. (g) Lateral view of an embryo co-stained for kni (green) and tll (red) mRNAs. (h) tll expression pattern in an embryo that lacks Kni and Hkb.

The pattern of kni closely matches with the ventral repression domain of tll [Fig. 4g], suggesting that Kni might repress tll. To test whether repression by Kni can account for incomplete expansion of tll in hkb null embryos, we examined tll expression in embryos that lack both Kni and Hkb. In these embryos, the tll pattern resembles that of Dl and Hkb double mutant embryos, with tll expressed nearly throughout the anterior pole [Fig. 4h]. Taken together, our results suggest that the anterior domain of tll expression is generated by a two-input feedforward loop, in which Bcd and MAPK signaling activate both tll and its repressors, such as Hkb and Kni.

Cic gradient as a regulator of posterior domains of tll and hkb

The posterior expression domains of both tll and hkb are eliminated in the absence of MAPK signaling [Figs. 1f, 1g]. This reveals that MAPK provides a key input for the posterior expression of tll and hkb. Genetic and biochemical studies revealed that Cic, which is distributed in a gradient, controls tll and hkb by directly binding to their enhancers.³⁵ We asked whether the Cic gradient can position the boundaries of these two genes. If this is the case, then the levels of Cic at the expression borders of tll and hkb should be different from each other. Furthermore, the position of these borders should be affected by changes in the levels of Cic.

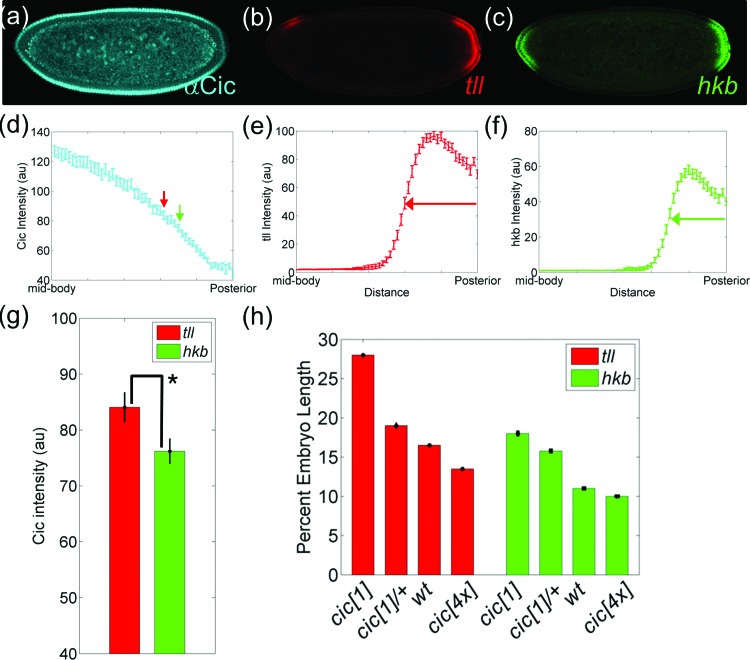
To test these predictions, we measured the sizes of the posterior expression domains of tll and hkb and relating them to the corresponding Cic levels. We used fluorescent in-situ hybridization (FISH) and antibody staining to detect Cic protein and tll and hkb mRNAs in the same embryo [Figs. 5a, 5b, 5c, 5d, 5e, 5f]. As an estimate for the expression border of these genes, we used the position at which the intensity of the FISH signal decays to 50% of its maximal level [Figs. 5d, 5e, 5f]. Based on this definition, we determined that tll and hkb expression boundaries are located at 17% and 15% embryo length from the posterior pole, respectively [Fig. 5h]. At each of these borders, we quantified the nuclear level of Cic. Thus, an image of a single embryo provides the levels of nuclear Cic at the expression borders of tll and hkb.

Figure 5.

Cic-dependent control of posterior domains of tll and hkb. (a)–(c) Simultaneous detection of Cic protein (a) and tll (b) and hkb (c) mRNAs in a single embryo using FISH. (d) Quantification of nuclear Cic in the posterior half of the embryo. The boundaries of tll and hkb are indicated by red and green arrows, respectively. (e) and (f) Normalized spatial gradient of tll (e) and hkb (f) mRNAs. (g) Bar graph of average intensities of Cic at the boundaries of tll (red) and hkb (green). Each bar represents an average of 52 data with error bars indicating s.e.m. (h) Changes in the boundaries of tll and hkb in embryos with different copies of cic gene (see Sec. 2 for details on the quantification). Posterior pole is denoted as 0% embryo length, and error bars are s.e.m. The number of embryos in each background are N = 65 (cic[1]), N = 56 (cic[1]/+), N = 49 (wt), and N = 32 (cic[4x]) for tll and N = 39 (cic[1]), N = 103 (cic[1]/+), N = 52 (wt), and N = 41 (cic[4x]) for hkb.

Based on a paired t-test comparison of the means of Cic levels in multiple embryos, we found that Cic levels at the two borders are statistically different from each other [Fig. 5g]. This is consistent with the model where the gradient of repression by Cic controls the nested expression patterns of tll and hkb at the posterior pole. As an additional test of this model, we examined whether posterior expression of tll and hkb are sensitive to the gene dosage of cic. First, we used embryos with two extra copies of cic (cic[4x]), which increased the level of Cic protein by ∼80% in the mid-body of the embryo without changing the shape of the gradient [Figs. 6c, 6d]. In these embryos, the posterior expression domains of both genes shift toward the posterior pole, consistent with the increased level of the repressor [Fig. 5h].

Similarly, in embryos from cic[1] heterozygous mothers, the posterior domains of tll and hkb expand toward the mid-body of the embryo [Fig. 5h]. Importantly, the levels of Cic at the expression borders of tll and hkb remain different from each other in both of these backgrounds. Considering that perturbing the cic copy number does not affect the normalized shape of the gradient [(Fig. 6c], our results suggest that the concentration of Cic rather than its relative difference from the maximum level is important in positioning gene expression boundaries of tll and hkb in the posterior region.

These observations suggest that the Cic gradient can establish the nested domains of tll and hkb at the posterior. In the simplest case, this gradient can work against uniformly distributed transcriptional activators, which can be either common for both genes or different. Examples of common activators are Zelda (Zld) and Stat92E, both of which positively control the expression of tll and hkb.^{36, 37} A dedicated activator is Lilliputian, which affects only hkb, but not tll.³⁸

Conceptual model of gene expression at the poles

A majority of our data and published observations made in studies of the terminal patterning system can be summarized by a model where the two-domain (anterior and posterior) expression patterns of the terminal genes are generated by different enhancers. In the simplest case, the anterior domain of a terminal gene, such as tll, is controlled by an enhancer that is it activated by a combination of Bcd and uniform activators, such as Zld, and repressed by a combination of Cic and Bcd target genes, such as Kni [Fig. 7a]. At the same time, posterior expression domains are established by uniform activators, such as Zld, working against the Cic gradient [Fig. 7b).

Figure 7.

A model for the regulation of tll and hkb. (a) A regulatory network of anterior tll and hkb by the three maternal signals. (b) A regulatory network of posterior tll and hkb by locally activated Torso. (c)–(e) Spatial distributions of Bcd (c), Cic (d), and nuclear Dl (e) gradients that provide spatially distributed inputs to the models shown in (a) and (b). (f) Bcd, Cic, and nuclear Dl gradients superimposed on the same embryo.

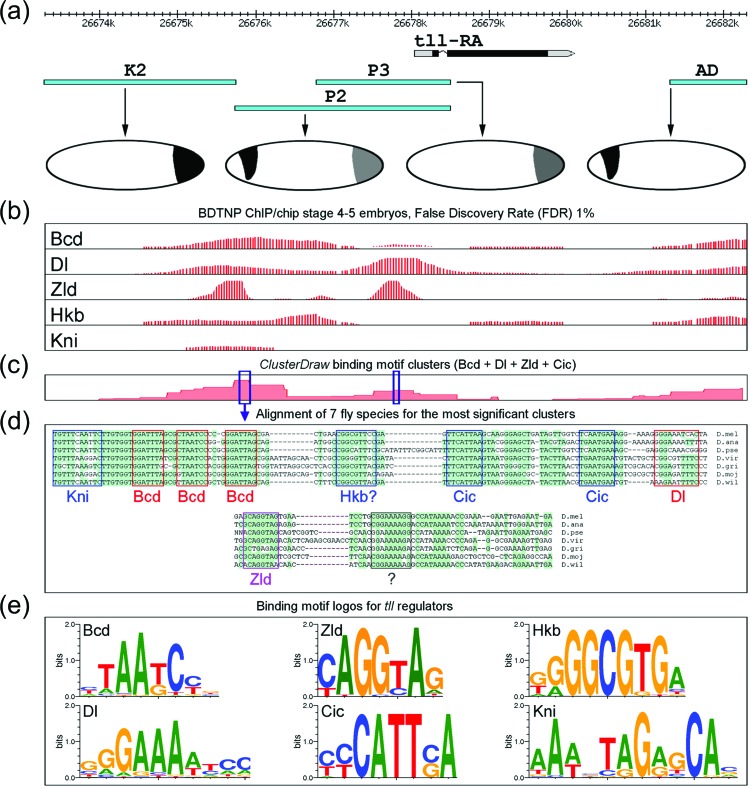
In addition to analysis of tll and hkb expression in multiple mutants, this model is supported by previous studies of tll and hkb enhancers.^{13, 39} These studies can be summarized as follows. First, experiments with transcriptional reporters of tll identified DNA sequences that display activity that either partially or completely matches the wild expression pattern [Fig. 8a]. Some of these sequences drive expression at the anterior pole, others are active at the posterior pole, and some are active at both poles.

Figure 8.

Sequence-specific analysis of tll enhancers. (a) Expression patterns of tll enhancers in vivo; fragments are named in accordance to the original publications.⁴⁶, ⁵¹ Fragments K2 and P3 reproduce the posterior pattern, fragment AD reproduces the anterior pattern and the fragment P2 reproduces both, the anterior and the posterior patterns. (b) In vivo binding patterns of five transcriptional regulators in the tll locus.⁵², ⁵³ (c) Results of sequence analysis: statistical significance of binding site density in the tll locus.⁴¹ Peaks (see the encircled numbers) correspond to significant clusters of binding sites for transcriptional regulators Bcd, Dl, Zld and Cic. (d) Alignment of DNA fragments corresponding to the identified clusters from seven species of Drosophila, binding site matches to regulatory motifs are boxed. Shaded areas mark regions highly conserved in evolution. (E) Binding motif logos for binding motifs of the transcriptional regulators used in the sequence analysis.³⁵, ⁵⁴, ⁵⁵, ⁵⁶

Second, chromatin immunoprecipitation (ChIP) studies established that Bcd, Kni, Hkb, and Dl proteins bind to the regulatory sequences of tll [Fig. 8b]. For example, the P2 region expressed at both anterior and posterior parts of the embryo, binds all four transcription factors, while the AD region, producing anterior tll pattern, binds only Bcd, Dl, and Hkb. Our analysis revealed strong Zld binding in enhancers active at the posterior pole. This is consistent with the results of a recent study that showed that the posterior expression of tll is strongly reduced in the absence of Zld.⁴⁰ Third, we found that the ChIP binding data are largely consistent with the information about the DNA binding preferences (position weight matrices) of these transcription factors⁴¹ [Figs. 8c, 8d, 8e]. Furthermore, the clusters of Bcd, Cic, Kni, and Dl sites in some of the enhancers are evolutionarily conserved. Two examples of conserved regions are shown in Fig. 8d.

Since Cic is downregulated at both termini, our model predicts that posterior enhancers of hkb and tll should be active at both anterior and posterior poles, which is not the case, at least for tll. In order to describe the wild-type pattern, we require that the posterior enhancer must be turned off at the anterior pole. How this happens is still unclear. Possible mechanisms for this coordination of enhancer activities include long-range and short-range transcriptional repression and MAPK substrate competition (see Sec. 5).

MATHEMATICAL MODEL

To illustrate our model, we formulated a simple mathematical description for the regulation of tll and hkb. We treat the anterior and posterior patterns as two independent systems. As inputs for this model, we use the spatial distributions of the Bcd, Cic, and Dl gradients [Figs. 7c, 7d, 7e, 7f], which we denote by $B(x)$, $C(x)$, and $D(y)$, respectively, where x and y directions along the AP and DV axes of the actual embryo. Given these inputs, gene expression borders can be predicted using a model where the rate of mRNA accumulation of a gene is equal to difference between transcript generation and first order degradation terms. When transcript degradation is fast, the local level of mRNA for a given gene is proportional to the rate of transcription, which in turn depends on the concentration of transcription factors.

Following a number of studies, we model the rate of transcription phenomenologically, using a Heaviside function, $H(u)$, of an aggregated variable u that depends on the appropriately chosen combination of the concentration of transcription factors.^{42, 43, 44}$H(u)=1$ when $u>0$ and zero otherwise. For instance, the posterior domains of hkb and tll are given by the following equations:

$$hk{b}^P(x,y)=H(A_{hkb,U}-r_{\mathit{h}\mathit{k}\mathit{b}}C),$$

$$tl{l}^P(x,y)=H(A_{tll,U}-r_{\mathit{t}\mathit{l}\mathit{l}}C).$$

Constants $A_{hkb,U}$ and $A_{tll,U}$ denote the effect of uniform activators, which can differentially affect the expression of the two genes. These constants combine the effect of the levels of transcription factors, which may be different for two genes. $r_{\mathit{h}\mathit{k}\mathit{b}}$ and $r_{\mathit{t}\mathit{l}\mathit{l}}$ model the effects of repressor.

Activities of anterior enhancers, denoted $hk{b}^A(x,y)$ and $tl{l}^A(x,y)$, are modelled as follows. We assume that Bcd and Dl act as independent activators of the anterior enhancer of hkb,^{45, 46} which act against uniform repressors and graded Cic

$$hk{b}^A\left(x,y\right)=H\left(a_{hkb,B}B+a_{hkb,D}D-r_{hkb,C}C-T_{\mathit{h}\mathit{k}\mathit{b}}\right),$$

where $r_{hkb,C}C+T_{hkb\hspace{0.17em}}$ is the local threshold value that must be overcome to induce the expression.

Since we propose that Kni acts as one of tll repressors at the anterior pole, we need a model of kni expression. Previous studies established that anterior expression of kni is activated by Bcd and Dl and repressed by Cic.³⁴ The simplest model capable of generating such a pattern is

$$kni(x,y)=H(a_{kni,DB}D\ast B-r_{kni,C}C-T_{\mathit{k}\mathit{n}\mathit{i}}).$$

In this equation, $a_{kni,DB}$ is the coefficient describing the combined activating effects of Bcd and Dl, $r_{kni,C}$ is the coefficient describing the repression strength of Cic, $T_{\mathit{k}\mathit{n}\mathit{i}}$ is space independent threshold. Consistent with experimental observations, this model predicts that kni expression vanishes in the absence of either Bcd or Dl and responds to changes in the gene dosage of Cic.

We assume that the spatial distributions of Hkb and Kni proteins follow the distribution of kni transcript and use them as inputs in the regulation of tll, which is activated by a uniform activator and Bcd and repressed by Hkb and Kni. The model also includes direct repression by Dl, which is represented by dashed repressive arrow in Fig. 7a

$$tl{l}^A(x,y)=H(a_{tll,B}B-r_{tll,D}D-r_{tll,C}C-r_{tll,K}Kni-r_{tll,H}Hkb-T_{\mathit{t}\mathit{l}\mathit{l}}),$$

where all coefficients are defined as before.

As discussed above, we assume that posterior enhancer is silenced at the anterior pole. The resulting model correctly predicts the AP asymmetric pattern of tll in wild-type embryos and how the spatial patterns of tll and hkb change in response to variations in the levels of anterior, terminal, and DV signals (Fig. 9). For instance, the expression patterns acquire AP symmetry in the absence of Bcd, which activates the anterior enhancer. Furthermore, the expression of tll loses DV polarity in the absence of Dl and fully covers the anterior pole in the absence of both Dl signaling and Hkb. Moreover, the expression borders of these genes respond to the quantitative changes in the levels of both Cic and Bcd.

CONCLUSIONS AND DISCUSSIONS

Terminal patterning of the early Drosophila embryo provides an excellent system for the in-depth analysis of context dependent interpretation of MAPK signaling, an effect that has been observed in multiple developmental systems. MAPK signaling is triggered by locally activated Torso RTK and downregulates the Cic repressor, relieving repression of several genes with Cic binding sites in their regulatory DNA. Previous studies established that the levels of MAPK activation at both poles are approximately equal to each other, but the expression patterns of multiple Cic target genes display a pronounced AP asymmetry.²⁶

Part of this asymmetry can be attributed to the MAPK substrate competition mechanism, whereby anteriorly localized MAPK substrates, such as Bcd, interfere with MAPK-dependent downregulation of Cic at the anterior pole. This mechanism accounts for the AP asymmetry in the expression of genes, such as zerknüllt (zen), which is expressed at the posterior pole, but repressed at the anterior.⁴⁷ The AP asymmetry of such patterns can be explained with a model where gene expression is controlled by a single enhancer that responds to a combination of nonuniformly distributed transcription factors.²⁶

Explaining the AP asymmetry of tll expression, which is expressed in a two-domain pattern, requires a more complex model. A key feature of this model is the presence of distinct enhancers responsible for the anterior and posterior parts of the patterns. The anterior enhancers are activated by Bcd and repressed by Cic. The anterior enhancer of tll is also repressed by Hkb and Kni, both of which are activated by the Bcd and Dl. The posterior patterns of tll and hkb are formed by a simpler mechanism, based on a gradient of Cic repression and uniformly distributed activators, such as Zld. This model can explain why the same signaling pathway elicits very different transcriptional responses in two different regions of the embryo, resulting in the asymmetric expression patterns of tll and hkb.

Our model requires that the posterior enhancer of tll is inactivated at the anterior pole and vice versa. The anterior enhancer is not active at the posterior pole because of the limited range of the Bcd gradient. The posterior enhancer can be silenced at the anterior pole in multiple ways. First, Bcd-dependent expression of Kni can directly repress posterior enhancer of tll. This possibility is supported by the presence of Kni binding sites in the posterior regulatory regions of tll. Second, repression of posterior enhancers can rely on a long-range repression, whereby silencing of one of the enhancers of a gene silences other enhancers.^{48, 49} The third mechanism can rely on the fact that anteriorly localized Bcd acts as a competitive inhibitor of MAPK-dependent downregulation of Cic.²⁷ This increases the level of Cic and can potentially repress the posterior regulatory elements of tll. Future work is required to determine the contributions of these different mechanisms to the wild-type pattern of tll.

The proposed model for the two-domain expression of tll is clearly a great simplification of reality and does not get everything right: When it comes to posterior expression of the terminal genes in our model, Cic is the only nonuniformly distributed regulator. According to this, the expression of tll and hkb should become uniform in the absence of Cic (Fig. 9). To test this, we examined the tll and hkb patterns in embryos from cic[1] flies, where the levels of Cic at the mid-body of the embryo are reduced to ∼10% of that of the wild-type [Fig. 6b]. The domains of the two genes were significantly expanded, but their expression was still confined to the terminal region [Figs. 5h, 9].

We also modeled the pattern of tll and hkb in cic[1] embryos by reducing the input level of Cic to 10% of the wild-type. The model predicted patterns of tll and hkb were indistinguishable from that of the absence of Cic. Thus, the model where Cic is only spatially distributed regulator of tll and hkb at the posterior pole accounts for only part of the data. This difference between model predictions and observations suggests the presence of additional repressors of the terminal genes in the mid-body of the embryo. One of these repressors can be Kni, which is expressed in the mid-body of the embryo,⁵⁰ and, according to our bioinformatics analysis, should bind tll enhancers active in the posterior pole. In the future, this can be incorporated into our model and integrated with models of gene regulation in the mid-body region.^{21, 42}