A Mathematical Model for Analyzing the Elasticity, Viscosity, and Failure of Soft Tissue: Comparison of Native and Decellularized Porcine Cardiac Extracellular Matrix for Tissue Engineering

Abstract

The clinical success of tissue-engineered constructs commonly requires mechanical properties that closely mimic those of the human tissue. Determining the viscoelastic properties of such biomaterials and the factors governing their failure profiles, however, has proven challenging, although collecting extensive data regarding their tensile behavior is straightforward. The easily calculated Young's modulus remains the most reported mechanical measure, regardless of its limitations, even though single-relaxation-time (SRT) models can provide much more information, which remain scarce due to a lack of manageable tools for implementing these models. We developed an easy-to-use algorithm for applying the Zener SRT model and determining the elastic moduli, viscosity, and failure profiles of materials under different mechanical tests in a user-independent manner. The algorithm was validated on the data resulting from tensile tests on native and decellularized porcine cardiac tissue, previously suggested as a promising scaffold material for cardiac tissue engineering. This analysis yields new and more accurate measurements such as the elastic moduli and viscosity, the model's relaxation time, and information on the factors governing the materials' failure profiles. These measurements indicate that the viscoelasticity and strength of the decellularized acellular extracellular matrix (ECM) are similar to those of native tissue, although its elasticity and apparent viscosity are higher. Nonetheless, reseeding and culturing the ECM with mesenchymal stem cells was shown to partially restore the mechanical properties lost after decellularization. We propose this algorithm as a platform for soft-tissue analysis that can provide comparable and unbiased measures for characterizing viscoelastic biomaterials commonly used in tissue engineering.

Introduction

Recent reports published by our group^1–5 and others^6–14 have demonstrated the use of constructs made of decellularized cardiac tissue as scaffolds for tissue engineering. Such scaffolds, to achieve clinical success, must have structural and mechanical properties that closely match human tissue. Specifically, they must possess adequate mechanical strength and the ability to retain their shape over time.¹⁵ Scaffolds with mismatched stiffness have failed to reduce infracted myocardial wall stress, whereas scaffolds with mismatched flexibility (as max. strain before yielding) failed to perform under myocardial contraction/expansion cycling, and did not conduct mechanical stimuli from the host myocardium.¹⁰ Moreover, only scaffolds that closely mimic the mechanical properties of the target tissue were shown to support the direction and propagation of progenitor cells associated with tissue regeneration, leading to a better functioning biomedical device.^16,17 Accordingly, for materials based on the extracellular matrix (ECM), as well as for many other viscoelastic biomaterials used in tissue engineering, not only must the stiffness be matched (average, time-independent), but the other viscoelastic parameters, which describe the time and rate dependency of the mechanical response to deformation, must also fit.¹⁴

In recent publications, we demonstrated the applicability of the decellularized ECM for tissue engineering applications, and the comparability of acellular and native tissue, including vascular grafts,¹⁸ thin myocardial patches,² and thick^3,5 left ventricle cardiac wall constructs. In particular, a perfusion-driven decellularization procedure (Trypsin- and Triton-based, more elaborately described in the Supplementary Data [Supplementary Data are available online at www.liebertpub.com/tec]) was found to achieve high acellularity of the thick porcine cardiac ECM as validated by histological analyses showing no cellular remains.³ Most importantly, the decellularized matrix was shown to be nonimmunogenic and cell supportive, while retaining its fiber morphology, structural characteristics, and collagen content—verified using multiphoton imaging, scanning electron microscopy, and mass spectrometry proteomic analysis. The previously reported biocompatibility of our decellularized cardiac tissue, as well as its structural and morphological similarity to native tissue, hints at its potential as a scaffold for cardiac tissue engineering. Aiming to be more clinically relevant, decellularized scaffolds might support tissue regeneration even without repopulating them with cells, as demonstrated previously with different natural and synthetic acellular materials transplanted into cardiac infarcts.^19–22 To do so, such scaffolds should primarily possess mechanical properties that resemble those of the native tissue^14,20,22,23 and that should be resolved so that they reflect a large variety of viscoelastic and failure characteristics, which will be addressed by this article.

Similar to the cardiac wall, most soft tissues under various modes of mechanical testing, exhibit viscoelastic behavior. In many cases, they also reveal a toe region, seen before the linear tensile region,^24,25 which is attributed to the straightening and alignment of fibrous proteins^26,27 and the deformation of the elastin.²⁸ While obtaining large amounts of data on the stress–strain behavior of such biomaterials is straightforward, analyzing it in a uniform, comparable, and user-independent manner is more challenging.²⁹ Despite significant advancements in highly correlative mechanistic models^30–38 for stress–strain analysis, most of the reported literature still relies on stiffness, as measured by the Young's modulus, as the primary mechanical measure for biological tissues. However, as tissues are subjected to many nonelastic deformation modes and their responses may differ significantly from ideal spring behavior, measuring only this characteristic can be misleading, at best. Therefore, and to design appropriate tissue replacements, an effort must be made to measure and match the viscoelastic properties of tissues more completely and comprehensively. One solution, in our opinion, lies in using our implementations of the Zener single-relaxation-time (SRT) model, suggested previously as appropriate for describing viscoelastic biomaterials,³⁹ yet seldom implemented due to practical limitations that we demonstrate how to remove in this article.

In comparison to the ideal spring model, SRT models, which are simple serial and/or parallel combinations of springs and dampers⁴⁰ (Fig. 1a), provide more information regarding material viscosity and elasticity. By setting varying boundary conditions into their constitutive differential equations, SRT models may accommodate several mechanical testing modes or response regions, which are depicted in a single time-continuous stress–strain curve. Such combinations of several modes and/or regions are not only common in many experiments, but also better resemble the physiological conditions in which these biomaterials are believed to operate.^41,42 Much like multiple relaxation time (MRT) models, SRT models are expected to correlate to a large extent with empirical data and may provide better assessments of viscoelastic properties than the Young's modulus alone,^43–45 with an advantage of avoiding the information redundancy commonly incurred by MRT models. SRT models may also facilitate the analysis of soft biomaterials, not as monolithic solids, but as a bundle of strings, each having the same elastic moduli and viscosity, but with different failure points, thereby enabling the modeling of such solids beyond their apparent linear viscoelastic region and into their failure region. Such analysis, producing new measures for elasticity and integrity failure, and providing better measures of toughness and strength, is crucial for evaluating and comparing biomaterials under harsh conditions and determining their applicability for regenerative medicine.

FIG. 1.

Schematic representation and typical stress–strain behavior of viscoelastic solids. (a) Schematic representation of three linear viscoelastic solids (models): Zener, Maxwell, and Kelvin–Voigt. The elastic modulus E or E₁ and E₂ correspond to the elastic components in the various solids, while η corresponds to the modulus of the dashpot/damper (the viscosity modulus). (b) Typical mechanical behavior of viscoelastic solids under tensile-relaxation test, spanning two testing modes—tensile (constant strain-rate) and stress-relaxation (constant strain)—resulting in two respective response regions. (c) Typical mechanical behavior of uniform viscoelastic solids under tensile-failure test, spanning a single testing mode (tensile, constant strain-rate), but resulting in various response regions: a linear viscoelastic region (LV region) before the point of elasticity loss, a nonelastic region after the elasticity loss (excluding Kelvin–Voigt), and a rupture above the integrity loss. The typical time continuous stress plots were derived from physical simulation of the various mechanical models under different tests using Simulink^® and Simscape^® as detailed in the Supplementary Data.

In common analysis, normalized data (e.g., moduli and compliance) can be used in simple models for comparing the viscoelastic behavior of different samples. Such data, readily attained for many synthetic materials, are much harder to come by when dealing with soft amorphous and heterogeneous biological tissues exhibiting complex behaviors under different testing modes. In cases when several mechanical testing modes or response regions (under a single stress–strain curve) are being simultaneously analyzed, their solutions frequently require researchers to resort to complex and elaborate models and mathematical transformations,^39,43 further obscuring their physical meaning. Additionally, the full potential of these models is seldom exploited, as they require the use of advanced mathematics and considerable programming abilities as well as computational capacities, which exceed that of common spreadsheet software and users. Accordingly, due to the lack of efficient, but simple tools to implement these models, most data collected from the stress–strain experiments remain unanalyzed and the significance of the measured properties of tested biomaterials is not thoroughly interpreted.

In this article, we present an efficient algorithm accompanied by an easy-to-use MATLAB^® code aimed at elucidating the viscoelastic parameters and determining the failure profiles of materials tested under experiments spanning various mechanical testing modes and/or stress–strain response regions. Our proposed analysis can provide highly indicative and new types of parameters, under more physiological-like conditions, which are essential for achieving a more complete mechanical characterization of soft-tissue constructs, especially in the context of tissue engineering. The suggested analysis, performed on thick (∼15 mm) porcine left ventricle wall cardiac tissue, reveals that although their viscosity and apparent elasticity might be different, the overall viscoelasticity and strength of the decellularized ECM resemble that of native tissue, supporting its utilization in tissue engineering applications. Preliminary studies of decellularized ECM reseeded with human bone marrow mesenchymal stem cells (MSCs), which were previously suggested as model cells and potential progenitors for cardiomyocytes,^46–48 reveal that most mechanical properties are partially restored following seeding and cultivation. The complete codes for algorithm implementation along with examples and documentation for the code execution are provided in the Supplementary Data.

Methods

Preparation of decellularized, native, and reseeded porcine tissue for mechanical testing

The porcine left ventricular myocardium was excised and decellularized to produce the acellular extracellular matrix (pcECM), using an enzymatic-based procedure, which was previously reported by us³ and is described in more detail in the Supplementary Data. For testing the reseeded pcECM, decellularized left ventricular wall pcECM slabs of 25 mm (w)×70 mm (l), in their full thickness, were seeded on the myocardium side, with 20×10⁶ human bone MSCs (Lonza™, Basal, Switzerland). The cell number was selected to achieve a maximal seeding density similar to the native cardiac tissue (∼10⁸ cells/cm³),^12–14 assuming 100% attachment and a maximal penetration depth of 100 μm under static culturing conditions.^49–51 Before being subjected to mechanical testing, the reseeded slabs were cultured for 2 weeks in the minimum essential medium Eagle, alpha modification (Sigma-Aldrich™, St. Louis, MO), supplemented with 10% Gibco^® fetal bovine serum, 1% l-glutamine, 5 ng/mL basic fibroblast growth factor, and 1% antibiotic–antimycotic (Invitrogen™, Carlsbad, CA). The cells were cultured at 37°C in a humidified incubator with 5% CO₂; the medium was replenished every other day.

Mechanical testing parameters

Independent samples of the reseeded pcECM as well as native and decellularized slabs, in their full thickness, which were cut into cuboidal slabs of 25 mm (w)×70 mm (l), were mounted onto an Instron™ 5567 (Norwood, MA) with a 500 N load cell for tensile testing. Complete mechanical characterization of the native (n=5) and decellularized pcECM (n=4) was conducted under both stress-relaxation and tensile-failure tests, whereas preliminary results for the reseeded pcECM (n=3) were obtained using the tensile-failure test only. For all samples, preloading was done for 13 cycles (0.05 mm/s to 15% strain), followed by unloading at the same rate. For stress-relaxation measurements (also termed tensile-relaxation tests), samples were stretched at a rate of 0.5 mm/s to 20% strain and held at constant displacement for an additional 600 s. For tensile-failure measurements (also termed stress-to-break tests), samples were stretched at a constant rate of 0.05 mm/s until failure. The results of the two tests were analyzed by several computational implementations of various mechanical models.

Tensile-relaxation analysis

The Zener and other viscoelastic models were implemented to resolve the behavior of the native and decellularized pcECM tested under a tensile-relaxation assay comprising two testing modes, namely, the tensile mode (constant strain-rate) and the stress-relaxation mode (constant strain), as shown in Figure 1b. Initially, a linear model (σ=σ₀+(ɛ−ɛ₀)E), corresponding to the Hook model, was fitted on data registered during the tensile mode to produce the Young's modulus (E as the slope) and the toe border (t₀) separating the toe region from the linear viscoelastic region (LV region). The elucidated toe border was used later as the starting point from which the Zener and other models were fitted.

The Zener model can be represented as a spring serially connected to a Kelvin–Voigt solid (Fig. 1a)^52,53 and described according to its typical constitutive differential equation (Eq. 1)⁴⁰ using the viscosity (η), and the elastic moduli (E₁ and E₂).

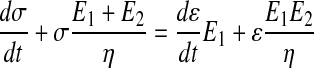(1)

By rearranging Equation 1, a multivariate linear correlation arises (Eq. 2) between the stress at time t (σ_t) and three apparently independent variables: (^dσ/_dt), (^dɛ/_dt), and ɛ.

(2)

Given that dσ, dɛ, and dt can be estimated based on their integral form (Δσ, Δɛ, and Δt), Equation 3 can be stipulated and used as an approximation of the constitutive differential Zener model.

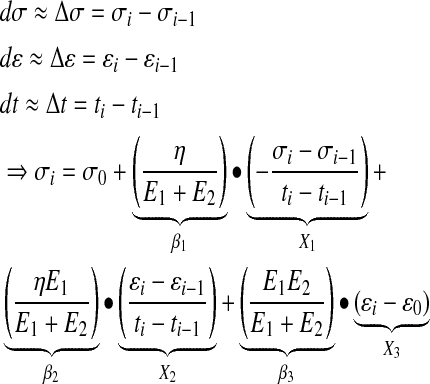(3)

By regressing the stress (σ_t) against X₁, X₂, and X₃ (according to Eq. 3), the regression coefficients can be elucidated (β₁, β₂, and β₃) and used to calculate the elastic moduli: E₁, E₂, and the viscosity designated by η. Since X₁, X₂, and X₃ are not entirely independent, as required for multivariate regression, the resulting parameters can only be regarded as estimates of the actual elastic moduli and viscosity.

The nonlinear form of the Zener model (Eq. 4) can be stipulated by integrating Equation 1 (see the Supplementary Data) using boundary conditions that correspond to the two prevalent modes: tensile, spanning from t₀ to t₁ with ^dɛ/_dt=v (while v represents the strain-rate used in the test) and stress-relaxation, from t₁ onward with ^dɛ/_dt=0. Finally, the integral nonlinear model stipulated in Equation 4 can be fitted with the empirical data and optimized to produce: E₁, E₂, and η.

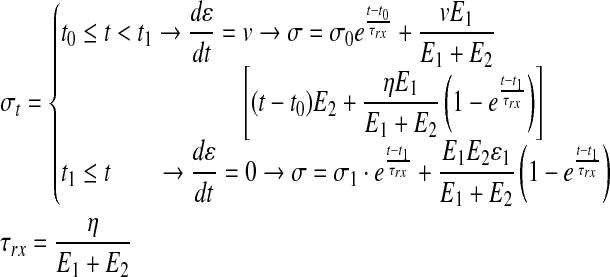(4)

For comparison, two other models (also shown in Fig. 1b), the Maxwell and Kelvin–Voigt models, were also fitted onto the data. The implementation of the Maxwell model is similar to that described for the Zener model (Eq. 4), but with E₂=0. The implementation of the Kelvin–Voigt model is according to Equation 5.

(5)

Tensile-failure analysis

A new method was designed to analyze the data drawn from tensile-failure tests. Unlike common analysis methods, this failure-enabling implementation of the Zener model was intended to analyze all the tensile-failure data without excluding the failure region. Accordingly, the following three assumptions (a–c) were made to accommodate data from both the failure and elastic response regions:

• (a) The analyzed material is regarded as a bundle of strings, instead of as a uniform monolithic solid. Since all strings belong to the same underlying material, they all have the same elastic moduli and viscosity; however, each string has its own unique failure points. Thus, the superposition of the individually failing strings, throughout the entire bundle, results in a global gradual failure.

• (b) Each string starts its mechanical response as a Zener solid, and then fails in a two-stage process. Elasticity loss occurs when the first failure point is reached. This point occurs when the spring denoted by E₁ is fully deformed, causing the Zener solid to lose its major elasticity and start behaving like a Kelvin–Voigt solid. Integrity loss occurs when a second point is reached, along the stress–strain continuum, at which the string can no longer hold its structural integrity, causing it to rupture.

• (c) Each failure point (for each string) is denoted as the multiplication product of the strain and stress (stress·strain) at the time of failure. The elasticity-loss measure (defined for each string as W_E≡Stress_E • Strain_E) is normally distributed throughout the bundled material with a mean of 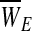and a variance of 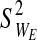. The integrity-loss measure (defined for each string as W_I≡Stress_I • Strain_I) is normally distributed throughout the bundled material with a mean of 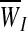and a variance of .

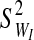Assuming all the above, Equation 6 can be stipulated to describe the stress on a single string, characterized by its own two failure points (W_E and W_I) and the parameters E₁, E₂, and η shared by all strings. Finally, when multiplying Equation 6 by the normal probability density functions of W_E and W_I (denoted by 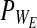and ), and then integrating the product according to 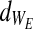and 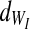, a new function is generated (Eq. 7) that describes the overall stress (σ_t) on a failing bundle of Zener strings. Equation 7 can be numerically solved as detailed in the Supplementary Data.

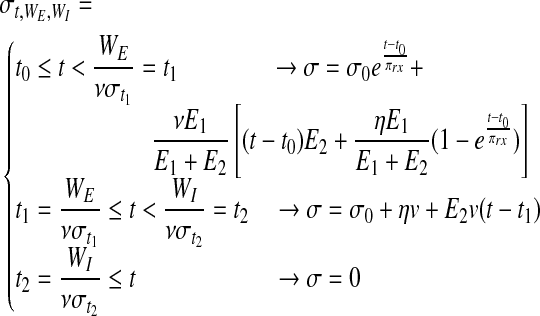(6)

(7)

To exemplify the behavior of the single strings, the failure profiles of three different uniform solids corresponding to the Zener, Maxwell, and Kelvin–Voigt models are depicted in Figure 1c. The Zener and Maxwell solids are experiencing simultaneous elastic and integrity failure; the Kelvin–Voigt solid, for which an elastic limit cannot be defined, is not experiencing such a failure.

Programming environment

All codes were written and executed using Matlab R2011a (The MathWorks, MA), supplemented with optimization and statistics toolboxes.

Statistical analysis

Results are expressed as the mean±SD. Statistical significance in the differences of the means was evaluated by the t-test. All R² in the text are adjusted (R²_adjusted) to correct for sample size and model complexity bias. A correlation of R²_adjusted≥0.9 was required to include any optimized parameters or results into our analysis.

Results

Tensile-relaxation analysis: typical curves

The decellularized ECM (Fig. 2a) and native tissue (Fig. 2b) were tested under tensile-relaxation and analyzed by our suggested implementation of the Zener model. The toe region border, the elastic moduli (E₁, E₂), and the viscosity (η) were elucidated, averaged, and utilized to plot the typical curves, representing the average tensile-relaxation behavior of the analyzed materials. The typical curves revealed a stiffer pcECM (Fig. 2c) exhibiting a substantially higher relaxation stress than native tissue under the same strain-rate conditions.

FIG. 2.

Typical tensile–relaxation curves. The theoretical tensile–relaxation curves for decellularized and native pcECM samples were plotted using the averaged viscosity and elastic moduli as well as the toe borders resulting from the suggested implementation of the Zener model. (a) Typical stress response of pcECM versus empirical data. (b) Typical stress response of native tissue versus empirical data. (c) Typical stress response of pcECM versus native tissue (time and stress are offset). pcECM, acellular extracellular matrix.

Tensile-relaxation analysis: elastic moduli and viscosity evaluation

The elastic behavior observed for the ECM and native tissue, in the tensile mode, was found to be correlated (R²>0.97) with the Hook (ideal spring) model, whereas the viscoelastic behavior, spanning both tensile and relaxation modes, matched (R²>0.94) the Zener model only (Fig. 3a). No differences (p>0.05) were found between the Young's modulus (E), derived from the Hook model, and the Zener elastic moduli (E₁ and E₂) calculated for the same materials, averaging 1.3±0.6 for the decellularized ECM and 0.3±0.1 (MN/m²) for native tissue (Fig. 3b). The equivalent static modulus , which is expected to be equivalent to the Young's modulus and is supposed to reflect the overall elasticity, was found to be smaller than the E₁, E₂, or Young's modulus for both materials (p<0.01). The Zener elastic moduli (E₁ and E₂) as well as the Young's modulus and the equivalent static modulus (E*) were found to be larger (>fourfold, p<0.05) for the decellularized ECM than for the native tissue. The viscosity (Fig. 3c) was also found to be almost three times larger (p<0.05) for the ECM (1.7×10²±50%) than for the native tissue, averaging 0.6×10²±50% (MN·s/m²). The resulting relaxation times 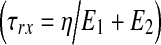, calculated according to the Zener viscosity and elastic moduli (Fig. 3d), were found to be significantly (p<0.05), yet not substantially longer for the native tissue than for the ECM.

FIG. 3.

The viscoelastic properties of decellularized and native pcECM analyzed under tensile-relaxation test. (a) The fit (correlation as R²_adjusted) between empirical data, resulting from analysis of decellularized and native pcECM samples, and between the following mechanical models: Hook (for data resulting from the tensile mode only), Zener, Maxwell, and Kelvin–Voigt. (b) The average elastic moduli of decellularized and native pcECM; Young's modulus E was calculated from the Hook model, while E₁, E₂, and E* (calculated based on E₁ and E₂) were determined according to the Zener model. (c) The viscosity modulus η according to Zener. (d) The relaxation (τ_rx) calculated based on Zener's viscosity and the elastic moduli. Statistical significance indicators: *p<0.05, **p<0.01.

Tensile-failure analysis: typical curves

The decellularized ECM (Fig. 4a) and native tissue (Fig. 4b) were tested under tensile-failure and analyzed using a particular implementation of the Zener model enabling the analysis of failing viscoelastic materials. The toe region border, the viscosity (η), and the elastic moduli (E₁, E₂) were elucidated, as well as the means and variance of the elastic and integrity load limits. These elucidated measures were averaged and used to plot the typical curves, representing the average tensile-failure behavior of the analyzed materials. The typical curves revealed a stiffer and tougher ECM (Fig. 4c), but with similar strength (maximal stress) as the native tissue.

FIG. 4.

Typical tensile-failure (stress-to-break) curves. The theoretical stress-to-break curves for decellularized and native pcECM samples were plotted using the averaged viscosity and elastic moduli and toe borders as well as the elastic and integrity limits (means and variance) resulting from the suggested failure-enabling implementation of the Zener model. (a) Typical stress response of pcECM versus empirical data. (b) Typical stress response of native tissue versus empirical data. (c) Typical stress response of pcECM versus native tissue (time and stress are offset).

Tensile-failure analysis: elastic moduli, viscosity, and load limit evaluation

The viscoelastic behavior and failure profiles, observed for both the ECM and native tissue, were found to be highly correlated (R²>0.94) with our suggested failure-enabling implementation of the Zener model as shown in the Supplementary Data (see examples for code execution). To further validate our model and its applicability, preliminary tensile-failure studies were also conducted on the acellular ECM that was reseeded and cultured with MSCs, as more elaborately described on the Supplementary Data. As can be seen from Figure 5a, while E₁ substantially increases (>10-fold, p<0.05) following decellularization, E₂ decreases and is practically zeroed for the decellularized ECM compared to the native tissue (p<0.01). After reseeding, both elastic moduli are partially restored, E₁ decreases and E₂ increases, moving closer to their original native values. The apparent viscosity values (η) were found to be similar for both the decellularized and native ECM as well as for the reseeded ECM (Fig. 5b) and the relaxation times were practically identical for all three groups (Fig. 5c). Here and unlike in the analysis of tensile-relaxation data, the relaxation times do not necessarily reflect a real-time measure. Nonetheless, it can still be regarded as an estimate for the overall viscoelasticity, given that it measures the ratio between the viscosity (η) and the sum of the elastic moduli (E₁+E₂). Despite the large variations between the tensile-failure (Fig. 3) and tensile-relaxation data (Fig. 5), the relaxation times drawn from those two tests are surprisingly comparable.

FIG. 5.

The viscoelastic properties and failure profile of decellularized, reseeded, and native pcECM analyzed using a tensile-failure test. The viscosity and elastic moduli as well as the stress·strain values at the failure points (means and variance) were elucidated, averaged, and plotted for samples of decellularized, acellular reseeded pcECM, and native pcECM samples using failure-enabling implementation of the Zener model (R²_adjusted>0.93). (a) The average elastic moduli. (b) The viscosity modulus η. (c) Relaxation (τ_rx) times calculated based on the Zener viscosity and the elastic moduli. (d) The stress·strain values at the failure points corresponding to the elasticity and integrity loss. Statistical significance indicators: *p<0.05, **p<0.01.

The failure points, designating the loss of elasticity and integrity, were normally distributed and measureable in terms of the multiplication products of the stress and strain at the time of failure. As can be seen in Figure 5d, the measure for elasticity loss was substantially larger for the decellularized (>7-fold, p<0.001) and reseeded (>100-fold, p<0.001) ECM compared with native tissue. The measure for integrity loss, however, was similar for both the native and reseeded ECM that was fourfold larger (p<0.001) than the same measure for the decellularized ECM. Apart from the large variance found in native tissue for the distribution of the elasticity loss (C.V.=80%), all other failure measures were narrowly distributed with coefficients of variance of <20%.

Discussion

The use of decellularized tissues or other complex biomaterials, as scaffolds for tissue engineering inevitably requires a thorough investigation of their viscoelastic and failure properties, which is often limited by the lack of easy-to-use tools to analyze the ample data resulting from standard mechanical tests.^15,17,54 The biomedical potential of our previously reported decellularized pcECM led us to develop several such analysis tools, reported upon herein. These tools were used to resolve the viscosity, the elastic moduli, and failure profiles of native and decellularized tissue tested under tensile-relaxation and tensile-failure tests.

This report sheds new light on the mechanical properties of cardiac tissue, which is imperative for any regenerative approach in this area. We also demonstrate and provide tools for analyzing other materials. Such analysis tools are presented as algorithms and codes for implementing a Zener-based analysis of data from both tensile-relaxation and tensile-failure experiments spanning several testing modes or response regions resulting from a single test-run or apparent on a continuous stress–strain curve. To remove user-bias, this algorithm attempts to require as little user input as possible, which in turn contributes to the analysis uniformity and repeatability.

Out of the four viscoelastic models (linear Zener, Zener, Maxwell, and Kelvin–Voigt), which can mathematically accommodate both tensile and stress-relaxation modes, only the Zener model was found to correspond to the mechanical response data collected from both testing modes. The resulting viscoelastic parameters (E₁, E₂, and η) were significantly higher for the decellularized pcECM than for the native tissue, implying an increased stiffness and apparent viscosity due to decellularization, which is also consistent with the measured increase in the Young's modulus. This increased stiffness, previously reported elsewhere,^7,10,12,55 and demonstrated herein for the decellularized pcECM using both analysis methods, can possibly be attributed to a denser and more compact ECM mainly composed of collagen fibers^10,46,56 as a result of the loss of cellular components. Yet the toe border strain (presented in the Supplementary Data) was similar for both the pcECM and native tissue, implying that the preservation of collagen and nonload-bearing proteins,^41,56 such as elastin, is also consistent with our previously reported results showing a minimal loss of such ECM components during decellularization.³

Unlike earlier analytical methods, which relied on graphical evaluation or estimations of single mechanical testing modes and lacked common ground for comparison, it is now possible to mathematically calculate the relaxation time, which is highly indicative of the materials' overall viscoelasticity.^29,35,36 Surprisingly, and despite the large variations between the native and decellularized pcECM, their relaxation times were found to be roughly comparable when tested under tensile-relaxation, and even quite similar for tensile-failure data. In other words, although the magnitudes of the viscoelastic responses (as measured by moduli) are vastly different for the decellularized and native tissues, the time dependency of these properties are roughly equivalent. These new crucial results, demonstrating this similar viscoelasticity, along with previously reported results indicating the same elastic hysteresis and toughness as native cardiac tissue,³ may definitively indicate the mechanical applicability of the decellularized pcECM for cardiac tissue engineering.

Using our suggested failure-enabling implementation of the Zener model, the overall viscoelasticity (in terms of relaxation time) drawn from the tensile-failure data was found to be not only similar for the pcECM and native tissue, but also comparable to the viscoelasticity determined using tensile-relaxation data. On the other hand, and as can be expected due to the different strain rates applied in the two tests, the viscosity and elastic moduli elucidated from the tensile-failure data differ in size from those drawn from the tensile-relaxation data. The strong agreement between the overall viscoelasticity as measured by the two tests further validates and reaffirms both the failure-enabling model and the simple Zener model as suitable for analyzing tensile-failure data and tensile-relaxation data, respectively. Unlike the simple failure analysis provided in the Supplementary Data, this model distinguished between the elastic and integrity failure stages, which were significantly different from one measure to another and from one material to another as well. These new measures not only provide better means for comparing the failure properties of analyzed materials, but also facilitate determination of the theoretical (typical) behavior of materials tested under tensile-failure conditions.

To further validate the applicability of our analysis method, samples of the acellular ECM were seeded with MSCs, cultured, and compared with the native and acellular ECM. As reported in the Supplementary Data, the cells grew sixfold in 2 weeks, uniformly covering the myocardial surface with a layer of aligned cells that also changed the overall appearance of the ECM, making it seem more like the native tissue. Tensile-failure analysis of the reseeded ECM has shown that most viscoelastic and failure properties were either partially restored (E₁, E₂, and the integrity loss) to their native values, or unchanged (η and τ_rx) if they had not initially differed between the decellularized ECM and native tissue. These results, achieved through tensile-failure analysis that also utilizes the basic implementation of the Zener model, further validate the model, and increase the prospects of this more biologically relevant reseeded scaffold to be suitable for regenerative medicine applications. We believe that regardless of these results, the comparison between the native and decellularized pcECM alone, which occupies the greater part of this article, is enough to prove the validity of our model for soft tissue analysis. Further, when taken together with our previously reported results, the mechanical similarity between the native and decellularized pcECM strengthens the applicability of the decellularized pcECM as a scaffold material for cardiac tissue engineering.

The striking mechanical similarities between the native and decellularized ECM, thoroughly characterized and demonstrated here for the first time, are not entirely unexpected as the collagen-rich proteinaceous scaffold, and not the cells, are supposed to govern the overall mechanical behavior.^48,56,57 Nonetheless, this comparison (native vs. ECM) does shed a new light on the mechanical contribution of the cells shown to reduce the elasticity (E₁ in both tests), viscosity (in tensile-relaxation), and elastic limit of the ECM, while increasing its integrity limit. These changes can be attributed to the decrease in the mechanical predominant collagen content (per weight) of the native tissue^7,8,10 compared to the ECM, and the additional strength provided by the cells^41,58,59—increasing the integrity limit. Surprisingly and unlike most parameters, which were partially restored after reseeding the ECM, the elastic limit increased instead of decreasing toward its native value. This phenomenon may be attributed to the ECM remodeling resulting in a different elastic limit than natural native tissue. This behavior and the overall mechanical contribution of the reseeded cells, which naturally change with culturing time and seeding densities, certainly raises more questions than what is briefly addressed in this article. Further research is, therefore, necessary, not only to answer these questions, but also to determine the effect of different culturing techniques (e.g., static vs. dynamic culturing, cocultures) and cell types (e.g., fibroblasts, endothelial) on the mechanical properties of the reseeded ECM.

In conclusion, we demonstrated efficient and easy-to-use analysis tools for further mechanical characterization of biomaterials, providing more accurate and substantial information regarding the viscoelastic behavior and failure profiles of biomaterials. In terms of our example, this additional information regarding the failure profiles of the pcECM is novel and much more indicative of the pcECM's viscoelastic properties than previously reported parameters graphically estimated or calculated from simple linear fittings.³ In particular, the additional information resulting from our analysis can now be used to estimate the mechanical compatibility and applicability of the acellular and reseeded pcECM as well as other constructs as scaffolds for tissue engineering. Finally, average viscosity and elastic moduli can easily be calculated for a certain material and test, which will in turn allow plotting of typical curves representing the theoretical stress–strain behavior of this material much better than a selected representative curve.

Further research is required to revalidate this analysis on a variety of other materials; however, we remain confident that this algorithm can be used as a common platform for soft-tissue analysis, providing comparable and user-independent measures to characterize the viscoelastic response and failure profiles. In particular, we reiterate two points. The first is that a single average Young's modulus value is not sufficient to characterize or compare different biomaterials, especially in applications where the matching of the time-dependent mechanical characteristics is crucial to the eventual success of the implanted scaffold or device. Second, truncating the stress–strain data and excluding response regions to fit simpler models may substantially influence the analysis and produce inaccurate and unreliable measures jeopardizing the mechanical compatibility and applicability of biomedical constructs. The code that was used herein to execute this algorithm and that appears in full in the Supplementary Data of this article should be seen as an invitation to alter and fit the model to other materials and needs.

Acknowledgments

This research is supported by the Singapore National Research Foundation under the CREATE program: The Regenerative Medicine Initiative in Cardiac Restoration Therapy Research Programme; and the Israeli Science Foundation (ISF) under grant No. 1563/10 entitled: “Thick acellular heart ECM with inherent vasculature: Towards engineering cardiac tissue replacement.” We further wish to thank Dr. Susan Liao for her help and assistance.

Disclosure Statement

No competing financial interests exist.