An Analysis of FMA Using Structural Self-Bisimilarity

Abstract

As ontologies are mostly manually created, they tend to contain errors and inconsistencies. In this paper, we present an automated computational method to audit symmetric concepts in ontologies by leveraging self-bisimilarity and linguistic structure in the concept names. Two concepts A and B are symmetric if concept B can be obtained from concept A by replacing a single modifier such as “left” with its symmetric modifier such as “right.” All possible local structural types for symmetric concept pairs are enumerated according to their local subsumption hierarchy, and the pairs are further classified into Non-Matches and Matches. To test the feasibility and validate the benefits of this method, we computed all the symmetric modifier pairs in the Foundational Model of Anatomy (FMA) and selected six of them for experimentation. 9893 Non-Matches and 221 abnormal Matches with potential errors were discovered by our algorithm. Manual evaluation by FMA domain experts on 176 selected Non-Matches and all the 221 abnormal Matches found 102 missing concepts and 40 misaligned concepts. Corrections for them have currently been implemented in the latest version of FMA. Our result demonstrates that self-bisimilarity can be a valuable method for ontology quality assurance, particularly in uncovering missing concepts and misaligned concepts. Our approach is computationally scalable and can be applied to other ontologies that are rich in symmetric concepts.

1. Introduction

Biomedical ontologies play an important role in health informatics and biomedical research. As mostly manually created formal representations of knowledge, potential errors and inconsistencies are inevitable [1]. A number of methods have been proposed for auditing ontologies [2, 3, 4]. They vary from lexical [5], structural [6, 7, 8, 9, 10], to semantic [11, 12, 13], statistical [14] and abstraction-network-based [15]. The entities audited are centered around concepts [16, 17] or relations [5, 6, 8, 9, 16].

In this paper, we introduce an auditing method that combines information from concepts and relations. We focus on symmetric concept pairs in the Foundational Model of Anatomy (FMA [18]), a commonly-used reference ontology in medicine. A pair of concepts is called symmetric if the concept names are the same except for the possible difference in a single occurrence of symmetric modifiers used. For example, (“Anterior part of deltoid,” “Posterior part of deltoid ”) is a symmetric concept pair in FMA involving the modifier pair anterior and posterior. We propose the use of bisimilarity (a.k.a. bisimulation) for auditing symmetric concepts in FMA. Bisimulation is a technique used in Computer Science to capture similar behaviors in transition systems [19, 20]. We say that two concepts are bisimilar if: 1) they are symmetric; 2) their parents are either bisimilar or the same. We use the word “self-bisimilarity” to indicate the fact that the bisimilar concepts come from the same ontology.

The motivating idea for this work is that most symmetric concept pairs should be bisimilar, so the “symmetry” carries over to all ancestors of the respective pairs until a shared concept is reached. Figure 1 shows two example configurations, where the arrows express the subsumption relationships (IS-A) in FMA.

Figure 1.

The two ideal cases for bisimilar concepts. Arrows express the subsumption relationships in FMA.

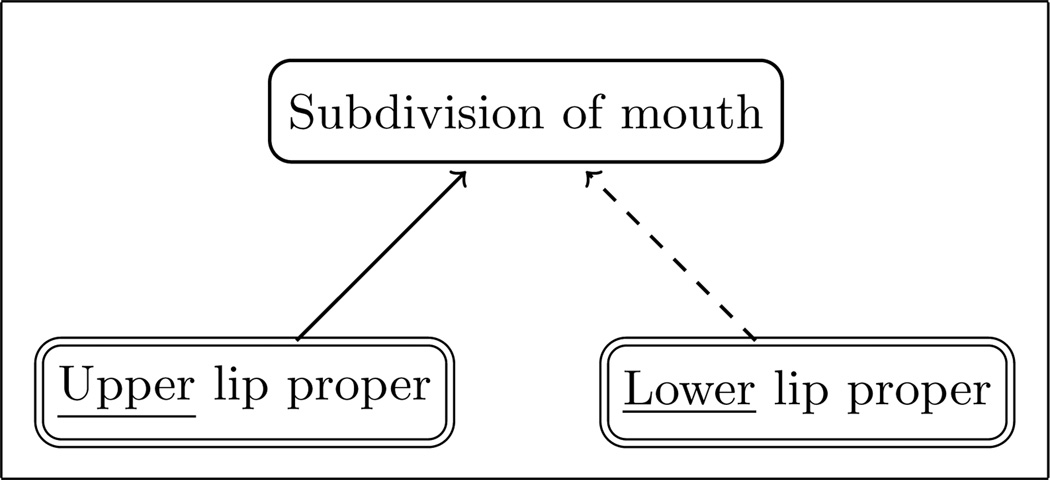
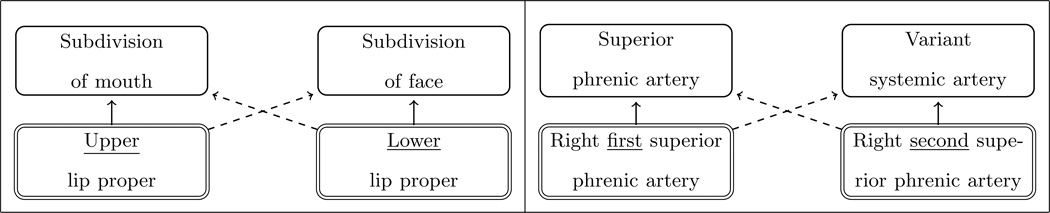
In some cases, the expected symmetric counterparts of some concepts do not exist in the ontology, which may be an indication of missing concepts. For example, while “Second toe” exists in FMA, “First toe” does not. It was confirmed by FMA experts that “First toe” should also appear in FMA. Moreover, even when both symmetric concepts exist, they may not exhibit bisimilar structures as illustrated in Figure 1. This can be seen from Figure 2: the symmetric pair (Upper lip proper, Lower lip proper) exists in FMA, however, they do not share a parent concept: “Lower lip proper” is not classified as a subclass of “Subdivision of mouth” in FMA, which represents a misaligned relationship.

Figure 2.

An example of abnormal structure. Dashed arrow indicates the absence of subsumption relationship between the nodes.

This paper provides a comprehensive study of substructures associated with symmetric concepts. We divide symmetric concept pairs into two groups:

1. Non-Matches, where only one member of a symmetric concept pair appears in the ontology. There are three cases in this group, distinguished by the possible appearances and types of their parents (Table 1).

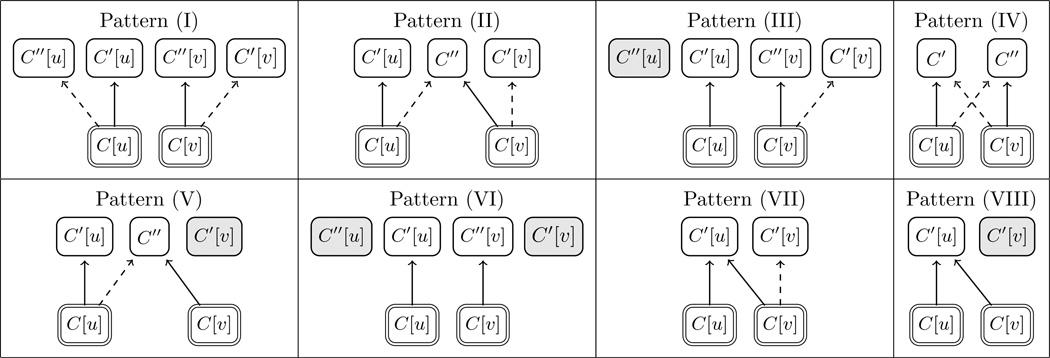
2. Matches, where both members of a symmetric concept pair appear in the ontology. There are five single-parent-context types (Table 2) and eight mixed-parent-context patterns representing the combination of these five types (Table 3).

Table 1.

Three Cases for Non-Matches. Shaded nodes represent absent concepts.

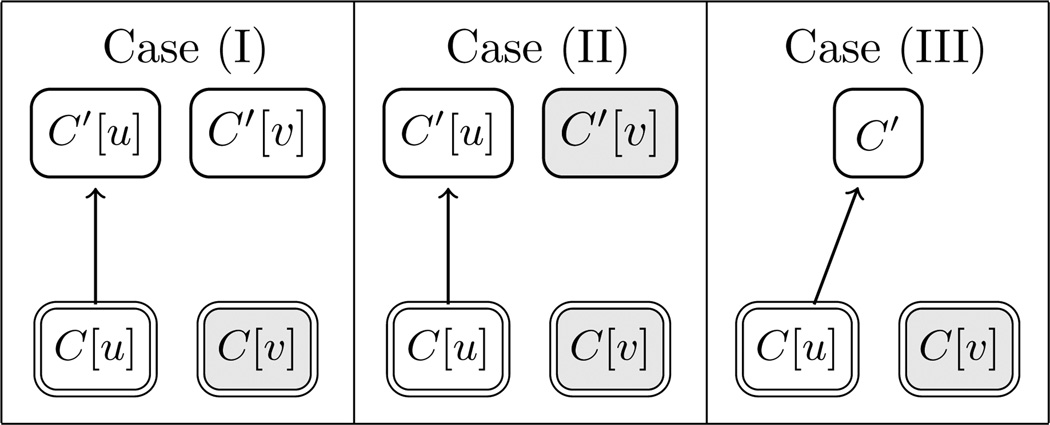Table 2.

Five Types for Matches. Shaded nodes represent absent concepts. Dashed arrows represent missing IS-A relationships.

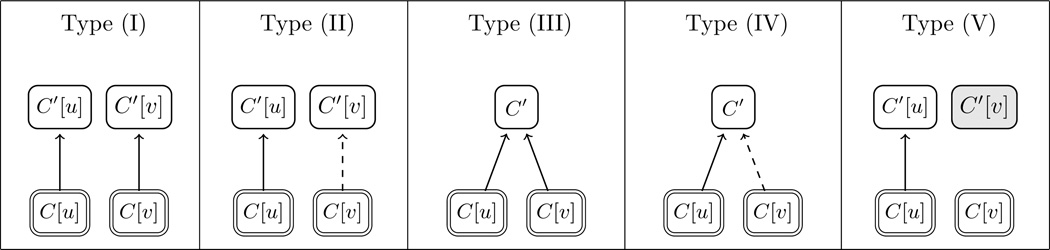Table 3.

The eight patterns of mixed parent contexts for problematic Matches. Shaded nodes represent absent concepts. Dashed arrows represent missing IS-A relationships.

In our experimentation, we automatically computed all the symmetric modifier pairs from FMA, and selected six of them as examples: (first, second), (anterior, posterior), (upper, lower), (ascending, descending), (superior, inferior), (left, right). As a result, 9893 Non-Matches and 221 abnormal Matches (out of a total number of 27267 Matches) were discovered for the six pairs in FMA. Manual evaluation by FMA domain experts on 176 selected Non-Matches and all the 221 abnormal Matches found 102 missing concepts and 40 misaligned concepts.

There are several related works: in [6], the authors used relationship auditing on FMA to discover problems such as cycles and inconsistencies, but did not specifically consider symmetric concepts. In our previous work [21], we used motifs to discover abnormal relations between mutually exclusive concepts, which is a structural relational auditing method. Lexical method was used in [22] to identify mismatches in ontology alignment. In [5], the authors used symmetric concepts for assessing the consistency of SNOMED and UMLS. They focused primarily on the existence of the concepts and relationships between them, without analyzing the structures for Matches or Non-Matches. Also, our recent work on dissecting the ambiguity of FMA concept names helps improve the accuracy for lexical auditing methods [23].

In all, we conduct a scalable, comprehensive analysis of all the possible structures for each symmetric pair, which is not just for detecting potential errors, for analyzing those scenarios, but more importantly, for exposing the sources of errors, and for guiding the creation of new ontologies with potential ontology design patterns [24, 25].

2. Background

Our methodology leverages the Semantic Web technology in three components: the Web Ontology Language (OWL), the Resource Description Framework (RDF), and its associated query language SPARQL. We explain the details of the methodology described in the subsequent sections. We begin with an overview of FMA.

2.1. The Digital Anatomist Foundational Model (FMA)

The FMA is both a theory of human anatomy and an computational artifact [18]. As a theory, it provides a unifying framework for the nature of the diverse entities that make up the bodily structure of biological organisms as well as the relationships between them. In particular, it is a theory of the canonical, phenotypic structure of the human organism at all biologically salient levels of granularity. As a theory of canonical anatomy, it ranges over those categories of entities which are idealizations of an organism’s body and its typical component parts. As a computational artifact, it is a formal representation of this theory, suitable for machine manipulation. The model underlying the FMA is a frame-based representation with 78,977 concepts including macroscopic, microscopic and sub-cellular canonical anatomy. For our analysis, we used the legacy version of the OWL translation of FMA from the Open Biomedical Ontology (OBO) Foundry [26]. The FMA OWL version from OBO foundry is distributed as an RDF/XML-based serialization that enables it to be stored in an RDF data store and made available to be queried via SPARQL over internet protocol.

Concepts in ontology are organized into a concept hierarchy with more generic concepts modeled as parents of more specific concepts using the subClassOf property (e.g., Right Hand subClassOf Hand). This relationship is called the IS-A relationship. Another important relationship in ontologies is the Part-Of relationship (e.g. Hand part of Free upper limb). In this paper, we only focus on the IS-A relationship.

2.2. Semantic Web Technology: OWL, RDF and SPARQL

In Semantic Web, RDF is used as a format to represent directed, labeled multi-graphs. It models entities in a triple structure consisting of a subject, predicate, and object [27]. The Web Ontology Language (OWL [28]) is a formal language for specifying the constraints of a particular domain, and is meant to govern the structure and meaning of the vocabulary used by RDF content. OWL ontologies are often distributed as RDF graphs in a document format.

The query language for RDF is called SPARQL [29]. SPARQL queries are comprised of patterns and logical combinations thereof. The patterns in a SPARQL query also have a triple structure, but the terms can also use variables that represent wildcards. They are evaluated against an RDF database (a.k.a. RDF store) that is typically hosted on a remote server over a standard, web-based protocol. SPARQL queries result in matching subgraphs as solutions, which map variables in the query to the variable terms that comprise the triple structure of an RDF graph in the data store.

3. Methods

A concept name can be divided into two parts: A modifier and a context which is the remainder of the term. We use u, v to represent modifiers and use C to represent context. C[u] then represents the concept name comprised of C and u, similarly with C[v]. Taking different modifiers and different positions of the modifiers into account, one concept name may have multiple divisions. For example, “Lumen of anterior ramus of right anterior segmental bronchus” has two divisions for the modifier “anterior”: “Lumen of anterior ramus of right anterior segmental bronchus” and “Lumen of anterior ramus of right anterior segmental bronchus,” where the underlined modifier is the one focused on.

We use pair (u, v) to represent symmetric modifiers. Putting the symmetric modifiers into the same context C results in a symmetric concept pair (C[u], C[v]). As a result, the above concept “Lumen of anterior ramus of right anterior segmental bronchus” has two symmetric concepts: “Lumen of posterior ramus of right anterior segmental bronchus” and “Lumen of anterior ramus of right posterior segmental bronchus.”

More than 80% of the concepts in FMA contain modifiers in their names. We provide an automatic approach to extract all the symmetric modifier pairs in FMA and rank them by their occurrences (The specific steps will be explained in Section 3.3). Six pairs of them are selected for further analysis.

3.1. Non-Matches

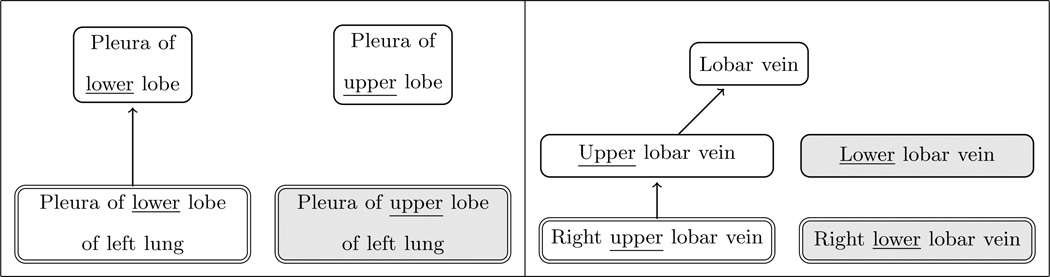
For a symmetric concept pair, if only the first member appears in the ontology, it is called a Non-Match. For example, for the pair (Pleura of lower lobe of left lung, Pleura of upper lobe of left lung), the first member appears in FMA and the second one does not. In this scenario, it is natural to trace back to the ancestors to investigate the original reason. As illustrated in the left diagram of Figure 3, we discover a concept “Pleura of lower lobe of left lung” whose symmetric concept “Pleura of upper lobe of left lung” is absent in FMA. When investigating its parent “Pleura of lower lobe,” we discover that the parent’s symmetric concept “Pleura of upper lobe” does exist. So the question is: why does “Pleura of upper lobe of left lung” not exist, and why is it not a child of “Pleura of upper lobe?” This kind of scenario is captured by Case (I) in Table 1.

Figure 3.

(1) Example of Case (I) in Table 1; (2) A Non-Match trace. Shaded nodes represent absent concepts.

Note that in our diagrams, we always use the solid arrow “−→” to represent the IS-A relationship rdfs:subClassOf. A dashed arrow “⤏” means that the IS-A relationship is missing between the head and tail, and a shaded node indicates that the corresponding concept does not appear in FMA at all.

There are two other cases for Non-Matches, as illustrated by Case (II) and Case (III) in Table 1, the details on all the cases are explained in the following:

• Case (I): C[u] exists in FMA while C[v] does not. The parent of C[u] also contains the modifier u but with a different context C′, and C′ [v] is a concept existing in FMA.

• Case (II): C[u] exists in FMA while C[v] does not. The parent of C[u] also contains the modifier u but with a different context C′. The same as C[v], C′[v] does not exist in FMA.

• Case (III): C[u] exists in FMA while C[v] does not, and the parent of C[u] does not contain the modifier u.

By looking into those cases we can discover that (II) is the only consistent case: the fact that C[v] does not exist in FMA is caused by the nonexistence of C′ [v] in FMA. If tracing back along Case (II) to their ancestors, we can always reach Case (I) or Case (III). For example, in the right diagram of Figure 3, by tracing back two steps, we reach Case (III). As a result, there exist clustered Non-Match trees where the roots belong to Case (I) or Case (III) while all the other nodes belong to Case (II). These kinds of roots are called Non-Match tree roots. While every pair in Case (II) must be a node in some tree, many pairs in Case (I) or Case (III) are just isolated nodes since they do not have any Non-Match descendant. As we can see, the tree roots help domain experts to limit and focus their effort when auditing ontologies.

3.2. Matches

If C[u] appears as a concept name in FMA, C[v] is supposed to be a concept name in FMA as well, and vice versa. When both C[u] and C[v] are concept names in FMA for some context C, the pair (C[u], C[v]) is called a Match. If we trace back to their parents, then ideally, there are supposed to be two cases, as illustrated by the examples in Figure 1 in Section 1: 1) Their parents are also a Match and contain the same modifiers with their children separately; 2) They share the same parent which does not contain the modifier u or v at all.

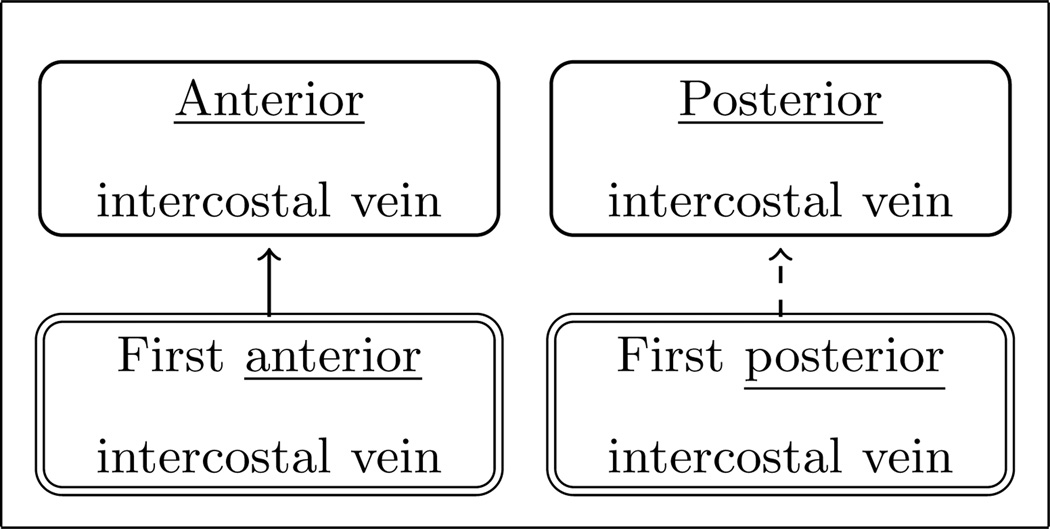
Even though most of the Matches in FMA maintain good bisimilar structures, there still exist abnormalities. The example shown in Figure 2 in Section 1 is only one such case. There are more abnormal structures on Matches. For example, there is a Match (First anterior intercostal vein, First posterior intercostal vein), where “First anterior intercostal vein” has parent “Anterior intercostal vein.” Although the symmetric concept for “Anterior intercostal vein” exists in FMA, it does not have “First posterior intercostal vein” as its child, as shown in Figure 4. This scenario is captured by Type (II) in Table 2.

Figure 4.

Another abnormal type for Match. Dashed arrow means a missing IS-A relationship.

For Matches, when considering only single parent context, we can classify all of them into five types, as shown in Table 2.

• Type (I): The parent of C[u] also contains the modifier u but with a different context C′, C′[v] also exists in FMA with C[v] being a sub-class of C′[v].

• Type (II): The parent of C[u] also contains the modifier u but with a different context C′, C′[v] also exists in FMA, but C[v] is not a sub-class of C′[v].

• Type (III): The parent of C[u] does not contain the modifier u, and C[u] and C[v] share the same parent.

• Type (IV): The parent of C[u] does not contain the modifier u, but C[u] and C[v] do not share the same parent.

• Type (V): The parent of C[u] also contains the modifier u but with a different context C′, but C′[v] does not exist at all.

It is clear that Type (I) is an ideal case. For Type (III), it is an ideal case when the parent C′ does not contain the modifier v neither. Other types indicate potential errors in the modeling procedure.

3.2.1. Patterns for abnormal matches

The calculation of the above five types is unilateral, i.e, it only considers single parent context. For those problematic non-symmetric ones (Type (II), (IV) and (V)), the type of (C[v], C[u]) may be different from that of (C[u], C[v]). As a result, there are nine mixed combinations, resulting in six different patterns considering the fact that some of them have symmetric structures. They are illustrated in Table 3 from Pattern (I) to Pattern (VI).

Besides the six patterns, there are two more patterns that can be easily ignored. As stated before, in Type (III) (Table 2), the parent C′ does not contain the modifier u, but may contain the modifier v. In that case, if we change the order of the members in the pair, the resulting type can be Type (II) or Type(V). For example, as illustrated in the left diagram of Figure 5, “C8 part of posterior division of brachial plexus” is child of “Branch of anterior ramus of eighth cervical nerve” instead of “Branch of posterior ramus of eighth cervical nerve” even though the latter one exists in FMA. In this case, from right to left, it is Type (III), but from left to right, the type is changed to Type (II). In another example, as shown in the right diagram of Figure 5, the type is Type (III) from right to left and is changed to Type (V) after we change the order of the members in the pair. As a result, we need to add Pattern (VII) and Pattern (VIII) to Table 3. Although pairs in these two patterns are rare, we still need to list them in order to be theoretically complete.

Figure 5.

(1) Example of Pattern (VII); (2) Example of Pattern (VIII). Shaded nodes represent absent concepts. Dashed arrows represent missing IS-A relationships.

The eight patterns we presented above provide the human editors of biomedical ontologies a full dimensional view of all the structures for Matches, which can be helpful in discovering and introducing new ontology design patterns [24, 25].

3.3. Implementation

The FMA OWL file was loaded into a Virtuoso RDF store [30], version 06.01.3127, hosted on a MacPro desktop machine with 32GB of RAM and one 2.8GHz Quad-Core Intel Xeon “Nehalem” processor, running Mac OS X Snow Leopard.

In order to retrieve all the modifier pairs, we first obtained all the class names in FMA and used Natural Language Processing (NLP) methods to obtain all the Noun-Phrase (NP) chunks without prepositions. As a result, 22510 NP chunks were obtained. For all the modifiers in those chunks, any two of them who share common context were selected out to form a modifier pair. Finally, we ranked all the modifier pairs by the number of common contexts the two members share. The first twenty pairs we obtained are: (left, right), (anterior, posterior), (superior, inferior), (lateral, medial), (first, second), (second, third), (first, third), (fourth, third), (fourth, second), (lateral, anterior), (first, fourth), (lower, upper), (fourth, fifth), (third, fifth), (deep, superficial), (second, fifth), (first, fifth), (posterior, lateral), (external, internal), (fourth, sixth).

We selected five pairs from the first twenty pairs and another pair from the remainder for experiment. For each input symmetric modifier pair (u, v), we employed an algorithm comprised of the following steps:

1. Query the RDF database, obtain all the concept names containing the modifier “u,” and their divisions on “u”

2. Replace “u” with “v” in each division, query the database again to see if the symmetric concept exists; obtain all the Matches and Non-Matches from “u” to “v”

3. Change “u” and “v” into each other, repeat step 1 and step 2; obtain all the Non-Matches from “v” to “u”

4. For all the Matches between “u” and “v,” query the database and get information about their parents, then divide them into the five types in Table 2

5. Check mixed parent context information for those problematic pairs from the above step, then divide them into the eight patterns in Table 3

6. For Non-Matches from “u” to “v,” query the database and get information about their parents; divide them into the three cases in Table 1, and obtain all the Non-Match tree roots

7. For Non-Matches from “v” to “u,” query the database and get information about their parents; divide them into the three cases in Table 1, and obtain all the Non-Match tree roots

One thing needs to be noted in our algorithm: When checking whether the concept name contains the same modifier as its parent do to decide the types in Table 2, if the modifier occurs multiple times in the term, context information around it has to be used. In our experiment, we use the words before and after the modifier as the helpers: if both modifiers in the parent and the child share the same words before or after them, they are considered the same modifier. For example, “Parenchyma of anterior part of right anterior bronchopulmonary subsegment” has parent “Parenchyma of anterior part of anterior bronchopulmonary subsegment.” When the first anterior is in question, to confirm that the parent contains the same modifier, context information “Parenchyma of ” was used. When the second anterior is in question, the other context information “bronchopulmonary subsegment” was used.

4. Results

After applying our automatic method for extracting modifiers in FMA, we discovered 1304 pairs of modifiers in which both members have at least 10 common contexts, and 34 pairs of modifiers in which both members have at least 100 common contexts. Six pairs of them that are most commonly used and most intuitively to introduce bisimilar concepts were selected for further experimentation: (left, right), (anterior, posterior), (first, second), (superior, inferior), (upper, lower), (ascending, descending).

For each symmetric modifier pair, Table 4 illustrates the total numbers of concept names, numbers of Matches and Non-Matches. For each number pair in the cells, the first member indicates the corresponding number for the first element in the modifier pair. Similarly for the second one. Since numbers of Matches should be the same for symmetric modifiers, the two numbers in each cell of the “Matches” column are the same.

Table 4.

The numbers of Matches and Non-Matches on the six symmetric modifier pairs

Modifiers	FMA classes		Matches	Non-matches
	Concepts	Divisions
(first, second)	(2502, 2902)	(2502, 2902)	(2317, 2317)	(185, 585)	(7.39%, 20.16%)
(anterior, posterior)	(3832, 5458)	(3936, 5586)	(2550, 2550)	(1386, 3036)	(35.21%, 54.35%)
(upper, lower)	(1423, 1379)	(1423, 1379)	(1227, 1227)	(196, 152)	(13.77%, 11.02%)
(ascending, descending)	(338, 313)	(338, 313)	(205, 205)	(133, 108)	(39.35%, 34.50%)
(superior, inferior)	(3317, 3089)	(3360, 3112)	(2263, 2263)	(1097, 849)	(32.65%, 27.28%)
(left, right)	(19482, 19442)	(19813,19763)	(18705, 18705)	(1108, 1058)	(5.59%, 5.35%)
Total Count	63477	64427	(27267, 27267)	9893	15.36%

As mentioned before, one concept name may have multiple divisions on the same modifier, due to the fact that the modifier may appear more than once in the concept. The column “divisions” in Table 4 shows the numbers of all the divisions on all the modifiers.

4.1. Non-Matches

The last column in Table 4 shows the percentages of Non-Matches on the total number of concepts containing the corresponding modifier. As it shows, more than half of the concepts whose names contain the modifier “posterior” do not have their symmetric concepts appearing in FMA. On the other hand, it is remarkable that for the pair (left, right), there are only about 5% of Non-Matches. For others, the percentages of Non-Matches are between 10% to 35%.

Table 5 illustrates the distribution of Non-Matches on the three cases we defined (see Table 1). The percentages are based on the total number of Non-Matches for each corresponding modifier pairs. As it shows, there are 9893 Non-Matches with 1219 Non-Match tree roots totally. Except for the pair (left, right), Case (II) occupies more than 50%, which is reasonable due to the fact that Case (II) is the consequence of Case (I) or Case (III). The last two columns of Table 5 record the numbers of Non-Match tree roots in Case (I) and Case (III) separately. As it shows, although Case (II) occupies a large part of the Non-Matches, after clustering, the number of trees they belong to is reduced dramatically. This emphasis on the tree roots helps save the effort of domain experts in the auditing process..

Table 5.

Distribution of Non-Matches on the three cases and the numbers of Non-Match tree roots in Case (I) and Case (III)

Modifiers	Case (I)		Case (II)		Case (III)		Tree Roots
							Case (I)	Case (III)
first → second	41	22.16%	96	51.89%	48	25.95%	15	30
second → first	24	4.10%	416	71.11%	145	24.79%	5	131
anterior → posterior	154	11.11%	810	58.44%	422	30.45%	88	147
posterior → anterior	159	5.24%	2512	82.74%	365	12.02%	101	186
upper → lower	57	29.08%	95	48.47%	44	22.45%	38	8
lower → upper	52	34.21%	76	50%	24	15.79%	33	4
ascending → descending	12	9.02%	75	56.39%	46	34.59%	12	17
descending → ascending	4	3.70%	70	64.81%	34	31.48%	2	18
superior → inferior	113	10.30%	668	60.89%	316	28.81%	41	156
inferior → superior	111	13.07%	454	53.48%	284	33.45%	57	90
left → right	147	13.27%	129	11.64%	832	75.09%	17	10
right → left	132	12.48%	83	7.84%	843	79.68%	6	7
Total Count	1006	10.17%	5484	55.43%	3403	34.40%	415	804

Except for tree roots, other pairs in Case (I) and Case (III) are isolated Non-Matches. For example, more than 75% of Non-Matches for the pair (left, right) are in Case (III). While there are only a few tree roots for this case, we can conclude that most of the pairs are isolated Non-Matches.

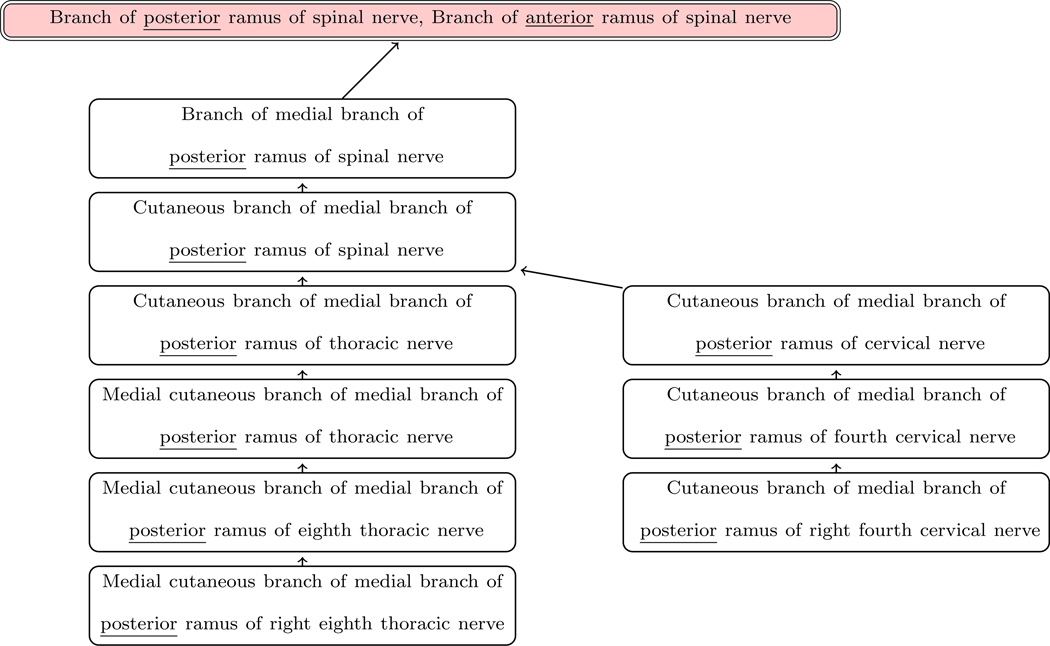
Figure 6 illustrates part of a tree with the tree root “Branch of medial branch of posterior ramus of spinal nerve” in Case (I). All descendants of the root have their corresponding symmetric concepts missing in FMA. It is clear that the absence of “Branch of medial branch of anterior ramus of spinal nerve” causes the absence of the other eight symmetric concepts for other descendants.

Figure 6.

The node in pink contains a symmetric concept pair. All descendants of it are Non-Matches with their corresponding symmetric concepts missing, where “Branch of medial branch of posterior ramus of spinal nerve” is the tree root.

4.2. Matches

Table 6 shows the results of the Matches for the six modifier pairs in FMA. The middle part illustrates the distribution of the Matches on the five types of single parent contexts (see Table 2); the right part illustrates the distribution of abnormal Matches on the eight patterns on mixed parent contexts (see Table 3). Except for the last row, the percentages in the last column are calculated on the total number of Matches for each corresponding modifier pairs. As indicated before, the one instance in Pattern (VII) and the four instances in Pattern (VIII) are special patterns derived from pairs in Type (III).

Table 6.

Distribution of Matches on single and mixed parent contexts: the middle part illustrates the distribution of the Matches on the five types (see Table 2); the right part illustrates the distribution of abnormal Matches on the eight patterns (see Table 3). The last row shows numbers of confirmed errors for each pattern after evaluation.

Modifiers	Matches on Types			Abnormal Matches on Mixed Patterns
	Type (I)	Type(III)	Others	I	II	III	IV	V	VI	VII	VIII	Total
(first, second)	1471	840	6				6					6	0.26%
(anterior, posterior)	1624	847	79		4	1	47	4	8/23	1	3	79+4	3.25%
(upper, lower)	877	320	30			2	17	1	10		1	30+1	2.53%
(ascending, descending)	124	76	5				5					5	2.44%
(superior, inferior)	1599	605	66	2	2	1	56	2	3			66	2.91%
(left, right)	149	18526	30		3	3	20		4			30	0.16%
Confirmed Errors					1	3	13	4	18		1	40	18%

As shown in Table 6, those abnormal Matches occupy a negligible portion of all the Matches (221 instances, less than 4%), which in turn confirmed our intuition that Type (I) and (III) are ideal situations. Among the eight patterns for abnormal Matches (Table 3), Pattern (IV) turns out to be the most common one with 151 instances, where the parents for the two symmetric concepts are two different contexts.

5. Evaluation

Manual evaluation was conducted by FMA experts from the Structural Informatics Group of the University of Washington, where the latest version of FMA is managed and maintained.

5.1. Non-Matches

Among the 9893 Non-Matches discovered by our algorithm, we randomly selected 176 tree roots for evaluation: the 13 Non-Match tree roots from “right” to “left,” the 27 tree roots from “left” to “right,” and the 136 tree roots from “second” to “first” (Table 5). Manual inspection confirmed 8, 4( 2 of them are deprecated) and 90 missing concepts for each group, respectively. In other words, 58% of them have been identified missing concepts that need to be or already has been added to the latest version of FMA. For example, the 10 missing concepts for the tree roots on (left, right) are:

• “Atrial branch of left coronary artery,”

• “Wall of trunk of atrial branch of left coronary artery,”

• “Lumen of trunk of atrial branch of left coronary artery,”

• “Set of branches of left middle cerebral artery,”

• “Branch of posterior ramus of left anterior segmental bronchus,”

• “Division of posterior part of left anterior segmental bronchial tree,”

• “Division of posterior part of left anterior bronchopulmonary subsegment,”

• “Parenchyma of division of posterior part of left anterior bronchopulmonary subsegment,”

• “Region of papillary muscle of right venrticle,” and

• “Epicardium of region of wall of right ventricle.”

Corrections for them have already been implemented by domain experts to the current version of FMA. Except for the 102 identified missing concepts, the other 74 instances are false positive results due to the traditional convention used in naming arteries, veins, nerves and lymphatic trees.

5.2. Matches

All the 221 abnormal Matches in Table 6 were evaluated by FMA experts. 40 true errors were found among them, including one deprecated term and 4 terms with misspellings. Their distribution on the eight patterns is shown in the last row of Table 6, where the percentage 18% is based on the number of all the abnormal Matches. Figure 7 illustrates two examples that were identified by FMA experts as true errors: for the example on the left, both “Upper lip proper” and “Lower lip proper” should have the same parent “Lip proper;” for the example on the right, both children should have the same parent “Superior phrenic artery.”

Figure 7.

Two detected error examples among the abnormal Matches. Arrows express the subsumption relationships. Dashed arrow indicates the absence of subsumption relationship between the nodes.

Recall the two examples in Figure 5, it was pointed out by domain experts that the parent assignments for the example on the left is correct. However, for the example on the right of Figure 5, “Inferior margin of left upper lobe” should have parent “Inferior margin of upper lobe of lung,” which was already implemented in the current version of FMA.

6. Discussions

We discovered 9893 Non-Matches and 221 abnormal Matches in FMA for the six symmetric modifier pairs. Manual evaluation by FMA domain experts on 176 Non-Matches and all the 221 abnormal Matches found 102 missing concepts and 40 misalignments in FMA.

If we classify the error types into (a) missing concept, and (b) misalignment, then all the Non-Matches cases are potential type (a) errors. For the eight patterns on mixed parent contexts in Table 3, Pattern (I), (II),(IV), and (VII) are likely type (b) errors. The other cases may represent a mixture of type (a) and type (b) errors, as illustrated by the example on the right of Figure 5.

The fact that there are false positive results among the Non-Matches and misaligned Matches discovered by our method is due to the traditional convention used in naming FMA concepts in tree structures such as arteries, veins, nerves and lymphatic trees. For example, “Left diagonal artery” is actually the diagonal branch of “left coronary artery.” There is no diagonal branch for the “right coronary artery,” hence no “right diagonal artery.” Another example for Matches: the class “Superior epigastric artery” is a branch (subtree) of “Internal thoracic artery,” hence has the parent class “Subdivision of internal thoracic artery;” while on the other hand, the class “Inferior epigastric artery” is a branch of “External iliac artery proper,” hence the child of “Subdivision of external iliac artery proper.” If we were to classify them based solely on location (epigastrium), then we would create a class called “Epigastric artery” which would then subsume both the superior and inferior types. However the location attribute as the primary axis for classification does not add more meaningful information or knowledge about the arteries.

As for now, we inspected a small portion (176) of the 9893 Non-Matches since manual checking on all of them require a lot of effort. The 58% rate of actual missing concepts among them indicates the effectiveness of our method. Incorporation of the missing tree roots on the pair (left, right) were already implemented by FMA experts after evaluation. We expect this to be an ongoing process as all cases are inspected.

For each symmetric concept pair, when defining the cases, types and patterns, we only look up to the parents without going down to the children at the same time, which might seem insufficient. However, if we switch to the children’s point of view, they become parents. So, it is not necessary to consider both directions.

Only binary symmetric modifiers are considered in this paper. To deal with non-binary relations such as (anterior, medial, lateral), one solution is to treat them pairwise, while the alternative is to treat them holistically. For the latter solution, we first need to extend Matches and Non-Matches from pairs to arrays, then define all the types and cases for them accordingly. However, it is predictable that the numbers of those types and cases will increase exponentially since all the possible combinations have to be taken into account. As a result, treating the non-binary relations pairwise and then combine the results may be a more feasible route.

7. Conclusion

We proposed a principled ontology auditing approach based on structural bisimilarity, and provided exhaustive analysis on six prominent modifier pairs. A significant amount of previously unknown errors were discovered and have been incorporated into the latest version of FMA. The uniqueness of our structural auditing method lies in three aspects. First, instead of manually providing the symmetric modifier pairs, we automatically compute all the pairs from FMA and rank them. Second, our methodology stems from the bisimulation theory in Computer Science. Different from randomly choosing some isolated structures for analysis, as is typical in the literature, the cases, types and patterns we define are theoretically complete. Third, we not only discover those concepts with high likelihood of errors, but also point out the roots where the errors were introduced. The eight patterns for the problematic Matches also help the domain experts trace back to the original conceptual errors, which can be useful in discovering and creating new design patterns in the processes of creating new ontologies [1, 24, 25].

We applied our methodology to the legacy version of FMA from the OBO foundry [26]. The algorithm we proposed is scalable and can be easily applied to other versions of FMA or other ontologies. Except for IS-A, the Part-Of relationship can be brought into the picture in our future work. The most prominent difference between IS-A and Part-Of relationships is that in the former, each concept can only have one parent in FMA, and in the latter, each concept can have multiple parents. Thus, the analysis of the Part-Of relationship will require more complex structures.

Highlights.

• We audit symmetric concepts in the Foundational Model of Anatomy.

• We extract modifier pairs from FMA and choose six of them for experimentation.

• We divide all symmetric concepts into two groups: Non-Matches and Matches.

• 9893 Non-Matches and 221 abnormal Matches were discovered with their substructures.

• Manual evaluation on a small portion of the results found 102 missing concepts and 40 misaligned concepts.

• Those substructures we defined help expose the sources of errors.