A clinical risk stratification tool for predicting treatment resistance in major depressive disorder

Abstract

Background

Early identification of depressed individuals at high risk for treatment-resistance could be helpful in selecting optimal setting and intensity of care. At present, validated tools to facilitate this risk stratification are rarely used in psychiatric practice.

Methods

Data were drawn from the first two treatment levels of a multicenter antidepressant effectiveness study in major depressive disorder, the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) cohort. This cohort was divided into training, testing, and validation subsets. Only clinical or sociodemographic variables available by, or readily amenable to, self-report were considered. Multivariate models were developed to discriminate individuals reaching remission with a first or second pharmacologic treatment trial from those not reaching remission despite two trials.

Results

A logistic regression model achieved an area under the receiver operating characteristic curve (AUC) exceeding 0.71 in training, testing and validation cohorts, and maintained good calibration across cohorts. Performance of three alternative models using machine learning approaches–a naïve Bayes classifier and a support vector machine, and a random forest model – was less consistent. Similar performance was observed between more and less severe depression, males and females, and primary versus specialty care sites. A web-based calculator was developed which implements this tool and provides graphical estimates of risk.

Conclusion

Risk for treatment-resistance among outpatients with major depressive disorder can be estimated using a simple model incorporating baseline sociodemographic and clinical features. Future studies should examine the performance of this model in other clinical populations and its utility in treatment selection or clinical trial design.

Registration

Sequential Treatment Alternatives to Relieve Depression (STAR*D); NCT00021528; www.star-d.org

Introduction

When an outpatient first presents for treatment of a major depressive episode, what is the likelihood that this specific patient will not reach symptomatic remission despite multiple treatment trials? So-called treatment-resistant depression has been repeatedly shown to be costly in both human and financial terms (1–3). If risk could be assessed readily on presentation, it might inform treatment planning, with some individuals referred for specialty care or consultation, or earlier consideration of combination treatment.

At present, no such tools are in common use in psychiatry. This is in marked contrast to other areas of medicine, such as oncology, cardiology, endocrinology, and critical care, where quantifying risk can be a crucial initial step in short- and long-term treatment planning (4–9). Psychiatric clinicians appear to rely either on extremes of severity (e.g., active suicidality, or psychosis), or on overall clinical impression, in making triage decisions: the American Psychiatric Association depression treatment guidelines, for example, simply distinguish strategies for more and less severe depressive episodes (10).

A recent area of enthusiasm has been development of biomarkers for risk stratification, but recent genetic investigation of antidepressant response suggests the limitations of these markers (11). At the same time, other studies indicate that biomarkers may be most useful when added to, rather than used to replace, existing clinical tools (12). To develop such a clinical decision making tool, data were drawn from the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) study, a large multicenter effectiveness study which incorporated sequential treatment trials to prospectively establish treatment resistance in major depressive disorder (MDD)(13). Multiple prediction models were developed using logistic regression as well as modern machine learning strategies, with the best-performing tool validated in an independent set of patients drawn from different regional centers in STAR*D.

Method

Clinical methods

General methodology for subject selection and treatment in STAR*D has been described elsewhere (13, 14). In brief, STAR*D was a multicenter study conducted in both primary and specialty care sites in the United States between 1999 and 2006. Eligible subjects were outpatients age 18–75, diagnosed with major depressive disorder by DSM-IV checklist, who presented requesting treatment and had a Hamilton Depression Rating Scale (HDRS) score of at least 14 (15). No advertising was allowed for recruitment in order to achieve a clinically-representative sample. All subjects signed written informed consent prior to participation, with the protocol approved by institutional review boards at participating institutions.

Treatment involved sequential interventions, or levels, beginning with citalopram treatment at level 1. In each 12-week level, individuals who reached symptomatic remission with a sufficiently tolerable regimen entered follow-up. The remaining patients were randomly assigned to next-step treatments, if they were willing to remain in treatment. At level 2, these included switch to sertraline, bupropion, or venlafaxine, or augmentation with bupropion or buspirone. Individuals could indicate a willingness to receive augmentation or switch, implementing equipoise-stratified randomization (16); therefore, assignment to these two groups of treatments was not balanced. (Subjects could also receive cognitive therapy alone or in addition to citalopram; as the present report focuses on pharmacotherapy, these subjects are not considered further here).

Outcomes

STAR*D included two protocol-specified primary outcomes, HDRS completed at level exit by a remote rater, and the 16-item Quick Inventory of Depressive Symptoms (QIDS-SR), a self-report measure completed at every visit (17, 18). Because data for the latter is available for more subjects, it has been the focus of most prior STAR*D reports and was therefore selected as the primary outcome here.

Specifically, the outcome of interest was remission by QIDS-SR of 5 or less at the first or second level of STAR*D, which was contrasted with failure to reach remission (QIDS-SR of 6 or greater) at study exit. Individuals who exited STAR*D following one level of treatment were censored from analysis, as it is impossible to determine their treatment resistance status from available data. Sensitivity analysis examined remission defined by HDRS score of 7 or less at study exit (from level 1 or 2), contrasted with nonremission following 2 antidepressant trials.

Variable Processing and Model Development

A challenge in multivariate models is selection of the set of variables to be included, particularly when a very large number of measures are available. While numerous automated methods are available for attribute or feature selection, many authors suggest that they should be informed by expert knowledge whenever possible (19). That is, some degree of manual variable selection can be useful in ensuring that all included variables are at least plausible predictors. (Prediction in this context should be distinguished from purely exploratory analysis, in which identifying a truly novel association might inform subsequent research efforts, which was not the goal of this study). On the other hand, because clinical variables may be correlated, and in order to maintain an adequate number of events or cases per variable (9), it is often necessary to perform some further pruning of variables prior to model development. This analysis utilized both approaches sequentially, with the author initially selecting a subset of clinically-plausible variables based upon manual review of those available in STAR*D, then applying an automated variable-selection approach to further prune the list and allow for more readily interpretable models. Figure S2 in the Supplement illustrates the process of variable selection and model development.

As the goal of this analysis was to identify a prediction tool using readily-available patient data, the only measures considered were those which are patient-rated, or ascertainable using simple patient reported questions; an example of the latter is perimenstrual mood worsening. This led to exclusion of variables likely to moderate outcome, but which are not amenable to patient report, such as comorbid medical illness, assessed in STAR*D using the Cumulative Illness Rating Scale, which requires clinician interview (20, 21). After review of all available STAR*D assessments, 4 sets of variables were examined (Table S1 in the Supplement). These included sociodemographic features available from the study entry form; individual items and total score on the QIDS-SR at study entry; presence or absence of psychiatric comorbidity on the Psychiatric Diagnostic Symptom Questionnaire (PDSQ)(22, 23); and measures of illness course and stressors completed at study entry, including duration of current episode, number of prior episodes, presence or absence of a prior suicide attempt, impact of family and friends on illness course, and perimenstrual mood worsening.

For PDSQ variables, only dichotomous (threshold for 90% specificity (22, 24)) variables were entered in the models, as well as a count of total number of DSM-IV diagnoses other than depression; as the PDSQ is not in the public domain, summary scores which would require use of that instrument were not included. Two screening subscales, mania and psychosis, performed poorly in validation studies [add refs]; in lieu of a 90% specificity threshold, variables were created which coded either presence or absence of at least screening symptom. Two additional individual questions drawn from the PDSQ were entered, reflecting lifetime history of witnessing or experiencing trauma, on the basis of growing evidence of gene-environment interaction in mediating depression risk.

After review of STAR*D screening assessments, two additional items were considered for model inclusion. The first was premenstrual mood worsening, based upon evidence that this symptom may be particularly responsive to SSRI treatment (25) – this is assessed by a single checklist item at entry into STAR*D: “In the course of the current MDE, does the patient regularly experience worsening of depressive symptoms 5–10 days prior to menses?” In an effort to assess degree of psychosocial supports, another variable considered was the family impact item from the demographic form collected in STAR*D: “The words and actions of family and friends can either help or make it more difficult for people to cope with depression. Please give us your judgment about the current overall impact of your family and friends on your condition.” This item is scored from 1 (very helpful) to 7 (much more difficult).

Standard approaches to missing data which rely only on subjects without missing observations, so-called complete cases analysis, have been suggested to be biased (26), necessitating some form of imputation to address the problem of missingness. In the present analysis, mean (for continuous/ordinal variables) or mode (for dichotomous variables) imputation was used to replace missing data. Alternative approaches to imputation, such as conditional imputation, have also been advocated (27). These strategies did not yield meaningfully different results in exploratory analyses, so were not further examined here. For all variables, less than 1% of data was missing.

Initial clinical review yielded 48 variables (Table S1 in the Supplement). In order to develop more parsimonious models for clinical application, while avoiding the limitations of standard stepwise approaches or univariate screens (9), an alternative strategy was applied in which a ‘wrapper’ was used to select attributes. In this approach, which is more computationally intensive but often yields superior accuracy to other types of feature selection using filters, multiple models are constructed on subsets of data using the same classification approach to be employed in the full model (28). For example, in a regression model, the performance of regression models using subsets of variables would be examined in subsets of data. While they do not eliminate the problem of overfitting entirely, recent developments make this approach increasingly practical and demonstrate its superiority to standard methods (29). (For a review of feature selection strategies, see reference (30)).

All models were implemented in the open-source Waikato Environment for Knowledge Analysis (WEKA) software (31), using the Best First greedy hill climbing search strategy combined with the Wrapper Subset Eval module, applying within-fold cross-validation to minimize overfitting. (That is, variable selection would be performed within the subset selected in each round of cross-validation, excluding the held-out data subset). This approach selected 15 variables for inclusion (Table 1).

Table 1.

Variables selected for model inclusion and coefficients in logistic regression model

Variable	coefficient	OR
QIDS-SR total	0.107	1.113
QIDS-SR middle insomnia	0.138	1.148
QIDS-SR late insomnia	0.073	1.076
QIDS-SR energy	0.129	1.137
Sex (male)	0.235	1.264
School (years of education)	−0.060	0.942
Marital status (currently married)	−0.297	0.743
School (years of education ^2)	1−e4	1.000
Race (African-American)	0.343	1.409
PTSD present	0.264	1.303
Recurrent episodes	0.179	1.195
Witnessed trauma	0.164	1.178
Experienced trauma	0.170	1.185
Psychosis screen positive	0.240	1.271
Family impact score	0.076	1.079
Intercept	−3.020

OR, odds ratio

QIDS-SR, Quick Inventory of Depressive Symptoms

Logistic regression, familiar to many clinical researchers, is a simple but powerful prediction approach which forms linear combinations of variables. In addition to logistic regression, three additional types of models were explored with the same 15 variables. These approaches were selected to encompass a diverse range of approaches to training a classifier using supervised learning, sometimes referred to as machine learning. These included a naïve Bayes classifier, a random forest model, and a support vector machine using a radial basis function kernel. Naïve Bayes classifiers implement Bayes’ theorem for probabilistic classification, multiplying probabilities conditional on a set of predictors (32, 33). While they assume that the predictors are conditionally independent, they often perform well even when this assumption does not fully hold, and compared to other algorithms may be more straightforward to interpret. Support vector machines are a newer machine learning approach which to date has been used relatively rarely in medical research (34) but more broadly in signal detection tasks (35). In essence, SVM algorithms take a set of training vectors and use one of several kernel functions to project them to a higher dimensional space, enabling identification of a separating hyperplane between classes (36). SVM requires manual tuning to determine optimal parameters for a given problem. Here, primary SVM results utilized a radial basis function as kernel; manual tuning was done using the training set only (see below).

Random forests utilize individual classification trees derived from applying recursive partitioning; the training data set is sequentially split, each time based on a single variable, attempting to form subgroups with greatest homogeneity (i.e., cases or controls). A key advantage of this approach is that it can incorporate interactions between variables, by placing them sequentially in the tree. For example, a sex-by-age interaction would be represented by splitting on sex, then on age. While it does categorize continuous variables, it identifies the optimal split (or splits) and therefore makes no assumption about distribution. While individual trees are readily interpretable, their predictive power is generally weak. Therefore, random forests generate a series of classification trees and integrate across them - it is thus a simple example of an ensemble classifier (37, 38). For primary results, parameters included maximum tree-depth of 8 nodes and random forest of 20 trees.

Model characterization, testing, and validation

The full STAR*D cohort was separated into a training (60%), testing (~20%), and validation (~20%) sample (Figure S1 in the Supplement). To increase informativeness about generalizability, the validation sample comprised 4 of the 14 regional centers, randomly selected to yield a sample of ~20% of the full cohort. Data from the remaining 10 centers was then divided randomly into training and testing sets. Performance of each model was initially assessed using 10-fold cross-validation in the training set to minimize overfitting. Relevant descriptions of model discrimination, including sensitivity, specificity, and area under the receiver operating characteristic (ROC) curve, were determined. The latter measure can be interpreted as the probability that, if a TRD case and treatment-responsive control are selected at random, the TRD case will have the greater score.

Even with the application of cross-validation, models are likely to overfit the training data set. Therefore, model performance was next estimated using the testing data set. This cohort was also used to examine three a priori selected subsets: males versus females, primary versus specialty care sites, and severe versus less severe depression as defined by QIDS-SR threshold of greater than or equal to, or less than, 16 (39).

The use of measures of discrimination, including ROC curves, has been criticized as neglecting another important aspect of model performance, namely calibration (40). That is, to what extent are intermediate categories of risk captured by model predictions. In addition to the Hosmer-Lemeshow chi2 test for goodness of fit (41), calibration curves were generated by risk quintile, to illustrate the relationship between predicted and observed risk in each quintile of estimated risk. Stata 10.1 (Statacorp, College Station, TX) was used for these analyses, with the hl package (42).

Finally, a persistent obstacle in clinical tool development is the lack of external model validation: even when researchers divide their data into a training and a testing set a priori, confidence in a model is increased further by examination of its performance in yet another data set. Unfortunately, this need to prospectively ascertain a second clinical cohort with similar phenotypic assessment makes this task almost impossible in a reasonable timeframe, and contributes to the paucity of such efforts in psychiatry. For this reason, in the present study, the optimal model developed in the first two cohorts was examined in a validation or generalizability set drawn from different regional centers. As noted above, the latter was intended to provide the most stringent test of performance, as these subjects were drawn from different study sites selected blindly, albeit with the same clinical and assessment protocol.

Calculator development

Another impediment to use of clinical decision support tools is the need to integrate data into a simple measure which can be readily applied by clinicians. Such a calculator was therefore implemented using Python, which allows the clinician to input relevant measures and outputs a classification score, as well as a visualization of risk relative to the STAR*D cohort in aggregate. The calculator can be accessed at [address to be specified by journal].

Results

Figure S1 in the Supplement illustrates derivation of the study cohorts. In the STAR*D cohort as a whole, 1348 subjects (33.5%) achieved remission at level 1 and 323 (8.0%) at level 2, excluding those assigned to CBT either as monotherapy or augmentation. Conversely, 884 (21.9%) subjects remained depressed after 2 treatment trials; 1341 (33.3%) remained depressed after a first trial and did not enter level 2. Table S2 in the Supplement compares individuals included in the modeling cohorts to those with missing or censored outcomes. In general, included individuals were more likely to be male, white, currently married, more educated, and to have fewer comorbidities. They were more likely to be seen in a specialty (versus primary) care center, and were slightly less depressed at study entry by QIDS-SR.

The full cohort was divided into training (n=1571; 61.5%), testing (n=523; 20.5%), and validation (n=461; 18.0%) cohorts. Sociodemographic and clinical descriptive features of these cohorts are indicated in Table S3 in the Supplement. As expected, they differed modestly in terms of some baseline clinical features, particularly proportion seen in primary versus specialty care, ethnicity, and episode duration. In the context of prediction, these differences between cohorts should make it more difficult to observe consistent test performance, yielding more conservative estimates.

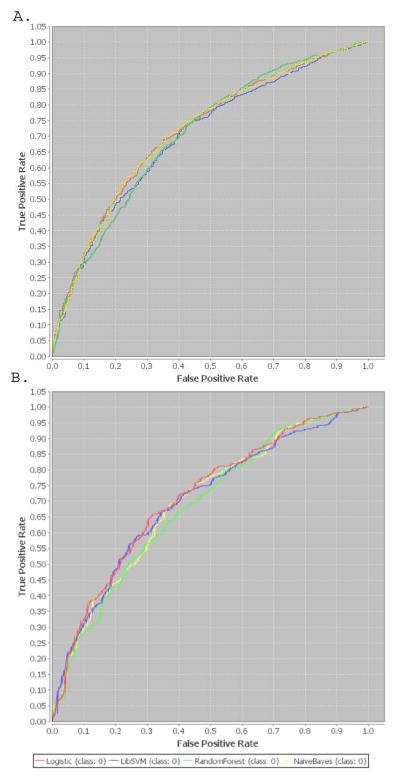
The variables selected for logistic regression are listed in Table 1, along with coefficients estimated in the training data set. To maximize comparability across models, these 15 variables were then incorporated in additional machine learning models as described in the methods. Table 2 shows the model performance for each of the machine learning algorithms using 10-fold cross validation in the training set, and in the full testing set. (Additional model features are presented in Table S4 in the Supplement). Receiver operating characteristic curves in the training and testing set are illustrated in Figure 1. Discrimination was greatest for logistic regression and Naïve Bayes in the training set, and for logistic regression and support vector machines in the testing set.

Table 2.

Comparison of model performance in training, testing, and validation data sets

	Logistic Regression		Naïve Bayes		Random Forest		Support Vector
Training set (cross-validation)
AUC	0.714	0.037	0.716	0.039	0.706	0.037*	0.697	0.042*
Specificity	0.867	0.031	0.783	0.035*	0.886	0.032^	0.917	0.041^
Sensitivity	0.353	0.058	0.519	0.064^	0.336	0.053*	0.217	0.068*
Testing set
AUC	0.712	0.023	0.698	0.024	0.693	0.024	0.706	0.023
Specificity	0.870	0.019	0.781	0.023	0.889	0.016	0.920	0.015
Sensitivity	0.332	0.033	0.492	0.036	0.337	0.033	0.241	0.029
	X2	p val	X2	p val	X2	p val	X2	p val
Calibration	4.09	0.5	102.73	<.001	5.04	0.4	17.02	0.005
Validation set
AUC	0.719	0.024
Specificity	0.911	0.016
Sensitivity	0.259	0.036
	X2	p val
Calibration	2.38	0.8

^{^}, superior to logistic regression (p<0.05)

^*, inferior to logistic regression (p<0.05)

AUC, area under receiver operating characteristic curve

Figure 1.

Receiver operating characteristic curves in training (a) and testing (b) data sets

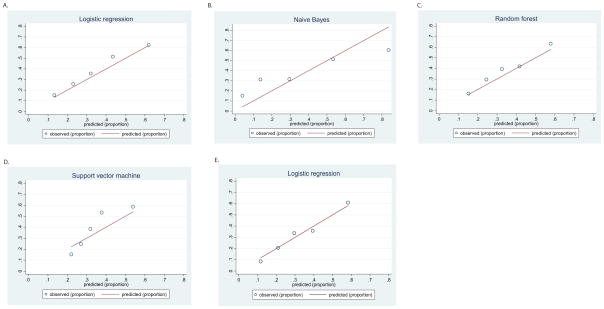
Calibration curves were also plotted for each model in the testing set (Figure 2), with the Hosmer-Lemeshow goodness-of-fit test calculated. The test was nonsignificant, indicating adequate calibration, in logistic regression and random forest models.

Figure 2.

Calibration curves in testing data set and validation data set

Next, performance of the logistic regression model was examined in specific patient subsets in the testing set. Discrimination was similar for the 207 males (AUC .712 (SE 0.35)) versus 316 females (AUC 0.706 SE 0.31); X2 (1 df)=0.02, p=0.9. Likewise, discrimination was similar for primary (n=221; AUC 0.73 SE 0.35) versus specialty care sites (n=302; AUC=0.693 SE 0.03); X2 (1 df)=0.73, p=0.4. Finally, performance was similar for severe (n=243; AUC 0.661 SE 0.35) versus less severe depression (n=280; AUC 0.684 SE 0.036); X2 (1 df)=0.23; p=0.6.

The best-performing model was then examined in the validation data set, with subjects also drawn from STAR*D but different regional centers (Table 2 and Figures 1 and 2). In this cohort, AUC was 0.719 (SE .025). Calibration remained good with Hosmer-Lemeshow X2 (5 df)=2.38 (p=0.8).

Lastly, to examine the ability of the model to predict clinician-rated rather than self-reported outcomes, we calculated discrimination using remission defined by HDRS, rather than QIDS-SR, still using the models derived based upon QIDS-SR. For the 359 subjects with HDRS data, AUC was similar to that observed for QIDS-SR: 0.719 (SE 0.028), while calibration remained acceptable (Hosmer-Lemeshow X2 (5 df)=5.33; p=0.4).

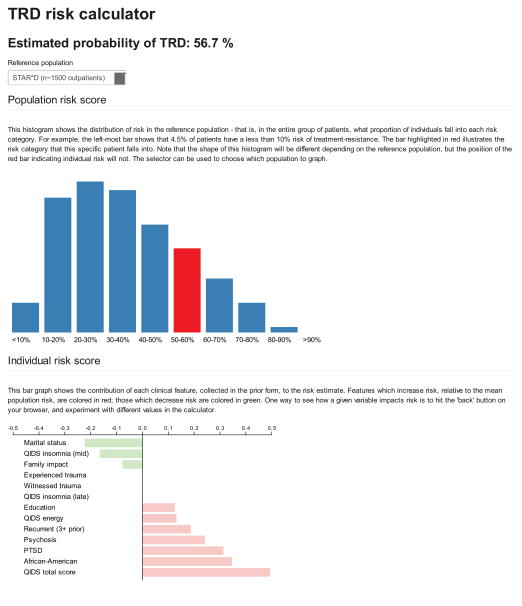
Figure 3 illustrates the output of a web-based calculator implementing the validated logistic regression model. The top portion depicts individual risk in the context of the STAR*D reference population; the reference population can be restricted particular subgroups (primary versus specialty care, male versus female). The bottom portion depicts relative contribution of individual clinical risk factors (specifically, the mean-centered value multiplied by the beta coefficient).

Figure 3.

Sample risk visualization screen from logistic regression model calculator

Discussion

Compared to the machine-learning approaches examined here, logistic regression provided similar discrimination, yielding an AUC of at least 0.71 in training, testing, and validation data sets. Calibration for this model was superior to that observed for naïve Bayes, SVM, and random forests, as these latter approaches attempt to maximize discrimination regardless of calibration. Most importantly, these results were consistent across two testing data sets, and similar to those observed using 10-fold cross-validation in the training data set, suggesting little evidence of overfitting. Discrimination was similar across patient subgroups (primary versus specialty care, male versus female), suggesting that the model should generalize well to other populations. In addition, considering clinician-rated remission based upon HDRS also yielded similar results, indicating that the model may also be applied in contexts where prediction of clinician rating is necessary.

Taken together, these results suggest that it is possible to rely solely on patient self-reported measures to identify at least a subset of individuals at greatest risk for treatment resistance. At a threshold of 0.5, assuming a prevalence of ~0.38 for TRD based on the testing set, positive predictive value is 0.61 and negative predictive value 0.68, so the model may be most useful in identifying a subset of higher-risk individuals. In other words, 61% of those with a positive test will have TRD, while 68% of those with a negative test will not. The optimal cutoff will depend on the clinical context for application; for example, employing a threshold of 0.6 yields positive predictive value of 0.72, with negative predictive value of 0.66. An important advantage of the regression model is that, because it is well-calibrated, intermediate risk categories should also be useful in categorizing an individual’s degree of risk.

The lack of effort to develop risk stratification approaches in psychiatry is notable because of its contrast with numerous other areas of medicine ranging from prediction of cardiac risk to utility of cancer screening to intensive care unit mortality (4–9). Indeed, in most of medicine, risk stratification plays an important role in treatment planning from the time of diagnosis. In acute care of myocardial infarction, efforts to develop treatment algorithms based on clinical presentation date back two decades, and are increasingly integrated in clinical practice (5). The absence of such tools in psychiatry is particularly ironic given that the utility of this approach, in comparison with clinical judgment alone, was first advocated by a psychologist more than 50 years ago (43).

One possible obstacle in psychiatry has been the lack of availability of biological markers of disease, and the perception that such markers are required in order to predict risk. In reality, the present results suggest that clinical features usefully predict outcome even in the absence of biology. Another obstacle may be the widespread misperception among clinicians and journal reviewers that a particular discrimination value (for example, a ‘magical’ AUC threshold of 0.8) is required before clinical adoption, which neglects the importance of considering clinical context. A recent commentary describes criteria for a useful clinical prediction tool; notably absent is the description of a specific degree of discrimination required (44). A recent comparison found most breast cancer prediction algorithms, including the widely-studied Gail score, to have AUC’s well below 0.7 (45). A final obstacle is the paucity of adequate independent data sets available for establishing the validity and transportability of a risk stratification tool; in part this arises from the lack of consistency of measures across studies.

How might this decision tool best be applied? This question requires further study targeted to specific interventions. For example, it is possible that individuals at high risk for TRD would benefit from early addition of cognitive-behavioral therapy, or from early use of combination pharmacotherapy or consideration of electroconvulsive therapy. Another potentially useful line of investigation is whether this algorithm identifies individuals less likely to respond to placebo treatment in antidepressant trials. Individuals at high risk for TRD may be particularly important to study with novel antidepressant interventions, as they may be most likely to require these next-step strategies. More generally, it will be useful to understand how clinicians, patients, and other stakeholders respond to risk data, as has been investigated in Alzheimer’s disease, for example (46).

Several limitations of this analysis should be noted. First, to maintain consistency with standard definitions of antidepressant treatment resistance, individuals who did not remit at level 1 and left the study prior to completing level 2 were censored, as it was hypothesized that predictors of attrition would not be the same as predictors of nonresponse. The problem of attrition (and nonadherence in general) as a contributor to apparent TRD merits further study. In addition, there are numerous other machine-learning approaches and variable coding strategies which might be considered in future work. Lastly, it will be important to examine the performance of this model and alternative models in truly independent data sets.

Notwithstanding these caveats, this report is one of the first to the author’s knowledge to describe and implement a clinical prediction algorithm for antidepressant treatment outcome in major depression, and applies many of the methodologic principles advocated in a recent review of risk stratification (9). The algorithm discriminates well even in a validation cohort selected from independent study sites, while maintaining acceptable calibration. The availability of a simple web-based calculator implementing this model should facilitate further investigation. At minimum, faced with modest progress in identification of clinically actionable biomarkers, these results suggest the utility of considering available clinical predictors in the meantime.