Abstract
We propose a probabilistic model for analyzing spatial activation patterns in multiple functional magnetic resonance imaging (fMRI) activation images such as repeated observations on an individual or images from different individuals in a clinical study. Instead of taking the traditional approach of voxel-by-voxel analysis, we directly model the shape of activation patterns by representing each activation cluster in an image as a Gaussian-shaped surface. We assume that there is an unknown true template pattern and that each observed image is a noisy realization of this template. We model an individual image using a mixture of experts model with each component representing a spatial activation cluster. Taking a nonparametric Bayesian approach, we use a hierarchical Dirichlet process to extract common activation clusters from multiple images and estimate the number of such clusters automatically. We further extend the model by adding random effects to the shape parameters to allow for image-specific variation in the activation patterns. Using a Bayesian framework, we learn the shape parameters for both image-level activation patterns and the template for the set of images by sampling from the posterior distribution of the parameters. We demonstrate our model on a dataset collected in a large multisite fMRI study.
Index Terms: Brain activation, functional magnetic resonance imaging (fMRI), hierarchical model
I. Introduction
Functional magnetic resonance imaging (fMRI) is widely used to study how the brain functions in response to external stimuli. In each run of an fMRI scan, data are collected as a time-series of 3-D voxel images while a subject is responding to external stimuli or performing a specific cognitive task. The temporal aspect of the time-series data for a run is often summarized as a β-map, a 3-D image of β coefficients that estimate the amount of activation at each voxel. An experiment often comprises multiple runs within a visit, and may also include multiple visits, and multiple subjects. There is also increasing interest in analyzing data taken at multiple different fMRI sites (machines) [1], [2].
In a typical approach to analysis of fMRI data, the activation maps are analyzed using voxel-by-voxel hypothesis testing. The set of voxels that are found to be statistically significant (e.g., based on t-statistics) are then used to define the activated region in the brain [3]. This approach assumes that the activation at each voxel is independent of the activation in neighboring voxels, and ignores the spatial information in the overall activation pattern. While spatial statistics that are derived from multiple neighboring voxels have been used to test significance of activations [4], [5], more recent approaches propose to directly take into account the spatial information in the activation pattern by modeling the shape of local activation regions explicitly. For example, Hartvig [6] represented the activation surface in fMRI as a parametric function consisting of a superposition of Gaussian-shaped bumps and a constant background level, and used a stochastic geometry model to find the number of bumps automatically. Penny and Friston [7] proposed a mixture model with each mixture component representing a local activation cluster. In earlier work we proposed a response surface model that represents an activation pattern as a superposition of Gaussian shaped parametric surfaces and demonstrated how the model could be used to characterize and quantify intermachine variability in multisite fMRI studies [8].
The methods discussed above for modeling spatial activation shape in fMRI data can handle only a single image. The problem of extracting spatial patterns from multiple images has not been addressed, even though detection and characterization of such patterns can in principle provide richer information (than voxel-level information) about cognitive activity and its variation across individuals, across time, and across machines. Previous approaches for spatial modeling in multiple images were based on first extracting spatial statistics from individual images, finding correspondences of those statistics across multiple images, and finding brain regions with significant activations in terms of the statistics matched across images [9]–[13]. Although the spatial statistics were extracted from multiple correlated voxels in the neighborhood of an activation region, their representation did not explicitly capture the activation shape information, and the overall approach did not provide a mechanism to systematically learn the variability across different images. A Bayesian hierarchial model has been proposed to account for spatial variability in activation across multiple images [14], but the spatial correlation was modeled through a covariance parameter between each pair of voxels, instead of using an explicit representation of activation shapes.
In this paper, we propose a new statistical approach that can characterize spatial fMRI activation patterns across multiple images1, where the multiple images could be repeated observations on an individual (as in a recent fMRI reliability study [1], [16]) or could be different individuals from a group in a clinical study. We model each activation cluster in an image as a Gaussian-shaped surface with parameters for 1) its height or peak value, representing the amount of activation, 2) the location of the cluster, modeling the center of activation in voxel-space, and 3) the width of the cluster. Given multiple activation images, we extract common activation clusters across images and learn the image-specific variation in the activation shape in each image. The general idea is illustrated in Fig. 1. At the bottom of Fig. 1 are fMRI activation images in the right motor region of the brain over four runs from the same subject performing a sensorimotor task. There are three activation clusters that appear in all or some of the four images, with image-specific variation in intensity and location. These types of variation are common in multiimage fMRI experiments, due to a variety of factors such as head motion and variation in the physiological and cognitive states of the subject. The underlying assumption in the model that we propose in this paper is that there is an unknown true activation pattern (as shown at the top of Fig. 1) in a subject’s brain given a particular stimulus, and that the activation patterns in the observed images (as shown in the middle row of Fig. 1) are noisy realizations of this true activation template, with variability in the activation patterns due to various sources. Our goal is to build a probabilistic model that infers both the overall template and image-specific activation patterns given multiple observed images.
Fig. 1.
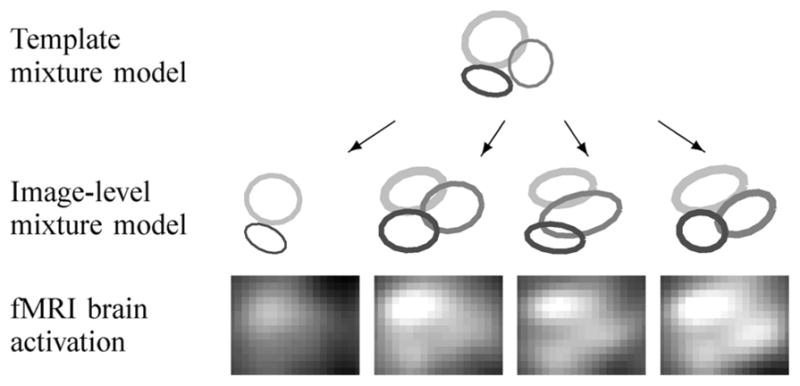
Illustration of image-level variations from the template model.
We base our probabilistic model for multiple images on a mixture of experts model with a Dirichlet process prior for a single image [8]. We model spatial activation patterns in a single activation image as a mixture of experts [17]–[19] with a constant background component and one or more activation components. Each local activation cluster is modeled using a parametric surface model with parameters for its peak value, the location of the cluster, and the width. The problem of estimating the number of such activation components is handled by combining this mixture of experts model with a Dirichlet process prior. A Dirichlet process prior is a nonparametric Bayesian prior that has been shown to be useful in learning the number of components in a mixture model from data without having to specify it a priori [20].
To model multiple activation images in a single probabilistic framework, we link the common components in multiple single-image models by introducing a hierarchy in the Dirichlet process prior. The hierarchical Dirichlet process is a model developed for handling multiple related mixture models with shared mixture components [21]. At the top of the hierarchy is a template mixture model with a set of components that are common across bottom-level mixture models. All of the bottom-level mixture models have components with the same fixed component parameters but are allowed to have their own mixing proportions. When we apply the hierarchical Dirichlet process to the specific problem of fMRI activation modeling, we can simultaneously infer both the top-level template and the image-level activation patterns from observed images, as well as the number of components at each level.
The hierarchical Dirichlet process assumes that the mixture component parameters (e.g., the intensities and locations of the Gaussian-shaped surface models we wish to use for fMRI activation modeling) are fixed across images. However, as can be seen in Fig. 1, there is image-specific local variation in the shape of activation clusters. In this paper, we introduce additional flexibility to the hierarchical Dirichlet process as follows: each image is allowed to have its own shape parameter, with a common prior distribution across images that has a mean shape in the activation template, and with a variance controlling the amount of image-specific random variation. This image-specific random variation added to the template shape parameters is sometimes referred to as random effects in the statistical literature [22]. By introducing random effects to the component parameters in the hierarchical Dirichlet process and estimating the random effects parameters, we can learn both the template activation shape and the image-specific random variation. In our experiments using data from a large multisite fMRI study, we demonstrate that the hierarchical Dirichlet process with random effects leads to systematically better results when compared to alternative approaches.
The rest of the paper is organized as follows. In Section II, we introduce a mixture of experts model with a Dirichlet process prior for a single image. In Section III, we propose a model for multiple images that uses a hierarchical Dirichlet process. In Section IV, we further extend this model by introducing random effects to the shape parameters in activation components. Section V provides a demonstration of the proposed models using multisite fMRI data. We conclude in Section VI with a brief discussion of future work.
II. Mixture of Experts Model With Dirichlet Process Prior for a Single Image
We begin by discussing the mixture of experts model for activation patterns in a single image, which we then generalize to multiple images in later sections.
A. The Model
We develop the model for the case of 2-D slices of β maps—the 3-D case can be derived as an extension of the 2-D case, but is not pursued in this paper. We assume that the β values yi, i = 1, …, N (where N is the number of voxels) are conditionally independent of each other given the voxel position xi = (xi1, xi2) and the model parameters. We then model the activation yi at voxel xi with a mixture of experts model [18], [23]
| (1) |
where ℭ = {cbg, cm, m = 1, …, M} is a set of component labels for the background cbg and the activation components (the cm’s), zi is the component label for the ith voxel, and represents the component parameters. The θbg and are parameters for the background component, and the θm’s and are used to model activation components as described below.
The first term on the right-hand side of (1) defines the spatial model or expert for a given mixture component. We model the activation component as a normal distribution having a mean that is a Gaussian-shaped surface centered at bm with width Σm and height km
| (2) |
where θm = (km, bm, Σm}, and a variance . The background component is modeled as a normal distribution with mean
where θbg = {μ}, and variance .
The second term in (1) is known as a gate function in the mixture of experts framework—it decides which model should be used to make a prediction for the activation level at position xi. Using Bayes’ rule we write this term as
| (3) |
where πz<sub>i</sub> is a class prior probability P(zi) [19], [24]. p(xi|zi, θ) is defined as follows. For the activation components with zi = cm, p(xi|zi, θ)is a normal density with mean bm and covariance Σm. The bm and Σm are shared with the Gaussian surface model in (2). This implies that the probability of activating the mth model or expert is highest at the center of the activation and gradually decays as xi moves away from the center. p(xi|zi, θ) for the background component is modeled as having a uniform distribution of 1/N for all positions in the brain, where N is the number of voxels in the image. If xi is not close to the center of any activations, the gate function selects the background expert for the voxel. The denominator of (3) provides an expression for the distribution of the input space as p(xi|θ) = Σc∈ℭ p(xi|c, θ)πc.
Combining the pieces results in a full generative-model specification [18], [24]
| (4) |
The second line in the above equation follows from (1) and the third line is obtained by applying (3).
Using a Bayesian modeling framework, we place prior distributions on the parameters as follows. We let the center of activation bm be a priori uniformly distributed inside or a half voxel away from the brain region in the image. We let the height parameter km be a priori uniformly distributed between 0 and a predefined value Kmax. The Kmax is set to a value about 15%–20% higher than the maximum β value in the image. For the width parameter Σm, we use a half-normal distribution with mean 0 and variance
as a prior for the variance terms in Σm and place a uniform prior over [−0.5, 0.5] on the correlation coefficients. This ensures that Σm always stays positive-definite. A normal distribution
 (0, τ02) is used as a prior on the background mean μ. The variances
and
are given half-normal prior distributions with mean 0 and variance
and
, respectively.
(0, τ02) is used as a prior on the background mean μ. The variances
and
are given half-normal prior distributions with mean 0 and variance
and
, respectively.
B. Dirichlet Process as a Prior
A practical issue with the finite mixture model approach is how to determine the number of components in the model [25], [26]. Nonparametric Bayesian approaches address this problem by assuming an infinite number of components a priori and then letting the data determine how many components exist in the posterior. In particular, Dirichlet processes are well-suited as a nonparametric Bayesian prior for mixture models [20], [27]. Using this approach, we can infer a posterior distribution over the number of components given the observed data.
A Dirichlet process [28] is a measure over probability measures denoted as DP(α, G0) with a concentration parameter α > 0 and a base distribution G0 as its two parameters. The Dirichlet process is most easily described by associating a component parameter vector φi with each voxel (xi, yi). We reserve the notation θc for a distinct component parameter; several φi’s may be equal to the same θc. We place a Dirichlet process prior DP(α, G0) on the parameters π = {πc’s, c ∈ ℭ} and θ as follows:
| (5) |
where G itself is a discrete probability measure in the form of
generated from DP(α, G0). The prior has an infinite number of components, but conditioned on the observed data, only a finite number of components exist in the posterior. We designate the first component as the only background component. All of the remaining components are activation components, and the model can have an arbitrary number of such components. A stick-breaking representation describes the construction of G from DP(α, G0) [29] as follows:
| (6) |
where π is constructed from a stick-breaking process Stick(α) as described below [29]
| (7) |
We can understand the process of generating πc’s via (7) as breaking a unit-length stick sequentially as follows. We sample from Beta(1, α), break the stick at , and set . We take the remainder of the stick of length ( ), select the second break-point by sampling from Beta(1, α), and set , and so on. It is straightforward to show that πc’s generated using (7) sum to 1. The component parameter θc associated with each πc is drawn from the base distribution G0, which is made up of the prior distributions defined in Section II-A for the activation component parameters {bm, km, Σm} and the background component parameter μ. We use a Gamma(a, b)distribution as a prior for the concentration parameter α.
If we integrate out G from the model described in (5), it can be shown that the labels (the zi’s) have the following clustering property [30]:
| (8) |
where represents the number of zi′ variables, i′ < i, that are assigned to component c, and K is the number of components that have one or more voxels in z1, …, zi−1 associated with them. The probability that zi is assigned to a new component is proportional to α. Note that the component with more observations already assigned to it has a higher probability of attracting the next observation. It can be shown that z1, …, zN are exchangeable under (8) [31].
C. Markov Chain Monte Carlo (MCMC) Sampling for Learning
Because of the nonlinearity of the model and nonconjugacy in the base distribution of the Dirichlet process prior, we rely on MCMC simulation methods to obtain samples from the posterior probability distribution of the parameters given the data. In a Bayesian mixture model framework it is common to augment the unknown parameters with the unknown component labels for observations and consider the joint posterior distribution p(θ, z|y, X) where y, X and z represent a collection of yi’s, xi’s and zi’s for i = 1, …, N and, . During each sampling iteration the component labels z and parameters θ are sampled alternately.
1) Sampling Component Labels
For each i we sample zi from its conditional posterior given as
| (9) |
where the first two terms on the right-hand side of the equation are data likelihoods, and the last term is given by (8), acting as if zi is the last item in a sequence like (8) that contains all N voxels.
Because of the nonconjugacy of the base distribution in the Dirichlet process prior, it is not possible to analytically compute the conditional posterior in (9), so we use a sampling method based on the Metropolis–Hastings algorithm for Dirichlet process mixtures with a nonconjugate prior [31]. We briefly describe the sampling algorithm as follows. If zi = zj for some j ≠ i (i.e., zi is a nonsingleton), we propose to reassign zi to a newly created component. If zi ≠ zj for all j ≠ i (i.e., zi is a singleton), we propose to reassign zi to one of the existing components with some other data points assigned to it. We accept the proposal based on the Metropolis–Hastings acceptance rule. To improve the mixing in the sampling algorithm, we use an additional partial Gibbs sampling step for nonsingletons [31].
As we sample from the conditional posterior in (9), the zi’s are associated with a finite number of components. Note that the number of components represented by the zi’s can change from one sampling iteration to the next. New components can get generated, and existing components can disappear if they become empty with no zi’s assigned to them. We are interested only in which observations are associated with the same component, regardless of the ordering of the components in the labeling scheme. From a Bayesian viewpoint, at the end of the sampling iterations, we obtain a posterior distribution of the number of components as a histogram of the sampled values over iterations. If we wish to report one fixed value for the number of components, we can (for example) select the sample with the highest posterior probability and use the associated assignments and components.
2) Sampling Component Parameters
Given the component labels z, we use a Gibbs sampling algorithm with some Metropolis steps to sample the component parameters. For the background mean μ and the concentration parameter α, it is possible to use the full conditional distribution of the parameter given all others. For the remaining parameters, we use a Metropolis algorithm with Gaussian random walk proposal distributions.
3) Initialization Methods
At the start of the MCMC sampling the model is initialized to one background component and one or more activation components. To initialize the model, we use a heuristic algorithm to find candidate voxels for local activation centers and assign a mixture component to each of the candidates. The heuristic procedure is as follows. To find candidate voxels, we take all of the positive voxels in an image, and repeatedly select the largest voxel among the voxels that have not been chosen and are at least several voxels apart from the previously selected voxels until there are no voxels left. The location and height parameters of the component are set to the position and the β-value of the candidate voxel respectively.
III. Hierarchical Dirichlet Processes for Multiple fMRI Images
To generalize the method of Section II so that it can learn common activation patterns from multiple images, we model each image as a mixture of experts model as described in Section II and let the components be shared among images by combining image-level models using a hierarchical Dirichlet process. A hierarchical Dirichlet process combines Dirichlet processes in a hierarchical manner to model multiple related mixture models with shared mixture components but different mixing proportions [21].
A. The Model
Assume that we have J images and that each image is modeled with a mixture of experts with a Dirichlet process prior as in Section II-A. To allow for the sharing of components across images, we combine Dirichlet processes hierarchically and model the base distribution G0 as coming from an upper-level Dirichlet process DP(γ, H). Let yji be the ith voxel (i = 1, …, Nj) in image j (j = 1, …, J). Then the complete model for a hierarchical Dirichlet process is given as
| (10) |
where H is a base distribution for the component parameters as defined in Section II, φji is the component parameter associated with the ith voxel in the jth image, and γ and α are concentration parameters for Dirichlet processes. The G0 in the above equation takes the following form:
| (11) |
where βc’s are generated from Stick(γ) and θc’s are distinct values in φji’s representing distinct component parameters sampled from the base distribution H. The Gj’s are given as
| (12) |
where πjc’s are mixing proportions for the mixture model of the jth image. It is important to notice that Gj comes from the Dirichlet process with a discrete distribution G0 as its base distribution. Thus, the components represented in the Gj’s are the ones present in G0, forcing the J images to have components with the same parameters.
We can derive a similar clustering property to (8) for hierarchical Dirichlet processes at each level of the hierarchy. At the bottom level, voxels yji for i = 1, …, Nj are assigned to one of the Tj local clusters within image j. When we integrate out Gj in (10), we obtain
| (13) |
where hji represents the label assignment of yji to one of the Tj local clusters, h−ji is all of the hji’s in the jth image excluding hji, and is the number of voxels assigned to the tth local cluster excluding yji.
At the top-level Dirichlet process, the local clusters are assigned to one of the global clusters with parameters θk. This assignment can be seen by integrating out G0 in (10)
| (14) |
where ljt maps the tth local cluster in image j to one of the K global clusters shared by all of the J images, l−jt represents the label assignments for all of the local clusters across J images excluding ljt, is the number of local clusters in image j assigned to the kth global cluster excluding ljt, and mk is the number of local clusters assigned to the kth global cluster.
According to (13) the probability that a new local cluster is generated within image j is proportional to α. This new cluster is generated according to (14). If a new component is selected in (14) the corresponding component parameter is drawn from the base distribution H.
Notice that more than one local cluster in image j can be linked to the same global cluster. It is the assignment of voxels to one of the K global clusters via local cluster labels that is of interest.
B. MCMC Sampling for Learning
To learn the model from a set of activation images we use an MCMC sampling algorithm to sample from the posterior distribution of the component labels and unknown parameters given a set of images. The quantities of interest are the local cluster labels hji’s, the global cluster labels ljt’s, and the parameters . We sample each of these in turn from its conditional posterior distribution in each iteration of Gibbs sampling. See Appendix A for more details.
IV. Hierarchical Dirichlet Processes With Random Effects for Multiple fMRI Images
To achieve the flexibility required to model the type of image-specific variation illustrated in Fig. 1, we further extend the model described in Section III by introducing random effects on component parameters.
A. The Model
We take the model in Section III-A and let the jth image have its own component parameters bmj’s, kmj’s, Σmj’s, and μj’s as follows. Let zji be the label assignment of the ith voxel in the jth image to one of the global clusters through hji’s and ljt’s. Then, the observation (yji, xji) in the jth image is modeled as
| (15) |
and if zji is a background component, the observation (yji, xji) in the jth image is modeled as
The image-specific parameters bmj’s and kmj’s, for each of the M activation components, and the μj’s are modeled as coming from a common prior distribution given by
| (16) |
where the bm’s and km’s define the unknown template activation shape for the mth component, and μ defines the overall background mean across images. The variance parameters Ψb<sub>m</sub>, , and represent the amount of variation in parameters bmj, kmj, and μj for each component across images. Thus, the bm’s, km’s, and μ can be viewed as defining templates, and the bmj’s, kmj’s, and μj’s as noisy observations of the template for image j with variances Ψb<sub>m</sub>’s, ’s, and , respectively. The width parameters Σmj’s are modeled as coming from a prior of a half-normal distribution for the variance elements and a uniform distribution over [−0.5, 0.5] for the correlations. We do not constrain Σmj’s across images through a population-level distribution. For ’s and in (16), we use half-normal distributions with mean 0 and predefined values for variances as priors. For Ψb<sub>m</sub>’s, we set the covariance elements to 0, assuming that bm<sub>1</sub> and bm<sub>2</sub> in bm = (bm<sub>1</sub>, bm<sub>2</sub>) are independent of each other, and use a half-normal prior on the variance elements.
We extend the clustering properties in (13) and (14) for hierarchical Dirichlet processes to describe the generative process of the model described above. The only difference is that if a global cluster selected using (14) (for the assignment of ljt) is a component that has not been used in the jth image, the image-specific shape parameters for the jth image needs to be generated from its prior.
B. Learning with MCMC Sampling
For inference we use an MCMC sampling scheme that is based on the clustering property of the model described in the previous section. In each iteration of the sampling algorithm we alternately sample labels h = {hji for all j, i}, 1 = {ljt for all j, t} and parameters
from their conditional posterior distributions. Details are given in Appendix B.
C. Demonstration of the Model on Simulated Data
We demonstrate the performance of the hierarchical Dirichlet process with random effects on simulated data, and compare the results with what we obtain from a simple thresholding scheme for a voxel-wise analysis. We assume a template activation pattern of three activation clusters of the same intensity located at b1 = (7, 7), b2 = (7, 19), and b3 = (15, 15) in a 20 25 region, and generate 10 observed images from this template, using 0.3, 0.8, and 1.2 as the variance element of Ψb<sub>m</sub>’s, and 0.3, 0.2, and 0.1 as φk<sub>m</sub>’s for m = 1, 2, 3. We further assume that the first three observed images contain all of the three activation clusters, the next three images contain two clusters, m = 1 and 2, and the remaining four images have a different subset of clusters, m = 2 and 3. Given the true parameters, the intensity value at each voxel of an image is determined by computing the intensity level for each of the activation and background components and taking the maximum value. The corresponding component with the maximum value is considered as the true cluster label for the voxel. Finally, we add noise generated from and to the intensity level of each voxel.
Illustrations demonstrating the fit of the hierarchical Dirichlet process with random effects to two sets of sample images are provided in Fig. 2(a) and (b). Fig. 2(a) shows the single MCMC draw with the highest posterior probability when the model is fit to data with low activation intensities and high noise levels (km = 1.0 and ). Fig. 2(b) shows the single MCMC draw with the highest posterior probability when the model is fit to data with high activation intensities and low noise levels (km = 2.0 and ). The left-most panel in Fig. 2(a) and (b) shows the true locations of the template activation clusters as ‘+’s and the region within one standard deviation as measured by the estimated Ψm’s is indicated by ellipses around each location. In the remaining panels of Fig. 2(a) and (b), we show the estimated image-specific activation clusters for seven (out of the ten) images in the image set as ellipses marking the region within one standard deviations (as measured by the estimated Σmj’s) of the image-specific location; the ellipses are overlaid on the images. In the high-noise case, Fig. 2(a), our model is able to determine the approximate locations of the two out of the three true activation components by combining the information across multiple images, even when the activation areas are not clear from individual images. When there is clear evidence for activation with low noise as in Fig. 2(b), our model is able to correctly identify the three true activation clusters.
Fig. 2.
Results on simulated data comparing the hierarchical Dirichlet process with random effects and a thresholding approach. The activation clusters estimated from the hierarchical Dirichlet process with random effects are shown for datasets simulated with (a) low activation intensities with high noise level (km = 1.0 and ), and (b) high activation intensities with low noise level (km = 2.0 and ). The results are based on the single MCMC sample with the highest posterior probability. The left-most images in Panels (a) and (b) show the true locations of the template activation clusters as ‘+’s, and estimated regions within one standard deviation (as measured by the Φm’s) as ellipses. In the next seven images in Panels (a) and (b), the estimated image-specific activation clusters are overlaid over the raw images as ellipses of width one standard deviations (as estimated by the Σmj’s). ROC curves for detecting the true activation voxels averaged over 20 simulated datasets are shown for (c) varying heights km’s (with fixed Σmj), and (d) varying widths, the variance elements of Σmj’s, of the activation clusters (for fixed km). In Panels (c) and (d), the three sets of ROC curves from the left to the right correspond to the noise levels , 0.6, and 1.0, respectively.
In order to systematically compare the performance of our method for detecting activated voxels and a benchmark thresh-holding approach, we simulate 20 sets of 10 images (each set of 10 generated as described above), and plot receiver operating characteristic (ROC) curves averaged over the 20 datasets. To obtain an ROC curve from the hierarchical Dirichlet process with random effects, we fit the model to each dataset, and use the following scheme to rank the voxels. Using the posterior samples for cluster labels hji’s from the MCMC sampling algorithm, we estimate the posterior probability of each voxel belonging to either background component or any of the activation components. We aggregate these probabilities so that we obtain for each voxel a single posterior probability of that voxel being part of an activation cluster (without regard to which cluster). We rank the voxels according these posterior probabilities of belonging to any of the activation components, compare the sorted list with the set of truly activated voxels, and plot type I errors and powers as an ROC curve. For the thresholding method, we simply rank the voxels according to their intensities to obtain ROC curves.
We compute ROC curves for varying values of the parameter defining activation heights (km = 1.0, 1.5, 2.0) in Fig. 2(c) with the width fixed (Σmj = 32), and then for varying values of the parameter defining activation widths (Σmj = 22, 32, 42) in Fig. 2(d) with the height fixed (km = 1.5). The three sets of ROC curves from the left to the right in Fig. 2(c) and (d) correspond to different levels of noise, , 0.6, and 1.0, respectively. The results show that across different values of shape parameters and noise levels our method outperforms the thresholding method that treats voxels independently of each other.
V. Experiments
Using data from a multisite fMRI study we experimentally compare the different models described in Sections II–IV, namely, the mixture of experts model with a Dirichlet process prior, the hierarchical Dirichlet process, and the hierarchical Dirichlet process with random effects.
A. Multisite Data Collection and Preprocessing
FMRI scans for the same five control subjects were collected from 10 different scanners as part of a multisite study of functional brain images, known as FIRST BIRN or fBIRN (Functional Imaging Research on Schizophrenia Test-bed Biomedical Informatics Research Network) [1], [32]. For each subject there were two visits to each site, and at each visit fMRI data were collected for four runs of a sensorimotor task and two runs of each of breathholding, resting, and cognitive recognition tasks, using a common protocol. The primary goal of this study is to better understand the variability of fMRI response patterns across runs, visits, scanners (sites) and subjects, so that future data collected across sites and subjects can be analyzed collectively and consistently (e.g., [16]). In the experiments below we use the data from the sensorimotor task, and focus on activation within specific regions of interest that are relevant to this task such as the left and right precentral gyri, the left and right superior temporal gyri, and the left and right occipital lobes. During the sensorimotor task subjects were presented with auditory and visual stimuli and were asked to tap fingers on each hand periodically. The brain regions analyzed correspond to areas expected to reflect visual, auditory, and motor activity.
Each run of the sensorimotor task produces a series of 85 scans that can be thought of as a time-series of voxel images. The set of scans for each run is preprocessed in a standard manner using SPM99 [33] with the default settings. The preprocessing steps include correction of head motion, normalization to a common brain shape, and spatial smoothing. Using the motion correction algorithm as implemented in SPM99 all of the four runs in each visit are realigned to the first image of the first run. The head motion correction is followed by a co-registration and normalization step that transforms the images into a standard space defined by the SPM eco-planar imaging (EPI) canonical template (Montreal Neurological Institute template, or MNI template). The normalized images are interpolated using bilinear interpolation and resliced to 2 × 2 × 2 mm voxels before being smoothed with an 8 mm full-width at half-maximum (FWHM) 3-D Gaussian kernel.
A general linear model is then fit to the time-series data for each voxel, yielding a regression coefficient β that estimates the amount of activation at each voxel. The design matrix used in the analysis includes the on/off timing of the sensorimotor stimuli measured as a boxcar convolved with the canonical hemodynamic response function. A β-map is a voxel image of the regression coefficients (β’s) that summarizes the activation across time as an activation map. Binary masks for regions of interest from the normalized atlas were then used to extract the β values for all voxels within a region. These β values serve as our data. The approach can be easily applied to other summary measures, e.g., t-statistics. We focus here on detecting areas of increased activation during the sensorimotor task relative to rest periods; the models outlined above could be modified to address expected decreases in activation as well.
B. Experimental Setup
In this section, we describe the setup for our application of the models to the FBIRN data, including specification of the prior distributions for the models used in our experiments and initialization methods for our algorithms. We selected a 2-D cross-section from each of the six regions of interest to fit the models. In all of the experiments we ran the sampling algorithm for 4000 iterations and used the samples over the last 3000 iterations after 1000 burn-in iterations to present the results. After a few initial runs of the sampling algorithm, we found that 4000 iterations with 1000 burn-in iterations were sufficient for convergence.
1) Single-Image Models
We set the prior distributions for the model as follows. We a priori assumed a small value of the concentration paramater α that tends to encourage a relatively small number of components, and hence set the prior for α to Γ(0.1, 1) in order to keep the mean of the gamma relatively small at 0.1. For the activation components, the priors for the width parameters Σm were set to a half-normal distribution with mean 0 and variance 100. We used a large variance in the half-normal prior to make the prior nearly uninformative within a fairly large range of values. We assumed an uninformative prior for the height parameters km, and used a uniform distribution over [0, Kmax] with Kmax set to a value 25% larger than the maximum intensity in the image. The initialization scheme described in Section II-C was used to initialize the model.
2) Multiple-Image Models
For our experiments with the two hierarchical Dirichlet process models (with and without random effects), we analyzed a single subject at a time, using a collection of 80 images (10 sites ×8 runs per site) of each region of interest for the given subject. Thus, the model has three layers of Dirichlet processes, corresponding to (from the top) the global template, the site-specific template, and the image-specific (or run-specific) activation model. At the bottom level of the hierarchy are the eight images from the eight runs at a specific site. In the previous analysis of the same dataset [16], it was shown that the visit variability is much smaller than the run variability. Thus, in our analysis, we combined the four runs from each of the two visits, and modeled them as if they were eight runs from one visit, although a simple extension of our model with an addition of another hierarchy would allow us to explicitly model the visit variability. The model with random effects had bm’s and km’s as global templates, and bmj’s and kmj’s as site-specific parameters for the jth site, modeled as coming from the distributions
 (bm,
Ψb<sub>m</sub>) and
, respectively. The activation component parameters bmjr’s and kmjr’s for an individual image of the rth run in the jth site were modeled as coming from the distributions
(bm,
Ψb<sub>m</sub>) and
, respectively. The activation component parameters bmjr’s and kmjr’s for an individual image of the rth run in the jth site were modeled as coming from the distributions
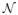 (bmj,
Ψb<sub>mj</sub>) and
, respectively. The model without random effects had bm’s and km’s in a global template fixed across all of the images.
(bmj,
Ψb<sub>mj</sub>) and
, respectively. The model without random effects had bm’s and km’s in a global template fixed across all of the images.
In all of our experiments, the prior distributions were set as follows. The priors for the concentration parameters at each of the three levels of Dirichlet processes were set, from the top level, to Γ(0.1, 1), Γ(2, 2), and Γ(2, 2), respectively. For the activation components, the prior for the width parameters and the height parameters in the global template were set in the same manner as in the single-image model. For the variance parameters in the random effects model, we used a half-normal (0, 4) and a half-normal (0, 0.4) as priors for Ψb<sub>m</sub>’s and ’s, respectively, at the top-level, and a half-normal (0, 2) and a half-normal (0, 0.2) as priors for Ψb<sub>mj</sub>’s and ’s, respectively, at the site-level. We a priori allowed the shape parameters to vary more at the top level than at the site-level by using a larger value for the variance in the half-normal priors for the top-level variance parameters. This is a reasonable assumption because intuitively we expect to see a larger variability in the activation patterns across sites, compared to across runs within a site.
We ran the heuristic clustering algorithm for initialization of the single-image model described in Section II-C on one of the 80 images (10 sites ×8 runs), and used the results as initial values for the number of components and component parameters. The output of this heuristic algorithm for the component labels of the single image was used to initialize the labels for all of the other images.
C. Illustrative Results for a Single Subject
To illustrate the methodology, we fit the two multiple-image models to the right precentral gyrus of subject 5. Using the single sample with the highest posterior probability, we show the estimated image-level (or run-level) activation patterns for the 8 runs in site 3 in Fig. 3 for the nonrandom effects model and the random effects model. In the first column of Fig. 3, we include the raw images, and in the second column in Fig. 3, we highlight the top 15% voxels with the highest intensities in each image, which would correspond to the results of single-voxel analyses. Ellipses are drawn to show a region of width standard deviation centered around the location parameters with the height parameters represented by the thicknesses of the ellipses. Ellipses with the same color across all sites and runs correspond to the same activation component.
Fig. 3.
Results for the right precentral gyrus for subject 5. Each row corresponds to an image from one of 8 runs for the same individual. In column 2, the top 15% voxels with the highest intensity levels are highlighted. In columns 3–5, estimated activation components are overlaid on the images. In column 3, a single-image model is fit to each of the 8 runs separately. In the case of multiple-image models (columns 4 and 5), we fit the models to all of the 80 images for subject 5 and show the estimated run-level activation patterns, using the single sample with the highest posterior probability.
For comparison, we fit the single-image model to each of the 8 images separately and show the results in the third column of Fig. 3. This single-image model correctly recognizes the high intensity areas as activation components, and finds other activation components with lower intensities. However, since this model analyzes each image separately it cannot link information across the eight runs even though the activation patterns are quite consistent among the images.
In the last two columns of Fig. 3 we see that the hierarchical Dirichlet process with random effects captures common activation clusters better than the model without random effects, in the presence of run-specific variations in activation shapes. For example, the random effects model recognizes the activation components with a relatively high intensity in the middle of the images as realizations of the same component shared among those images, whereas the nonrandom effects model fits the same activation clusters with different combinations of multiple components in the different images. This shows that having a fixed set of parameters for all of the images does not give the model enough flexibility to model the variability due to sites and runs. The random effects model found a more compact summary of the site-specific activation pattern than the model without random effects.
Histograms of the number of components over the last 3000 iterations are shown in Fig. 4. The posterior mass is peaked around a larger number of components for the hierarchical Dirichlet process without random effects than for the model with random effects. This is because the hierarchical Dirichlet process generates a larger number of components to summarize the activation pattern in the same set of images, compared to the model with random effects. Since the hierarchical Dirichlet process has one set of fixed parameters shared across all of the images, it tries to explain the local variability in activation shape through additional activation components.
Fig. 4.

Histograms of the number of components over the last 3000 iterations for the right precentral gyrus for subject 5. For the single-image model, the histogram for run 1 in visit 1 is shown.
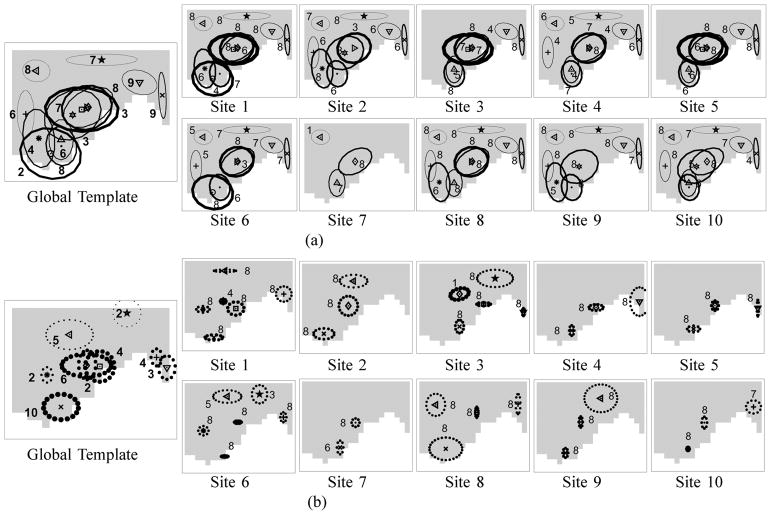
Using the same sample, we show the estimated top-level and site-level template activation patterns in Fig. 5(a) for the hierarchical Dirichlet process and in Fig. 5(b) for the model with random effects. For the model without random effects in Fig. 5(a), the activation components are drawn as ellipses with size proportional to one standard deviation of the width parameters Σm’s centered around the location parameters bm’s, and with the thickness of the ellipses proportional to the height parameters km. In Fig. 5(a), the site-specific images on the right contain a subset of exact copies of components from the global template on the left. For the model with random effects in Fig. 5(b), the global template shows the template activation components as ellipses centered around the location parameters bm’s with the height parameters km’s as thicknesses. For the same model, we show the site-level templates on the right, using the site-specific shape parameters, bmj’s and kmj’s, to draw the ellipses. Note that the radii of the dotted-lined ellipses for the model in Fig. 5(b) are proportional to 1.5 times the standard deviation of the covariance parameters Ψb<sub>m</sub>’s and Ψb<sub>mj</sub> that in turn represent the variation in the locations of activation components.
Fig. 5.
The global template (on the left) and site-level templates (on the right) estimated by (a) a hierarchical Dirichlet process and (b) a hierarchical Dirichlet process with random effects, using the right precentral gyrus of subject 5. Note that the solid ellipses in (a) represent the widths of the activation components, whereas the dotted ellipses in (b) represent the variation in the location parameters of activation clusters. The single sample with the highest posterior probability is shown. The frequencies of each activation component appearing in any of the 10 sites for the subject are shown as numbers next to each ellipse in the global template. Similarly, the frequencies of each activation component appearing in any of the eight runs in each site for the subject are shown in the site-level templates.
As we can see in Fig. 5, once again, the random effects model finds a more compact summary of the activation pattern than the model without random effects by using a smaller number of components to explain the activation pattern.
We notice that the across-run variability represented as Ψb<sub>mj</sub>’s in Fig. 5(b) (on the right) is generally smaller than the across-site variability represented as Ψb<sub>m</sub>’s (on the left). The frequencies of each activation component appearing in any of the ten sites for the subject are shown as numbers next to each ellipse in the global template in Fig. 5. Similarly, the frequencies of each activation component appearing in any of the eight runs in each site for the subject are shown in the site-level templates. Most of the components are common across all of the eight runs within a site. This again shows that activation patterns are fairly consistent across runs within a site.
As for the computation time, it took 71 min to run the MCMC sampling algorithm for the hierarchical Dirichlet process model on the 80 images used in Figs. 3 and 5, and 101 min for the model with random effects on the same set of images. These computation times could be considerably shortened by code optimization and/or by parallelizing the algorithms for execution on multicore machines or grid architectures.
D. Comparison of Models across Subjects
We fit the model with random effects to the fMRI data for each subject for the left precentral gyrus and right superior temporal gyrus and show the estimated global activation templates in Fig. 6. The estimated activation components are shown as ellipses that correspond to 1.5 times the covariance Ψb<sub>m</sub> in the component location parameters, centered around the location parameters bm, with the height parameters km as thicknesses. The number of times that each component appears in the 10 site-specific templates is shown next to the ellipses. We show only those components that appear in 5 or more sites.
Fig. 6.
Hierarchical Dirichlet processes with random effects fit to the left precentral gyrus and the right superior temporal gyrus of subjects 1, 2, 3, 4, and 5. The global template activations based on the single sample with the highest posterior probability are shown as ellipses of 1.5 standard deviation of the covariances Ψb<sub>m</sub> centered at the locations bm’s with the heights km’s as thicknesses. The frequencies of each activation component appearing in any of the 10 sites for the subject are shown as numbers next to each ellipse.
Even though each subject is analyzed separately, there are several activation clusters in the results shown in Fig. 6 that appear consistently across subjects within a region of interest. For example, in the left precentral gyrus in Fig. 6, the models found an activation cluster in the upper left of the image in all of the subjects. For the right superior temporal gyrus all of the subjects show two activation clusters on the right of the images.
E. Analysis of Variability in Activation Patterns
The model with random effects can be used to estimate how much variability in the activation patterns is due to different sources, e.g., run-to-run versus site-to-site variability. The results from Fig. 5(b) suggest that site variability is larger than run variability in terms of the locations of activation clusters, since for most of the clusters, the Ψb<sub>m</sub>’s are larger than the Ψb<sub>mj</sub>’s. Here we quantify more precisely the overall variation in the height and location parameters due to sites and runs on a per-subject basis. Given the estimated parameters for each region of interest (from the sample with the highest posterior probability from the model) we compute the overall site variability in the height parameters Var(height,site) by taking an average of the variance parameters ’s over all of the components as follows:
Similarly, we compute the overall run variability in the height parameters Var(height,run) by taking an average of the variance parameters ’s over all of the sites and components as follows:
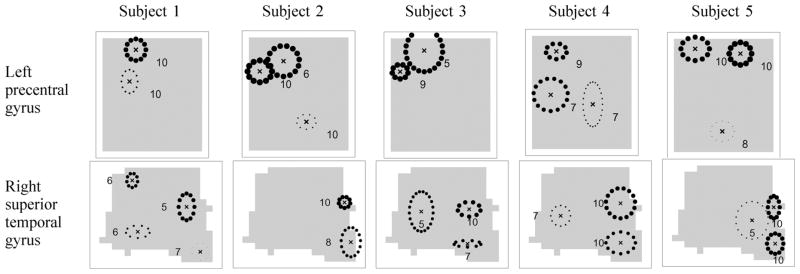
We plot the results for the right precentral gyrus in Fig. 7(a). As we expected, for all of the subjects, the site variability is much larger than the run variability.
Fig. 7.
Analysis of variability in activation patterns. (a) Variability in height parameters, (b) variability in location parameters, and (c) average rate of occurrence of activation components across images.
We perform the same analysis for the location parameters. We summarize the information in the 2×2 covariance matrices Ψb<sub>m</sub>’s by taking the sum of the two variance elements and Ψb<sub>m</sub> (1,1) and Ψb<sub>m</sub> (2,2). We can compute the overall site variability in the location parameters Var(loc,site) as
and, similarly, the overall run variability in the location parameters Var(loc,run) as
The results are shown in Fig. 7(b) for the right precentral gyrus. Again, we see that in location parameters the site variability is larger than the run variability. These results are consistent with those of Friedman et al. [16], who analyzed images from the same experiment using analysis of variance models applied to statistics such as the maximum and median values of percent signal change and contrast-to-noise ratio within each region of interest.
In Fig. 7(a) and (b), the difference between the site and run variability is larger for the height parameters than for the location parameters. A plausible explanation is that there are scanner-specific characteristics such as the magnet strength that affect the heights of activation clusters more than the locations.
In Fig. 5(b), we notice that most of the activation components are shared among all of the images across runs in the same site, whereas this persistency is weaker across sites. In order to quantify how persistent an activation component is across sites or runs, we compute the average rate of occurrence of an activation component among the 10 sites or the 8 runs. We compute the measure for site as follows:
Similarly, we use the following as the measure for runs:
If the values for Fsite or Frun are close to 1, most of the images across sites or runs share common components. We plot the results in Fig. 7(c). As we expected, activation components are more persistent across runs than across sites.
F. Evaluation of Predictive Performance
To evaluate the predictive benefit of adding random effects to the hierarchical Dirichlet process model, we conducted a number of cross-validation experiments. Specifically, we compute the logP score, p(Dtest|Dtrain), of test data Dtest given training data Dtrain for each model in each fold of the cross validation. The logP score is a fair estimator of the predictive power of a model (irrespective of how many parameters the model has), as it evaluates how much probability mass a model assigns to unseen test data, higher probability values being better (e.g., [34]). We compute the predictive log density p(Dtest|Dtrain) using Monte Carlo integration over the parameters (the component labels and random effects parameters) as follows. We draw parameters from their posterior distribution given the training data, evaluate the likelihood of the test data given these parameters, and compute an average of this likelihood over multiple posterior draws of the parameters.
For a given subject and region of interest, we perform cross-validation at two different levels, one at the run level and the other at the site level. For run-level cross-validation, we leave out one run from each of the 10 sites, use those held-out 10 images as test data, and perform an 8-fold (across 8 runs) cross-validation. For each set of held-out runs, we train the model on the remaining 70 images from the 10 sites, and compute the predictive log-likelihood (or logP score) of the 10 held-out test images (one per site). In the site-level cross-validation, we leave out one site at a time, use the 8 images in the held-out site as test set, and perform a 10-fold cross-validation. We use the 9 × 8 = 72 images in the other 9 sites as training set, learn the model, and compute the predictive log-likelihood of the 8 images at the test site. Intuitively, there should be more uncertainty in a future observation when the same subject is scanned at a new site, compared to when the same subject is scanned for another run at the same site. Thus, we expect to see a lower predictive logP score per image for the leave-one-site-out than for the leave-one-run-out cross-validation.
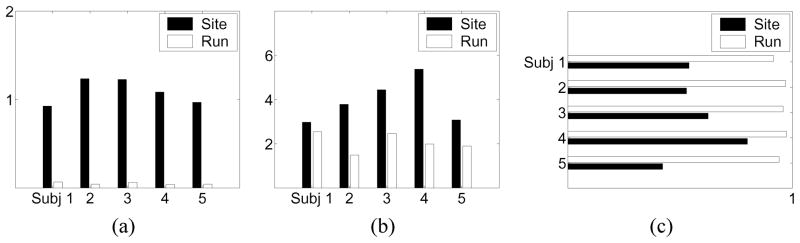
We show the average per-voxel logP scores of test data for the right precentral gyrus in Fig. 8. The figure shows the scores for the five subjects from leave-one-run-out and leave-one-site-out cross-validation. In Fig. 8(a), the x-axis represents logP scores from the model with random effects, and the y-axis from the model without random effects. For all of the subjects, the model with random effects shows systematic improvement in logP scores compared to the hierarchical Dirichlet process in both leave-one-run-out and leave-one-site-out cross-validations.
Fig. 8.
Results from cross-validations for right precentral gyrus. (a) With random effects versus without random effects. Each letter corresponds to leave-one-site-out or leave-one-run-out cross-validations for each of the five subjects. (b) Leave-one-site-out versus leave-one-run-out. Each letter corresponds to the models with or without random effects for each of the five subjects.
In Fig. 8(b), we plot the logP scores of the five subjects for both models using the x-axis as the scores from the leave-one-run-out cross-validation and the y-axis as the scores from the leave-one-site-out cross-validation. In all of the cases, the subjects shown as letters lie under the x = y line, confirming our intuition that the leave-one-site-out cross-validation would give a lower logP score.
VI. Conclusion
In this paper, we proposed a probabilistic framework for analyzing spatial activation patterns in multiple fMRI activation images. Each image was modeled as a mixture of a background component and a number of activation components with each activation component representing an activation cluster as a Gaussian-shaped surface. We combined multiple single-image models through a hierarchical Dirichlet process. With the hierarchical Dirichlet process we were able to infer the activation clusters that appear commonly in all or a subset of the images. The number of activation components was inferred from the data using a nonparametric Bayesian framework with a hierarchical Dirichlet process. To allow further flexibility in the model we incorporated random effects in the activation shape parameters and let each individual image have image-specific variation in the activation shape rather than forcing all images to have a fixed set of activation shape parameters as is the case in the hierarchical Dirichlet process. In this probabilistic framework we were able to learn the unknown template activation shape as well as the random effects parameters for each image, and we demonstrated this on a dataset from a multisite fMRI study.
The model we proposed in this paper assumes that the group-specific variation in parameters in any single mixture component is independent of the variation in parameters of other components. A possible extension would be to model additional systematic group variation in the mixture component parameters such as global translations of the template (or a subset of the components) in an image, e.g., due to different MRI machine characteristics or head positioning. We could also include across-subject variability in the model instead of analyzing each subject separately, and model the interaction between subjects and sites in terms of variation in the activation shape.
Other information could also be used to further enhance the model. For example, in this paper we focused on activation maps that summarize the voxel time-series into a single image. To take advantage of all of the information present in the dataset, a useful extension would be to model spatial patterns over time, e.g., combining the proposed Dirichlet process framework with the time-dependent model of Penny and Friston [7]. Furthermore, structural MRI scans collected for a subject could be used as a spatial prior to constrain modeled activation areas to gray matter regions in the brain (e.g., as proposed in [35]).
Another useful direction would be to extend the hierarchical Dirichlet process with random effects proposed in this paper to model differences between labeled groups of individuals, e.g., in studies of controls and patients for a particular disorder. This could be done by introducing a variable for a group label in the model, whose value is known in the training data, but is unknown at prediction time.
Appendix A. Sampling Algorithm for Hierarchical Dirichlet Processes
Sampling Component Labels
To sample the component labels we use the sampling algorithm based on the clustering properties of (13) and (14). We sample the local cluster labels hji’s by drawing each of the hji’s in turn from the conditional posterior distribution, given as
where θ is the set of all component parameters, θjt is the parameters of one of the K components associated with the tth local cluster in image j, and
| (17) |
We sample the global cluster labels ljt’s using the conditional posterior distribution given as shown in (18) at the bottom of the page.
Since we do not have conjugate priors for the component parameters in this model for fMRI data, it is not possible to evaluate the integrals in (17) and (18) analytically for a new component. We approximate the integrals by drawing a sample from the prior and evaluating the likelihood using this sample [31].
Sampling Component Parameters
Given the sample for component labels we sample the component parameters. We use Gibbs sampling to sample the background mean μ and the Metropolis algorithm with the normal distribution as a proposal for all of the other parameters. We place a gamma prior on α and γ and sample values for these parameters from their conditional posterior distributions [21].
Appendix B. Sampling Algorithm for Hierarchical Dirichlet Processes With Random Effects
Sampling Component Labels
Because of the presence of image-specific shape parameters, the sampling methods for component labels for a hierarchical Dirichlet process in (17) and (18) cannot be directly applied to its extension with random effects. In a hierarchical Dirichlet process, since image-level shape parameters are exact copies of the corresponding component parameters in the template activation pattern, whenever we decide to generate a new local cluster for an image-specific activation pattern, we can simply copy the parameters from the template. However, in the model with random effects, each image inherits a perturbed version of the parameters in the template, and we should consider two separate cases of known and unknown image-specific parmaters for each of the template component, when generating a new local cluster. The known image-specific parameters indicate that the component in the template pattern has been introduced to the image before, whereas such parameters do not exist for the component being introduced to the image for the first time. We modify the sampling equations for hierarchical Dirichlet processes to take into account image-specific parameters as described below.
| (18) |
We sample hji’s using the following conditional distribution:
where ujt is the image-specific activation component parameters associated with the tth local cluster in image j and
| (19a) |
| (19b) |
| (19c) |
In (19a) the summation is over components in A = {k| some hji′ for i′ ≠ i is assigned to k}, representing global clusters that already have some local clusters in image j assigned to them. In this case, since ujk is already known, we can simply compute the likelihood p(yji, xji|ujk). In (19b) the summation is over B = {k| no hji′ for i′ ≠ i is assigned to k}, representing global clusters that have not yet been assigned in image j. In (19c) we model the case where a new global component gets generated. The integrals in (19b) and (19c) cannot be evaluated analytically, so we approximate the integral by sampling new values for ujk and θk from their prior distributions and evaluating the likelihood p(yji, xji|ujk) [31].
Samples for ljt’s can be obtained from the conditional distribution given as shown in (20) at the bottom of the page. As in the sampling of hji, we cannot evaluate the integrals in (20) analytically. We approximate the integrals by sampling new values for ujk and θk from the priors and evaluating the likelihood.
| (20) |
Sampling Component Parameters
Given h and 1 we use Gibbs sampling to sample the background means μ and μj’s and use the Metropolis algorithm with a normal distribution as a proposal for all of the other parameters.
In practice, this MCMC scheme for the hierarchical Dirichlet process with random effects can mix poorly and get stuck in local maxima where the labels for two image-level components are swapped relative to the same two components in the template. To address this problem and restore the correct correspondence between template components and image-level components we propose a move that swaps the labels for two group-level components at the end of each sampling iteration and accepts the move based on a Metropolis acceptance rule.
Footnotes
This paper extends results that were presented earlier in preliminary form as a short conference paper [15].
Contributor Information
Seyoung Kim, Email: sssykim@cs.cmu.edu, Machine Learning Department, School of Computer Science, Carnegie Mellon University, Pittsburgh, PA 15213 USA.
Padhraic Smyth, Email: smyth@ics.uci.edu, Department of Computer Science, University of California, Irvine, CA 92697 USA.
Hal Stern, Email: sternh@uci.edu, Department of Statistics, University of California, Irvine, CA 92697 USA.
References
- 1.Zou K, Greve D, Wang M, Pieper S, Warfield S, White N, Manandhar S, Brown G, Vangel M, Kikinis R, Wells W. Reproducibility of functional MR imaging: Preliminary results of prospective multi-institutional study performed by Biomedical Informatics Research Network. Radiology. 2005;237:781–789. doi: 10.1148/radiol.2373041630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Friedman L, Glover G. Reducing scanner-to-scanner variation of activation in multi-center fMRI studies: Adjustment for signal-to-fluctuation-noise-ratio. NeuroImage. 2006;33(2):471–481. doi: 10.1016/j.neuroimage.2006.07.012. [DOI] [PubMed] [Google Scholar]
- 3.Friston KJ, Holmes AP, Worsley KJ, Poline JB, Frith CD, Frackowiak RSJ. Statistical parametric maps in functional imaging: A general linear approach. Human Brain Map. 1995;2:189–210. [Google Scholar]
- 4.Hayasaka S, Nichols TE. Validating cluster size inference: Random field and permutation methods. NeuroImage. 2003;20:2343–2356. doi: 10.1016/j.neuroimage.2003.08.003. [DOI] [PubMed] [Google Scholar]
- 5.Flandin G, Penny W. Bayesian fMRI data analysis with sparse spatial basis function priors. NeuroImage. 2007;34(3):1108–1125. doi: 10.1016/j.neuroimage.2006.10.005. [DOI] [PubMed] [Google Scholar]
- 6.Hartvig N. A stochastic geometry model for fMRI data Dept. Theoretical Stat. Univ Aarhus, Res Rep. 1999;410 Research Report 410. [Google Scholar]
- 7.Penny W, Friston K. Mixtures of general linear models for functional neuroimaging. IEEE Trans Med Imag. 2003 Apr;22(4):504–514. doi: 10.1109/TMI.2003.809140. [DOI] [PubMed] [Google Scholar]
- 8.Kim S, Smyth P, Stern H. Parametric response surface models for analysis of multi-site fMRI data. Proc 8th Int Conf Med Image Computing Computer Assist Intervent. 2005;2:217–224. doi: 10.1007/11566465_44. [DOI] [PubMed] [Google Scholar]
- 9.Thirion B, Pine P, Tucholka A, Roche A, Ciuciu P, Mangin JF, Poline JB. Structural analysis of fMRI data revisited: Improving the sensitivity and reliability of fMRI group studies. IEEE Trans Med Imag. 2007 Sep;26(9):1256–1269. doi: 10.1109/TMI.2007.903226. [DOI] [PubMed] [Google Scholar]
- 10.Opertol G, Clouchoux C, Bulot R, Anton J, Coulon O. Surface-based structural group analysis of fMRI data. Proc 11th Int Conf Med Image Computing Computer-Assist Intervent. 2008:959–966. doi: 10.1007/978-3-540-85988-8_114. [DOI] [PubMed] [Google Scholar]
- 11.Uthama A, Abugharbieh R, Palmer SJ, Traboulsee A, McKeown MJ. SPHARM-based spatial fMRI characterization with intersubject anatomical variability reduction. IEEE J Selected Topics Signal Process. 2008;2(6):907–18. [Google Scholar]
- 12.Ng B, Abugharbieh R, Huang X, McKeown MJ. Spatial characterization of fMRI activation maps using invariant 3-D moment descriptors. IEEE Trans Med Imag. 2009 Feb;28(2):261–268. doi: 10.1109/TMI.2008.929097. [DOI] [PubMed] [Google Scholar]
- 13.Ng B, Abugharbieh R, Hamarneh G, McKeown MJ. Random walker based estimation and spatial analysis of probabilistic fMRI activation maps. Proc. Med. Image Computing Computer-Assist. Intervent. Workshop Stat. Model. Detection Issues Intra- and Inter-Subject Functional MRI Data Anal; 2009. pp. 37–44. [Google Scholar]
- 14.Bowman D, Caffo B, Bassett SS, Kilts C. A Bayesian hierarchical framework for spatial modeling of fMRI data. NeuroImage. 2008;39:146–56. doi: 10.1016/j.neuroimage.2007.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kim S, Smyth P. Advances in Neural Information Processing Systems. Vol. 19. Cambridge, MA: MIT Press; 2007. Hierarchical Dirichlet processes with random effects; pp. 697–704. [Google Scholar]
- 16.Friedman L, Stern H, Brown G, Mathalon D, Turner J, Glover G, Gollub R, Lauriello J, Lim K, Cannon T, Greve D, Bockholt H, Belger A, Mueller B, Doty M, He J, Wells W, Smyth P, Pieper S, Kim S, Kubicki M, Vangel M, Potkin S. Test-retest and between-site reliability in a multicenter fMRI study. Human Brain Map. 2008;29(8):958–972. doi: 10.1002/hbm.20440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rasmussen C, Ghahramani Z. Advances in Neural Information Processing Systems. Vol. 14. Cambridge, MA: MIT Press; 2002. Infinite mixtures of Gaussian process experts; pp. 881–888. [Google Scholar]
- 18.Jacobs R, Jordan M, Nowlan S, Hinton G. Adaptive mixtures of local experts. Neural Computat. 1991;3(1):79–87. doi: 10.1162/neco.1991.3.1.79. [DOI] [PubMed] [Google Scholar]
- 19.Xu L, Jordan M, Hinton G. Advances in Neural Information Processing Systems. Vol. 7. Cambridge, MA: MIT Press; 1995. An alternative model for mixtures of experts; pp. 633–640. [Google Scholar]
- 20.Escobar M, West M. Bayesian density estimation and inference using mixtures. J Am Stat Assoc. 1995;90(430):577–588. [Google Scholar]
- 21.Teh Y, Jordan M, Beal M, Blei D. Hierarchical Dirichlet processes. J Am Stat Assoc. 2006;101(476):1566–1581. [Google Scholar]
- 22.Laird N, Ware J. Random-effects models for longitudinal data. Biometrics. 1982;38(4):963–974. [PubMed] [Google Scholar]
- 23.Kim S, Smyth P, Stern H. A nonparametric Bayesian approach to detecting spatial activation patterns in fMRI data. Proc. 9th Int. Con. Med. Image Computing Computer Assist. Intervent; Germany. 2006. pp. 217–224. [DOI] [PubMed] [Google Scholar]
- 24.Meeds E, Osindero S. Advances in Neural Information Processing Systems. Vol. 18. Cambridge, MA: MIT Press; 2006. An alternative infinite mixture of Gaussian process experts; pp. 883–890. [Google Scholar]
- 25.McLachlan G, Peel D. Finite Mixture Models. New York: Wiley-Interscience; 2000. [Google Scholar]
- 26.Titterington DM, Smith AFM, Makov UE. Statistical Analysis of Finite Mixture Distributions. New York: Wiley; 1985. [Google Scholar]
- 27.Rasmussen C. Advances in Neural Information Processing Systems. Vol. 12. Cambridge, MA: MIT Press; 2000. The infinite Gaussian mixture model; pp. 554–560. [Google Scholar]
- 28.Ferguson T. A Bayesian analysis of some nonparametric problems. Ann Stat. 1973;1(2):209–230. [Google Scholar]
- 29.Sethuraman J. A constructive definition of Dirichlet priors. Stat Sinica. 1994;4:639–650. [Google Scholar]
- 30.Blackwell D, MacQueen J. Ferguson distribution via Polya urn schemes. Annals of Statistics. 1973;1:353–355. [Google Scholar]
- 31.Neal R. Markov chain sampling methods for Dirichlet process mixture models. J Computat Graphical Stat. 2000;9:249–265. [Google Scholar]
- 32.Potkin S, Andreasen N, Brown G, Glover G, Kikinis R, Lauriello J, Lieberman J, Lim K, McCarley R, McCarthy G, Rosen B, Toga A. Multi-site brain fMRI imaging studies in schizophrenia using the BIRN methodology and federated database approach. Proc. 41st Annu. Meeting Am. College Neuropsychopharmacol; 2002. pp. 252–253. [Google Scholar]
- 33.Veltman D, Hutton C. SPM99 Wellcome Dept Imag Neurosci, Univ College London, Tech Rep. 2000. [Google Scholar]
- 34.Smyth P. Model selection for probabilistic clustering using cross-validated likelihood. Stat Comput. 2000;10(1):63–72. [Google Scholar]
- 35.Ou W, Golland P. From spatial regularization to anatomical priors in fMRI analysis. Proc. 19th Int. Conf. Inf. Process. Med. Imag; 2005. pp. 88–100. [DOI] [PMC free article] [PubMed] [Google Scholar]