SimTB, a simulation toolbox for fMRI data under a model of spatiotemporal separability

Abstract

We introduce SimTB, a MATLAB toolbox designed to simulate functional magnetic resonance imaging (fMRI) datasets under a model of spatiotemporal separability. The toolbox meets the increasing need of the fMRI community to more comprehensively understand the effects of complex processing strategies by providing a ground truth that estimation methods may be compared against. SimTB captures the fundamental structure of real data, but data generation is fully parameterized and fully controlled by the user, allowing for accurate and precise comparisons. The toolbox offers a wealth of options regarding the number and configuration of spatial sources, implementation of experimental paradigms, inclusion of tissue-specific properties, addition of noise and head movement, and much more. A straightforward data generation method and short computation time (3–10 seconds for each dataset) allow a practitioner to simulate and analyze many datasets to potentially understand a problem from many angles. Beginning MATLAB users can use the SimTB graphical user interface (GUI) to design and execute simulations while experienced users can write batch scripts to automate and customize this process. The toolbox is freely available at http://mialab.mrn.org/software together with sample scripts and tutorials.

1. Introduction

Simulating functional magnetic resonance imaging (fMRI) data is an important strategy for evaluating processing and analysis methods. These methods include fMRI data preprocessing (Allen et al., 2010; Della-Maggiore et al., 2002), algorithm comparisons and activation detection techniques (Erhardt et al., 2011; Correa et al., 2007; Li et al., 2007; Ma et al., 2007; Lu et al., 2003; Dimitriadou et al., 2004; Worsley et al., 2005), hypothesis testing strategies (Logan and Rowe, 2004; Marchini and Presanis, 2004), and motion-correction algorithms (Ardekani et al., 2001; Freire and Mangin, 2001; Pickens et al., 2005; Morgan et al., 2007).

For dozens of studies, a specific one-time simulation has been developed to understand a model or analysis method (e.g., LeVan and Gotman, 2009; Esposito and Goebel, 2011; Moosmann et al., 2008; Schmithorst and Holland, 2004; Li et al., 2007; Yourganov et al., 2011). Comparing across these one-time simulations, many are based on different models having different assumptions. Some models have as few as three sources including baseline, source of interest, and noise (Della-Maggiore et al., 2002; Logan and Rowe, 2004; Marchini and Presanis, 2004; Baumgartner et al., 2000; Lu et al., 2003; Dimitriadou et al., 2004; Baumgartner et al., 1998; Beckmann and Smith, 2004; Bellec et al., 2006; Bullmore et al., 2001; Jahanian et al., 2004). Other fMRI simulation software use first principles of the MR physics (Drobnjak et al., 2006; Xu et al., 2007; Kim et al., 2008), bootstrap from real data (Bellec et al., 2009), or interpolate to introduce motion (Ardekani et al., 2001; Freire and Mangin, 2001; Pickens et al., 2005). Some of these are computationally demanding, requiring hours or days for a single simulation, others rely on existing fMRI subject data, and others are too simple or specialized to be of general use (see Sec. 4.1). An unintended consequence of a one-time simulation is the possibility that the simulation design may be biased to present a particular method favorably.

Here we introduce a simulation toolbox, SimTB, running under the crossplatform MATLAB environment (The Mathworks, Inc.). The toolbox allows for exible generation of fMRI datasets under a model of spatiotemporal separability¹ and is designed to facilitate the testing of a variety of analytic methods. The spatiotemporal model is well-supported because similar spatiotemporal networks are inferred in real fMRI data whether using spatial or temporal independent component analysis (ICA) (Calhoun et al., 2009), general linear model (GLM), seed-based (Whitfield-Gabrieli et al., 2009), or clustering approaches (Van Den Heuvel et al., 2008). Users have full control over data generation including the creation and manipulation of spatial sources, implementation of block- and event-related experimental designs, inclusion of tissue-specific baselines, addition of head movement, and more. Importantly, all simulation features are controlled by a relatively small number of parameters, providing a level of abstraction that makes it possible to answer questions that would be impossible to address in real data. Because of its exibility, the toolbox has broad application for the testing of preprocessing strategies (e.g., motion correction, spatial/intensity normalization), univariate analyses (e.g., GLM), multivariate anlayses (e.g., ICA), and connectivity analyses (e.g., seed-based correlation). We have used SimTB to extensively explore subject variability within the group ICA framework (Allen et al., 2011a). Simulation parameters can be selected through a graphical user interface (GUI) or defined in a batch script called from the command line.

The rest of the manuscript continues as follows. In Section 2 we provide the exposition of the model generating the data. In Section 3 we demonstrate use of the toolbox with a simple simulation and some output from the toolbox. In Section 4 we discuss other functions of the toolbox and compare SimTB with other fMRI simulation software.

2. Materials and methods

2.1. Model

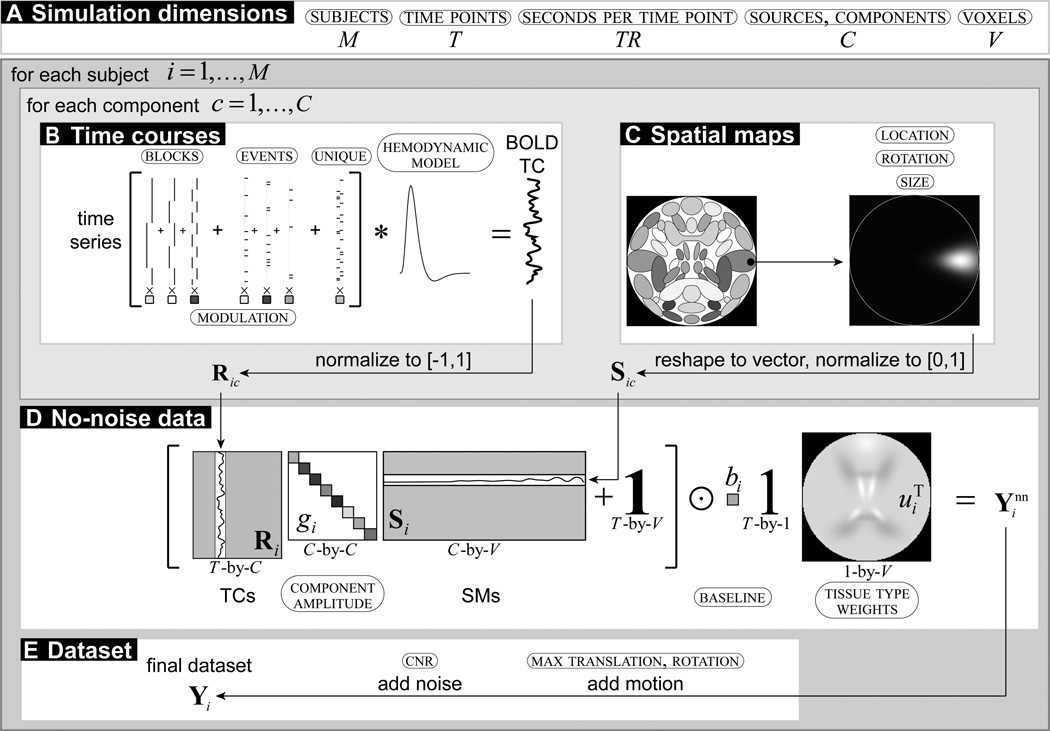
In SimTB, we adopt a data generation model consistent with spatiotemporal separability, that is, data can be expressed as the product of time courses (TCs) and SMs. A high-level owchart of the data generation is in Figure 1. Specifically, for each subject, i = 1, …, M, we assume there are up to C sources or components, each consisting of a spatial map (SM), activation TC, and an amplitude. The no-noise (nn) data is a linear combination of amplitude-scaled and baseline-shifted TC and SM sources,

$$\underset{T·V}{\underbracket{{\mathbf{Y}}_i^{\text{nn}}}}=[\underset{T·C}{\underbracket{{\mathbf{R}}_i}}\underset{C·C}{\underbracket{\text{diag}({\mathbf{g}}_i)}}\underset{C·V}{\underbracket{{\mathbf{S}}_i}}+\underset{T·V}{\underbracket{{\mathbf{J}}_T^V}}]\odot \underset{1·1}{\underbracket{b_i}}\underset{T·1}{\underbracket{{\mathbf{J}}_T^1}}\underset{1·V}{\underbracket{{\mathbf{u}}^{\top }}},$$ (1)

where ${\mathbf{Y}}_i^{\text{nn}}$ is the time-by-voxel (T-by-V) no-noise data for subject i, R_i is a matrix of C column vectors of TCs, S_i is a matrix of C row vectors of SMs, g_i is a vector of C source amplitudes defined as a percent signal change of the baseline, b_i is a baseline intensity scalar, u is a vector of voxel tissue type baseline modifiers, ${\mathbf{J}}_T^V$ is a T-by-V matrix of ones, and ⊙ denotes the Hadamard (element-wise) matrix product. These and other variables are further defined in the following sections, as well as the method for producing the final subject data.

Figure 1. Flowchart of data generation.

Values in small caps and circled indicate parameters to be specified. (A) Simulation dimension is determined by the number of subjects, time points (and seconds per time point), and voxels (representing a number of selected sources). (B) Time courses are the sum of task block, task event, and unique event time series modeled into a blood oxygen level-dependent (BOLD) TC and normalized. (C) Spatial maps are selected, translated, rotated, resized, and normalized. (D) The no-noise data combines the TCs and SMs scaled by component amplitudes, and scaled to a tissue type weighted baseline. (E) The final dataset includes motion and noise.

2.1.1. Spatial sources

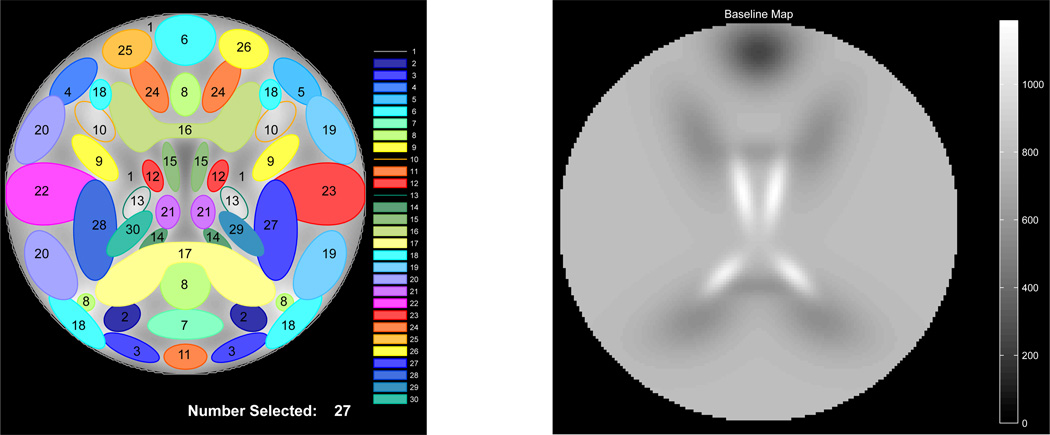
A template of the 30 default SMs is shown in Figure 2A on a square image of $V=\sqrt{V}\times \sqrt{V}$ voxels, where side length $\sqrt{V}$ is specified by the user. SimTB has no requirements regarding the shape of the SMs (or TCs), and users can specify SMs using any 2-D function defined on x, y ∈ [−1, 1]. Default SMs are modeled after sources commonly seen in axial slices of real fMRI data and most are created by combinations of simple Gaussian distributions. For example, a source with a single region of activation can be defined as

$${\mathbf{S}}_{\mathit{\text{ic}}}=\text{exp}(-{[w_{\mathit{\text{xic}}}\{(x-x_{0\mathit{\text{ic}}})\text{ cos}({\theta }_{\mathit{\text{ic}}})-(y-y_{0\mathit{\text{ic}}})\text{ sin}({\theta }_{\mathit{\text{ic}}})\}]}^2)\times \text{ exp}(-{[w_{\mathit{\text{yic}}}\{(x-x_{0\mathit{\text{ic}}})\text{ sin}({\theta }_{\mathit{\text{ic}}})+(y-y_{0\mathit{\text{ic}}})\text{ cos}({\theta }_{\mathit{\text{ic}}})\}]}^2)$$

where location (x_0ic, y_0ic), orientation θ_ic, and width (w_xic, w_yic) parameterize the activation. Users can vary the location (x_0ic, y_0ic) and orientation θ_ic of activation blobs across subjects, i = 1, …, M, and sources, c = 1, …, C. The spatial extent of the whole source can also be varied with the “spread” parameter, ρ_ic. SMs are normalized to have a maximum intensity of 1 and are transformed as ${\mathbf{S}}_{\mathit{\text{ic}}}^{\prime }={\mathbf{S}}_{\mathit{\text{ic}}}^{1/{\rho }_{\mathit{\text{ic}}}}$, where ρ_ic describes the expansion (ρ_ic > 1) or contraction (ρ_ic < 1) of the source and ${\mathbf{S}}_{\mathit{\text{ic}}}^{\prime }$ is the modified SM for subject i. Finally, a little Gaussian noise distributed as 𝒩(0, 2.5 × 10⁻⁵) is added so that each subject SM is unique.

Figure 2.

(A) Configuration of default sources and (B) default tissue baseline. Sources are labeled and 27 of 30 have been selected for a simulation. Spatial maps are designed to represent sources observed in axial slices of real fMRI data.

We recommend specifying base parameters related to the dimensions and quality of data to fall within the range of values typically reported for whole-brain fMRI studies at conventional voxel sizes and field strengths. For the example simulation (AOD experiment) presented herein we use fewer voxels than are typically present in real data (~17,000 versus ~50,000 intracranial voxels) in order to keep dataset size and computational time manageable. Accordingly, we set the true number of sources to be proportional to the number of components that can be consistently and stably estimated in real data, which appears to be in the range of 70 to 100 (Kiviniemi et al., 2009; Ystad et al., 2010; Abou-Elseoud et al., 2010; Allen et al., 2011b). We note that the SimTB framework allows users to specify and define the shapes of any number of sources, making it exible and potentially suitable for a number of testing applications.

2.1.2. Time courses

Each source TC is T time points in length, where the user specifies the repetition time (TR) in seconds per sample. TCs are constructed under the assumption that source activations result from underlying neural events as well as noise. Neural events can follow block or event-related experimental designs, or can represent unexplained, random deviations from baseline. We refer to an underlying event time series as TS to distinguish it from the subsequent TC that is created with a hemodynamic model.

Experimental paradigms are designed with task blocks and task events which can be assigned to several sources and can be identical across subjects, while unique events refer to unexplained deviations that are unique to each source and subject. Each task block is described by a block length and an inter-stimulus interval. If multiple task blocks are defined, their order is pseudo-randomized so that each task block occurs roughly an equal number of times. Task events and unique events are defined by a probability of occurrence at each TR. For a given source, the TS is created by adding together amplitude-scaled task blocks, task events, and unique events. Amplitudes for task inputs can be negative or positive (indicating suppression or activation with the task), or can be zero (indicating that source activation does not follow the task).

Generating the fMRI blood oxygen level-dependent (BOLD)-like TCs from the event TS may be done in several ways, including linear convolution with a canonical hemodynamic response function (HRF) (difference of two gamma functions) (Friston et al., 1995) and the Windkessel balloon model (Buxton and Frank, 1997; Buxton et al., 1998; Mandeville et al., 1999; Friston et al., 2000). Users may vary hemodynamic parameters between sources and subjects, and define their own TC source models. After creation of the TCs, each source TC is scaled to have a peak-to-peak range of one. As with the SMs, Gaussian noise distributed as 𝒩(0, 2.5 × 10⁻⁵) is added to ensure non-zero TCs.

2.1.3. Baseline intensity

A baseline intensity, b_i, is specified for each subject. An optional tissue-type modifier ${\mathbf{u}}_i^{\top }$ scales the baseline for each voxel. Tissue types with corresponding intensity levels, ω are assigned to each source. Tissue types are assigned to each source and voxel intensity levels are then determined by

$${\mathbf{u}}_i^{\top }={\mathbf{J}}_T^V+{\displaystyle \sum _{c=1}^C}({\omega }_c-1)|{\mathbf{S}}_{\mathit{\text{ic}}}|.$$

For example, Figure 2B displays the default baseline intensity map where four tissue types are defined: sinus signal dropout (ω₆ = 0.3), cerebrospinal uid (CSF) (ω_14,15 = 1.5), white matter (ω_16,17 = 0.7) and gray matter (ω_c = 1 for all other sources). By default, b_i = 800, thus the intensity map ranges from 0.3 × 800 = 240 in areas with signal dropout to 1.5 × 800 = 1200 in CSF.

2.1.4. Dataset, putting it all together

SMs and TCs are scaled according to the source amplitudes, g_i, which are specified in terms of peak-to-peak percent signal change relative to the local baseline. Source features are linearly combined to form the no-noise dataset as in equation 1. Motion may then be added by specifying the maximum x- and y-translation and rotation for each subject. Rotation and translation timeseries are generated via an autoregressive process of model order 1, AR(1), with parameter 0.95, which is a relatively smooth, but effectively bounded, random walk. This model assumes that the head moves randomly between time points but tends toward a central position more than extremes. The dataset is transformed accordingly by linear interpolation at each time point. Datasets are padded with an enlarged bounding box to accommodate translation. Incorporating more complex motion patterns based on the estimated motion parameters from real data will be in upcoming software versions.

To construct the noisy subject data matrix, Y_i, we add Rician noise to the data relative to a specified contrast-to-noise ratio (CNR) (Gudbjartsson and Patz, 1995). We define CNR as σ̂_s/σ̂_n, where σ̂_s is the temporal standard deviation of the true signal and σ̂_n is the temporal standard deviation of the noise. We calculate σ̂_s as the 30% trimmed mean of the standard deviations of the no-noise voxel timeseries (i.e., columns of ${\mathbf{Y}}_i^{\text{nn}}$). The CNR level for each subject is chosen by the user, and the noise standard deviation is then calculated as σ̂_n = σ̂_s/CNR. Each element of Y_i is then $Y_{\mathit{\text{itv}}}=\sqrt{{(Y_{\mathit{\text{itv}}}^{\text{nn}}+{\nu }_{1\mathit{\text{tv}}})}^2+{\nu }_{2\mathit{\text{tv}}}^2}$, t = 1, …, T and v = 1, …, V, where ν_1tv and ν_2tv are distributed as $𝒩(0,{\widehat{\sigma }}_{\mathrm{n}}^2)$.

The final dataset, Y_i, is saved to disk in .mat or .nii format along with the simulation parameters, the true SMs and TCs, and the motion parameters. When saved in a standard imaging format (.nii), simulated datasets can be used with pre-processing or analysis streams developed in any of the standard functional imaging analysis packages (e.g., SPM², AFNI³, and FSL⁴).

3. Results

3.1. Auditory Oddball paradigm

To demonstrate use of SimTB, we simulate data consistent with an auditory oddball (AOD) experiment, which consists of detecting an infrequent target sound within a series of standard sounds and different novel sounds (Kiehl et al., 2001). In this event-related paradigm, three stimuli are presented to each participant in random order. The standard stimulus is a baseline tone that occurs frequently, the target stimulus is a distinct tone that subjects should press a button upon hearing, and the novel stimulus is a random digital noise. We model distinct effects of standard, target, and novel tones on the BOLD signals of different sources. In addition, we adjust the baseline intensity and temporal properties of sources to match the statistical moments found in real data.

3.2. Simulation parameters

Below, we describe the simulation parameters and their implementation. Simulation parameters can be selected through the GUI. Alternatively, parameters can be defined in a batch script that is called at the command line. The batch script for the AOD experiment described here is distributed with SimTB. With either method, the final step in creating the parameter structure involves a validation procedure where parameters are checked for consistency with each other and for appropriate values overall. This step helps users to avoid mistakes and conflicts in simulation design.

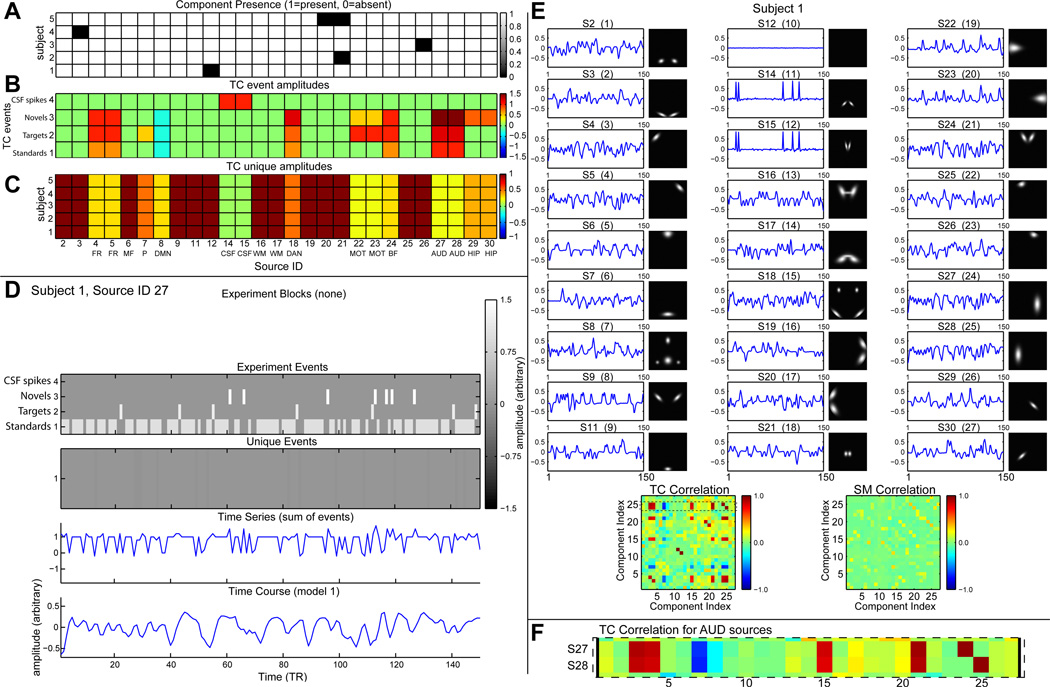
We simulate M = 5 subjects, each with up to C = 27 sources in a dataset with V = 148 × 148 voxels and T = 150 time points collected at TR = 2 seconds. Selected sources are those filled in Figure 2A. Some sources are not “of interest” and are present with probability 0.9 (S2, S3, S9, S11, S12, S19, S20, S21, S25, and S26), that is, some sources may be absent for each subject. A built-in display function can be used to visualize parameter values. For example, Figure 3A shows the component presence for all subjects and sources. Black squares indicated the few sources that are absent from the datasets of individual subjects.

Figure 3. Selected parameters for all subjects and output for Subject 1.

(A) Source presence/absence for each subject and source. For components not “of interest”, presence was random with 0.9 probability of being present. (B) Amplitudes for task events and (C) unique events for each subject and source. The amplitude for unique events are reduced for task event-related sources. (D) For Subject 1, Source 27, the task event and unique event TCs are combined, modeled into a BOLD signal, and scaled to have standard deviation one, then a little Gaussian noise is added. (E) Summary of the final data for subject 1 including TCs and SMs, with correlations. (F) TC correlation between AUD Sources 27 and 28 is high with other sources having task events.

To mimic between-subject spatial variability, the sources for each subject will be given a small amount of translation, rotation, and spread via normal deviates. Translation in the horizontal and vertical directions of each source have a standard deviation of 0.1 voxels, rotation has a standard deviation of 1 degree, and spread has a center of 1 and standard deviation of 0.03.

To define the TCs, we use task events and unique events. We define four task event types which occur in a random order for each subject. In addition to the three task event types mentioned earlier (1=standards, 2=targets, and 3=novels), we include a spike event (4) that occurs rarely (probability of occurrence at each TR is 0.05) and is assigned only to CSF sources to match the TC skewness of CSF seen in real data. Task-related stimuli occur at each TR with probability 0.6, 0.075, and 0.075, respectively (8:1:1 ratio), thus no auditory stimulus occurs on a quarter of the TRs (see experiment events in Figure 3D).

Sources are separately modulated by each event type (Fig. 3B). As can be seen in Figure 3B), auditory sources (AUD) are modulated strongly by novel, target and standard tones, whereas motor sources (MOT) are mostly modulated by targets (to which subjects should respond), the precuneus (P) is only modulated by targets, and the hippocampus (HIP) is only modulated by novels. Note that the default mode network (DMN) component is negatively modulated (decreases activity) to all stimuli.

All sources have unique events that occur with a probability of 0.2 at each TR (see unique events in Figure 3D). Unique event amplitudes are displayed in Figure 3C. For sources not of interest (no task modulation), the unique event amplitude is 1. For task-modulated sources, unique events are added with small amplitudes (0.2 to 0.5) so that sources responding to the same events have similar but not identical activation. CSF sources have smaller unique events (amplitude of 0.05).

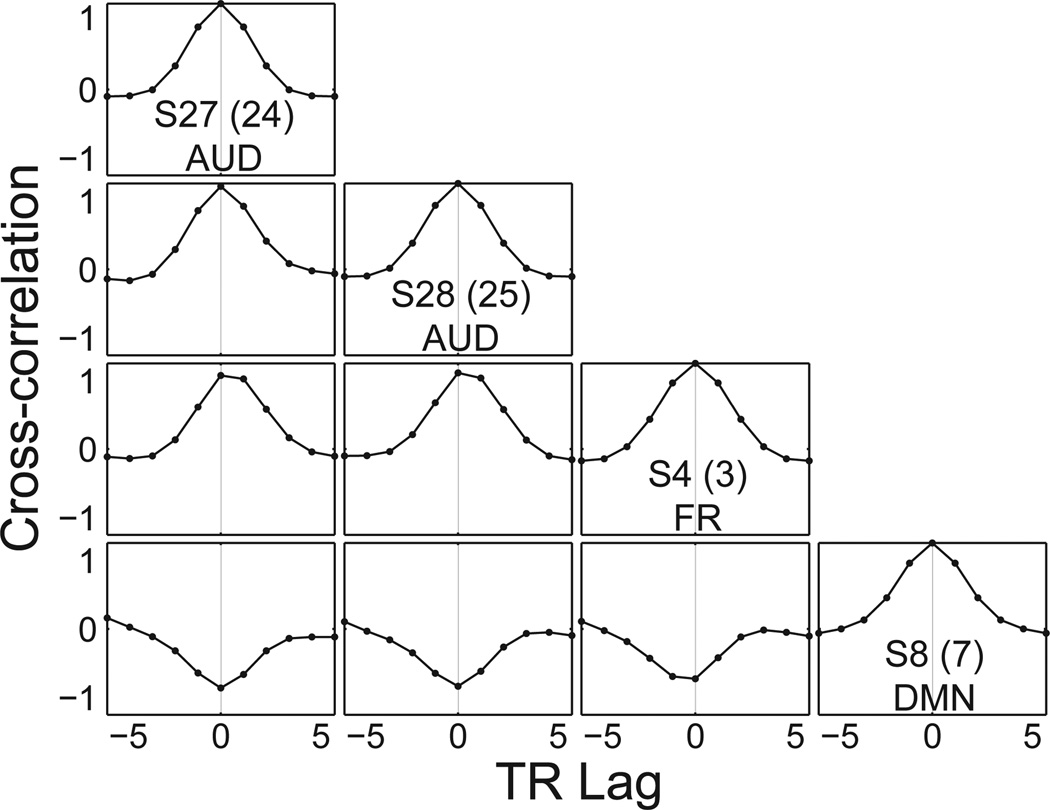
From the event time series, TCs are generated using convolution with a canonical HRF. In general, each source may be generated with a different set of hemodynamic parameters. Here, we use the same set of parameters for all but four sources. The two frontal sources (FR: S4 and S5) have a 1 second onset delay relative to other sources (Fig 4). The two CSF sources (CSF: S14 and S15) use a spike model which has much faster dynamics than the canonical HRF (e.g., peak at about 3 seconds rather than about 6 seconds). Figure 3D shows the construction of the TC for auditory Source 27 for Subject 1, as generated with a display function provided in SimTB. Here the relative frequencies and amplitudes of Standard, Novel, and Target events is evident. Unique events for auditory S27 are common but of low amplitude. Note the lack of CSF spike events since they only appear for the CSF sources.

Figure 4. Cross-correlation of selected components for Subject 1.

S27 and S28 are highly correlated. S4 has a one-second HRF delay relative to other components, so peak cross-correlation is between 0 and 1 TR lag. S8 is negatively correlated with the task.

A summary of all the TCs and SMs including their pairwise correlations for Subject 1 is shown in Figure 3E. Here, we see the relationships between simulation parameters and resulting SMs and TCs. For instance, the absence of S12 in Subject 1 in Figure 3A is reected in the at TC and blank SM in Figure 3E. Note that sources not modulated by the task, such as S1 (see Figure 3B) still have activation TCs as specified by convolution with unique events. We can also see the distinct “spike-like” behavior of CSF TCs (S12 and S13) which is created by a hemodynamic model with faster dynamics, rare positive events, and low noise (unique events). Correlation plots at the bottom of Figure 3E reflect the similarity between the TCs due to shared task events and SMs due to spatial overlap. For example, Figure 3F highlights the two TC correlation rows for AUD sources (S27 and S28). High correlation values with other sources (e.g., S4, S5, S18, etc.) reflect the shared task events in Figure 3B.

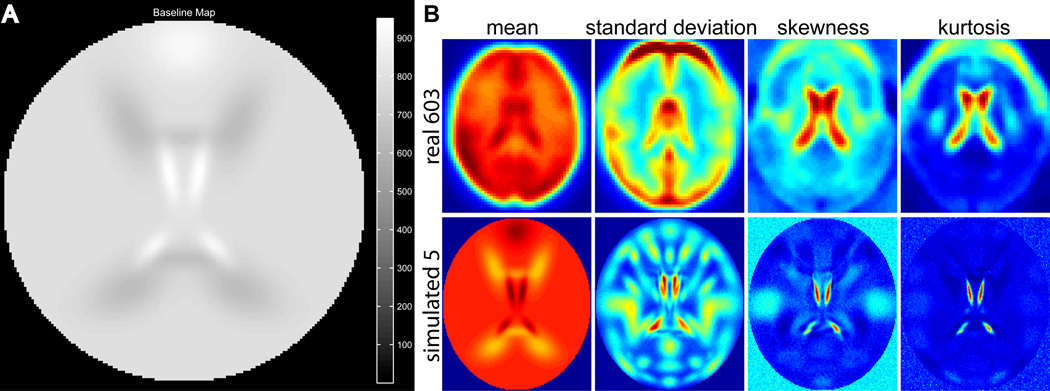
The baseline intensity for all subjects is b_i = 800, though in general this value can be different for each subject. For all “gray matter” components, percent signal change is centered at g_ic = 3 with a standard deviation of 0.25. To approximate the statistical moments of real data, the tissue-type modifier u is increased for CSF (S14 and S15 are 1.2 times larger), decreased for white matter (WM S16 and S17 are 0.8 times as large), and increased for the frontal component (S6 is 1.15 times larger). The resulting dataset baseline is displayed in Figure 5A. With component activations as specified above, we are able to match the statistical moments in real data quite well (Figure 5B).

Figure 5.

(A) Tissue type map used for simulation. Note, compared to the default (Fig. 2B), WM is 0.8 (up from 0.7), CSF is 1.2 (down from 1.5), and frontal is 1.15 (up from 0.3). (B) First four statistical moments in real data averaged over 603 healthy normal controls over T = 148 time points (Allen et al., 2011b), as well as simulated data for 5 subjects with T = 150 time points. Except for real-data edge effects from warping and movement, the first four central statistical moments (mean, variance, skewness, and kurtosis) can be closely matched with simulated data.

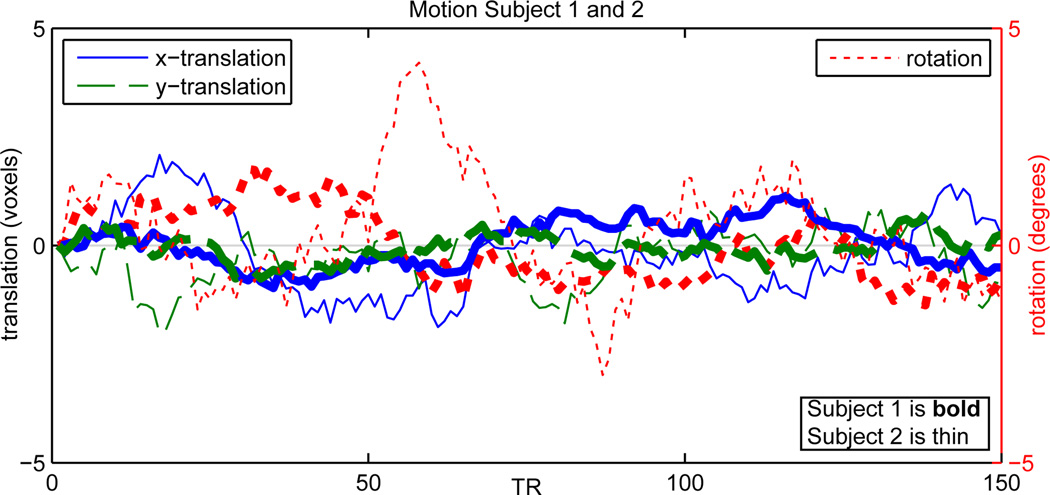
Rician noise is added to the data of each subject to reach the desired CNR level. Here, CNR is uniformly distributed over subjects from 0.65 to 2, reflecting the range of typical CNR values for BOLD contrast at conventional voxel sizes and field strengths. In addition, we simulate head motion with a maximum translation of 0.02 of the image length, and a maximum rotation of 5 degrees. Note that the extent of motion for each subject can also be controlled. As an example, we designate Subject 1 to move up to 0.5 of the maximum. Resulting motion parameters for Subjects 1 and 2 are shown in Figure 6, where greater rotational and translational motion can be seen for Subject 2.

Figure 6. Motion for Subjects 1 and 2.

Parameters for x-translation, y-translation, and rotation are shown, where Subject 1 has half the motion of Subject 2.

4. Discussion

In the above example, we showed that by specifying relatively few parameters, one can generate datasets that model distributed and differential activation to numerous stimuli, approximate statistics found in real fMRI data, and incorporate inter-subject variability. To our knowledge, there is no other available simulation framework that allows for such flexible and easy data generation and we envision that SimTB will be useful in a variety of applications. For example, in a recent study (Allen et al., 2011a) we use SimTB extensively to consider performance of group ICA methods under various forms of inter-subject variability. Other applications might include comparisons of methods to estimate effective connectivity, which can be simulated by setting the onset time of the HRF (or other BOLD model) to delay between selected sources (see Fig 4). A whole-brain spatial source is included for those interested in the effect of global mean regression (Murphy et al., 2009). SimTB can also be useful for assessing preprocessing techniques, such as estimating motion. Data normalization methods in a group setting is possible, such as voxelwise or datawise z-scoring or intensity normalization because baseline intensity and contrast-to-noise ratios are subject specific (Allen et al., 2010). Smoothing methods may also be compared, for example, by defining small spatial sources aligned differently between subjects and imposing different smoothing strategies. Coregistration may be compared by first modifying each subject’s structural map by varying the location spatial sources with different tissue types, then further by post-hoc applying a warping/alignment to the simulated data. SimTB is useful for almost any analysis where testing on a simulation first is important with strict control of input parameters.

There are a number of ways to introduce further realism into the analyses. By capitalizing on the flexibility of the toolbox and the large number of customizable parameters, users may incorporate increasingly realistic sources of noise/artifacts using their own models in order to create datasets that are most appropriate for testing particular methods. For example, physiological noise may be simulated by adding a spatially diffuse source (such as the whole-brain source S1) and time course consistent with the spectral content of physiological noise. Susceptibility artifacts might be simulated by defining regions with altered signal intensity (this is controlled via the tissue type parameter) as well as specifying altered percent signal change in these regions. Furthermore, 2D maps may be approximated from 3D networks in real data, though many decomposition methods make no distinction⁵. For example, if the shape of the spatial map is in consideration, then a simple strategy would be to model a 2D map from a slice of the 3D map (essentially this has already been done for many of the default sources). If, instead of shape, the distributional properties (e.g., kurtosis) are of consideration, then one might calculate the moments of a 3D map, then design a 2D source to approximate those statistics.

The toolbox includes a number of other functions to help with tasks related to simulation and analysis. There are multiple ways to visualize the parameters (Fig. 3), tissue maps (Fig. 2B), task-modulated TCs, and many of these are available “on-the-fly” as the simulation is being created so it can be stopped and tweaked if needed. After simulation, a movie of the dataset is available to assess differences in activation and motion over time. Contour maps of SMs across subjects can be viewed. For analysis, a function is included for automatic source matching between the simulated and estimated SMs derived from an analysis.

4.1. Comparing SimTB with other fMRI simulation tools

Because SimTB captures the fundamental structure of the data in a simple way and controls every aspect of the simulation (not derived from real data), while ignoring the additional realism that is often not essential to understand an estimation method, precise comparisons are possible. SimTB simulates datasets quickly (3–10 seconds for each subject) and is much faster compared to physics-oriented simulated scanner for understanding MRI (POSSUM), part of FSL (FMRIB’s software library), allowing the practitioner to simulate and analyze many datasets to potentially understand a problem from many angles. However, POSSUM uses concepts of MR physics to help understand effects of specified scanning parameters, including tools for pulse sequence generation, slice profile, B0 field inhomogeneities, signal generation, noise addition, motion, and image reconstruction (Drobnjak et al., 2006). SimTB simulates data entirely from a model and defined parameters, whereas some methods require existing fMRI data to simulate fMR images, such as POSSUM, bootstrap resampling of real data (Bellec et al., 2009), and the METU-fMRISim toolbox which requires a structural MRI anatomic brain volume (Türkay, 2009). As an aside, efMRI software (Rorden, 2009) can be used in conjunction with SimTB to optimize statistical efficiency of an experimental design (Friston et al., 1999).

5. Conclusion

SimTB is well-suited for a variety of applications. Though the model makes assumptions (spatiotemporal separability), the simulated data captures the fundamental structure of fMRI data. Importantly, the model does so without relying on real datasets, which have unknown features that cannot be completely modeled.