Capturing inter-subject variability with group independent component analysis of fMRI data: a simulation study

Abstract

A key challenge in functional neuroimaging is the meaningful combination of results across subjects. Even in a sample of healthy participants, brain morphology and functional organization exhibit considerable variability, such that no two individuals have the same neural activation at the same location in response to the same stimulus. This inter-subject variability limits inferences at the group-level as average activation patterns may fail to represent the patterns seen in individuals. A promising approach to multi-subject analysis is group independent component analysis (GICA), which identifies group components and reconstructs activations at the individual level. GICA has gained considerable popularity, particularly in studies where temporal response models cannot be specified. However, a comprehensive understanding of the performance of GICA under realistic conditions of inter-subject variability is lacking. In this study we use simulated functional magnetic resonance imaging (fMRI) data to determine the capabilities and limitations of GICA under conditions of spatial, temporal, and amplitude variability. Simulations, generated with the SimTB toolbox, address questions that commonly arise in GICA studies, such as: (1) How well can individual subject activations be estimated and when will spatial variability preclude estimation? (2) Why does component splitting occur and how is it affected by model order? (3) How should we analyze component features to maximize sensitivity to inter-subject differences? Overall, our results indicate an excellent capability of GICA to capture between-subject differences and we make a number of recommendations regarding analytic choices for application to functional imaging data.

1. Introduction

Spatial independent component analysis (ICA) has emerged as a powerful technique for the analysis of functional neuroimaging data. Based on the optimization of spatial independence, ICA identifies brain regions with temporally coherent activity and linearly decomposes data into a set of spatial components with corresponding activations (McKeown et al., 1998, 2003; Calhoun et al., 2009). Unlike conventional regression approaches, ICA does not require an explicit temporal model, making it an ideal tool for applications where brain activation is difficult to specify a priori, such as complex cognitive paradigms or resting-state studies. The development of group ICA (GICA) frameworks (Calhoun et al., 2001b; Beckmann and Smith, 2005) has further increased the utility and popularity of this data-driven approach, permitting straightforward application of ICA to multi-subject datasets without post-hoc matching or merging of components (Calhoun et al., 2001a; Esposito et al., 2005; Schöpf et al., 2010). Using temporal concatenation of individual datasets, GICA identifies group-level spatial components that can be back-projected to estimate subject-specific components, comprised of individual spatial maps (SMs) and activation time courses (TCs). This approach has been utilized in numerous studies to describe inter-subject differences in intrinsic networks in both health and disease, e.g., (Calhoun et al., 2008; Jafri et al., 2008; Filippini et al., 2009; Beckmann et al., 2009; Biswal et al., 2010; Allen et al., 2011).

Despite successful application, it is important to consider that multi-subject data may not be consistent with the spatial stationarity assumption of ICA models. That is, by estimating sources at the group level, we implicitly assume that spatial activations occur at the same position and with the same shape in all individuals. However, striking neuroanatomic variations exist across individuals, both with regard to topology and function (Ono et al., 1990; Rademacher et al., 1993; Thompson et al., 1996; Uylings et al., 2005). Though gross differences in size and shape can be moderated by spatially normalizing subjects into a common anatomical space, it is well established that considerable variability in functional localization persists (Amunts et al., 2000; Xiong et al., 2000; Wilms et al., 2005; Duncan et al., 2009; Derrfuss et al., 2009).

The impact of inter-subject spatial variability on GICA is largely unknown. Such questions are difficult to address in real data, where the true shape and extent of activations are typically not available, but are well-posed for simulation studies where variability can be parameterized and estimated features can be compared to a known ground truth. Previous studies have used simulations to study spatial variability as an all-or-none phenomena, where subjects either do or do not have a component. In a demonstration of the GICA framework, Calhoun et al. (2001b) showed that if only 1 in 9 subjects exhibited a particular component it could be faithfully reconstructed for the individual without erroneous activation in other subjects. Later work by Schmithorst and Holland (2004) supported these findings and determined that a given component need be present in as few as 10–15% of subjects to be well estimated at the group level. While these simulations provide important information for the application of GICA, they do not accurately model the spatial variability that exists between individuals, nor do they address the effect of spatial variability on estimation quality. Additionally, previous studies have not fully investigated the ability of GICA to capture inter-subject variability in other domains, such as differences in component amplitude and temporal coherence.

Motivated by the sparsity of published work and guidelines in this area, we have undertaken a comprehensive set of simulation-based experiments to evaluate estimation quality of subject activations under conditions of spatial, temporal, and amplitude variability. Simulations are constructed with the SimTB toolbox (Erhardt et al., 2011a) and are modeled after typical fMRI datasets with realistic dimensions, spatiotemporal activations, and noise characteristics. Experiments 1–3 address inter-subject spatial variability. Guided by studies describing variable functional organization between subjects (Xiong et al., 2000; Wilms et al., 2005; Duncan et al., 2009; Derrfuss et al., 2009), we vary both component shape (Experiment 1) and component location (Experiments 2 and 3) to determine the effects on estimation and identify the point at which subject reconstruction fails. In Experiments 4 and 5, we vary the level of activation (i.e., component amplitude) across subjects and determine the most appropriate method to estimate amplitude information from subject components. Notably, the estimation of component amplitude is strongly affected by the absence (Experiment 4) or presence (Experiment 5) of spatial variability. Experiment 6 focuses on the temporal domain, and investigates the estimation of functional network connectivity (FNC), the temporal correlation between component TCs (Jafri et al., 2008), when this quantity varies across individuals. Experiment 7 continues the study of temporal features, but rather than incorporate differences between subjects, we examine factors that encourage the separation of sources into distinct components, so-called “component splitting”. Finally, Experiment 8 incorporates all the aforementioned types of inter-subject variability and models a common scenario where the goal is to compare components between two groups. We use this experiment to determine analysis strategies that maximize sensitivity to group differences and we recommend a set of best practices for feature analysis in real data. Throughout the experiments, we consider ICA model order as an additional factor that affects the ability of researchers to appropriately compare subject activations. We address the estimation and choice of model order in the Discussion, along with a thorough treatment of the limitations and benefits of multi-subject analyses.

2. Materials and methods

Experiments involved manipulations of simulation parameters around a set of base values that are listed in Table 1. Base parameters controlling the dimensions and quality of data were specified to fall within the range of values typically reported for whole-brain fMRI studies at conventional voxel sizes and field strengths. To keep dataset size and computational time manageable, we used fewer voxels than are typically present in real data (~17,000 versus ~50,000 intracranial voxels). Accordingly, we set the true number of sources to be roughly one third the number of components that can be consistently and stably estimated in real data, which appears to be in the range of 70 to 100 (Kiviniemi et al., 2009; Ystad et al., 2010; Abou-Elseoud et al., 2010; Allen et al., 2011).

Table 1.

Base parameter values.

Parameter	Notation	Value
subjects	M	30
components	C	25
voxels	V	148 × 148
timepoints	T	150
repetition time	TR	2
percent signal change	g	3
contrast-to-noise ratio	CNR	1

Below we provide the details of simulations and experimental manipulations, the implementation of GICA, and the metrics used to assess the accuracy of GICA estimation. MATLAB code for all data generation and analysis are available from the authors upon request.

2.1. Simulations

Simulated data are generated with the MATLAB toolbox, SimTB (Erhardt et al., 2011a), which we have developed to facilitate the testing of different analytic methods for multi-subject datasets and is freely available for download (http://mialab.mrn.org/software). In SimTB, we adopt a data generation model that is consistent with the assumptions of ICA, that is, data can be expressed as the product of activation TCs and non-Gaussian sources (SMs). For subjects i = 1, …,M, we model C components, each consisting of a SM and corresponding TC. In our base simulation, M = 30 subjects and C = 25 components. SMs have V = 148×148 voxels and TCs are T = 150 time points in length with a repetition times (TRs) of 2 seconds per sample.

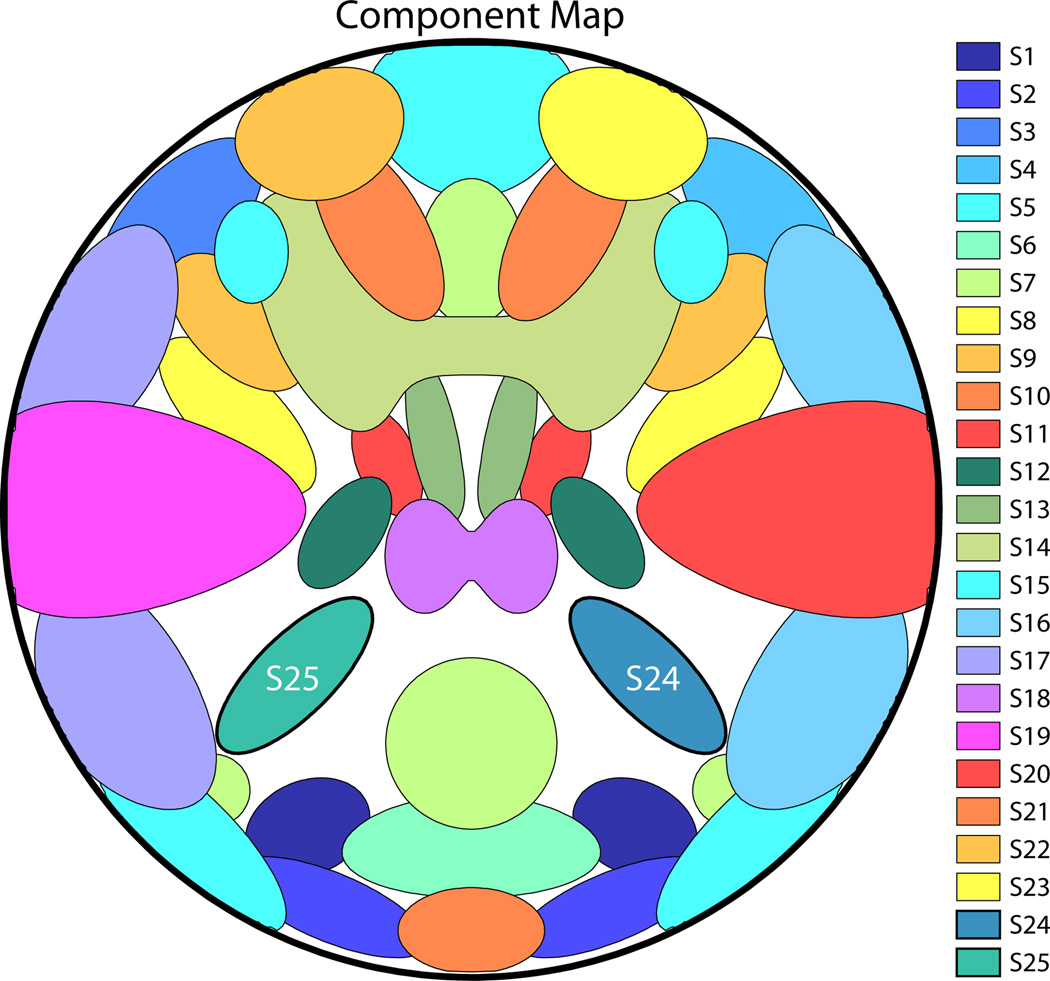
SMs are defined by 2-D density functions that can independently be rotated, translated, and contracted or expanded for each subject. Figure 1 displays the C = 25 components used in our base simulation. Sources are all super-Gaussian and are modeled after activation patterns typically seen in axial slices of real fMRI data. SMs are normalized to have values in [0, 1] and for each subject, SMs are reshaped as the 1 × V row-vectors S_ic and are concatenated to form the C × V matrix S_i.

Figure 1.

Component map, showing the spatial configuration of the C = 25 components in the base simulation. SM boundaries in this and subsequent figures are drawn at 30% of the maximum value. Sources S25 and S24, which are manipulated in Experiments 1–7, are labeled.

Component TCs are simulated as the convolution of a canonical hemodynamic response function (HRF) (difference of two gamma functions) with “neural” events (Friston et al., 1995). In most experiments, events occur with a probability of 0.5 at each TR and are unique to components and subjects. In experiments 6 and 7, where we explore the effects of temporal correlation on source estimation, components of interest share common events in addition to unique events. For each subject, TCs are normalized to have a peak-to-peak range of one and the TC column-vectors, R_ic, are concatenated to form the T × C matrix R_i.

The no-noise (nn) subject data matrix, ${\mathbf{Y}}_i^{\text{nn}}$, is constructed as a linear combination of the amplitude-scaled component pairs:

$${\mathbf{Y}}_i^{\text{nn}}=[{\mathbf{R}}_i\text{diag}({\mathbf{g}}_i){\mathbf{S}}_i+{\mathbf{J}}_T^V]\odot b_i{\mathbf{J}}_T^1{\mathbf{u}}_i^{\mathrm{{\rm T}}},$$

where g_i is the C × 1 vector of component amplitudes defined as percent signal changes from the baseline, ${\mathbf{J}}_T^V$ is a T × V matrix of ones, b_i is the baseline intensity, ${\mathbf{J}}_T^1$ is a T × 1 column of ones, u^Τ is the V × 1 vector describing the spatial intensity profile, and ⊙ denotes the Hadamard (element-wise) matrix product. For simplicity, all subjects have the same arbitrary baseline intensity of b_i = 800 and spatial profile ${\mathbf{u}}_i^{\mathrm{{\rm T}}}$, which is uniform ones inside the “head” and zero outside. In most experiments, we set the component amplitude (peak-to-peak percent signal change) g_ic = 3 for all subjects and components. In experiments 4, 5, and 8, we study component amplitude and vary g_ic around 3.

To construct the noisy subject data matrix, Y_i, we add Rician noise to the data relative to a specified contrast-to-noise ratio (CNR) (Gudbjartsson and Patz, 1995). Here, we define CNR as σ̂_s/σ̂_n, where σ̂_s is the temporal standard deviation of the true signal and σ̂_n is the temporal standard deviation of the noise. We calculate σ̂_s as the 30% trimmed mean of the standard deviations of the no-noise voxel timeseries (i.e., columns of ${\mathbf{Y}}_i^{\text{nn}}$). Each element of Y_i is then $Y_{\mathit{\text{itv}}}=\sqrt{{(Y_{\mathit{\text{itv}}}^{\text{nn}}+{\nu }_{1\mathit{\text{tv}}})}^2+{\nu }_{2\mathit{\text{tv}}}^2}$, t = 1,…,T and v = 1,…,V, where ν_1tv and ν_2tv are distributed as Normal$(0,{\widehat{\sigma }}_{\mathrm{n}}^2)$.

2.2. Experiment 1: Spatial Rotation

Experiment 1 examines the effect of variable component shape. This is done in order to simulate activation patterns across subjects which share a common peak but differ along individual gyration patterns (Rademacher et al., 1993; Ono et al., 1990; Thompson et al., 1996; Uylings et al., 2005). A single component of interest (S25) is stretched to form an oblong ellipse (Figure 2A, red box) and is rotated such that subject SMs are equally spaced over the range of rotation (Δθ). In a set of five simulations, we parametrically increase Δθ to be 0°, 45°, 90°, 135°, and 180° for Steps 1 through 5, respectively. Thus, in Step 1, subject SMs overlap perfectly and in Step 5 they are maximally distributed around the circle and have minimal overlap. Note the peak position is common across the M = 30 subjects in all simulations. Each step of the experiment is repeated ten times to reduce variability, with noise and TC activations varying between repetitions.

Figure 2. Experiment 1: effects of spatial rotation.

A) Component map highlighting S25 (red box) which is rotated across subjects. B) Contour maps showing the configuration of true (top) and estimated (bottom) S25 for subjects 1 to 30 (black to gray). Δθ indicates the range of rotation angles across subjects at each step. C) Examples of subject SMs for a single repetition of Step 4 with ICA model order 25. D) R² statistics between true and estimated subject SMs (top) and TCs (bottom) plotted over subjects. Black data points indicate the mean over 10 repetitions and error bars denote ±1 standard error (SE) of the mean. Gray curves show the model fit (see Section 2.11). For Step 1, where θ is constant, the gray line simply denotes the mean across subjects. Red dots in Step 4 correspond to the subjects displayed in panel C.

2.3. Experiment 2: Spatial Translation

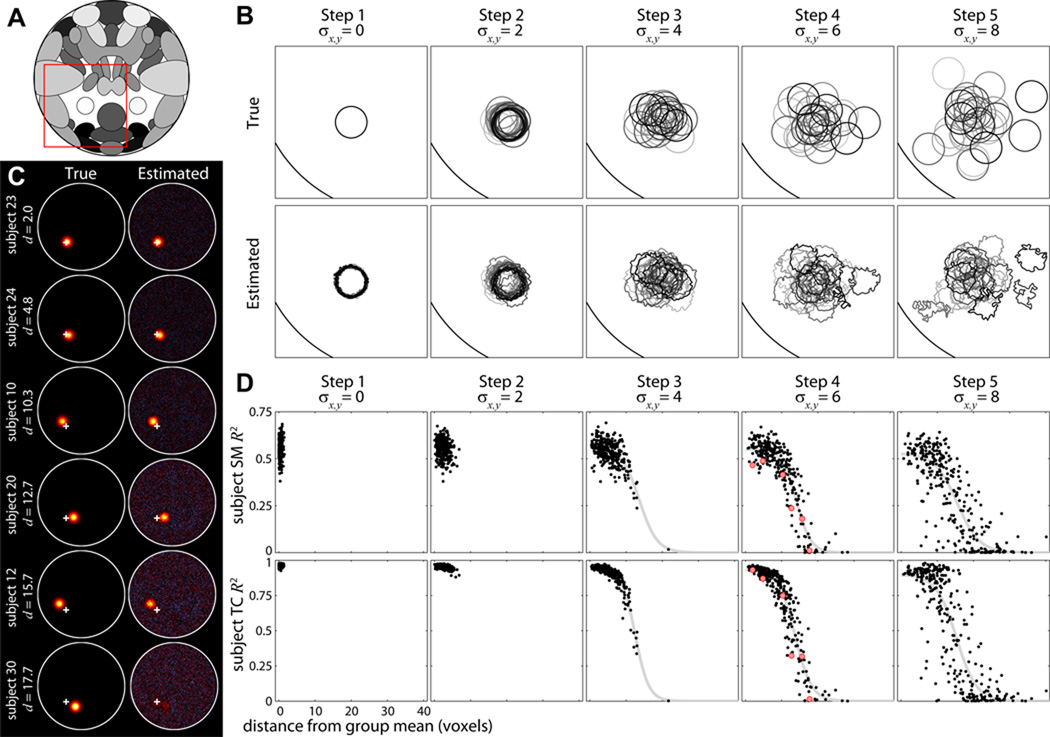
Experiment 2 studies the effect of variable component position. We simulate the well known case of variable activation locations (Rademacher et al., 1993; Amunts et al., 2000; Xiong et al., 2000; Wilms et al., 2005; Duncan et al., 2009; Derrfuss et al., 2009). S25 is circular with a FWHM of 12.3 voxels (Figure 4A, red box) and is translated across subjects according to a bivariate normal distribution with mean zero and specified standard deviation σ_x,y. In a set of five simulations, σ_x,y is specified as 0, 2, 4, 6, and 8 voxels for Steps 1 through 5, respectively. S25 is relatively isolated and has little overlap with other sources, though exceptions occur with extreme translations in Steps 4 and 5. The experiment is performed with M = 30 subjects and is repeated ten times with randomized noise, TCs, and component translations.

Figure 4. Experiment 2: effects of spatial translation.

A) Component map. Red box highlights S25 and corresponds to the bounding box in B. B) Contour maps showing the configuration of true (top) and estimated (bottom) S25 for subjects 1 to 30 (black to gray) in a single repetition. Translations in x and y are normally distributed with mean zero and standard deviation σ_x,y. Note that for Steps 4 and 5, contours of estimated SMs for some subjects are greatly distorted or completely absent. C) Examples of subject SMs for a single repetition of Step 4 with ICA model order 25. Subjects are displayed in order of increasing distance (d) from the group mean, which is indicated by the white cross. D) R² statistics between true and estimated subject SMs (top) and TCs (bottom) for all subjects and repetitions, plotted as a function of d. Gray curves show the fit of the Boltzmann sigmoid model (see Section 2.11). We do not fit the model for Steps 1 or 2 where d varies little between subjects. Red dots in Step 4 correspond to the subjects displayed in C.

2.4. Experiment 3: Translation of Multiple Components

Experiment 3 builds on Experiment 2 and explores the scenario where several neighboring sources may be poorly aligned across subjects, see e.g., Amunts et al. (2000). S25 is again circular in a relatively isolated region and is translated vertically according to a normal distribution with mean zero and standard deviation σ_y (Figure 5A, red box). A second component of interest, S24, is surrounded by sources S1 and S12 (Figure 5A, blue box). All three components are vertically translated together according to σ_y. For Steps 1 through 5, σ_y is 0, 1.25, 2.5, 3.75, and 5 voxels, respectively. As σ_y increases, sources S1, S12 and S24 will be increasingly misaligned across subjects, e.g., S24 of subject i may be spatially coincident with S12 of subject j. Because S25 is designed to serve as a control for S24 (i.e., translation in isolation versus translation with overlap), we explicitly match the distribution of vertical displacements for S24 and S25. That is, for each simulation we draw a set of M = 30 translations for S25, which are permuted across subjects and assigned to S1, S12, and S24. Thus, we ensure that any difference in the estimation quality between S24 and S25 is due to source misalignment. The experiment is repeated ten times with randomized noise, TCs, and component translations.

Figure 5. Experiment 3: effects of spatial translation of multiple components.

A) Component map. Red box highlights S25. Blue box highlights S24 and neighboring sources S12 and S1 (top and bottom, respectively). B) Composite contour maps showing the configuration of true (top) and estimated (bottom) S25 (left) and S24 (right) for subjects 1 to 30. Bounding boxes correspond to the red (left) and blue (right) boxes in A. Components are vertically translated according to σ_y, with S12, S24 and S1 translated together in each subject. S25 undergoes the same translations, permuted over subjects. For reference, the true contours of S12 (green) and S1 (blue) are shown for the subjects with the largest positive (dark circle) and negative (light circle) displacements. Their influence can be seen in the distorted estimated contours of S24 (bottom). C) Examples of subject SMs for a single repetition of Step 4, in order of positive to negative vertical displacements (Δ_y). Left column shows a composite of the true S25 and S24 SMs for subjects with matching translations; middle and right columns show the corresponding estimated SMs (eS). The group mean is indicated by the white cross. D) R² statistics between true and estimated subject SMs (top) and TCs (bottom) as a function of distance from the group mean. Black squares denote S25, gray circles indicate S24, and curves show the sigmoidal fits. Red symbols in Step 4 correspond to the subjects displayed in C.

2.5. Experiment 4: Amplitude Variation

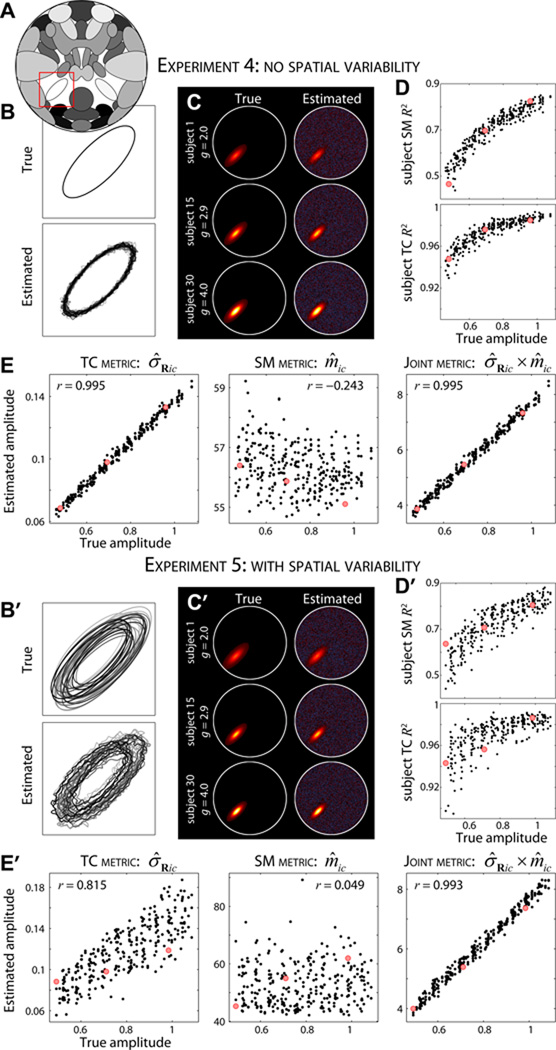
Experiment 4 evaluates how well GICA can capture inter-subject differences in component amplitude. The spatial configuration of S25 is identical to the base simulation (Figure 6A, red box) and is constant across subjects. Component amplitude (g_i25) is varied linearly over subjects from 2 to 4 in 10 steps. For M = 30, groups of three subjects share the same amplitude, facilitating characterization of amplitude estimation as homoscedastic or heteroscedastic. Because there is a natural scaling ambiguity in ICA (i.e., scale and sign information can be captured in SMs and TCs), we use this simple experiment to help us identify and assess metrics proposed to estimate subject-specific component amplitudes. The experiment is repeated ten times with randomized noise and TCs.

Figure 6. Experiments 4 and 5: effects of amplitude variation.

A) Component map, highlighting S25 (red box). B, B′) Contour maps of true (top) and estimated (bottom) S25 for subjects 1 to 30 in Experiment 4 (B) and Experiment 5 (B′). In Experiment 4 (B) the spatial properties of S25 are identical across subjects; in Experiment 5 (B′) component position and size are varied slightly. In both experiments component amplitude of S25 is increased linearly from g₁ = 2 to g₃₀ = 4. C, C′) Examples of true (left) and estimated (right) SMs for subjects 1, 15, and 30 in order of increasing amplitude. D, D′) R² statistics between true and estimated subject SMs (top) and TCs (bottom) for all subjects and repetitions as a function of component amplitude. E, E′) Scatter plot of true versus estimated subject-specific amplitudes using TCs standard deviation, σ̂_Ric (left), SM maximum, m̂_ic (middle), and their product σ̂_Ric × m̂_ic (right) as the amplitude metrics. Red dots in D, E and D′, E′ correspond to the subjects displayed in C and C′, respectively. Note that the true and estimated SMs in C, C′ are displayed with scaling information, i.e., g_icS_ic and σ̂_RicŜ_ic, respectively.

2.6. Experiment 5: Amplitude and Spatial Variation

Experiment 5 builds on Experiment 4 and simulates the more realistic case of inter-subject differences in component amplitude in the presence of spatial variability. Component amplitudes are varied as in Experiment 4 and S25 is translated over subjects following a bivariate normal distribution with σ_x,y = 2 voxels. In addition, the size of S25 is slightly varied across subjects. For a normalized SM S_ic, we compute ${\mathbf{S}}_{\mathit{\text{ic}}}^{\prime }={\mathbf{S}}_{\mathit{\text{ic}}}^{1/\rho }$, where ρ is a scalar describing the expansion (ρ > 1) or contraction (ρ < 1) of the component and ${\mathbf{S}}_{\mathit{\text{ic}}}^{\prime }$ is the modified SM for subject i. For S25, ρ is varied linearly from 0.7 and 1.6 and randomized to subjects. The experiment is performed with M = 30 subjects repeated ten times with randomized noise, TCs, and component translations.

2.7. Experiment 6: Functional Network Connectivity

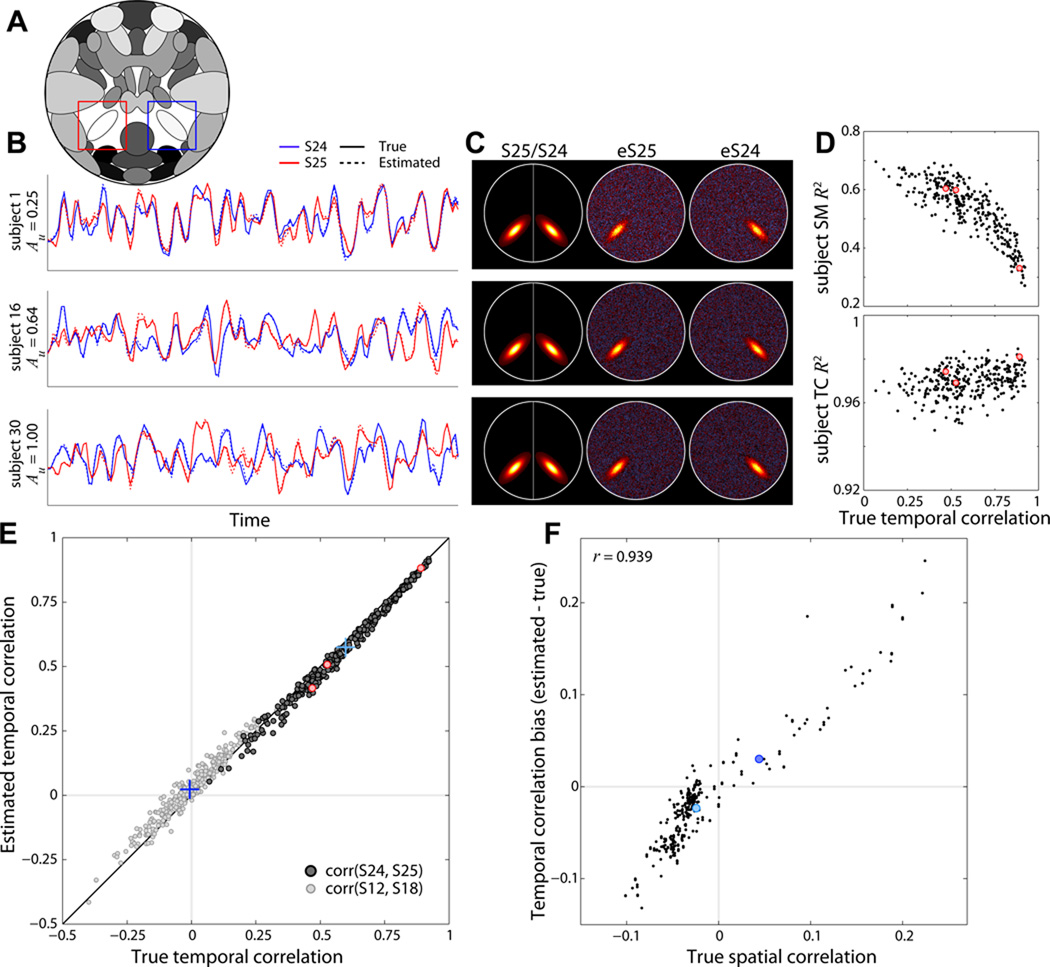
Experiment 6 evaluates how well the FNC between components can be estimated for individual subjects (Jafri et al., 2008). Temporal similarity between components S24 and S25 (Figure 7A, blue and red boxes) is varied across M = 30 subjects by modifying relative amplitudes of unique and shared events. For all subjects, the TCs of S24 and S25 are simulated with the same set of shared events (probability of occurrence is 0.5 at each TR) along with additional unique events (probability of occurrence is 0.5). The amplitude of unique events (A_u) relative to shared events is increased linearly over subjects from 0.25 to 1. Thus subjects with greater A_u values will have decreased temporal correlation between S24 and S25 TCs. The experiment is repeated ten times with randomized noise and TCs.

Figure 7. Experiment 6: effects of variable functional network connectivity.

A) Component map, highlighting S25 (red box) and S24 (blue box). B) Examples of true (solid lines) and estimated (dotted lines) component TCs for subjects 1, 16, and 30. S25 (red) and S24 (blue) TCs become more distinct as amplitude of unique events (A_u) is increased (see Section 2.7). C) Examples of true and estimated SMs for the subjects shown in B. Left column shows a composite of the true S25 and S24, middle and right columns show estimated SMs for S25 and S24, respectively. D) R² statistics between true and estimated subject SMs (top) and TCs (bottom) for S25 as a function of the true FNC value (temporal correlation) between S24 and S25. E) Scatter plot of true versus estimated FNC values for all repetitions and subjects between S24 and S25 (dark gray dots) and between S12 and S18 (light gray dots). Correlations between S24 and S25 are designed, thus FNCs values are strong and positive; correlations between S12 and S18 arise by chance and follow a null distribution. Blue crosses denote the true and estimated mean FNCs values for each component pair. F) Estimation bias (FNC_est − FNC_true) for all $\left(\begin{array}{c}\hfill 25\hfill \\ \hfill 2\hfill \end{array}\right)=300$ component pairs plotted as a function of their true spatial correlation. Red dots in D,E correspond to the subjects displayed in B,C. Blue dots in F correspond to the component pairs (crosses) displayed in E.

2.8. Experiment 7: Component Separation

Experiment 7 continues the study of temporal correlation between components, focusing on factors that cause sources to separate into distinct components. As in Experiment 6, S24 and S25 TCs are composed of shared events as well as unique events. In a set of thirty simulations we parametrically increase A_u from 0 to 3, where higher A_u values indicate more distinct component TCs. Here the sampling of A_u is uneven (very fine steps at low values and coarser steps at larger values) to focus on the range of A_u that causes the largest changes in decomposition. Note that in this experiment all M = 5 subjects have the same spatial and temporal parameters. To study the inuence of additional factors on component separation, we also repeat the set of simulations (Steps 1 to 30) while varying other parameters of interest around their base values. Factors of interest include the number of time points (nT = [75, 300], base value = 150), contrast-to-noise ratio (CNR = [0.5, 2.0], base value = 1.0), spatial extent of S24 and S25 (ρ = [0.5, 2.0], base value = 1.0), and the spatial overlap of S24 and S25 (high overlap versus no overlap in the base simulation). Note that each parameter is varied in turn (i.e., not a factorial approach), which corresponds to exploring the primary axes of the parameter space where the base simulation is the origin. All simulations are repeated ten times with randomized noise and TCs.

2.9. Experiment 8: Detecting Group Differences

Experiment 8 simulates a typical study where the objective is to compare component features between groups. We model two groups, A and B, that differ in four ways as described in detail below. Each group has 30 subjects, for M = 60 subjects total. Additional sources are included to fill the “head” (see Figure 10A) and all sources undergo mild spatial variation across subjects. SMs are translated according to a bivariate normal distribution with mean zero and standard deviation σ_x,y = 0.75 voxels, and are rotated by normally distributed angles with mean zero and a standard deviation of 1°. Note that each cluster of activation is rotated separately. SM size is also randomized, with ρ uniformly distributed between 0.85 and 1.15. Unless otherwise noted, component amplitudes are distributed normally with a mean of 3 and standard deviation of 0.3.

Figure 10. Experiment 8: detecting group differences in component shape and amplitude.

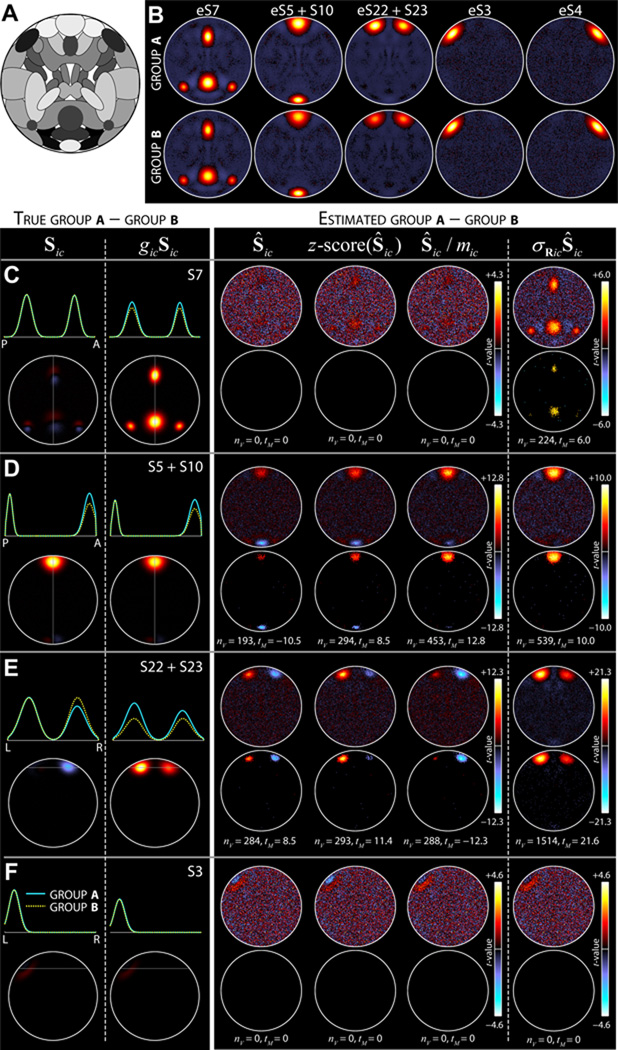
A) Component map of sources used in Experiment 8. B) Estimated average SMs of groups A (top) and B (bottom) for components of interest. These average maps are computed relative to the scaled subject components, σ̂_RicŜ_ic. C–F, left) True group differences for S7 (C), S5+S10 (D), S22+S23 (E), and S3 (F). Differences are computed for both unscaled (S_ic, left) and scaled (g_icS_ic, right) SMs. Top panels show average intensity profiles for Group A (cyan) and Group B (dotted yellow) at the slice with maximal activation (indicated by gray line). Bottom panels show the difference maps, calculated as A–B. C–F, right) Estimated group differences as determined with four different scaling approaches, from left to right, Ŝ_ic, z-score(Ŝ_ic), Ŝ_ic/m̂_ic, and σ̂_RicŜ_ic (see Section 2.9). Differences are displayed as two-sample t-statistics (top) that are thresholded at α = 0.05 in bottom panels, with the number of significant voxels (n_V) and maximum significant t-statistic (t_M) indicated. Estimated differences in Ŝ_ic, z-score(Ŝ_ic), and Ŝ_ic/m̂_ic should be compared to the true differences in S_ic (left of dashed line); differences in σ̂_RicŜ_ic should be compared to differences in g_icS_ic (right of dashed line). Data in B–F show the results of a single repetition.

Group differences are as follows. (1) Group A has larger component amplitude for S7 than Group B. This is modeled by distributing g_i7 as normal with mean 3.3 and standard deviation 0.3 for Group A, and mean 2.7, standard deviation 0.3 for Group B. (2) Groups A and B have different shapes for a network composed of S5 and S10. The network is modeled by assigning shared events between S5 and S10 and setting A_u = 0, creating identical TCs. For Group A, the amplitude of S5 is g_i5 = 0.75 × g_i10, whereas for Group B g_i5 = 1 × g_i10. Thus, Group B has a network where the anterior node (S5) is weaker than the posterior node (S10) and Group A has two nodes of equivalent strength. (3) Groups A and B have different shapes and different amplitudes for a network composed of S22 and S23. For Group A, g_i23 = 0.8 × g_i22, where g_i22 is distributed normally with mean 5 and standard deviation 0.3. For Group B, g_i23 = 1 × g_i22, where g_i22 is distributed normally with mean 3 and standard deviation 0.3. Thus, Group A has a lateralized network where the left node is stronger than the right and Group B has a bilaterally symmetric network. Furthermore, the amplitude of the network for Group A is much larger than the amplitude for Group B. (4) Group B has stronger FNC between sources S3 and S4 than Group A. This is modeled by first designating shared events between S3 and S4, then distributing A_u as uniform between [0.5,1.0] for Group A and between [0.65, 1.15] for Group B. The experiment is performed ten times with randomized component amplitudes, spatial parameters, event amplitudes and TCs. Note that although we use 29 sources in the simulation, two pairs of sources are joined together as networks, S5+S10 and S22+S23, thus the true dimensionality is C = 27.

2.10. Group ICA

GICA is performed with the GIFT toolbox (http://icatb.sourceforge.net/) which uses a temporal concatenation approach to combine data across subjects (Calhoun et al., 2001b, 2002). A formal treatment of the procedure can be found in Appendix A. Prior to the ICA decomposition, subject datasets are orthogonalized and whitened using principal components analysis (PCA) such that the T₁ retained eigenvectors have a norm of 1. We retain T₁ = T − 1 principal components since a relatively large number of subject-specific principal components (PCs) has been shown to improve reconstruction of subject components (Erhardt et al., 2011b). Whitened subject datasets are temporally concatenated to form the aggregate data matrix and a group-level PCA reduces the dimension of the aggregate data to T₂, the number of components to be estimated with ICA. In most experiments we set T₂ = C, where C is the known true number of sources. In some cases, we explicitly use T₂ = C − 1 or T₂ = C +5 to explore the effects of under- and over-fitting, respectively. Spatial ICA (McKeown et al., 1998) is performed using the Infomax algorithm with 20 repetitions in Icasso to estimate  and Ŝ, the T₂ × T₂ group mixing matrix and the T₂ × V aggregate SMs, respectively (Hyvärinen et al., 2001; Bell and Sejnowski, 1995; Himberg et al., 2004). Individual subject maps, Ŝ_i, and TCs, R̂_i, are then estimated by back-projecting the aggregate mixing matrix  to the subject space based on the PCA reducing matrices (Calhoun et al., 2001b, 2002). As noted in Erhardt et al. (2011b) and detailed in Appendix A, this back-projection method is very closely related to dual regression which defines subject SMs and TCs by least-squares regression onto the original data (Calhoun et al., 2004; Filippini et al., 2009). For the analyses here we expect and have verified no difference between direct back-projection and dual regression estimation, thus our results are applicable to a broad range of GICA implementations.

2.11. Statistical Analysis

In all experiments we calculate the R² statistic (coefficient of determination) between true and estimated component features. For the aggregate SM, subject SMs, and subject TCs, we compute R²(Ŝ_c, S̄_c), R²(Ŝ_ic, S_ic), and R²(R̂_ic, R_ic), respectively, where ${\overline{\mathbf{S}}}_c=\frac{1}{M}{\displaystyle {\sum }_{i=1}^M}{\mathbf{S}}_{\mathit{\text{ic}}}$ is defined as the true group SM for component c.

Where appropriate, we use simple models to describe the relationship between a parameter of interest and R² statistics of a component feature. For example, in Experiment 1 we fit the linear model z = β₀+β₁ cos(θ)+β₂ sin(θ), where θ is a vector of component rotation angles and z is the vector of TC or SM R² statistics for all subjects and repetitions. Similarly, for Experiments 2 and 3 involving component translation, we fit the Boltzmann sigmoid model,

$$\mathbf{z}=\frac{z_{\mathit{\text{max}}}-z_{\mathit{\text{min}}}}{1+e^{\eta (\mathbf{d}-d_{50})}}+z_{\mathit{\text{min}}},$$

where d is the vector of component distances from the group mean. Sigmoid parameters z_max and z_min define the maximum and minimum R² values, respectively, η defines the sigmoid slope, and d₅₀ is the distance at which R² values fall to half their maximum. The four sigmoid parameters are estimated by minimizing the residual sum of squares using the lsqnonlin function in MATLAB with the Levenberg-Marquardt algorithm. Model fits are considered statistically significant at an α = 0.05 level.

For Experiments 4 and 5, where we are interested in capturing the amplitude variability across subjects, we compute the Pearson correlation coefficient between the vector of true subject amplitudes for a given component, g_c, and the vector of estimated amplitudes, ĝ_c. We compare three proposed metrics for estimating amplitude: (1) the standard deviation of component TCs, σ̂_Ric, (2) the maximum intensity of component SMs, m̂_ic, and (3) their product, σ̂_Ric × m̂_ic, which combines scaling information from TCs and SMs. Note that in computing m̂_ic, we average intensity values over the top twenty voxels (roughly 0.1%) to reduce the influence of noise.

For evaluations of FNC (Experiment 6), we compute correlations between the estimated TCs of each subject and compare these values with the true correlations. In Experiment 7 we are interested in factors that contribute to differences in source decomposition and limit our analyses to the aggregate SMs. Because estimated SMs can represent S24 and S25 joined together in a single component or split apart into distinct components, we compute R² statistics for both possible ground truths, R²(Ŝ_c, S̄₂₄ +S̄₂₅), and R²(Ŝ_c, S̄₂₄) and R²(Ŝ_c, S̄ ₂₅), respectively.

For Experiment 8, we investigate how analysis choices may affect sensitivity to detect group differences. For components of interest, we perform voxelwise two-sample t-tests for the group difference (Group A - Group B). Voxelwise tests are corrected for multiple comparisons at an α = 0.05 significance level using false discovery rate (FDR) (Genovese et al., 2002). Prior to computing t-statistics, component SMs are scaled using one of four different approaches: (1) no scaling, Ŝ_ic, where estimated subject SMs are left in their original units, (2) scale normalization, notated z-score(Ŝ_ic), where SMs are transformed to have mean zero and standard deviation 1, (3) removal of scale, Ŝ_ic/m̂_ic, where SMs are divided by their maximum value, and (4) joint scaling, σ̂_RicŜ_ic, which incorporates scale information from component TCs into SMs. Note that methods (2) and (3) reflect attempts to remove scaling information and capture only shape. Estimated group differences are compared to the true differences in component maps, S_ic, and scaled maps, g_icS_ic.

3. Results

3.1. Experiment 1: Spatial Rotation

Figure 2 displays the results from Experiment 1 at an ICA model order of 25. Qualitatively, subject SMs are captured very well for all ranges of rotation angles (Figure 2B, Steps 1–5). Examples of subject SMs for Step 4 (Δθ = 135°) demonstrate remarkable estimation of highly variable component shapes (Figure 2C). Quantitative assessment is provided in Figure 2D, which displays the R² statistics for subject SMs (top) and TCs (bottom) averaged over repetitions. As the range of rotation increases from Δθ = 0° to Δθ = 180°, estimation quality decreases on average, with particular detriment to subjects at the edges of the group. The angle of rotation accounts for a significant portion of variance in the R² values for all steps except 5 (α = 0.05), which is expected given the circular symmetry of the SMs in this simulation (see Figure 2B).

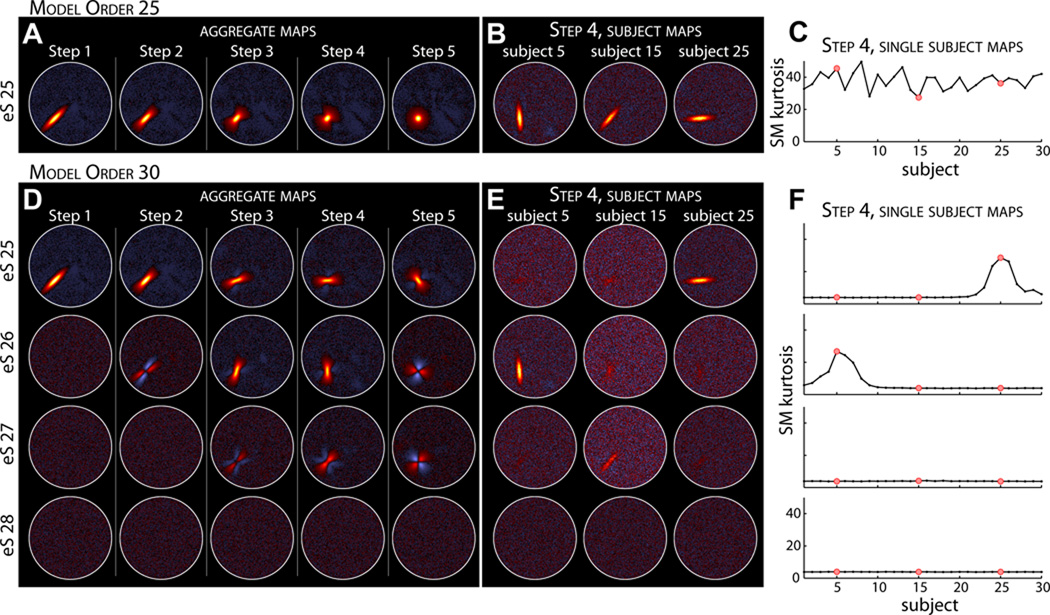
Figure 3 displays the results from the same experiment when the model order is increased to 30. For Step 1, where there is no spatial variability between subjects, the five “extra” estimated aggregate SMs are essentially noise and lack any spatial structure (Figure 3D, first column). However for Steps 2–5, where there is inter-subject spatial variability, S25 can be estimated as two or three different sources (Figure 3D, columns 2–5). This type of decomposition has a substantial effect on the subject SMs, examples of which are shown in Figure 3E for Step 4. In contrast to the results at a model order of 25 (Figure 3B), at higher model order no single estimated component captures the SMs of all subjects, and some subjects may have their component represented by a combination of several sources (e.g., Subject 15, Figure 3E, center column). Such a GICA decomposition makes comparisons difficult and may obfuscate between-subject differences. We note that the kurtosis of subject SMs reliably indicates whether individual components contain spatial structure (Figure 3C,F), suggesting a heuristic to identify sources that are not consistently estimated across subjects (see Discussion).

Figure 3. Experiment 1: effects of increasing model order from 25 (A–C) to 30 (D–F).

A,D) Estimated aggregate SMs for Steps 1–5. For Step 1 of model order 30 (D, left column), all “extra” estimated sources (eS) are essentially noise and lack any spatial structure. At steps with spatial variability between subjects, S25 is split into two or three estimated sources. Note that we do not display eS29 or eS30 since these additional estimated sources were simply noise for all steps. B,E) Examples of subject SMs for Step 4. At higher model order no single component captures the SM for all subjects. C,F) Kurtosis of the subject SMs. Red dots in C, F correspond to the subjects displayed in B, E, respectively.

3.2. Experiments 2 and 3: Spatial Translation

Results from Experiment 2 at a model order of 25 are displayed in Figure 4. Contour maps of estimated SMs (Figure 4B, bottom) suggest that subject components are captured well when spatial translations are small or moderate but not when translations are more extreme. As seen in Steps 4 and 5, subjects with SMs far from the group mean have greatly distorted or absent contours. Examples of subject SMs for Step 4 (Figure 4C) also show that estimation deteriorates as subject SMs move further from the group mean (top to bottom) and ultimately fails when the translation distance becomes too large (e.g., Subject 30, Figure 4C, bottom).

In Figure 4D we plot the R² statistics for subject SMs (top) and TCs (bottom) as a function of component distance from the group mean. For Steps 1–4, estimation quality of subjects with small translations is relatively constant and seems largely unaffected by increasing σ_x,y. In Step 5, where the spatial overlap between subjects is reduced and some subject SMs are translated into neighboring components (see Figure 4B, rightmost panel), estimation quality becomes more variable for all subjects. The drop-off in estimation quality with distance in Steps 3–5 suggests consistent sigmoidal behavior that is reasonably well-captured with the Boltzmann sigmoid model. The sigmoidal fits provide estimates for d₅₀, the distance at which estimation quality drops to 50% of the maximal value. Parameter estimates, listed for each [Step] in units of voxels, are [3] d₅₀ = 13.6, [4] d₅₀ = 14.1, and [5] d₅₀ = 15.5 for SMs, and [3] d₅₀ = 12.5, [4] d₅₀ = 13.7, [5] d₅₀ = 15.3 for TCs. Notably, these values are similar to the full-width at half-maximum (FWHM) of S25 (12.3 voxels) suggesting a rule of thumb regarding sufficient overlap of subject SMs (see Discussion).

We also decomposed the data from this experiment at an ICA model order of 30. Parallel to the findings from Experiment 1, S25 can be estimated as multiple components at higher model order and no single component captures the SMs or TCs of all subjects (data not shown). Together, these results suggest that model order can profoundly affect GICA decomposition in the presence of inter-subject spatial variability, and that using a dimensionality that exceeds the true number sources (i.e., over-fitting) can produce an undesirable splitting of components.

In Experiment 3, we further investigate the effects of spatial translation when several components are translated together and may be poorly aligned across subjects. Figure 5A–B displays the spatial configuration of components of interest, S25 (left) and S24 (right). Both S25 and S24 are translated vertically according to σ_y, however S25 is in relative isolation whereas S24 is translated together with S12 and S1 (top and bottom, respectively). As seen in the contour maps of Steps 4 and 5 (Figure 5B, top row), S24 SMs for some subjects overlap with S1 (filled blue contours) or S12 (filled green contours). This misalignment leads to distortions in the estimated SMs of S24, which contain erroneous activations related to S1 and S12 (Figure 5B, bottom row, right panels). This can also be seen in examples of subject SMs for Step 4 (Figure 5C). For subjects with positive vertical displacements (Δy > 0, Figure 5C, top), the position and shape of S24 is reasonably well captured, but estimated SMs have additional prominent deactivation in locations consistent with S12 and more subtle extraneous positive activation in the region of S1. For subjects with negative displacements (Δy < 0, Figure 5C, bottom), the same pattern is present but with deactivations over S1 and positive activation related to S12. These distortions are more apparent as translations increase in magnitude. Note that S25, which undergoes translations of the same extent, is quite well estimated for all subjects in all steps (Figure 5B, bottom row, left panels and Figure 5C, middle column).

Quantitative comparison of estimation quality for S24 and S25 is provided in Figure 5D, which displays the R² statistics for subject SMs (top) and TCs (bottom) as a function of SM distance from the group mean. For all steps, estimation quality for subjects with small translations is roughly equivalent between S24 (gray circles) and S25 (black squares), however as translation distances increase in Steps 3–5, R² statistics for S24 deviate from S25 and drop much faster as a function of distance. We again use sigmoidal fits to describe the behavior of the R² statistics and estimate the distance at which estimation quality drops to 50% of the maximal value. For S25, d₅₀ estimates are similar to the values observed in Experiment 2: [5] d₅₀ = 13.0 for SMs and [5] d₅₀ = 12.7 for TCs. Parameter estimates for S24 are considerably smaller, [4] d₅₀ = 8.1 and [5] d₅₀ = 8.0 for SMs, and [4] d₅₀ = 8.0 and [5] d₅₀ = 8.0 for TCs, demonstrating the vulnerability of single-subject estimation to misalignment of functional regions.

3.3. Experiments 4 and 5: Amplitude Variation

Results from Experiments 4 and 5 at an ICA model order of 25 are provided in Figure 6. SMs for all subjects are well captured both when spatial properties of S25 are identical (Figure 6B) and vary slightly (Figure 6B′) across subjects. The sizes of components are estimated quite accurately despite the considerable variability in component amplitude. Figures 6C and 6C′ display examples of estimated subject SMs and show increasing signal intensity relative to background noise with increasing amplitude. As would be expected, greater amplitude confers greater estimation quality which is easily seen by plotting SM and TC R² statistics as a function of component amplitude (Figure 6D, D′). The relationship between amplitude and estimation quality is notably tighter in Experiment 4 (Figure 6D) due the additional factors of displacement and component size that also affect estimation in Experiment 5 (Figure 6D′).

The primary objective in performing 4 and 5 was to determine an appropriate estimator for single-subject component amplitudes. In Figure 6E and Figure 6E′ we display the accuracy of amplitude estimation for three proposed metrics (see Section 2.11). In the absence of spatial variability, scaling information is captured primarily in TCs. The standard deviation of each TC, σ̂_Ric, provides an excellent estimate of amplitude that is highly correlated with the true amplitude (r = 0.995, Figure 6E, left). Maximum SM intensity, m̂_ic, is weakly negatively correlated with the truth (r = −0.243, Figure 6E, middle), however the product σ̂_Ric × m̂_ic also provides a very good estimate of component amplitude (r = 0.995, Figure 6E, right). In the presence of spatial variability, both TCs and SMs contain scaling information. The TC standard deviation σ̂_Ric is moderately well correlated with the true amplitude (r = 0.815, Figure 6E′, left) and SM maximum m̂_ic is poorly correlated (r = 0.049, Figure 6E′, middle), however their product estimates component amplitude very well (r = 0.993, Figure 6E′, right). The plots in Figure 6E,E′, suggest that amplitude estimation is homoscedastic, that is, the variability in estimation is roughly equivalent across the range of true amplitudes. From these experiments we conclude that single-subject component amplitudes can be well captured, provided that amplitude metrics combine scaling information from both TCs and SMs, and that inferences regarding amplitude will be best made when considering component features jointly.

3.4. Experiment 6: Functional Network Connectivity

Results from Experiment 6 at a model order of 25 are displayed in Figure 7. In this experiment, component amplitude and spatial characteristics are constant while the temporal similarity between S24 and S25 TCs is varied across subjects (see Section 2.7). Figure 7B–C shows examples of subject TCs and SMs for components S25 (red) and S24 (blue). Inspection of the subject SMs suggests that estimation suffers when S24 and S25 TCs are highly similar (Figure 7B–C, subject 1) as compared to when TCs are more distinct (Figure 7B–C, subject 30). This effect is seen clearly in Figure 7D, where we plot R² statistics for S25 as a function of the true FNC (temporal correlation) between S24 and S25. Degradation of SM estimation results from the difficulty and ambiguity in decomposing sources with highly similar TCs. Conversely, TCs estimation improves slightly with temporal correlation (Figure 7D, bottom, r = 0.29, p < 10⁻⁶) since there is converging evidence of the TC shape.

The accuracy of FNC estimation is addressed in Figure 7E–F. Overall, FNC values are well estimated, both for strong positive correlations between S24 and 25 that are modeled explicitly (Figure 7E, dark gray dots) and for weaker correlations between S12 and S18 (and other non-linked component pairs) that follow a null distribution (Figure 7E, light gray dots). While inter-subject differences in FNC are captured quite well, we noticed small but consistent biases in the estimated values. For example, the average true temporal correlation between S12 and S18 is −0.007 ± 0.007 (mean ± SE), but the estimated mean is 0.023 ± 0.007, a small but highly significant difference (t = −18.6, p < 10⁻⁵⁰). In exploring possible causes for this difference, we noted that the largest positive bias, FNC_est −FNC_true = 0.25, is between neighboring components S2 and S10, whereas the largest negative bias, −0.13, is between S19 and S20 which are large “lateralized” components with no overlap (see Figure 1). As shown in Figure 7F, this pattern extends to FNC estimates for all component pairs: estimation bias in temporal correlation is highly associated (r = 0.94, p < 10⁻¹⁴⁰) with the true spatial correlation between components. The link between spatial correlation and FNC bias results from an incongruence between simulated datasets and assumptions of the ICA model. ICA decomposes data based on maximal independence between sources, however the sources in our simulations are not statistically independent. As shown in Figure 7F, many sources are weakly spatially correlated. However ICA maximally decorrelates the components spatially, forcing erroneous correlations into the temporal domain. Note that there is no association between the spatial correlation of estimated components and FNC bias (r = −0.09, p = 0.13) because the spatial correlations have largely been removed in the decomposition (range of true spatial correlations: 0.33; range of estimated spatial correlations: 0.10). In summary, while estimated FNC values are quite precise and capture differences across subjects, the estimates values may be slightly biased by the extent that the true SMs are spatially correlated.

3.5. Experiment 7: Component Separation

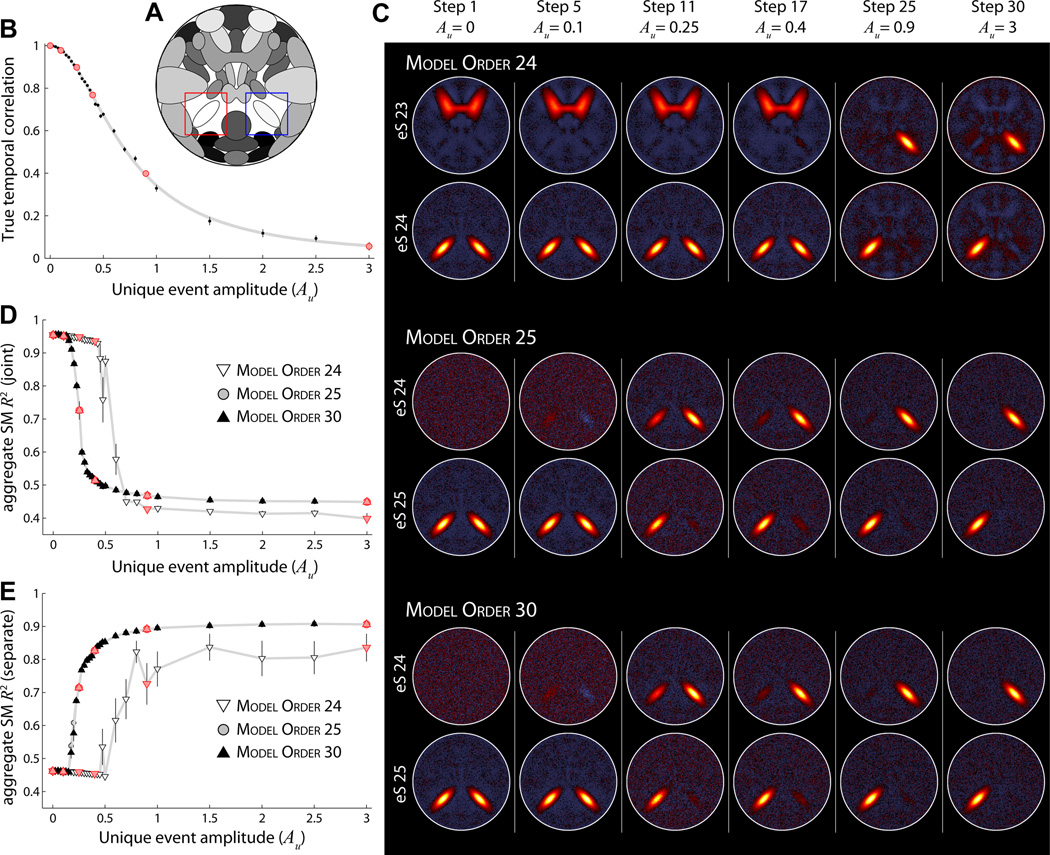
Experiment 7 focuses on source decomposition at the group level and investigates parameters that affect component separation. In a set of thirty simulations, we steadily decrease the similarity between S24 and S25 TCs by increasing the amplitude of unique events (see Section 2.8). As seen in Figure 8B, the true temporal correlation between S24 and S25 decreases from exactly 1 when A_u = 0 to just above 0 when A_u = 3. The effect of increasing A_u on estimated aggregate maps is displayed in Figure 8C. At a model order of 24 (Figure 8C, top), sources S24 and S25 are estimated as a single component for a large range of A_u values. Based on R² statistics between the aggregate SMs and a “joint” ground truth (Figure 8D, white triangles), as well as with a “separate” ground truth (Figure 8E, white triangles), sources S24 and S25 are not fully estimated as distinct components until A_u ≈ 0.8. Note that when S24 and S25 are estimated as two components, a model order of 24 is too low for the decomposition. One of the sources (S14, refer to Figure 1) is no longer estimated as its own component and instead appears very weakly as negative activation in most other components (e.g., Figure 8C, top, Step 30). Component mixing can also be seen in earlier steps (e.g., Figure 8C, top, Step 17) where erroneous activation from S24 is weakly present in the estimated S14 SM.

Figure 8. Experiment 7: effects of model order on component separation.

A) Component map, highlighting S25 (red box) and S24 (blue box). B) The true temporal correlation between S24 and S25 as A_u increases from 0 to 3 in thirty steps. C) Examples of estimated aggregate SMs at ICA model order 24 (top), 25 (middle), and 30 (bottom). SMs are shown for select values of A_u, as denoted by the red circles in panel (A). D–E) R² statistics between true and estimated aggregate SMs as a function of A_u at model order 24 (white downward triangles), model order 25 (gray circles), and model order 30 (black upward triangles). Note that R² statistics for model order 30 overlay almost perfectly with those for model order 25. In panel D, R² statistics are computed with respect to the “joint” ground truth, R²(Ŝ_c, S̄₂₄+S̄₂₅). In E, R² statistics are with respect to the “separate” ground truth, computed as the average of R²(Ŝ_c, S̄₂₄) and R²(Ŝ_c, S̄₂₅), (see Section 2.11). In B,D,E symbols indicate the mean across all M = 5 subjects and 10 repetitions; error bars show ±1 SE.

When the ICA model increases to 25 or 30 (Figure 8C, middle and bottom, respectively), sources S24 and S25 are estimated as distinct components at much lower values of A_u. In both cases, splitting begins at A_u ≈ 0.2 and the two sources are recognizable at A_u ≈ 0.4, though they continue to separate through A_u = 3 (Figure 8C–E). Thus, for a given level of similarity between S24 and S25, a lower model order estimates the sources as joined while a higher model order decomposes the sources as separate components. We note the great improvement in estimation quality of separated components when the ICA model order is sufficiently large (T₂ ≥ C; Figure 8C,E). Also, there is no decrement in estimation quality when the model order is greater than the true dimensionality (T₂ > C). In fact the R² statistics for T₂ = 25 and T₂ = 30 are nearly identical (Figure 8D–E) and we have observed the same result for model orders as high as T₂ = 50.

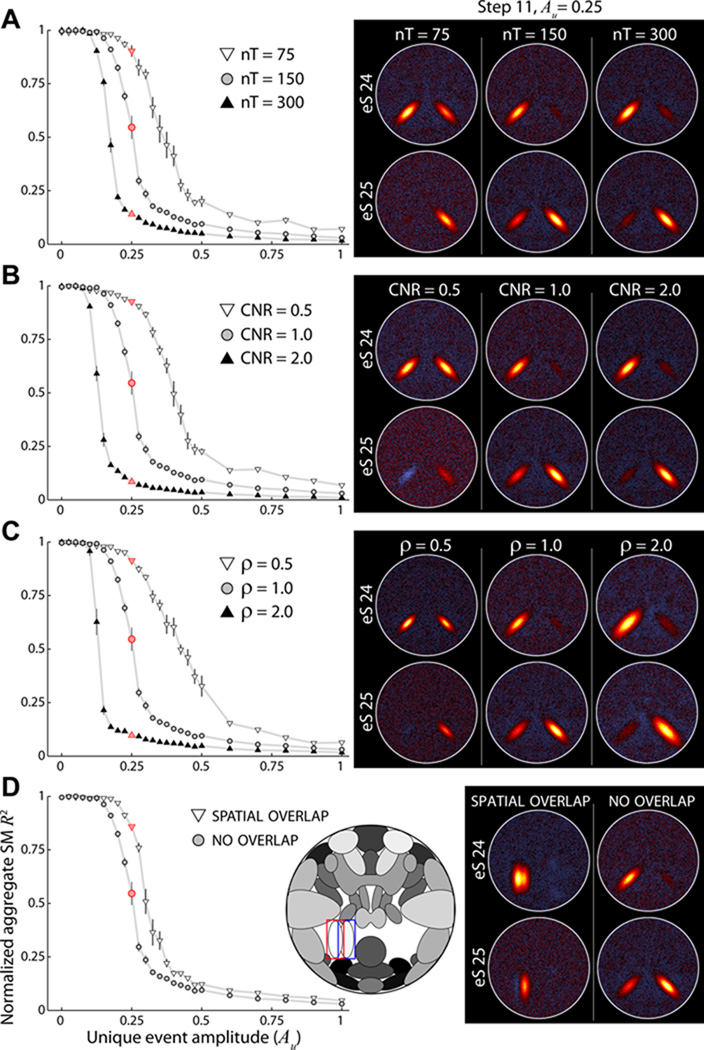
In Figure 9 we further investigate component separation by examining the impact of various dataset parameters. For each set of simulations, we vary a single simulation parameter around its base value (see Table 1) and compare the estimated aggregate SMs as a function of A_u. Here, ICA model order is fixed at T₂ = 25. All investigated parameters, including the number of time points (Figure 9A), dataset CNR (Figure 9B), spatial size of S24 and S25 (Figure 9C) and spatial overlap between S24 and S25 (Figure 9D) affect the likelihood of component separation. As one would expect, when parameters increase the amount of information or quality of information related to S24 and S25, the sources are estimated as distinct components at lower values of A_u (i.e., leftward shift of curves in Figure 9). Conversely, when fewer instances (time points) or samples (voxels related to S24 and S25) are available for the GICA decomposition, the sources must have more distinct activations to be estimated as separate components (i.e., rightward shift of curves in Figure 9). Thus, it is not just model order that affects the likelihood of component separation, but also a large number of factors that effect the quantity and quality of information pertaining to the sources. The separation or joining of sources may be related more to their sizes and spatial proximity than to the similarity between their TCs.

Figure 9. Experiment 7: effects of simulation parameters on component separation.

A–D) R² statistics with respect the “joint” ground truth for aggregate SMs as a function of A_u (left) and examples of estimated SMs at A_u = 0.25 (right), as denoted by red symbols at left. ICA model order is 25 for all decompositions. Symbols indicate the mean across subjects and repetitions; error bars show ±1 SE. In each panel, component separation is studied while varying a single simulation parameter at values below (white downward triangles) and above (black upward triangles) the base simulation level (gray circles). Parameters of interest are the number of time points (A), CNR (B), spatial size (C), and spatial overlap (D). In D, we compare high spatial overlap (see component map inset, true spatial correlation between S24 and S25 = 0.20) with no overlap in the base simulation (see Figure 7A, spatial correlation = −0.02). To facilitate visual comparison, data points are shown only over the range A_u = [0, 1] and R² statistics are normalized such that R² = 1 when A_u = 0 and R² = 0 when A_u = 3.

3.6. Experiment 8: Detecting Group Differences

In Experiment 8 we examine how analysis choices affect to the ability to detect group differences. Figure 10B displays the estimated components of interest for a single repetition of the experiment. Group differences are apparent in the mean maps for Group A (top) and Group B (bottom), which are computed by averaging over the scaled SMs (σ̂_RicŜ_ic) for subjects in each group. Specifically, S7 has greater amplitude for Group A than Group B. Component S5+S10 has a shape difference between groups: Group B has weaker anterior activation relative to the posterior node, whereas both nodes are equally active in Group A. Component S22+S23 has subtle shape difference, where the network is lateralized for Group A (left > right) but symmetric for Group B. In addition, S22+S23 has a strong amplitude difference, with Group A greater than Group B. Estimated SMs for S3 and S4 appear similar across groups, which is expected given that these sources were modeled with only temporal differences (see Section 2.9).

Figure 10C–F addresses the detection of group differences using several approaches to component scaling. Component scaling is often performed before making voxelwise comparisons between groups or subjects in an effort to maximize sensitivity to differences in component shape and minimize inuences of scale. We consider four scaling methods that may be sensitive to differences in component shape and/or amplitude. These include (1) no scaling, Ŝ_ic, which leaves subject SMs in their original units, (2) scale standardization, z-score(Ŝ_ic), which transforms SMs to have mean zero and unit standard deviation, (3) removal of scale, Ŝ_ic/m̂_ic, which divides SMs by their maximum value, and (4) joint scaling, σ̂_RicŜ_ic. Methods 2 and 3 reflect explicit attempts to remove scaling information and capture only shape. Method 4 shows the effect of incorporating all amplitude information into the SMs. Estimated group differences are compared to the differences in true component maps, S_ic, as well as the true scaled maps, g_icS_ic.

True (left) and estimated (right) group differences for S7 are displayed in Figure 10C. Scaling methods 1, 2, and 3 show no significant difference between groups at FDR corrected α = 0.05 while Method 4, which is sensitive to component amplitude, shows significant differences at regions with large activations. For the S5+S10 network (Figure 10D) all four scaling methods detect the shape difference between the groups, though with varying sensitivity. Over ten repetitions, the absolute maximum significant t-statistic is 10.6±1.2 (mean ± SD), 9.2 ± 1.0, 12.3 ± 1.4, and 10.2 ± 1.3 for methods 1 through 4, respectively. Using the non-parametric Wilcoxon signed-rank statistic (W₊) to test for differences between scaling methods, we find that peak t-statistics obtained with method (3) are significantly larger than those obtained with the other methods (W₊ ≤ 5, p < 0.05 for all comparisons). In terms of spatial extent, Method 4 identifies the most significant voxels (n_V = 540 ± 80), which is consistently larger than the number identified by method 1 (n_V = 241 ± 55), 2 (n_V = 308 ± 67), or 3 (n_V = 481 ± 67). We note that the number of voxels detected with Method 3 is also consistently greater than Method 1 or 2 (W₊ = 0, p = 0.002 for both comparisons). For component S22+S23 (Figure 10D) Methods 1–3 reflect the group difference in component shape (again with varying sensitivity), while Method 4 is dominated by the difference in component amplitude. Focusing on Methods 1–3, all scaling approaches identify roughly the same number of significant voxels (n_V = 294±59; n_V = 307±58; n_V = 293±45; W₊ ≥ 13.5, p > 0.15 for all comparisons), though method 3 again yields larger peak t-statistics (t_M = 9.2 ± 1.2; t_M = 11.2 ± 1.1; t_M = 12.7 ± 1.6; W₊ ≤ 6, p < 0.05 for both comparisons.) As a control analysis, we also examined group differences between components S3 and S4 which are modeled with temporal but no spatial differences. None of the scaling methods identified significant group differences in any repetition (e.g., Figure 10F), implying that temporal differences are not erroneously captured in the spatial domain.

Summarizing the above results, scaling methods 1, 2 and 3 capture differences in component shape and are relatively insensitive to component amplitude. Method 4 can also detect differences in shape though these may be weakened or confounded by co-occurring differences in scale (e.g., Figure 10D–E) thus it is not the preferred approach for identifying distinctions in network structure. Comparing methods 1–3, dividing SMs by their maximum intensity, Ŝ_ic/m̂_ic, provides the most sensitive approach both in terms of the maximum t-statistic (Figure 10E–F) and the number of significant voxels identified (e.g., Figure 10E). Leaving subject SMs in their original units or z-scoring tends to distribute localized differences over several regions, reducing statistical power in a voxelwise, univariate approach.

4. Discussion

By manipulating specific parameters in a controlled simulation environment, we evaluated the performance of GICA under conditions of spatial, amplitude, and temporal variability. Additionally, we determined analysis choices that can maximize sensitivity to inter-subject differences. As with any simulation study, the relevance of our findings depends on the extent to which simulations capture the properties in real data. Our data generation model (see Section 2.1) attempts to mimic the general structure of fMRI data while providing for a level of simplification and abstraction that makes in-depth investigation possible. Thus while we have certainly not replicated all the complexities inherent to multi-subject datasets, we believe we have captured a number of fundamental properties that permit conceptual extension of our findings. We discuss these results in the context of ICA studies typically performed on real multi-subject datasets.

4.1. Spatial Variability

In the current construction of GICA we temporally concatenate individual subject datasets to form an aggregate data matrix on which ICA is performed (see Appendix A). With temporal concatenation, we implicitly assume that spatial sources are consistent across subjects despite known variability in anatomical and functional localization. In Experiments 1–3, we evaluated how robust the GICA approach is to violations of spatial stationarity. Generally, experiments indicated that (1) given a sufficient degree of overlap across the group, individual subject activations can be estimated extremely well, (2) on average, estimation quality decreases as inter-subject spatial variability increases, and (3) subjects with activations most similar to the group mean will always be the best estimated. Specifically, when subject components share the same peak but have different shapes (Experiment 1), activations are well captured for all individuals at all investigated levels of spatial variability (Steps 1 to 5). This is true even when fewer subjects are used (M = 5 and M = 15), which reduces the absolute degree of overlap between subjects (data not shown for brevity). When subject activations vary in location (Experiments 2 and 3), estimation quality decreases sigmoidally as a function of the Euclidean distance from the group peak. We estimate that subject components will be adequately well captured if they are displaced from the group mean by less than the FWHM of the component, but that estimation may be poor or fail completely when displacement is more than this value (e.g., see subject 30 in Figure 4C). In Experiment 3, we found that component estimation is further deteriorated when spatial variability induces misalignment between homologous regions, that is, Source A in subject i is more spatially coincident with Source B than Source A in subject j. Though such misalignments cause considerable distortions in estimated sources at relatively mild displacements (see Figure 5C), it is worth nothing that the peak location is still correctly determined, thus such decompositions may still prove useful in situations where localization of a functional domain is the primary concern.

An important step in this work is relating our simulation-based findings to the inter-subject spatial variability observed in real data. In Table 2, we summarize the results of several recent studies on variability in functional localization. Despite large differences in methodology and regions of interest, the studies consistently suggest that on average, locations of subject activations are between 8 and 15 mm from the group peak. Given this degree of spatial variability, we can estimate how large activations should be in order to allow detection for most subjects. Assuming that displacements in activation are normally and isotropically distributed (supported by Xiong et al. (2000)), Euclidean distances from the group peak will follow a generalized χ distribution with three degrees of freedom. For an average distance of d̄ = 8 mm (SD = 3.4 mm), there is a 90% probability that subject activations will be within 12.5 mm of the group peak. If spatial variability is greater (d̄ = 15 mm, SD = 6.3mm), there is a 90% chance that individual peaks will be within 23.5 mm. Based on our findings that the distance from the group peak should be less than the FWHM of the component, activations in real data should have a FWHM of between 12.5 and 23.5 mm in order for most subjects (90%) to be adequately estimated. This corresponds to a volume of between 1 cm³ and 6.8 cm³, assuming spherical activations. Note that for real data, image smoothing is almost always used to increase the extent of activation for each subject and improve correspondence across individuals. While blurring undoubtedly increases activation overlap and enhances signal detection on the whole (White et al., 2001; Mikl et al., 2008), typical smoothing may be ineffective when activations are small and spatial variability is high. Consider that smoothing a signal of size FWHM_s with a Gaussian kernel of size FWHM_k will yield an activation with ${\text{FWHM}}_a=\sqrt{{\text{FWHM}}_s^2+{\text{FWHM}}_k^2}$. Thus if the necessary activation size FWHM_a is between 12.5 and 23.5 mm, a conventional smoothing kernel of FWHM_k = 8 mm would only slightly decrease the necessary extent of the true signal FWHM_s to between 9.6 and 22.1 mm (0.46 cm³ and 5.6 cm³).

Table 2.

Inter-subject spatial variability reported for functional areas. In all studies subject datasets were spatially normalized prior to group analysis. VOTC = ventral occipito-temporal cortex; LOTC = lateral occipito-temporal cortex; IFJ = inferior-frontal junction; BA = Brodmann area; SMA = supplementary motor area; ACC = anterior cingulate cortex; STG = superior temporal gyrus; IFG = inferior temporal gyrus.

Study	Method	n	Region	Group peak (MNI)	Average distance ± SD
Wilms et al. (2005)	fMRI	14	right V5/MT+	51; −72; 10	9.5 ± 7.6 mm
Wilms et al. (2005)	fMRI	14	left V5/MT+	−45; −76; 14	8.7 ± 3.9 mm
Duncan et al. (2009)	fMRI	45	left VOTC	−42; −50; −20	15.0 ± 5.0 mm
Duncan et al. (2009)	fMRI	45	left LOTC	−40; −58; −20	9.0 ± 3.0 mm
Derrfuss et al. (2009)	fMRI	14	left IFJ	−39; 2; 32	8.2 ± 3.8 mm
Xiong et al. (2000)	PET	20	SMA, BA 6	0; 15; 51	9.4 ± 3.4 mm
Xiong et al. (2000)	PET	20	ACC, BA 32/24	3; 26; 28	9.7 ± 4.4 mm
Xiong et al. (2000)	PET	20	left M1, BA 4/6	−44; −7; 38	13.4 ± 5.6 mm
Xiong et al. (2000)	PET	20	left STG, BA 22	−54; −35; 10	11.9 ± 5.1 mm
Xiong et al. (2000)	PET	20	left IFG, BA 44	−46; 21; 7	11.7 ± 4.7 mm
Xiong et al. (2000)	PET	20	left IFG, BA 47	−38; 32; −19	13.1 ± 5.4 mm

From the calculations above, we estimate that the current GICA framework and those with similar constructions, e.g. (Beckmann and Smith, 2004; Filippini et al., 2009), will perform extremely well on large-scale components, such as motor and visual networks which tend to have volumes greatly exceeding 20 cm³ (Allen et al., 2011), but will be less effective (i.e., may fail to estimate components for some subjects) when activations are smaller than a few cm³ in volume. Other approaches to multi-subject ICA, such as tensorial ICA (Beckmann and Smith, 2005; Guo and Pagnoni, 2008) or CanICA (canonical correlation analysis coupled with ICA) (Varoquaux et al., 2010), are also predicated on spatial consistency across subjects and will have similar limitations. Of course, conventional group analyses such as the general linear model (GLM) are subject to the same constraints. As reviewed by Brett et al. (2002), if functional areas do not align well between individuals, there will be no significant activation at the group level even if all subjects have significant activations in homologous regions.

To avoid the assumption of spatial correspondence, one could perform a multi-subject ICA by concatenating subject datasets along the spatial domain, as suggested by Svensén et al. (2002). However, because this approach assumes temporal consistency it will suffer from variability in response latency and shape, similar to group temporal ICA on event related EEG responses (Moosmann et al., 2008), and in general is not suitable for resting-state investigations. These limitations may be overcome by performing ICA in the frequency domain on amplitude spectra, e.g., (Calhoun et al., 2003; Damoiseaux et al., 2006), though it has been shown that for fMRI data, spatial concatenation is inferior to temporal concatenation in terms of source estimation (Schmithorst and Holland, 2004).

Another approach is to perform ICA on each subject separately (Calhoun et al., 2001a), allowing subjects to have unique temporal and spatial features. This method can potentially identify activations that would be poorly estimated in a group analysis and might be the preferred technique in situations where one expects a very high degree of spatial variability. However, if the ultimate goal is to make comparisons between subjects, one faces the difficulty of matching and combining components from different decompositions. Component matching may be sensitive to manual inspection (Calhoun et al., 2001a) or spatial congruence with a predefined template (Greicius et al., 2004). To avoid these problems, algorithms have recently been developed to automate the identification of common components without templates using self-organized clustering (Esposito et al., 2005) and cross-correlation (Schöpf et al., 2010). Unfortunately, these algorithms ultimately rely on spatial correlation between subject maps to determine functionally homologous networks, thus they are also vulnerable to spatial variability and may mismatch or fail to identify components that are disparate from the group mean. Furthermore, single-subject ICA may generally be limited by the low signal-to-noise ratio (SNR) in individual datasets. The increased SNR in GICA greatly facilitates the estimation of sources that would otherwise be difficult or impossible to resolve in single-subject analyses without additional constraints or prior information (Lin et al., 2010).

We can conclude that all current approaches to group analysis are somewhat limited by inter-subject spatial variability despite smoothing, particularly when areas of activation are small and the degree of variability is high. Improvements in spatial normalization methods may ameliorate correspondence, but variability in functional localization relative to anatomical landmarks (Rademacher et al., 1993; Crivello et al., 2002; Derrfuss et al., 2009) suggests that novel approaches to normalization must take function into consideration (Thirion et al., 2006). As noted by Kriegeskorte and Bandettini (2007), solutions to the challenge of inter-subject functional correspondency will become increasingly important as the spatial resolution of fMRI increases.

4.2. Model Order

As demonstrated in several experiments, the choice of model order can have a large effect on ICA decompositions. Using a model order that is too low may cause distortions in estimated sources, such as erroneous background activation (e.g., Figure 8C, top). In the case of under-fitting, we found that sources with low amplitude or those that are spatially diffuse (lower kurtosis) were the most likely to be subsumed into other components. This is consistent with observations from Abou-Elseoud et al. (2010) and our own experiments with real data that white matter components, which are weaker and larger than localized cortical sources, begin to emerge as model order increases.

Increasing model order to and beyond the true dimensionality permits sources that lack strong temporal coherence or spatial consistency across subjects to split into multiple components. Note that variability of spatial patterns across time points and across subjects are viewed equivalently from the perspective of the ICA algorithm, however have very different interpretations on the part of the researcher. As discussed below in Section 4.3, component splitting due to temporal differences may be viewed as resolving “subnetworks” or determining a finer level of functional segmentation (Kiviniemi et al., 2009; Smith et al., 2009; Abou-Elseoud et al., 2010). In contrast, component splitting due to spatial variability across subjects (see Figure 3) is highly undesirable as is precludes meaningful inter-subject and between-group comparisons. It is not known how often this type of splitting occurs in real data where the true sources are unknown. Occurrence may be quite rare since temporal differences should be more prevalent and cause splitting at lower model orders, however based on the discussion of spatial variability above (Section 4.1), researchers should be cautious when using higher model orders that yield relatively small components.

Though the estimation of dimension for fMRI data is still an open and challenging problem (Yourganov et al., 2010), we found that both analytic approaches based on information-theoretic criteria (ITC) and empirical methods provided quite reasonable results. We briefly comment on their performance and applicability to real data. For the simulated datasets used here, the Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and Minimum Description Length (MDL) all provided excellent estimates of dimensionality. Variability across subject datasets was low (range between 1 to 3) and median estimates were consistently equal to the true dimension. Application of ITC to real fMRI data has not been as successful due to structured noise that is both temporally and spatially correlated (Cordes and Nandy, 2006; Li et al., 2007). To overcome this limitation, Li et al. (2007) proposed a sub-sampling scheme to obtain a set of effectively independent data samples on which the ITC formulae may be applied. Using these modified ITC on smoothed simulated data (FWHM_k = 2.5 times the voxel width), we again found excellent correspondence between estimated and true dimensionality. Note, however, that the modified algorithms performed poorly on unsmoothed data (variable estimates were too low in the case of MDL and too high for AIC and KIC), and the original algorithms performing poorly on smoothed data (estimates were two to three times the true dimensionality), reflecting the lack of robustness of these methods under non-ideal conditions.

The variable performance of theoretic measures has led to development of empirical approaches aimed to optimize stability and reproducibility (Yourganov et al., 2010). For ICA, stability can be assessed by iterating decompositions over bootstrap resamplings or randomized initial parameters and performing a clustering analysis on the full set of components (Himberg et al., 2004). This process, implemented in the Icasso toolbox, provides a quality index (I_q) for each component cluster which ranges from 0 to 1 and reflects the difference between intra-cluster and extra-cluster similarity. Previous studies (Li et al., 2007; Ystad et al., 2010) suggest that an appropriate model order can be determined from the “knee” in the I_q curve, i.e., the point at which components transition from relatively stable (e.g., I_q > 0.8) to less reliable. Applying this method to the simulated datasets, we found that it worked perfectly for group datasets with no spatial variability, but tended to over-estimate the optimal model order when inter-subject spatial variability was pronounced. Note that we make a distinction here between desired model order and true dataset dimension. When spatial variability is present, the true dimensionality in the group dataset will be larger than that of any subject dataset, and I_q correctly reflects the stable estimation of additional (though undesirable) components (e.g., eS26 and eS27 in Steps 4–5 of Figure 3D). To mitigate over-estimation, our results suggest that subject SM kurtosis may be used in conjunction with I_q to identify components that are consistently estimated at the subject level. Using the “knee” in the I_q curve as a starting point, researchers might iteratively reduce model order until component SMs exhibit relatively high kurtosis for the majority of subjects. While this heuristic requires validation in real data, we are hopeful that the SimTB toolbox will encourage further development and improvement of dimensionality estimation methods for fMRI.

4.3. Component Separation

Experiment 7 extensively investigated the separation of sources into distinct components as a result of temporal dissimilarity. Our results replicate findings from resting-state data showing that higher model order encourages the separation of functionally distinct regions (Smith et al., 2009; Abou-Elseoud et al., 2010). Additionally, we found that a number of other factors also contribute to the likelihood of component splitting. For a given model order and level of temporal similarity between components, separation was affected by the number of time points, CNR, component size, and degree of component overlap (see Figure 9). These findings suggest that researchers should very cautiously interpret decompositions at different model orders as representing different levels of “functional hierarchy” (Smith et al., 2009). Though we can infer that a component separates because of distinct temporal activation in individual sub-components, we cannot conclude that a component remains stable because of homogeneous activation. A lack of splitting may signify a stable network, or may simply indicate that sub-networks are small with high spatial overlap. While ICA undoubtedly provides useful information about functional networks, their sub-divisions, and the relationships between networks, formal investigations of hierarchical organization and modularity may be best pursued with alternative methods, e.g., Meunier et al. (2009). As a final comment on component separation, we note that the most appropriate model order for any analysis will be a function of data quantity and quality. Because dataset dimensions (M, T, and V) and CNR will affect the ability to decompose components, we recommend that researchers estimate and optimize model order for their own datasets (using the approaches discussed in Section 4.2) rather than use a value that is frequently reported in the literature.

4.4. Feature Analysis

One major aim of the GICA framework is to facilitate between-subject comparisons. Numerous investigations have used this approach to describe alterations in intrinsic networks related to basic demographic factors, e.g., (Biswal et al., 2010; Allen et al., 2011) or neurodegenerative and psychiatric disorders, e.g., (Calhoun et al., 2008; Jafri et al., 2008; Filippini et al., 2009), with an eye towards diagnostic classification. Typical analyses compare component TC spectra, SM intensity, and FNC to make inferences regarding network activation, network shape, and the temporal similarity between networks, respectively. In Experiments 4/5 and 8, we compared the performance of various analytic approaches to detect inter-subject differences in these features. Our results, presented in Figures 6 and 10, draw attention to the scaling ambiguity inherent in ICA, that is, for a generic decomposition X = ÂŜ, a scalar α_c multiplied with one of the sources Ŝ_c can be canceled by dividing the corresponding column of  by the same scalar:

$$\mathbf{X}=\widehat{\mathbf{A}}\widehat{\mathbf{S}}={\displaystyle \sum _{c=1}^C}(\frac{1}{{\alpha }_c}{\widehat{\mathbf{A}}}_c)({\alpha }_c{\widehat{\mathbf{S}}}_c).$$

Though arbitrary scaling has long been discussed in the context of ICA (Hyvärinen et al., 2001), the implications for GICA have not been appreciated. In the presence of spatial variability, even slight differences in SMs will cause scaling information to be captured differently across subjects. Subjects with SMs closest to the mean will have larger amplitude in component maps (Ŝ_i), whereas subjects with more disparate SMs will have lower intensities in component maps and larger amplitude in component TCs (R̂_i). While inconsistencies in scaling could hinder comparisons across subjects, we found that the true scaling information can be easily recovered by considering a joint amplitude metric (see Figure 6E,E’). Thus, we propose to consider subject components as a product of three features, ${\widehat{\mathbf{R}}}_i^{\mathrm{N}}{\widehat{\mathbf{g}}}_i{\widehat{\mathbf{S}}}_i^{\mathrm{N}}$, where ĝ_i is the vector of estimated component amplitudes, and ${\widehat{\mathbf{R}}}_i^{\mathrm{N}}\text{ and }{\widehat{\mathbf{S}}}_i^{\mathrm{N}}$ are the amplitude normalized TCs and SMs, respectively. In this study, we have constructed a joint metric using the TC standard deviation, which is a well-characterized estimator of the spread or dispersion based on all the time points, and the SM maximum value, which indicates the amplitude of the voxel most strongly associated with the corresponding TC and more importantly is not be sensitive to differences in component shape. While other constructions are certainly possible, we found that this joint estimator performed extremely well in multiple scenarios and thus suggest ĝ_ic = σ̂_Ric × m̂_ic, ${\widehat{\mathbf{R}}}_{\mathit{\text{ic}}}^{\mathrm{N}}={\widehat{\mathbf{R}}}_{\mathit{\text{ic}}}/{\widehat{\sigma }}_{\mathbf{R}\mathit{\text{ic}}},\text{ and }{\widehat{\mathbf{S}}}_{\mathit{\text{ic}}}^{\mathrm{N}}={\widehat{\mathbf{S}}}_{\mathit{\text{ic}}}/{\widehat{m}}_{\mathit{\text{ic}}}$.

In comparing component features, researchers must determine where and how to consider amplitude information. For example, if the question pertains to the level of network activation, one might compare amplitude, ĝ_ic, as its own feature (as in Experiments 4 and 5), or might combine amplitude with TCs, ${\widehat{\mathbf{R}}}_{\mathit{\text{ic}}}^{\mathrm{N}}{\widehat{g}}_{\mathit{\text{ic}}}$, and use Fourier analysis to evaluate power as a function of frequency. If the question relates to differences in network shape, one might perform analysis on amplitude normalized SMs, ${\widehat{\mathbf{S}}}_{\mathit{\text{ic}}}^{\mathrm{N}}$. As addressed in Experiment 8, leaving SMs in their original units or z-scoring components tends to distribute localized differences and reduce statistical power in a voxelwise, univariate approach. Utilizing ${\widehat{\mathbf{S}}}_{\mathit{\text{ic}}}^{\mathrm{N}}={\widehat{\mathbf{S}}}_{\mathit{\text{ic}}}/{\widehat{m}}_{\mathit{\text{ic}}}$ (or a similar construction) may maximize sensitivity to regional differences. Alternatively, researchers might also be interested in the scaled SMs, ${\widehat{g}}_{\mathit{\text{ic}}}{\widehat{\mathbf{S}}}_{\mathit{\text{ic}}}^{\mathrm{N}}$, which provides information regarding network activity and shape. As detailed in Appendix B, this is exactly the quantity that is estimated in dual regression when TCs are variance normalized prior to the second regression, see e.g., Zuo et al. (2010). While scaled SMs may be the most relevant feature in some cases, we note that considering shape and amplitude together can obfuscate or confound differences in these domains (see Figure 10E) and we recommend conducting analysis of each feature separately.

In contrast to TCs and SMs, estimates of FNC (which are based on the similarity between component TCs) are unaffected by amplitude and will be identical whether considering R̂_i and ${\widehat{\mathbf{R}}}_i^{\mathrm{N}}$. We note, however, that FNC estimates may be influenced by the interplay between temporal and spatial features. For example, the TCs of spatially correlated components are estimated to be more similar than the true TCs due to the optimization of independence (and hence de-correlation) in the spatial domain (Figure 7F). As a second example, increased temporal similarity between components can deteriorate estimation of corresponding SMs due to the ambiguity in decomposition (see Figure 7D). It is possible that such interplay could “contaminate” temporal and spatial differences, though our results from Experiment 8 provide an example where differences in FNC are not erroneously captured in the spatial domain (Figure 10F). We conclude that estimates of FNC are generally quite precise and accurately reflect inter-subject differences (e.g., Figure 7E), though researchers should be aware of possible biases associated with the assumptions of spatial independence.

Appendix A. Back-projection and Dual Regression

Let Y_i be the T × V data matrix for subject i, where T time points over V voxels are simulated for M subjects. The whitened subject dataset is ${\mathbf{F}}_i^{-}{\mathbf{Y}}_i$, where ${\mathbf{F}}_i^{-}$ is the T₁ × T eigenvector matrix and T₁ is the number of principal components retained for each subject. Note that ${\mathbf{F}}_i^{-}$ is standardized, meaning that the eigenvectors are scaled by the inverse square root of their eigenvalues. Whitened subject datasets are concatenated to form the MT₁ × V aggregate data matrix:

$${\mathbf{Y}}^{*}=\left[\begin{array}{c}\hfill {\mathbf{F}}_1^{-}{\mathbf{Y}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{F}}_M^{-}{\mathbf{Y}}_M\hfill \end{array}\right].$$ (A.1)

The PCA-reduced aggregate data is

$$\mathbf{X}\equiv {\mathbf{G}}^{-}{\mathbf{Y}}^{*},$$ (A.2)

where G⁻ is the T₂ × MT₁ standardized reducing matrix. Following noise-free ICA, we write

$$\mathbf{X}=\widehat{\mathbf{A}}\widehat{\mathbf{S}}$$ (A.3)

and estimate  and Ŝ, the T₂ × T₂ mixing matrix and the T₂ × V aggregate SMs, respectively.

To estimate subject SMs and TCs, we follow Calhoun et al. (2001b, 2002) and back-project the aggregate mixing matrix  to the subject space based on the PCA reducing matrices. Subject-specific TCs are defined as R̂_i ≡ F_iG_iÂ, and subject-specific SMs are Ŝ_i ≡ Â⁻¹(F_iG_i)⁻Y_i, where G_i is the partition of G corresponding to subject i.

We note that the recently developed dual regression method (Calhoun et al., 2004; Filippini et al., 2009), which defines subject TCs and SMs by least-squares regression onto the original data, is closely related to the back-projection formulations above. In dual regression, subject TCs and SMs are estimated as Ṙ_i ≡ Y_iŜ⁻ and ${\dot{\mathbf{S}}}_i\equiv {\dot{\mathbf{R}}}_i^{-}{\mathbf{Y}}_i$, respectively. The correspondence between back-projection and dual regression can be seen by expressing Ṙ_i in terms of the subject and aggregate PCA matrices. For subject i, we first multiply R̂_i by the subject reducing matrix to obtain:

$${\mathbf{F}}_i^{-}{\dot{\mathbf{R}}}_i={\mathbf{F}}_i^{-}{\mathbf{Y}}_i{\widehat{\mathbf{S}}}^{-}.$$ (A.4)

Concatenating the subject matrices we have

$$\left[\begin{array}{c}\hfill {\mathbf{F}}_1^{-}{\dot{\mathbf{R}}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{F}}_M^{-}{\dot{\mathbf{R}}}_M\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathbf{F}}_1^{-}{\mathbf{Y}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{F}}_M^{-}{\mathbf{Y}}_M\hfill \end{array}\right]{\widehat{\mathbf{S}}}^{-}.$$ (A.5)

Note from equation A.1 that the right-hand side of A.5 becomes Y^*Ŝ⁻. Substituting in equation A.3 we can write Y^*(Â⁻¹X)⁻ which simplifies to Y^*(X)⁻Â because X^Τ is orthogonal. Using the definition of X from equation A.2, we write Y^*(G⁻Y^*)⁻Â. Because both Y^* and G⁻ are orthogonal over rows, the pseudoinverse simplifies to Y^*(Y^*)⁻GÂ = GÂ. Substituting this expression into equation A.5, we have

$$\left[\begin{array}{c}\hfill {\mathbf{F}}_1^{-}{\dot{\mathbf{R}}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{F}}_M^{-}{\dot{\mathbf{R}}}_M\hfill \end{array}\right]=\mathbf{G}\widehat{\mathbf{A}}=\left[\begin{array}{c}\hfill {\mathbf{G}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{G}}_M\hfill \end{array}\right]\widehat{\mathbf{A}}.$$ (A.6)

The expression for subject i is then ${\mathbf{F}}_i^{-}{\dot{\mathbf{R}}}_i={\mathbf{G}}_i\widehat{\mathbf{A}}$. Note that if ${\mathbf{F}}_i^{-}$ is full rank, we can pre-multiply by F_i and arrive at Ṙ_i = F_iG_i = Ṙ_i. Thus, when the subject data is not reduced, TCs estimated with dual regression and back-projection are identical. Because Ŝ_i can be expressed as ${\widehat{\mathbf{S}}}_i={\widehat{\mathbf{R}}}_i^{-}{\mathbf{Y}}_i$, subject SMs will also be identical under this condition. When ${\mathbf{F}}_i^{-}$ reduces the information retained from subject datasets, R̂_i and Ṙ_i will not be identical and their similarity will decrease as ${\mathbf{F}}_i{\mathbf{F}}_i^{-}$ diverges from the identity matrix.

For the results presented in the current study, ${\mathbf{F}}_i^{-}$ has full rank (rotates and whitens subject data but does not reduce information), therefore differences between back-projection and dual regression are within computational precision.

Appendix B. Joint Scaling in Dual Regression

In dual regression, subject TCs and SMs are defined as Ṙ_i ≡ Y_iŜ⁻ and ${\dot{\mathbf{S}}}_i\equiv {\dot{\mathbf{R}}}_i^{-}{\mathbf{Y}}_i$, respectively. In practice, sometimes SMs are estimated in the second regression step using TCs that have been normalized to have unit variance (see e.g., Zuo et al. (2010)). Let ${\ddot{\mathbf{R}}}_i={\dot{\mathbf{R}}}_i{\mathbf{D}}_i^{-1}$ be the matrix of variance normalized TCs, where D_i is the T₂×T₂ diagonal matrix whose entries are the standard deviations of each component TC. The modified SMs are then

$${\ddot{\mathbf{S}}}_i\equiv {\ddot{\mathbf{R}}}_i^{-}{\mathbf{Y}}_i={({\dot{\mathbf{R}}}_i{\mathbf{D}}_i^{-1})}^{-}{\mathbf{Y}}_i={\mathbf{D}}_i{\dot{\mathbf{R}}}_i^{-}{\mathbf{Y}}_i={\mathbf{D}}_i{\dot{\mathbf{S}}}_i.$$ (B.1)

Thus, variance normalizing TCs before performing the second regression is equivalent to multiplying the original SMs by the standard deviations of the TCs.