Paradoxical psychometric functions (“swan functions”) are explained by dilution masking in four stimulus dimensions

Abstract

The visual system dissects the retinal image into millions of local analyses along numerous visual dimensions. However, our perceptions of the world are not fragmentary, so further processes must be involved in stitching it all back together. Simply summing up the responses would not work because this would convey an increase in image contrast with an increase in the number of mechanisms stimulated. Here, we consider a generic model of signal combination and counter-suppression designed to address this problem. The model is derived and tested for simple stimulus pairings (e.g. A + B), but is readily extended over multiple analysers. The model can account for nonlinear contrast transduction, dilution masking, and signal combination at threshold and above. It also predicts nonmonotonic psychometric functions where sensitivity to signal A in the presence of pedestal B first declines with increasing signal strength (paradoxically dropping below 50% correct in two-interval forced choice), but then rises back up again, producing a contour that follows the wings and neck of a swan. We looked for and found these “swan” functions in four different stimulus dimensions (ocularity, space, orientation, and time), providing some support for our proposal.

1. Introduction

1.1. The generic problem for spatial vision

During the 1970s and 1980s, experiments with luminance-modulated stimuli revealed much about early visual analysis (Graham, 1989, 2011). The model that emerged is one in which millions of visual analysers decompose the retinal image into local measures along multiple image dimensions including space, orientation, spatial frequency, colour, and motion. The purpose of this is obvious. The visual objects that we are interested in contain smaller parts whose details contribute to the identification of the object. Therefore, some form of image decomposition is necessary to analyse the parts and this is usually attributed to population coding within each of the feature dimensions.

However, visual objects themselves do not appear fragmented, so something else is needed to link the parts back together to build representations of higher order structures. Much of what we now know about grouping and linking stems from early 20th-century observations by the Gestalt psychologists, albeit now usually set in a contemporary psychophysical context (e.g. Dickinson & Badcock, 2007; Field, Hayes, & Hess, 1993; Jones, Anderson, & Murphy, 2003; Levi & Klein, 2000; Morgan & Hotopf, 1989; Motoyoshi & Nishida, 2004; Moulden, 1994; Parkes, Lund, Angelucci, Solomon, & Morgan, 2001; Sassi, Vancleef, Machilsen, Panis, & Wagemans, 2010; Wilson & Wilkinson, 1998; see Graham, 1989, 2011 for reviews). However, none of the above studies on feature integration considered the implications in terms of luminance contrast (hereafter, simply contrast). This is curious, because contrast is the fundamental coding dimension of the primary visual cortex (V1). Perhaps the reluctance to use image or target contrast as a dependent variable stems from the finding that contrast increment detection does not improve when the size (area) of a grating patch is increased (Legge & Foley, 1980). This has been taken to imply that contrast integration (over area) does not take place above threshold. For a given pattern or object, the preliminary analysers (basic mechanisms of V1) presumably contribute to feature integration in some manner, but a simple summing operation will not suffice, because this would confound object contrast with the number of analysers involved (Hess, Dakin, & Field, 1998).

This actually posed little concern for much of the work on spatial vision in the late 20th century, because most authors were content to end their story at the level of the preliminary analysers in V1 (though see Olzak & Thomas, 1999, for an early example of a body of work that progressed this). However, more recent work (Foley, Varadharajan, Koh, & Farias, 2007; Manahilov, Simpson, & McCulloch, 2001; Meese, 2010; Meese & Summers, 2009; Watson & Ahumada, 2005) suggests that the outputs of these mechanisms converge in a way capable of achieving contrast integration, and several factors have been identified (Meese, 2010; Meese & Summers, 2007) that explain why this process was often overlooked in the earlier textbook studies. Furthermore, the long-standing view that contrast integration (over area) is abolished above detection threshold (Legge & Foley, 1980) is now quashed (Meese & Baker, 2011; Meese & Summers, 2007) and the principle of integration of the contrast response across multiple mechanisms has been firmly established.

In this paper, we present a general scheme that is able to achieve contrast integration over any dimension of interest for which there are multiple analysers. The scheme involves a simple arrangement of summation and counter-suppression such that at threshold, the contrast sensitivity of the system benefits by extending the stimulus along the relevant dimension, whereas above threshold, the contrast response is clamped by the gain control (Meese & Baker, 2011; Meese & Summers, 2007).

1.2. A generic model of contrast integration: Signal combination and counter-suppression

Our generic model is simply a development of standard models of contrast transduction (e.g. Legge & Foley, 1980) and contrast gain control (Foley, 1994). It shares the basic design of previous models that were developed for specific stimulus dimensions, such as eye (Meese, Georgeson, & Baker, 2006), area (Meese & Summers, 2007), or both (Meese & Baker, 2011). Here, the model has been stripped back to the basic operations of summation and counter-suppression. It lacks the detail to provide quantitative fits to more complex data sets from previous studies, but it serves to illustrate the general points of interest.

We use the term “target” to refer to the signal increment that the observer is trying to detect and the term “pedestal” to refer to the uninformative contrast against which this judgement is being made. The term “mask” is sometimes preferred over “pedestal” particularly when the mask and target differ along one or more stimulus dimensions. However, our model involves summation across all of the relevant target and mask components and so contrast increments of the target are always detected against the background activity of the mask in the output mechanism (resp), regardless of any stimulus differences between the target and mask. Therefore, we find the term “pedestal” to be appropriate here, but tend to use the more general term “mask” with reference to related work by others.

To generalize across stimulus dimensions, we refer to pairs of stimulus component contrasts as A and B, expressed as percent contrast. In this study, these can derive from the left and right eyes, or adjacent locations in space, time, or orientation. We assume that different elementary mechanisms are responsive to A and B, and that the outputs of those mechanisms are combined to give a single response described by the equation

(1)

where Z is a constant and the exponents p and q were set to typical values of 2.4 and 2, respectively (Legge & Foley, 1980). The model assumes late additive noise, added to the resp, and assumes that in a two-interval discrimination task the observer chooses the interval with the higher resp. The slope of the dipper function handle for contrast discrimination is set by the difference between p and q and the position of the transition between the dipper region and handle is influenced by Z. For the simulations here, we set Z = 2, but this value was not critical. Our analysis of the slope of the psychometric function is affected little if at all by the details of any of these parameters (within a normative range).

For contrast discrimination with a single component (e.g. where the target and pedestal each contribute to the contrast in the A mechanism and B = 0), the model reduces to the familiar Legge and Foley (1980) equation, which leads to dipper-shaped functions relating discrimination threshold to pedestal contrast (blue curve in Figure 1a). Activating both component mechanisms equally (so that A and B each contain target plus pedestal contrasts) produces a similar dipper function, which is shifted downwards and to the left (red curve in Figure 1a). This reveals a summation effect (the model is more sensitive to A + B than to A alone) at weak pedestal contrasts, but the dipper handles converge at higher contrasts where the denominator terms dominate the saturation constant, Z. This behaviour is found empirically in both the binocular (Legge, 1984; Maehara & Goryo, 2005; Meese et al., 2006) and spatial (Legge & Foley, 1980; Meese, Hess, & Williams, 2005; Meese & Summers, 2007) dimensions.

Figure 1.

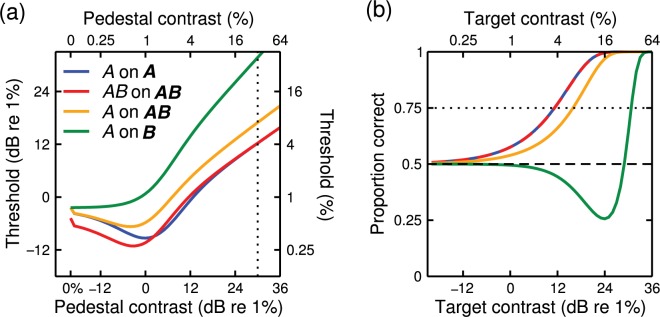
Predictions of the generic contrast integration model. (a) Dipper functions in four arrangements of pedestal and target. Components are denoted as A and B, to represent separate locations along the dimension of interest (space, time, eye, or orientation). Pedestal components are denoted in bold and target components in plain font. (b) Psychometric functions at a high (32%) pedestal contrast for the same four arrangements. The dotted line in panel (a) indicates the pedestal contrast for which psychometric functions are shown in panel (b), and the dotted line in panel (b) indicates the threshold at 75% correct. The target contrast levels at which the dotted lines intersect with the model predictions are therefore equivalent across the two panels. Matlab code to produce this figure is provided in Appendix B.

We now consider more complex stimulus arrangements. For convenience, when referring to target and pedestal components, we set pedestal components in bold (AB) and leave target components in plain font (AB). When the pedestal consists of both components, but the target increment is in only one (A on AB), the dipper function (orange curve in Figure 1a) is a vertical translation of the AB on AB condition (red curve). This comparison across conditions reveals the effects of increasing the number of targets (from A to AB) whilst keeping the suppressive gain control from the pedestals constant (AB). The result is consistent with our previous work that has found evidence for strong summation (greater than probability summation) at all pedestal contrasts in both the binocular (Meese et al., 2006) and spatial (Meese & Summers, 2007) dimensions, just as the model predicts. However, the reasons for such strong summation in the model are not as obvious as they might seem. The modelling by Meese and Summers (2007) showed that the benefit in the AB on AB condition derives from the effects of both signal summation (A + B), and the detrimental effects of dilution masking in the A on AB condition against which it is compared. Dilution masking is a specific form of masking (described in detail in the following section) that involves the inappropriate combination of the B pedestal component with the A signal on the numerator of Equation (1).

Another configuration of interest is when target and pedestal are different components (A on B). For binocular vision, this is dichoptic pedestal masking (pedestal in one eye, target in the other), where the threshold elevation is so strong that the target contrast must equal or exceed that of the pedestal in order to be detected (Baker & Meese, 2007; Legge, 1979; Meese et al. 2006). This is precisely the behaviour predicted by Equation (1) and shown by the green curve in Figure 1(a). Note that the masking function is steeper and more severe than in the other three conditions. While investigating the model predictions for the A on B condition, we observed an unusual form to the psychometric function at high pedestal contrasts. We describe this observation in the following section.

1.3. Dilution masking, swan functions, and negative d′

In a typical contrast discrimination experiment, the pedestal is presented in each two-interval forced choice (2IFC) task and drives the overall response of the generic model equation (Equation (1)) equally across them. Adding a target to the pedestal increases the model response in the target interval. Because performance (d′) is determined by the difference in responses between intervals scaled by the observer's internal noise, performance improves as target contrast increases, and (the so-called) threshold is reached at some criterion level of performance (e.g. 75% correct). In the generic contrast integration model, this is precisely what happens for the A on A and AB on AB conditions, and psychometric functions are the familiar monotonic sigmoidal functions of target contrast, as shown by the red and blue curves in Figure 1(b).

In the A on B condition, however, the combined effects (in Equation (1)) of mandatory summation and suppression between the A and B mechanisms produce very different behaviour from above. The existence of cross-mechanism suppressive effects becomes more readily apparent if Equation (1) is rewritten as follows:

(2)

For sufficiently high pedestal contrasts, the model response to the target (A) is very weak because of strong suppression from the pedestal (B). This means that the target contrast must be high for it to be detected. However, as the target contrast increases, it produces a substantial suppressive effect of its own and this diminishes the contribution that the pedestal (B) makes to the overall response of the model (note that the target (A) and pedestal (B) are summed before the decision stage). It turns out that at intermediate target contrasts (a little below detection threshold), the detrimental (suppressive) effect of the target exceeds its positive contribution to the overall model response. This means that the model output is lower in the target interval than in the null interval. (This is a bit like turning up the dimmer switch for your lighting and finding that the light level decreases!) An observer selecting the interval with the greater response (e.g. the higher perceived contrast) will choose the null interval and be incorrect. This means that performance will drop below 50% correct in a 2IFC task, an example of negative d-prime.¹ At higher target contrasts, the nonlinear properties of the model mean that d-prime becomes positive, and the rising part of the psychometric function is very steep, with small increases in target contrast producing substantial improvements in performance.

The green curve in Figure 1(b) illustrates this unusual behaviour, which leads to a nonmonotonic psychometric function that we refer to as a “swan function” (because it resembles the wings and neck of a swan) or sometimes a paradoxical psychometric function (because over the initial part of the function, an increase in signal strength produces a drop in performance). More generally, we refer to the masking process that underlies the swan functions (for A on B) as dilution masking. The terminology derives from the fact that the potency of the target is diluted by its inappropriate combination with a pedestal that has been suppressed by the target. Meese and Summers (2007) identified this form of masking in their work on the A on AB configuration. Dilution masking is distinct from conventional within-channel masking (Legge & Foley, 1980)—where the pedestal and target are unavoidably combined within the same initial mechanism—and cross-channel masking (Foley, 1994)—where the mask suppresses the signal but is not combined with it.

In summary, the three hallmarks of A on B masking in our generic model are as follows:

• High thresholds

• Steep psychometric functions (the “neck” of the swan function)

• A region of negative d-prime in the psychometric function (the “wings” of the swan function).

Recently, Foley (2011) reported a series of experiments that produced unusual, nonmonotonic psychometric functions that resemble the swan functions predicted by our model. In one such experiment, a brief (100 ms) target was presented (temporally) in-between two high contrast maskers, each of 1000-ms duration. The proportion of correctly identified targets decreased below chance performance (i.e. <50% correct for 2IFC, implying negative d-prime) at medium target contrasts, and then increased above chance at higher contrasts, producing a highly unusual “trough” region in the psychometric function (see Foley, 2011, Figures 5 and 8). Encouraged by this finding, and our earlier observations of this phenomenon in the ocular dimension (Meese et al., 2005), we tested the predictions of the generic contrast integration model experimentally across four stimulus dimensions (space, time, eye, and orientation) in order to examine the generality of the proposed model. To anticipate our results, we found evidence for all three of the properties above in each stimulus dimension (see Baker, Meese, & Georgeson, 2010, for a preliminary report). This provides good support for the generic model of contrast integration and suggests a broader context in which to interpret Foley's (2011) findings.

2. Methods

2.1. Apparatus and stimuli

All experiments used a ViSaGe stimulus generator (Cambridge Research Systems, Ltd., Kent, UK) controlled by a PC. Stimuli were presented on a Nokia Multigraph 445X monitor, except for when eye of presentation was manipulated. These conditions used a Clinton Monoray monitor and ferro-electric shutter goggles (CRS, FE-01) that presented display frames alternately to the left and right eyes. Both monitors ran at 120 Hz, so no flicker was seen even with frame alternation. The mean luminance of the Nokia monitor was 60 cd/m². Viewed through the goggles (which attenuate luminance by a factor of eight), the Clinton monitor had a mean luminance of 10 cd/m². There were four experiments, investigating different dimensions (space, time, eye, and orientation), for which stimuli are now described. We use decibel (dB) units when presenting log contrast, defined as C_dB = 20log₁₀ (C_%), where C_% = 100(L_max − L_min)/(L_max + L_min) is Michelson contrast in percent.

In each of the following four dimensions, we devised A and B component stimuli, where contrast sensitivity was (approximately) the same for A and B and where the A + B compound was continuous in the dimension of interest. We reasoned that this would encourage grouping by the Gestalt law of good continuation in the relevant dimension.

2.1.1. Space

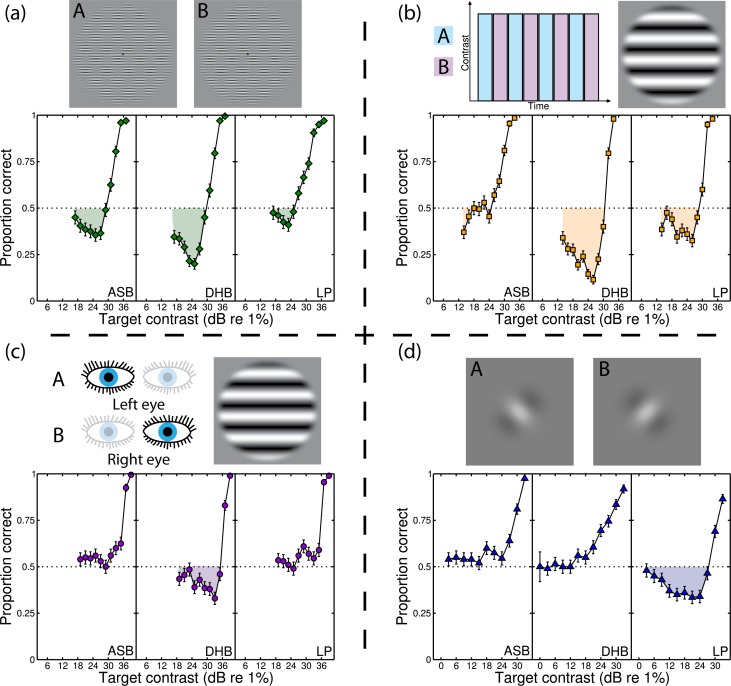
We used “Swiss cheese” stimuli, first introduced by Meese and Summers (2007). These consist of a carrier grating (horizontal, 4 c/deg, 10° wide), the contrast of which was modulated over space by a raised plaid envelope to produce “check” regions of high and low contrast (A or B components). The modulator spatial frequency was such that there were four carrier cycles per modulator check, and the entire stimulus was windowed by a circular raised cosine envelope (8° plateau, 1° cosine ramp around the boundary). The A and B components were derived by using positive and negative phases of the plaid modulator (see examples in Figure 3a). Summing A and B recreates the original unmodulated carrier grating. The stimulus duration was 200 ms.

Figure 3.

Psychometric functions for the A on B condition in each of four stimulus dimensions. Functions were sampled at 200 trials per target contrast level. There is evidence for nonmonotonicity and negative d-prime within each dimension. Above each plot are high contrast examples of the stimuli and icons indicating the arrangement of the A and B stimuli. The dimensions were (a) space, (b) time, (c) eye, and (d) orientation. Error bars are binomial errors.

2.1.2. Time

Spatially, the AB target was a 1 c/deg horizontal sine-wave grating windowed by a raised cosine envelope (3° plateau, 1° cosine ramp around the boundary). An example is given in Figure 3(b). The total stimulus duration was 266.67 ms, with A and B component contrasts modulated by a 15 Hz raised square wave, which produced pulses of 33.33-ms duration (see the inset in Figure 3b). Odd-spaced pulses formed the A stimulus, and even-spaced pulses the B stimulus. Viewed in isolation, each component had on–off flicker, but their sum was a temporally unmodulated grating (i.e. it is the temporal equivalent of the spatial modulation described above).

2.1.3. Eye

The binocular AB eye stimulus was spatially identical to that used in the time condition, but was presented continuously for 200 ms. Monocular components A and B were shown to the left and right eyes, respectively. This was achieved using the shutter goggles, which have negligible crosstalk between the eyes.

2.1.4. Orientation

Our AB stimulus was an isotropic (circularly symmetric) difference of Gaussians (DoG) stimulus with a centre frequency close to 1 c/deg. It was constructed to have zero mean luminance by using standard deviations for the positive and negative Gaussian functions of 0.21° and 0.31°, respectively, and amplitudes of unity and 0.44, respectively. To generate the A and B components, the DoG was orientation filtered in the Fourier domain as follows. The filter was a raised sine function of polar angle in Fourier space with a period of 180° of orientation. Positive and negative phases of angular modulation produced component stimuli with orthogonal orientations (±45°), which resembled Gabor wavelets (see Figure 3d). Summing the A and B components reconstructed the original isotropic DoG. (See the companion paper by Meese & Baker, 2013, for supporting diagram.) Stimulus duration was 200 ms. We abandoned initial attempts to devise an analogous stimulus in the spatial frequency dimension because the complicating factor of the contrast sensitivity function made it difficult to devise A and B stimuli for which sensitivity was similar.

2.2. Procedure

The monitor was viewed from a chin-and-head rest, at a distance of 114 cm (Nokia) or 57 cm (Clinton). For the “eye” experiment, the goggles were mounted in the head rest. We used a 2IFC paradigm (ISI of 400 ms) and the method of constant stimuli for all experiments. Psychometric functions were measured at 11 target contrast levels, determined by pilot experiments, for a single pedestal contrast level (36 dB for the “eye” experiment and 30 dB for the rest). Observers indicated which interval appeared to have the greater contrast using a two-button mouse (for cross-reference, this is equivalent to Foley's (2011) “normal” response rule). There was no feedback to indicate response correctness, as this would mislead observers if our hypothesis about a negative d-prime region of the psychometric function were correct.

For each of the four experiments, there were four combinations of the target and pedestal, A on A, AB on AB, A on AB, and A on B. Although this nomenclature always describes component “A” as the target, in practice half of the trials were carried out with component “B” as the target, and the results were pooled across the two arrangements. Trials from all four pedestal/target combinations were interleaved. This was important, particularly in the “time” experiment, where we were concerned that observers might have used flicker amplitude instead of luminance contrast as a cue to the target interval in the A on B condition (the target interval would always have the lower flicker amplitude). This cue was eliminated by interleaving the other three conditions, in particular the A on AB condition, for which the target interval had the greater flicker amplitude.

Sessions for each experiment were carried out in 10 blocks, each consisting of 20 trials per contrast level at each condition. This produced psychometric functions with 200 trials per level, and a total of 2,200 trials per function. We estimated the threshold (75% correct) and slope (equivalent Weibull β) of each function using Probit analysis (Finney, 1971).

2.3. Observers

Three psychophysically experienced observers completed all conditions. One was the first author (DHB), the other two (ASB and LP) were volunteers who were unaware of the purpose of the experiments. Observers had normal stereopsis and wore appropriate optical correction if necessary.

2.4. Model simulations

To illustrate model behaviour for dipper functions (e.g. in Figures 1a and A2), we calculated thresholds by finding target contrasts that satisfied the following equation:

(3)

where the “resp” terms are model outputs (e.g. from Equation (1) or the alternative models considered in Appendix A) in the null and target intervals, d is the performance level at “threshold” (for 75% correct, d = 0.95) and σ is a deterministic representation of the observer's internal noise. For the simulations here σ = 0.2. This value was not critical and merely influences overall sensitivity and the location of the transition between the dipper region and the dipper handle.

Model psychometric functions (e.g. in Figures 1b and A1) were produced by evaluating Equation (3) for a range of target contrasts and converting the resulting d′ values to proportion correct according to

(4)

where Φ denotes the normal integral and p is proportion correct for a 2IFC task (see MacMillan & Creelman, 2005). We fitted the simulated psychometric functions using Probit analysis to produce threshold and slope estimates to compare with our empirical results (e.g. grey crosses in Figure 2). Note that the negative d in the swan functions (see Section 1) derive from the fact that resp_null is larger than resp_target (Equation (3)) in that region. In turn, this causes Equation (4) to drop below 50% correct.

Figure 2.

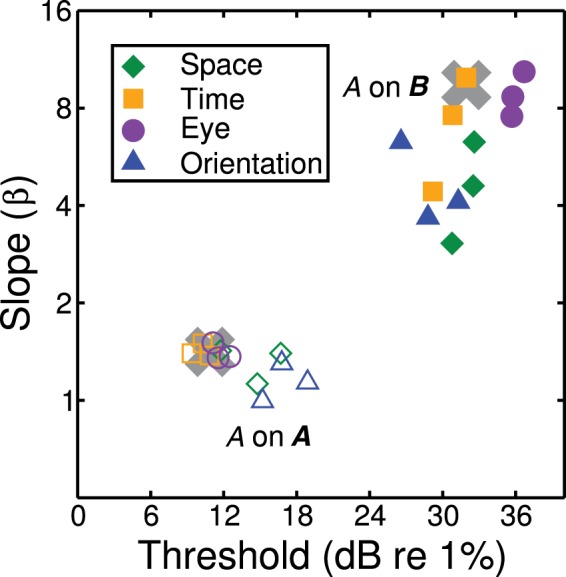
Thresholds and slopes for two arrangements of target and pedestal. Open symbols are for the A on A condition, and filled symbols for the A on B condition. Colour and symbol denote the stimulus type, with one data point per observer for each condition. Slopes are equivalent Weibull β values, estimated from the fitted cumulative log-Gaussian psychometric function using the approximation β = 10.3/σ, where σ is the Gaussian standard deviation in dB. Note that the fitting procedure ignores values below the guess rate (50% correct) so the slope of the positive d-prime portion of the function is not affected by negative d-prime regions. The grey crosses give the threshold and slope predictions for the generic contrast integration model.

3. Results

We first compare the threshold and slope values between the A on A and A on B conditions. In these two conditions, the pedestal contrast is the same: all that differs is the arrangement of pedestal and target across the dimension of interest. The results are shown in Figure 2 and are very different across the two conditions. The A on A condition (open symbols) is characterized by moderate thresholds (<20 dB) and shallow psychometric slopes (1 < β < 2) consistent with previous work on contrast discrimination (e.g. Bird, Henning, & Wichmann, 2002; Meese et al., 2006), and similar to the A on AB and AB on AB conditions (not shown). The A on B condition (filled symbols in Figure 2) produced high thresholds (∼30 dB) and steep psychometric functions (β > 3).

Both of these results are consistent with the predictions of the generic model of contrast integration (grey crosses). In the model, slopes are shallow for A on A because the effective contrast transducer at high pedestal contrasts is equivalent to a power function with exponent p − q = 0.4. For small contrast increments (around the size of a contrast discrimination threshold), this function is effectively linear (i.e. the local curvature of the C^0.4 power law is approximately zero). Thus, it is often said that a pedestal “linearizes” the contrast response to the target. This has the effect of reducing the psychometric slope to that for a linear system, which is β ∼ 1.3 (e.g. Tyler & Chen, 2000). In the A on B condition, however, the slopes become steeper because of the effects of dilution masking described in Section 1.

We now consider psychometric functions for the A on B condition. These are shown for each of the four stimulus dimensions and three observers in Figure 3. In each plot, the horizontal dotted line indicates chance performance for standard 2IFC (d = 0). Points falling below this line indicate negative d-prime, highlighted by the shaded regions. Recall that each point on the psychometric function represents 200 trials, so their binomial errors are low (see error bars). Only the A on B condition produced the negative d-prime effects—the other arrangements of target and pedestal produced conventional monotonic psychometric functions (not shown). We find evidence for nonmonotonic behaviour for all three observers in the spatial dimension (Figure 3a), clear evidence for two observers in the time dimension (Figure 3b), and evidence for one observer in each of the eye (DHB, Figure 3c) and orientation (LP, Figure 3d) dimensions. We consider possible explanations for these individual differences in Section 4. In summary though, examples of negative d-prime were found for all four stimulus dimensions, as predicted by the model.

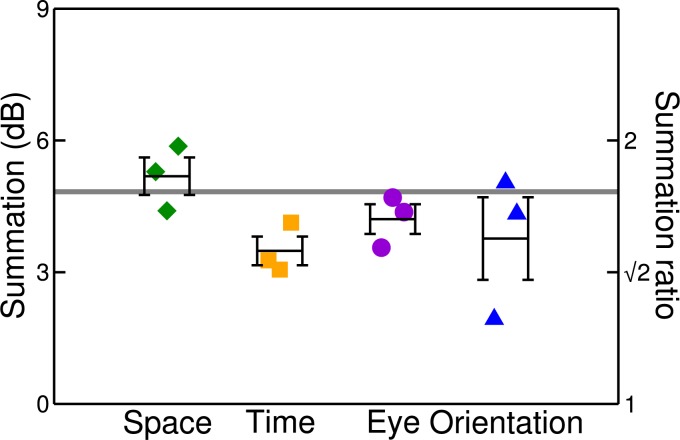
Finally, we estimated the level of summation across the A and B components by comparing thresholds in the A on AB condition with those in the AB on AB condition. Symbols in Figure 4 indicate summation ratios (the threshold difference in dB, which equals 20 times the log of the ratio of thresholds in linear units) for individual observers, for each of the four stimulus dimensions. The black bars are the averages, with error bars indicating ±1 SE. The mean level of summation on a pedestal lies between 3 and 6 dB, consistent with previous findings for eye and space (Meese & Summers, 2007; Meese et al., 2006). The levels of summation are close to those predicted by the generic contrast integration model (grey horizontal line), which was not critically dependent on the values of its four parameters (Z, p, q, and σ).

Figure 4.

Summation ratios in four stimulus dimensions (symbols) and model prediction (horizontal line). Symbols show results for each of the three observers, with the average shown by the black bars. In all cases, summation is calculated as the dB threshold difference between the A on AB and AB on AB conditions. Error bars show ±1 SE.

4. Discussion

We tested several predictions of a generic contrast integration model of vision in each of four stimulus dimensions (space, time, eye, and orientation). As predicted, we found that detection thresholds and the slopes of the psychometric function depended on whether the pedestal was the same as or different from the target (Figure 2), indicating that our stimulus manipulations were successful in recruiting multiple mechanisms (i.e. the A and B components excited different front-end mechanisms; see Appendix A for details). Furthermore, we found that the simultaneous excitation of these mechanisms improved performance, consistent with signal summation across them (Figure 4). Further still, when the target and pedestal were different (termed A on B) we found evidence for nonmonotonic psychometric functions with a clear region of negative d-prime in more than half of them. Because of the shape of these functions, we refer to them as “swan” functions (Figure 3). This surprising behaviour is predicted by our generic contrast integration model as described in Section 1.

In what follows, we will discuss swan functions that have been found in other studies and possible explanations for the individual differences in our results. We will consider and reject alternative models of our results in Appendix A.

4.1. Swan functions in other studies

As mentioned in Section 1, Foley (2011) described psychometric functions that have a nonmonotonic shape similar to our swan functions under some of his conditions. Foley's stimulus arrangement that produced this behaviour (a temporal “mask–target–mask” sequence) is very similar to our “time” condition described above (four repetitions of “mask–target”), and so it is plausible that the processes underlying the nonmonotonic effects might be the same across the two studies. However, our model involves summation of mask and target, but in Foley's model the signals are subtracted. We compare our model with Foley's and several others in Appendix A, and conclude that only our model can account for all of the findings in our study here.

In other work, swan functions have also been reported in the motion dimension. Serrano-Pedraza and Derrington (2010) judged perceived direction of motion for a 3 c/deg Gabor target moving at 4 deg/sec, superimposed on a static 1 c/deg Gabor mask. When the stimulus was quite large (3.3° full width at half-height [FWHH]), the psychometric function relating target contrast to proportion of correct direction judgements was steep and nonmonotonic, with a similar form to those in Figure 3. The negative d-prime region was so severe (particularly for one observer) that for some contrasts every trial was perceived incorrectly (e.g. 0% correct). When the stimulus was small (0.82° FWHH), psychometric functions were shallower and had a monotonic sigmoidal shape.

Are the results of Serrano-Pedraza and Derrington (2010) related to ours? The model they propose takes the MAX response across noiseless and mutually suppressive mechanisms sensitive to different spatial frequencies. The combination of subtractive suppression and a MAX operator produces appropriate nonmonotonic psychometric functions but does not predict the summation of A and B stimuli (Figure 4). This makes it inconsistent with our full set of results. Our own implementation of a MAX-based model in Appendix A suffers the same fate. However, the MAX approach might well be appropriate in Serrano-Pedraza and Derrington's (2010) motion paradigm where the existence of a competitive opponent motion process is well established (e.g. the “winner takes all” in choosing between two potential motion directions). Consistent with this is their finding that detection of motion for the individual components shows no summation of duration thresholds (their Figure 2b). Thus, although there are qualitative similarities between the swan functions here and those in the motion dimension, the details of their origins are quite possibly different.

More broadly, our findings may relate to other “paradoxical” contrast behaviours, such as those reported by Stevenson and Cormack (2000). In their experiments, performance deteriorated when there was a contrast imbalance between the eyes (for stereopsis; see also Legge & Gu, 1989), or between two components in a vernier task, or adjacent frames of a motion stimulus. Both Legge and Gu (1989) and Kontsevich and Tyler (1994) proposed models for the stereo case, the latter being closely related to ours, involving mutual suppression followed by signal combination. Finally, the nonmonotonic behaviour may be related to the well-known Fechner paradox in dichoptic brightness matching (e.g. Curtis & Rule, 1980).

4.2. Possible explanations for individual differences

Although we found examples of negative d-prime in all four stimulus dimensions, the effects were not uniform across observers. In particular, for eye and orientation, only one of our three observers produced swan functions, though for the eye condition we have found them in three out of four other observers outside of this study (unpublished observations; and Baker, 2008). Even where all observers do show the effect (e.g. for space, Figure 3a), there is much more variation in the magnitude of the paradoxical trough region than in the threshold or slope values (Figure 2).

We consider three possible explanations for these individual differences, though others doubtless exist. The first is that the level of suppression between the A and B mechanisms might vary across observers. This can be modelled in Equation (2) by including a multiplicative weight parameter on each of the cross-mechanism denominator terms. Reducing the level of suppression attenuates the negative d-prime region, but it also reduces threshold and slope. Therefore, it cannot explain the data for most of the observers and conditions in which the trough was absent, yet thresholds and slopes remained roughly homogeneous (Figure 2). However, it could perhaps explain the results for DHB in the orientation condition.

A second possibility is that observers might not select the interval that produces the greatest internal response. An alternative decision rule might be to respond to the stimulus that differs from an internal representation of the null interval, consistent with choosing abs(d′). To a first approximation, this would flip the negative d-prime region upside down, producing a hump above 50% correct, much like using the “reverse” rule described by Foley (2011). There is some limited evidence for this for observer ASB in the time, eye, and orientation conditions (Figure 3b–d), and observer LP in the eye condition (Figure 3c). Of course, alternating between these two rules on different trials or sessions would average out the trough and the hump leaving performance at chance (50% correct) in that part of the psychometric function, just as we found in some of our results.

The third explanation is that observers might have access to the individual component mechanisms—i.e. mechanisms in which the A and B components are not summed. For example, for the “Swiss cheese” stimuli from the spatial dimension, the different spatial regions corresponding to the A and B components can be readily resolved when the stimulus is above threshold. However, it is less clear that this could happen in the other dimensions. In the binocular dimension, the consensus from the literature is that observers cannot identify the eye to which a stimulus has been presented (i.e. utrocular discrimination is difficult or impossible; see Blake & Cormack, 1979). Arguably though, this is not important: so long as observers are able to access the output of monocular mechanisms it does not matter whether those mechanisms are labelled for eye of origin. Regardless of the details, if observers were able to access nonoverlapping component mechanisms, this would abolish both the threshold elevation and negative d-prime effects caused by the pedestal. This is clearly not the case for any of our observers, but one could construct a model in which a partial contribution from such mechanisms reduces one or both effects. However, our results do not provide sufficient constraint to attempt this here.

4.3. The generic integration model and population coding

In the experiments here, we have sampled the dimension of interest in just two places (the A and B components). Nonetheless, we envisage extended integration where appropriate, and we have presented evidence for this elsewhere (e.g. Baker & Meese, 2011). However, from one point of view, the generic model that we propose might appear puzzling: what is the point of integrating signal over a stimulus dimension if it is then to be suppressed by a similar integration over the same dimension? The first part of the answer is that the counter-suppression helps to maintain the invariance of contrast perception with the variable extent of integration. In the case of binocular summation, we have referred to this as ocularity invariance (Meese et al., 2006). However, this operation appears to throw away the benefit of performing integration in the first place. Meese and Baker (2011) offered a possible answer to this conundrum by proposing a population of integrators, where the suppressive integration region (the gain control) extends over the maximum extent of the relevant dimension, but the extent of the excitatory region varies across the mechanisms within the population. Thus, the general arrangement of suppression and counter-suppression that we propose is not as counterproductive as it might seem, because it provides the potential basis for a population code at a global (or object) level of analysis.

5. Conclusions

We have found evidence for nonmonotonic psychometric functions (swan functions) in each of four stimulus dimensions. They occur only when the target and mask patterns stimulate different early visual mechanisms—different eyes, different positions, different orientations, or at different times. This unusual behaviour is predicted by our generic model of contrast integration, which involves summation and counter-suppression across mechanisms within each stimulus dimension. It remains to be seen whether this framework extends beyond the low-level stimulus dimensions we have tested to higher level visual operations, such as object or face processing, or into other sensory modalities such as hearing and touch.

Biography

Daniel H. Baker studied Psychology at the University of Nottingham from 2000 to 2003. He then worked in industry for a year before beginning a PhD at Aston University under the supervision of Tim Meese. Daniel held a postdoctoral position at the University of Southampton (2007–09), and is currently a research fellow at Aston University. His main research interests are spatial vision, binocular vision (including binocular rivalry), and motion perception. For more information visit http://www1.aston.ac.uk/lhs/staff/az-index/daniel-baker/.

Tim S. Meese worked as a telecommunications engineer for five years before studying Psychology and Computer Science at the University of Newcastle-Upon-Tyne, where he graduated in 1989. He did his PhD at the University of Bristol and is now Professor of Vision Science at Aston University. His main research interests are in binocular and spatial vision and depth perception. He has been on the executive committee of the Applied Vision Association for more than 15 years and is now one of the chief editors of Perception and i-Perception.

Mark A. Georgeson studied Mathematics and Experimental Psychology at Cambridge University, then worked for his DPhil on spatial vision at Sussex University. He has held academic posts at Bristol, Birmingham, and Aston Universities, and published about 80 research papers on visual psychophysics and computational modelling. The work aims to understand how spatial vision, motion perception, and binocular vision work in the human brain. He co-authored the widely used textbook Visual Perception: Physiology, Psychology and Ecology (1996, 2003), is active in the Applied Vision Association, and is on the editorial boards of several research journals.

Appendix A

Alternative models

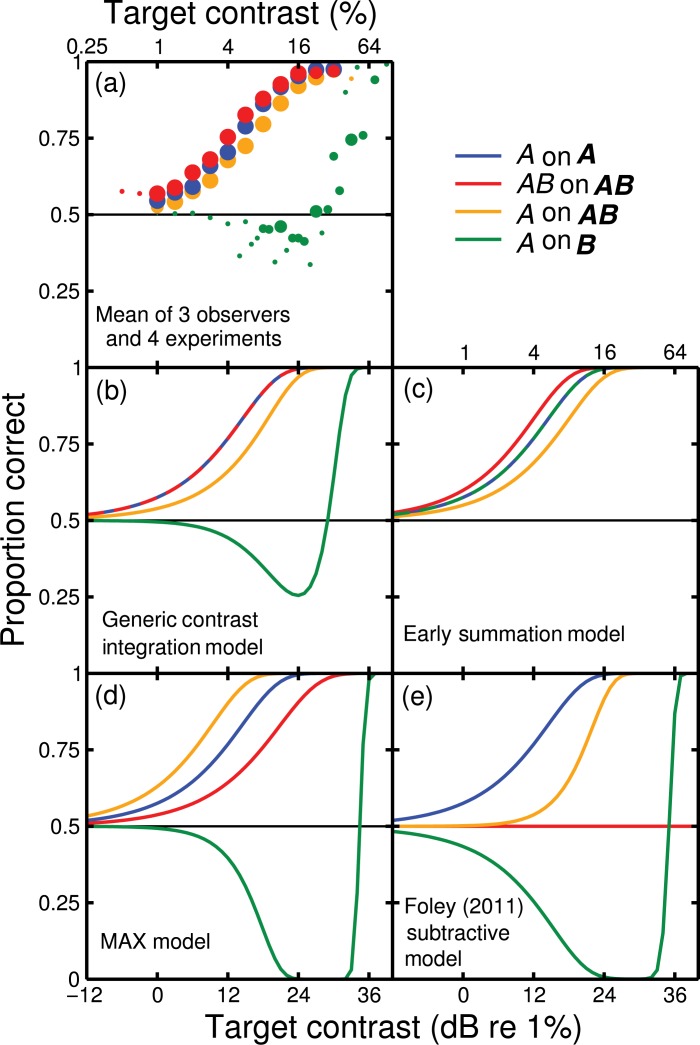
Here, we consider several alternative functional models of our results. The pooled data across all observers and experiments are shown in Figure A1(a), and the successful predictions of our generic contrast integration model are shown in Figure A1(b) for comparison. We first show that other model arrangements do not predict all aspects of our data. We then show that our generic model can predict some aspects of Foley's (2011) results.

Figure A1.

Pooled data and predictions of four functional models for each of four arrangements of pedestal and target (legend). The data were combined across observers and experiments, with symbol size representing the total number of trials at each contrast level (the largest symbols represent 2,400 trials each). See text for descriptions of the four models.

A.1. Early summation

An alternative to pooling signals after exponentiation is to pool them before it. This is to assume that the selectivity of the initial filtering mechanisms is sufficiently broad to respond to each of the A and B components. The model equation is given by

(A1)

with all terms as described in the main body of the report. As shown in Figure A1(c), this model fails badly for the A on B condition. This is because the linear summation between the two components means that the model is blind to which is the pedestal and the target. Thus, it predicts exactly the same behaviour for A on B arrangement as it does for the A on A arrangement, and is inconsistent with the swan functions and high thresholds that we find empirically for A on B.

A.2. A MAX operation instead of linear summation

Instead of summing the two terms in Equation (2), we could select the most active mechanism:

(A2)

with all terms as described in the main body of the report. This model does predict the nonmonotonic character of the swan functions for A on B. In fact, the severity of the paradoxical region is even greater than for the generic contrast integration model (compare the green functions in Figures A1d with A1b). However, it fails to predict the correct ordering of the other contrast discrimination conditions, as follows. In the MAX model, the psychometric function for the A on AB condition (yellow) appears to the left of that for the AB on AB condition (red). This implies a negative summation effect, which occurs because suppression from the additional target in the AB on AB case outweighs the (non-existent) benefit of including it.

For simplicity, the model calculations in Figure A1(d) were derived analytically. A stochastic version of the MAX model with independent Gaussian noise added to each term in Equation (A2) behaved in a very similar way, with the ordering of the conditions unchanged at high pedestal levels (not shown). This is in spite of the benefit from probability summation at threshold (e.g. Tyler & Chen, 2000; Appendix A of Meese & Summers, 2007), which is hidden by the strong suppression from the pedestals.

A.3. Foley's subtractive model

Foley (2011) proposed a model in which the mask contrast is subtracted from that of the target. A simplified version, following our present conventions, can be written as

(A3)

where “abs” indicates the absolute (unsigned) value. Note that Foley's original model also included weight terms on both the numerator and denominator. We have omitted these here for simplicity, but including them makes little difference to the qualitative behaviour of the model (at least for the range of values considered by Foley, 2011). Figure A1(e) confirms that this arrangement predicts the swan function for the A on B condition considered by Foley (2011). However, the other three arrangements of mask and pedestal considered here are less well predicted. In particular, the AB on AB condition produces a model response of zero, since the A and B terms cancel on the numerator of Equation (A3). This could be fixed by including additional mechanisms (as proposed by Foley, 2011). However, achieving the strong summation effects that we report will most likely require something similar to our generic model, which also predicts the nonmonotonic effects without the need for a subtractive term.

Given the similarity between our swan functions and those reported by Foley (2011; e.g. his Figure 5) it is clear that our model (Equation (1)) can at least provide a qualitative account of his results. A precise quantitative fit would likely require additional free parameters (such as weights to account for the different durations of mask and target) and is beyond the scope of this study.

Notwithstanding the above, we should also point out that one of the useful properties of Foley's (2011) model is that it is well disposed to describing some interesting “straddle” adaptation effects reviewed by Graham (2011) (occasionally referred to as “Buffy” adaptation). It is beyond the scope of this article to provide details of those experiments here, and it remains to be seen whether our generic contrast integration model can be extended to account for those results as well.

A.4. The generic contrast integration model predicts Foley's (2011) dipper functions

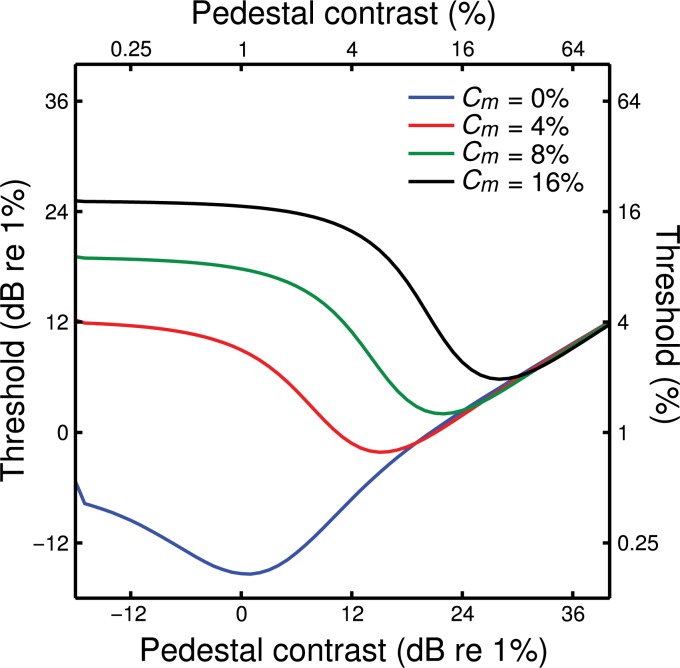
Experiment 1 of Foley (2011) measured contrast discrimination (dipper) functions for a 100-ms target (and pedestal) interleaved between two 1,000-ms masks, with the same spatial properties. As the mask contrast increased from zero, the dippers were shifted upwards and to the right such that the dipper handles superimposed, similar to findings with other masks (e.g. cross-orientation masks, Foley, 1994; dichoptic pedestal masks, Baker, Meese, & Georgeson, 2007). The amount of facilitation (depth of the dip) also increased in the presence of a mask. In Figure A2, we show the predictions of the generic contrast integration model, when the target and pedestal are the A component, and the mask is the B component. It is clear that the diagonal translation of the dippers is also predicted by our model (Equation (1)). We also note that this pattern of dippers is similar to that we have reported previously, when target and pedestal are shown to one eye, and a fixed contrast mask is shown to the other eye (Baker et al., 2007).

Figure A2.

Predictions for Foley's (2011) dipper functions. The diagonal translation of these functions with increasing mask contrast mirrors the pattern found empirically (see Foley, 2011). Note that the dipper handles converge at high pedestal contrasts, and that facilitation is strongest for high mask contrasts.

Appendix B

Matlab code to produce model diagrams

At the request of an anonymous reviewer, we have included Matlab code to produce the graphs in Figure 1.