Spatial arrangement in texture discrimination and texture segregation

Abstract

We investigated the role of spatial arrangement of texture elements in three psychophysical experiments on texture discrimination and texture segregation. In our stimuli, oriented Gabor elements formed an iso-oriented and a randomly oriented texture region. We manipulated (1) the orientation similarity in the iso-oriented region by adding orientation jitter to the orientation of each Gabor; (2) the spatial arrangement of the Gabors: quasi-random or regular; and (3) the shape of the edge between the two texture regions: straight or curved. In Experiment 1, participants discriminated an iso-oriented stimulus from a stimulus with only randomly oriented elements. Experiment 2 required texture segregation to judge the shape of the texture edge. Experiment 3 replicated Experiment 2 with Gabors of a smaller spatial extent in a denser arrangement. We found comparable performance levels with regular and quasi-random Gabor positions in the discrimination task but not in the segregation tasks. We conclude that spatial arrangement plays a role in a texture segregation task requiring shape discrimination of the texture edge but not in a texture discrimination task in which it is sufficient to discriminate an iso-oriented region from a completely random region.

1. Introduction

In natural visual perception, we organize a scene in coherent perceptual units. This task of perceptual organization involves two related processes: perceptual grouping and texture processing. Perceptual grouping refers to the process of combining elements into larger chunks or configurations and follows the Gestalt principles introduced by Wertheimer (1938); (see Wagemans et al., 2012, for a recent review). With texture processing, we refer to two processes: texture discrimination and texture segregation (Landy & Graham, 2004; Norman, Heywood, & Kentridge, 2011; Wolfson & Landy, 1998). Wolfson and Landy (1998) define these processes:

Segregation implies that the observer “instantaneously” perceives a distinct edge between abutting regions. This perceived edge can be used for tasks such as shape discrimination (e.g. Landy & Bergen, 1991; Wolfson & Landy, 1995). On the other hand, discrimination is used to indicate the observer can distinguish between regions (using the appearance of each region's texture) regardless of whether a distinct edge is perceived where the textures abut. (p. 439)

In the following paragraphs, we will first discuss the relationship between perceptual grouping and texture processing as a larger context for our study. Subsequently, we will explain how we attempt to bring research in perceptual grouping and texture processing closer together by investigating the influence of a factor that is known to play an important role in perceptual grouping (i.e. spatial arrangement of the elements) in the context of texture segregation. We will briefly review the handful of studies that have addressed the role of spatial arrangement of elements in both texture discrimination and segregation. We conclude that a direct comparison between regular and random element placement in both texture tasks is missing, which is what we provide in this study.

1.1. Relationship between perceptual grouping and texture processing

Perceptual grouping and texture processing are largely intermingled in the organization of natural scenes. In Figure 1(a), for instance, the texture elements of the surfaces and objects are clearly distinct from those of the background in spatial frequency content, orientation spectrum, colour, luminance, etc. In many natural scenes, texture cues and grouping cues go hand in hand to distinguish objects from the background, and texture segregation and grouping seem to constitute two sides of the same coin. When they do not, objects are much harder to detect, as in cases of camouflaged animals (see Figure 1b). The segregation and grouping cues here would give rise to the perception of a stick in the foreground and some segments of twigs that may be grouped in elliptic or circular configurations, but the grouping of elements belonging to the frog (in the centre of the image) with elements from the background prevents to segregate the frog from the background. Ben-Av, Sagi, and Braun (1992) describe grouping and texture segregation as related processes that prepare the input for figure-ground segregation. According to Treisman (1982), grouping is a special case of a texture in which the elements are discrete and above a certain minimum size. In addition, both processes can occur largely without attention and they specify candidates for object recognition.

Figure 1.

Perceptual organization in natural vision and research. In natural scenes, perceptual grouping and segregation can (a) go hand in hand and facilitate object detection or (b) make segregation of the frog from the forest floor difficult. Despite these interactions in natural vision, research traditions in perceptual organization make use of very different stimuli: e.g. (c) a dot lattice for studying perceptual grouping (adjusted from Kubovy, Holcombe, & Wagemans, 1998), and (d) a texture pattern (reproduced with permission from Lamme, Rodriguez-Rodriguez, & Spekreijse,1999). In a more integrated approach, we can, for example, study (e) snake detection in which grouping based on collinearity facilitates segregation of a curve from the background noise, (f) texture segregation based on orientation similarity, (g) contour and texture surface interactions in radial frequency patterns, and (h) in everyday objects.

Despite the close relation between the processing of texture and grouping in natural vision (e.g. Ben-Av et al., 1992; Treisman, 1982), they have mostly been studied in isolation using different types of stimuli. For instance, perceptual grouping is often studied with rather sparse stimuli containing several dots in regular positions (called “dot lattices,” see Figure 1c; e.g. Kubovy & Wagemans, 1995; Kubovy et al., 1998). In texture processing, stimuli often consist of more dense arrays of oriented line fragments in more random positions (see Figure 1d), so that two areas can be segregated from each other based on differences in orientation of the line fragments (e.g. Lamme et al., 1999). This traditional approach has led to valuable knowledge of perceptual grouping and texture processing as isolated processes. However, research on their interrelationships would be facilitated by reducing some of the differences between stimuli used to study grouping and texture processing. For instance, by orienting some Gabor elements tangentially along a curve (see Figure 1e), the curve (or “snake”) can be segregated from the background of random oriented Gabors by grouping based on collinearity (e.g. Field, Hayes, & Hess, 1993). One could also create a texture segregation stimulus similar to the grouping stimuli, consisting of the same Gabors with comparable positioning and density (see Figure 1f), and differing only in the distribution of the Gabor orientations. With such stimuli, observers can be asked to perform similar tasks in the grouping and segregation cases, for instance, to detect the presence of a snake or texture edge or to discriminate two types of snakes or texture edges (e.g. straight vs. curved, different global orientations, different types of curvature).

Previous attempts to bridge the gaps between the stimulus domains of the two research traditions focused predominantly on the interaction between contour and surface information in the context of figure-ground segregation. For instance, Machilsen and Wagemans (2011) have used stimuli such as the one in Figure 1(g) to compare the detection of (closed) snakes, texture regions, and their combination. They found that the information provided by the contour and surface cues was integrated in a way that did not differ from an optimal linear combination rule. Sassi, Vancleef, Machilsen, Panis, and Wagemans (2010) have used stimuli such as the one in Figure 1(h) and found different identification rates of everyday objects as a function of the overall orientation in the foreground and the background. They also observed an interaction with the contour defined by aligned Gabors. In these studies, however, the stimuli were rather different from traditional texture segregation stimuli (such as those in Figures 1d and f), containing texture regions surrounded by background regions (instead of two abutting regions). This approach induced additional processes of figure-ground segregation and shape perception that might obscure the grouping-texture interaction. In addition, two kinds of perceptual grouping were present: orientation similarity within the texture region and orientation alignment along the edge of the region (or the contour path).

In this study, we take one step further in studying the relations between grouping and texture segregation by examining the effect of spatial arrangement, which has mainly been studied in grouping, on texture processing, while at the same time staying rather close to the prototypical stimuli in the texture segregation literature, with two abutting regions and region grouping only.

1.2. Spatial arrangement of the elements in perceptual grouping and texture processing

In the following paragraphs, we will first describe the role of spatial arrangement in grouping in the context of psychophysical experiments and computational modelling. Next, we argue for the importance of studying spatial arrangement in texture processing. Afterwards, we describe the indirect and direct evidence for a role of spatial arrangement in both texture discrimination and texture segregation.

Perceptual grouping has been investigated in different research traditions, which differ rather substantially in the nature of the stimuli, experimental paradigms, modelling, and so forth. One of the key differences concerns the spatial arrangement of the elements (random or regular) in the stimuli. For example, one tradition (e.g. Kubovy & Wagemans, 1995; Kubovy et al., 1998) measures the strength of perceptual grouping by proximity by presenting regular dot lattices, and asking for reports of perceived global orientation of parallel lines. They modelled overall response frequencies and applied the same procedure in other kinds of regular stimuli (including so-called Gabor lattices; Claessens & Wagemans, 2005). In another tradition, grouping models have been formulated by van Oeffelen and Vos (1982) and Compton and Logan (1993) that predict perceptual organization for individual stimuli with completely randomly positioned dots. Surprisingly, models designed for random dot stimuli are not applicable to regular dot stimuli and vice versa (Kubovy & Wagemans, 1995).

Spatial arrangement is also important for texture processing. Landy (1996) indicated that natural textures can be regular (e.g. brick walls and honeycomb) or random (e.g. forest floor), and he argued that texture processing should be studied with both types of stimuli (as it is the case in the different stimulus traditions on grouping). He also highlighted the importance of spatial arrangement of the texture elements (random or regular) for further developments in research on texture perception and relating texture segregation to perceptual grouping processes. In addition, Harrison and Keeble (2008) point to a distinction between computational models of texture segregation that account for the influence of spatial arrangement (e.g. neural diffusion models) and models that omit this effect (e.g. filter–rectify–filter models).

An indirect comparison between random and regular spatial arrangements of the texture elements can be made since different studies on texture processing have used different spatial arrangements so far. For instance, to study the underlying mechanisms of texture segregation, Wolfson and Landy (1998) used random positioning of the elements, while Giora and Casco (2007) and Norman et al. (2011) positioned their elements regularly. Ignoring the details of these different studies, both lines of work generally arrived at similar conclusions, which suggests that spatial arrangement does not play a big role in texture processing.

More systematic research specifically targeted on the influence of spatial arrangement (random or regular) of the elements in texture processing is limited, although several authors (e.g. Norman et al., 2011) agree with Landy (1996) that this would be quite useful. When giving an overview of the direct comparisons between regular and random spatial arrangement, we should make a distinction between studies focusing on texture discrimination and studies focusing on texture segregation.

In texture discrimination, (uniform) texture regions can be distinguished regardless of the presence of an edge (e.g. sometimes the different textures are in different stimuli). The difference between random and regular positioning of the elements was investigated in two studies by Keeble and his colleagues in 1995 and 1997. In the first study (Keeble, Kingdom, Moulden, & Morgan, 1995), observers were presented with uniform textures of line elements placed in either random or grid positions. Participants had to discriminate between the iso-oriented texture and a randomly oriented texture. A decrease in performance was found for regularly positioned elements. However, when controlling for the density difference between the random and regular conditions, this difference disappeared. In the second study (Keeble, Kingdom, & Morgan, 1997), observers were again presented with uniform textures in which line or Gabor elements were placed in either random or grid positions, but participants now had to discriminate between different orientation distributions of the textures. The regular arrangement of the line elements led to a reduction in performance for one participant for short presentation durations (105 ms). In all other conditions (i.e. longer presentation time and Gabor elements) and for all other participants, no systematic difference between spatial arrangements was observed. Apart from the case reported by Keeble et al. (1997), these results indicate that the spatial arrangement of the elements is irrelevant for texture discrimination.

With regard to texture segregation, in which an edge between texture regions differing in element orientation can be perceived, only one study directly compared the effect of random and regular element positioning (Pearson & Kingdom, 2001). When studying the interference of colour and orientation information in texture segregation, Pearson and Kingdom (2001) observed impaired performance with random element positioning compared to regular positioning. They explained this result by suggesting that the induced variability in the inter-element distances in random stimuli leads to a general drop in the contrast gradient defining the edge. Hence, the weaker representation of the edge results in impaired performance in the random condition.

To conclude, from the existing literature it is not clear whether spatial arrangement has an influence in texture processing. There are several reasons. First, the comparison between different studies is complicated by the diversity of their research goals: context effects (Harrison & Keeble, 2008), model comparison (Giora & Casco, 2007; Norman et al., 2011; Wolfson & Landy, 1998), orientation distributions of the elements (Keeble et al., 1995, 1997), and interference of colour- and orientation-based texture segregation (Pearson & Kingdom, 2001). In addition, another limitation of some of the above-mentioned studies (Giora & Casco, 2007; Harrison & Keeble, 2008; Keeble et al., 1995, 1997) is that task differences (discrimination vs. segregation) and stimulus differences (uniform textures vs. textures with adjacent regions differing in orientation) are confounded: uniform textures are typically used in combination with a discrimination task, while textures with different regions are frequently combined with a segregation task. This raises the additional question whether stimulus or task characteristics determine the effect of spatial arrangement, if one were to be found reliably. Differences in stimuli, tasks, and research goals make it difficult to draw a clear conclusion about the role of spatial arrangement of elements in texture processing from the limited number of studies so far. These limitations highlight the need for a more systematic study of the difference between random and regular positioning of texture elements in two typically employed tasks (texture discrimination and texture segregation) with the same stimuli. It is this gap in the literature that this study aims to fill.

1.3. The present study

Since the distinction between regular and random positions of the elements seems to have important implications for models of perceptual grouping, a relevant question is whether the position of elements is also an important factor in texture processing. In this study, we systematically investigate the influence of spatial arrangement in discrimination and a segregation tasks while using textures with two abutting regions. In contrast to the uniform textures typically used in the texture discrimination literature, our stimuli are simultaneously suitable for both a discrimination and a texture segregation task. With these stimuli, participants performed a task in which they had to discriminate an iso-oriented texture from a random texture (Experiment 1). One could call this task “detection of iso-oriented texture” but we prefer to call this task the discrimination task as discrimination is the essential task characteristic. Subjects have to discriminate between a texture with only random orientations and a texture with two regions: a random region and an iso-oriented region. Although the stimuli would allow segregation of the texture regions, this is not necessary for the task; noticing an iso-oriented region or a difference between an iso-oriented and a randomly oriented region in the textures is sufficient. Because this task does not really require (but only allows) segregation of the regions, a second task was added (Experiment 2) in which participants were forced to segregate the texture into two regions in order to make a judgment about the shape of the segregation edge (a completely straight edge or one with a straight and a curved part). One could call this task “discrimination of the shape of the texture edge” but, in line with the literature and the reasoning outlined above, we prefer to call this task the segregation task. To control for the role of the correspondence between the spatial scale of the texture and the spatial scale of the shape difference in the texture edge, we repeated the segregation experiment with denser stimuli (Experiment 3).

2. Experiment 1: Texture discrimination

2.1. Methods

2.1.1. Participants

Nine experienced psychophysical observers volunteered for the study (four males and five females). They were aged between 20 and 47 years. All reported normal or corrected-to-normal vision. Four participants were naïve with respect to the hypotheses of the study, the other five were authors.

2.1.2. Stimuli

Stimuli were generated offline with some precursor functions of GERT, the Grouping Elements Rendering Toolbox (Demeyer & Machilsen, 2012) for MATLAB (MathWorks). They consisted of oriented Gabor patches positioned on a uniform grey background (107 cd/m²). Example stimuli are presented in Figure 2.

Figure 2.

Some example stimuli of Experiments 1 and 2. (a) A stimulus with random positions; (b) a stimulus with regular positions.

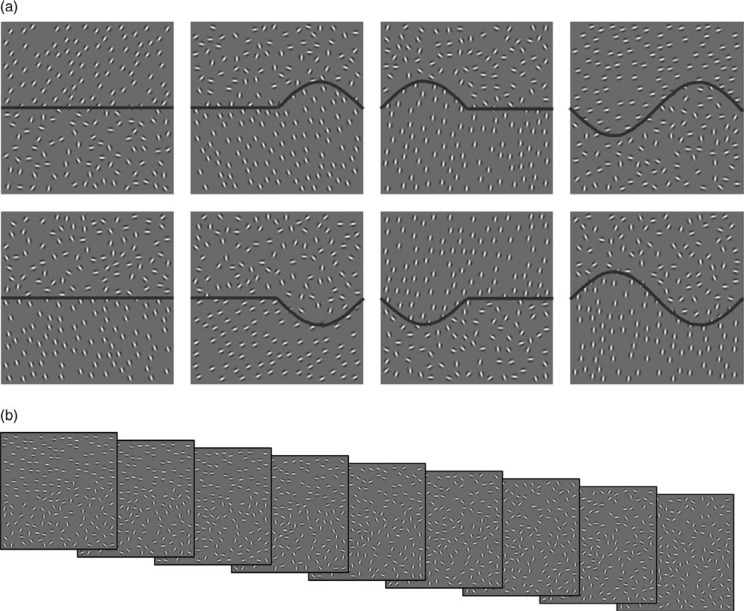
First, the positions of the Gabors were manipulated. In the random position condition, Gabor elements were placed at quasi-random positions in the stimulus (minimal inter-element distance of 0.52°). In the regular position condition, Gabor elements were placed at the crossings of a grid (horizontal and vertical inter-element distance of 0.78°). Second, the orientations of the Gabors were manipulated. For the target stimuli, Gabors in one area all had a common orientation; in the other area, the orientation of each Gabor was picked randomly, so one area could be segmented from the other area based on differences in orientation similarity (maximal in one area, minimal in another area). In other words, the target stimulus stimuli were divided in two regions of similar size: one with randomly oriented Gabors and another with uniformly oriented Gabors (called “iso-oriented”). The implicit edge between the two regions was centred vertically and continued horizontally from the left to the right side of the stimulus. It could take on seven different shapes, depending on the combination of straight and curved segments (Figure 3a). For the distracter stimuli, all orientations were determined randomly, so no two areas were defined. In all stimuli, (common) orientations were randomly chosen from a uniform distribution between −90° and 90°. Third, to manipulate the difficulty level of the segregation, element orientation in the iso-oriented region varied from perfectly iso-oriented (strong grouping) to almost random (no grouping). This was done in nine steps. The orientation jitter was sampled uniformly from a distribution with minimum zero and maximum ±0°, 10°, 20°, 30°, 40°, 50°, 60°, 70°, or 80°, depending on the jitter level (Figure 3b).

Figure 3.

Stimulus manipulations. (a) Each stimulus consists of two areas; the implicit edge is formed by discontinuities in orientation of the elements. For illustrative purposes, lines are drawn on the stimuli to show the different shapes they can take. Stimuli as presented to the participants are shown in Figure 2. All shapes are used in Experiment 1. In Experiment 2, only the six shapes at the left are shown. (b) The nine levels of orientation jitter are presented for one stimulus: 0°, 10°, 20°, 30°, 40°, 50°, 60°, 70°, and 80°.

The Gabor patches were even symmetric and were constructed by multiplying a cosine luminance grating with a circular Gaussian. The grating had a spatial frequency of 3.64 cycles per degree and the Gaussian envelope was characterized by a standard deviation of 0.1° of visual angle. The number of Gabor elements (169) was held constant in every stimulus and their spatial distribution was proportional to the surface area of each region. In this way, any local or global density differences were avoided. Stimuli subtended 10° × 10° of visual angle at a viewing distance of 50 cm (259 × 259 pixels).

2.1.3. Apparatus and set-up

Participants were seated in a dark and silent room. They rested their head in a chin-and-forehead rest and viewed the centre of the stimuli binocularly. The stimuli were presented on a colour-calibrated CRT monitor (View Sonic Graphics Series G90fB: 17 inch, screen resolution 1024 × 768 pixels, refresh rate 60 Hz). To guarantee precise luminance control and accurate timing in stimulus presentation and response registration, a visual stimulus generator (ViSaGe, Cambridge Research Systems) graphic card controlled stimulus presentation. Responses were registered by a Cedrus response box (RB-530, Cambridge Research Systems). The MATLAB environment (MathWorks) was used to operate the ViSaGe.

2.1.4. Procedure

In a temporal two-alternative forced choice (2AFC) task, similar to Keeble et al. (1995), participants were asked to indicate which interval contained a stimulus with an iso-oriented region. Each trial consisted of a fixation cross (800 ms), a blank interstimulus interval (250 ms), the first stimulus interval (150 ms), a blank interstimulus interval (500 ms), the second stimulus interval (150 ms), and a response screen that was presented until response. The stimulus intervals were accompanied by different tones (first interval: 649 Hz; second interval: 779 Hz) indicating the different intervals. To encourage the participants, their responses were followed by a feedback tone (correct response: 909 Hz; incorrect response: 519 Hz). After each block of 104 trials, feedback on performance and interval bias was provided by indicating the percentage correct for that block and the instruction to press the left or right button more often if the proportion of left button presses (“target in first interval”) fell behind or exceeded the proportion of targets in the first interval by 15% or more. In this experiment, all edge shapes presented in Figure 3(a) were used. To balance the occurrence of straight and curved segments at either side, the condition with a completely straight line was presented twice as often as each of the other conditions resulting in eight shape conditions. We used the method of constant stimuli: nine fixed levels of orientation jitter for both the regular and random position conditions. With 104 trials for every data point, we balanced the occurrence of the different shape conditions of the edge (13 trials per shape condition). In total, each participant performed 1,872 trials (2 position conditions by 9 orientation jitter levels by 104 trials), divided in 18 blocks of 104 trials, in which all orientation jitter levels and position conditions were randomly intermingled. The session could be terminated after each block and most participants completed the experiment in two sessions.

2.1.5. Data analyses

Data were analysed by fitting several generalized linear mixed models (Bolker et al., 2009; Jaeger, 2008) to the group data. In this section, we first give a general description of this type of models. Subsequently, advantages of generalized linear mixed models over ANOVA and fitting individual psychometric functions are explained. In the last paragraph, we give more specific details on how we applied the technique to our data.

Generalized linear mixed models can model binary outcome data (correct/incorrect). The binary data are logistically transformed with a lower asymptote at 50% correct to model the guess rate in our experiments. Predictors can be included in the model to account for general effects in the data. These general effects are called fixed effects and are observed within subjects. In addition to these general effects, generalized linear mixed models offer the advantage of modelling variability between subjects by including random effects. The random effects allow for individual variability on the estimated parameters of the fixed effects.

Because the variability between subjects can be modelled, generalized linear mixed models have an advantage over ANOVA and fitting psychometric functions (Jaeger, 2008; Quené & van den Bergh, 2008). First, by modelling the variability in the data we increase the power of our analysis compared with an ANOVA on the percentages correct or d′. The values entered in the ANOVA are generally based on averaging over trials of each condition and therefore reduce the richness of the data set, while in generalized linear mixed models there is no need for averaging and more variance in the data can be explained (general variability is explained by fixed effects and variability between subjects is explained by random effects). Second, by comparing fitted psychometric functions, sampling variability in our data might mask general trends. In addition, generalized linear mixed models allow for more objective conclusions than the conclusions based on qualitative comparison between subjects in individual analyses. For all these reasons, we opted for an overall group analysis by generalized linear mixed models as our main analysis instead of ANOVA or fitting individual psychometric functions. To validate our approach, we also fitted psychometric functions to the data of each individual subject and performed an overall group analysis on the thresholds. Overall, the results of these analyses support the conclusions from the generalized linear mixed models, but as they provide additional insight in inter-individual differences, we have included a detailed report of these analyses as supplementary material at http://gestaltrevision.be/en/resources/supplementary-material.

Analyses were performed in SAS (SAS Institute Inc.), a software package for statistical computing. We applied these techniques by including fixed main effects and two-way interaction effects of orientation jitter (0°−80° in steps of 10°), position condition (random or regular), and shape (straight or curved) in the model. We allowed the effect of orientation jitter, the main effect of position condition (comparable to threshold differences between position conditions), and the interaction between position condition and orientation jitter (comparable to differences in slopes between position conditions) to vary over participants and therefore included random effects of these predictors. In search of a satisfying model, we started with a model including all aforementioned effects and applied a backward stepwise procedure. This means that we excluded non-significant effects in each step until we obtained a model that only included significant effects. We evaluated the effect of a predictor in explaining the data by performing a t-test. For non-nested models, we compared the Akaike information criterion (Akaike, 1974) and the Bayesian information criterion (Schwarz, 1978) to compare the goodness of fit of different models. These criteria indicate the goodness of fit of a statistical model taking into account model complexity. To meet convergence criteria of the iterative parameter estimation procedure, the factor orientation jitter was centred on 40°.

2.2. Results and discussion

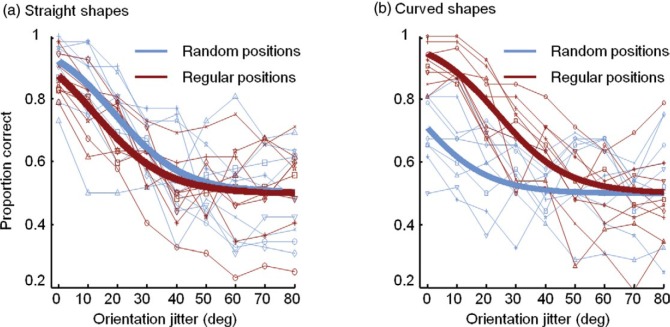
The final model contained a significant effect of orientation jitter (parameter estimate = −0.0810, SE = 0.0070, t(6) = −11.62, p < 0.001). As expected, performance declined with increasing orientation jitter (Figure 4). An increase of 10° of orientation jitter was associated with a decrease of 56% of the odds for a correct answer, with all other factors held constant (estimated odds ratio (${\displaystyle \widehat{\mathit{OR}}}$) = 0.56). No significant effects were observed for position condition (parameter estimate = 0.1909, SE = 0.2125, t(6) = 0.90, p = 0.40).

Figure 4.

Individual data and model predictions for performance in the discrimination task (Experiment 1). Thin lines show the performance on an individual level (each symbol represents one subject). The thick lines are the model predictions on a group level. The predicted curves for regular and random positioned elements are very similar (almost no difference between the thick red and blue lines, respectively).

We observed similar performance levels for random and regular positioned elements in a texture discrimination task. In this task, grouping similar elements in a smaller region is sufficient to detect the iso-oriented pattern and precise knowledge about the segregation edge (e.g. location, shape and orientation) was not necessary even though the stimuli would allow segregation of the two regions because the stimuli had a clear segregation edge. To tap more directly into the segregation process, we designed a second experiment in which segregation was necessary to solve the task. Participants were presented with the same stimuli but now had to judge the shape of the implicit edge.

3. Experiment 2: Texture segregation

3.1. Methods

In this experiment, participants, stimuli, and set-up were identical to Experiment 1. Participants performed a yes/no task with one stimulus presented on each trial. In the segregation task, the participants judged whether the shape of the edge was completely straight (“straight”) or contained a curved part (“curved”). Note that this implies a similar type of distinction at the level of the texture edge in this experiment (completely straight or with a non-straight part) as in the previous experiment at the level of the texture as a whole (completely random or with a non-random part). This also implies that the distinction can be made either by comparing two parts (two regions of the whole texture or two parts of the implicit texture edge) or by detecting the diagnostic part (the non-random region in the texture or the non-straight segment of the texture edge). In spite of these similarities, a pilot experiment showed that the segregation task was too difficult at the original presentation time of 150 ms. This already implies that the focus of the task on the shape of the edge as such increased the task difficulty, which was to be expected because additional processes were now needed to segregate the two texture regions, to make the edge explicit, and to process its shape (curvature). Increasing the presentation time to 500 ms resulted in data that nicely covered the whole range of the psychometric function. The shapes of the texture edge were restricted to the six shapes containing straight segments, that is, all but those in the rightmost column of Figure 3(a). To balance the occurrence of straight and curved shapes, the straight shape was presented four times as often as each of the curved conditions. Analyses were performed in the same way as in Experiment 1.

3.2. Results and discussion

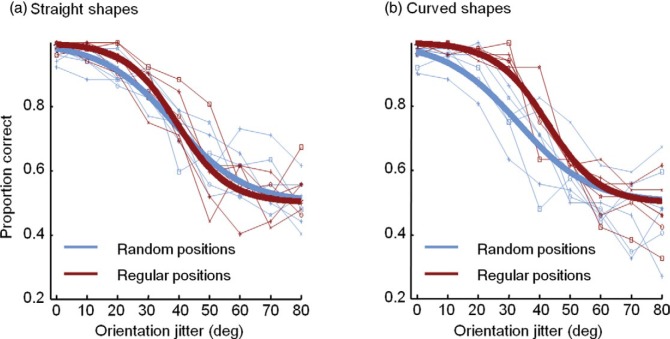
For the segregation task (Experiment 2), the observed and predicted percentages correct are plotted in Figure 5. We found a significant main effect of orientation jitter (parameter estimate = −0.0854, SE = 0.0047, t(6) = −18.08, p < 0.001). Here, an increase of 10° of orientation jitter was associated with a decrease of 57% of the odds for a correct answer given all other factors are constant (${\displaystyle \widehat{\mathit{OR}}}$ = 0.57). In this experiment, other predictors were significant in the final model. Overall, the task was significantly easier in the regular position condition than in the random position condition (estimated difference = 2.3946, SE = 0.2404, t(6) = 9.96, p < 0.001, ${\displaystyle \widehat{\mathit{OR}}}$ = 10.96). In addition, there was a significant effect of shape (estimated difference = 1.8966, SE = 0.1862, t(6) = 10.67, p < 0.001), indicating lower performance for the curved shapes than for the straight shapes (${\displaystyle \widehat{\mathit{OR}}}$ = 7.29). However, an interaction between shape and position condition (parameter estimate = −2.9646, SE = 0.2406, t(6) = −12.32, p < 0.001) was also obtained, showing a greater difference between the position conditions in the curved trials than in the straight trials. For the curved shapes, regular positioning of the elements made the task easier for most levels of orientation jitter, except for high levels of orientation jitter (floor effect).

Figure 5.

Individual data and model predictions for performance in the segregation task (Experiment 2). Thin lines show the performance on an individual level (each symbol represents one subject). The thick lines are the model predictions on a group level. For straight shapes the predicted curves for regular and random positioned elements do not differ much for most jitter levels, except for a small benefit of the random position at the highest jitter levels (a). However, for curved shapes segregation is easier for regular positioned elements at all levels of orientation jitter, although the benefit is larger for the lower jitter levels (b).

In sum, the main conclusion from this experiment is that for curved shapes, performance is better with regular than with random positioning of the elements. However, spatial scale differences could be a confounding factor in this experiment: The observed difference between random and regular spatial arrangement could be due to undersampling of the curve in the random positioning. In the case of regular positioning, the spatial scale of the elements is similar to the scale of the texture's curved edge which makes shape discrimination of the edge easier in comparison with random placement in which sampling of the edge is noisier. Although it is not immediately clear how this account would explain all the details of the complex interaction between position and shape (better performance for regular positioning in curved shapes but not in straight shapes), it is clear that the correspondence between the spatial scale of the element placement in the textures as a whole and the spatial scale of the curvature differences of the texture edges as such could determine the task difficulty. To test the role of this factor, we reduced the size of the Gabor elements and increased the density of the stimulus in Experiment 3. In this way, the inhomogeneities in the texture are on a different spatial scale than the spatial scale of the curvature of the edge. So, if we replicate the differences between random and regular positioning in the more dense stimuli, we can rule out the specific contribution of the correspondence in spatial scale between the element placement and the edge shape, and we can generalize the effects of element positioning on texture segregation to a wider set of conditions.

4. Experiment 3: Texture segregation with dense textures

4.1. Methods

Six psychophysical observers volunteered for the study (three males, three females). They were aged between 22 and 31 years. All reported normal or corrected-to-normal vision. Three participants were naïve with respect to the hypotheses of the study, and the other three were authors. Here, we reduced the size of the Gabors by a factor 2 while increasing the density by a factor 2 (Figure 6). Density was increased by reducing the minimal inter-element distance from 0.52° to 0.26° in the random positioning condition. In the regular positioning condition, the distance between the elements was reduced from 0.78° to 0.39°. The number of Gabors in each stimulus was increased to 676. To reduce the size of the Gabor patches, a grating with a spatial frequency of 7.28 cycles per degree was multiplied with a Gaussian envelope that was characterized by a standard deviation of 0.05° visual angle. Other stimulus parameters were identical to Experiments 1 and 2. Apparatus, set-up, procedure, and data analyses were equivalent to Experiment 2.

Figure 6.

Example stimuli used in Experiment 3 (with a straight and curved part in the texture edge) for which the spatial arrangement of elements is regular (a) and random (b).

4.2. Results and discussion

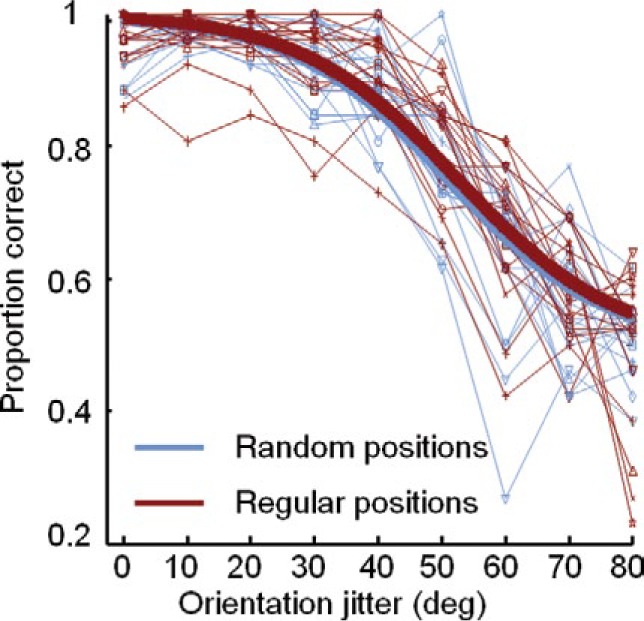
The final model contained a significant effect of orientation jitter (parameter estimate = −0.0849, SE = 0.0045, t(3) = −18.93, p < 0.001, ${\displaystyle \widehat{\mathit{OR}}}$ = 0.57). Although we changed the spatial scale of the elements, we still observed a significant effect of spatial arrangement: regular positions made segregation easier in comparison to random positions (estimated difference = 0.8879, SE = 0.2021, t(3) = 4.39, p = 0.022, ${\displaystyle \widehat{\mathit{OR}}}$ = 2.436). Results for each position condition are shown in Figure 7. Similar to Experiment 2, we found that straight shapes were significantly easier to segregate than curved shapes (estimated difference = 0.4486, SE = 0.1378, t(3) = 3.25, p = 0.047, ${\displaystyle \widehat{\mathit{OR}}}$ = 1.57). The interaction between position condition and orientation jitter was significant (parameter estimate = −0.0337, SE = 0.0077, t(3) = −4.39, p = 0.022), indicating a smaller difference between regular and random arrangement at high orientation jitter at which performance is at chance level (floor effect) and at low orientation jitter (ceiling effect). In addition, we also observed a significant interaction between shape and position condition (parameter estimate = −0.8083, SE = 0.2134, t(3) = −3.79, p = 0.032), showing a greater difference between the position conditions in the curved shape trials than in the straight shape trials, similar to what was found in Experiment 2.

Figure 7.

Individual data and model predictions for performance in the segregation task with more dense stimuli (Experiment 3). Thin lines show the performance on an individual level (each symbol represents one subject). The thick lines are the model prediction on a group level.

In denser stimulus arrays, we again found a significant difference in texture segregation between conditions with regular and random placement of the elements. This finding argues against the alternative explanation that our results from Experiment 2 are due to an undersampling of the curved shape edge in the random element condition. Note that the observed increase in performance with denser stimuli in Experiment 3 compared with sparser stimuli used in Experiment 2 was more pronounced in the random condition. This might indicate that, in theory, performance in the random condition could approximate the performance level of the regular condition at some very high densities for which the sampling of the curved-shape edge in the random condition is even better. However, we were not able to test this because increasing the density more than in Experiment 3 (while keeping the stimulus size the same) would require very small Gabors for which their orientation would become difficult to discriminate. Although we cannot completely rule out the alternative explanation, the present findings of Experiments 2 and 3 suggest that the texture segregation task, which requires the processing of the shape of the texture edge, is easier when the elements are placed in regular than in random positions.

5. General discussion

5.1. Summary of the findings

We investigated the importance of spatial arrangement of elements (random vs. regular positioning), an important characteristic in grouping, in the context of texture segregation stimuli in a discrimination task (Experiment 1) and in a segregation task (Experiments 2 and 3). Our results show that texture segregation stimuli alone are not sufficient to observe an effect of element position (random or regular), the effect is only present if the task requires segregation. We found no effect of element position on performance in the discrimination task in which it is sufficient to discriminate an iso-oriented region from a completely randomly oriented stimulus, while in the segregation task requiring shape discrimination of the texture edge, we did find a difference between both position conditions. This difference was probably independent of the spatial scale of the Gabor elements.

5.2. Relation to previous findings

Although Landy (1996) has emphasized the importance of the distinction between random and regular textures more than 15 years ago, research on this topic has remained rather limited so far. Convergent results in studies using different spatial arrangements suggest that the distinction is not crucial (Giora & Casco, 2007; Norman et al., 2011; Wolfson & Landy, 1998). In the study of Wolfson and Landy (1998), the elements were positioned at random positions in the stimulus, while in Giora and Casco (2007) and Norman et al. (2011) the elements were positioned in a grid but the results were generally similar.

One study directly comparing random and regular positioned elements was performed by Keeble et al. (1995), who compared random and regular element position in texture discrimination and found no differences when they controlled for density differences. In addition, Keeble et al. (1997) only found a small difference for one participant under specific conditions in a similar experiment. These results seem congruent to our findings of Experiment 1, but contradictory to Experiments 2 and 3, because in this experiment we found a difference between random and regular arrangement over all participants. However, in both studies of Keeble and colleagues, participants were presented with uniform textures in a discrimination task, while we investigated texture segregation stimuli (with two different texture regions within a single stimulus) in a discrimination task (Experiment 1) and in a segregation task (Experiments 2 and 3). In the study of Pearson and Kingdom (2001), participants also had to perform a segregation task, but their participants had to segment a figure from a background and localize this figure while in our task participants had to segment two equivalent regions and make a judgment about the shape of the edge. They found better performance for the regular arrangement than for random element arrangement. This is in accordance with our results.

Taken together, this pattern of results suggests that spatial arrangement does not play a role in texture discrimination (Keeble et al., 1997, 1995; Experiment 1), but it is important when texture segregation is required (Pearson & Kingdom, 2001; Experiments 2 and 3), regardless of whether the stimuli are uniform (as they are often are in discrimination tasks) or non-uniform (as they always are in segregation tasks).

5.3. Possible explanations of the findings

Before discussing the most plausible interpretation of the findings reported in this study, we discuss some alternative explanations that we consider less likely.

First, the correspondence in spatial scale between the placement of the elements and the curvature of the edge in Experiment 2 might have resulted in a better sampling of the curve in the regular condition than in the random condition. We have tried to rule out this explanation in Experiment 3 with smaller Gabor elements and higher density textures. Because we still observed an effect of spatial arrangement with these stimuli, the alternative explanation of spatial scale correspondence is unlikely. It cannot be completely ruled out, however, because performance obtained with denser stimuli (Experiment 3) was better than that obtained with sparser stimuli (Experiment 2, and the difference between random and regular placement might disappear with even denser stimuli).

Second, presentation duration might be a possible confounding factor: in Experiment 1, stimuli were presented for 150 ms, while in Experiments 2 and 3 presentation time was extended to 500 ms as the segregation task was too difficult at 150 ms. Perhaps spatial arrangement only plays a role after 150 ms. Under different experimental conditions, Keeble et al. (1995) compared random and regular element positions for stimuli presented for 150 and 1,000 ms and found no differences, indicating that the effect of spatial arrangement is independent of presentation time. In addition, Pearson and Kingdom (2001) presented stimuli for 150 ms and observed an effect of spatial arrangement. Their findings suggest that the effect of spatial arrangement is independent of presentation time.

Third, Experiments 1 and 2 also differed in the psychophysical method: in Experiment 1, a 2AFC task was used, while in Experiments 2 and 3 participants performed a yes/no task. The major difference between both methods lies in the risk for response bias. In a 2AFC task, this risk is minimal, while in a yes/no task response bias is more common. Therefore, one could argue that the observed effect of spatial arrangement is related to response bias. We calculated the response bias for each subject for our experiments by dividing the proportion of “second interval” answers by the proportion of trials with the target in the second interval. No significant difference was observed between the bias in the 2AFC task of Experiment 2 and the yes/no task of Experiment 1 (paired t-test: t₈ = 0.40, p = 0.70) and between the bias in the 2AFC task of Experiment 3 and the yes/no task of Experiment 1 (unpaired t-test: t₁₃ = 0.91, p = 0.38), making this explanation unlikely.

Fourth, one could argue that it is possible to judge the shape of the edge based on local information. One could, for instance, pay attention only to the central area of the stimulus to solve the task. In our opinion, this strategy would not change our results because local information sampling is as likely for random as for regular element positions. Moreover, given that both conditions were randomly intermingled in the experiments, it is unlikely that participants used separate strategies for regular and random spatial arrangements.

A fifth explanation centres on the distinction between spatial alignment and collinearity. In most of the literature on grouping and segregation, spatial alignment refers to similar orientations of the elements in an organized region, while collinearity refers to the alignment of the elements with the orientation of the contour (in grouping studies) or the edge (in texture segregation studies). In texture stimuli, collinearity occurs in the special case that the elements are parallel to the edge; in our stimuli, this would be the case for horizontal element orientations. It is known that collinearity facilitates texture segregation (Nothdurft 1992; Wolfson & Landy, 1995). Harrison and Keeble (2008) showed that collinearity of the texture elements (without spatial alignment of the Gabor phases) facilitates texture segregation. However, comparing their results with our results is difficult because they defined spatial alignment as collinearly oriented Gabor elements which additionally have the same phase. This means that in their study, spatial alignment of orientation is always confounded with collinearity. In some of our regular stimuli, spatial alignment and collinearity might have co-occurred, making it difficult to know which factor (spatial alignment or collinearity) might have had the strongest effect. However, if we define collinear stimuli as stimuli with element orientations in the iso-oriented region between −5° and 5°, the percentage of collinear stimuli in the whole stimulus set is probably too small (7%) to account completely for the observed effect of spatial arrangement. Moreover, a repeated measures ANOVA showed that the interaction between position condition and collinearity was not significant (F_1,8 = 2.84, p = 0.13). So, all in all, we do not think that collinearity as such or its interaction with spatial arrangement can explain the obtained difference between regular and random positions.

Because all the above explanations can be ruled out, we think that the observed effect of spatial arrangement has to do with the nature of the task: discrimination versus segregation. The fact that we observed no effect of spatial arrangement in Experiment 1, while we did find such an effect in Experiment 2, is most likely related to the task requirements of both experiments. Because the segregation task in Experiment 2 requires finer judgments, some kind of interference between the shape and the position cue could influence the responses and be a possible explanation for the difference between the spatial arrangements. In our stimuli, two cues are present: orientation and position. The orientation information is equivalent in the random and regular position conditions, but the position information differs between these conditions. In the random condition the positions give no structural information, while in the regular condition the position information results in an overall structure of horizontal or vertical straight lines (a grid). In the segregation task, participants have to evaluate the shape of the edge. Here the straight line configuration created by the positional information can provide a reference frame (a grid) and facilitate the detection of a deviation from a straight line in the curved shapes.

5.4. Possible implications for models of texture processing and contour integration

When relating our results to models of texture segregation, we have to make a distinction between two categories: edge-based models and region-based models. First, in edge-based models the focus is on the detection of discontinuities at the edge (Bergen & Landy, 1991; Kehrer & Meinecke, 2003; Landy & Graham, 2004; Motoyoshi & Nishida, 2004; Thielscher & Neumann, 2005). In the second model category, region-based grouping, similar texture elements are detected and the activity of neighbouring similar elements is enhanced by linking operations (Caelli, 1985; Jain & Farrokhnia, 1991), spreading the activity to the boundaries of the texture. Experiment 1 permits integration over a large region and therefore could reflect a region-based approach. In Experiments 2 and 3, the relevant information is limited to the edge and therefore an edge-based approach is more suitable. In this regard, we observed no effect of spatial arrangement on the region-based approach (Experiment 1) and a significant effect on the edge-based approach (Experiments 2 and 3). Regarding the models, the pattern of results obtained in this study implies that the edge-based process in Experiments 2 and 3 should be influenced by the spatial arrangement of the elements while the region-based process in Experiment 1 is not.

Another way to relate our findings to mechanisms is to distinguish between grouping within a texture region (Experiment 1), which is not sensitive to the regularity of the element spacing, and grouping along the texture edge (Experiments 2 and 3), which is sensitive to the regularity of the element spacing. In this regard, it is useful to point out that the grouping process that operates along the edge and that seems necessary to discriminate the shape of the edge has strong similarities with contour integration. In the association field model of Field et al. (1993), elements are grouped in a contour in case of high association strength between elements. Association strength is influenced not only by orientation similarity but also by position of the elements: only nearby aligned elements are grouped in contours. Relating this model to our findings, this could suggest that the regular spatial arrangement of elements along the texture edge increases the association strength compared with the random spatial arrangement of the elements. This stronger association could result in better discrimination of the edge's shape even though orientation information does not vary.

Although there is no direct evidence that the same grouping process occurs in contour integration and in texture segregation, as far as we know, others have shown that in shape perception of the contour, not only orientation information but position information is also important. Gheorghiu and Kingdom (2009) and Hancock and Peirce (2008) showed that curvature is an intermediate-level feature that is computed from a combination of local orientations and/or positions along the contour. Moreover, Day and Loffler (2009) pointed to the important role of position information besides orientation information in a shape perception task of contours of radial frequency patterns, a task that bears more similarity to our segregation task.

Bell, Gheorghiu, Hess, and Kingdom (2011) also showed that position and orientation are integrated into curves prior to encoding global shape. Therefore, our results on the relevance of position information in the shape judgment task in Experiments 2 and 3 are in line with effects found in contour integration. Further research will be necessary to investigate to what extent the underlying mechanisms of contour integration and texture segregation are similar or not.

Our finding of a different effect of spatial arrangement depending on the nature of the task might seem to contradict the results of a recent study on contour integration by Robol, Casco, and Dakin (2012). Building on a paradigm introduced by Dakin and Baruch (2009), these authors investigated the effect of neighbouring elements on contour-shape discrimination and contour detection of snakes and ladders. They specifically introduced near-parallel and near-perpendicular surrounds and compared these with random surrounds tested. They found that the effect of spatial arrangement of nearby elements was very similar regardless of whether the task was to localize and determine the shape of the contour or to localize the contour without explicit shape discrimination. Although it is tempting to attribute the differences between our and their findings to differences between the mechanisms involved in texture and contour processing, it is useful to indicate a number of crucial differences between the two studies. Instead of manipulating spatial arrangements of the elements based on the random or regular distribution of the element positions, as we did, their conditions differed by the element orientations. In addition, their spatial arrangement conditions differed in the nearby elements only, not with respect to the entire display as in our conditions. Finally, our experiments were concerned with texture segregation and discrimination, and theirs with contour integration. So, the differences between the two studies are substantial. In line with the overall motivation of this study, it would be interesting to compare both paradigms more directly in a single study with similar stimulus parameters and task requirements.

Our study has contributed a first step in this direction by systematically examining the role of element positioning (which is typically included in studies of perceptual grouping) in texture processing (where it has been largely ignored so far).

6. Conclusion

In sum, we investigated the role of spatial arrangement of the elements in texture discrimination and texture segregation. Our results show that the position of the elements is important in a texture segregation task, but not in a texture discrimination task. Because the same stimuli were used in both tasks, the explanation must be situated at the level of the task demands. The discrimination task could be performed on the basis of the grouping of the texture elements within a region, while the segregation task required additional processing steps in terms of texture segregation, grouping along the texture edge, and shape processing. That only the latter, more demanding task is affected by the regularity of the element spacing is compatible with a range of different models of possible underlying mechanisms (e.g. edge-based vs. region-based texture processing, association field models of curvilinear grouping, and processing curvature).

Biography

Kathleen Vancleef (1985) obtained her Master's degree in Psychology from the University of Leuven. Currently, she is working on a PhD thesis under supervision of Johan Wagemans (Leuven) and Glyn Humphreys (Oxford). Central to her research are questions about texture segregation and contour integration, which she studies with psychophysical and neuropsychological paradigms. Besides her experimental work, she applies her theoretical knowledge by developing clinical diagnostic tools for visual impairment.

Tom Putzeys (1985) obtained a Master's degree in experimental psychology from the University of Leuven and completed a PhD project in 2012, supervised by Johan Wagemans (Leuven), Matthias Bethge (Tübingen), and Robbe Goris (NYU). In his research, he combines psychophysics and computational modelling to investigate how information represented in low-level visual areas is decoded when forming decisions in simple behavioural tasks.

Elena Gheorghiu (1973) obtained her PhD in physics from Utrecht University, the Netherlands. After receiving her PhD, she worked as a postdoctoral research fellow at McGill University, Canada, and the University of Leuven, Belgium. Her studies focus on understanding the relationship between the low-level stages of vision that detect local features and the intermediate-to-higher stages of vision that connect these features to form contours, textures, surfaces, and shapes. Her current research interests are in a number of interrelated domains including stereopsis, curvature processing, contour and texture perception, shape, colour, and motion (see http://mvr.mcgill.ca/Elena/).

Michaël Sassi (1983) received his Master's degree in experimental psychology from the University of Leuven, where he is currently working on a PhD project supervised by Johan Wagemans. His research aims to investigate the potential influences of global or large-scale stimulus properties as well as high-level processing on perceptual grouping in general and contour integration in particular.

Bart Machilsen (1980) studied psychology at the University of Leuven, where he did his PhD research under supervision of Johan Wagemans. He is currently a postdoctoral fellow in the Laboratory of Experimental Psychology. In collaboration with Dr. Maarten Demeyer, he refined and integrated the stimulus construction algorithms described in the current research paper into an open-access Matlab toolbox (www.gestaltrevision.be/gert). His present research interests include processes of perceptual organization, temporal aspects of visual perception, natural scene statistics, and predictive coding.

Johan Wagemans (1963) has a BA in psychology and philosophy, an MSc and a PhD in experimental psychology, all from the University of Leuven, where he is currently a full professor. His current research interests are mainly in so-called mid-level vision (perceptual grouping, figure-ground organization, depth and shape perception) but stretching out to low-level vision (contrast detection and discrimination) and high-level vision (object recognition and categorization), including applications in autism, arts, and sports (see www.gestaltrevision.be).