Abstract
This study investigates bone-tooth association under compression to identify strain amplified sites within the bone-periodontal ligament (PDL)-tooth fibrous joint. Our results indicate that the biomechanical response of the joint is due to a combinatorial response of constitutive properties of organic, inorganic, and fluid components. Second maxillary molars within intact maxillae (N=8) of 5-month-old rats were loaded with a μ-XCT-compatible in situ loading device at various permutations of displacement rates (0.2, 0.5, 1.0, 1.5, 2.0 mm/min) and peak reactionary load responses (5, 10, 15, 20 N). Results indicated a nonlinear biomechanical response of the joint, in which the observed reactionary load rates were directly proportional to displacement rates (velocities). No significant differences in peak reactionary load rates at a displacement rate of 0.2 mm/min were observed. However, for displacement rates greater than 0.2 mm/min, an increasing trend in reactionary rate was observed for every peak reactionary load with significant increases at 2.0 mm/min. Regardless of displacement rates, two distinct behaviors were identified with stiffness (S) and reactionary load rate (LR) values at a peak load of 5 N (S5 N=290–523 N/mm) being significantly lower than those at 10 N (LR5 N=1–10 N/s) and higher (S10N–20 N=380–684 N/mm; LR10N–20 N=1–19 N/s). Digital image correlation revealed the possibility of a screw-like motion of the tooth into the PDL-space, i.e., predominant vertical displacement of 35 μm at 5 N, followed by a slight increase to 40 μm at 10 N and 50 μm at 20 N of the tooth and potential tooth rotation at loads above 10 N. Narrowed and widened PDL spaces as a result of tooth displacement indicated areas of increased apparent strain within the complex. We propose that such highly strained regions are “hot spots” that can potentiate local tissue adaptation under physiological loading and adverse tissue adaptation under pathological loading conditions.
1. INTRODUCTION
The bone-tooth fibrous joint is a dynamic organ that responds to several extrinsic factors to maintain occlusal function (Herring, 2012; Ten Cate, 1998). One prominent extrinsic factor is functional load (Herring, 2012; Popowics et al., 2009). Loads within physiological threshold limits permit soft and hard tissue turnover and maintain optimum periodontal ligament (PDL)-space between the tooth and bone (McCulloch et al., 2000; Niver et al., 2011; Ten Cate, 1998). However, changes in PDL-space can be caused by aberrant loads, eliciting a positive feedback that perpetuates mineral forming and/or resorbing areas in both vascularized bone and cementum. Changes to the adjacent mineralized tissues can increase and/or decrease PDL-space, eventually altering the ability of the PDL to optimally transmit occlusal loads. (Graber and Vanarsdall, 1994; Hurng et al., 2011; McCulloch et al., 2000). As such, mechanical loads on the fibrous joint could induce local strains within the bone-PDL-cementum complex that can generate site-specific physiological changes to maintain the PDL-space or pathological tissue adaptations if loads exceed physiological threshold limits (Bartold, 2012; Wolff, 1986).
Over time, organ-related biomechanics, including tooth deformation, have been investigated using strain gauges (Jantarat et al., 2001; Popowics et al., 2009; Popowics et al., 2004), photoelasticity (Asundi and Kishen, 2000, 2001), Moiré interferometry (Wang and Weiner, 1998; Wood et al., 2003), electronic speckle pattern interferometry (Zaslansky et al., 2005; Zaslansky et al., 2006), digital image correlation (DIC) (Qian et al., 2009; Zhang et al., 2009), and in situ loading devices coupled to X-ray microscopes (Naveh et al., 2012). However, strain maps using photoelastic, finite element, and numerical methods are limited due to assumptions of constitutive properties of tissues and their interfaces (Cattaneo et al., 2005; Komatsu et al., 2004). Among other technique-related problems, Moiré and ESPI are surface-sensitive and do not provide bone-root association unless the organ is sectioned to expose internal structures. In addition, observed PDL mechanics have been predominantly limited to transverse block sections of the bone-PDL-cementum complex (Chiba and Komatsu, 1993; Komatsu et al., 2004). The approach presented in this study exploits technology to date by using a mechanical testing device coupled to a high resolution X-ray microscope (Lin et al., 2012; Naveh et al., 2012) and subsequent use of DIC to identify displacement fields within the bone-tooth fibrous joint.
The objective of this study is to identify the mechanical response of an intact, healthy bone-tooth fibrous joint to simulated compressive loads. Mechanical response of the bone-tooth fibrous joint will be discussed in three steps: 1) mapping the displacement response of the tooth within the alveolar socket in relation to compressive load; 2) correlating the load-displacement curves to the bone-tooth association qualitatively and quantitatively; 3) mapping local displacements within the bone-PDL-cementum complex by digitally correlating 2D virtual cross sections (2D sections taken from 3D tomographic data sets) at no-load and loaded conditions. This experimental approach allows performing higher resolution imaging without disturbing the loading scheme and the organ. Using DIC as a post processing tool and eliminating the need for sample preparation (Qian et al., 2009; Ziegler et al., 2005) opens a new area of investigation in understanding dynamic processes of different complexes under various loading scenarios (Dickinson et al., 2012; Okotie et al., 2012). Through a hierarchical study from joint function to tissue-level strains, strain concentrated and amplified regions will demonstrate “hot spots”. By analyzing these hot spots, we can predict dominant tensile, compressive, and/or shear strains within soft and hard tissues, including the PDL-bone and PDL-cementum interfaces of the fibrous joint.
2. MATERIALS AND METHODS
All animal experiments conducted in this study were housed in pathogen-free conditions in compliance with the guidelines of the Institutional Animal Care and Use Committee (IACUC) of UCSF and the National Institute of Health (NIH). Eight five-month-old male Sprague Dawley rats (Charles River Laboratories, Inc., Wilmington, MA) on a hard-pelleted diet (hard-pellet diet is the normal diet for rats) and bred within a germ-free environment were used. The intact maxillae were freshly harvested after euthanasia and stored in Hank’s balanced salt solution (HBSS) with 0.2% sodium azide (Carvalho et al., 1996) for compression tests.
2.1. In situ compression stage
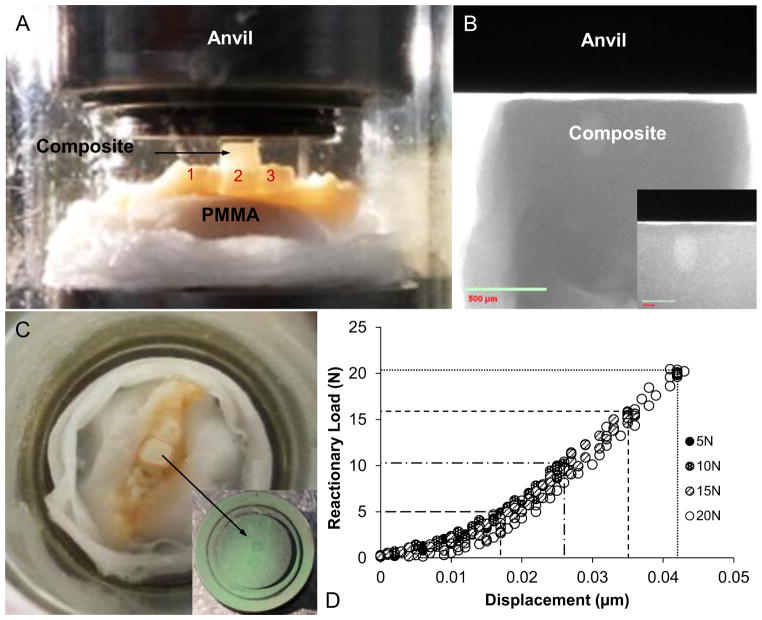
Following specimen preparation (Fig. 1) for compression testing (see Supplemental Information including Fig. S1 for evaluation of compression stage stiffness), contact with the occlusal composite was ensured by initiating a compression load of 0.2N. The second molar was loaded at various displacement rates (velocities) of 0.2, 0.5, 1.0, 1.5, and 2.0 mm/min (Hiiemae, 2004; Thomas and Peyton, 1983) until various peak reactionary load responses of 5, 10, 15, and 20 N (Nies and Ro, 2004) were detected by the transducer.
Figure 1. Specimen preparation for in situ mechanical testing.
(A) A hemimaxilla secured on to a steel stub with poly(methyl methacrylate) (PMMA) and with occlusal buildup on the second maxillary molar for uniform loading and compression by using an in situ loading device. (B) A μ-XCT radiograph shows the relationship of the leveled-composite surface with the opposing anvil (inset). (C) Uniform loading on the occlusal build-up is indicated by the contact area marked with ink sprayed on the anvil surface (green, inset). (D) A representative output of loading and unloading load-displacement curves for various peak reactionary loads.
2.2. Analysis of load-displacement curves
Stiffness (S in N/mm) was determined by using a linear regression model fit to the last 30% of the load/displacement data of each compression cycle (Fung, 1993; Popowics et al., 2009) (see Supplemental Information, Fig. S2). Loading rate (N/s) was also calculated in a similar fashion, but by using the load–time data (see Supplemental Information, Fig. S2). Specifically, the loading curve was used as we are interested in the response of the fibrous joint to compressive loads during mastication (represented by the loading curve) rather than to its recovery. Strain rates as a result of displacement rates for loading and unloading can be different accounting for different rates of interstitial fluid during efflux and influx.
2.3. Micro-X-ray computed tomography (μ-XCT) analysis of the loaded fibrous joint
Before scanning, the tooth was displaced at a constant rate of 2.0 mm/min to a peak reactionary load of 5 N, 10 N, and 20 N respectively. The specimens were scanned with X-rays after the load equilibrated (Fig S2). X-ray imaging was performed using a tungsten anode with a setting of 75 KVp at 8 W at binning 2 and a quartz silica (SiO2) filter designed specifically for biological specimens. The second molar and bone was kept within the field of view by using a 4x lens. 1800 projections were collected at an exposure time 6 s for each projection.
2.4. Digital Image Correlation (DIC)
The DIC method enables identification of tooth displacement with respect to the alveolar bone by using equivalent mesial–distal and buccal–lingual virtual sections, respectively, at no load (0N) and loaded conditions (5, 15, 20N). 2D virtual sections at respective loads were selected from μ-XCT tomographs. Virtual sections were digitally correlated using commercial software VEDDAC (CWM GmbH, Chemnitz). The software calculates the displacement of the tooth relative to the adjacent bone by comparing the two images with an image processing correlation algorithm while correcting for rigid body movement.
3. RESULTS
3.1. Fibrous joint response to compressive loads
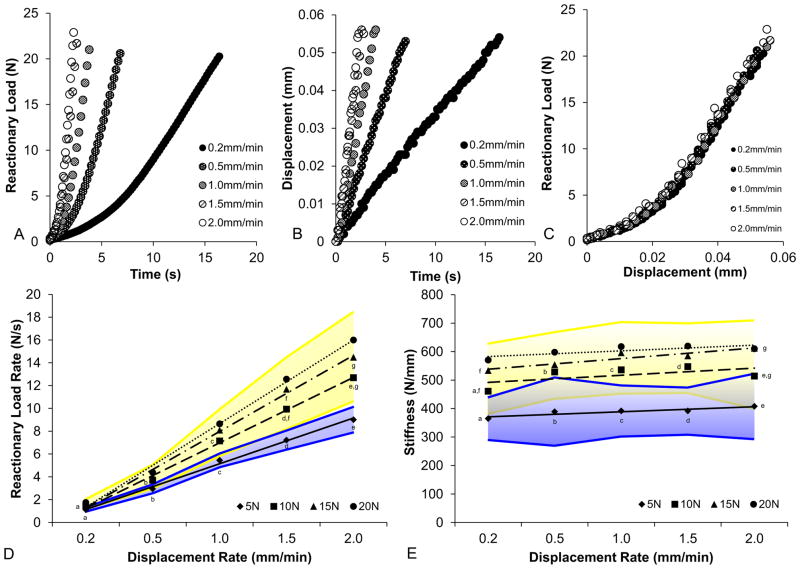
The stiffness of the mechanical testing device was significantly higher than the experimental specimen under investigation (Fig. S1). Representative displacement-time curves confirm the sensitivity of the compression stage in detecting changes in displacement based on varied loading velocities as inputs for compression of the second maxillary molar within an intact maxilla (Fig. 2a). Representative load-time curves showed that load rate response increased as the velocities increased (Fig. 2b). With increased velocity, load-displacement curves continued to exhibit a nonlinear biomechanical response of the fibrous joint (Fig. 2c). For each given displacement rate, load-displacement curves at all peak reactionary loads overlapped (Fig. 1d). No significant differences in load–displacement response of the fibrous joint were observed with changes in velocity (Fig. 2c) or peak reactionary loads. Reactionary load rates at 5 N were significantly lower than reactionary load rates at peak reactionary loads greater than and including 10 N (Student’s t-test with unequal variance, P<0.05). At velocities of 1.5 mm/min and 2.0 mm/min, reactionary load rates at 10 N were significantly lower than those at 15 N (Student’s t-test with unequal variance, P<0.05). There were no significant differences in reactionary load rates between 15 N and 20 N across all displacement rates (Fig. 2d).
Figure 2. Fibrous joint response to compression as represented through load rate and load-displacement.
Representative graphs illustrate load response vs. time (A), displacement vs. time (B), and load vs. displacement (C) for each displacement rate. Averages of reactionary load rates (D) and stiffness values (E) for each peak reactionary load are also plotted against displacement rate. Shaded regions illustrate upper and lower limits within one standard deviation of average reactionary load rates (D, blue – 5 N, yellow – greater than 10 N) and stiffness values (E, blue – 5 N, yellow – greater than 10 N) across all experimental conditions. a,b,c,d,e,f,g Indicates significant difference (Student’s t-test, P<0.05).
At each peak reactionary load, a positive correlation between stiffness and displacement rate was observed (Fig. 2e). Across all displacement rates, two distinct groups of stiffness values were identified. The stiffness values at 5 N were significantly lower than those at 10, 15, and 20 N (Student’s t-test with unequal variance, P<0.05). Stiffness values at 10 N were significantly lower than stiffness values at 15 N at displacement rates of 0.2 mm/min and 2.0 mm/min (Student’s t-test with unequal variance, P<0.05). No significant differences in stiffness values between 15 N and 20 N across all displacement rates were identified, but stiffness values at 15 N and 20 N converged with increasing displacement rates.
3.2. Bone-PDL-tooth association using an in situ loading device coupled to a μ-XCT
The fibrous joint response to compression was visualized in 2D mesial-distal and buccal-lingual virtual sections through the lingual roots and distal roots, respectively (Fig. S3a, b; please open movies with QuickTime™). Comparisons between no load, 5, 10, and 20 N peak reactionary loads were made by maintaining the alveolar bone as a reference. Overall, the lack of identical sections through the crown and roots when under load, showed that the tooth displaces out of the sectional plane presumably due to out-of-plane rotation and/or displacement normal to the virtual section. The tooth exhibited predominantly vertical displacement into the PDL-space and interradicular bone at 5 N and 10 N (Fig. S3). With increasing compressive load above 10 N, minimal vertical tooth movement was observed. In the coronal regions, decreased PDL-space adjacent to the distal and buccal surfaces of each root and increased PDL-space adjacent to mesial and lingual surfaces of each root were observed (Fig. S3a, b). Apical regions exhibited opposing effects with decreased PDL-space adjacent to the mesial and lingual surfaces of each root and increased PDL-space adjacent to distal and buccal surfaces of each root.
3.3. Digital imaging correlation illustrates tooth displacement relative to bone
The rigid body motion in Figures 3a, 3b, and 3c was corrected by using an extra tool, VEDDAC, where all calculated displacements were made relative to bone. Figures 3a and 3b show DIC results of the displacement in occlusal (Y) direction in mesial-distal and buccal-lingual virtual sections at different loads to which rigid body correction was applied (30 μm at 5 N, 40 μm at 10 N, and 50 μm at 20 N). The colored regions represent areas that were digitally correlated. The colors were selected such that a displacement range of almost 10 μm is visualized by the same color. The areas which did not move during loading are colored yellow and correspond to a displacement of −5μm to 5μm. DIC on mesial–distal sections (Fig. 3a) illustrated approximately half of the displacement for a quarter of the maximum load, where both roots moved equally in the Y-direction. No significant displacement in X-direction was found in the mesial-distal section at a load of 5 N (not shown) and for an increased load of 10 to 20 N. However, when loaded to 10 N the buccal root moved more in the Y-direction than the lingual root, indicating rotation of the tooth (Fig. 3b, c). This rotation was confirmed by a displacement in the X-direction as shown at 20 N in the buccal-lingual section (Figure 3c).
Figure 3. Digital imaging correlation (DIC) used for displacement mapping of the second maxillary molar (tooth) in relation to alveolar bone (AB) at 4x magnification.
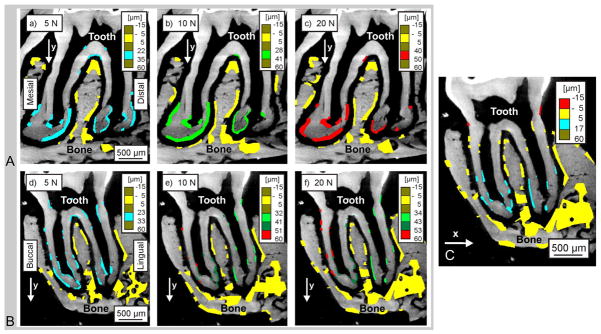
2D virtual mesial-distal (A) and buccal-lingual (B,C) sections indicate regions analyzed at 5 N (a, d), 10N (b, e), and 20 N (c, f, and C) of peak reactionary load. All comparisons were made against conditions of no load (0 N). Color-coded regions indicate areas analyzed for changes in horizontal (x shift) and vertical (y shift) displacement fields.
4. DISCUSSION
This study seeks to predict areas of “heightened” adaptive potential within a bone-tooth organ by investigating: 1) the mechanical response of the intact fibrous joint, 2) the degrees of freedom of tooth movement in relation to the alveolar socket, and 3) the resulting areas of increased PDL and/or mineralized tissue compression. It has been suggested that the mandible during mastication rotates upward and protrusively along an elliptical path, resulting in the upward and forward movement of mandibular molars during mastication (Hiiemae, 1971; Hiiemae, 1967; Hunt et al., 1970). Therefore, the opposing maxillary molars are speculated to displace both vertically into and mesially within the alveolar socket. As such, specimens were loaded uniaxially – a principal component of in vivo occlusal loads. Results illustrated an in situ behavior of the PDL and a 3D relationship of the root surface with the inner surface of the alveolar bone in an intact fibrous joint.
Cellular responses due to function-induced strains promote PDL-turnover (Beertsen et al., 1997; Berkovitz, 1990; McCulloch et al., 2000), perpetuate bone remodeling and modeling (McCulloch et al., 2000; Roberts, 1999), and control cementum growth (Luan et al., 2007; Niver et al., 2011). Strain-related tissue changes are dependent on both the diet hardness (magnitude of load) and the frequency of loading (Niver et al., 2011). In this study, it is plausible that frequency of chewing loads is comparable to loading rates of the tooth in the alveolar socket (Fig. 2a), and diet hardness is comparable to the magnitude of reactionary loads (Fig 1d). As a result, the rate at which the tooth is displaced into the alveolar socket and the reactionary loads that are felt are dependent on the dominance of an individual constituent or a combinatorial effect of polyphasic constituents that make up and act as key players within the tissues and the complex.
Periodontal tissues and their interfaces contain various stress and strain relieving components such as mineral; fibrillar proteins including collagen, fibronectin, elastin; globular proteins, such as glycoproteins and polyanionic proteoglycans. The globular proteins interact with fibrillar proteins, interstitial fluid (including bound and unbound water) and blood (Embery et al., 2000; Ho et al., 2005; Nanci and Bosshardt, 2006; Ten Cate, 1998). These components with respective constitutive properties could have different load-bearing responses individually or combinatorially depending on the rate of loading (Papadopoulou et al., 2011). This effect is evident in Figures 2b–2e, which highlights varying reactionary loads depending on the rate at which the tooth is displaced in the socket. Although these measurements are not significantly different, the upward trends of increasing range of reactionary load rates with increasing velocities are noticeable (from 1.0–2.0 mm/min at 0.2mm/min to 8.0–18.5 mm/min) (Fig. 2). This is because, at lower velocities, such as 0.2 mm/min, unbound interstitial fluids within the joint could have enough time to move, resulting in a similar reactionary rate response (Fig. 2d). Hence, if a virtual scan were to be performed at a displacement rate of 0.2 mm/min, regardless of the peak reactionary loads, the corresponding root association with bone would be similar. This is because the energy due to displacement of the tooth and resulting PDL compression at a displacement rate of 0.2 mm/min, regardless of reactionary loads (5–20 N), could manifest into shear between different components in addition to fluid flow through the organic network and blood vessel channels within PDL and bone. Interestingly, with an increase in velocity, the rate at which reactionary loads are sensed increases (Fig. 2d). Increased reactionary response from 0.5 mm/min and above could be due to inadequate time for fluid flow (Fig. 2b). As such, higher velocities could manifest into a strain hardening-like characteristic contributed by both the viscous and elastic constituents, making the complex apparently elastic in nature. These effects are observed at loads greater than 10 N.
Despite the linear behavior between velocity and reactionary load rate (Fig. 2d), it should be noted that the effect from viscous constituents is highlighted by the nonlinear behaviors of load with time (Fig. 2b) and load with displacement (Fig. 2c) regardless of the displacement rate. Hence, it can be argued that the load bearing nature of the bone-PDL-tooth complex in this study at and above 10 N is dependent on a combinatorial response of all phases equivalent to an elastic response. This equivalent elastic response is echoed by the statistically significant lower range of stiffness (S5N = 290–523 N/mm) and reactionary load rate (LR5N = 1–10 N/s) values at 5 N, compared to 10N and higher (S10N-20N = 380–684 N/mm; LR10N- 20N = 1–19 N/s) across all displacement rates (Fig. 2e). In between peak reactionary loads of 5 N and 10 N, the viscous constituents could play a dominant role. It can also be argued that the interdependency of the viscous and elastic contributions can be decoupled within appreciable limits by removing the effect of the viscous constituents using enzymes to digest PGs, elastin, and/or collagen (Ho et al., 2005; Komatsu, 2010; Ujiie et al., 2008). However, a lack of the viscous component would imply decreased strain relaxation, dampening mechanism, and fracture resisting characteristics, of the tooth and bone. The lack of significant differences in the stiffness values across displacement rates for each peak reactionary load (Fig. 2e) is most likely due to the lower range of displacement rates that the instrument offers for which the fibrous joint was tested (Fig. 2c). This argument is further reinforced by previous studies that have confirmed a significant change in the load-displacement behavior of greater ranges of displacement rates of 1–104 mm/24 hours (Komatsu and Chiba, 1993).
Effects of strain relaxation and as a result the association of the root with the bone were identified in our virtual sections. Before scanning the specimen under loaded conditions, it is necessary to bring the system to an equilibrium state, i.e. under static load. During this process, we were able to map the decay of peak reactionary loads (Fig. S2) and, as a result, displacements (Fig. 3) within the complex. For a higher peak reactionary load of 20 N, higher strain relaxation was observed (Fig. S2c). Following an equilibrated position, the relative position of the root to the bone was analyzed using DIC. It should be noted that while the load-displacement curves provided the total displacement of the tooth into the alveolar socket at any given instance of time, the displacement observed using DIC was equivalent to the equilibrated condition at the time of scanning the specimen. During the time taken to equilibrate which is equivalent to 1 hour, it is only inevitable that complex could have recovered to a displacement equivalent to a reactionary load of 16–17 N (Fig. S1a). As such, we suspect that DIC calculations of tooth position would be more accurate under loading conditions at 0.2 mm/min, during which there is decreased strain hardening (Fig. S2c – decay curves for a peak reactionary load of 20 N compared to 5 N), and resultant delayed tooth movement.
Lack of identical tooth sections despite having identical AB sections illustrated a seminal biomechanical response of the tooth relative to the bone. Results illustrate that in response to uniaxial loading, the tooth could initially undergo vertical displacement predominantly in the first 5 N (Fig. 3, 4a.1.) of reactionary load, during which uncrimping of collagen (Miller et al., 2012) and partial pumping of interstitial fluid into endosteal and bone marrow spaces could occur (S5N = 290–523 N/mm) (Bergomi et al., 2010). Upon increased loading, strain hardening of collagen and hydrostatic pressure of tissues could play a significant role (Fig. 4a.2.), with contribution from mineralized tissues coming into play at loads above 10 N (S10N-20N = 380–684 N/mm; Fig. 4a.3). Fracture of alveolar bone was observed in some specimens at 15 N and 20 N of load response (Fig. 4a.4.). The increase in hard tissue influence at intermediate loads (10–15 N) and fracture of bone at higher loads (15–20 N) could have contributed to the lack of significant differences in stiffness and reactionary load rate between 15 N and 20 N of peak reactionary load. As such, 15 N is the suggested upper limit for future studies on fibrous joint mechanics of rat maxilla with the loading system used in this study.
Figure 4. Biomechanical response model of a rat molar within the AB socket.
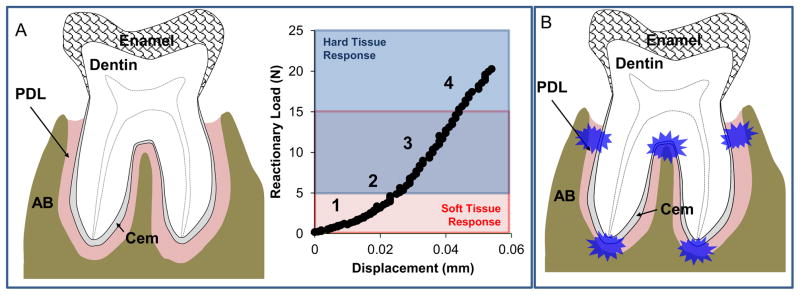
Soft (red box) and hard (blue box) tissue responses are demarcated within a representative load-displacement curve derived from compression testing. Numbered segments within the curve represent different stages of the progression of tooth movement within the alveolar socket. The response of the fibrous joint is illustrated in the subsequent images: (1) response to initial tooth movement up to 5 N response to uniaxial load, (2) increasing tension and compression of PDL with strain hardening effects along with (3) possible deformation of hard tissues within the tooth and AB under higher loads, and (4) fracture of the alveolar bone and/or tooth under increased loading. (B) Proposed concentrated areas of strain within PDL are illustrated in blue.
Based on DIC results, compressive loads can promote a see-saw like motion about the interradicular fulcrum coupled with torsion (i.e., screw-motion) (Fig. S3a, b; Supplemental Videos 1 and 2, please open movies with QuickTime™) (Chattah et al., 2009; Christiansen and Burstone, 1969). Hence, the downward screw-motion can promote opposing strain fields within the complex. These can be compression and tension fields within local regions that occur as “hotspots” within the bone-PDL-cementum complex depending on the direction in which the tooth rotates and translates (Fig. 4b). As a result, it is likely that cyclic loading due to chewing can promote a compression zone opposing a tension zone within the same complex. While the rotation could be in excess of load-direction and also depends on the morphology of the bone-PDL-tooth joint, results presented in the manuscript arguably should be viewed as a condition indicative of natural tooth biomechanics in the animal. The in vivo horizontal force vectors on the maxillary molar could promote a greater rotational displacement within the socket than seen in our predominantly axial loading experiments, and in turn can increase the number of experimentally observed “hot spots”. Regardless, compression-based strain fields are known to promote resorption in bone, while tension-based strain fields are known to promote mineral formation. As such, with cyclic chewing loads, it is expected that tension-based and compression-based strain fields in the complex can promote subsequent cellular response for continuous physiological remodeling and maintenance (Beertsen et al., 1997; Herber et al., 2012) or pathological adaptations leading to function impairment (Bartold, 2012; Hurng et al., 2011; Wolff, 1986).
Supplementary Material
Supplemental Figure 1. Validation of the in situ loading device with polydimethylsiloxane (PDMS), poly(methyl methacrylate) (PMMA), and aluminum (Al). Characteristic loading curves were plotted in (A) load vs. time for PDMS (1:5, 1:25, 1:45), Al, and PMMA; (B) displacement vs. time at 2.0 mm/min for PDMS (ratios of 1:5, 1:25, 1:45), Al, and PMMA; and (C) load vs. displacement for PDMS (ratios of 1:5, 1:25, 1:45), Al, and PMMA. Averages of reactionary load rates (D) and stiffness values (E) across peak reactionary loads for each PMMA crosslinking density were plotted against displacement rate. Note: 1:45 PDMS did not exhibit a detectable load rate response because material deformation exceeded the limits of the instrument. Reactionary load rate (N/s) and stiffness (N/mm) were calculated from the linear region of curves representative of respective peak reactionary loads. Shaded regions illustrate upper and lower limits within one standard deviation of average reactionary load rates (D, red – 1:5 PDMS, blue – 1:25 PDMS) and stiffness values (E, red – 1:5 PDMS, blue – 1:25 PDMS) across all peak reactionary loads at each displacement rate. ¥ Parameters indicating increased stiffness of the mechanical testing device as determined by compressing Al.
Supplemental Figure 2. Effect of time on reactionary load during mechanical testing (shorter time) and tomography (longer time). (A) Representative load vs. time curves from the point of initial contact to the peak reactionary load are shown for loading at an input displacement rate of 2.0 mm/min. The illustrated load-time curves are the loading portion of the load relaxation curves shown in C (box). (B) Corresponding representative load-displacement curves for each peak reactionary load are illustrated. (C) Representative load relaxation curves illustrate higher load decay when loaded to 20N compared to 5N.
Supplemental Figure 3. Tooth displacement through the fibrous joint in response to increasing occlusal compression. Top row: Superposition of 2D virtual sections illustrate the position of the mesial-distal roots (A) and buccal-lingual roots (B) of the second maxillary molar in the alveolar socket in different views (4x magnification) at various peak reactionary loads (no load, 5, 10, 20 N) and displacement rate of 2.0 mm/min (Note: please open movies using QuickTime™); Bottom row: 3D rendering using Avizo illustrates the relationship of the second maxillary molar (green, middle) to bone (purple), highlighting maximum displacement at the interradicular tooth region and interradicular bone (circle), at no load (C) and 5 N (35 μm, D), 10 N (40 μm, E), and 20 N (50 μm, F) of load.
Acknowledgments
The authors thank Dr. Dwayne Arola, University of Maryland Baltimore County, Baltimore, Maryland, U.S.; Drs. Stephen Weiner and Gili Naveh, Weizmann Institute of Science, Rehovot, Israel; Dr. Ron Shahar, The Hebrew University of Jerusalem, Israel for their insightful discussions specific to the in situ loading device. The authors also like to thank Biomaterials and Bioengineering MicroCT Imaging Facility, UCSF for the use of Micro XCT, and in situ loading device. Support was provided by NIH/NIDCR R00DE018212, NIH/NIDCR R01DE022032, NIH/NIDCR T32 DE07306-14, NIH/NCRR S10RR026645, and Departments of Preventive and Restorative Dental Sciences and Orofacial Sciences, UCSF.
Footnotes
We acknowledge that all authors do not have conflict of interest, and were fully involved in the study and preparation of the manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Asundi A, Kishen A. A strain gauge and photoelastic analysis of in vivo strain and in vitro stress distribution in human dental supporting structures. Archives of oral biology. 2000;45:543–550. doi: 10.1016/s0003-9969(00)00031-5. [DOI] [PubMed] [Google Scholar]
- Asundi A, Kishen A. Advanced digital photoelastic investigations on the tooth-bone interface. Journal of biomedical optics. 2001;6:224–230. doi: 10.1117/1.1344587. [DOI] [PubMed] [Google Scholar]
- Bartold PM. Bone and Tooth Interface: Periodontal Ligament. In: McCauley LK, Somerman MJ, editors. Mineralized Tissues in Oral and Craniofacial Science Biological Principles and Clinical Correlates. 1. Vol. 224. A John Wiley & Sons, Inc; 2012. p. 227. [Google Scholar]
- Beertsen W, McCulloch CA, Sodek J. The periodontal ligament: a unique, multifunctional connective tissue. Periodontology 2000. 1997;13:20–40. doi: 10.1111/j.1600-0757.1997.tb00094.x. [DOI] [PubMed] [Google Scholar]
- Bergomi M, Cugnoni J, Botsis J, Belser UC, Anselm Wiskott HW. The role of the fluid phase in the viscous response of bovine periodontal ligament. Journal of biomechanics. 2010;43:1146–1152. doi: 10.1016/j.jbiomech.2009.12.020. [DOI] [PubMed] [Google Scholar]
- Berkovitz BK. The structure of the periodontal ligament: an update. European journal of orthodontics. 1990;12:51–76. doi: 10.1093/ejo/12.1.51. [DOI] [PubMed] [Google Scholar]
- Carvalho RM, Yoshiyama M, Pashley EL, Pashley DH. In vitro study on the dimensional changes of human dentine after demineralization. Archives of oral biology. 1996;41:369–377. doi: 10.1016/0003-9969(95)00115-8. [DOI] [PubMed] [Google Scholar]
- Cattaneo PM, Dalstra M, Melsen B. The finite element method: a tool to study orthodontic tooth movement. Journal of dental research. 2005;84:428–433. doi: 10.1177/154405910508400506. [DOI] [PubMed] [Google Scholar]
- Chattah NLT, Shahar R, Weiner S. Design strategy of minipig molars using electronic speckle pattern interferometry: comparison of deformation under load between the tooth-mandible complex and the isolated tooth. Advanced Materials. 2009;21:413–418. [Google Scholar]
- Chiba M, Komatsu K. Mechanical responses of the periodontal ligament in the transverse section of the rat mandibular incisor at various velocities of loading in vitro. Journal of biomechanics. 1993;26:561–570. doi: 10.1016/0021-9290(93)90017-9. [DOI] [PubMed] [Google Scholar]
- Christiansen RL, Burstone CJ. Centers of rotation within the periodontal space. American journal of orthodontics. 1969;55:353–369. doi: 10.1016/0002-9416(69)90143-2. [DOI] [PubMed] [Google Scholar]
- Dickinson AS, Taylor AC, Browne M. The influence of acetabular cup material on pelvis cortex surface strains, measured using digital image correlation. Journal of biomechanics. 2012;45:719–723. doi: 10.1016/j.jbiomech.2011.11.042. [DOI] [PubMed] [Google Scholar]
- Embery G, Waddington RJ, Hall RC, Last KS. Connective tissue elements as diagnostic aids in periodontology. Periodontology 2000. 2000;24:193–214. doi: 10.1034/j.1600-0757.2000.2240109.x. [DOI] [PubMed] [Google Scholar]
- Fung YC. Biomechanics: Mechanical Properties of Living Tissues. 2. Springer-Verlag New York, Inc; New York, New York: 1993. [Google Scholar]
- Graber TM, Vanarsdall JR. Bone Physiology, Metabolism, and Biomechanics in Orthodontic Practice, Orthodontics Current Principles and Techniques. Mosby-Year Book, Inc; St. Louis, Missouri: 1994. pp. 210–228. [Google Scholar]
- Herber RP, Fong J, Lucas SA, Ho SP. Imaging an adapted dentoalveolar complex. Anat Res Int. 2012;2012:782571. doi: 10.1155/2012/782571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herring SW. Biomechanics of teeth in bone: function, movement, and prosthetic rehabilitation. In: McCauley LK, Somerman MJ, editors. Mineralized Tissues in Oral and Craniofacial Sceince Biological Principles and Clincal Correlates. 1. A John Wiley & Sons Inc; 2012. p. 255. [Google Scholar]
- Hiiemae K. The structure and function of the jaw muscles in the rat (Rattus norvegicus L.) Zoological Journal of the Linnean Society. 1971;50:111–132. [Google Scholar]
- Hiiemae K. Mechanisms of food reduction, transport and deglutition: how the texture of food affects feeding behavior. Journal of Texture Studies. 2004;35:171–200. [Google Scholar]
- Hiiemae KM. Masticatory function in the mammals. Journal of dental research. 1967;46:883–893. doi: 10.1177/00220345670460054601. [DOI] [PubMed] [Google Scholar]
- Ho SP, Sulyanto RM, Marshall SJ, Marshall GW. The cementum-dentin junction also contains glycosaminoglycans and collagen fibrils. Journal of structural biology. 2005;151:69–78. doi: 10.1016/j.jsb.2005.05.003. [DOI] [PubMed] [Google Scholar]
- Hunt HR, Rosen S, Hoppert CA. Morphology of molar teeth and occlusion in young rats. Journal of dental research. 1970;49:508–514. doi: 10.1177/00220345700490030701. [DOI] [PubMed] [Google Scholar]
- Hurng JM, Kurylo MP, Marshall GW, Webb SM, Ryder MI, Ho SP. Discontinuities in the human bone-PDL-cementum complex. Biomaterials. 2011;32:7106–7117. doi: 10.1016/j.biomaterials.2011.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jantarat J, Palamara JE, Messer HH. An investigation of cuspal deformation and delayed recovery after occlusal loading. Journal of dentistry. 2001;29:363–370. doi: 10.1016/s0300-5712(01)00018-5. [DOI] [PubMed] [Google Scholar]
- Komatsu K. Mechanical strength and viscoelastic response of the periodontal ligament in relation to structure. Journal of dental biomechanics. 2010;2010 doi: 10.4061/2010/502318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komatsu K, Chiba M. The effect of velocity of loading on the biomechanical responses of the periodontal ligament in transverse sections of the rat molar in vitro. Archives of oral biology. 1993;38:369–375. doi: 10.1016/0003-9969(93)90207-3. [DOI] [PubMed] [Google Scholar]
- Komatsu K, Kanazashi M, Shimada A, Shibata T, Viidik A, Chiba M. Effects of age on the stress-strain and stress-relaxation properties of the rat molar periodontal ligament. Archives of oral biology. 2004;49:817–824. doi: 10.1016/j.archoralbio.2004.04.002. [DOI] [PubMed] [Google Scholar]
- Lin JD, Özcoban H, Ryder MI, Ho SP. Loading rate response of a diseased bone-tooth fibrous joint. 41st Annual Meeting & Exhibition of the American Association for Dental Research; Tampa, FL. 2012. p. Abstract number 106. [Google Scholar]
- Luan X, Ito Y, Holliday S, Walker C, Daniel J, Galang TM, Fukui T, Yamane A, Begole E, Evans C, Diekwisch TG. Extracellular matrix-mediated tissue remodeling following axial movement of teeth. The journal of histochemistry and cytochemistry: official journal of the Histochemistry Society. 2007;55:127–140. doi: 10.1369/jhc.6A7018.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCulloch CA, Lekic P, McKee MD. Role of physical forces in regulating the form and function of the periodontal ligament. Periodontology 2000. 2000;24:56–72. doi: 10.1034/j.1600-0757.2000.2240104.x. [DOI] [PubMed] [Google Scholar]
- Miller KS, Connizzo BK, Feeney E, Tucker JJ, Soslowsky LJ. Examining differences in local collagen fiber crimp frequency throughout mechanical testing in a developmental mouse supraspinatus tendon model. Journal of biomechanical engineering. 2012;134:041004. doi: 10.1115/1.4006538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nanci A, Bosshardt DD. Structure of periodontal tissues in health and disease. Periodontology 2000. 2006;40:11–28. doi: 10.1111/j.1600-0757.2005.00141.x. [DOI] [PubMed] [Google Scholar]
- Naveh GR, Shahar R, Brumfeld V, Weiner S. Tooth movements are guided by specific contact areas between the tooth root and the jaw bone: A dynamic 3D microCT study of the rat molar. Journal of structural biology. 2012;177:477–483. doi: 10.1016/j.jsb.2011.11.019. [DOI] [PubMed] [Google Scholar]
- Nies M, Ro JY. Bite force measurement in awake rats. Brain research. Brain research protocols. 2004;12:180–185. doi: 10.1016/j.brainresprot.2003.11.003. [DOI] [PubMed] [Google Scholar]
- Niver EL, Leong N, Greene J, Curtis D, Ryder MI, Ho SP. Reduced functional loads alter the physical characteristics of the bone-periodontal ligament-cementum complex. Journal of periodontal research. 2011;46:730–741. doi: 10.1111/j.1600-0765.2011.01396.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okotie G, Duenwald-Kuehl S, Kobayashi H, Wu MJ, Vanderby R. Tendon strain measurements with dynamic ultrasound images: evaluation of digital image correlation. Journal of biomechanical engineering. 2012;134:024504. doi: 10.1115/1.4006116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papadopoulou K, Keilig L, Eliades T, Krause R, Jager A, Bourauel C. The time-dependent biomechanical behaviour of the periodontal ligament--an in vitro experimental study in minipig mandibular two-rooted premolars. European journal of orthodontics. 2011 doi: 10.1093/ejo/cjr134. [DOI] [PubMed] [Google Scholar]
- Popowics T, Yeh K, Rafferty K, Herring S. Functional cues in the development of osseous tooth support in the pig, Sus scrofa. Journal of biomechanics. 2009;42:1961–1966. doi: 10.1016/j.jbiomech.2009.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popowics TE, Rensberger JM, Herring SW. Enamel microstructure and microstrain in the fracture of human and pig molar cusps. Archives of oral biology. 2004;49:595–605. doi: 10.1016/j.archoralbio.2004.01.016. [DOI] [PubMed] [Google Scholar]
- Qian L, Todo M, Morita Y, Matsushita Y, Koyano K. Deformation analysis of the periodontium considering the viscoelasticity of the periodontal ligament. Dental materials: official publication of the Academy of Dental Materials. 2009;25:1285–1292. doi: 10.1016/j.dental.2009.03.014. [DOI] [PubMed] [Google Scholar]
- Roberts WE. Bone dynamics of osseointegration, ankylosis, and tooth movement. J Indiana Dent Assoc. 1999;78:24–32. [PubMed] [Google Scholar]
- Ten Cate R. Oral histology: development, structure, and function. Mosby-Year Book, Inc; 1998. [Google Scholar]
- Thomas NR, Peyton SC. An electromyographic study of mastication in the freely-moving rat. Archives of oral biology. 1983;28:939–945. doi: 10.1016/0003-9969(83)90090-0. [DOI] [PubMed] [Google Scholar]
- Ujiie Y, Shimada A, Komatsu K, Gomi K, Oida S, Arai T, Fukae M. Degradation of noncollagenous components by neutrophil elastase reduces the mechanical strength of rat periodontal ligament. Journal of periodontal research. 2008;43:22–31. doi: 10.1111/j.1600-0765.2007.00990.x. [DOI] [PubMed] [Google Scholar]
- Wang RZ, Weiner S. Strain-structure relations in human teeth using Moire fringes. Journal of biomechanics. 1998;31:135–141. doi: 10.1016/s0021-9290(97)00131-0. [DOI] [PubMed] [Google Scholar]
- Wolff J. The law of bone remodelling. Springer-Verlag; Berlin; New York: 1986. [Google Scholar]
- Wood JD, Wang R, Weiner S, Pashley DH. Mapping of tooth deformation caused by moisture change using moire interferometry. Dental materials: official publication of the Academy of Dental Materials. 2003;19:159–166. doi: 10.1016/s0109-5641(02)00025-8. [DOI] [PubMed] [Google Scholar]
- Zaslansky P, Currey JD, Friesem AA, Weiner S. Phase shifting speckle interferometry for determination of strain and Young’s modulus of mineralized biological materials: a study of tooth dentin compression in water. Journal of biomedical optics. 2005;10:024020. doi: 10.1117/1.1891505. [DOI] [PubMed] [Google Scholar]
- Zaslansky P, Friesem AA, Weiner S. Structure and mechanical properties of the soft zone separating bulk dentin and enamel in crowns of human teeth: insight into tooth function. Journal of structural biology. 2006;153:188–199. doi: 10.1016/j.jsb.2005.10.010. [DOI] [PubMed] [Google Scholar]
- Zhang D, Mao S, Lu C, Romberg E, Arola D. Dehydration and the dynamic dimensional changes within dentin and enamel. Dental materials: official publication of the Academy of Dental Materials. 2009;25:937–945. doi: 10.1016/j.dental.2009.01.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziegler A, Keilig L, Kawarizadeh A, Jager A, Bourauel C. Numerical simulation of the biomechanical behaviour of multi-rooted teeth. European journal of orthodontics. 2005;27:333–339. doi: 10.1093/ejo/cji020. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Figure 1. Validation of the in situ loading device with polydimethylsiloxane (PDMS), poly(methyl methacrylate) (PMMA), and aluminum (Al). Characteristic loading curves were plotted in (A) load vs. time for PDMS (1:5, 1:25, 1:45), Al, and PMMA; (B) displacement vs. time at 2.0 mm/min for PDMS (ratios of 1:5, 1:25, 1:45), Al, and PMMA; and (C) load vs. displacement for PDMS (ratios of 1:5, 1:25, 1:45), Al, and PMMA. Averages of reactionary load rates (D) and stiffness values (E) across peak reactionary loads for each PMMA crosslinking density were plotted against displacement rate. Note: 1:45 PDMS did not exhibit a detectable load rate response because material deformation exceeded the limits of the instrument. Reactionary load rate (N/s) and stiffness (N/mm) were calculated from the linear region of curves representative of respective peak reactionary loads. Shaded regions illustrate upper and lower limits within one standard deviation of average reactionary load rates (D, red – 1:5 PDMS, blue – 1:25 PDMS) and stiffness values (E, red – 1:5 PDMS, blue – 1:25 PDMS) across all peak reactionary loads at each displacement rate. ¥ Parameters indicating increased stiffness of the mechanical testing device as determined by compressing Al.
Supplemental Figure 2. Effect of time on reactionary load during mechanical testing (shorter time) and tomography (longer time). (A) Representative load vs. time curves from the point of initial contact to the peak reactionary load are shown for loading at an input displacement rate of 2.0 mm/min. The illustrated load-time curves are the loading portion of the load relaxation curves shown in C (box). (B) Corresponding representative load-displacement curves for each peak reactionary load are illustrated. (C) Representative load relaxation curves illustrate higher load decay when loaded to 20N compared to 5N.
Supplemental Figure 3. Tooth displacement through the fibrous joint in response to increasing occlusal compression. Top row: Superposition of 2D virtual sections illustrate the position of the mesial-distal roots (A) and buccal-lingual roots (B) of the second maxillary molar in the alveolar socket in different views (4x magnification) at various peak reactionary loads (no load, 5, 10, 20 N) and displacement rate of 2.0 mm/min (Note: please open movies using QuickTime™); Bottom row: 3D rendering using Avizo illustrates the relationship of the second maxillary molar (green, middle) to bone (purple), highlighting maximum displacement at the interradicular tooth region and interradicular bone (circle), at no load (C) and 5 N (35 μm, D), 10 N (40 μm, E), and 20 N (50 μm, F) of load.