Evaluating efficiency-equality tradeoffs for mobile source control strategies in an urban area

Abstract

In environmental risk management, there are often interests in maximizing public health benefits (efficiency) and addressing inequality in the distribution of health outcomes. However, both dimensions are not generally considered within a single analytical framework. In this study, we estimate both total population health benefits and changes in quantitative indicators of health inequality for a number of alternative spatial distributions of diesel particulate filter retrofits across half of an urban bus fleet in Boston, Massachusetts. We focus on the impact of emissions controls on primary fine particulate matter (PM_2.5) emissions, modeling the effect on PM_2.5 concentrations and premature mortality. Given spatial heterogeneity in baseline mortality rates, we apply the Atkinson index and other inequality indicators to quantify changes in the distribution of mortality risk. Across the different spatial distributions of control strategies, the public health benefits varied by more than a factor of two, related to factors such as mileage driven per day, population density near roadways, and baseline mortality rates in exposed populations. Changes in health inequality indicators varied across control strategies, with the subset of optimal strategies considering both efficiency and equality generally robust across different parametric assumptions and inequality indicators. Our analysis demonstrates the viability of formal analytical approaches to jointly address both efficiency and equality in risk assessment, providing a tool for decision-makers who wish to consider both issues.

1. Introduction

When comparing pollution control strategies, risk managers may be concerned with both the magnitude and distribution of costs and benefits. While methods to quantify total population health benefits have been well defined and extensively applied ^(1-3), there have been fewer examples where the distribution of benefits has been simultaneously and quantitatively evaluated. Previous studies have developed approaches to quantify inequality in health risks either with a focus on baseline distributions of risk ^(4-6) or with consideration of how control strategies would influence measures of inequality for a defined health outcome ⁽⁷⁾. In the study focused on control strategies, the measures of inequality were chosen to adhere to axioms ⁽⁸⁾ that allowed the measures to be interpretable from a benefit-cost analysis perspective. Using these inequality indicators, measures of efficiency (the total public health benefits) and inequality (the distribution of those benefits given baseline health risks and characteristics of at-risk individuals) could be compared across control scenarios. This would allow risk managers to rule out the subset of control strategies that are worse from both efficiency and equality perspectives, formally consider the tradeoffs between efficiency and equality for the remaining control strategies, and ultimately choose strategies given tradeoff preferences.

While these studies have provided a template for the joint consideration of efficiency and equality when evaluating control strategies, some significant limitations remain. First, studies that focused on cancer endpoints ^{(5, 6)} did not consider dimensions of vulnerability that may follow defined spatial patterns and contribute to concerns about health inequality. An application looking at the impact of power plant pollution control on fine particulate matter (PM_2.5) mortality ⁽⁷⁾ did consider differential baseline mortality rates by county, a level of geographic resolution appropriate for emissions from tall stacks, but this may mask within-county heterogeneity that may contribute significantly to risk inequality for mobile or area sources. No studies specifically addressed spatial patterns of mobile source primary air pollutants (those directly emitted, as opposed to secondary pollutants formed over time in the atmosphere), for which many limitations are heightened. Given relatively steep concentration gradients ⁽⁹⁾, risk assessments may need to be conducted at fine spatial scales, posing challenges for exposure modeling and development of appropriate concentration-response functions.

In this study, we consider a case example of tailpipe emission controls for primary PM_2.5 emitted by diesel buses in an urban area. In many cities around the world, there is substantial interest in designing and implementing pollution control strategies for diesel buses. While fleet upgrades can be made by purchasing new compressed natural gas or emission-controlled diesel buses, many cities and states are also considering retrofits to existing buses given the long lifespan of diesel engines and the potential reduced cost of retrofits compared to new vehicle procurement. One common retrofit under consideration involves retrofitting post-1995 buses with diesel particulate filters (DPFs), which reduce primary PM_2.5 emissions by 80-95% while significantly reducing carbon monoxide and hydrocarbon emissions as well ^{(10, 11)}.

A city or transportation authority may lack the funding to retrofit every bus in its fleet. A crucial question would involve how to best utilize limited funding to maximize public health benefits while simultaneously considering health inequality. The latter concern would be salient in this context, given the strong interest within many urban community organizations in addressing diesel vehicle emissions and the desire among many stakeholders to reduce existing health disparities in urban settings. The question of how to best utilize a fixed amount of pollution control funding given system constraints and multiple attributes of interest to decision makers can be generalized to many settings beyond urban bus retrofits.

In this study, we develop a hypothetical case based on the bus fleet of the Massachusetts Bay Transportation Authority (MBTA). We assume that the MBTA has funds available to retrofit exactly half of existing buses on defined routes. This does not correspond with an actual MBTA policy decision (in fact, many buses have already been retrofitted with DPFs), but is illustrative of a risk management decision optimizing use of limited resources. We utilize dispersion modeling outputs ⁽¹²⁾ and quantify exposure reductions under a variety of possible control scenarios. We link this information with spatially-resolved baseline mortality rate data, using concentration-response functions derived from the epidemiological literature, and quantify the impact of each control scenario on the public health benefits and the change in the spatial distribution of mortality risks across the impacted area. We consider the degree to which efficiency-equality tradeoffs exist as well as the characteristics of optimal control strategies, and determine the sensitivity of our conclusions to key model assumptions.

2. Methods

2.1. Bus route selection

We presumed for this hypothetical analysis that only those bus routes found entirely within Boston were under consideration for controls. We also assumed that a bus would travel on the same route each day, so that retrofitting a bus involved reducing emissions on a selected route (alternatively, the control scenarios could be considered as selecting routes to control, with corresponding selection of buses given usage patterns). While these assumptions may not correspond with actual practices, they make our analysis computationally feasible and more readily interpretable, and the methods are generalizable to more complex scenarios.

To determine which routes would be included and which road segments were covered by these routes, we used ESRI StreetMap 8.3 data. These data are derived from 2000 US Census TIGER files and match well with census block boundaries (a census block generally corresponds with a city block in urban areas). The StreetMap road segments were linked with an electronic shapefile from the Central Transportation Planning Staff of the Boston Metropolitan Planning Organization (MPO), which included a separate record for each of 1,068 bus route variations. These route variations were consolidated into two variations (inbound and outbound) for each route that covered the entire spatial extent of all of the variations. Given differences of as much as 30 to 50 m in the locations of the StreetMap road centerlines and the MPO bus route locations, we linked the MPO street map bus routes to the nearest StreetMap segments, and errors were manually corrected by visual inspection. This resulted in 45 bus routes that were included in our study, which spanned much of the city (Figure 1).

Figure 1.

Location of 45 bus routes considered for control scenarios, overlaid on census tract boundaries with age-adjusted mortality rates among populations over age 30.

2.2. Emissions

The primary PM_2.5 emissions avoided through use of the DPF are the product of the uncontrolled diesel bus emissions (g/vehicle mile), the DPF efficiency, and the number of miles traveled per bus per day. For the calculation of mileage, the length of each bus route was obtained from summing the lengths of the road segments in each route in ArcGIS, and the average number of loops per day per bus was estimated from a Spring 2006 route operations table provided by the MBTA ⁽¹³⁾.

Uncontrolled PM_2.5 emissions during operation were estimated to vary between 0.17 and 0.51 g/vehicle mile ⁽¹⁴⁾. The DPF efficiency for PM_2.5 is quite high, typically over 90% ⁽¹⁰⁾. For our base calculations, we assumed uncontrolled diesel emissions of 0.32 g/vehicle mile and DPF efficiency of 90%, resulting in control benefits of 0.29 g/vehicle mile, but tested the sensitivity of our conclusions to alternative values of 0.14 g/vehicle mile (assuming 0.17 g/vehicle mile at baseline and 85% control efficiency) and 0.50 g/vehicle mile (assuming 0.51 g/vehicle mile at baseline and 99% control efficiency). While uniform changes in values such as per-vehicle emissions reductions would not influence the rank-ordering of health benefits estimates across control scenarios, they could in theory influence the rank-ordering of changes in some inequality measures, so we conduct a series of sensitivity analyses to determine the robustness of our findings. However, we do not conduct formal uncertainty propagation given limited information for key parameters and our focus on characterizing efficiency-equality tradeoffs rather than explicitly determining net benefits of controls.

2.3. Exposure modeling

Given that 5,232 individual road segments (as defined by ArcGIS) were covered by the 45 selected bus routes, atmospheric dispersion modeling accounting for local conditions for each road segment across multiple control scenarios was implausible. Instead, we relied on modeling work conducted previously for all road segments in the Boston metropolitan core ⁽¹²⁾. In this study, the CAL3QHCR line-source dispersion model was applied to each road segment for each hour of the year, using unit emissions and presuming no differences in meteorology, orientation, or topography across road segments. While the latter assumptions will contribute uncertainty to the analysis, the use of unit emissions contributes minimal uncertainty given a generally linear relationship between emissions and incremental concentrations for primary pollutants (i.e., if emissions on a roadway doubled, the incremental concentrations associated with that roadway alone, excluding background, would approximately double as well).

For each road segment, we estimated its contribution to annual average PM_2.5 concentrations (given the health outcome of interest) at each census block within 5000 m of the roadway. The CAL3QHCR model outputs included impacts of unit emissions at various fixed distances from the roadway. We interpolated concentrations at other distances with a log-log regression of concentration estimates as a function of distance, which fit the CAL3QHCR outputs extremely well (R² > 0.99). The concentration increments associated with unit emissions were then combined with estimated bus route emissions reductions to estimate exposure reductions. The spatial extent of the dispersion modeling was greater than what is typically used for CAL3QHCR, given our interest in estimating public health benefits and previous findings that indicated the potential contribution of populations at longer range ⁽¹⁵⁾.

To determine the importance of spatial resolution of exposure assessment, we also estimated exposures at the lower-resolution census tract level. Census tracts average about 4,000 people and are established to be relatively demographically homogeneous. We assigned all individuals within the census tract to the exposure estimated at the centroid of the tract, and compared the results with the census block-level exposure assessment.

Along with the direct concentration outputs, we also estimated the primary PM_2.5 intake fraction for each road segment, reflecting the fraction of emissions inhaled by the population ⁽¹⁶⁾. This measure is an indicator of which roadways would yield the greatest population exposure reductions (a function of both concentration gradients and population density) if controlled by the same amount. The intake fractions were used to develop a subset of the control scenarios, as described below. The intake fractions were calculated on populations age 30 and over, to correspond with the concentration-response function; these values were highly correlated (r > 0.99) with total population intake fractions and would yield identical rankings of routes by population exposure reductions.

2.4. Concentration-response functions

In this analysis, we focus on premature mortality from PM_2.5, which has previously been shown to dominate monetized health benefits of PM_2.5 controls ^{(1, 17)}. Furthermore, we focus on long-term rather than short-term exposures, since cohort study estimates have generally dominated time-series estimates from a health benefits perspective. Of the published cohort studies yielding concentration-response functions for premature mortality ⁽¹⁸⁾, the Harvard Six Cities study and the American Cancer Society study provide the most applicable estimates, given their focus on general populations and extensive peer review and re-analysis. Recent Six Cities publications report central estimates between 1.2% ⁽¹⁹⁾ and 1.6% ⁽²⁰⁾ increases in all-cause mortality per μg/m³ increase in annual average PM_2.5. The most recent publication from the full American Cancer Society cohort ⁽²¹⁾ yielded a central estimate of a 0.6% increase in all-cause mortality per μg/m³ increase in annual average PM_2.5.

However, these publications used coarse spatial resolution exposure measures to develop their concentration-response functions, which may result in exposure misclassification (and is not aligned with the fine spatial resolution of our exposure assessment). An analysis of a subset of the American Cancer Society cohort using more spatially refined exposure characterization yielded a central estimate of a 1.7% increase in all-cause mortality per μg/m³ increase in annual average PM_2.5 ⁽²²⁾, indicating that past studies may have underestimated the effects of PM_2.5. Given the totality of evidence, we consider a 1% increase in all-cause mortality per μg/m³ increase in annual average PM_2.5 to represent a reasonable central estimate for our primary calculations. We test the sensitivity of our conclusions to plausible alternative concentration-response function values, meant to capture general uncertainty within the epidemiological literature, issues related to the differences in spatial resolution between our exposure estimates and the concentration-response functions, and any potential differences in toxicity between diesel primary PM_2.5 and PM_2.5 as a whole. We consider a lower-bound value of 0.3% and an upper-bound value of 2.0%. These represent the median values across experts for the 5^th and 95^th percentiles of the uncertainty distribution for this concentration-response function, respectively, in an expert elicitation study conducted for the US EPA ⁽²³⁾. Given the population structures in these cohort studies, we apply the function only to individuals age 30 and older.

2.5. Background mortality rates

Because of our interest in patterns of mortality risk at high spatial resolution, information not available from public databases, we obtained records for all individual deaths in the region of interest from the Massachusetts Department of Public Health. Each individual's residential location at time of death was geocoded by TeleAtlas (Lebanon, NH) and associated with a 2000 US census tract. To yield stable mortality rate estimates, we used all deaths from 1995 through 2004, considering census tracts within 5000 m of any road segments included in our study (portions of Suffolk, Middlesex, and Norfolk Counties). To estimate per capita mortality rates for inequality calculations and control scenario development, we used population data from the 2000 US Census, representing a year in the center of the range of dates included in the mortality database. Both deaths and population numbers were stratified by age, allowing us to calculate death rates among those age 30 and older and to estimate both raw and age-adjusted mortality rates (with the latter estimated using Year 2000 standard population data).

2.6. Inequality indicators

Although multiple dimensions of inequality may be of concern for decision makers, we presume that the spatial distribution of mortality risk is of primary interest. Previous studies ⁽²⁴⁾ demonstrated that census tract-level premature mortality in Boston varies significantly and is correlated with poverty rates, indicating that a concern about spatial inequality would be similar to a concern about socioeconomic disparities in this health outcome.

We use the Atkinson index as our primary measure of inequality, as previous studies showed that it was the most interpretable measure for health benefits analysis ⁽⁸⁾. The Atkinson index is defined as:

$$1-{\left[\frac{1}{n}\sum _{i=1}^n{\left[\frac{X_i}{\overline{X}}\right]}^{1-\epsilon }\right]}^{\frac{1}{1-\epsilon }}$$ [1]

where x_i represents the mortality risk for each individual i, n represents the number of individuals affected, and ε is an inequality parameter, where a minimum value of zero indicates no concern about inequality and increasing positive values indicate increasing aversion toward inequality. As with many inequality indicators, the Atkinson index ranges from 0 (perfect equality) to 1 (maximum inequality).

An advantage of the Atkinson index is that the risk analyst does not need to impose any value judgment about what portions of the distribution are more or less important (i.e., relative weights at different percentiles of the distribution), and instead can determine the sensitivity of policy conclusions to the choice of ε. Of note, the Atkinson index was originally constructed for income inequality ⁽²⁵⁾ and displays greater sensitivity to low values than to high values, especially for increasing ε. However, for health risk, we would be more concerned with high values from an inequality standpoint. We therefore apply the Atkinson index both directly to mortality risk and to the inverse of mortality risk, determining the sensitivity of our conclusions to the differing formulation.

As done previously ^{(7, 8)}, we focus on the difference between the Atkinson index at baseline and the Atkinson index subsequent to the implementation of controls, as we are less concerned with the distribution of benefits per se than with the degree to which these benefits exacerbate or ameliorate existing health inequalities. In other words, it is not the fact that some populations receive greater benefits than others from risk management efforts that would be of concern, but rather the degree to which the distribution of these benefits influences current distributions of risk. In addition, we focus on age-adjusted mortality rates at the census tract level, weighted by the population of individuals age 30 and older within the tract. While raw mortality rates are used to calculate health risks, if these values were used in the Atkinson index, it would imply that geographic areas with a preponderance of elderly or younger individuals would be highly influential (particularly concerning given small spatial aggregates), and this would not capture the most common concerns about inequality. As a result, we calculate the changes in the Atkinson index using age-adjusted mortality rates, but use raw mortality rates as well to determine the degree to which our conclusions are affected by the age adjustment.

In addition, while previous work ⁽⁷⁾ showed modest sensitivity to the measure used for baseline inequality characterization (e.g., total mortality vs. PM_2.5-related mortality), the lack of available PM_2.5 concentration data at census tract resolution implies that total mortality is the most useful measure for this application. We test the sensitivity of our conclusions to the use of the Gini index, the mean log deviation, and Theil's entropy index, alternative inequality indicators whose formulation and rationale for inclusion in sensitivity analyses are described elsewhere ⁽⁸⁾.

2.7. Control scenarios

Our aim is to capture control scenarios hypothesized to span the efficiency-equality space, as well as to include more common control strategies for comparison. We obtained a table from the MBTA of the number of vehicles, headways (the time between buses, or inverse of frequency), and mileage per route ⁽¹³⁾. Across the 45 bus routes, we determined that approximately 192 buses were used per day (averaged across weekdays and weekends), so we constructed control scenarios in which 96 buses were retrofit in each case.

We considered control scenarios that included control of half of vehicles on all routes, focusing controls on the highest (or lowest) intake fraction roadways, focusing controls on the highest (or lowest) emission reductions per bus, and focusing controls on routes passing through the highest (or lowest) background mortality rate neighborhoods (Table I). We additionally constructed control scenarios that explicitly maximized (or minimized) health benefits and that represented random selection across routes. The intent of these control scenarios was not to be exhaustive or represent actual strategies the MBTA would likely adopt, but rather to capture a range of distributions of controls that could allow us to examine efficiency-equality tradeoffs.

Table I.

Specified control scenarios for efficiency-equality tradeoff analysis.

Scenario	Retrofit definition
A	50% of buses on each route
B	Starting from the longest routes (higher emissions), going down
C	Starting from the shortest routes (lower emissions), going up
D	Starting from the highest intake fractions (highest population exposure per unit emissions), going down
E	Starting from the lowest intake fractions (lowest population exposure per unit emissions), going up
F	Starting from the highest emissions per bus per day, going down
G	Starting from the lowest emissions per bus per day, going up
H	Starting from the highest population-weighted and concentration-weighted mortality rates in tracts intersected by road segments, going down
I	Starting from the lowest population-weighted and concentration-weighted mortality rates in tracts intersected by road segments, going up
J	Starting from the highest age-adjusted population-weighted and concentration-weighted mortality rates in tracts intersected by road segments, going down
K	Starting from the lowest age-adjusted population-weighted and concentration-weighted mortality rates in tracts intersected by road segments, going up
L	Starting from the highest health benefits per bus, going down
M	Starting from the lowest health benefits per bus, going up
N-R	Random control scenarios (routes chosen at random)

2.8. Analytical framework

For our primary output, we calculate the health benefits of applying DPF retrofits according to the control scenarios outlined in Table I, using the central estimates for all uncertain parameters, and plot these benefits against the change in health inequality using the Atkinson index (with ε = 0.75, in the middle of the range typically applied in the literature ⁽²⁶⁾). Such a plot provides information about which control scenarios are worse from both efficiency and equality perspectives. The remaining strategies involve tradeoffs between efficiency and equality and would be candidates for selection. We term this subset of strategies the optimal efficiency-equality frontier.

We then conduct a series of sensitivity analyses, considering the degree to which any uncertain parameters influence the subset of control scenarios on the optimal efficiency-equality frontier or the rank ordering of different control scenarios from an efficiency or inequality perspective. We focus on the emissions reductions per DPF, the use of census block vs. census tract resolution exposure assessment, the concentration-response function for PM_2.5 mortality, the inequality indicator applied (including different values of ε for the Atkinson index), and the values used within the inequality indicators (including the inverse of health risk and raw rather than age-adjusted mortality rates).

Of note, while it would be most decision-relevant in principle to calculate the net benefits of each control scenario (monetized health benefits less control costs), in this case the control costs are identical across all scenarios, so net benefits would be perfectly correlated with non-monetized health benefits. We therefore omit the valuation step for the sake of brevity and interpretability. All calculations were conducted in SAS version 9.1.

3. Results

As indicated in Figure 1, age-adjusted annual mortality rates among those over age 30 vary across the census tracts within 5000 m of any road segments under study. While the population-weighted average rate is 11.7 deaths per 1000 people per year, the tract-specific rates range from 3.1 to 34 per 1000, with most observations falling within a factor of two of the average (5^th percentile of 7 per 1000, 95^th percentile of 17 per 1000). As shown previously ⁽²⁴⁾, higher rates are found in lower-socioeconomic status census tracts, with heterogeneity observed both between and within neighborhoods. When the inequality indicators were applied to baseline age-adjusted mortality rates, the resulting values were 0.025 for the Atkinson index with ε = 0.75 (values of 0.008, 0.048, and 0.11 for ε = 0.25, 1.5, and 3.0 respectively), 0.031 for Theil's entropy index, 0.032 for the mean log deviation, and 0.13 for the Gini index. There is limited interpretability of the relative magnitudes of these values across indicators or the significance of the value of any one indicator absent the risk management context.

The mortality reduction per retrofitted bus per year varied by approximately a factor of 10 across the routes considered (Table II). This was influenced both by an order of magnitude variation in the emissions reductions per bus (influenced by the number of miles per day a bus travels on a given route) and a factor of three variation in the population exposure per unit emissions reduction (influenced by population density near the roadways). Heterogeneity in baseline mortality rates among the populations exposed to each bus route was influential as well, although the incremental concentration- and population-weighted mortality rate varied across routes by less than a factor of two.

Table II.

Emissions, exposure, and mortality reductions per bus, using central estimates for all parameters. Bus routes are sorted by mortality reduction per bus per year.

Bus route1	Primary PM2.5 emissions reduction per bus (g/day)	Population exposure reduction per unit emissions (intake fraction2)	Mortality reduction per bus per year
192	96	5.3E-06	3.0E-03
191	91	6.0E-06	2.9E-03
16	78	5.0E-06	2.3E-03
11	44	5.8E-06	1.9E-03
45	67	5.2E-06	1.9E-03
9	47	6.2E-06	1.8E-03
20	64	4.5E-06	1.8E-03
10	46	6.1E-06	1.7E-03
120	43	5.9E-06	1.7E-03
15	53	5.9E-06	1.6E-03
43	34	9.1E-06	1.5E-03
55	44	7.3E-06	1.5E-03
3	55	3.7E-06	1.3E-03
26	51	5.1E-06	1.3E-03
30	59	3.9E-06	1.3E-03
37	52	3.5E-06	1.3E-03
44	41	5.4E-06	1.3E-03
8	40	5.2E-06	1.2E-03
23	40	5.4E-06	1.2E-03
31	49	4.6E-06	1.2E-03
39	35	6.3E-06	1.2E-03
7	46	3.4E-06	1.0E-03
50	43	3.7E-06	1.0E-03
22	33	5.4E-06	9.8E-04
38	37	3.6E-06	9.8E-04
41	34	5.2E-06	9.8E-04
14	32	5.0E-06	9.5E-04
36	40	3.1E-06	9.5E-04
40	42	3.3E-06	9.5E-04
28	33	5.0E-06	8.8E-04
42	34	4.7E-06	8.8E-04
18	25	5.9E-06	8.6E-04
21	33	4.8E-06	8.4E-04
17	25	6.1E-06	8.2E-04
29	30	5.0E-06	8.1E-04
19	23	5.6E-06	6.8E-04
24	36	3.5E-06	6.7E-04
48	18	5.8E-06	5.4E-04
6	17	5.6E-06	4.9E-04
32	26	3.3E-06	4.8E-04
5	9	6.4E-06	4.5E-04
121	9	6.5E-06	3.5E-04
4	11	4.7E-06	3.0E-04
27	14	4.0E-06	3.0E-04
277	8	7.2E-06	2.9E-04

¹These route numbers were obtained from a database from the Metropolitan Area Planning Commission and do not in all cases correspond to current MBTA route numbers.

²As conventionally defined, intake fraction is a unitless measure equal to the product of population and concentration change, multiplied by a nominal breathing rate and divided by the emission rate. A nominal breathing rate of 20 m³/day is only used in this case for ease of interpretability and is not a component of the risk calculation. In addition, only the population over age 30 is used in the calculation, given the structure of the risk estimates.

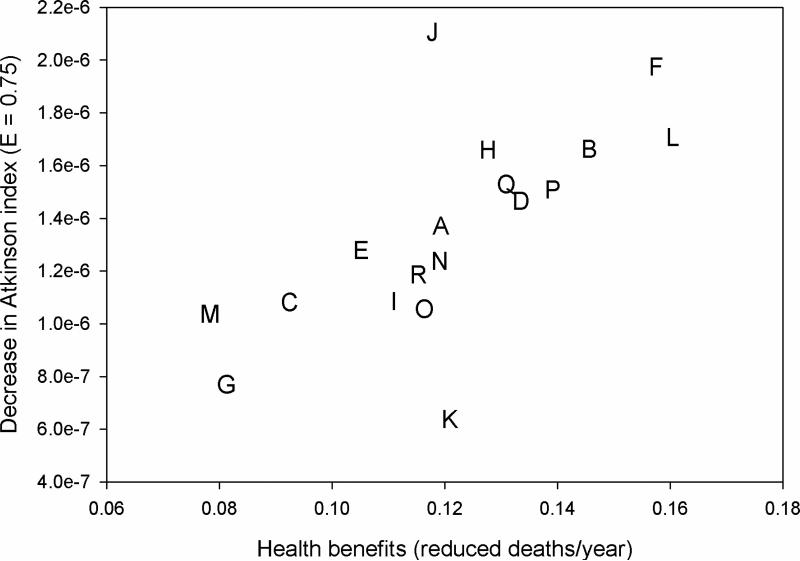
In our base case model (Figure 2), the public health benefits of the control scenarios varied by more than a factor of two, with heterogeneity in the changes in the Atkinson index as applied to age-adjusted mortality rates (ε = 0.75) as well. As would be anticipated, scenario L (control the routes with the highest health benefits per bus first) yielded the greatest public health benefits, while scenario M (control the routes with the lowest health benefits per bus first) was least efficient. The control scenario that most improved health equality was scenario J (control in high age-adjusted mortality regions first), while scenario K (control in low age-adjusted mortality regions first) had the least improvement. Three control scenarios are on the optimal efficiency-equality frontier – scenario J, scenario L, and scenario F (control high-emitting buses first). All other control scenarios are worse for both efficiency and equality, although some of the simpler scenarios were near-optimal (e.g., controlling the longest routes first in scenario B). In many cases, the more efficient scenarios also demonstrated greater reductions in health inequality.

Figure 2.

Annual decrease in mortality and change in the inequality of per-capita age-adjusted mortality risk for mobile source control scenarios. The inequality indicator is the difference in the Atkinson index (ε = 0.75) between the baseline and post-control mortality distribution, where positive values indicate reductions in inequality. The letters represent control scenarios listed in Table I, and points to the upper-right section of the graph represent preferred strategies.

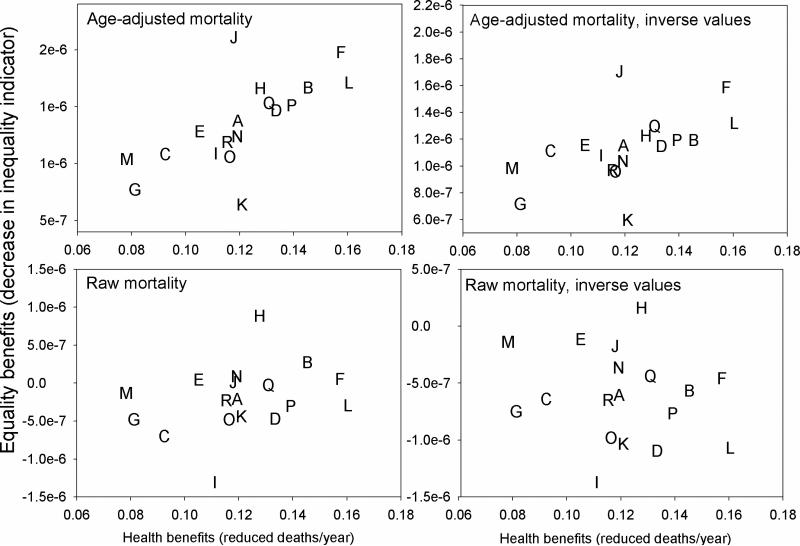
Within our sensitivity analyses, we first consider whether the optimal subset of scenarios is robust to the choice of inequality indicator. Applying our base case model to alternative indicators (including alternative values of ε for the Atkinson index), we find that the optimal frontier is unchanged, and that there are only minor changes in the rank-ordering of control scenarios (results not shown).

Figure 3 presents the sensitivity of our conclusions to the input data used in the inequality indicator. Findings for the Atkinson index (ε = 0.75) are presented, but the conclusions are similar for other inequality measures. When using raw mortality rates rather than age-adjusted rates in the inequality indicators, control scenario H (which uses raw mortality rates) replaces control scenario J on the optimal frontier, and there are some changes in the rank-ordering of control scenarios (Figure 3). When using the inverse of mortality risk within the inequality indicators, the optimal frontiers are unaffected, but other control scenarios change to some degree in their inequality rankings.

Figure 3.

Annual decrease in mortality and change in the inequality of per-capita mortality risk for mobile source control scenarios, using multiple input values within the Atkinson index (ε = 0.75). In each case, the inequality indicator represents the difference between the baseline and post-control mortality distribution, where positive values indicate reductions in inequality. The letters represent control scenarios listed in Table I, and points to the upper-right section of the graph represent preferred strategies.

Testing the sensitivity of our conclusions to the parametric assumptions made for the emissions reduction and the mortality concentration-response function, across all combinations of values for these parameters, there were no changes in the optimal control scenarios or the rank-ordering of control scenarios across all inequality indicators and input values (results not shown).

Finally, we can compare the results of the analysis using census block resolution for exposure assessment with the results had we assigned exposures directly at the census tract level. When benefits are aggregated by bus route, the ratio between block-resolution and tract-resolution benefits ranges from 0.5 to 2.0 (median of 1.1, 5^th percentile of 0.7, 95^th percentile of 1.6), indicating some effect but relatively little systematic bias. When estimated by road segment, the ratio ranges from 0.01 to 11 (median of 1.2, 5^th percentile of 0.6, 95^th percentile of 2.3), indicating that in a small number of cases the population health impact of a given road segment could be misestimated by an order of magnitude or more if exposure assessment were conducted at the census tract level rather than the block level. Thus, spatially refined exposure data would have a greater influence on the distribution of bus route control benefits than on the magnitude of those benefits, especially at the tails of the distribution.

4. Discussion and Conclusions

Our analysis demonstrated the viability of an approach for quantifying both the total public health benefits and changes in health inequality within a single framework. The control scenarios on the optimal frontier in at least one sensitivity analysis, and particularly those that are robust across different parametric assumptions, would be ideal strategies for risk managers concerned about both efficiency and equality. In this case, three control scenarios were robust across all parametric perturbations, provided that the decision-maker was concerned about age-adjusted mortality inequality. Some of these control scenarios are intuitive and could have been selected without a formal analysis (e.g., strategies that explicitly maximize public health benefits will by definition always reside on the optimal efficiency-equality frontier), but our analytical framework is generalizable to any risk management decision aimed at influencing public health.

Interestingly, more efficient control scenarios also tended to do better from an inequality perspective, as shown previously for power plants ⁽⁷⁾. This is because controlling in areas with high baseline risk will tend to be advantageous from both efficiency and equality perspectives. While this concordance between efficiency and equality will not exist in all settings, it will tend to exist when baseline disease rates vary, risk management options can target high-risk areas, and population density is reasonably uniform or positively correlated with baseline disease rates. GIS-based mapping and descriptive statistics for key parameters could therefore help to quickly identify control strategies that may be close to the optimum.

In general, the importance of adopting our framework depends in part on the nature of the control decision. For example, although the benefits per bus varied by an order of magnitude, given an emissions control strategy involving retrofitting half of buses, the benefits per control strategy only varied by a factor of two. As the percentage of buses retrofitted increases, the differences across control scenarios in both health benefits and changes in inequality indicators are reduced, lessening the significance of choosing a sub-optimal strategy. This is due to the fact that the control strategies are increasingly similar, becoming identical as the percentage of buses retrofitted approaches 100%. As the retrofit percentage changes, the efficiency and equality measures change, but the optimal scenarios and qualitative findings are insensitive to the percentage of buses retrofitted. In addition, a control decision related to primary pollutants emitted by mobile sources will tend to have public health impacts clustered closer to the source, increasing the likelihood that control strategies based on near-roadway population density and at-risk populations will perform well. Control decisions involving secondary pollutants from point sources may be less likely to be optimal in the absence of analysis or more careful evaluation of the spatial extent of impact.

In spite of the interpretability and utility of our findings, there are some key limitations. Within our health inequality calculations, we have only captured a subset of dimensions of vulnerability, omitting: 1) potential differential relative risks based on health status or demographic factors; 2) attributes other than age and census tract that could influence baseline mortality risks; and 3) differential exposure based on ambient concentration “hot spots” or differences between ambient concentrations and personal exposures. On the first two of these points, while some studies have demonstrated approaches to model differential baseline and relative risks for PM_2.5-related mortality ⁽²⁷⁾, further stratifying baseline mortality data at the census tract level by factors such as educational attainment would have led to unstable mortality rate estimates. In addition, the use of mortality risk estimates at the census tract level, a geographic aggregate designed to be relatively homogeneous with respect to demographics and socioeconomic status, should capture a number of key sources of baseline risk heterogeneity.

On the third point, given evidence of a linear concentration-response function for PM_2.5-related mortality throughout the range of concentrations in Boston ⁽¹⁹⁾, spatial variability in ambient concentrations would have minimal influence on our findings. However, the magnitude and distribution of benefits could be influenced by time-activity patterns, time spent in transportation microenvironments, and so forth. Our analysis did not address these factors, effectively presuming that residential outdoor concentrations correspond with personal exposures. Differences between ambient concentrations and personal exposures that were demographically patterned, based on factors such as residential air conditioning, would tend to increase the benefits of emission controls for bus routes in low-socioeconomic status neighborhoods, potentially increasing both the efficiency and equality benefits for control strategies targeting these areas. Neither our study nor the epidemiological literature had sufficient data to model personal exposure changes at fine geographic scales, but further exploration of this topic would be warranted.

In addition, our dispersion modeling was somewhat simplified, effectively presuming that residential proximity to roadways was the only predictor of exposure to a vehicle on those roadways, which neglects the influence of street canyons, differential wind patterns in different areas of the city, and other micro-scale effects. While this clearly omits some sources of heterogeneity, the exponential decay associated with primary pollutant fate and transport implies that the influence of proximity overwhelms many other effects, and our calculation of exposure at the census block level provides a high-resolution exposure estimate often not available in urban-scale mobile source risk assessments. This does create a potential disconnect with concentration-response functions based on central site monitoring data, but our tradeoff conclusions were robust across different concentration-response function values. Using CAL3QHCR out to 5000 m clearly contributed uncertainty at longer range, although the fact that the CAL3QHCR outputs were well explained by a log-log regression model as a function of distance enhances the interpretability of our findings.

Our use of mortality rate estimates at the census tract level offered better resolution than often used in PM_2.5 health risk assessments, but the estimates were correspondingly more uncertain. Some of the spatial patterns of baseline mortality rates may be artifacts of small sample sizes in individual census tracts or of errors in the estimated baseline populations. Other studies ⁽²⁴⁾ have addressed this concern by developing smooth functions across geographic aggregates in a multilevel modeling framework, but such an analysis was beyond the scope of our study. In theory, this could influence the specific control strategies on the optimal frontier if the spatial patterns of baseline mortality rates were significantly different than implied by the raw data. That being said, the aim of our study was to demonstrate a theoretical framework and determine its implications, and any direct translation to risk management decisions would need to consider this uncertainty along with those previously discussed.

Our analysis focused on mortality risk, as the endpoint that dominates monetized health benefits within benefit-cost analyses, but other health endpoints could be of interest to risk managers, especially given concerns about health disparities. For example, asthma hospitalization rates demonstrate significant spatial and demographic heterogeneity across Boston ⁽²⁸⁾. It is possible that the optimal control strategy for asthma hospitalizations or other PM_2.5-related outcomes could differ from the optimal strategy for mortality. However, low-income areas tend to have high baseline rates for multiple morbidity and mortality outcomes, and population density would be consistent across outcomes (although varying somewhat for different age groups), so it would seem unlikely that optimizing on mortality would be a poor strategy for morbidity. Optimizing on quality-adjusted life years or monetized health benefits would be one approach to address this concern, potentially examining the geographic and demographic distribution of gains and losses, although this would complicate characterization of baseline rates within the inequality indicators.

We omitted any pollutants other than primary PM_2.5; inclusion of other primary pollutants or secondary PM_2.5 formation would increase the benefits and potentially change the spatial patterns of impacts, although the benefits of DPFs would likely be driven by primary PM_2.5. We also assumed that the spatial distribution of mortality risks would be unchanged over time; if other factors (e.g., demographic shifts in selected neighborhoods) led these distributions to change during the lifetime of the DPF, there would be a need to formally address the time dimension of the analysis. In general, any quantification of net benefits would need to consider the capital and operating costs of the DPF, any time lags for health benefits, and so forth, providing a template in which time-variant distributional information could be incorporated.

Finally, our framework does not address the question of whether the degree of inequality in mortality risks should be considered problematic, what magnitude of inequality indicator change should be considered significant, or to what extent small changes in inequality should be traded off against small changes in population health benefits. While the baseline measures of mortality inequality are generally low relative to commonly-seen values for income inequality ^{(26, 29)}, this would be anticipated given that income can vary by orders of magnitude while age-adjusted all-cause mortality rates would generally vary to a lesser extent across geographic aggregates. Also, there would be differences in the extent to which differences in income or health would be deemed tolerable by risk managers, and comparing these magnitudes is therefore uninformative. The changes in inequality and mortality risk associated with our control strategies were quite small, but this is unsurprising given control of one pollutant from fewer than 100 vehicles, and this fact by itself does not imply that our framework is not applicable. The key is to understand the extent to which control strategies would alter the distribution of health risks, ruling out control strategies dominated across efficiency and inequality measures, and further study would be required to better understand willingness to trade off efficiency and equality. Our framework also presumes that equalizing health risk is a primary risk management goal. Some risk managers may have different decision rules (such as equalizing emissions reductions for all neighborhoods). Our approach does not preclude this decision rule, but helps to determine the implications of it.

In spite of these and other limitations, our modeling framework offers some useful insights for decision makers faced with allocation of limited resources across sources of emissions and given concerns about both efficiency and inequality. Given information about the baseline distribution of health risks, our framework provides specific insight about the subset of control strategies that maximize public health benefits and minimize inequality in health outcomes, addressing simultaneous concerns of benefit-cost and environmental justice analyses. Our framework also readily addresses uncertain parameters and the sensitivity of conclusions to the choice and formulation of the inequality indicator, helping to clarify the subset of control strategies that are dominant or dominated across different model assumptions. More generally, the characteristics of optimal strategies can help risk managers determine useful rules of thumb absent a comprehensive modeling effort, and the process of formally considering efficiency and equality tradeoffs can help motivate consideration of a broad array of control strategies, which by itself could lead to improved risk management outcomes.