Role of microprojections in myoendothelial feedback – a theoretical study

Abstract

We investigated the role of myoendothelial projections (MPs) in endothelial cell (EC) feedback response to smooth muscle cell (SMC) stimulation using mathematical modelling. A previously developed compartmental EC–SMC model is modified to include MPs as subcellular compartments in the EC. The model is further extended into a 2D continuum model using a finite element method (FEM) approach and electron microscopy images to account for MP geometry. The EC and SMC are coupled via non-selective myoendothelial gap junctions (MEGJs) which are located on MPs and allow exchange of Ca²⁺, K⁺, Na⁺ and Cl⁻ ions and inositol 1,4,5-triphosphate (IP₃). Models take into consideration recent evidence for co-localization of intermediate-conductance calcium-activated potassium channels (IK_Ca) and IP₃ receptors (IP₃Rs) in the MPs. SMC stimulation causes an IP₃-mediated Ca²⁺ transient in the MPs with limited global spread in the bulk EC. A hyperpolarizing feedback generated by the localized IK_Ca channels is transmitted to the SMC via MEGJs. MEGJ resistance (R_gj) and the density of IK_Ca and IP₃R in the projection influence the extent of EC response to SMC stimulation. The predicted Ca²⁺ transients depend also on the volume and geometry of the MP. We conclude that in the myoendothelial feedback response to SMC stimulation, MPs are required to amplify the SMC initiated signal. Simulations suggest that the signal is mediated by IP₃ rather than Ca²⁺ diffusion and that a localized rather than a global EC Ca²⁺ mobilization is more likely following SMC stimulation.

Key points

• Endothelial microprojections (MPs) are cellular extensions of endothelial cells (ECs) that may be involved in regulation of smooth muscle cell (SMC) constriction in blood vessels.

• We developed computational models to investigate the role of MPs in generating EC feedback during SMC stimulation. The models account for the geometry of MPs and heterogeneous distribution of membrane channels and receptors in an EC.

• Simulations show that SMC stimulation causes calcium release in and around EC MPs that activates hyperpolarizing currents in ECs and moderates SMC constriction.

• The results help us better understand the mechanisms that regulate blood flow and pressure.

Introduction

Myoendothelial communication plays an important role in vascular tone regulation. Complex bidirectional pathways exist between the endothelial cell (EC) and smooth muscle cell (SMC) layers which regulate SMC constriction and vessel diameter. Agonist stimulation of SMCs may lead to a calcium (Ca²⁺) response in ECs sufficient to initiate Ca²⁺-dependent vasodilatory signals such as the endothelium-derived hyperpolarizing factor (EDHF). Such EC response can moderate SMC constriction and is referred to as myoendothelial feedback. The presence of endothelial feedback after SMC stimulation was first suggested by Dora et al. (1997) and remains a topic of active investigation (Dora et al. 2008; Ledoux et al. 2008a; Sandow et al. 2009b; Tran et al. 2012). Different aspects of this feedback response remain unresolved including the identity of the main mediator in SMC-to-EC communication (Ca²⁺ or inositol 1,4,5-triphosphate (IP₃)) and the characteristics of the EC response, as well as whether attenuation of this mechanism contributes to vessel pathology (Sandow et al. 2009b; Kerr et al. 2012).

Myoendothelial projections (MPs) are cellular extensions from ECs and/or SMC that extend over the internal elastic lamina and come in close contact with the other cell type (Heberlein et al. 2009; Sandow et al. 2009b). In spite of their early discovery in 1957 (Moore & Ruska, 1957), the functional importance of MPs has only recently begun to be appreciated (Kerr et al. 2012). Electron microscopy studies confirm the presence of MPs in many different vessels, including in rat mesenteric arteries (Ledoux et al. 2008a; Sandow et al. 2009b; Tran et al. 2012). MPs vary both in number and size among different vascular beds, age, species, sex and diseased states of animals (Sandow et al. 2009a). An increase in incidences of MPs with decrease in vessel diameter is often reported (Heberlein et al. 2009; Sandow et al. 2009a), which correlates with an increase in EDHF action (Garland et al. 1995; Shimokawa et al. 1996; Hill et al. 2000, 2002) but not with the activity of the endothelium-derived relaxing factor (EDRF) whose efficacy often diminishes with decrease in vessel size (Luksha et al. 2009).

Recent immunohistochemical labelling studies show evidence for localization of IP₃ receptors (IP₃Rs), intermediate conductance Ca²⁺-activated potassium channels (IK_Ca) and connexins in MPs (Crane et al. 2003; Sandow et al. 2006; Dora et al. 2008; Isakson, 2008; Ledoux et al. 2008a; Sandow et al. 2009b). Myoendothelial gap junctions (MEGJs) are often located on top of these projections and are responsible for electrochemical communication between ECs and SMCs (Heberlein et al. 2009; Sandow et al. 2009a,b). It has been proposed that a small amount of IP₃ and/or Ca²⁺ entering from the stimulated SMC can accumulate in the restricted space of MPs and activate localized IP₃Rs, leading to rapid release of Ca²⁺ from the endoplasmic reticulum (ER) stores and amplification of Ca²⁺ response. In support of this theory, spontaneous and agonist initiated local Ca²⁺ events like ‘pulsars’ (Ledoux J, 2008b) and ‘wavelets’ (Tran et al. 2012) have been shown to occur in and around MP sites in ECs following both EC as well as SMC stimulation. The occurrence of these Ca²⁺ events in the vicinity of localized IK_Ca channels is consistent with a role for the EDHF in closing the myoendothelial feedback loop. Endothelial nitric oxide synthase (eNOS) may also colocalize at MPs, but evidence indicates a limited role for NO in the feedback response (Nausch et al. 2012).

Mathematical modelling can assist in further analysis of the experimental data, but few theoretical studies have investigated EC–SMC communication. In a recent study, Brasen et al. (2012) describe a 2D-axisymmetric model incorporating the anatomical structure of MPs to show the spatiotemporal modulation of Ca²⁺ and IP₃ in EC, SMC and MPs during EC and SMC stimulation. In this model, they highlight the competence of MPs in rectification of Ca²⁺ signals by the virtue of their structure and location. However, the role of the membrane potential (V_m), the effect of plasma membrane channels, the localization of channels and receptors, and the myoendothelial feedback in the heterocellular communication have yet to be modelled. In our previously developed EC–SMC model (Kapela et al. 2009), we integrated detailed single cell EC (Silva et al. 2007) and SMC (Kapela et al. 2008) models with electrical, chemical and NO coupling pathways. Agonist stimulation of ECs increased Ca²⁺ in ECs, activated EDHF and EDRF pathways, hyperpolarized SMC, and reduced SMC Ca²⁺. Ca²⁺ fluxes from stimulated SMC or EC did not elevate global Ca²⁺ in the other cell. EC feedback response to SMC stimulation was observed only when we significantly increased gap junction permeability to IP₃ and EC IP₃R density relatively to previously suggested values.

In this study, we develop computational models to investigate the role of MPs in myoendothelial communication. We extend our previously developed EC–SMC model to incorporate a subcompartment within the EC that simulates the presence of MPs (Fig. 1A). We also present a continuum model capable of incorporating accurate MP geometry from electron microscopy images (Fig. 2A) and account for spatial localization of IK_Ca and IP₃Rs as suggested in experimental studies (Crane et al. 2003; Sandow et al. 2006; Isakson, 2008; Ledoux et al. 2008a). The current models provide theoretical insights into the role of MPs.

Figure 1.

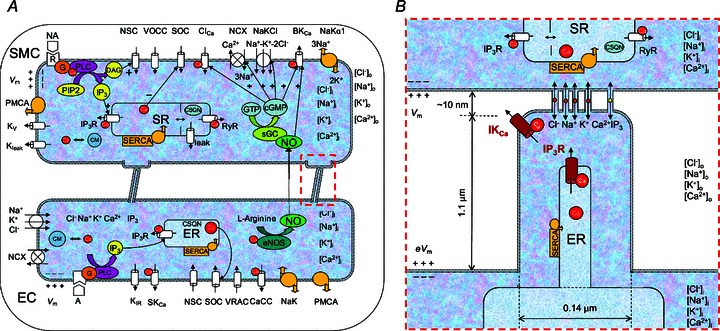
A, schematic diagram showing all the channels and pumps incorporated in the EC–MP–SMC compartmental model. B, characteristics of the EC microprojections (MP). Localized (high density) IK_Ca channels and IP₃Rs are present in the MP. All other channels and pumps are distributed proportionally to the volumes of the EC bulk and MP (the other channels in MP are not shown for clarity).

Figure 2.

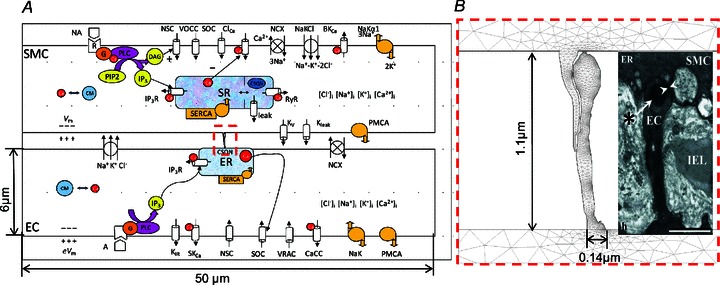
A, 2D FEM model geometry with SMC and EC as rectangular segments and with a MP whose shape is imported from electron microscopy image by (Sandow et al. 2009b) (inset in B). Ion channel currents are uniformly distributed along the top and bottom boundaries of each cell. B, EC projection with mesh. IK_Ca channels and IP₃Rs are localized in the MP. All other channels and pumps are also present in MP membrane, but proportionally to MP volume. The ER is homogeneously spread across the entire EC including the MPs.

Methods

Compartmental model

The current model is based on our previously developed two-cell EC–SMC model (Kapela et al. 2009). The earlier models were optimized for a specific tissue (i.e. model descriptions and parameters were based on experimental data obtained primarily from rat mesenteric resistance arteries). We modified the EC by partitioning it into two compartments representing the bulk EC and the MP as shown in Fig. 1A. Parametric studies were performed to determine the influence of certain parameters on model responses.

Geometric parameters

Figure 1B shows the dimensions used to calculate effective volume, area and diffusion parameters for the EC MP compartment. The length and width of MPs are taken from electron microscopy images of rat mesenteric artery (Sandow et al. 2009b). 2.7 MEGJs per endothelial cell were assumed (Dora et al. 2008) and that every projection contains one gap junction. The total EC volume (1 pl; Schuster et al. 2003) is divided into bulk EC volume and a much smaller MP volume. MP volume is calculated by assuming the MP to be cylindrically shaped with dimensions as shown in Fig. 1B. Membrane area, whole cell capacitance and the ER/SR are divided between the two compartments proportionally to their volume ratios. This allows for appropriate division of intracellular fluxes between the two compartments.

Ionic channel distributions

The model schematic is shown in Fig. 1A. The whole cell conductances of the channels and pumps are maintained the same as in the previous EC and SMC models (Silva et al. 2007; Kapela et al. 2008). The following channels are assumed uniformly distributed across the membrane of EC and their maximum conductances are scaled by the bulk and MP volumes: Inwardly rectifying potassium channel (K_ir), non-selective cation channel (NSC), small conductance calcium activated potassium channel (SK_Ca), store-operated channel (SOC), calcium activated chloride channel (CaCl), sodium-potassium pump (NaK_α1), Na⁺–Ca²⁺exchanger (NCX), plasma membrane Ca²⁺-ATPase (PMCA), sarco(endo)plasmic reticulum Ca²⁺-ATPase (SERCA). IK_Ca (Crane et al. 2003; Sandow et al. 2006, 2009b; Dora et al. 2008; Ledoux et al. 2008a) and IP₃R (Isakson, 2008; Ledoux et al. 2008a; Sandow et al. 2009b) are localized to MPs as shown in Fig. 1B. The maximum conductance of IK_Ca channel (G_IKCa) has been measured in porcine arteries (Bychkov et al. 2002), and was rescaled in our lumped EC model (Silva et al. 2007). Immunohistochemistry data suggest a high presence of IK_Ca channels and IP₃Rs in the vicinity of MPs (Sandow et al. 2006; Dora et al. 2008; Isakson, 2008; Ledoux et al. 2008a; Sandow et al. 2009b). IK_Ca labelling is very punctuated and colocalized with MPs in some vascular beds, e.g. rat mesenteric arteries (Dora et al. 2008; Ledoux et al. 2008a; Sandow et al. 2009b), but more dispersed in others (McNeish et al. 2006; Tran et al. 2012) and therefore their distribution between MPs and the rest of the cell is likely to vary. Thus, under control conditions we assume that the majority of IK_Ca channels are concentrated in MPs (Table 1) and we also performed simulations for different levels of IK_Ca localization. Similarly, a significant percentage (i.e. 10% under control conditions) of the total IP₃Rs is assumed to be localized inside the MPs and the remaining distributed in the bulk of EC. This corresponds to a much higher IP₃R density in MP than in the bulk of EC. (The distribution of IP₃Rs is controlled by the maximum current parameter (I_IP3R,max, Table 1).) The degree of localization (10%) was assumed based on the fact that IP₃Rs are not as highly colocalized with MPs as IK_Ca (Ledoux et al. 2008a; Sandow et al. 2009b). In the SMC model, single cytosolic compartment integrates currents through the following channels: voltage-dependent L-type calcium channel (VOCC), delayed rectifier potassium channel (K_v), NSC, ATP activated potassium channel (K_ATP), large conductance calcium activated potassium channel (BK_Ca), SOC, CaCl, NCX, and PMCA and NaK_α1 pumps. Norepinephrine (NA) stimulation generates IP₃ through Ca²⁺-dependent phospholipase-C (PLC). MEGJs connect the MP compartment to the SMC (Sandow & Hill, 2000; Dora et al. 2003). Permeability of gap junctions is calculated based on experimental data for the total MEGJ resistance (R_gj; Yamamoto et al. 2001). MEGJs are assumed to be non-selective and permeable to Na⁺, K⁺, Ca²⁺, Cl⁻ ions and IP₃. The EDRF–NO pathway is blocked for all simulations.

Table 1.

List of parameters describing dimensions of MPs and microdomains along with values of diffusion constants of ions and IP₃ in the cytosol

Parameter	Value	Description
GIKCa	Bulk EC: 0.0 nS	Maximum IKCa channel conductance
	MP: 1.72 nS (Kapela et al. 2009)
IIP3R,max	Bulk EC: 1.053 ×103 pA mm−1	Maximum current through IP3R per concentration difference
	MP: 0.117 × 103 pA mm−1
Kd_act	Low: 130 nm (Jacobsen et al. 2007)	[Ca2+] for half-maximal activation of IP3R
	High: 350 nm (assumed)
f	Control: 1.75	Diffusional restriction between MP and bulk EC
	No MP : 10−3
DCa	300 μm2 s−1 (Allbritton et al. 1992)	Diffusivity of free calcium in cytosol
DK	744 μm2 s−1	Diffusivity of potassium in cytosol
DNa	505 μm2 s−1	Diffusivity of sodium in cytosol
DCl	900 μm2 s−1	Diffusivity of chloride in cytosol
DIP3	283 μm2 s−1 (Allbritton et al. 1992)	Diffusivity of IP3 in cytosol
Amp	0.0154 μm2 (Sandow & Hill, 2000)	Area of a single MP
Lmp	3.5 μm (Sandow & Hill, 2000)	Diffusion length from MP to bulk EC
Nmp	2.7 (Dora et al. 2008)	Number of MEGJ/EC
F	96487.0 C mol−1	Faraday's constant
R	8341 mJ (mol K)-1	Universal gas constant
T	293 K	Temperature
zK, zNa, zCa, zCl	1, 1, 2, –1	Ion valency of K+, Na+, Ca2+, Cl−

Coupling between MPs and bulk EC: diffusion currents

We used (electro) diffusion equations to describe fluxes of the four ions and IP₃. The equations account for fluxes between two compartments and their dependence on V_m as well as concentration difference:

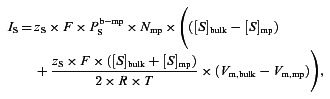(1)

(2)

where S represents Na⁺, K⁺, Ca²⁺ and Cl⁻. Suffixes ‘mp’ and ‘bulk’ represent the MP and bulk compartments in EC. 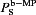is the permeability of species S between the MP and the bulk of the cell. A first approximation for its value can be acquired from the species diffusivity (D_s), MP cross-sectional area (A_mp) and the MP length (L_mp), i.e.

A correction factor (f) was also utilized to account for the effects of buffering/degradation/extrusion and/or the presence of subcellular organelles that can further limit the exchange of species between the two compartments.

The ER in MP is coupled with the bulk ER using diffusion equation for Ca²⁺ transport:

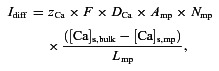(3)

where [Ca]_s is the concentration of Ca²⁺ in the ER stores. All parameter values and their description are listed in Table 1.

Calcium-induced calcium release (CICR)

The default IP₃R kinetics in the EC bulk and MP is the same as in the previous EC-SMC model (Silva et al. 2007; Kapela et al. 2009), comprising of IP₃-dependent activation and Ca²⁺-dependent inactivation terms:

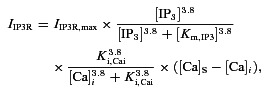(4)

where [Ca]_S and [Ca]_i represent the ER and cytosolic calcium concentrations respectively and [IP₃] represents intracellular IP₃ concentration. K_m,IP3 and K_i,Cai are the half-activation and -inhibition constants for IP₃ activation and Ca²⁺-dependent inhibition of the IP₃R current.

To test the potential of intercellular Ca²⁺ flux to induce CICR through IP₃Rs, the IP₃R current in the EC was modified to include a calcium-dependent activation component (P_Ca) as shown in eqns (5) and (6).

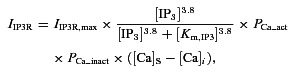(5)

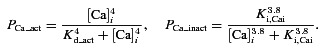(6)

Two values of K_{d_act} were examined as listed in Table 1. The lower value of K_{d_act} was taken from a model of SMCs (Jacobsen et al. 2007), and the second value is an average from various cell types (Finch et al. 1991; Atri et al. 1993).

Numerical methods

All other model equations are described in detail in previous studies (Silva et al. 2007; Kapela et al. 2008, 2009). The compartmental EC and SMC models are implemented using 20 and 26 ordinary differential equations, respectively. Table 1 lists any changed or newly introduced parameter values. The rest of the parameter values remain unchanged from the previous EC–SMC model. The equations are coded in Fortran 90 and solved numerically using Gear's backward differentiation formula method for stiff systems (IMSL Numerical Library routine). The maximum time step was 1 ms and the tolerance for convergence was 0.0005.

Finite element method (FEM) model

The compartmental EC–MP model described above does not allow us to predict intracellular concentration gradients, the spatiotemporal nature of Ca²⁺ mobilization and the localization of the Ca²⁺ signal. Furthermore, preliminary simulations revealed that the feedback response depends significantly on the permeability between the MP and the bulk EC cytosol (adjusted through the factor ‘f’’). Calculation of fluxes between two unequal compartments (MP and bulk EC) needs to take into account a variable diffusion area, boundary fluxes, buffering of Ca²⁺ and degradation of IP₃ which are difficult to accurately capture through lumped diffusion parameters used in the compartmental model. Thus, we developed a FEM model to account for the spatial gradients of Ca²⁺ inside the EC MP and for the diffusion of species from the MP to the bulk EC with higher accuracy. A 2D model also allows us to incorporate accurate MP geometry by importing MP images from experimental studies and to account for spatial localizations of IK_Ca and IP₃Rs within the MPs.

The model is developed using the Chemical Engineering module of COMSOL, similarly to (Kapela & Tsoukias, 2011). While a 3D cylindrical axisymmetric model of EC and SMC was implemented in (Kapela & Tsoukias, 2011), here we assumed a simplified geometry and EC and SMC are represented as rectangular structures with dimensions as shown in Fig. 2A. The model implements only half of the EC and SMC. The results in the remaining half are assumed to be symmetrical. The shapes of the projections are imported from experimental electron microscopy images (Heberlein et al. 2009; Sandow et al. 2009b; Tran et al. 2012; Fig. 5). Volume of MP is calculated assuming the MP to be cylindrical with diameter and length as shown in Fig. 2B. Two rectangular domains connect the SMC and EC MPs to represent MEGJs. Differences in height (depth) of the cell's bulk, MPs, and MEGJs have been accounted for by appropriate scaling of fluxes at the boundaries between MEGJ and MP and at boundary between MP and bulk cytosol.

Figure 5.

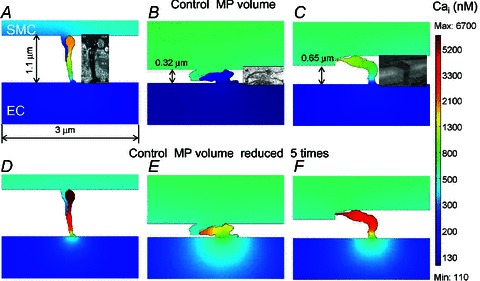
Predicted Ca²⁺ concentration inside the MP after NA stimulation of SMC for different MP geometries: (A–C) control MP volume and shape, (D–F) MP volume reduced five-fold. Insets in (A–C) show the original electron microscopy images of the projections reproduced with permission from John Wiley and Sons, and The American Physiological Society (Heberlein et al. 2009; Sandow et al. 2009b; Tran et al. 2012).

Nernst-Planck equations describe the electrodiffusion of the ions in the EC, MP, SMC and MEGJs:

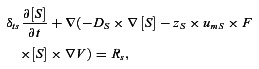(7)

where [S] is the intracellular concentration of the four ionic species (Ca²⁺, Na⁺, K⁺, Cl⁻), D_s is the diffusivity of the respective ions, 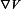is the electrical gradient, z_S is the charge, F is the Faraday constant, and u_mS is the mobility of the respective ion. R_s is the source/sink term which includes expressions for Ca²⁺ release/uptake from the ER/SR, and Ca²⁺ buffering in EC bulk and MP. In SMC, fast Ca²⁺ buffering is represented by the Ca²⁺-dependent function δ_ts. Diffusion of IP₃ and buffered Ca²⁺ in the cytosol, and Ca²⁺ in ER/SR is implemented using diffusion equations inside the SMC, EC, MP and MEGJs domains:

(8)

where [S] is the concentration of either species (IP₃, Ca²⁺_S, Ca²⁺_buffered). In EC, IP₃ production is introduced by the R_s term, while in SMC agonist receptors and IP₃ formation are described by an embedded weak boundary equation.

All model equations describing the membrane and store channels are the same as in the compartmental model. The membrane currents are defined as boundary fluxes across the top and bottom boundaries of EC, SMC and all boundaries of the MP. The left and right boundaries of the cell are assumed insulated. To distribute the channels uniformly, the currents are divided between the MP and bulk cytosol according to the volumes of MP and bulk cytosol. Similarly to the compartmental model, the whole maximum conductance of IK_Ca channels (G_IKCa) and 10% of IP₃R_max current were placed in EC MPs. 900 MΩ is used as control R_gj unless stated otherwise.

The equations are solved using the SPOOLES direct solver with absolute and relative tolerances of 10⁻³ and 10⁻² respectively. The solution time was 30 s with a time stepping of 0.1 s. The different geometries were divided into ∼1000 elements. Unless stated otherwise, the NO pathway is blocked for all simulations.

Results

Global vs. local Ca²⁺ and IP₃ changes

Figure 3 shows Ca²⁺ and IP₃ changes in bulk EC and MP compartments during SMC (Fig. 3A) and EC (Fig. 3B) agonist stimulations. Following SMC stimulation with NA (Fig. 3A), the IP₃ diffusing from SMC into the EC MP causes a high IP₃ transient in the MP, which does not spread into the bulk of EC. A large Ca²⁺ transient is generated in the MP by activation of IP₃Rs localized in the MP. Like IP₃, Ca²⁺ in the MP does not spread much into the bulk EC compartment. IK_Ca channels localized in the MPs are activated by the Ca²⁺ transients and generate hyperpolarizing current that spreads through gap junctions to moderate SMC depolarization (Fig. 3C). The high Ca²⁺ and IP₃ transients in the MP after NA stimulation of SMC are attributed to the small volume of the MP, the localization of IP₃Rs and the restricted diffusion between the MP and bulk EC. Thus, the magnitude of the Ca²⁺ and IP₃ transients depend on the assumed value of effective permeability . Simulations with a wide range of permeability values were performed by varying parameter f (data not shown). Correction factor f < 0.1 makes the bulk and MP well mixed and effectively lacking a functional MP compartment, while f≫ 1.75 (control) creates excessive electrical resistance and the two compartments are no longer near isopotential.

Figure 3.

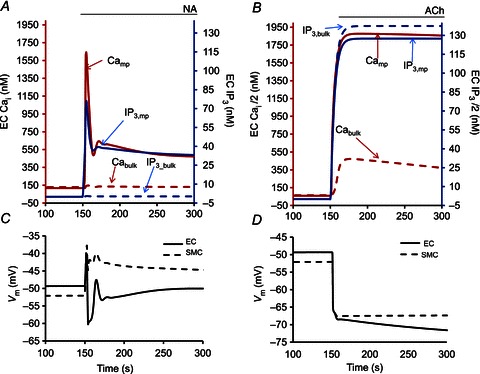
Compartmental model results showing Ca²⁺ and IP₃ concentrations in the EC MP (continuous lines) and EC bulk (dashed lines) during 1 μm NA stimulation of SMC (A) and ACh stimulation of EC (B). Corresponding V_m in EC (continuous lines) and SMC (dashed lines) are shown in C and D. MEGJ resistance is maintained at 900 MΩ with restricted diffusion between the projection and bulk EC. 10% of IP₃Rs are concentrated in the MP compartment.

Acetylcholine (ACh) stimulation of bulk EC compartment increases the global Ca²⁺ concentration through the production of IP₃ (Fig. 3B) and opening of IP₃Rs in ER. Diffusion of IP₃ from the bulk to MP generates a Ca²⁺ increase ∼7 times higher than in bulk EC because of the localization of IP₃Rs in the small volume of MPs and restricted diffusion between the two compartments. The Ca²⁺ increase in the bulk and MP compartments opens SK_Ca and IK_Ca channels and hyperpolarizes the EC. This change in EC V_m is transmitted through MEGJs as EDHF and hyperpolarizes SMC (Fig. 3D).

In agreement with the compartmental model, the 2D FEM model predicts that NA stimulation of SMC generates high IP₃ (Fig. 4C) and Ca²⁺ (Fig. 4A) transients inside the EC MP with minimal spread into the bulk EC. Simulations with ACh stimulation (Fig. 4B and D) are also consistent with the compartmental model (Fig. 3B). In Fig. 5, we examined the effect of MP geometry on the spread of Ca²⁺ from the MP into the bulk EC. The three MP geometries examined are from the electron microscopy studies of rat mesenteric arteries (Sandow et al. 2009b), mouse cremaster arterioles (Heberlein et al. 2009), and hamster vessels (Tran et al. 2012). Under control MP volume, the long MP with comparatively small diffusion area yielded a large Ca²⁺ transient which did not spread much into the bulk of EC (Fig. 5A). The transients decreased with smaller heights and larger surface areas of the MPs (Fig. 5B and C). The short MP with large surface area did not have a significant Ca²⁺ transient in the MP (Fig. 5B). If the volume of each MP was reduced 5 times, effectively making it flatter, the predicted Ca²⁺ transients in the MPs increased significantly in all three cases (Fig. 5D–F), but the MP with higher surface area (Fig. 5E) allowed for a comparatively bigger spread of Ca²⁺ into the bulk of EC.

Figure 4.

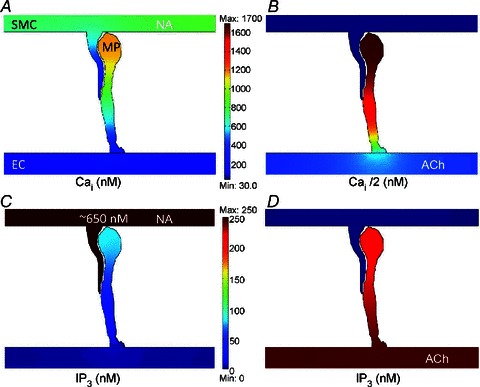
2D FEM model results for NA stimulation of SMC (A, C) and ACh stimulation of EC (B, D). Predicted Ca²⁺ concentration inside the MP after NA stimulation of SMC (A) and bulk EC stimulation with ACh (B). The corresponding IP₃ transients in the MP for SMC and EC stimulation are shown in C and D, respectively. Ca²⁺ and IP₃ concentration profiles are shown 7.5 s after 1 μm NA stimulation of SMC and 2 s after ACh stimulation of EC, respectively.

Effect of MPs

Figure 6 shows the effect of EC MPs on feedback in SMC V_m. In the presence of MPs, an approximately 2–3 mV feedback can be achieved, compared to the model with a single well-mixed EC compartment (Fig. 6A, continuous vs. dashed lines). The feedback is lost in the model without MPs because NA cannot generate a Ca²⁺ transient in the single compartment model (Fig. 6B, dashed vs. continuous lines)_. In fact, the global EC Ca²⁺ decreases in the model without MPs (Fig. 6B, dashed line) because of SMC depolarization transmitted through MEGJs to EC. Large increases in the gap junction permeability (∼10²-fold; R_gj= 9 MΩ), and maximum IP₃R current (∼10³-fold) in the single EC compartment model could compensate partially for the absence of MPs (Fig. 6A and B, dotted lines). From the results, it is evident that the presence of MPs facilitates the production of a hyperpolarizing feedback from EC to SMC following SMC stimulation.

Figure 6.

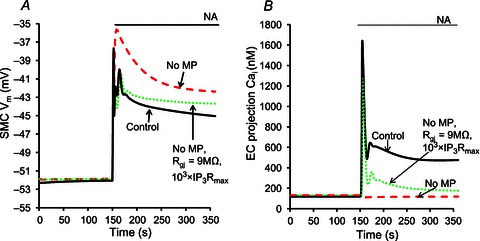
SMC V_m (A) and EC MP Ca²⁺ (B) under three scenarios: no MP (dashed lines), control (continuous lines), and no MP with MEGJ resistance reduced from control 900 MΩ to 9 MΩ and the maximum IP₃R current increased 10³-fold (dotted lines).

IP₃ vs. Ca²⁺ signalling

Figure 7 examines the relative contributions of IP₃ and Ca²⁺ diffusion from stimulated SMC to EC to the generation of MP Ca²⁺ transients and the myoendothelial feedback. Average Ca²⁺ from MP in the 2D FEM model after SMC stimulation is plotted for different MEGJ resistances before (Fig. 7A) and after (Fig. 7B) blockade of intercellular IP₃ diffusion. Under control R_gj (900 MΩ as estimated by Yamamoto et al. 2001), IP₃ diffusion appears to be the major signalling molecule (Fig. 7A, continuous line), as the Ca²⁺ transient achieved by intercellular Ca²⁺ diffusion during IP₃ blockade (Fig. 7B, continuous line) is insignificant. In contrast, blocking Ca²⁺ diffusion did not cause a significant change in the MP Ca²⁺ transient (Fig. 7B, inset, dashed line vs. continuous line). Along with the Ca²⁺ transient, the feedback in SMC V_m is also abolished by blockade of IP₃ diffusion from SMC to EC (Fig. 7C, continuous vs. dashed lines). At low R_gj values (250 MΩ > R_gj > 50 MΩ, based on 70 MΩ from Sandow & Hill, 2000), The Ca²⁺ transient arising purely from diffusion of Ca²⁺ (Fig. 7B) becomes significant and might cause a minor feedback. In general, the predicted Ca²⁺ transient in MP increases with decrease in R_gj and is mediated mainly by IP₃ rather than Ca²⁺ diffusion.

Figure 7.

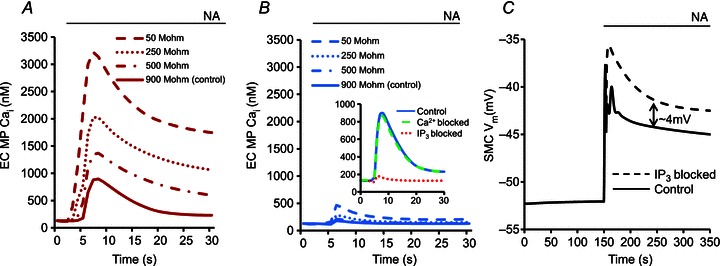
Ca²⁺ transients in the MP after NA stimulation of SMC in the 2D FEM model under control conditions (A) and with IP₃ diffusion across MEGJs blocked (B), for different MEGJ resistances. The variation in R_gj is based on resistances estimated in experimental studies (Sandow & Hill, 2000; Yamamoto et al. 2001). C, SMC V_m under control conditions (continuous line) and with IP₃ diffusion from SMC to EC blocked in the compartmental model after NA stimulation of SMC. The arrow line (⇕) shows the magnitude of the feedback mediated by the IP₃ diffusion.

Effect of IK_Ca distribution

Experimental studies suggest that the quantity of IK_Ca channels in MPs is likely to vary between vascular beds and vessel types (Crane et al. 2003; Sandow et al. 2006; Dora et al. 2008; Ledoux et al. 2008a; Tran et al. 2012). Figure 8 shows the effect of varying IK_Ca distribution between MP and bulk EC on myoendothelial feedback in the compartmental model. The myoendothelial feedback after SMC stimulation increases with increased localization of IK_Ca channels in the MP (Fig. 8A), although the amount of IK_Ca channels in the MP does not affect the Ca²⁺ transient in the MP (Fig. 8B). The maximum feedback is achieved under control conditions with 100% IK_Ca channels present in the MP (Fig. 8A, continuous line). With uniform distribution of IK_Ca channels (Fig. 8A, dashed line), the model loses its ability to generate feedback and resembles the output of the model with no MP (Fig. 6A, dashed line).

Figure 8.

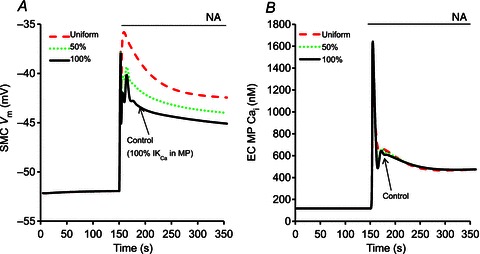
Compartmental model results showing SMC V_m (A) and Ca²⁺ concentration in the EC MP (B) after stimulation with NA under different IK_Ca distribution in EC. Uniform IK_Ca (dashed lines), 50% of IK_Ca channels in MP (dotted lines), and all IK_Ca channels in MP (continuous lines).

Effect of R_gj

Values for the myoendothelial R_gj reported in the literature vary significantly. A lower value of 70 MΩ has been reported based on morphological observations. A higher value of 900 MΩ presents perhaps a better estimate as it was derived from electrical measurements (Sandow & Hill, 2000; Yamamoto et al. 2001; de Wit & Griffith, 2010). The effect of varying R_gj on the feedback is shown in more detail in Fig. 9. In all simulations, both IP₃ and Ca²⁺ coupling are present and the permeability of MEGJs to IP₃ and Ca²⁺ is inversely proportional to the assumed MEGJ resistance. Consistent with Fig. 7A, reduction of R_gj enhances the feedback in SMC V_m (Fig. 9A) and SMC Ca²⁺ (Fig. 9B). For low values of MEGJ resistances (<250 MΩ), IP₃ diffusion from SMC induces large Ca²⁺ responses in MP (Fig. 7A) and hyperpolarizing current from IK_Ca channels can overcome NA-induced SMC depolarization (Fig. 9A). This non-physiological response suggests that the combination of high IP₃R density in MP and low R_gj are not physiological. The magnitude of the feedback in SMC V_m and SMC Ca²⁺ vs. R_gj is shown in Fig. 9C and D. The feedbacks are calculated as the difference between SMC V_m (or Ca²⁺) in the model with given R_gj and SMC V_m (or Ca²⁺) in the model with no MP after 200 s of NA stimulation of SMC. The simulations without MP (and R_gj= 900 MΩ) are taken as the reference because no feedback response is generated in this scenario.

Figure 9.

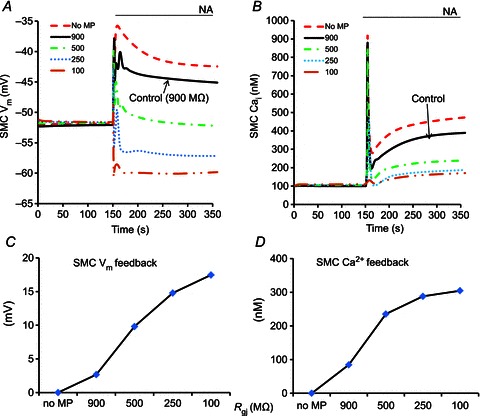
Compartmental model predictions of SMC V_m (A) and SMC Ca²⁺ transients (B) after SMC stimulation with NA for different R_gj values as shown in panel keys. The magnitude of the feedback in SMC V_m (C) and Ca²⁺ (D) is calculated at the end of simulation as a difference between the model with given R_gj and the ‘no MP’ model(dashed lines).

Effect of IP₃Rs

Immunohistochemical labelling techniques report a significant localization of IP₃Rs in the MPs, but their density and activation characteristics remain unclear and it is likely that they vary across different vascular beds (Isakson, 2008; Ledoux et al. 2008a; Ledoux J, 2008b; Sandow et al. 2009b). Figure 10 shows the predicted magnitude of the myoendothelial feedback as a function of IP₃R distribution. In these simulations, the IP₃R current was calculated according to eqn (4), which includes only IP₃-dependent (but not Ca²⁺-dependent) activation. Greater feedback is achieved with higher IP₃R density in the MP and around 6 mV of hyperpolarizing feedback can be achieved with 30% IP₃R localization in MP (Fig. 10C, long dashed line). Under control conditions (10% IP₃Rs in MP), the maximum feedback achieved is around 3 mV (Fig. 9A, continuous vs. dashed lines) under the assumed parameter values.

Figure 10.

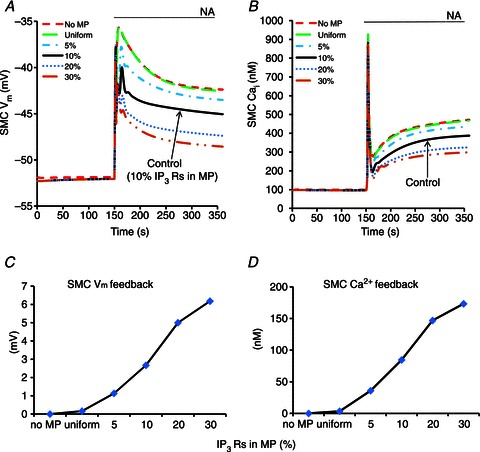
Compartmental model predictions of SMC V_m (A) and SMC Ca²⁺ transients (B) for different IP₃R densities inside the MP as shown in panel keys. The magnitude of the feedback in SMC V_m (C) and SMC Ca²⁺ (D) is calculated at the end of simulation as a difference between the model with given IP₃R distribution and the ‘no MP’ model(dashed lines).

Figure 11 examines whether the incorporation of Ca²⁺-dependent activation of IP₃Rs and presence of basal IP₃ can increase the role of intercellular Ca²⁺ diffusion in the feedback response. In these simulations, the IP₃R current was calculated according to eqn (5), which includes both IP₃- and Ca²⁺-dependent activations. SMC V_m at rest and following NA stimulation (1 μm) and is plotted as a function of basal IP₃ concentration in EC (i.e. EC prestimulation). Simulations are repeated after blocking Ca²⁺ diffusion (dashed line), blocking IP₃ diffusion (dotted line) and blocking both Ca²⁺ and IP3 diffusion (dashed-dotted line) between bulk EC and MP. The difference between the dashed-dotted and continuous lines is the amount of feedback. Simulations are performed for two different sensitivities of IP₃R activation to Ca²⁺ (i.e. K_{d_act}).

Figure 11.

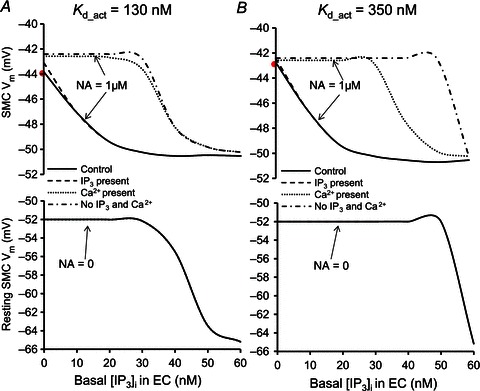
Compartmental model predictions of SMC V_m after 200 s of NA stimulation and at rest (NA = 0) for different basal IP₃ concentrations in the EC, with control MEGJ coupling (continuous lines), IP₃ diffusion alone (Ca²⁺ diffusion blocked) (dashed lines), Ca²⁺ diffusion alone (IP₃ diffusion blocked) (dotted lines), and no IP₃ or Ca²⁺ diffusion (dashed-dotted lines). A, simulations with low EC IP₃R K_{d_act}= 130 nm. B, simulations with high EC IP₃R K_{d_act}= 350 nm.

A first observation is that for both K_{d_act} values (Fig. 11A and B) SMC hyperpolarization when IP₃ exchange is present is the same as in control (dashed and continuous lines). Thus, IP₃ diffusion alone can produce maximum feedback response regardless of the contribution or not from Ca²⁺. With a low Ca²⁺-dependent IP₃R activation parameter (K_{d_act}= 130 nm), Ca²⁺ diffusion alone does not generate significant feedback at any basal IP₃ in EC (Fig. 11A, dotted vs. dashed-dotted line). IP₃ diffusion generates feedback of a few millivolts at low basal IP₃, and larger feedback at intermediate concentrations of basal IP₃ (∼25 nm; Fig. 11A, dashed vs. dashed-dotted line). Ca²⁺ diffusion has a small synergistic effect with IP₃ diffusion at low basal IP₃, but it has no effect at intermediate and high basal IP₃ (Fig. 11A, dashed vs. continuous line). High basal IP₃ (>35 nm) activates EC independently from SMC and limits the feedback response.

With a high Ca²⁺-dependent activation parameter (K_{d_act}= 350 nm), Ca²⁺ diffusion alone could generate significant feedback in the presence of appropriate basal IP₃ in EC (Fig. 11B, dotted vs. dashed-dotted line). EC prestimulation with basal IP₃ in the range of 30–45 nm partially activates IP₃Rs and elevates resting Ca²⁺ near K_{d_act}. At this point IP₃Rs in MP are sensitized to small Ca²⁺ fluxes from SMC, and significant myoendothelial feedback can be mediated without IP₃ coupling. IP₃ diffusion generates weak feedback at low basal IP₃, and large feedback at intermediate concentrations of basal IP₃ (<45 nm; Fig. 11B, dashed vs. dashed-dotted line). In the presence of IP₃ coupling, Ca²⁺ diffusion has little or no effect on the feedback (Fig. 11A, dashed vs. continuous line). In general, basal IP₃ can sensitize EC to IP₃ and Ca²⁺ fluxes from SMC. However, IP₃ diffusion can initiate a significant feedback response under many scenarios of parameter values and conditions, while Ca²⁺ diffusion is required only when IP₃ diffusion is blocked and its potential for feedback is conditional on an appropriate value for the sensitivity of the IP₃R to Ca²⁺ and the existence of basal IP₃ levels within a narrow concentration window.

Discussion

The primary aim of this study was to understand the role of MPs in myoendothelial signalling. Using the proposed models, we examined the effect of MPs on the intracellular Ca²⁺ gradients in EC during SMC stimulation and the resulting NO-independent vasodilatory feedback response from EC to SMC. Simulations show the effect of MP geometry, MEGJ coupling, R_gj, IK_Ca distribution, IP₃R density and activation parameters, and basal IP₃.

EC-to-SMC communication

Endothelial control of vascular tone is attributed to an increase in EC Ca²⁺ followed by the activation of Ca²⁺-dependent vasodilatory pathways such as EDRF, prostacyclin (PGI₂) and EDHF (Dora et al. 1997; Sandow, 2004; Feletou & Vanhoutte, 2006) among others. Both the compartmental and 2D FEM models could simulate SMC relaxation induced by ACh stimulation of EC and mediated by EDHF, consistent with experimental data and the previous EC–SMC model (Dora et al. 1997; Oishi et al. 2001; Schuster et al. 2001; Lamboley et al. 2005; Kapela et al. 2009). ACh stimulation increased IP₃ and Ca²⁺ in EC bulk and MP (Fig. 4A and B), leading to activation of SK_Ca and IK_Ca channels. The hyperpolarizing current from SK_Ca and IK_Ca channels was transmitted by the MEGJs to SMC and reduced SMC Ca²⁺. Presence of MP did not compromise EDHF, and EC MP was effectively isopotential with EC bulk.

SMC-to-EC communication

An increasing amount of evidence shows the existence of local EC Ca²⁺ events such as ‘pulsars’ and ‘wavelets’ in and around EC MPs following SMC stimulation without significant global spread (Kansui et al. 2008; Ledoux et al. 2008b; Tran et al. 2012). Similarly, following SMC stimulation in the models, the IP₃ and Ca²⁺ increase in EC was confined to the MPs and its spread into the bulk EC was rather limited (Fig. 3A, 4A and C). The amplitude of Ca²⁺ transients in the MPs depended upon the size and shape of the projection (Fig. 5) and the area available for diffusion of ions into the bulk EC. Theoretical estimations suggest that passive diffusion of Ca²⁺ and/or IP₃ into EC is insufficient for a global Ca²⁺ mobilization (Nagaraja et al. 2012). The small size of MP as compared to the bulk cytosol and restricted diffusivity from MP into bulk EC allows for significant accumulation of IP₃ and/or Ca²⁺ following SMC stimulation. RyRs and/or IP₃Rs like those found in MPs can further amplify the weak fluxes of Ca²⁺ and IP₃ to induce local Ca²⁺ transients and EC hyperpolarization (Isakson, 2008; Ledoux et al. 2008a).

In earlier studies, a global Ca²⁺ increase in EC after SMC stimulation has also been reported (Dora et al. 1997; Yashiro & Duling, 2000; Schuster et al. 2001; Tuttle & Falcone, 2001; Jackson et al. 2008). The reason for this discrepancy may be attributed to differences in the experimental techniques employed. Our results suggest that if a global response does happen, a mechanism to amplify the small local events is necessary. The presence of a currently unidentified regeneration mechanism cannot be excluded. In fact, in a recent theoretical study Brasen et al. (2012) showed that a Ca²⁺ transient in the MP, induced by IP₃ elevation in SMC, could subsequently spread into the entire EC as a Ca²⁺ wave through CICR in IP₃Rs. CICR was possible because of sensitization of EC bulk with basal IP₃ levels (0.1 μm) and not because of IP₃ spread from the SMC and MP to EC bulk. This study did not account for membrane electrophysiology. In our model, sub-threshold levels of IP₃ enhanced significantly the feedback without generating global EC Ca²⁺, while further elevation of basal IP₃ hyperpolarized resting V_m (Fig. 11). These results show that fine tuning of the system's excitability may allow facilitation of Ca²⁺ spread, but at least in our model, NA-induced Ca²⁺ transients are more likely to have limited spread, in agreement with recent experimental studies (Kansui et al. 2008; Ledoux et al. 2008b; Tran et al. 2012).

MPs amplify feedback

In the model, the local Ca²⁺ transients and IK_Ca channels in the EC MPs generated a hyperpolarizing feedback in SMC of around 3 mV (Fig. 6A, continuous line). In simulations with no diffusional resistance between the MPs and bulk EC and thus effectively no MPs, the feedback was lost (Fig. 6A, dashed line), in spite of the IP₃R and IK_Ca localization still present near the MEGJs. In the absence of a restricted space like the MPs, the IP₃ and Ca²⁺ entering the MPs from the stimulated SMC rapidly diffused into the entire endothelial cell and failed to produce a local or global Ca²⁺ increase (Fig. 6B, dashed line), because of dilution in large cytosolic volume, Ca²⁺ sequestration and buffering, and IP₃ degradation by one to five phosphatases present in the cytosol. Increasing the gap junction permeability 10²-fold and maximum IP₃R current 10³-fold failed to fully compensate the lack of MPs (Fig. 6A, continuous vs. dotted lines). Thus, it appears that in conjunction with the localization of IK_Ca and IP₃Rs, the presence of a restricted space like a MP within the EC is essential for Ca²⁺ mobilization in the EC and facilitation of feedback following SMC stimulation. It is important to note here that the differences in Ca²⁺ and IP₃ concentration between the MPs and bulk EC, as well as the spread of MP Ca²⁺ into the bulk EC, will depend on the relative size, surface area and volume of the MP with respect to the bulk of EC (Fig. 5).

Ca²⁺ accumulation may be further enhanced by the close proximity of ER and mitochondria to the plasma membrane. The presence of organelles at the base of the MP, for example, will restrict diffusion to the bulk of EC, enabling significant Ca²⁺ transients in the vicinity of MP which could activate components that are not necessarily placed within the MP. Thus, in general, small spaces restricted by MP and/or subcellular structures seem to be imperative for amplification of SMC initiated signals causing local Ca²⁺ events and the experimentally observed feedback of a few millivolts (Tran et al. 2012). The inhibition of SK_Ca/IK_Ca channels enhanced NA-induced depolarization by ∼3.5 mV and was associated with about 10% smaller diameter of NA-constricted vessels (Tran et al. 2012). Since the resistance to flow is inversely proportional to diameter to the fourth power (i.e. Poiseuille equation), this change corresponds to a very significant (more than 50%) increase in resistance.

MEGJs and R_gj

MEGJs are the primary NO-independent pathway for transfer of agonist induced EC hyperpolarization to the SMC (Sokoya et al. 2006; Isakson et al. 2007; Kansui et al. 2008). Their presence has been documented in various vascular beds (Figueroa et al. 2004), including rat mesenteric arteries (Hill et al. 2000; Sandow & Hill, 2000), using direct as well as indirect methods like electron microscopy and dye coupling between two cells (Little et al. 1995; Beny, 1997). MEGJs also transmit V_m changes from SMC to EC, although differences in input resistances of endothelial and smooth muscle layers can cause asymmetric ME responses (Emerson & Segal, 2000; Diep et al. 2005). Furthermore, the highest occurrences of MEGJs have been observed in small arteries and arterioles coincidental with a high number of MPs and high EDHF activity (Hwa et al. 1994; Sandow et al. 2009a). Myoendothelial signalling is highly diminished or even abolished in the presence of gap junction blockers like 18-glycyrrhetinic acid (18-GA) and carbenoxolone (Hill et al. 2000; Goto et al. 2002; Hill et al. 2002; Dora et al. 2003; Sandow et al. 2004; Mather et al. 2005; Sokoya et al. 2006; Dora et al. 2008), but not after eNOS inhibition (Nausch et al. 2012). Some vessels may lack MEGJs and functional ME coupling (Sandow et al. 2002; Siegl et al. 2005). Gap junctions are believed to be non-selective in nature, with similar permeabilities for small ions (Christ et al. 1996; Brink et al. 2000). Experimentally estimated values of R_gj are spread over a large range, 70–900 MΩ, depending on the particular tissue and experimental conditions and the type of cells being examined (Sandow & Hill, 2000; Yamamoto et al. 2001; de Wit & Griffith, 2010). In the simulations, a decrease in R_gj is associated with increased permeability of MEGJs to Ca²⁺ and IP₃ and and increase in Ca²⁺ transients in the EC MP (Fig. 7A). This in turn led to higher feedback in terms of SMC Ca²⁺ and SMC V_m (Fig. 9). Under control density of IP₃Rs and IK_Ca channels in MP and with Ca²⁺ and IP₃ diffusion through MEGJs, resistances below 500 MΩ caused Ca²⁺ transients in the MP to be high enough to counteract the SMC depolarization to NA stimulation (Fig. 9A). This suggests lower IP₃R density in MPs and/or higher R_gj.

Localization of IP₃Rs

IP₃R localization will be an important determinant of amplitude of Ca²⁺ transients in the MP (Lamboley et al. 2005; Isakson, 2008; Sandow et al. 2009b). While a significant number of IP₃R clusters seem to be present along the projections (Ledoux et al. 2008a; Sandow et al. 2009b), IP₃Rs in the rest of the EC are primarily responsible for experimentally observed global Ca²⁺ increase in EC after ACh stimulation, which is most likely initiated from the luminal side of the EC, opposite to the location of MPs. Results from the compartmental model showed an increase in feedback in terms of SMC V_m and SMC Ca²⁺ with increase in IP₃R localization in the MP, predicting a hyperpolarizing feedback of up to 6 mV with 30% IP₃R localization (Fig. 10C). ER is a dynamic and flexible structure spread throughout the EC and undergoing constant change. ER provides a single continuous space for the movement of Ca²⁺ ions and can direct Ca²⁺ movement in the cell by concentrating IP₃Rs in a particular cellular region (Diambra & Marchant, 2009; Taylor et al. 2009). Perhaps, for this reason, ER localizes at the base and inside of some projections so as to increase the density of IP₃R in the projection to form a local regulating module to enhance the feedback of EC to SMC. With better quantification of the relative densities of these receptors in the MP as compared to the whole EC, we can obtain a better estimate of the feedback capacity of MPs.

Localization of IK_Ca channels

The co-localization of IK_Ca channels close to IP₃Rs is crucial for facilitation of feedback by MPs. Experimental studies in some tissues show a spatial separation of the two types of K_Ca channels expressed in the ECs (Crane et al. 2003; Sandow et al. 2006; Dora et al. 2008). In rat mesenteric arteries, IK_Ca channels are predominantly expressed in and around the MPs (Dora et al. 2008; Ledoux et al. 2008a; Sandow et al. 2009b), while SK_Ca channels are mostly confined to the bulk of EC near EC–EC tight junctions (Crane et al. 2003; Sandow et al. 2006). MPs contain most of the IK_Ca channels that along with SK_Ca channels are responsible for EC hyperpolarization during EC stimulation (Doughty et al. 1999; Crane et al. 2003; Tran et al. 2012). This segregation of IK_Ca and SK_Ca channels might be a way to separate the respective roles of the very closely related and similarly activated K_Ca channels. Because of their localization in the MP, IK_Ca channels might be engaged in a local feedback mechanism through MP Ca²⁺. Model predictions showed that, during SMC stimulation, the concentration of Ca²⁺ in the MPs increased as high as the global Ca²⁺ concentration in EC during ACh (a potent vasodilator) stimulation of EC (Fig. 3A vs. B) Therefore, this unique orientation of IK_Ca channels near the local Ca²⁺ transients might dismiss the need of a global response. This is also reflected in the fact that for the same Ca²⁺ transient in the MP (Fig. 8B), the feedback generated with the control model (100% IK_Ca channels localized to MP) was lost with uniform distribution of these channels (Fig. 8A, continuous vs. dashed lines). The feedback progressively decreased with a decrease in the number of IK_Ca channels localized in the MP. For these simulations, R_gj and IP₃R density were maintained at their respective control values.

IP₃ diffusion

Experimental results suggest that Ca²⁺ mobilization in EC after SMC stimulation can be attributed mostly to diffusion of IP₃ rather than Ca²⁺ (Lamboley et al. 2005; Isakson et al. 2007; Tran et al. 2012). Vascular co-culture studies by Isakson et al. showed that IP₃R blockade in ECs inhibits Ca²⁺ flashes in ECs induced by agonist stimulation of BAPTA-loaded SMCs (Isakson et al. 2007; Isakson, 2008). A similar blocking of IP₃Rs in SMC following EC stimulation, however, did not alter SMC response due to lack of IP₃R localization on the SMC side of the myoendothelial junction and an abundance of IP₃ metabolizer 5-phosphatase (Isakson, 2008). Experiments on rat mesenteric arteries by Lamboley et al. (2005) showed that blocking of any component of the IP₃ signalling pathway (PLC inhibition in SMC, IP₃R blocking in EC) led to a severe reduction in Ca²⁺ transients in ECs following SMC stimulation. In a recent study in hamster vessels, Tran et al. (2012) showed that blockade of EC IP₃Rs inhibits feedback in SMC V_m (by ∼4 mV) during SMC stimulation with an IP₃ releasing vasoconstrictor (PE), as seen in our simulations (Fig. 7C, dashed line). A similar blockade of EC IP₃Rs did not alter SMC depolarization and constriction due to a non-IP₃ releasing voltage-dependent potassium channel (K_v) blocker, 4-aminopyridine (4-AP) (Tran et al. 2012). In agreement with the experimental observations, the 2D FEM model results under control (Fig. 7A) and blocked IP₃ diffusion (Fig. 7B) conditions for different R_gj values predicted a significant reduction (∼4 times) in Ca²⁺ transients by blockade of IP₃ diffusion from SMC to EC, which suggests that the majority of Ca²⁺ transient can be attributed to the diffusion of IP₃ and not Ca²⁺.

Ca²⁺ diffusion

Earlier studies suggested that Ca²⁺ mobilization in EC after SMC stimulation is mediated by diffusion of Ca²⁺ ions (Dora et al. 1997; Schuster et al. 2001), but this hypothesis has not been supported experimentally. In our control model, blocking of Ca²⁺ diffusion from SMC to EC did not alter the MP Ca²⁺ transient (Fig. 7B, inset). Ca²⁺ diffusion alone appears to produce some Ca²⁺ increase in the MP only at low values of R_gj (<50 MΩ; Fig. 7B, dashed line). In the model with Ca²⁺- and IP₃-activated IP₃Rs (eqn (5)), Ca²⁺ diffusion can activate IP₃Rs in synergy with IP₃ diffusion (Fig. 11A) or in the presence of basal IP₃ levels in the EC (Fig. 11B). The basal concentration of IP₃ needs to be adequate enough to sensitize IP₃R in ECs to weak Ca²⁺ flux, but at the same time it should not increase the resting EC MP Ca²⁺ levels and induce CICR prior to SMC stimulation (Nagaraja et al. 2012). Hence, there appears to be a narrow window of basal IP₃ levels for which Ca²⁺ might be able to contribute to the feedback response. The adequacy of basal IP₃ will be influenced by the degree of IP₃R localization and the half-maximum activation concentration (K_{d_act}) of both IP₃ and Ca²⁺ for the IP₃R. So far, there is no direct evidence for simultaneous existence of all these conditions in the EC. In our model, for a limited set of parameters (K_{d_act}= 350 nm; basal IP₃ between 30–50 nm), Ca²⁺ diffusion could produce a hyperpolarizing feedback of up to 6 mV for control values of R_gj, IP₃R and IK_Ca localization (Fig. 11B, dotted line). However, for this high value of K_{d_act}, the IP₃R activation and feedback (∼0.5 mV) are much smaller in the absence of basal IP₃ compared to the control model.

Limitations

A number of parameter values have not been accurately quantified. In this study, we try to remain consistent with our previous EC–SMC model with respect to parameter values and whole cell currents (i.e. most parameters were derived in this earlier study from rat mesenteric artery data). The important deviations were the maximum IP₃R current and permeability of MEGJs to IP₃. These parameters had been increased 10³- and 10²-fold in the earlier EC–SMC model to compensate for the lack of MPs and to allow for myoendothelial feedback. The models’ behaviour is sensitive to a number of tissue specific parameters such as channel conductances, myoendothelial IP₃ permeability, dimension and number of MPs, localization and density of IP₃Rs, SK_Ca/IK_Ca channels, and MEGJs inside the MPs. This limitation was partially addressed through parametric studies that examine the effect of parameter uncertainty on the models’ predictions.

The compartmental model captures well the electrical aspects of the myoendothelial coupling, but cannot accurately simulate subcellular concentration gradients and exchange of species. The 2D model is better suited to simulate Ca²⁺ transients in the vicinity of MPs and to account for the MP geometry and the spatial distribution of channels and receptors. The 2D model is limited, however, by the absence of quantification for the spatial distribution of these important cellular components. The integrated CICR mechanism is not sufficient to facilitate significant Ca²⁺ spread in the models. Other regenerative mechanisms might also exist that could enhance Ca²⁺ and IP₃ diffusion. For example, IP₃ generation by Ca²⁺ (via Ca²⁺-dependent PLC) in ECs might lead to global Ca²⁺ mobilization in the EC. At this point, however, such mechanisms have not been established experimentally.

By assuming only a single EC and SMC pair, the model simulates an average behaviour spatiotemporally. That is, every EC in the vessel is hyperpolarized to the same level for the entire duration. In reality, only a small percentage of ECs will exhibit NA-induced MP Ca²⁺ wavelets at any given time (Tran et al. 2012). Depending on the number of active sites, the duration and frequency of the events, the IK_Ca current required per MP must be stronger to compensate for current loss to other ECs. The model does not account for the transient/stochastic behaviour of Ca²⁺ mobilization seen in the experimental studies. Figures 8–10 show, however, that a single MP is capable of generating much stronger hyperpolarizing currents.

Conclusions

The models developed in this study present a first attempt to capture the role of MPs in the myoendothelial feedback. The models predict that even in the absence of NO signalling pathway, EC is able to generate the few-millivolt (i.e. 2–3 mV) feedback observed experimentally, thanks to the presence of signalling microdomains composed of MPs with small cytosolic volume, restricted permeability to bulk EC, and localized IP₃Rs and IK_Ca channels. In agreement with recent experimental evidence (Tran et al. 2012) the model predicts that IP₃, rather than Ca²⁺, diffusion from SMC to EC is the mechanism responsible for the Ca²⁺ transients in the EC MPs after SMC agonist stimulation. These Ca²⁺ transients are localized primarily within the MPs, with limited spread into EC bulk. A global spread would thus require the presence of a regeneration mechanism in the bulk of EC. The amount of feedback depends on various parameters, but simulations suggest that MPs are required for a significant feedback. Thus, our results highlight the importance of MPs in myoendothelial communication by amplifying local Ca²⁺ increase and facilitating the generation of feedback response to SMC constriction.

Glossary

ACh

acetylcholine

CICR

calcium-induced calcium release

EC

endothelial cell

EDHF

endothelium-derived hyperpolarizing factor

EDRF

endothelium-derived relaxing factor

ER

endoplasmic reticulum

FEM

finite element method

IK_Ca

intermediate-conductance Ca²⁺-activated K⁺ channels

IP₃

inositol 1,4,5-triphosphate

IP₃R

IP₃ receptor

MEGJ

myoendothelial gap junctions

MP

myoendothelial projection

NA

noradrenaline

SMC

smooth muscle cell

Author contributions

S.N., A.K., C.H.T., D.G.W. and N.M.T are responsible for conception and design of the research. S.N., A.K. and N.M.T implemented the models, performed the simulations, and drafted the manuscript. C.H.T. and D.G.W. edited and revised the manuscript. S.N., A.K., C.H.T., D.G.W. and N.M.T approved the final version of the manuscript.